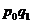|
Группы
регионов по числу автобусов
|
Число
регионов, Единиц fi
|
Середины
интервалов xi
|
Накопленные
частоты S
|
xi
fi
|
(xi
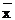-  )2
∙ fi
|
|
0
- 31.25
|
11
|
15.63
|
11
|
171.88
|
9357.64
|
|
31.25
- 62.5
|
12
|
46.88
|
23
|
562.5
|
52.08
|
|
62.5
- 93.75
|
5
|
78.13
|
28
|
390.63
|
5555.56
|
|
93.75
- 125
|
2
|
109.38
|
30
|
218.75
|
8342.01
|
|
Итого
|
30
|
-
|
-
|
1343.75
|
23307.29
|
Среднее арифметическое значение признака:
Вывод: среднее значение числа
автобусов общего пользования равно 44
Мода:
Мода - наиболее часто встречающееся
значение признака у единиц данной совокупности.
где x0 - начало модального
интервала; h - величина интервала; f2 -частота, соответствующая модальному
интервалу; f1 - предмодальная частота; f3 - послемодальная частота.
Выбираем в качестве начала интервала
159.2, так как именно на этот интервал приходится наибольшее количество.
Наиболее часто встречающееся
значение ряда - 35.16
Вывод: в большинстве регионов число
автобусов составляет 35,16
Медиана делит выборку на две части:
половина вариант меньше медианы, половина - больше.
В интервальном ряду распределения
сразу можно указать только интервал, в котором будут находиться мода или
медиана. Медиана соответствует варианту, стоящему в середине ранжированного
ряда. Медианным является интервал 159.2 - 247, т.к. в этом интервале
накопленная частота S, больше медианного номера (медианным называется первый
интервал, накопленная частота S которого превышает половину общей суммы
частот).
Таким образом, 50% единиц
совокупности будут меньше по величине 41.67
Вывод: в 50% регионов число
автобусов общего пользования более 41,67, а в 50% регионов менее 41,67.
Квартили - это значения признака в
ранжированном ряду распределения, выбранные таким образом, что 25% единиц
совокупности будут меньше по величине Q1; 25% будут заключены между Q1 и Q2;
25% - между Q2 и Q3; остальные 25% превосходят Q3.
Таким образом, 25% единиц
совокупности будут меньше по величине 21.31
совпадает с медианой, Q2 = 41.67
Остальные 25% превосходят значение
61.2.
Вывод: В четверти регионов число
автобусов общего пользования составляет менее 21,31, и у четверти более 21,31.
Среднеквадратическое отклонение:
Дисперсия - характеризует меру
разброса около ее среднего значения (мера рассеивания, т.е. отклонения от
среднего).
Среднее квадратическое отклонение
(средняя ошибка выборки).
Каждое значение ряда отличается от
среднего значения 44.79 в среднем на 27.87
Коэффициент вариации:
Поскольку v>30% ,но v<70%, то
вариация умеренная.
Проверка теоремы о разложении
дисперсии (расчет дисперсий производится по результативному признаку (по
признаку-результату) - число автобусов общего пользования на 100 тыс. населения)
Правило сложения дисперсий: общая
дисперсия равна сумме межгрупповой дисперсии и средней из внутригрупповых
дисперсий.
; 
; 
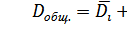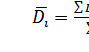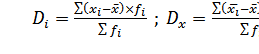
. Находим средние значения каждой
группы.
Общее средние значение для всей
совокупности:
. Дисперсия внутри группы при
относительном постоянстве признака-фактора возникает за счет других факторов
(не связанных с изучением). Эта дисперсия называется остаточной:
Расчет для группы: 1.4 - 99.48
(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22)
Определим групповую (частную)
дисперсию для 1-ой группы:
Расчет для группы: 99.48 - 197.56
(23,24,25,26,27,28)
Определим групповую (частную)
дисперсию для 2-ой группы:
Расчет для группы: 197.56 - 295.64
()
Определим групповую (частную)
дисперсию для 3-ой группы:
Расчет для группы: 295.64 - 393.72
()
Определим групповую (частную)
дисперсию для 4-ой группы:
Расчет для группы: 393.72 - 491.8
(29)
Определим групповую (частную)
дисперсию для 5-ой группы:
Расчет для группы: 491.8 - 589.88
(30)
Определим групповую (частную)
дисперсию для 6-ой группы:
. Внутригрупповые дисперсии
объединяются в средней величине внутригрупповых дисперсий:
Средняя из частных дисперсий:
. Межгрупповая дисперсия относится
на счет изучаемого фактора, она называется факторной
δ2 = ((45.27-46.37)2*22 +
(54.83-46.37)2*6 + (0-46.37)2* + (0-46.37)2* + (30-46.37)2*1 + (36-46.37)2*1 +
...)/30 = 27.73
Определяем общую дисперсию по всей
совокупности, используя правило сложения дисперсий:
σ2 = 886.97 + 27.73 = 914.7
Расчёт коэффициента корреляции
Изобразим корреляционное поле.
Построим уравнение регрессии и определим тесноту связи между признаками,
используя дисперсионный и корреляционный анализ.
Формально критерий МНК можно
записать так:
= ∑(yi - y*i)2 → min
Система нормальных уравнений.
a•n + b∑x
= ∑y∑x + b∑x2 = ∑y•x
Для наших данных система уравнений
имеет вид
a + 2706.9 b = 1391
.9 a + 697199.33 b = 114134.5
Из первого уравнения выражаем а и
подставим во второе уравнение:
Получаем эмпирические коэффициенты
регрессии: b = -0.02511, a = 48.6327
Уравнение регрессии (эмпирическое
уравнение регрессии):
= -0.02511 x + 48.6327
Эмпирические коэффициенты регрессии
a и b являются лишь оценками теоретических коэффициентов βi, а само
уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.
Выборочные средние.
Выборочные дисперсии:
Среднеквадратическое отклонение
Коэффициент корреляции
Ковариация.
Рассчитываем показатель тесноты
связи. Таким показателем является выборочный линейный коэффициент корреляции,
который рассчитывается по формуле:
Линейный коэффициент корреляции
принимает значения от -1 до +1.
Связи между признаками могут быть
слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
.1 < rxy < 0.3: слабая;
.3 < rxy < 0.5: умеренная;
.5 < rxy < 0.7: заметная;
.7 < rxy < 0.9: высокая;
.9 < rxy < 1: весьма высокая;
В нашем примере связь между
признаком Y фактором X слабая и обратная.
Кроме того, коэффициент линейной
парной корреляции может быть определен через коэффициент регрессии b:
Уравнение регрессии (оценка
уравнения регрессии).
Линейное уравнение регрессии имеет
вид y = -0.0251 x + 48.63
Коэффициентам уравнения линейной
регрессии можно придать экономический смысл.
Коэффициент регрессии b = -0.0251
показывает среднее изменение результативного показателя (в единицах измерения
у) с повышением или понижением величины фактора х на единицу его измерения. В
данном примере с увеличением на 1 единицу y понижается в среднем на -0.0251.
Коэффициент a = 48.63 формально
показывает прогнозируемый уровень у, но только в том случае, если х=0 находится
близко с выборочными значениями.
Но если х=0 находится далеко от
выборочных значений х, то буквальная интерпретация может привести к неверным
результатам, и даже если линия регрессии довольно точно описывает значения
наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или
вправо.
Подставив в уравнение регрессии соответствующие
значения х, можно определить выровненные (предсказанные) значения
результативного показателя y(x) для каждого наблюдения.
Связь между у и х определяет знак
коэффициента регрессии b (если > 0 - прямая связь, иначе - обратная). В
нашем примере связь обратная.
Таблица 2.5 - Расчетная таблица для
определения линейного коэффициента корреляции
|
x
|
y
|
x2
|
y2
|
x
• y
|
|
44.3
|
92
|
1962.49
|
8464
|
4075.6
|
|
24.7
|
27
|
610.09
|
729
|
666.9
|
|
39.6
|
15
|
1568.16
|
225
|
594
|
|
49.8
|
48
|
2480.04
|
2304
|
2390.4
|
|
34.5
|
15
|
1190.25
|
225
|
517.5
|
|
84.2
|
61
|
7089.64
|
3721
|
5136.2
|
|
25.7
|
44
|
660.49
|
1936
|
1130.8
|
|
36.2
|
72
|
1310.44
|
5184
|
2606.4
|
|
2.6
|
92
|
6.76
|
8464
|
239.2
|
|
180.5
|
6
|
32580.25
|
36
|
1083
|
|
416.8
|
30
|
173722.24
|
900
|
12504
|
|
589.9
|
36
|
347982.01
|
1296
|
21236.4
|
|
176.8
|
89
|
31258.24
|
7921
|
15735.2
|
|
144.5
|
47
|
20880.25
|
2209
|
6791.5
|
|
15.1
|
14
|
228.01
|
196
|
211.4
|
|
83.9
|
28
|
7039.21
|
784
|
2349.2
|
|
144.9
|
65
|
20996.01
|
4225
|
9418.5
|
|
54.5
|
62
|
2970.25
|
3844
|
3379
|
|
55.4
|
98
|
3069.16
|
9604
|
5429.2
|
|
1.4
|
125
|
1.96
|
15625
|
175
|
|
7.8
|
16
|
60.84
|
256
|
124.8
|
|
74.7
|
0
|
5580.09
|
0
|
0
|
|
75.5
|
24
|
5700.25
|
576
|
1812
|
|
49
|
33
|
2401
|
1089
|
1617
|
|
112.9
|
61
|
12746.41
|
3721
|
6886.9
|
|
101
|
61
|
10201
|
3721
|
6161
|
|
50.3
|
15
|
2530.09
|
225
|
754.5
|
|
3.6
|
44
|
12.96
|
1936
|
158.4
|
|
12.5
|
156.25
|
1296
|
450
|
|
14.3
|
35
|
204.49
|
1225
|
500.5
|
|
2706.9
|
1391
|
697199.33
|
91937
|
114134.5
|
Изображение корреляционного поля и построение на
нём ломаной регрессии.
На основе полученных данных построим график.
Рис. 2.7 - Корреляционное поле зависимости
В нашем примере связь между признаком Y фактором
X слабая и обратная.
Задание №3
. Используя результаты расчетов, выполненных в
задании 2 работы по признаку 1, и полагая, что эти данные получены при помощи
собственно-случайного 40% бесповторного отбора, определить:
а) пределы, за которые с доверительной
вероятностью 0,954 не выйдет значение признака, рассчитанное по генеральной
совокупности;
б) как нужно изменить объем выборки, чтобы
снизить предельную ошибку средней величины на 50%.
. Используя результаты расчетов, выполненных в
задании № 2 работы по признаку 2 и полагая, что эти данные получены при помощи
повторного отбора, определить:
а) пределы, за которые в генеральной
совокупности не выйдет значение доли предприятий, у которых индивидуальные
значения признака превышают моду (уровень доверительной вероятности установите
по своему усмотрению);
б) как изменить объем выборки, чтобы снизить
предельную ошибку доли на 30%.
. а) Пределы, за которые не выйдет среднее
значение признака
Средняя ошибка выборки для признака
№ 1:
(тыс.км.кв.)
Т.к. величина выборки: n = 30
регионов - 40%
Значит: N = 75 регионов - 100%
Теория устанавливает соотношение
между предельной и средней ошибкой выборки, гарантируемое с некоторой
вероятностью:
∆ = µ * t , где
∆ - предельная ошибка выборки
µ - средняя ошибка выборки-
коэффициент доверия.
При этом, коэффициент доверия
определяется в зависимости от того, с какой достоверной вероятностью надо
гарантировать результаты выборочного исследования. Для определения коэффициента
доверия пользуются готовыми таблицами. Некоторые наиболее часто встречающиеся
значения этого коэффициента приведены ниже:
|
Доверительная
вероятность
|
Коэффициент
доверия
|
|
0,683
|
1
|
|
0,954
|
2
|
|
0,990
|
2,5
|
|
0,997
|
3
|
Предельная ошибка выборки для признак-фактора
∆ = 15,91* 2 = 31,82 тыс.км.кв.
Таким образом, границы доверительного интервала
признак фактора могут быть представлены как:
, то есть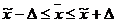 
где
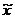- среднее значение переменной в
выборке (выборочное среднее)
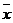- среднее генеральной совокупности.
Границы доверительного интервала
признак-фактора могут быть определены:
, то есть 
или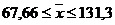 
б) Определение объема выборки для
снижения предельной ошибки средней величины на 50%
Чтобы снизить предельную ошибку
средней величины на 50% (в 2 раза) необходимо, чтобы предельная ошибка выборки
(∆) уменьшилась в два раза, поэтому необходимая численность выборки
составит:
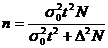
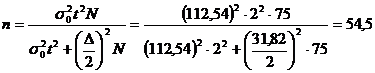регион
Следовательно, для того, чтобы
снизить предельную ошибку средней величины на 50%, необходимая численность
выборки должна составлять 55 регионов.
. а) Определение пределов, за
которые в генеральной совокупности не выйдет значение доли регионов, у которых
индивидуальные значения признака превышают моду
Возможные расхождения между
характеристиками выборочной и генеральной совокупности измеряются средней
ошибкой выборки, которая представляет собой среднее квадратическое отклонение
возможных значений выборочных характеристик (оценок) от генеральных. Она
определяется в зависимости от метода обора.
Доля альтернативного признака в выборочной
совокупности определяется по формуле:
р = m / n ,где
- число элементов совокупности,
которые больше моды ( m =17).- объем выборочной совокупности
р = 17 / 30 = 0,566*100%=56,66%
При повторном отборе, когда каждая
отобранная и обследованная единица возвращается в генеральную совокупность, где
ей опять предоставляется возможность попасть в выборку, средняя ошибка выборки
определяется следующим образом:
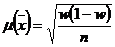
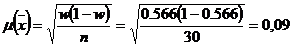
Теория устанавливает соотношения
между предельной и средней ошибкой выборки, гарантируемая с некоторой
вероятностью. Выберем доверительную вероятность 0,954. Значит, коэффициент
доверия равен 2.
∆ = µ * t , где
∆ - предельная ошибка выборки
µ - средняя ошибка выборки
t - коэффициент доверия.
∆ =0,09 *2= 0,18
Определим пределы, за которые не выйдет значение
доли регионов, у которых Число собственных легковых автомобилей на 1000 человек
населения выше моды:
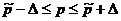
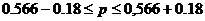
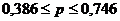
б) Определение объема выборки для
снижения предельной ошибки доли на 30%
При повторном отборе необходимая
численность выборки:
= (w*(1 - w)*t2 ) / ∆2 (1)
Считая w маломеняющейся при
изменении выборки, имеем:
= (w*(1 - w)*t2 ) / (0,7∆)2
(2)
Разделив (1) на (2) имеем:
Из (1) выражаем: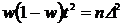 
и подставим
во (2) :
= 
61,2региона.
При повторном отборе необходимая
численность выборки должна составлять 62 региона.
Задание №4
. Пользуясь данными из
статистических ежегодников, составить 2 динамических ряда для характеристики
изменения социально-экономических показателей по районам Псковской области.
Районы и направление определяются
для каждого студента по последним цифрам номера зачетной книжки.
. Рассчитать:
а) Среднегодовой уровень динамики;
б) Цепные и базисные показатели
динамики: абсолютный прирост, темп роста, темп прироста;
в) Средний абсолютный прирост,
средний темп роста, средний темп прироста.
. Произвести сглаживание ряда
динамики трехлетней скользящей средней.
. Произвести аналитическое
выравнивание ряда динамики.
. Изобразить фактический и
выровненный ряды динамики графически.
. Сделать сравнительные выводы и
прогнозы по районам. Дать общую характеристику развития районов по данному
направлению.
. Одним из показателей, который
наиболее ярко характеризует население в различных районах области, является
численность населения и ее динамика.
Таблица 4.1 - Динамика численности
населения в Себежском районе в 2005-2012 годах
|
Год
|
Численность
населения, тыс. чел.
|
|
2005
|
37,2
|
|
2006
|
36,8
|
|
2007
|
36,5
|
|
2008
|
36,1
|
|
2009
|
35,7
|
|
2010
|
35,8
|
|
2011
|
35,8
|
|
2012
|
35,9
|
|
Всего
|
290,0
|
Таблица 4.2 - Динамика численности населения в
Пыталовском районе в 2005 - 2012 годах
|
Год
|
Численность
населения, тыс. чел.
|
|
2005
|
27,2
|
|
2006
|
26,8
|
|
2007
|
26,2
|
|
2008
|
26,2
|
|
2009
|
25,8
|
|
2010
|
25,3
|
|
2011
|
24,7
|
|
2012
|
22,7
|
|
Всего
|
204,9
|
.Среднегодовой уровень динамики рассчитывается
по формуле средней арифметической простой, так как промежутки между периодами
равные и распределение нечастотное.
y =( y1/2+y2+y3+y4+y5+y6+y7+(y8
/2))/ n-1
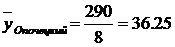(тыс. чел.)
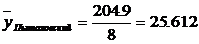(тыс. чел.)
Базисные и цепные показатели
динамики в Себежском районе
Таблица 4.3 - Базисные и цепные показатели
динамики численности населения в Себежском районе в 2005 - 2012 годах
|
Год
|
Численность
населения, тыс. чел.
|
Базисные
показатели динамики
|
Цепные
показатели динамики
|
|
|
∆,
тыс. чел.
|
Тр,
%
|
Тпр,
%
|
∆,
тыс. чел.
|
Тр,
%
|
Тпр,
%
|
|
2005
|
37,2
|
0
|
100
|
0
|
-
|
-
|
-
|
|
2006
|
36,8
|
-0,4
|
98,92
|
-1,08
|
-0,4
|
98,92
|
-1,08
|
|
2007
|
36,5
|
-0,7
|
98,12
|
-1,88
|
-0,3
|
99,18
|
-0,82
|
|
2008
|
36,1
|
-1,1
|
97,04
|
-2,96
|
-0,4
|
98,90
|
-1,10
|
|
2009
|
35,7
|
-1,5
|
95,97
|
-4,03
|
-0,4
|
98,89
|
-1,11
|
|
2010
|
35,8
|
-1,4
|
96,24
|
-3,76
|
0,1
|
100,28
|
0,28
|
|
2011
|
35,8
|
-1,4
|
96,24
|
-3,76
|
0
|
100,00
|
0,00
|
|
2012
|
35,9
|
-1,3
|
96,51
|
-3,49
|
0,1
|
100,28
|
0,28
|
Базисные показатели динамики:
Абсолютный прирост:
∆i =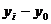 
Темп роста:
Тр =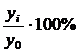 
Темп прироста:
Тпр =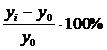 
= Тр - 1
Цепные показатели динамики:
Абсолютный прирост:
∆i = 
Темп роста:
Тр = 
Темп прироста:
Тпр =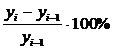 
= Тр - 1
Средние показатели динамики:
Средний абсолютный прирост:
= 
= 
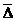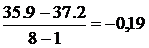(тыс. чел.)
Средний темп роста:
Средний темп прироста
Вывод:
Базисные показатели динамики:
Численность населения в Себежском районе с 2005
года до 2012 года уменьшилась на 1,3 тыс. человек. Изменение численности
населения в Себежском районе за эти годы произошло в 0,965 раз. Темп роста
составил 96,51%. Таким образом, можно отметить, что численность населения в
Себежском районе в 2012 году по сравнению с 2005 годом уменьшилась на 3,49%.
Цепные показатели динамики:
В 2012 году по сравнению с 2011 годом
численность населения в Себежском районе увеличилась на 0,1 тыс. человек.
Изменение численности населения в Себежском районе за 1 год произошло в 1,003
раз. Темп роста численности населения составил 100,3%. Увеличение численности
населения в Себежском районе произошло на 0,3%.
Средние показатели динамики:
Среднее уменьшение численности населения в
Себежском районе за 2005 - 2012 годы составило 0,19 тыс. человек. Средний
базисный темп роста равен 99,5%. Среднее уменьшение численности населения
составило 0,5%.
Базисные и цепные показатели динамики в
Пыталовском районе
Таблица 4.4 - Базисные и цепные показатели динамики
численности населения в Пыталовском районе в 2005 - 2012 годах
|
Год
|
Численность
населения, тыс. чел.
|
Базисные
показатели динамики
|
Цепные
показатели динамики
|
|
|
∆,
тыс. чел.
|
Тр,
%
|
Тпр,
%
|
∆,
тыс. чел.
|
Тр,
%
|
Тпр,
%
|
|
2005
|
27,2
|
0
|
100
|
0
|
-
|
-
|
-
|
|
2006
|
26,8
|
-0,4
|
98,53
|
-1,47
|
-0,4
|
98,53
|
-1,47
|
|
2007
|
26,2
|
-1
|
96,32
|
-3,68
|
-0,6
|
97,76
|
-2,24
|
|
2008
|
26,2
|
-1
|
96,32
|
-3,68
|
0
|
100,00
|
0,00
|
|
2009
|
25,8
|
-1,4
|
94,85
|
-5,15
|
-0,4
|
98,47
|
-1,53
|
|
2010
|
25,3
|
-1,9
|
93,01
|
-6,99
|
-0,5
|
98,06
|
-1,94
|
|
2011
|
24,7
|
-2,5
|
90,81
|
-9,19
|
-0,6
|
97,63
|
-2,37
|
|
2012
|
22,7
|
-4,5
|
83,46
|
-16,54
|
-2
|
91,90
|
-8,10
|
Средние показатели динамики:
Средний абсолютный прирост:
= = 
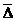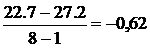(тыс. чел.)
Средний темп роста:
Средний темп прироста
Вывод:
Базисные показатели динамики:
Численность населения в Пыталовском
районе с 2005 года до 2012 года уменьшилась на 4,5 тыс. человек. Изменение
численности населения в Пыталовском районе за эти годы произошло в 0,8346 раз.
Темп роста составил 83,46%. Таким образом, можно отметить, что численность
населения в Пыталовском районе в 2012 году по сравнению с 2005 годом
уменьшилась на 16,54%.
Цепные показатели динамики:
В 2012 году по сравнению с 2011
годом численность населения в Пыталовском районе уменьшилась на 2,0 тыс.
человек. Изменение численности населения в Пыталовском районе за 1 год
произошло в 0,919 раз. Темп роста численности населения составил 91,9%. Уменьшение
численности населения в Пыталовском районе произошло на 8,1%.
Средние показатели динамики:
Среднее уменьшение численности
населения в Пыталовском районе за 2005 - 2012 годы составило 0,62 тыс. человек.
Средний базисный темп роста равен 97,5%. Среднее уменьшение численности
населения составило 2,5%.
Сглаживание ряда динамики трехлетней
скользящей средней.
Таблица 4.5 - Динамика численности
населения в Себежском районе в 2005 - 2012 годах
|
Год
|
Численность
населения, тыс. чел.
|
Скользящие
средние
|
|
2005
|
37,2
|
*
|
36,8
|
36,83
|
|
2007
|
36,5
|
36,47
|
|
2008
|
36,1
|
36,10
|
|
2009
|
35,7
|
35,87
|
|
2010
|
35,8
|
35,77
|
|
2011
|
35,8
|
35,83
|
|
2012
|
35,9
|
*
|
|
Всего
|
290,0
|
*
|
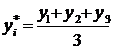(трехлетняя скользящая средняя)
|
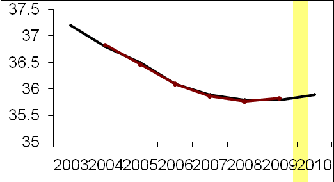
Рис.
4.1 - Динамика численности населения в Себежском районе в 2005-2012 годах
|
Вывод: В данном случае удалось выявить основную
закономерность (тренд) в изменении численности населения в Себежском районе;
было выяснено, что численность населения в Себежском районе до 2010 года
уменьшалась, а после 2010 года стала увеличиваться.
Таблица 4.6 - Динамика численности населения в
Пыталовском районе в 2005 - 2012 годах
|
Год
|
Численность
населения, тыс. чел.
|
Скользящие
средние
|
|
2005
|
27,2
|
*
|
|
2006
|
26,8
|
26,73
|
|
2007
|
26,2
|
26,40
|
|
2008
|
26,2
|
26,07
|
|
2009
|
25,8
|
25,77
|
|
2010
|
25,3
|
25,27
|
|
2011
|
24,7
|
24,23
|
|
2012
|
22,7
|
*
|
|
Всего
|
204,9
|
*
|
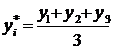(трехлетняя скользящая средняя)
|
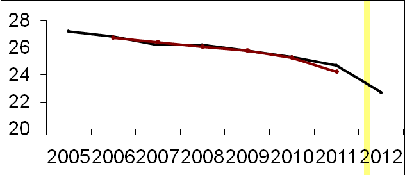
Рис.
4.2 - Динамика численности населения в Пыталовском районе в 2005 - 2012 годах
|
Вывод: В данном случае удалось выявить основную
закономерность (тренд) в изменении численности населения в Пыталовском районе;
было выяснено, что численность населения в Пыталовском районе с каждым годом
уменьшается, т.е. имеет отрицательный тренд.
. Аналитическое выравнивание ряда динамики.
Таблица 4.6 - Динамика численности населения в
Себежском районе в 2005 - 2012 годах
|
Год
|
Численность
населения, тыс. чел.
|
tусл.
|
(tусл.)2
|
y·tусл.
|
|
|
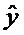
2005
|
37,2
|
-7
|
49
|
-260,4
|
36,9
|
|
2006
|
36,8
|
-5
|
25
|
-184
|
36,7
|
|
2007
|
36,5
|
-3
|
9
|
-109,5
|
36,5
|
|
2008
|
36,1
|
-1
|
1
|
-36,1
|
36,3
|
|
2009
|
35,9
|
1
|
1
|
35,9
|
36,2
|
|
2010
|
35,8
|
3
|
9
|
107,4
|
36,0
|
|
2011
|
35,8
|
5
|
25
|
179
|
35,8
|
|
2012
|
35,9
|
7
|
49
|
251,3
|
35,6
|
|
Всего
|
290,00
|
0,00
|
168,00
|
-16,40
|
290,0
|
Функция при аналитическом
выравнивании имеет вид прямой линии. Введем условное время по порядку года
таким образом, чтобы 
=0.
Параметры a0 и a1 находятся из системы нормальных уравнений:
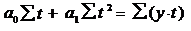
8∙a0 =
290
∙a1 =
-16,4= 36,25= -0,097
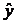= a0 + a1·t = 36,25 -
0,097·tусл. -
теоретическая функция.
Интерпретация коэффициентов
теоретической функции:
Коэффициент a0 = 36,25 показывает
среднее значение численности населения в Себежском районе за восемь лет.
Коэффициент a1 = -0,097 показывает,
что с каждым годом численность населения в Себежском районе уменьшается на
0,097 тыс. человек.
|
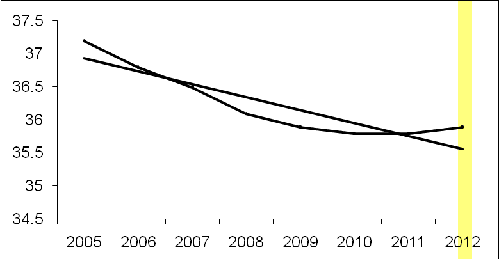
Рис.
4.3 - Динамика численности населения в Себежском районе в 2005 - 2012 годах
|
Так как известна аналитическая функция, то можно
сделать прогноз динамики численности населения в Себежском районе на 2015 год.
В данном случае tусл.= 13. Подставляя это значение в функцию, получим:
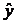= a0 + a1·t = 36,25 - 0,097∙13
= 34,98 (тыс. чел.)
Вывод: В данном случае удалось выявить основную
закономерность динамики численности населения в Себежском районе. Численность
населения в Себежском районе уменьшается примерно на 0,097 тыс. человек в год.
Таким образом, можно сделать прогноз численности населения в Себежском районе
на 2015 год (более долгосрочные прогнозы будут неточными вследствие влияния
факторов, не учтенных в данной модели). В 2015 году численность населения в
Себежском районе составит примерно 34,98 тыс. человек.
Таблица 4.7 - Динамика численности населения в
Пыталовском районе в 2005 - 2012 годах
|
Год
|
Численность
населения, тыс. чел.
|
tусл.
|
(tусл.)2
|
y·tусл.
|
|
|
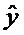
2005
|
27,2
|
-7
|
49
|
-190,4
|
27,5
|
|
2006
|
26,8
|
-5
|
25
|
-134
|
27,0
|
|
2007
|
26,2
|
-3
|
9
|
-78,6
|
26,4
|
|
2008
|
26,2
|
-1
|
1
|
-26,2
|
25,9
|
|
2009
|
25,8
|
1
|
1
|
25,8
|
25,3
|
|
2010
|
25,3
|
3
|
9
|
75,9
|
24,8
|
|
2011
|
24,7
|
5
|
25
|
123,5
|
24,3
|
|
2012
|
22,7
|
7
|
49
|
158,9
|
23,7
|
|
Всего
|
204,90
|
0,00
|
168,00
|
-45,10
|
204,9
|
Функция при аналитическом
выравнивании имеет вид прямой линии. Введем условное время по порядку года
таким образом, чтобы =0.
Параметры a0 и a1 находятся из системы нормальных уравнений:
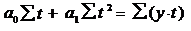
∙a0 = 204,9
∙a1 = -45,1= 25,61= -0,268
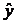= a0 + a1·t = 25,61-0,268·tусл. -
теоретическая функция.
Интерпретация коэффициентов
теоретической функции:
Коэффициент a0 = 25,61 показывает
среднее значение численности населения в Пыталовском районе за восемь лет.
Коэффициент a1 = -0,268 показывает,
что с каждым годом численность населения в Пыталовском районе уменьшается на
0,268 тыс. человек.
|
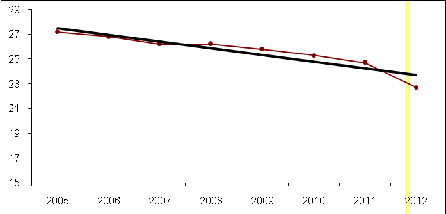
Рис.
4.4 - Динамика численности населения в Пыталовском районе в 2005 - 2012 годах
|
Так как известна аналитическая функция, то можно
сделать прогноз динамики численности населения в Пыталовском районе на 2015
год. В данном случае tусл.= 13. Подставляя это значение в функцию, получим:
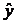= a0 + a1·t = 25,61 - 0,268∙13
= 22,126 (тыс. чел.)
Вывод: В данном случае удалось
выявить основную закономерность динамики численности населения в Пыталовском
районе. Численность населения в Пыталовском районе уменьшается примерно на
0,268 тыс. человек в год. Таким образом, можно сделать прогноз численности
населения в Пыталовском районе на 2015 год (более долгосрочные прогнозы будут
неточными вследствие влияния факторов, не учтенных в данной модели). В 2015
году численность населения в Пыталовском районе составит 22,126 тыс. человек.
группировка признак мода
медиана
Задание №5
Пользуясь таблицами, сформировать
таблицу исходных данных.
определить индивидуальные индексы:
физического объема,
цены,
стоимости.
Определить общие индексы:
физического объема,
цены,
стоимости.
Объяснить экономический смысл
каждого из индексов, показать взаимосвязь между ними.
Определить абсолютное изменение
стоимости произведенной продукции в текущем периоде по сравнению с базисным, в
том числе за счет изменения цен и за счет изменения выпуска продукции.
Считая продукцию однородной,
определить, как изменилась средняя цена единицы продукции и как при этом
повлияло изменение цен и структуры выпускаемой продукции. Объяснить полученные
результаты.
Используя данные таблицы 5,
рассчитать, как в среднем изменилась себестоимость единицы и выпуск продукции.
Формируем таблицу исходных данных
(приложение).
Индивидуальный индекс физического
объема показывает, как изменится объем проданного товара в текущем периоде по
сравнению с базисным, по каждому виду продукции и рассчитывается по формуле:
.
В нашем случае объем проданного
товара по виду продукции С уменьшился на 21%. По видам продукции А и В в
произошло увеличился на 46% и 6% соответственно.
Индивидуальный индекс цены
рассчитывается по формуле:
и показывает как изменились цены по
каждому виду продукции. По всем видам продукции произошло уменьшение по виду А
- на 5%, по виду В увеличился на 14%, по виду увеличился С - на 80%.
Индивидуальный индекс стоимости
показывает изменение стоимости продукции по ее видам и рассчитывается по
формуле: 
. Таким
образом по всем видам продукции произошло увеличение по виду А - на 38%, по
виду В - на 21%, по виду С - на 41%.
Общий индекс физического объема
товарооборота будет иметь вид:
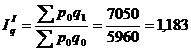или 118,3%,
Т.е. реализация продукции в текущем
периоде по сравнению с базисным увеличилась на 18,3% .
Общий индекс цены показывает как в
целом на предприятии изменились цены на продукцию и рассчитывается по формуле:
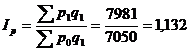или 113,2%,
Т.е. цены на всю продукцию
предприятия в текущем периоде по сравнению с базисным увеличились на 13,2%.
Общий индекс стоимости показывает
как в среднем изменилась стоимость продукции в текущем периоде по сравнению с
базисным и рассчитывается по формуле:
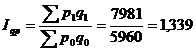или 133,9%,
Т.е. стоимость продукции в среднем
по предприятию увеличились на 33,9% в текущем периоде по сравнению с базисным.
Проверка:
.
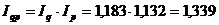Абсолютное изменение стоимости
проданной продукции в текущем периоде по сравнению с базисным определяется по
формуле:
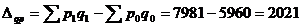тыс.руб.
в том числе:
За счет изменения цен на отдельные
виды продукции
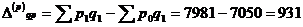тыс.руб.
За счет изменения физического объема
продукции
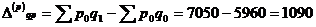тыс.руб.
Таким образом, увеличение стоимости
продукции в текущем периоде по сравнению с базисным на 2021 тыс.руб. произошло
за счет изменения объема проданной продукции на 1090 тыс.руб. и за счет
изменения цен на отдельные виды продукции на 931 тыс. руб.
Индексы структурных сдвигов
Изменение средней цены единицы
продукции определяем, считая эту продукцию однородной, следовательно:
Т.е. средняя цена единицы продукции
увеличилась в текущем периоде по сравнению с базисным на 30,7%.
В том числе а) за счет
непосредственного изменения цен на отдельные виды продукции:
,
цены на всю продукцию предприятия в
текущем периоде по сравнению с базисным увеличились на 13,2%.
За счет изменения структуры (объема)
продукции:
,
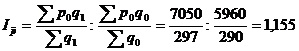средняя цена на продукцию
предприятия увеличилась на 15,5% за счет изменения объема продукции
Список используемой литературы
1. Методические указания
по выполнению курсовой работы по ред. Л.Н. Гальдикас и Л.И. Стрикуновой., 2011
г.
. Муниципальные районы и
городские округа Псковской области - основные характеристики: стат. сборник в 2
томах, Псковоблкомстат, 2013.-142 с.
. Псковский
статистический ежегодник. 2013: Cтат. сб. В 2 т. Т.1 / Псковстат - П., 2013. -
198 с.
. Нименья И.Н..
Статистика. М: Финансы и статистика, 2005 г.
. Теория статистики:
Учебник/Под ред. проф. Р.А. Шмойловой. - 3-е изд.,. перераб. - М.: Финансы и
статистика, 2002. -560 с.
6. Федеральная
служба государственной статистики <#"827205.files/image071.gif">
