Статистические методы поиска

Введение

Ускорение научно-технического прогресса, потребовало существенно поднять эффективность труда инженерно-технических работников, создателей новой техники. Повышение эффективности творческой составляющей труда предусматривает овладение широким спектром методических средств. К ним следует отнести и методы поиска новых технических идей и решений. В настоящее время известно немало таких методов. В отечественной литературе они, однако, чаще всего даются разрозненно или небольшими группами и большинство из них поэтому остается незнакомыми широкому читателю.

Настоящая работа представляет собой обзор большой группы методов и имеет целью дать материал для ориентации преподавателя при подготовке к теме "Обзор методов поиска новых технических решений".

Приведенная в работе информация носит, как правило, конспективный характер, поскольку даже краткое изложение всех методов привело бы к непомерному увеличению объема материала. В большинстве случаев здесь поэтому приведены только блок-схемы и краткие характеристики этапов. Не включены в работу и примеры использования методов. Конспективно описаны методы мозгового штурма, морфологического ящика, алгоритм решения изобретательских задач, функционально - стоимостный анализ. Это оправдано тем, что учебные пособия по данным методам готовятся отдельно. По той же причине в работе не нашли отражения разработки в области машинной поддержки процесса поиска новых технических решений.

Несмотря на ограниченный объем материала, где это возможно, будут приводиться полные тексты, перечни рекомендаций и контрольные вопросы.

1. Статистические методы поиска

.1 Статистические методы или методы случайного поиска

Статистические методы или методы случайного поиска получили достаточно широкое распространение при построении оптимальных решений в различных приложениях. Это объясняется в первую очередь тем, что с ростом размерности задач резко снижается эффективность регулярных методов поиска (детерминированных), так называемое “проклятие размерности”. Во-вторых, зачастую информация об оптимизируемом объекте слишком мала для того, чтобы можно было применить детерминированные методы. Статистические алгоритмы часто используют при поиске оптимального решения в системах управления, когда отклик можно получить только при задании управляющих воздействий  на входах системы. В таких ситуациях статистические алгоритмы могут оказаться значительно эффективнее детерминированных.

Рис. 1

Статистические методы наиболее эффективны при решении задач большой размерности или при поиске глобального экстремума.

Под случайными или статистическими методами поиска будем понимать методы, использующие элемент случайности либо о сборе информации о целевой функции при пробных шагах, либо для улучшения значений функции при рабочем шаге. Случайным образом может выбираться направление спуска, длина шага, величина штрафа при нарушении ограничения.

Статистические алгоритмы обладают рядом достоинств:

·   простота реализации и отладки программ;

·   надежность и помехоустойчивость;

·   универсальность;

·   возможность введения операций обучения;

·   возможность введения операций прогнозирования оптимальной точки.

Основными недостатками являются большое количество вычислений минимизируемой функции, медленная сходимость в районе экстремума.

Принято считать, что преимущество статистических методов проявляется с ростом размерности задач, так как вычислительные затраты в детерминированных методах поиска с ростом размерности растут быстрее, чем в статистических алгоритмах.

.2 Простой случайный поиск

Пусть нам необходимо решить задачу минимизации функции  при условии, что . В этой области по равномерному закону выбираем случайную точку 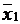 и вычисляем в ней значение функции 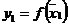. Затем выбираем таким же образом случайную точку  и вычисляем 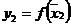. Запоминаем минимальное из этих значений и точку, в которой значение функции минимально. Далее генерируем новую точку. Делаем  экспериментов, после чего лучшую точку берем в качестве решения задачи (в которой функция имеет минимальное значение) среди всех случайно сгенерированных.

Рис. 2

Пусть  - размерность вектора переменных. Объем -мерного прямоугольника, в котором ведется поиск минимума, . Если необходимо найти решение с точностью , , по каждой из переменных, то мы должны попасть в окрестность оптимальной точки с объемом .

Вероятность попадания в эту окрестность при одном испытании равна . Вероятность не попадания равна .

Испытания независимы, поэтому вероятность не попадания за  экспериментов равна 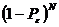. Вероятность того, что мы найдем решение за  испытаний: . Нетрудно получить оценку для необходимого числа испытаний  для определения минимума с требуемой точностью:

.

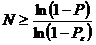Опираясь на заданную точность , , 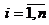величину , можно определить  и, задаваясь вероятностью , посмотреть, как меняется требуемое количество экспериментов  в зависимости от  и  (см. табл.).

Таблица

При решении экстремальных задач на областях со сложной геометрией обычно эту область вписывают в -мерный параллелепипед, в котором генерируют случайные точки по равномерному закону, оставляя только те, которые попадают в допустимую область.

Рис.3

Различают направленный и ненаправленный случайный поиск:

1. Ненаправленный случайный поиск. Все последующие испытания проводят совершенно не зависимо от результатов предыдущих. Сходимость такого поиска очень мала, но имеется важное преимущество: возможность решать многоэкстремальные задачи (искать глобальный экстремум). Примером является рассмотренный простой случайный поиск.

2. Направленный случайный поиск. В этом случае отдельные испытания связаны между собой. Результаты проведенных испытаний используются для формирования последующих. Сходимость таких методов, как правило, выше, но сами методы обычно приводят к локальным экстремумам.

.3.Локальный случайный поиск с возвратом

В данном методе первоначально производится фиксированный шаг в случайно выбранном направлении. Если значение функции качества в новом состоянии 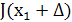 превышает исходное значение  или остается неизменным, т.е. случайный выбор оказался неудачным, то происходит возврат в исходное состояние , откуда осуществляется новый шаг в случайном направлении. Если значение  уменьшилось, то следующий шаг в случайном направлении делается уже из точки .

Алгоритм поиска можно записать в следущем рекуррентном виде;

(1)

На рисунке 7 представлена блок-схема алгоритма. В начальный момент система делает шаг  в случайном направлении из исходного состояния , причем в памяти уже находится значение функции качества  для этого состояния. Затем определяется новое значение функции качества , которое сравнивается с запомненным . В случае уменьшения функции качества 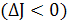 вновь делается случайный шаг  и запоминаются на компоненты. В случае увеличения функции качества система делает обратный шаг компоненты которого были запомнены раньше. Функция качества в этом состоянии  определяется вновь и запоминается, после чего делается новый шаг в случайном направлении. Алгоритм эффективен даже в случае нестационарных функций качества, изменяющихся во времени по тем или иным причинам.

.4 Локальный случайный поиск с пересчетом

Этот поиска отличается от предыдущего тем, что система не возвращается при неудачном шаге назад в исходное состояние, а делает “пересчитанный” случайный шаг в новое состояние, при котором учитывается исходное состояние.

Алгоритм поиска записывается в виде следующей рекуррентной формулы

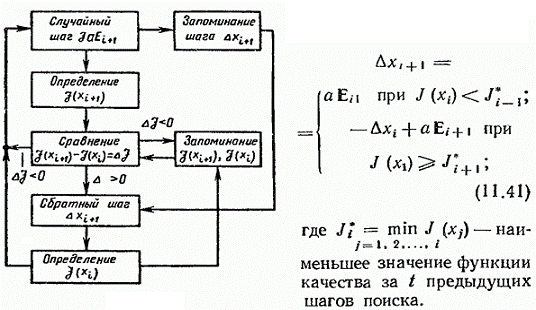
Рис.4

Рис.5

Этот алгоритм используется в основном для случаев стационарной функции качества или при отсутствии помех. Поиск с пересчетом сокращает количество измерений функции качества, что оправдано при отсутствии помех.

Блок-схема поиска представлена на рисунке на 8 . Из схемы видно, что в процедуре поиска отсутствует определение  после неудачного шага, а устройство памяти  освобождается от дополнительной информации.

.5 Локальный случайный поиск по наилучшей пробе

Данный метод поиска содержит операцию накопления, состоящую из нескольких пробных шагов. По совокупности независимых проб принимается решение о выборе наиболее удачного состояния.

В соответствии с методом из исходного состояния  делается m случайных пробных шагов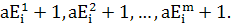

В полученных смещенных точках , где j=1, 2,…, m, производится вычисление значений функции качества  и запоминается состояние, которое привело к минимальному значению:

(2)

Далее производится рабочий шаг в этом выбранном направлении:

 (3)

Где  случайный единичный вектор наилучшей пробы.

С увеличение числа пробных шагов m случайно выбранное направление поиска все больше приближается к направлению, обратному градиенту.

Алгоритм поиска имеет недостаток , связанный с возможностью попадания в такую зону, когда рабочий шаг делается в сторону увеличения функции качества, например если все пробные шаги привели к увеличению функции качества. Модификация в этом случае осуществляется таким образом:

(4)

В соответствии c (4) система сделает рабочий шаг вдоль наилучшей пробы только тогда, когда минимальное значение  из всех проб не превышает исходного значения . Если это условие не выполняется, тогда повторяется цикл из m пробных шагов.

.6 Локальный случайный поиск статистическому градиенту

Данный метод поиска используется в тех случаях, когда функцию качества J (x) нельзя представить в регулярном виде и она определяется в зависимости от регулярных параметров  а также от случайных параметров ). Такая ситуация возможна, например, при поиске экстремума в условиях действия помех.

Так как случайный поиск по статистическому градиенту близок по своей сущности к методам стохастической аппроксимации, то рассмотрим предварительно некоторые процедуры стохастической аппроксимации.

При наличии случайных параметров ) регулярную функцию качества J (x) представим в виде случайной функции

), (5)

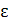где x= -- вектор состояний поиска; =),- вектор случайных помех.

Зная вероятностные характеристики параметров , например плотность распределения p(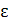), можно усреднить функцию H (x,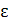) по этим параметрам и перейти вновь к осредненной регулярной функции качества

 (6)

Или

 (7)

где  - математическое ожидание.

Из (6) можно сделать вывод о том, что получение функции качества в детерминированном виде связано с необходимостью вычисления интеграла либо при жестких ограничениях на характер случайных воздействий е, либо при известных вероятностных характеристиках изменения таких воздействий. Однако обычно имеется только информация об отдельных реализациях случайной функции

При поиске экстремума дифференцируемой функции качества J(x) все n частных производных  i=1,2,…, n, должны обращаться одновременно в нуль, т. е.

grad J(x)=0 (8)

В результате замены J(x) на  условия экстремума принимают следующий вид:

grad =0 (9)

или, учитывая линейность операций, можно записать

(10)

Осуществляя итеративную процедуру стохастической аппроксимации. определяем состояние 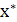. соответствующее экстремальному значению  , постепенно приближаясь к нему:

. (11)

Таким образом, при отсутствии точного знания функции качества J(x) следует заменить ее стохастической оценкой  и далее оперировать с этой оценкой при поиске точки экстремума .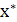

В том случае, если  представима в виде скалярной функции скалярного аргумента х и случайного параметра е, процедура стохастической аппроксимации сводится к процедуре определения корня этой скалярной функции или к так называемой процедуре Роббинса-Монро.

Пусть

, (12)

где -скалярная функция от параметра состояния x.

Функцию можно представить в виде суммы регулярной составляющей f(x) и случайной составляющей е, причем математическое ожидание М (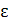) - 0, т. е. случайная составляющая центрирована.

В результате поиска определяют корень 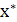регулярной составляющей f(x), т. е.

 (13)

в соответствии с процедурой

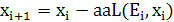 (14)

где а - знак наклона регулярной составляющей f(x) в точке 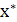 (для минимума «+», для максимума «-»); а - постоянная, определяющая наклон аппроксимированной прямой к f(x).

Если функция  является однопараметрической функцией регрессии, задана своими реализациями  и можно дать точечную оценку ее градиента grad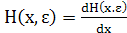 , т. е.

 (15)

где  - интервал оценки производной, то поиск экстремума функции  сводится к поиску корня функции регрессии регулярной части в соответствии с процедурой Кифера-Вольфовица:

 (16)

Где a=

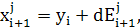В случайном поиске по статистическому градиенту из исходного состояния х{ делается т случайных пробных шагов: a В новых точках  i=1,2,…, m, вычисляют значения функции качества ,i=1,2,…,m, и соответствующие приращения функции качества:

 (17)

После этого вычисляется вектор статистической оценки градиента в точке , т. е.

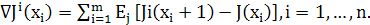 (18)

В пределе при т статистическая оценка  совпадает с направлением градиента функции качества, поэтому рабочий шаг производится в направлении полученной оценки

Рис.6

 (19)

где -норма вектора статистического градиента; а - величина рабочего шага.

Таким образом, в случайном поиске по статистическому градиенту число точечных измерений статистической оценки градиента может быть меньше по сравнению с методами стохастической аппроксимации (т < п).

Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов. Процедура поиска значительно усложняется в тех случаях, когда функция качества является не унимодальной, а многоэкстремальной. Практически все рассмотренные способы поиска локального экстремума не могут быть использованы без специальных модификаций для поиска глобального экстремума. Исключение составляет метод полного перебора. Однако на практике им пользоваться бывает неудобно из-за слишком больших затрат времени на поиск. Как правило, методы поиска глобального экстремума базируются на статистических принципах.

Это объясняется тем, что поиск статистическими методами позволяет управлять плотностью распределения независимых пробных шагов и сосредоточивать поисковые шаги в местах наиболее вероятного нахождения глобального экстремума.

(20)

Где 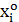- это i-е пробное состояния, выбранное случайно и сохраненное в памяти в случае удачной пробы;  - вычисленное в i-м пробном состоянии значение функции качества и сохраненное в памяти в случае удачной пробы; -пробный шаг; J()-значение функции качества на i-м пробном шаге.

При равномерной плотности распределения пробных шагов поиск разделяется на к этапов из 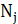 пробных шагов, где j = 1. 2..... к.

Каждый пробный этап осуществляется внутри гиперпараллелепипеда в пространстве состояний X, т. е.

, i=1,2,…, n, ( 21)

причем стороны гиперпараллелепипеда с каждым j-м этапом уменьшаются в с > 1 раз по сравнению с (j - 1)-м этапом в соответствии с формулой:

(22)

где 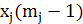 - точка, соответствующая пробному шагу с наименьшим значением функции качества из всех проб на (j - 1)-м этапе.

Несмотря на равномерную плотность распределения пробных шагов внутри каждого этапа, происходит увеличение плотности распределения от этапа к этапу за счет уменьшения зоны поиска (23), т. е.

 (23)

где  - плотность распределения пробных шагов на j-м этапе;

 - объем гиперпараллелепипеда на j-м этапе.

Таким образом, на каждом пробном этапе осуществляются случайные пробные шаги, из которых выбирается шаг с наименьшим значением функции качества, а затем зона поиска сужается около этой выбранной точки и снова производятся случайные пробные шаги до попадания в окрестность глобального экстремума.

Иногда целесообразно пробные шаги на каждом последующем этапе распределять не равномерно, а по нормальному закону, например

(24)

 - исходная дисперсия; 0 < < q < 1.

Итак, случайные пробные шаги нормально распределены со средним значением, совпадающим с наилучшей величиной функции качества из всех проб этапа, а дисперсия уменьшается при неудачных шагах и увеличивается до исходного значения при удачных шагах.

Обычно время, отводимое на поиск, ограничено, поэтому целесообразно управлять не только плотностью распределения пробных шагов внутри этапов, но и количеством таких проб. Например, в начале поиска количество пробных шагов внутри этапа может быть относительно небольшим, что связано с приблизительным выделением «подозреваемой» на глобальный экстремум подобласти, а затем для более точного определения положения глобального экстремума используется оставшееся количество пробных шагов.

оптимизатор гиперквадрат алгоритм случайный

2. Примеры поисковых самонастраивающихся систем

Самонастраивающаяся система с поиском по методу градиента. Блок-схема системы представлена на рис. 10. Система работает по принципу синхронного детектирования с модуляцией, основанному на методе градиента.

На рабочее движение системы накладывается гармоническое поисковое движение с небольшой амплитудой, вырабатываемое генератором Г и устройством формирования опорного сигнала УОС, т. е.

 (25)

На выходе объекта колебательная составляющая функции качества J(x) изменяет фазу в зависимости ст текущего положения рабочей точки относительно экстремума (рис. 11).

Рис. 7

С помощью синхронного детектора фазы ДФ осуществляется перемножение сигнала У (х) и опорного сигнала с генератора:

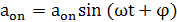 (11.66)

После отфильтрования переменной составляющей с помощью фильтра Ф получают сигнал, пропорциональный производной функции качества по х, т. е.dJ(x)/dx, поступающий на исполнительное устройство ИУ. В точке экстремума этот добавочный сигнал равен нулю.

.1 Многоканальный статистический оптимизатор со случайным поиском

Схема и принципы работы самонастраивающейся системы со случайным поиском описаны в 121. В системе реализован ряд шаговых алгоритмов поиска, например поиск с возвратом, поиск с пересчетом и т. д. Система состоит из одинаковых, параллельно работающих каналов, выбранных по числу оптимизируемых параметров объекта. Блок-схема одного из каналов представлена на рис. 12(а)

Рис.8

Рис. 9

Основный блоком оптимизатора является блок генераторов случайных сигналов, с помощью которого вырабатываются последовательности разнополярных импульсов с одинаковой амплитудой и длительностью. Эти импульсы через ключевые схемы поступают на исполнительные устройства для изменения регулируемого параметра объекта в положительную и отрицательную стороны поиска экстремума. В результате воздействия исполнительных устройств изменяется функция качества. Знак приращения функции качества фиксируется и запоминается в блоке определения знака. Работа оптимизатора осуществляется циклически с помощью блока команд, на вход которого подается сигнал.

л ,

где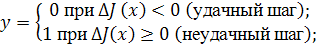

Сигнал  измеряют следующим образом:

Значение  определяют так:

(26)

На рис. 12, б, и представлены направленные графы последовательного изменения состояний блока команд для поиска с возвратом и пересчетом. Индексы у стрелок, соединяющих вершины графа, соответствуют возможному переходу блока команд из одного состояния в другое в зависимости от поданного сигнала р, определяемого из (11.68).

Состояния блока команд пронумерованы следующим образом: / - определение знака приращения показателя качества ДУ (х)\ 2 - запоминание показателя качества; 3 - обратный шаг; 5 - сброс памяти генератора случайных сигналов; 6 - запуск генератора случайных сигналов; 7 - рабочий шаг; 8 - установление функции качества на выходе объекта.

3. Простейшие алгоритмы направленного случайного поиска

.1 Алгоритм наилучшей пробы с направляющим гиперквадратом

Внутри допустимой области строится гиперквадрат. В этом гиперквадрате случайным образом разбрасывается  точек , в которых вычисляются значения функции. Среди построенных точек выбираем наилучшую. Опираясь на эту точку, строим новый гиперквадрат. Точка, в которой достигается минимум функции на -м этапе, берется в качестве центра нового гиперквадрата на -м этапе.

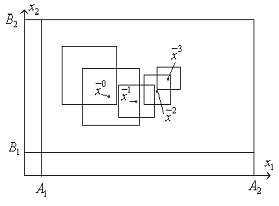
Рис. 10

Координаты вершин гиперквадрата на -м этапе определяются соотношениями

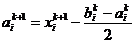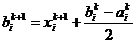, , (27)

где  - наилучшая точка в гиперквадрате на -м этапе.

В новом гиперквадрате выполняем ту же последовательность действий, случайным образом разбрасывая  точек, и т.д. Таким образом на 1-м этапе координаты случайных точек удовлетворяют неравенствам , и  - точка с минимальным значением целевой функции.

В алгоритме с обучением стороны гиперквадрата могут регулироваться в соответствии с изменением параметра  по некоторому правилу. В этом случае координаты вершин гиперквадрата на -м этапе будут определяться соотношениями

, . (28)

Хорошо выбранное правило регулировки стороны гиперквадрата приводит к достаточно эффективному алгоритму поиска.

В алгоритмах случайного поиска вместо направляющего гиперквадрата могут использоваться направляющие гиперсферы, направляющие гиперконусы.

.2 Алгоритм парной пробы

В данном алгоритме четко разделены пробный и рабочий шаги. Пусть 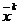 - найденное на -м шаге наименьшее значение минимизируемой функции . По равномерному закону генерируется случайный единичный вектор  и по обе стороны от исходной точки 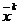 делаются две пробы: проводим вычисление функции в точках

где 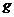-величина пробного шага. Рабочий шаг делается в направлении наименьшего значения целевой функция. Очередное приближение определяется соотношением

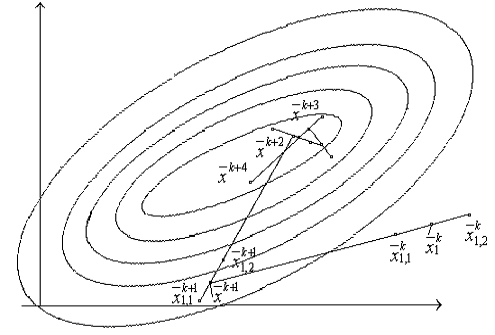
Рис.11

Особенностью данного алгоритма является его повышенная тенденция к “блужданию”. Даже найдя экстремум, алгоритм уводит систему в сторону.

.3 Алгоритм наилучшей пробы

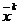На -м шаге мы имеем точку . Генерируется  случайных единичных векторов . Делаются пробные шаги в направлениях 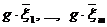 и в точках  вычисляются значения функции. Выбирается тот шаг, который приводит к наибольшему уменьшению функции

И в данном направлении делается шаг . Параметр  может определяться как результат минимизации по определенному направлению или выбирается по определенному закону.

С увеличением числа проб выбранное направление приближается к направлению .

Рис.12

.4 Метод статистического градиента

Из исходного состояния 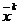 делается  независимых проб  и вычисляются соответствующие значения минимизируемой функции в этих точках. Для каждой пробы запоминаем приращения функции

После этого формируем векторную сумму

В пределе при  она совпадает с направлением градиента целевой функции. При конечном  вектор  представляет собой статистическую оценку направления градиента. Рабочий шаг делается в направлении . Очередное приближение определяется соотношением

При выборе оптимального значения , которое минимизирует функцию в заданном направлении, мы получаем статистический вариант метода наискорейшего спуска. Существенным преимуществом перед детерминированными алгоритмами заключается в возможности принятия решения о направлении рабочего шага 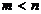при . При  и неслучайных ортогональных рабочих шагах, направленных вдоль осей координат, алгоритм вырождается в градиентный метод.

Рис.13

.5 Алгоритмы глобального поиска

Случайный поиск приобретает решающее значение при оптимизации многоэкстремальных задач и объектов. В общем случае решение многоэкстремальных задач без элемента случайности практически невозможно.

Алгоритм 1. В допустимой области  случайным образом выбирают точку . Приняв ее за исходную и используя некоторый детерминированный метод или алгоритм направленного случайного поиска, осуществляется спуск в точку локального минимума .

Затем выбирается новая случайная точка  и по той же схеме осуществляется спуск в точку локального минимума  и т.д.

Рис.14

Поиск прекращается, как только заданное число раз не удается найти точку локального экстремума со значением функции меньшим предыдущих.

Алгоритм 2. Пусть получена некоторая точка локального экстремума . После этого переходим к ненаправленному случайному поиску до получения точки такой, что .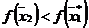

Из точки  с помощью детерминированного алгоритма или направленного случайного поиска получаем точку локального экстремума , в которой заведомо выполняется неравенство .

Далее с помощью случайного поиска определяем новую точку , для которой справедливо неравенство , и снова спуск в точку локального экстремума  и т.д.

Поиск прекращается, если при генерации некоторого предельного числа новых случайных точек не удается найти лучшей, чем предыдущий локальный экстремум, который и принимается в качестве решения.

Алгоритм 3. Пусть  - некоторая исходная точка поиска в области , из которой осуществляется спуск в точку локального экстремума  со значением . Далее из точки  двигаемся либо в случайном направлении, либо в направлении  до тех пор, пока функция снова не станет убывать (выходим из области притяжения ). Полученная точка  принимается за начало следующего спуска. В результате находим новый локальный экстремум  и значением функции .

Если , точка  забывается и ее место занимает точка . Если , то возвращаемся в точку  и движемся из нее в новом случайном направлении.

Рис.15

Процесс прекращается, если не удается найти лучший локальный минимум после заданного числа попыток или “случайного” направления, в котором функция снова начинает убывать.

Этот метод позволяет найти глобальный экстремум в случае многосвязных допустимых областей.

Алгоритм 4. В допустимой области  разбрасываем  случайных точек и выбираем из них наилучшую, то есть ту, в которой значение функции минимально. Из выбранной точки осуществляем локальный спуск. А далее вокруг траектории спуска образуем запретную область. В оставшейся области случайным образом разбрасываем новую совокупность случайных точек, и из лучшей точки осуществляем спуск в точку локального экстремума. Вокруг новой траектории также строим запретную область и т.д.

Рис.16

Поиск прекращается, если в течение заданного числа попыток не удается найти лучшего локального экстремума.

Замечание: Комбинация случайного поиска с детерминированными методами применяется не только для решения многоэкстремальных задач. Часто к такой комбинации прибегают в ситуациях, когда детерминированные методы сталкиваются с теми или иными трудностями (застревают на дне узкого оврага, в седловой точке и т.д.). Шаг в случайном направлении порой позволяет преодолеть такую тупиковую ситуацию для детерминированного алгоритма.

Заключение

Методы статистического поиска хорошо применимы для решения задач оптимизации так как направление поиска выбирается случайно, путем выбора n случайных чисел, равномерно распределенных на отрезке [-1,1) из генератора случайных чисел который есть в каждом ЭВМ.

Список использованной литературы

1.   Поляк Б.Т. Введение в оптимизацию. - М.: Наука. - 1983. -384с.

2.      Карманов В.Г. Математическое программирование. - М.: Наука.- 1980. - 256с.

.        Растригин Л.А. Системы экстремального управления. -М.:Наука. - 1974.- 632с.

.        Растригин Л.А. Статистические методы поиска. -М: Наука. - 1968. -376с.

.        Растригин, Л. А., Тарасенко Г.С. Об одном адаптивном алгоритме случайного поиска / Л. А. Растригин//Проблемы случайного поиска. - Рига: Зинатне. -1974. -Вып.3. -С.108-112.

.        Цыпкин Я. З. Основы теории обучающихся систем. - М.: Наука. - 1981. -251с.

.        Цыпкин Я.З. Адаптация и обучение в автоматических системах. - М.: Наука. - 1968. -400с.

.        Крутиков В.Н. Управление распределением испытаний в алгоритмах случайного поиска// Тезисы докладов 4 Всесоюзного совещания: Статистические методы теории управления. -М.: Наука. -1978. -С.27-28.

.        Теория автоматического управления: Учеб. для вузов по спец. «Автоматика и телемеханика». В 2-х ч. Ч. II. Теория нелинейных и специальных систем автоматического управления. / А. А. Воронов, Д. П. Ким, В. М. Лохин и др.; Под ред. А. А. Воронова.- 2-е изд., перераб. и доп. М.: Высш. шк., 1986.- 504 с.