Основы научных исследований

Основы научных исследований

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФГБОУ ВПО УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ЛЕСОТЕХНИЧЕСКИЙ

УНИВЕРСИТЕТ

Кафедра технологии переработки пластических масс

Дисциплина «Основы научных исследований»

КОНТРОЛЬНАЯ РАБОТА

«Основы научных исследований»

Необходимость и цели опытно-конструкторских работ

конструкторский количественный катализатор регрессионный

Необходимость опытно-конструкторских работ обусловлена значительным снижением степени риска при организации промышленного производства нового объекта в условиях масштабного перехода от лабораторных исследований к промышленным.

Цели ОКР включают в себя:

конструирование и подборка наиболее подходящего аппаратурного оформления процессов, средств контроля и автоматизации при переходе от лабораторных установок к промышленным;

отработка мероприятий по охране окружающей среды при переходе от лабораторных установок к промышленным;

решение вопросов транспортировки сырья и продукции, ее расфасовки и упаковки.

Опишите возможные способы поиска научно-технической информации средствами Интернет

Поиск необходимой информации в Интернете можно осуществлять различными способами:

Поиск с помощью поисковых машин по ключевому слову

Поиск с помощью классификаторов поисковых машин

Каталоги и коллекции ссылок (более общие понятия)

Рейтинги (самые популярные ресурсы)

Конференции, чаты

Страницы ссылок (“Links”) на тематических сайтах (редкие, специализированные вещи)

Несетевые способы (советы друзей, знакомых; реклама в печатных изданиях).

В зависимости от типа информации определяются и пути поиска. Условно можно выделить 4 типа информации:

тип - общая (например: история Российской империи),

тип - менее общая (например: император Александр II),

тип - конкретная (например: реформы Александра II),

тип - более конкретная (например: отмена крепостного права).

Информация 1 типа ищется с помощью классификаторов поисковых машин. Если сразу сайты с требуемой информацией не находятся, то следует просматривать найденные по классификатору каталоги и страницы ссылок (“Links”), которые находятся сайтах подобной тематике. Эти сайты приводятся в классификаторе по теме и найденных каталогах.

Информация 2 типа ищется подобно поиску для 1 типа, но с преимуществом поиска по каталогам и страницам ссылок.

Информация 3 типа - по ключевым словам, которые вводятся в строку поиска поисковых машин, каталогам, страницам ссылок.

Информация 4 типа - по подробным данным, которые вводятся в строку поиска. Данные находятся согласно способам поиска изложенных для 2 и 3 типов.

Необходимо оценить количественную зависимость выхода сахаров при гидролизе древесных отходов от температуры и концентрации катализатора. Используйте для этого метод математического планирования эксперимента для проведения регрессионного анализа и составьте матрицу линейного плана полного двухуровневого факторного эксперимента с кодированными значениями факторов

Уравнение регрессии количественной зависимости выхода сахаров при гидролизе древесных отходов у от температуры х1 и концентрации катализатора х2 (k=2):

у=b0+b1x1+ b2x2

Необходимое число опытов:

необх ≥ k + 1 ≥ 2 + 1 ≥ 3; Nнеобх ≥ L + 1 ≥ 3 + 1 ≥ 4; Nнеобх ≥ 4.

соотношению N ≥ Nнеобх отвечают планы типа 2(k-а) при условии, что (k-a) ≥ 2 и cсоответственно N ≥ 4. Из совокупности планов с N ≥ 4 выберем план ПФЭ типа 22 как наиболее экономный по числу опытов (N = 4) и позволяющий получить наиболее точные оценки коэффициентов уравнения регрессии.

План-матрица эксперимента типа 22

Данный план является ортогональным и D-оптимальным.

Проведите регрессионный анализ с использованием линейной модели процесса следующих результатов эксперимента:

В эксперименте каждый опыт повторялся дважды при одном времени реакции. Средняя дисперсия воспроизводимости всех опытов эксперимента при определении выхода продукта равна 1(% мас.)2 при ее степени свободы f=15.

Искомое уравнение регрессии:

.

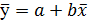Так как дана средняя дисперсия воспроизводимости всех опытов эксперимента, то делаем допущение о нормальном законе распределения y и равенстве дисперсий (одинаковой случайной ошибке при любом значении х).

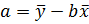; = 0.96 (мас. %/мин.)

а = 8,18 (мас. %).

Выборочный коэффициент корреляции:

= 0,91.

Коэффициент корреляции очень близок к единице, следовательно, зависимость между х и у является практически линейной в изученном диапазоне:

.

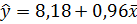Оценка значимости коэффициентов проводится по критерию Стьюдента:

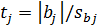
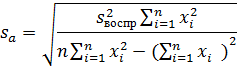
= 0,46 (% мас.)2= 0,011 (% мас.)2= 17,78 (мас.% мин)-1

tb =87,27 (мас.% мин)-1> tр(f) и tb > tр(f) для р=0,05 и f=15, следовательно коэффициенты значимо отличаются от нуля и являются значимыми.

Адекватность уравнения проверяется по критерию Фишера:

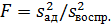
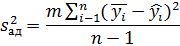
1092,19 (% мас.)2

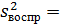958,48 (% мас.)2= 1,14

Значение соотношения F меньше табличного значения квантиля распределения Фишера при уровне значимости р = 0,05 и числе степеней свободы f1 = 14 и f2 = 15, значит уравнение адекватно эксперименту.

Округлите следующие числа до двух значащих цифр:

,35622; 0,00591; 1,00483; 996,61959

Ответ: 1000; 0,0059; 1,005; 1000.