Обработка результатов полного факторного плана для получения математической модели результатов полного факторного плана

Обработка результатов полного факторного плана для получения математической модели результатов полного факторного плана

Курсовая работа

по дисциплине: «Основы научных исследований в деревообработке»

на тему: «Обработка результатов полного факторного плана

для получения математической модели»

Содержание

Введение

. Цель и задачи исследования

. Методика проведения эксперимента

.1 Выбор метода проведения эксперимента

.2 Выбор управляемых факторов и уровней их варьирования

.3 Выбор математической модели

.4 Определение необходимого числа поставленных опытов

.5 Составление плана эксперимента

.6 Методика проведения эксперимента

.7 Результаты определения выходной величины

. Математическая обработка результатов эксперимента

.1 Отбрасывание грубых ошибок

.2 Проверка однородности дисперсии

.3 Расчет коэффициентов уравнения регрессии

. Статистический анализ уравнения регрессии

.1 Оценка значимости коэффициентов уравнения регрессии

.2 Проверка адекватности математической модели

.3 Проверка эффективности математической модели

. Перевод уравнения регрессии из кодированных обозначений факторов в натуральные

. Построение графиков зависимости выходной величины от управляемых факторов

.1 График зависимости выходной величины Y от фактора Х₁

.2 График зависимости выходной величины Y от фактора Х₂

.3 График зависимости выходной величины Y от факторов Х₁ и Х₂

Заключение

Библиографический список

Введение

Технический прогресс в деревообработке неразрывно связан с достижениями науки. Перед работниками деревоперерабатывающей промышленности поставлена задача более полного использования резервов повышения эффективности производства. Одним из путей её решения является широкое проведение исследований и внедрение результатов их в производственную практику.

Научно-технический прогресс предъявляет новые возросшие требования к творческому потенциалу специалистов, их умению ориентироваться в потоке информации, овладевать методами. Потребность в классифицированном применении методов научных исследований в деревообработке возрастает с каждым годом. Инженеры-исследователи всё чаще сталкиваются в своей работе с задачами, требующими кроме профессиональной подготовки знаний методов обработки результатов наблюдений, планирования эксперимента, математических методов моделирования и оптимизации.

Научные исследования в деревообработке имеют ряд особенностей: сфера научных исследований очень широка, так как деревообрабатывающая промышленность объединяет самые разнообразные технологические процессы.

Другая особенность связана со спецификой исходного материала-древесины. Древесина, как естественный объект биологического происхождения, обладает чрезвычайно сложной микро- и макроструктурой. Научные исследования трудоёмки, энергоёмки, поэтому на производстве они проводятся на заключительных этапах. Многие вопросы недостаточно проработаны теоретически (нет единой теории резания, адгезии). Большинство научных исследований носят прикладной характер, т.е. имеют практическую направленность.

Несмотря на трудности научных исследований в деревообработке, они необходимы для создания более прогрессивных технологий производства.

1. Цель и задачи исследования

Основными целями и задачами планирования эксперимента являются:

1)      Планирование эксперимента с целью математического описания объекта. Целью данного эксперимента является получение математической модели методом регрессионного анализа.

2)      Отсеивающие эксперименты в технологических исследованиях. Задача здесь заключается в том, чтобы в сложных мало изученных процессах выделить доминирующие факторы среди очень большого числа априорно принятых

)        Планирование эксперимента при поиске оптимальных условий. Целью этого эксперимента является отыскание таких значений варьируемых факторов, при которых выходная величина объекта принимает экстремальное, т.е. максимальное или минимальное, значение. Методами такого исследования является регрессионный анализ или математическое моделирование

)        Планирование эксперимента с качественными факторами. Методами обработки являются дисперсионный анализ или экспертные оценки (априорное моделирование). Применение этого метода диктуется необходимостью раздельной оценки рассеяния, обусловленного различными источниками.

)        Планирование эксперимента при изучении свойств смесей. Объектом исследования является смесь некоторого числа компонентов, а варьируемые факторы - процентное содержание каждого из них в смеси. Тогда в сумме величины всех этих факторов составляют 100%, то есть варьируемые факторы в данном случае независимыми не являются. Методы планирования экспериментов при построении диаграмм состав-свойство широко используется при исследовании очень сложных поверхностей отклика. Задача заключается в том, чтобы найти оптимальное в некотором смысле расположение точек в факторном пространстве с целью описания диаграммы состав-свойство в виде полинома.

)        Планирование эксперимента при эволюционной оптимизации производственных процессов. Этот метод заключается в непрерывном проведении, как правило, факторного эксперимента в рабочей области процесса. Постановка таких экспериментов базируется на предположении, что варьируемые (в узких пределах) переменные измеримы. Задача сводится к необходимости непрерывно экспериментировать в сложных производственных условиях, чтобы приспосабливаться к неконтролируемому временному дрейфу эксперимента.

Целью данной курсовой работы является получение математической модели упрессовки сырого шпона и отработка методики обработки результатов эксперимента.

дисперсия математический уравнение регрессия

2. Методика проведения эксперимента

.1 Выбор метода проведения эксперимента

Различают эксперименты активный и пассивный, однофакторный и многофакторный.

Активным называют эксперимент, условия которого можно целенаправленно менять. Преимущества активного эксперимента:

возможность обеспечить высокую точность проведения каждого опыта;

возможность повторения его при тех же значениях фактора;

воспроизводимость опытов.

Активный эксперимент чаще проводится в лабораторных условиях.

Пассивным называют эксперимент, условия проведения которого не могут быть управляемыми. Эксперимент заключается в наблюдении над протекающим процессом. Чаще всего пассивные эксперименты проводятся в условиях действующего производства, т.е. на объектах, работающих в режиме нормальной эксплуатации (контроль прочности фанеры, в течение месяца, года).

Однофакторный эксперимент является классическим. Однофакторным называется такой эксперимент, когда изучается воздействие на объект, исследование только одного варьируемого фактора. Остальные факторы, влияющие на объект исследования фиксируются на постоянном уровне. Преимуществом однофакторного эксперимента являются простота, возможность обнаружения ошибки на стадии проведения эксперимента.

Многофакторным экспериментом называется эксперимент, все факторы в котором варьируются одновременно. Основное преимущество многофакторного эксперимента меньшее количество проводимых опытов, меньшие затраты времени. Недостаток многофакторного эксперимента - сложность обработки результатов, невозможность обнаружения ошибки на стадии эксперимента. Ошибки в проведении многофакторного эксперимента выявляются на стадии статистической обработки результата эксперимента.

В данном эксперименте используем метод активного многофакторного эксперимента.

.2 Выбор управляемых факторов и уровней их варьирования

В курсовой работе ставится эксперимент с двумя варьируемыми факторами. Уровни этих факторов заданы в натуральном обозначении. Необходимо представить диапазоны варьированных факторов в натуральных и кодированных обозначениях, определить для каждого фактора основной (нулевой) уровень и интервал варьирования.

Заданные варьируемые факторы - манометрическое давление Р, кгс/см ² и продолжительность прессования τ,мин. Диапазон варьирования факторов в натуральных и кодированных обозначениях:

≤ P ≤ 80; 0.5≤ τ ≤ 1;

≤ X₁≤ +1; -1 ≤ X₂ ≤ +1.

Таблица 2.1

Наименование фактора	Обозначения фактора		Уровни варьирования			Интервал варьирования Δi
	Натуральное	Кодированное	-1	0	+1
1. Давление, кгс/см2	P	X1	40	60	80	20
2. Продолжительность прессования, мин	τ	X2	0.5	0.75	1	0.25

Нулевой уровень каждого фактора X_i⁽⁰⁾ определяется по формуле

X_i⁽⁰⁾ = (X_i^(-1) + X_i⁽⁺¹⁾) / 2, (2.1)

где X_i^(-1) - нижний уровень i-го фактора;

X_i⁽⁺¹⁾ - верхний уровень i-го фактора.

P⁽⁰⁾ = (40+80) /2 =60 (кгс/см²);

τ⁽⁰⁾ = (0.5+1)/2=0.75 мин.

Интервал варьирования фактора Δ_i определяется по формуле

Δ_i = X_i⁽⁰⁾ - X_i^(-1) = X_i⁽⁺¹⁾ - X_i⁽⁰⁾, (2.2)

Δ _{i 1} = 60 - 40 = 20 (кгс/см²);

Δ _{i 2} = 0.75-0.5 = 0.25 (мин.).

2.3 Выбор математической модели

Регрессионная модель y=f(X₁, X₂, …, X_к) - зависимость выходной величины y от варьируемых факторов X₁, X₂, …, X_к, полученная с применением регрессионного анализа. Регрессионный анализ включает метод отыскания параметров математической модели (метод наименьших параметров) и статистическую обработку данных.

Регрессионную модель можно искать в виде многочлена определенного порядка, в виде экспоненты, тригонометрического многочлена и т.д.

Линейная модель 1 порядка вида

y=B_o+B₁X₁+B₂X₂+…. +B_kX_k (2.3)

предполагает отсутствие эффектов взаимодействия факторов. График представляет семейство параллельных прямых (рис. 2.1а).

Линейная модель с эффектами взаимодействия между факторами - частный случай квадратичной модели, которая имеет вид (для двух факторов)

y=B_o+B₁X₁+B₂X₂+B₁₂X₁X₂ (2.4)

графики линейной модели с эффектом взаимодействия представлены на рис. 2.1 б, в.

Квадратичную математическую модель можно представить в виде (для двух факторов)

у=В₀+В₁Х₁+В₂Х₂+В₁₁Х₁²+В₂₂Х₂²+В₁₂Х₁Х₂ (2.5)

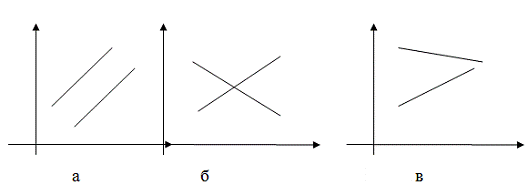
Рис. 2.1. Графики линейной модели: а - с отсутствием эффекта взаимодействия; б, в - с эффектом взаимодействия

Линейная модель дает приближенное представление о влиянии факторов на объект. Применение таких моделей оправдано в следующих случаях: 1) на начальных этапах исследования или в ситуации, когда экспериментатора удовлетворяет ограниченная точность линейной модели; 2) при жестком ограничении на количество опытов, поскольку планы, позволяющие получить линейную модель, являются экономными; 3) когда экспериментатор априорно уверен в достоверности линейной модели.

В данном эксперименте будем использовать линейную математическую модель, т. к. нас устраивает ограниченная точность модели и в условиях учебных занятий трудно провести большое количество опытов.

2.4 Определение необходимого числа поставленных опытов

Для полного факторного плана (ПФП) число опытов N определяется по формуле

N = 2^к , (2.6)

где к - число варьируемых факторов.

В нашем случае N = 2² = 4

.5 Составление плана эксперимента

Построить ПФП значит составить матрицу планирования эксперимента путем перебора всех возможных сочетаний верхних и нижних уровней факторов. Матрицы экспериментов в кодированных и натуральных значениях факторов представлены в таблицах 2.2 и 2.3

Таблица 2.2

№	X1	X2
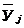
1	+	+	19,67
2	-	+	6,525
3	+	-	16,677
4	-	-	9,127

Таблица 2.3

№	P	τ
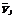
1	80	1	19,67
2	40	1	5,525
3	80	0.5	16,677
4	40	0.5	9,127

Значение выходной величины 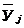 заносится в матрицы после проведения эксперимента и первичной статистической обработки его результатов.

.6 Методика проведения эксперимента

В эксперименте отбирается 4 листа шпона толщиной 1,5 ± 0,1мм или 1,15 ± 0,05 мм. Смешивание разных номинальных толщин в одном эксперименте недопустимо. Шпон размечается произвольно. Наносим на каждый из листов по 12 меток, в которых будем замерять толщину шпона.

Выбор точности измерительного инструмента. Предельная допустимая погрешность измерительного инструмента Δ определяется по формуле

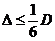, (2.4)

где D - поле допуска на данный размер.

D=0,2 тогда 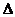=1/6*0,2=0,03. Исходя из полученных значений, измерительный инструментом, выбираемым нами для проведения наших экспериментов, будет микрометр с Ц_д=0.01 мм.

Выбрав измерительный инструмент, замеряют толщину шпона в каждой точке, замеры заносят в таблицу 2.4. Затем первый лист упрессовываем под давлением 80 кг*с/см² и продолжительностью прессования 1 минуту; потом меняем давление на 40 кг*с/см²,а время оставляем тем же и упрессовываем второй лист; третий лист упрессовываем под давлением 80 кг*с/см² и продолжительностью 0,5 минуты; четвертый лист упрессовываем под давлением 40 кг*с/см², и продолжительностью прессования 0,5 минуты. Измеряем толщину всех упрессованных листов в двенадцати точках и записываем результаты замеров в таблицу 2.5.

Выходная величина - упрессовка y определяется по формуле

y=((hсыр.- hсух.)/ hсыр.)*100 (2.8)

Значения упрессовки записываем в таблицу 2.6.

.7 Результаты определения выходной величины

Таблица 2.4. Результаты замеров толщины сырого шпона, мм

Лист	1	2	3	4	5	6	7	8	9	10	11	12
1	1,39	1,41	1,44	1,39	1,42	1,42	1,39	1,41	1,41	1,41	1,42	1,42
2	1,46	1,47	1,43	1,46	1,44	1,45	1,44	1,46	1,44	1,45	1,43	1,45
3	1,42	1,42	1,39	1,43	1,43	1,44	1,42	1,41	1,41	1,43	1,44	1,42
4	1,38	1,42	1,43	1,45	1,43	1,42	1,39	1,41	1,42	1,39	1,43	1,44

Таблица 2.5. Результаты замеров толщины сухого шпона, мм

Лист	1	2	3	4	5	6	7	8	9	10	11	12
1	1,29	1,28	1,26	1,27	1,26	1,28	1,29	1,29	1,28	1,27	1,26	1,28
2	1,38	1,37	1,34	1,34	1,33	1,35	1,34	1,32	1,35	1,36	1,36	1,34
3	1,29	1,21	1,18	1,19	1,19	1,17	1,18	1,17	1,18	1,19	1,18	1,19
4	1,14	1,08	1,12	1,04	1,10	1,09	1,20	1,15	1,23	1,24	1,04	1,09

Таблица 2.6. Упрессовка шпона, %

Результаты Уi в точках												Режим
1	2	3	4	5	6	7	8	9	10	11	12
7,19	9,22	12,5	8,63	11,26	9,85	7,19	8,51	9,22	9,23	11,2	18,5	9,127	P =80 τ =1
5,47	6,80	6,29	8,21	7,63	6,89	6,94	9,59	6,25	6,20	4,89	6,20	6,525	P =40 τ =1
9,15	14,78	16,78	16,78	18,7	16,9	17,02	16,3	16,78	18,0	16,2	16,67	P =80 τ =0,5
17,3	23,94	24,4	28,27	23,08	23,2	13,6	18,44	13,3	10,79	23,2	37,5	19,67	P =40 τ =0,5

3. Математическая обработка результатов эксперимента

.1 Отбрасывание грубых ошибок

Опыт 1. Выстраиваем результаты опыта в ранжированный ряд.

Уi	7,19	8,51	8,63	9,22	9,23	9,85	18,54	11,26	12,50
mi	2	1	1	2	1	1	1	1	1

Определяем среднее арифметическое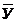

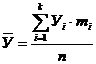 , (3.1)

где У_i - i-е значение выходной величины У;

m_i - частота повторения данного значения;

n - число замеров в выборке.

Определяем среднее квадратическое отклонение S

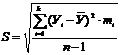 (3.2)

=9,49

S=1,59

Для проверки выборки на наличие грубых ошибок воспользуемся критерием Стьюдента. Расчетное значение tp определяется для минимального и максимального элементов выборки:

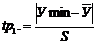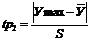 ,  (3.3)

Табличное значение критерия Стьюдента t_T определяется по уровню значимости q = 0.05 и числу степеней свободы выборки ƒ = n -1.

Если выполняется соотношение t_p ≤ t_т, (3.4), проверяемый элемент не является грубой ошибкой.

t_p1 =|7,19-9,4925|/1,5976=1,4412 t_p2 =|12,50-9,4925|/1,5925=1,9207

t_T (q = 0,05, ƒ = 11) = 2,20.

t_p1 < t_T, t_p2 < t_T.

Вывод: выборка не содержит грубых ошибок.

Опыт 2. Выстраиваем результаты опыта в ранжированный ряд.

Уi	4,89	5,47	6,20	6,25	6,29	6,80	6,89	6,94	7,63	8,21	9,59
mi	1	1	2	1	1	1	1	1	1	1	1

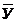=6,78=1,2498

t_p1 =|16,67-24,09|/3,956=1,5125 t_p2 =|28,77-24,09|/3,956=2,2483

t_p1 < t_T , t_p2 > t_T.

Вывод: выборка содержит грубую ошибку.

Опыт 3. Выстраиваем результаты опыта в ранжированный ряд.

Уi	9,15	14,78	15,10	16,20	16,31	16,78	16,90	17,02	18,05	18,75
mi	1	1	1	1	1	3	1	1	1	1

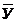=16,67=1,1326

t_p1 =|9,15-16,05|/2,8436=2,8436 t_p2 =|14,78-16,67|/1,1326=1,6971

t_p1 > t_T , t_p2 < t_T.

Вывод: выборка содержит грубую ошибку.

Опыт 4. Выстраиваем результаты опыта в ранжированный ряд.

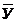=21,453

S=7,9948

Уi	10,79	13,38	13,67	17,39	18,44	23,08	23,24	23,27	24,94	24,47	28,27	3750
mi	1	1	1	1	1	1	1	1	1	1	1	1

t_p1 =|0,79-21,45|/7,99=1,3341 t_p2 =|37,50-21,453|/7,99=2,0083

t_p1 < t_T , t_p2 < t_T.

Приводим к равномерному дублированию.

N1=n2=n3=n4=11

Опыт 1.

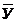=9.127

S=1.256

Опыт 2.

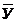=6,525

S=0.925

Опыт 3.

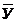=16,677

S=1.132

.2 Проверка однородности дисперсии

Для проверки используем G -критерий Кохрена

, (3.5)

где G_p - расчетное значение критерия Кохрена;

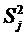 - дисперсия в j - м опыте;

S²_max - максимальная из дисперсий.

Табличное значение критерия Кохрена G_T определяется по уровню значимости q = 0,05, числу степеней свободы каждой выборки ƒ = n - 1 и количеству выборок m.

Если выполняется условие G_p ≤ G_T, (3.6), дисперсии всех выборок однородны, все выборки принадлежат одной и той же генеральной совокупности, а различие между ними объясняется влиянием случайных ошибок. Таблица 3.

m = 4, ƒ = 11.

N
1	1,57
2	0,85
3	1,132
4	36,13

G_{T =0,482}

G_p= 1,09

G_p < G_T.

Вывод: Дисперсии всех выборок однородны.

.3 Расчет коэффициентов уравнения регрессии

Для линейной математической модели вида

у = b₀ + b₁x₁ + b₂x₂ + b₁₂x₁x₂

коэффициенты уравнения регрессии b_i (i = 0, 1, …, k) находятся по формуле

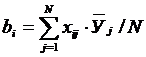, (3.7)

где x_ij - значение i -го фактора в j -м опыте;

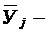 среднее значение выходной величины в j -м опыте;

N - число опытов.

Эффект взаимодействия двух факторов b₁₂ определяется по формуле

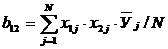. (3.8)

Таблица 3.1

N	x1	x2
1	+	+	19,67
2	-	+	6,525
3	+	-	16,677
4	-	-	9,127

b₀ =(19,67+6,525+16,67+9,12)/4=12,99

b₁=(19,67-6,525+16,67-9,12)/4=5,17

b₂=(19,67+6,525-16,67-9,12)/4= 0,01

b₁₂=(19,67-6,525-16,67+9,12)/4= 1,39

После расчета коэффициентов b_i получили математическую модель

У = 12,99+5,17X₁ + 0,1X₂ +1,39X₁X₂

4. Статистический анализ уравнения регрессии

.1 Оценка значимости коэффициентов уравнения регрессии

1. Дисперсия воспроизводимости 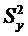определяется по формуле

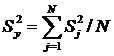, (4.1)

где  - дисперсия в j -м опыте.

Число степеней свободы дисперсии воспроизводимости:

N
1	1,57
2	0,85
3	1,132
4	36,13

ƒ_y = N·(n - 1). (4.2)

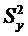=(39,895)/4=9,958

ƒ_y = 4·10 = 40

. Дисперсия коэффициентов уравнения регрессии S²{b_i} определяется по формуле

S² {b_i} = S²_y /(n·N), (4.3)

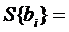
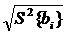 (4.4)

S² {b_i}=9,958/44=0,226

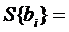0,475

3. Критическое значение коэффициентов уравнения регрессии

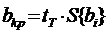, (4.5)

где t_T - табличное значение критерия Стьюдента, определенное по уровню значимости q = 0.05 и числу степеней свободы дисперсии воспроизводимости ƒ_У . Коэффициент уравнения b_i является значимым, если выполняется условие:

|b_i| > b_kp, (4.6)

в противном случае он не является значимым и подлежит удалению из уравнения регрессии.

t_T (q = 0.05, ƒ_У = 40) = 2,02 b_kp=2,02*0,475=0,959 .

,99>0,959 → b₀ значим; 0,1>0,959→ b₂ не значим;

5,17>0,959 → b₁ значим; 1,39>0,959 → b₁₂ значим.

Модель остается в прежнем виде У = 12,99+5,17X₁ +1,39X₁X₂

.2 Проверка адекватности математической модели

Можно проверить адекватность модели только для ненасыщенных планов, т.е. таких, для которых выполняется условие

р < N, (4.7)

где р - число значимых коэффициентов уравнения регрессии.

Дисперсия адекватности 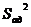 определяется по формуле

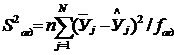, (4.8)

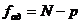, (4.9)

где n - число дублированных опытов;

 - среднее значение выходной величины в j-ом опыте;

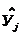 - значение выходной величины, рассчитанное по уравнению регрессии для j-ого опыта;

f_α∂ - число степеней свободы дисперсии адекватности.

Проверим однородность дисперсии адекватности S_α∂² и дисперсии воспроизводимости S_y², воспользуемся для этого критерием Фишера:

F_p = S_α∂²/S_y², (4.10)

F_т (q = 0.05, f_α∂, f_y). (4.11)

Если выполняется условие F_p ≤ F_т , (4.12)

дисперсии S_α∂² и S_y² однородны, математическая модель адекватна, т.е. предсказывает значение выходной величины с той же точностью, что и результаты эксперимента.

Вычислим по уравнению регрессии значения выходной величины 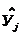 для каждого опыта, занесем их в таблицу 4.1.

У = 12,99+5,17X₁ +1,39X₁X₂

Таблица 4.1

	X1	X2
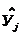
1	+	+	16,67	19,55
2	-	+	6,525	6,43
3	+	-	16,67	16,77
4	-	-	9,12	9,21

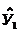=12,99+5,17+1,39=19,55

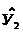 =12,99-5,17-1,39=6,43

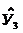 =12,99+5,17-1,39=16,77

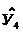 =12,99-5,17+1,39=9,21

4.3 Проверка эффективности математической модели

Для проверки эффективности, т.е. информационной ценности модели вычисляют дисперсию относительно среднего значения S_c², остаточную дисперсию S_ост² и коэффициент информационной ценности

F_и = S_c²/S_ост².(4.13)

Модель имеет информационную ценность, т.е. эффективна, если

F_и > 3. (4.14)

. Дисперсия относительно среднего значения отклика

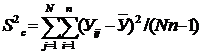, (4.15)

Где У_ij - значение выходной величины в i-ом дублированном опыте j-го опыта;

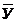- среднее значение выходной величины по всем N сериям опытов.

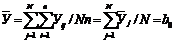
S_c²=(7,19-12,99)²+(7,19-12,99)²+(8,51-12,99)²+(8,63-12,99)²+(9,22-12,99)²+(9,22-12,99)²+(9,23-12,99)²+(9,85-12,99)²+(9,85-12,99)²+(11,26-12,99)²+(11,26-12,99)²+(4,89-12,99)²+(5,47-12,99)²+(6,20-12,99)²+(6,20-12,99)²+(6,25-12,99)²+(6,29-12,99)²+(6,80-12,99)²+(6,89-12,99)²+(6,94-12,99)²+(7,63-12,99)²+(8,21-12,99)²+(14,76-12,99)²+(15,10-12,99)²+(16,20-12,99)²+(16,3-12,99)²+(16,78-12,99)²+(16,78-12,99)²+(16,78-12,99)²+(16,90-12,99)²+(17,02-12,99)²+(18,05-12,99)²+(18,75-12,99)²+(10,79-12,99)²+(13,38-12,99)²+(13,67-12,99)²+(17,39-12,99)²+(18,44-12,99)²+(23,08-12,99)²+(23,24-12,99)²+(23,27-12,99)²+(23,94-12,99)²+(24,47-12,99)²+(28,27-12,99)²/43=38,457

2 Остаточная дисперсия

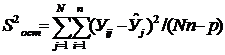 (4.16)

) 19,55

) 6,43

) 16,27

) 9,21

S_ост² = (7,19-19,55)²+(7,19-19,55)²+(8,51-19,55)²+(8,63-19,55)²+(9,22-19,55)²+(9,22-19,55)²+(9,23-19,55)²+(9,85-19,55)²+(9,85-19,55)²+(11,26-19,55)²+(11,26-19,55)²+(4,89-6,43)²+(5,47-6,43)²+(6,20-6,43)²+(6,20-6,43)²+(6,25-6,43)²+(6,29-6,43)²+(6,80-6,43)²+(6,89-6,43)²+(6,94-6,43)²+(7,63-6,43)²+(8,21-6,43)²+(14,76-16,77)²+(15,10-16,77)²+(16,20-16,77)²+(16,31-16,77)²+(16,78-16,77)²+(16,78-16,77)²+(16,78-16,77)²+(16,90-16,77)²+(17,02-16,77)²+(18,05-16,77)²+(18,75-16,77)²+(10,79-9,21)²+(13,38-9,21)²+(13,67-9,21)²+(17,39-9,21)²+(18,44-9,21)²+(23,08-9,21)²+(23,24-9,21)²+(23,27+9,21)²+(23,94-9,21)²+(24,47-9,21)²+(28,27-9,21)²/41=68,446

F_и =38,457/68,446=0,562

,562 <3.

Математическая модель не имеет информационной ценности ,т.е. не эффективна.

3. Проверим, на сколько различаются значения выходной величины, рассчитанные по уравнению регрессии, и результаты эксперимента

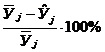
. (19,67-19,55)/19,67*100%= 0,6%

. (6,525-6,43)/6,525*100%= 1,5%

. (16,67-16,77)/16,67*100%= -0,6%

. (9,12-9,21)/9,12*100%= -0,98%

Результаты отличаются не больше чем на 1,5%

5. Перевод уравнения регрессии из кодированных обозначений факторов в натуральные

Заменим кодированные обозначения факторов Х_i на натуральные х_i

X_i = (x_i - x_i⁰)/Δ_i, (5.1)

гдеx_i⁰ - значение i-го фактора на нулевом уровне;

Δ_i - интервал варьирования i-го фактора.

Х₁ = (Р - 60)/20,Х₂ = (τ - 0.75)/0.25;

У = 12,99+5,17X₁ +1,39X₁X₂

У = 12,99+5,17(Р - 60)/20 +1/39((τ - 0.75)/0.25= 9,99+0,05Р-16,68τ +0,278Рτ

У= 9,99+0,05Р-16,68τ +0,278Рτ

Проверим правильность перевода уравнения в натуральные обозначения факторов.

Таблица 5.1

N	P	τ
1	80	1	19,549
2	1	6,43
3	80	0.5	16,78
4	40	0.5	9,21

=9,99+0,05*80-16,68*1+0,278*80*1=19,549

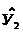=9,99+0,05*40-16,68*1+0,278*40*1=6,43

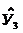=9,99+0,05*80-16,68*0,5+0,278*80*0,5=16,77

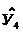 =9,99+0,05*40-16,68*0,5+0,278*40*0,5=9,21

Уравнение правильно переведено из кодированных в натуральные обозначения.

6. Построение графиков зависимости выходной величины от управляемых факторов

Графики строим по уравнению регрессии в кодированных обозначениях факторов.

У = 12,99+5,17X₁ +1,39X₁X₂

.1 График зависимости выходной величины У от фактора Х₁

Зафиксируем значение фактора Х₂ на уровне +1: Х₂ = +1.

При X₁ = +1Х₁ = -1

У = 19,55У = 6,43

Если Х₂ = -1,

У = 12,99+5,17X₁ -1,39X₁X₂

При X₁ = +1;Х₁ = -1;

У =16,78 У = 9,21

6.2 График зависимости выходной величины У от фактора Х₂

У = 12,99+5,17X₁ +1,39X₁X₂

Х₁= +1

При X₂ = +1Х₂ = -1

У =19,55У =16,77

ЕслиХ₁ = -1

У = 12,99+5,17X₁ -1,39X₁X₂

При X₂ = +1Х₂ = -1

У =6,43 У=9,21

6.3 График зависимости выходной величины У от факторов Х₁ и Х₂

Х₁ = + 1 Х₁ = - 1 Х₁ = + 1Х₁ = - 1

Х₂ = + 1Х₂ = + 1Х₂ = - 1Х₂ = - 1

У =19,55 У =16,77У =6,43У = 9,21

Заключение

Интерпретируем уравнение регрессии в кодированных обозначениях, т.к. в этом случае факторы варьируются в одинаковых диапазонах от «-1» до «+1», что позволяет их численно сравнивать.

В нашем случае математическая модель имеет вид

У = 12,99+5,17X₁ +1,39X₁X₂

.        Коэффициент b₀ показывает значение выходной величины, когда факторы находятся на нулевом уровне, в данном случае упрессовка шпона составит 26,38%, когда манометрическое давление Р = 60 кг*с/см², а продолжительность прессования τ = 0,75 мин.

.        Наибольшее влияние на упрессовку шпона оказывает эффект взаимодействия давления и продолжительности прессования.

.        Знак коэффициента уравнения регрессии показывает, как изменится выходная величина с изменением фактора. При увеличении манометрического давления х₁ выходная величина будет увеличиваться, а при увеличении времени прессования x₂ упрессовка шпона будет убывать.

.        Эффект взаимодействия может увеличивать или уменьшать упрессовку. При одновременном возрастании или при одновременном убывании давления и продолжительности прессования упрессовка будет уменьшаться от эффекта взаимодействия. Если один из факторов будет возрастать, а другой в это время убывать, эффект взаимодействия будет увеличивать упрессовку.

.        При изменении давления Р на 20 кг*с/см² упрессовка шпона изменится на 5,17%, а при изменении времени подпрессовки на 0,25 минут прессовка изменится на. При одновременном изменении Р и τ на интервал варьирования упрессовка изменится на 1,39%. В геометрической интерпретации значение коэффициента уравнения регрессии - это тангенс угла наклона графика зависимости выходной величины к соответствующей оси.

Библиографический список

1. Пижурин А.А., Розенблит М.С. Исследование процессов деревообработки. - М.: Лесная промышленность, 2010. - 232 с.

. Вахнина Т.Н. Научные исследования в деревообработке: Методические указания для выполнения курсовой работы. - Кострома: КГТУ, 2009. - 20 с.