Моделирование спроса на жилье в небольшом городе в условиях депопуляции
Введение
В моей работе будет рассмотрен один из аспектов такой
проблемы как «депопуляция населения малых городов России», а именно как влияет
миграция на уровень цен жилой недвижимости. Такое решение было связанно с
научно-исследовательскими работами (НИР) кафедры Автоматизированные системы
обработки информации и управления (АСОИУ) Камышинского технологического
института(КТИ) филиал Волгоградского государственного технического университета
(ВолгГТУ). Работы кафедра выполняет по гранту Российского фонда фундаментальных
исследований (РФФИ) (финансируется из средств РФФИ и администрации
Волгоградской области), проект р-Поволжье-а №13-07-97033 «Модели и алгоритмы
для подсистем управления качеством жизни небольшого города, препятствующие его
депопуляции (на примере города Камышина Волгоградской области.)»
Одна из наиболее значимых и сложных социальных проблем в
России - жилищная проблема. Доставшаяся в наследство еще с советских времен,
сегодня проблема доступного и качественного жилья не приблизилась, а, скорее отдалилась
от своего решения. Действительно, социальное жилье почти не строится, а цены на
коммерческое таковы, что купить его могут только очень богатые люди.
Жилищная проблема в России является одной из важнейших
проблем современной экономики. Сегодня 8% россиян проживают
либо в общежитиях и служебных квартирах, либо снимают жилье. Арендуют жилье
люди с недостаточно высоким уровнем доходов, из них 58% малообеспеченные семьи,
37% - семьи со средним обеспечением и лишь 5% можно отнести к сравнительно благополучным
слоям населения. Более того, основная часть арендаторов имеет жилье с маленьким
метражом и не всеми коммунальными удобствами. Еще около 6% проживают в
коммунальных квартирах или в части дома, не имеющих коммунальных удобств. [1]
Активная миграция населения из российской глубинки в
мегаполисы оставляет вымершими деревни. К той же участи постепенно приближаются
и малые города России.
Почти весь миграционный прирост в межрайонной внутренней
миграции получают 10 наиболее привлекательных регионов страны -- 93% в
2005--2007 гг. При этом Московская область и Москва приняли 28 и 26% внутренних
мигрантов соответственно, а вместе -- 54%.
Центром притяжения общероссийского масштаба является также
Санкт-Петербургская агломерация. Кроме того, на такую роль могут претендовать
Краснодарский край и Белгородская область, а с некоторой оговоркой --
Калининградская область и Ставропольский край. Мощными региональными лидерами
являются Республика Татарстан, Свердловская, Самарская, Ярославская области. К
региональным лидерам второго плана можно отнести Карелию, Волгоградскую,
Саратовскую, Кемеровскую области, Хабаровский край. Подавляющее же большинство
регионов России теряет население, причем потери по регионам распределяются
довольно равномерно.
За 2005--2007 гг. города в целом росли на 62% за счет
международной, на 26% -- внутрирегиональной и на 12% -- внутренней
межрегиональной миграции. Село потеряло 70% мигрантов в пользу городских
поселений своего региона, 30% -- других регионов, при этом международная
миграция восполнила потери села на 67%. Мигранты, как внутренние, так и
внешние, стремятся в крупные города, где много возможностей для
трудоустройства, получения высоких заработков, самореализации. Из 13 регионов,
возглавлявшихся городами-миллионниками, в 2001--2005 гг. восемь имели
устойчивый миграционный прирост, в 2006 г. -- 10, в 2007 г. -- 11. При этом и
само число городов-миллионников в 2004 г. сократилось до 12 (в результате
сокращения населения Перми), а в 2005 г. -- до 11 (из группы
городов-миллионников выбыл также Волгоград).
Население региональных столиц прирастает за счет его
постепенного стягивания из других городов и сельской местности
«подведомственной» территории и регионов-соседей. Даже в регионах, где
наблюдается устойчивый миграционный отток населения, столицы прирастают за счет
мигрантов. Пример -- города Иркутской и Красноярской агломераций. Региональные
столицы (включая Москву) в равной мере росли за счет внутрирегиональной и
межрегиональной миграции, при этом роль внутренней миграции составляла 60% от
общего миграционного прироста (рис. 6.14) Нестоличные крупные города имели
близкий к нулевому миграционный баланс внутрироссийской миграции и прирастали
только за счет международной миграции. Средние и малые города теряли население
в межрегиональном обмене, но восполняли эти потери за счет обмена с сельской
местностью. Поскольку в России потенциал сельско-городской миграции близок к
исчерпанию, малым и средним городам практически нечем пополнять население.
Только в начале 1990-х гг., когда миграционный приток русского и русскоязычного
населения, в том числе вынужденных переселенцев, был ориентирован в
значительной мере на малые и средние города и сельскую местность (здесь
переселенцам проще было решить жилищную проблему), они получали миграционную подпитку.
В последние годы рост экономики восстановил спрос на труд прежде всего в
крупных городах, что послужило стимулом для миграции из малых городов. [2]
Значит, строительство в них невыгодно, инвесторы вкладывают
средства в города - миллионщики. При этом стремятся получить земельные участки
в престижных старых районах и построить в них дорогое элитное жилье.
Однако, если люди уезжают из населённого пункта будь то
деревня село или малый город, то значит они освобождают свои дома и квартиры.
Но налоги и коммунальные платежи всё равно надо платить, а в последние годы
цены на энергоносители только растут. Поэтому остается только два выхода:
сдавать свою собственность в аренду или продать её. Чем дольше ты живешь вдали
от свой недвижимости, тем больше затраты на неё. Поэтому надо как то решать эту
проблему. Самый простой вариант это продать, но вот тут уже возникает
интересная ситуация:собственники желаю продать товар подороже, но таких
предложений на рынке довольно много в связи миграцией в большие города, поэтому
что бы продать нужно уменьшать цену. И такая ситуация будет сохраняться до тех
пор пока количество людей покидающих населённый пункт будет больше чем людей
желающих переехать в данную местность.
На основе таких выводов было сделано предположение, что цена
на недвижимость будет постепенно падать, до тех пор пока не измениться ситуация
или пока недвижимость не станет привлекательной для переезда.
Для подтверждения данной гипотезы были поставлены следующие
цели:
- Провести анализ сделок с недвижимостью по предыдущим
годам.
- Проверить существование связи между ценой
на недвижимость и миграцией населения.
- При установлении данной связи
формализовать её характеристики и параметры.
- Смоделировать изменение цен на жилье на
основе выявленной связи.
1.
Основная часть
1.1
Принцип формирования цен на недвижимость
имитационный недвижимость программный корреляционный
Существует две принципиальные стратегии формирования цены на
недвижимость, которые на прямую отражают особенность двух рынков недвижимости:
первичного и вторичного.
На первичном рынке продавец часто является одновременно как
застройщиком так и собственником. Поэтому в первую очередь для него важна
прибыль. Как следствие цены на недвижимость формируются следующим образом:
Цена=Затратам_на_сторительство+ожидаемая_прибыль
Конечно учитывается как и на любом рынке тут действует закон
Спроса и предложения. Поэтому если застройщик предполагает что затраты не
окупятся то он может либо избавиться от объекта, либо заморозить строительство.
Всё зависит от активов и состояния конкурентной среды.
На вторичном рынке действие закона Спроса и Предложения
первично. Формирование цены на этом рынке может быть описано следующим образом.
«Цена продавца» - сумма денег, за которую продавец готов
уступить свои права на объект недвижимости.
Наиболее типичными для продавца при установлении цены
являются такие аргументы, как:
понесенные продавцом когда-то затраты («Я купил эту квартиру
(дом, участок и пр.) за 50 тысяч долларов, да еще вложил в него еще столько же,
так что меньше, чем за 100 тысяч я ее не продам»);
цены на равнозначные, по его мнению, объекты («Мне нужна
двухкомнатная квартира, так что я готов продать мой дом за сумму, которой мне
хватит, чтобы ее купить»)
уровень текущих и будущих доходов продавца («Я выхожу на пенсию
и мне нужно, чтобы вырученных от продажи денег хватило на жизнь»
услышанные или полученные из средств массовой информации
сведения о ценах на аналогичные, по мнению продавца, объекты («Моя знакомая
продала такую же, как у меня квартиру, за 5 миллионов рублей, так что ниже этой
суммы она не стоит»)
«Цена покупателя» - сумма денег, которую покупатель готов
отдать за права на объект недвижимости.
У покупателя - свои резоны о приемлемом уровне цены:
уровень финансовых возможностей (« Я могу заплатить за эту
квартиру не больше, чем 4 миллиона рублей»);
информация, полученная из тех же средств массовой информации,
статей, рассказов (« В Интернете сейчас висят предложения на такие же квартиры
по цене на полмиллиона рублей меньше»);
характеристики настоящего жилья («У меня сейчас кухня 20 кв.
метров, а Вы мне предлагаете только с 9 кв.метрами»).
Как видим, «цена продавца» и «цена покупателя» - это
отражение субъективных представлений продавца и покупателя о той желаемой с их
точки зрения цене, за которую они готовы продать/приобрести объект
недвижимости.
Субъективность в оценках продавца и покупателя, однако, вовсе
не означает, что у них нет объективной основы. На деле такие представления
всегда базируются на множестве факторов и информации, которая имеет разную природу
- отчасти объективную, отчасти субъективную, на которой и базируется их
представления о разумной и справедливой цене.
Цена в любой конкретной сделке, в конечном счете, будет
результатом столкновения представлений продавца и покупателя и родится она в
результате их переговоров. Задача риэлтора - квалифицированно
проконсультировать участников сделки о реально возможном уровне цены на объект
недвижимости, являющийся ее предметом. Для этого нужно показать, какой может
быть наиболее вероятная разумная цена, по которой может быть продан/приобретен
тот или иной объект недвижимости. Как ее определить.
1.2
Факторы формирования цены на объекты недвижимости
Все факторы, влияющие на уровень цен на объекты недвижимости,
могут быть разделены на две группы:
- Факторы, определяющие уровень цена национальном и
региональных рынках в целом.
- Факторы, определяющие уровень цены на конкретный
объект недвижимости.
К первой группе относятся такие общеэкономические факторы как
уровень развития страны, объемы валового внутреннего продукта (ВВП) на душу
населения, уровень занятости, уровень доходов населения в стране и пр.
Исследование их влияния на рынок недвижимости, его активность, уровень цен и
арендной платы - особая большая тема
Во-первых, уровень цен на объекты недвижимости в каждый
данный момент времени определяется соотношением предложения и спроса на рынке.
Так, если предложение превышает спрос, то у покупателя больше возможности
диктовать свои условия, в том числе и относительно уровня цены. Такая ситуация
называется «рынок покупателя» и цена, при прочих равных обстоятельствах, будет
снижаться.
Предложение превышает спрос - «рынок покупателя»: цена падает
Если, напротив, спрос превышает предложение, то возможности
диктовать свои условия выше у продавца. В этом случае мы имеем дело с «рынком
продавца» и цена будет расти.
Спрос превышает предложение - «рынок продавца»: цена растет
Во-вторых, динамика цен на рынке определяется такими
факторами, как динамика доходов приобретателей недвижимости и динамика
строительных издержек.
Рост доходов приобретателей (покупателей) недвижимости ведет
к росту спроса на объекты недвижимости а, значит, и цен на них. Но зависимость
здесь совсем не прямая, поскольку, как правило, между уровнем доходов
покупателя и уровнем цен на объекты недвижимость существует значительный
разрыв.
Например, уровень годового дохода семьи из трех человек в 1
000 000 рублей по состоянию на 2008 г. для Санкт-Петербурга может считаться
вполне приличным. Но стоимость трехкомнатной квартиры будет составлять около 5
000 000 рублей, так что соотношение «Цена квартиры/годовой доход» будет равно 5
(это соотношение часто называют «коэффициент доступности жилья». Предположим,
что доход вырастет на 20% и составит 1 200 000 рублей, а цена квартиры
увеличится даже на 10%, т.е. станет 5 500 000 рублей. Коэффициент доступности
жилья изменится, но изменится незначительно - лишь до 4,6. Значит, даже
существенный рост текущих доходов не ведет к такому же росту спроса.
Нужно иметь в виду, что рынок аренды в этом отношении заметно
отличается от рынка продаж, потому что здесь уже нет такого разрыва - арендная
плата составляет лишь часть дохода арендатора и потому зависимость между ростом
доходов арендаторов и ростом их спроса на аренду может быть заметно более
явной.
Аналогичным образом обстоит дело и тогда, когда мы имеем дело
с использованием ипотечного кредитования. Оно как раз и построено на том, что
платежи по кредиту составляют лишь часть дохода заемщиков, так что рост их
доходов может быть важным фактором роста спроса на приобретение недвижимости в
собственность.
Что касается строительных издержек, то понятно, что если
растет стоимость материалов: цемента, кирпича и пр., уровень заработной платы в
строительстве, то не может не расти и стоимость строительной продукции - домов
и квартир.
В-третьих, следует иметь в виду, что на спрос на данные
объекты недвижимости (а, значит, и на цены) может повлиять ситуация с
объектами, которые их могут заменить.
Например, при росте цен на квартиры на первичном рынке,
очевидно, вырастет спрос на аналогичные квартиры на вторичном рынке, что, через
какое-то время вызовет и здесь рост цен. Другой вариант: в строящихся домах
запланировано недостаточное, по сравнению со спросом, количество однокомнатных
квартир. Очевидно, что это может вызвать рост спроса с последующим ростом цен
на двухкомнатные квартиры малой площади. Или, еще одна возможность: быстро
растет арендная плата. Это может привести к тому, что как альтернативный
вариант будет рассматриваться приобретение квартир с использованием ипотечных кредитов.
Следовательно, спрос на такой вариант решения жилищной проблемы также может
вырасти.
Конкретных вариантов такого влияния может быть достаточно
много: первичный рынок вместо вторичного, аренда вместо покупки, двухкомнатные
квартиры вместо однокомнатных и пр. Задача риэлтора - видеть возникающие на
рынке возможности и использовать их в своей деятельности.
Вторая группа факторов, это факторы, определяющие наиболее
вероятную цену на конкретный объект недвижимости.
Эти факторы также можно разделить на две группы:
- характеристики объекта,
- характеристики сделки.
Характеристики объекта - это его физические параметры,
отличающие данный объект от других. На наиболее массовом рынке - рынке квартир
и комнат в многоэтажных домах к числу таких факторов относятся такие, как:
- характеристики местоположения;
- характеристики здания, в котором
расположен объект сделки;
- характеристики объекта сделки (квартиры
или комнаты).
Местоположение как экономическая характеристика объекта
недвижимости находит свое отражение в двух основных параметрах: окружении и
доступности.
Под окружением объекта понимается характер окружающей объект
застройки, уровень благоустройства окружающей территории, ландшафт и пр. Любой
объект может как выиграть, так и проиграть от своего окружения.
Надо заметить, что роль одного и того же окружения может быть
различна для объектов недвижимости разного типа. Так, расположение в самой
непосредственной близости от метро может быть фактором, повышающим ценность
торговой или офисной недвижимости, и рассматриваться как негативный фактор для
элитного, клубного жилья.
Под доступностью объекта понимается близость или отдаленность
объекта с точки зрения его пользователя от места проживания, работы
пользователя, от маршрутов общественного транспорта, автомагистралей и пр.
1.3
Общие сведения о демографической ситуации
По численности населения город Камышин занимает третье место
среди муниципальных образований Волгоградской области, уступая только городам
Волгоград и Волжский.
В Камышине сосредоточено 6,1% городского населения области. В
таблице 1 представлены данные о численности городского населения и о динамике
ее изменения за период с 2003 по 2011год, с прогнозом на период 2012…2014 года.
Здесь и ниже периоды времени, по которым использованы прогностические данные,
отмечены символом «*».
На рисунке 1 показана диаграмма изменения численности
населения, из которой следует, что тенденция уменьшения численности населения,
начавшегося в кризисные девяностые годы двадцатого века, в период с 2009 года
была временно преодолена, и численность стабилизировалась на уровне 118 000
человек. Однако, судя по прогнозу на период до 2014 года, ожидается дальнейшее
снижение численности.
Для предотвращения депопуляции города необходимы специальные
меры, предусмотренные программой развития городского округа - города Камышина
на период до 2020 года. На рисунке 2 приведены данные о рождаемости и
смертности и о динамике этих показателей за период 2003-2011 года с прогнозом
до 2014 года.
Таблица 1 - Население города Камышина и динамика изменения
численности
|
Годы
|
Численность на
конец года
|
Родилось, чел.
|
Умерло, чел.
|
Коэффициент
рождаемости (на 1000 чел.)
|
Коэффициент
смертности (на 1000 чел.)
|
|
2003
|
125503
|
1049
|
1942
|
8,4
|
15,5
|
|
2004
|
123747
|
1093
|
1882
|
8,8
|
15,2
|
|
2005
|
121829
|
1032
|
2001
|
8,5
|
16,4
|
|
2006
|
119997
|
1075
|
1897
|
9
|
15,8
|
|
2007
|
118533
|
1081
|
1707
|
9,1
|
14,4
|
|
2008
|
117297
|
1214
|
1687
|
10,3
|
14,4
|
|
2009
|
120939
|
1167
|
1715
|
9,6
|
14,2
|
|
2010
|
119634
|
1128
|
1813
|
9,4
|
15,2
|
|
2011
|
118605
|
1154
|
1703
|
9,7
|
14,4
|
|
2012*
|
118280
|
1160
|
1705
|
9,8
|
14,4
|
|
2013*
|
117262
|
1166
|
1704
|
9,9
|
14,5
|
|
2014*
|
116259
|
1170
|
1703
|
10,1
|
14,6
|
По данным Областного комитета государственной статистики в
докризисный период коэффициент рождаемости превосходил коэффициент смертности,
что благоприятно сказывалось на демографической ситуации. В последующие периоды
количество родившихся стабильно ниже количества умерших; разность между
родившимися и умершими, максимальная в 2005 году (- 969 человек), к 2008 году
стабилизировалась на уровне 530 человек. Негативные явления, связанные с
отрицательным балансом родившихся и умерших, прогнозируются вплоть до 2014
года. По коэффициенту рождаемости/смертности город Камышин занимает
соответственно двадцать шестое/девятнадцатое места среди муниципальных
образований Волгоградской области.
Данные о возрастной структуре населения города Камышина
приведены в таблице 2.
Таблица 2 - Показатели, характеризующие возрастную структуру
населения города Камышина
|
Показатели
|
Ед. измерения
|
1989г
|
1995г.
|
2000г
|
2006г
|
2011г
|
|
Число лиц
моложе трудоспособного возраста
|
% к общей
численности населения
|
23,4
|
21,7
|
19,0
|
14,8
|
Нет данных
|
|
Число лиц
трудоспособного возраста (мужчины 16-59 лет, женщины 16-54 лет)
|
____ «» ____
|
59,0
|
58,3
|
58,8
|
62,9
|
Нет данных
|
|
Число лиц
старше трудоспособного возраста
|
____ «» ____
|
17,6
|
20,0
|
22,2
|
22,8
|
Нет данных
|
|
Естественная
убыль (прирост) населения
|
На 1000 чел.
|
2,9
|
- 4,1
|
- 7,6
|
- 6,8
|
Нет данных
|
Согласно таблице 2, наблюдается неуклонный рост
количества пенсионеров и неуклонное снижение количества лиц моложе
трудоспособного возраста. Такая тенденция в будущем приведет к снижению
числа лиц трудоспособного возраста по сравнению с численностью пенсионеров, что
может привести к утрате статуса города как одного из промышленных центров
области. Дополнительные данные по возрастной структуре населения приведены в
таблицах 3 и 4.
Таблица 3 − Возрастной состав детей по городу Камышину
|
Показатели
|
Ед. измерения
|
2007г
|
2008г.
|
2009г
|
2010г
|
2011г
|
|
Число
родившихся
|
Чел.
|
1081
|
1110
|
1130
|
1150
|
Нет данных
|
|
Число детей в
возрасте до 1 года
|
Чел.
|
1081
|
1110
|
1130
|
1150
|
Нет данных
|
|
Число детей
дошкольного возраста
|
Чел.
|
5510
|
5550
|
5570
|
5590
|
Нет данных
|
|
Число детей
школьного возраста
|
Чел.
|
11551
|
11260
|
11005
|
10760
|
Нет данных
|
|
Число детей до
16-летнего возраста
|
Чел.
|
18142
|
17920
|
17705
|
17500
|
Нет данных
|
Таблица 4 - Динамика изменения численности пенсионеров по
городу Камышину (в расчете на 1000 человек населения)
|
Показатели
|
Ед. измерения
|
2004г
|
2005г.
|
2006г
|
2007г
|
2011г
|
|
Число
пенсионеров
|
На 1000 чел.
|
270
|
273
|
279
|
281
|
Нет данных
|
Статистические данные, рассмотренные выше, показывают, что в
городе происходят неблагоприятные изменения численности населения и его
возрастного состава. При наблюдающемся общем уменьшении числа жителей рост
количества людей пенсионного возраста происходит ускоренными темпами, при этом
уменьшается число детей до шестнадцати лет. Начиная с 2010 года, негативные
тенденции постепенно преодолеваются (в частности, благодаря правительственным
мерам по стимулированию рождаемости и по улучшению состояния здравоохранения),
но в целом явления депопуляции и старения населения по-прежнему сохраняются.
Общие выводы о социально-экономическом положении города
Камышина и об особенностях демографической ситуации. В период, предшествующий
перестройке хозяйственного механизма, значение города Камышина для страны
определялось формулой: «Камышин - город текстильщиков». В настоящее время
определяющее значение текстильной промышленности для города утрачено
(по-видимому, безвозвратно). В связи с этим инерционный путь развития города
бесперспективен. Необходимо найти новое главное направление развития города, которое
послужило бы цели его самоидентификации, определило бы «точки роста» и
позволило бы осознать ряд конкурентных преимуществ города по сравнению с
мегаполисами. Без этого нельзя ожидать, что город будет соответствовать миссии:
будет утрачена его привлекательность для молодежи и инвесторов, могут наступить
кризисные явления в промышленности, возрастет уровень безработицы, усилится
отток населения (главным образом, работоспособной и хорошо обученной молодежи)
в более привлекательные регионы.
В таблице 5 приведена сводка состояния и перспектив развития
города Камышина в терминах SWOT-анализа
(Strength-Weakness-Opportunities-Troubles analysis, анализ сильных и слабых
характеристик текущей ситуации, а также благоприятных тенденций и опасностей в
будущем). По его итогам в Камышине есть все необходимые компоненты для развития
на основе имеющихся ресурсов большого агропромышленного комплекса.
Таблица 5 - SWOT-анализ состояния и перспектив развития в
городе Камышине
|
Сильные стороны
|
Слабые стороны
|
|
-
Привлекательное географическое положение (центр европейской части России,
близость к столице и к городам-мегаполисам Волгограду и Саратову, наличие
огромного водного бассейна - Волгоградского водохранилища);
|
- Утрата
«собственного лица» города после утраты роли Камышинского хлопчатобумажного
комбината как градообразующего предприятия; - Низкий уровень заработной
платы, в разы отличающийся от уровня зарплаты в столице и заметно уступающий
уровню зарплат в г.Волгограде, Волжском, Михайловке;
|
|
- Компактность
города, благодаря которой затраты времени на перемещения между местом работы
и жилья невелики; по сравнению с жителями мегаполисов у горожан остается
значительно больше времени на воспитание детей, общение, самообразование,
спорт и отдых; - Отсутствие одной из главных опасностей XXI века - дефицита
пресной воды; - Здоровый климат с большим числом солнечных дней; - Хорошее
состояние воздушного бассейна (благодаря удачному размещению промышленных
предприятий и небольшой доли вредных производств - Развитая образовательная
среда (дошкольное, школьное общеобразовательное и дополнительное,
профессиональное - начальное, среднее профессиональное и высшее); - Богатые
культурные традиции, развитая культурная среда (театр, дворцы культуры,
музеи, картинные галереи, библиотеки); - Хорошие условия для занятий спортом
и реализации здорового образа жизни (наличие пляжей, стадионов, плавательных
бассейнов, спортивных клубов и школ); - Развитая технологическая и -
промышленная среда, наличие резервных мощностей на многих предприятиях; - Достаточно
высокий уровень общей и технической грамотности населения, массовое
использование компьютерной техники и сложных электронных устройств на
производстве и в быту; - Высокий уровень развития телекоммуникаций, систем
стационарной и мобильной связи; - Наличие мощной водной транспортной артерии;
- Мощная торговая сеть; - Трудолюбие населения, традиции возделывания
высококачественных овощей и фруктов на дачных участках; Высокое качество
местных продуктов питания (молоко, мясо и продукты их переработки, плодоовощная
продукция).
|
- Камышина на
экономические и социальные процессы в стране и области и недостаточным
развитием - развлекательного комплекса; - Запущенность ряда районов, ветхость
многих домостроений, износ большей части тротуаров, мусор на улицах; - Низкая
экологическая культура населения, приводящая к засорению прибрежных зон
Волгоградского водохранилища и Камышинского залива, тротуаров, парков и
других зон отдыха; - Элементы деградации ряда показателей, характеризующих
качество жизни (старение и недостаточное обновление состава школьных
учителей, высокая степень износа инженерных сетей, срывы сроков капитальных
ремонтов многоэтажных панельных зданий, ухудшение состояния зеленых
насаждений).
|
|
- Интеграция
города Камышина и Камышинского района, превращение Камышина в индустриальный,
торговый, образовательный и культурный центр Камышинского района; - Хорошие
условия для создания и развития производств, связанных с интеграцией Камышина
и Камышинского района. В частности: производство работ в районе по электрификации,
инженерным сетям, производству строительных материалов, строительству дорог,
информационным сетям; по ремонту и обслуживанию сельскохозяйственной техники;
по механизации и автоматизации ирригационных систем; по созданию аппаратов и
технологий переработки сельскохозяйственной продукции (консервирования,
замораживания, сублимации) и др.; - Возможности развития альтернативной
энергетики (ветровой и солнечной); - Конкурентоспособность местных продуктов
питания, возможность снабжения армии и северных регионов страны экологически
чистыми продуктами; - Возможность повышения эффективности подготовки
квалифицированных кадров для города и района за счет создания
образовательного кластера, объединяющего начальное, среднее специальное и
высшее профессиональное образование; - Благоприятные условия для развития
зон отдыха, курортов, водного спорта и туризма.
|
- Утрата
статуса города областного значения из-за депопуляции и недостаточного
значения города для экономики области; - Углубление необходимости в дотациях к городскому бюджету из-за
недостаточности доходной части бюджета и из-за роста числа пенсионеров и
безработных; - Нарастание
социальной напряже-нности из-за низкого уровня заработной платы; - Ухудшение кадрового потенциала города
из-за оттока способной молодежи в крупные города с более престижной жизнью и
более высоким уровнем зарплаты; - Снижение активности населения в области создания новых
производств и малых предприятий - социальное и гражданское безразличие, отсутствие стремления к
карьерному росту у заметной части населения, опасность алкоголизации; - Увеличение частоты и продолжительности
аварий инженерных сетей в связи с их износом; - Загрязнение вод Волгоградского во-дохранилища и Камышинского
залива, приводящее к опасному для здоровья ухудшению качества питьевой воды; - Деградация зеленой зоны ГНУ
Нижневолжская станция по селекции древесных пород (городское название
«Питомник»); - Перегруженность
транспортной арте-рии, соединяющей северный и южный районы города, рост
частоты и продолжительности пробок в районе бухты и Бородинского моста.
|
1.4
Корреляционный анализ
Корреляционный анализ - метод обработки статистических
данных, с помощью которого измеряется теснота связи между двумя или более
переменными. Корреляционный анализ тесно связан с регрессионным анализом (также
часто встречается термин «корреляционно-регрессионный анализ», который является
более общим статистическим понятием), с его помощью определяют необходимость
включения тех или иных факторов в уравнение множественной регрессии, а также
оценивают полученное уравнение регрессии на соответствие выявленным связям
(используя коэффициент детерминации).[3]
Термин "корреляция" означает "связь". В
эконометрике этот термин обычно используется в сочетании "коэффициенты
корреляции". Рассмотрим линейный и непараметрические парные коэффициенты
корреляции.
Обсудим способы измерения связи между двумя случайными
переменными. Пусть исходными данными является набор случайных векторов 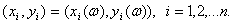 Выборочным коэффициентом корреляции,
более подробно, выборочным линейным парным коэффициентом корреляции К. Пирсона,
как известно, называется число
Выборочным коэффициентом корреляции,
более подробно, выборочным линейным парным коэффициентом корреляции К. Пирсона,
как известно, называется число
 (2)
(2)
Если rn = 1, то 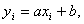 причем a>0. Если же rn = - 1, то
причем a>0. Если же rn = - 1, то 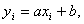 причем a<0. Таким образом,
близость коэффициента корреляции к 1 (по абсолютной величине) говорит о
достаточно тесной линейной связи.[4]
причем a<0. Таким образом,
близость коэффициента корреляции к 1 (по абсолютной величине) говорит о
достаточно тесной линейной связи.[4]
Выявить наличие или отсутствие корреляции между двумя величинами
можно путем визуального анализа полей корреляции и оценкой величины выборочного
коэффициента корреляции.
Для независимых случайных величин коэффициент корреляции равен
нулю, но он может быть равен нулю для некоторых зависимых величин, которые при
этом называются некоррелированными. Коэффициент корреляции характеризует не
всякую зависимость, а только линейную. Если случайные величины x и y связаны точной
функциональной линейной зависимостью 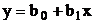 , то
, то 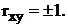 . В общем случае, когда величины связаны
произвольной стохастической зависимостью, коэффициент корреляции может иметь
значение в пределах
. В общем случае, когда величины связаны
произвольной стохастической зависимостью, коэффициент корреляции может иметь
значение в пределах 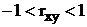 .
.
1.5
Регрессионный анализ
Регрессионный анализ - это статистический метод исследования
зависимости случайной величины у от переменных (аргументов) хj
(j = 1, 2,..., k), рассматриваемых в регрессионном анализе как
неслучайные величины независимо от истинного закона распределения xj.
Обычно предполагается, что случайная величина у имеет
нормальный закон распределения с условным математическим ожиданием 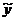 = φ(x1,..., хk), являющимся
функцией от аргументов хj и с постоянной, не зависящей от
аргументов дисперсией σ2.
= φ(x1,..., хk), являющимся
функцией от аргументов хj и с постоянной, не зависящей от
аргументов дисперсией σ2.
Для проведения регрессионного анализа из (k + 1)-мерной генеральной совокупности (у, x1, х2,..., хj,..., хk) берется выборка объемом n, и каждое i-е наблюдение (объект) характеризуется
значениями переменных (уi, xi1, хi2,..., хij,..., xik), где хij - значение j-й переменной для i-го наблюдения (i = 1, 2,..., n), уi -
значение результативного признака для i-го наблюдения.
Наиболее часто используемая множественная линейная модель
регрессионного анализа имеет вид
 (3)
(3)
где βj - параметры
регрессионной модели;
εj - случайные ошибки
наблюдения, не зависимые друг от друга, имеют нулевую среднюю и дисперсию σ2.
Отметим, что модель (3) справедлива для всех i = 1,2,..., n,
линейна относительно неизвестных параметров β0, β1,…, βj, …, βk и аргументов.
Как следует из (3) коэффициент регрессии Bj показывает, на
какую величину в среднем изменится результативный признак у, если переменную хj
увеличить на единицу измерения, т.е. является нормативным коэффициентом.
В матричной форме регрессионная модель имеет вид
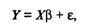 (4)
(4)
где Y - случайный вектор-столбец размерности п
х 1 наблюдаемых значений результативного признака (у1, у2,....
уn); Х- матрица размерности п х (k + 1) наблюдаемых
значений аргументов, элемент матрицы х,, рассматривается как неслучайная
величина (i = 1, 2,..., n; j=0,1,..., k; x0i, = 1); β - вектор-столбец размерности (k + 1) х 1 неизвестных,
подлежащих оценке параметров модели (коэффициентов регрессии); ε - случайный вектор-столбец размерности п х 1 ошибок
наблюдений (остатков). Компоненты вектора εi не зависимы друг от
друга, имеют нормальный закон распределения с нулевым математическим ожиданием
(Mεi = 0) и неизвестной
постоянной σ2 (Dεi = σ2).
На практике рекомендуется, чтобы значение п превышало
k не менее чем в три раза.
В модели (4)
 (5)
(5)
В первом столбце матрицы Х указываются единицы при
наличии свободного члена в модели (3). Здесь предполагается, что существует
переменная x0, которая во всех наблюдениях принимает
значения, равные единице.
Основная задача регрессионного анализа заключается в
нахождении по выборке объемом п оценки неизвестных коэффициентов
регрессии β0, β1, …, βk модели (3) или вектора β в (4).
Так как в регрессионном анализе хj
рассматриваются как неслучайные величины, a Mεi = 0, то согласно (3) уравнение регрессии имеет
вид
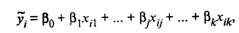 (6)
(6)
для всех i = 1, 2,..., п, или в матричной форме:
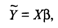 (7)
(7)
где 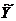 - вектор-столбец с элементами
- вектор-столбец с элементами 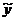 1...,
1..., 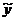 i,...,
i,..., 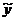 n.
n.
Для оценки вектора-столбца β наиболее часто используют метод наименьших
квадратов, согласно которому в качестве оценки принимают вектор-столбец b,
который минимизирует сумму квадратов отклонений наблюдаемых значений уi от
модельных значений 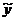 i, т.е. квадратичную форму:
i, т.е. квадратичную форму:
 (8)
(8)
где символом «Т» обозначена транспонированная матрица.
Дифференцируя, с учетом (7) и (6), квадратичную форму Q по β0, β1, …, βk и приравнивая частные производные к нулю,
получим систему нормальных уравнений
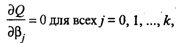 (9)
(9)
решая которую получим вектор-столбец оценок b, где b
= (b0, b1,..., bk)T. Согласно методу
наименьших квадратов, вектор-столбец оценок коэффициентов регрессии получается
по формуле
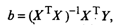 (10)
(10)

ХT -
транспонированная матрица X;
(ХTХ)-1 - матрица, обратная матрице ХTХ.
Зная вектор-столбец b оценок коэффициентов регрессии,
найдем оценку  уравнения регрессии
уравнения регрессии
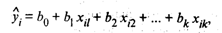 (11)
(11)
или в матричном виде:
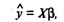 (12)
(12)
 [9]
[9]
1.6
Множественная нелинейная регрессия
Несколько явлений могут быть соединены между собой
нелинейными соотношениями. В этом случае для описания зависимостей следует
воспользоваться множественной нелинейной регрессией. Здесь также различают
множественную нелинейную регрессию первого и второго классов.
Исходя из логических соображений процедура построения
уравнения множественной нелинейной регрессии должна быть аналогична процедуре
определения простой нелинейной регрессии. Рассмотрим следующий пример
квазилинейной регрессии, ограничившись двумя объясняющими переменными:
 (13)
(13)
Если профессионально-теоретический анализ экономического
явления позволяет функции от объясняющих переменных представить в виде
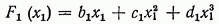 (14)
(14)
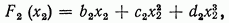 (15)
(15)
то зависимость (13) выражается так:
 (16)
(16)
Применяя метод наименьших квадратов, находят параметры a, b1…d1 Но в этом случае
уравнение (16) можно относительно просто свести к линейному виду, переобозначив
переменные. Ограничившись только этим указанием, не будем записывать уравнение
в линейной форме.
Из функций множественной нелинейной регрессии второго класса,
которые допускают линеаризацию, представляют большой экономический интерес
производственные функции. Понятие производственной функции трудно описать вербально.
Производственные функции вначале использовались для исследования
причинно-следственных отношений в производственной сфере. Затем они стали очень
популярным средством анализа экономических явлений, что объясняется как
простотой вида этих функций, так и широкими возможностями их применения в самых
разных ситуациях.
Исторически первой производственной функцией явилась
степенная функция Кобба-Дугласа
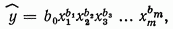 (17)
(17)
где у обозначает выпуск продукции, национальный доход и т. xi- влияющие факторы; b0- нормировочный
множитель; b1,...bm- коэффициенты эластичности. Если ограничиться рассмотрением
товарной продукции y затратами труда x1 и основными фондами x2, то (17) примет вид:
 (18)
(18)
Логарифмируя обе части равенства, получим
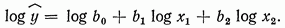 (19)
(19)
Из (19) легко найти оценки параметров. Если вводится требование  (линейная гомотетичность), т. е. b1=1-b2 то уравнение (18) приобретает вид:
(линейная гомотетичность), т. е. b1=1-b2 то уравнение (18) приобретает вид:
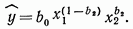 (20)
(20)
Путем простого преобразования можно получить
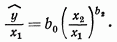 (21)
(21)
Записывая (21) в логарифмическом виде и применяя
преобразования, находят b0 и b2
Далее был разработан класс линейно-гомотетичных функций: CES (Constant Elasticity of Substitution) - функция с постоянной
эластичностью замены и VES (Variable Elasticity of Substitution) - функция с
изменяющейся во времени эластичностью замены. Этот класс функций дает
возможность моделировать изменение эластичности, замены факторов производства с
изменением уровня выпуска:
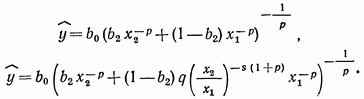 (22)
(22)
(23)
Исходя из дифференциальных уравнений этих функций можно
определить p,q и s.Но часто они
устанавливаются в соответствии с экономии требованиями, так что из уравнений
(22) и (23), так же как из (21), находят только параметры регрессии b0и b2.
Наконец, укажем еще одну производственную функцию для
описания научно-технического прогресса;
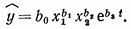 (23)
(23)
В этом соотношении научно-технический прогресс
рассматривается как экспоненциальная функция от времени, показатель b3 характеризует темп
научно-технического прогресса. Насколько эта функция имеет экономическое
содержание и соответствует эмпирическим данным, должно быть проверено обширными
исследованиями. Вообще нужно отметить, что множественная нелинейная регрессия
лучше отражает многообразие связей в экономике. Применение ЭВМ снимает все
вычислительные проблемы, которые раньше были препятствием для создания
нелинейных многофакторных моделей. [16]
2.
Выбор средств реализации
2.1
Выбор и обоснование программной среды реализации
Так как задача подразумевается обработку статистических
данных относительно не большего объема до 20 тысяч записей,то на первом этапе
логично использовать электронными таблицами. Как наиболее знакомую и изученную
я выбрал Microsoft Office Excel.
Excel - популярная офисная программа от Microsoft.
Возможности Excel весьма велики, поэтому их не стоит игнорировать не только
рядовым трейдерам и инвесторам, но и более искушенным в анализе данных
специалистам Excel может стать очень полезным инструментом для изучения рынка и
повседневной торговой деятельности, если знать, на что он способен и иметь
практические навыки его использования.
Хоть Excel и уступает по мощности специальным пакетам
анализа, таким как MATLAB или Statistica, у него есть своя ниша и определенные
преимущества.
К их числу можно отнести широкую распространенность и
доступность самой программы, интуитивно понятный интерфейс, русскоязычный
интерфейс. пользовательские функции, можно относительно легко решить практически
любую вычислительную задачу. При проведении сложного статистического или
инженерного анализа можно упростить процесс и сэкономить время, используя
надстройку "Пакет анализа". Чтобы выполнить анализ с помощью этого
пакета, следует указать входные данные и выбрать параметры. Расчет будет
выполнен с использованием подходящей статистической или инженерной
макрофункции, а результат будет помещен в выходной диапазон. Некоторые
инструменты позволяют представить результаты анализа в графическом виде.
В Excel имеется довольно много штатных статистических
функций. Наиболее актуальные для анализа данных:
- ДИСП() - дисперсия;
- КОВАР() - ковариация;
- КОРРЕЛ() - корреляция;
- ЛОГНОРМРАСП() -
логнормальное распределение;
- МАКС() - максимум;
- МЕДИАНА() - медиана;
- МИН() - минимум;
- МОДА() - мода;
- НОРМРАСП() - нормальное
распределение;
- СКОС() - коэффициент
асимметрии;
- СРГЕОМ() - среднее
геометрическое;
- СРЗНАЧ() - среднее
арифметическое (доходность);
- СТАНДОТКЛОН() -
стандартное отклонение (волатильность);
- ТЕНДЕНЦИЯ() - линейный
тренд;
- ЭКСЦЕСС() - коэффициент
эксцесса.
- Корреляция;
- Ковариация;
- Описательная статистика;
- Экспоненциальное
сглаживание;
- Гистограмма;
- Скользящее среднее;
- Генерация случайных
чисел;
- Регрессия.
А вот на втором этапе - моделировании нужно использовать
специализированные математические пакеты.
Основное отличие Mathcad от аналогичных программ - это
графический, а не текстовый режим ввода выражений. Для набора команд, функций,
формул можно использовать как клавиатуру, так и кнопки на многочисленных
специальных панелях инструментов. В любом случае - формулы будут иметь
привычный, аналогичный книжному, вид. Вычисления с введенными формулами
осуществляются по желанию пользователя или мгновенно, одновременно с набором,
либо по команде. Обычные формулы вычисляются слева направо и сверху вниз
(подобно чтению текста). Любые переменные, формулы, параметры можно изменять,
наблюдая воочию соответствующие изменения результата. Это дает возможность
быстро отладить модель.- система компьютерной алгебры из класса систем
автоматизированного проектирования, ориентированная на подготовку интерактивных
документов с вычислениями и визуальным сопровождением, отличается легкостью
использования и применения для коллективной работы
Разработчики Mathcad сделали ставку на расширение системы в
соответствии с потребностями пользователя. Для этого назначены дополнительные
библиотеки и пакеты расширения, которые можно приобрести отдельно и которые
имеют дополнительные функции, встраиваемые в систему при установке, а также
электронные книги с описанием методов решения специфических задач, с примерами
действующих алгоритмов и документов, которые можно использовать непосредственно
в собственных расчетах. Кроме того, в случае необходимости и при условии
наличия навыков программирования в C, есть возможность создания собственных
функций и их прикрепления к ядру системы через механизм DLL.содержит сотни
операторов и встроенных функций для решения различных технических задач.
Программа позволяет выполнять численные и символьные вычисления, производить
операции со скалярными величинами, векторами и матрицами, автоматически
переводить одни единицы измерения в другие.
Среди возможностей Mathcad можно выделить:
- Решение дифференциальных уравнений, в том
числе и численными методами
- Построение двумерных и трёхмерных графиков
функций (в разных системах координат, контурные, векторные и т. д.)
- Использование греческого алфавита как в
уравнениях, так и в тексте
- Выполнение вычислений в символьном режиме
- Выполнение операций с векторами и
матрицами
- Символьное решение систем уравнений
- Аппроксимация кривых
- Выполнение подпрограмм
- Поиск корней многочленов и функций
- Проведение статистических расчётов и
работа с распределением вероятностей
- Поиск собственных чисел и векторов
- Вычисления с единицами измерения
- Интеграция с САПР-системами, использование
результатов вычислений в качестве управляющих параметров
В частности в Mathcad 14 добавились такие инструменты решения
дифференциальных уравнений,- по метод Адамса, BDF и комбинированным
Adams/BDF[10]
3.
Анализ данных
3.1
Сбор данных
Анализ сделок с недвижимостью проводился,на основании данных
представленных на сайте Росстата «Мониторинг сделок с недвижимостью»[5]. В базе
данных Росстата зарегистрировано 21575 сделок с жилой недвижимостью заключенных
с 1996 года по февраль 2013 года заключенных в городе Камышин. После проверки
часть данных пришлось отбраковать, так как они являлись дублирующими записями.
Количество сделок занесенных в базу за 1996-2005 года
является не достаточным для получения достоверных оценок и дальнейшего
построение на их основе модели прогнозирования. Поэтому для обработки были
использованы только записи за 2006-2013года.
Данные о миграция населения были взяты с портала «Единая
межведомственная информационно-статистическая система»[6] по запросам:
«Миграционный прирост населения по городам с числом жителей
100 тыс. человек и более»
«Выбыло населения по городам с числом жителей 100 тыс.
человек и более»
«Прибыло населения по городам с числом жителей 100 тыс.
человек и более»
А том числе с портала ЕМИСС был взят такой показатель как
«Индексы потребительских цен на товары и услуги» как в помесячном разрезе,так и
годовом.
Научным руководителем была предоставлена статистическая
информация по различным аспектам экономической, финансовой и социальной сфере
жизни -деятельности города Камышина.
Такой показатель как Среднемесячная заработная плата
работников организаций был взят из отчетов Главы городского округа, которые
находятся на официальном сайте администрации города Камышин[7]
3.2
Предварительная обработка и составление сводных таблиц
Записи на сайте Росстата в разделе-«Мониторинг сделок с
недвижимостью»,включают большое число атрибутов:
- Номер объекта
- Вид объекта недвижимости
- Кадастровый квартал
- Площадь, кв.м.
- Тип сделки
- Дата сделки
- Дата регистрации/ предложения
- Цена сделки/ предложения, руб.
- Удельная цена сделки/ предложения,
руб./кв.м.
- Доля в праве на объект недвижимости
- Назначение/Категория земель
- Разрешенное использование
- Количество надземных этажей
- Подземная этажность
- Ограничения (обременения) вещных прав
- Жилая площадь, кв.м.
- Наименование
- ОКАТО
- Субъект
- Район
- Город
- Населенный пункт
- Улица
- Номер этажа
- Количество объектов в сделке
- Источник данных
- Организация
- Материал наружных стен
- Год ввода в эксплуатацию
- Год завершения строительства
- Вид жилого помещения в многоквартирном
доме
- Тип информации
- Идентификатор записи
Требуется выбрать необходимые нам данные и провести
дополнительную проверку выбранных значений. Из всех граф представленных на
портале для исследования достаточно всего 5:
- Дата сделки
- Цена сделки/ предложения, руб.
- Удельная цена сделки/ предложения,
руб./кв.м.
- Наименование
- Площадь, кв.м.
При проверке на аномальный уровень оставшихся данных были
исправлены только несколько записей являющиеся примером ошибки первого рода.
Проверка остальных ошибок затруднена так неизвестно ошибкой какого рода она
является.
Под аномальным уровнем понимается отдельное значение уровня
временного ряда, которое не отвечает потенциальным возможностям исследуемой
экономической системы и которое, оставаясь в качестве уровня ряда, оказывает
существенное влияние на значения основных характеристик временного ряда, в том
числе на соответствующую трендовую модель. Причинами аномальных наблюдений
могут быть ошибки технического порядка, или ошибки первого рода: ошибки
при агрегировании и дезагрегировании показателей, при передаче информации и
другие технические причины. Ошибки первого рода подлежат выявлению и
устранению. Кроме того, аномальные уровни во временных рядах могут возникать
из-за воздействия факторов, имеющих объективный характер, но проявляющихся
эпизодически, очень редко - ошибки второго рода; они
устранению не подлежат.[8]
Проведя первичную обработку сделок с недвижимостью, оценим
изменение цен визуально на графике, с линий тренда представленном в графическом
приложении рисунок 1.Можно отметить постепенный рост средних цен за один
квадратный метр жилой площади, начиная с 2006,и их фиксацию на уровне в
22000-23000 тысячи за квадратный метр. Но для объективного сравнения уровня
цен, необходимо учитывать инфляцию. Использую сведения о помесячной инфляции и
простейший алгоритм, реализованный на внутреннем языке MathCAD, приведем цены к базовым
значениям относительно выбранных годов,2006 и 2013.Индексы цен представлены в
таблице 6:
Таблица 6 - Изменение индекса цен по месяцам за 2006-2013
года.
|
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
2012
|
2013
|
|
январь
|
101.54
|
100.73
|
101.02
|
101.73
|
100.47
|
101.56
|
100.59
|
100.43
|
|
февраль
|
101.45
|
100.47
|
100.99
|
101.91
|
100.32
|
100.51
|
100.46
|
100.51
|
|
март
|
100.14
|
100.4
|
101.51
|
101.4
|
100.52
|
101.06
|
100.61
|
100.21
|
|
апрель
|
100.14
|
100.11
|
101.57
|
100.58
|
100.07
|
100.23
|
100.23
|
100.23
|
|
май
|
100.27
|
100.01
|
101.25
|
100.43
|
100.21
|
100.09
|
100
|
100.19
|
|
июнь
|
99.84
|
100.35
|
100.9
|
99.75
|
100.29
|
100.37
|
100.16
|
99.95
|
|
июль
|
100.84
|
101.13
|
101.1
|
100.37
|
100.47
|
100.23
|
100.42
|
100.45
|
|
август
|
100.65
|
102.26
|
101.19
|
100.48
|
100.78
|
100.36
|
100.5
|
100.48
|
|
сентябрь
|
100.61
|
101.67
|
101.38
|
100.64
|
101.19
|
100.38
|
100.5
|
100.87
|
|
октябрь
|
100.61
|
102.03
|
101.04
|
100.33
|
100.6
|
100.45
|
100.26
|
100.5
|
|
ноябрь
|
100.87
|
101.12
|
100.67
|
100.32
|
100.7
|
100.04
|
100.16
|
100.46
|
|
декабрь
|
100.38
|
100.48
|
100.34
|
100.23
|
100.53
|
100.42
|
100.33
|
100.19
|
На графика цен получившихся после индексации рисунок 2 и
рисунок 4 графического приложения, становится заметно падения среднего уровня
цен. Особенно хорошо это заметно в ценах 2006 года.
После подтверждения предположения о том, что средний уровень
цен на квадратный метр падает переходим к следующему пункту из списка целей:
- Проверить существование связи между ценой на
недвижимость и миграцией населения.
3.3
Проверка существования связи между ценой на недвижимость и миграцией населения
Для этого найдем основные статистические показатели по годам
для всех трех, абсолютного (текущего) и относительных(индексированных) цен.
Результатом проведенной статистической оценки собранных
таблица показателей цены на квадратный метр на недвижимость по годам,
представленных в приложении А на странице 48-49.
Составим сводную таблицу графами которой будут:
- год
- Стоимость одного квадратного метра в ценах
текущего года
- Стоимость одного квадратного метра в ценах 2013
года
- Стоимость одного квадратного метра в ценах 2006
года
- Число сделок
- Убыло
- Прибыло
- Средняя заработная плата
- Квартплата
Сама таблица находится в приложении А на странице 50.
Для этой таблицы проведем корреляционный анализ по сводной
таблице. Результаты анализа корреляционной таблицы показали с сильную связь
между числом сделок и миграцией населения в обоих направлениях. Для
прибывающего населения коэффициент корреляции составил 0.902175, для уезжающих
- 0.81374.
3.4
Формализация связи
Для установления вида и параметров уравнения связывающего
миграцию населения и количество сделок с недвижимостью применим регрессионный
анализ. Для этого проверим наиболее часто применимые регрессионные модели, в
первую очередь логарифмическую, являющуюся линеаризация степенной функции,
которая широко используется в эконометрических исследованиях при изучении
спроса [15].
Проверка полинома второй степени.
Оценка уравнения регрессии.
Определим вектор оценок коэффициентов регрессии. Согласно
методу наименьших квадратов, вектор s получается из выражения:
= (XTX)-1XTY
(24)
Матрица X представлена в таблице 7.
Таблица 7 - Матрица значений X
|
1
|
5.13
|
6.51
|
26.29
|
42.43
|
33.4
|
|
1
|
4.72
|
5.87
|
22.28
|
34.41
|
27.69
|
|
1
|
6.13
|
6.96
|
37.61
|
48.5
|
42.71
|
|
1
|
4.79
|
5.74
|
22.94
|
32.92
|
27.48
|
|
1
|
5.88
|
6.84
|
34.57
|
46.73
|
40.19
|
|
1
|
4.34
|
5.69
|
18.84
|
32.4
|
24.7
|
|
1
|
5.84
|
6.79
|
34.09
|
46.11
|
39.65
|
|
1
|
5.08
|
5.87
|
25.8
|
34.5
|
29.84
|
|
1
|
6.51
|
6.97
|
42.39
|
48.61
|
45.39
|
|
1
|
5.57
|
6.09
|
31.06
|
37.11
|
33.95
|
|
1
|
6.85
|
7.19
|
46.92
|
51.7
|
49.25
|
|
1
|
5.65
|
6.39
|
31.94
|
40.86
|
36.12
|
|
1
|
6.89
|
7.49
|
47.43
|
56.11
|
51.59
|
|
1
|
4.89
|
5.81
|
23.94
|
33.74
|
28.42
|
Матрица Y представлена в таблице 8.
Таблица 8 - Матрица значений Y
|
27
|
|
17
|
|
270
|
|
73
|
|
763
|
|
408
|
|
709
|
|
764
|
|
1216
|
|
1018
|
|
1315
|
|
1178
|
|
1437
|
|
301
|
Матрица XT представлена в таблице 9.
Таблица 9 - Транспонированная матрица значений X
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
5.13
|
4.72
|
6.13
|
4.79
|
5.88
|
4.34
|
5.84
|
5.08
|
6.51
|
5.57
|
6.85
|
5.65
|
6.89
|
4.89
|
5.87
|
6.96
|
5.74
|
6.84
|
5.69
|
6.79
|
5.87
|
6.97
|
6.09
|
7.19
|
6.39
|
7.49
|
5.81
|
|
26.29
|
22.28
|
37.61
|
22.94
|
34.57
|
18.84
|
34.09
|
25.8
|
42.39
|
31.06
|
46.92
|
31.94
|
47.43
|
23.94
|
|
42.43
|
34.41
|
48.5
|
32.92
|
46.73
|
32.4
|
46.11
|
34.5
|
48.61
|
37.11
|
51.7
|
40.86
|
56.11
|
33.74
|
|
33.4
|
27.69
|
42.71
|
27.48
|
40.19
|
24.7
|
39.65
|
29.84
|
45.39
|
33.95
|
49.25
|
36.12
|
51.59
|
28.42
|
Умножаем матрицы, (XTX),результат представлен в
таблице 10.
Таблица 10 - Умножение транспонированной матрицы значений X
на матрицу значений X
|
14
|
78.27
|
90.21
|
446.1
|
586.13
|
510.38
|
|
78.27
|
446.07
|
510.32
|
2590.33
|
3354.75
|
2942.6
|
|
90.21
|
510.32
|
586
|
2942.36
|
3838.24
|
3354.37
|
|
446.1
|
2590.33
|
2942.36
|
15312.13
|
19562.35
|
17278.33
|
|
586.13
|
3354.75
|
3838.24
|
19562.35
|
25339.4
|
22224.14
|
|
510.38
|
2942.6
|
3354.37
|
17278.33
|
22224.14
|
19561.76
|
В матрице, (XTX) число 14, лежащее на пересечении
1-й строки и 1-го столбца, получено как сумма произведений элементов 1-й строки
матрицы XT и 1-го столбца матрицы X
Умножаем матрицы, (XTY),результат представлен в
таблице 11.
Таблица 11 - Умножение транспонированной матрицы значений X
на матрицу значений Y
|
12396
|
|
72436.05
|
|
81860.36
|
|
430723.84
|
|
544989.05
|
|
483778.15
|
Находим обратную матрицу (XTX)-1
результат представлен в таблице 12.
Таблица 12 - Значения транспонированной матрицы (XTX)-1
|
5555.96
|
1317.41
|
-2867.47
|
106.99
|
390.45
|
-389.52
|
|
1317.41
|
496.44
|
-838.98
|
52.02
|
136.81
|
-166.56
|
|
-2867.47
|
-838.98
|
1617.75
|
-78.17
|
-239.79
|
265.09
|
|
106.99
|
52.02
|
-78.17
|
10.1
|
17.02
|
-25.46
|
|
390.45
|
136.81
|
-239.79
|
17.02
|
40.41
|
-50.59
|
|
-389.52
|
-166.56
|
265.09
|
-25.46
|
-50.59
|
69.72
|
Вектор оценок коэффициентов регрессии равен (25).Результат
данной операции представлен в таблице 13.
Y(X) = (XTX)-1XTY =
(25)
Таблица 13 - Значения матрицы Y(X)
|
-695.09
|
|
-1668.76
|
|
1774.46
|
|
-378.76
|
|
-606.67
|
|
1013.4
|
Уравнение регрессии (оценка уравнения регрессии)
Y = -695.09-1668.76X1 + 1774.46X2-378.76X3-606.67X4
+ 1013.4X5 (26)
Матрица парных коэффициентов корреляции.Число наблюдений n =
14. Число независимых переменных в модели равно 5, а число регрессоров с учетом
единичного вектора равно числу неизвестных коэффициентов. С учетом признака Y,
размерность матрицы становится равным 7. Матрица, независимых переменных Х
имеет размерность (14 х 7).
Матрица, составленная из Y и X, представлена в таблице 14.
Таблица 14 - Таблица значений Y и X
|
1
|
427
|
5.13
|
6.51
|
26.29
|
42.43
|
33.4
|
|
1
|
817
|
4.72
|
5.87
|
22.28
|
34.41
|
27.69
|
|
1
|
1270
|
6.13
|
6.96
|
37.61
|
48.5
|
42.71
|
|
1
|
773
|
4.79
|
5.74
|
22.94
|
32.92
|
27.48
|
|
1
|
763
|
5.88
|
6.84
|
34.57
|
46.73
|
40.19
|
|
1
|
408
|
4.34
|
5.69
|
18.84
|
32.4
|
24.7
|
|
1
|
709
|
5.84
|
6.79
|
34.09
|
46.11
|
39.65
|
|
1
|
764
|
5.08
|
5.87
|
25.8
|
34.5
|
29.84
|
|
1
|
1216
|
6.51
|
6.97
|
42.39
|
48.61
|
45.39
|
|
1
|
1018
|
5.57
|
6.09
|
31.06
|
37.11
|
33.95
|
|
1
|
1315
|
6.85
|
7.19
|
46.92
|
51.7
|
49.25
|
|
1
|
1178
|
5.65
|
6.39
|
31.94
|
40.86
|
36.12
|
|
1
|
1437
|
6.89
|
7.49
|
47.43
|
56.11
|
51.59
|
|
1
|
301
|
4.89
|
5.81
|
23.94
|
33.74
|
28.42
|
Транспонированная матрица представлена в таблице 15.
Таблица 15- Транспонированная матрица значений Y и X
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
427
|
817
|
1270
|
773
|
763
|
408
|
709
|
764
|
1216
|
1018
|
1315
|
1178
|
1437
|
301
|
|
5.13
|
4.72
|
6.13
|
4.79
|
5.88
|
4.34
|
5.84
|
5.08
|
6.51
|
5.57
|
6.85
|
5.65
|
6.89
|
4.89
|
|
6.51
|
5.87
|
6.96
|
5.74
|
6.84
|
5.69
|
6.79
|
5.87
|
6.97
|
6.09
|
7.19
|
6.39
|
7.49
|
5.81
|
|
26.29
|
22.28
|
37.61
|
22.94
|
34.57
|
18.84
|
34.09
|
25.8
|
42.39
|
31.06
|
46.92
|
31.94
|
47.43
|
23.94
|
|
42.43
|
34.41
|
48.5
|
32.92
|
46.73
|
32.4
|
46.11
|
34.5
|
48.61
|
37.11
|
51.7
|
40.86
|
56.11
|
33.74
|
|
33.4
|
27.69
|
42.71
|
27.48
|
40.19
|
24.7
|
39.65
|
29.84
|
45.39
|
33.95
|
49.25
|
36.12
|
28.42
|
Матрица ATA представлена в таблице 16.
Таблица 16 - Умножение транспонированной матрицы значений ATна
матрицу значений A
|
14
|
12396
|
78.27
|
90.21
|
446.1
|
586.13
|
510.38
|
|
12396
|
12682716
|
72436.05
|
81860.36
|
430723.84
|
544989.05
|
483778.15
|
|
78.27
|
72436.05
|
446.07
|
510.32
|
2590.33
|
3354.75
|
2942.6
|
|
90.21
|
81860.36
|
510.32
|
586
|
2942.36
|
3838.24
|
3354.37
|
|
446.1
|
430723.84
|
2590.33
|
2942.36
|
15312.13
|
19562.35
|
17278.33
|
|
586.13
|
544989.05
|
3354.75
|
3838.24
|
19562.35
|
25339.4
|
22224.14
|
|
510.38
|
483778.15
|
2942.6
|
3354.37
|
17278.33
|
22224.14
|
19561.76
|
Полученная матрица имеет следующее соответствие
представленные в таблице 17.
Таблица 17 - Соответствие смысловых значений таблицы 16
|
∑n
|
∑y
|
∑x1
|
∑x2
|
∑x3
|
∑x4
|
∑x5
|
|
∑y
|
∑y2
|
∑x1
y
|
∑x2
y
|
∑x3
y
|
∑x4
y
|
∑x5
y
|
|
∑x1
|
∑yx1
|
∑x1
2
|
∑x2
x1
|
∑x3
x1
|
∑x4
x1
|
∑x5
x1
|
|
∑x2
|
∑yx2
|
∑x1
x2
|
∑x2
2
|
∑x3
x2
|
∑x4
x2
|
∑x5
x2
|
|
∑x3
|
∑yx3
|
∑x1
x3
|
∑x2
x3
|
∑x3
2
|
∑x4
x3
|
∑x5
x3
|
|
∑x4
|
∑yx4
|
∑x1
x4
|
∑x2
x4
|
∑x3
x4
|
∑x4
2
|
∑x5
x4
|
|
∑x5
|
∑yx5
|
∑x1
x5
|
∑x2
x5
|
∑x3
x5
|
∑x4
x5
|
∑x5
2
|
Вычисление парных коэффициентов корреляции представлены в
таблице 18 и 19.
Таблица 18 - Вспомогательные значения необходимые для
вычисления коэффициентов корреляции Y и X
|
Признаки
x и y
|
∑xi
|
∑yi∑xiyi
|
|
|
|
|
|
Для
y и x1
|
78.27
|
5.59
|
12396
|
885.43
|
72436.05
|
5174
|
|
Для
y и x2
|
90.21
|
6.44
|
12396
|
885.43
|
81860.36
|
5847.17
|
|
Для
y и x3
|
446.1
|
31.86
|
12396
|
885.43
|
430723.84
|
30765.99
|
|
Для
y и x4
|
586.13
|
41.87
|
12396
|
885.43
|
544989.05
|
38927.79
|
|
Для
y и x5
|
510.38
|
36.46
|
12396
|
885.43
|
483778.15
|
34555.58
|
|
Для
x1 и x2
|
90.21
|
6.44
|
78.27
|
5.59
|
510.32
|
36.45
|
|
Для
x1 и x3
|
446.1
|
31.86
|
78.27
|
5.59
|
2590.33
|
185.02
|
|
Для
x1 и x4
|
586.13
|
41.87
|
78.27
|
5.59
|
3354.75
|
239.62
|
|
Для
x1 и x5
|
510.38
|
36.46
|
78.27
|
5.59
|
2942.6
|
210.19
|
|
Для
x2 и x3
|
446.1
|
31.86
|
90.21
|
6.44
|
2942.36
|
210.17
|
|
Для
x2 и x4
|
586.13
|
41.87
|
90.21
|
6.44
|
3838.24
|
274.16
|
|
Для
x2 и x5
|
510.38
|
36.46
|
90.21
|
6.44
|
3354.37
|
239.6
|
|
Для
x3 и x4
|
586.13
|
41.87
|
446.1
|
31.86
|
19562.35
|
1397.31
|
|
Для
x3 и x5
|
510.38
|
36.46
|
446.1
|
31.86
|
17278.33
|
1234.17
|
|
Для
x4 и x5
|
510.38
|
36.46
|
586.13
|
41.87
|
22224.14
|
1587.44
|
Таблица 19 - Вспомогательные значения необходимые для
вычисления коэффициентов корреляции Y и X
|
Признаки
x и y
|
|
|
|
|
|
|
Для
y и x1
|
0.61
|
121924.53
|
0.78
|
349.18
|
0.82
|
|
Для
y и x2
|
0.34
|
121924.53
|
0.58
|
349.18
|
0.7
|
|
Для
y и x3
|
78.39
|
121924.53
|
8.85
|
349.18
|
0.83
|
|
Для
y и x4
|
57.16
|
121924.53
|
7.56
|
349.18
|
0.7
|
|
Для
y и x5
|
68.25
|
121924.53
|
8.26
|
349.18
|
0.79
|
|
Для
x1 и x2
|
0.34
|
0.61
|
0.58
|
0.78
|
0.94
|
|
Для
x1 и x3
|
78.39
|
0.61
|
8.85
|
0.78
|
1
|
|
Для
x1 и x4
|
57.16
|
0.61
|
7.56
|
0.78
|
0.94
|
|
Для
x1 и x5
|
68.25
|
0.61
|
8.26
|
0.78
|
0.99
|
|
Для
x2 и x3
|
78.39
|
0.34
|
8.85
|
0.58
|
0.94
|
|
Для
x2 и x4
|
57.16
|
0.34
|
7.56
|
0.58
|
1
|
|
Для
x2 и x5
|
68.25
|
0.34
|
8.26
|
0.58
|
0.98
|
|
Для
x3 и x4
|
57.16
|
78.39
|
7.56
|
8.85
|
0.95
|
|
Для
x3 и x5
|
68.25
|
78.39
|
8.26
|
8.85
|
0.99
|
|
Для
x4 и x5
|
68.25
|
57.16
|
8.26
|
7.56
|
0.98
|
Матрица парных коэффициентов корреляции представлена в
таблице 20.
Таблица 20 - Значение парных коэффициентов корреляции
|
-
|
y
|
x1
|
x2
|
x3
|
x4
|
x5
|
|
y
|
1
|
0.82
|
0.7
|
0.83
|
0.7
|
0.79
|
|
x1
|
0.82
|
1
|
0.94
|
1
|
0.94
|
0.99
|
|
x2
|
0.7
|
0.94
|
1
|
0.94
|
1
|
0.98
|
|
x3
|
0.83
|
1
|
0.94
|
1
|
0.95
|
0.99
|
|
x4
|
0.7
|
0.94
|
1
|
0.95
|
1
|
0.98
|
|
x5
|
0.99
|
0.98
|
0.99
|
0.98
|
1
|
Для отбора наиболее значимых факторов xi
учитываются следующие условия:
связь между результативным признаком и факторным должна быть
выше межфакторной связи;
связь между факторами должна быть не более 0.7. Если в
матрице есть межфакторный коэффициент корреляции rxjxi > 0.7, то
в данной модели множественной регрессии существует мультиколлинеарность.;
при высокой межфакторной связи признака отбираются факторы с
меньшим коэффициентом корреляции между ними.
В нашем случае rx1 x2, rx1 x3, rx1
x4, rx1 x5, rx2 x3, rx2 x4, rx2 x5,
rx3 x4, rx3 x5, rx4 x5 имеют |r|>0.7, что
говорит о мультиколлинеарности факторов и о необходимости исключения одного из
них из дальнейшего анализа.
Модель регрессии в стандартном масштабе.
Модель регрессии в стандартном масштабе предполагает, что все
значения исследуемых признаков переводятся в стандарты (стандартизованные
значения) по формулам:
(27)
где хji - значение переменной хji в
i-ом наблюдении.
(28)
Таким образом, начало отсчета каждой стандартизованной
переменной совмещается с ее средним значением, а в качестве единицы изменения
принимается ее среднее квадратическое отклонение S.
Если связь между переменными в естественном масштабе
линейная, то изменение начала отсчета и единицы измерения этого свойства не
нарушат, так что и стандартизованные переменные будут связаны линейным
соотношением:
ty = ∑βjtxj (29)
Для оценки β-коэффциентов применим
МНК. При этом система нормальных уравнений будет иметь вид:
rx1y=β1+rx1x2•β2 +... + rx1xm•βm x2y=rx2x1•β1 + β2 +... + rx2xm•βm (30)xmy=rxmx1•β1 + rxmx2•β2 +... + βm
Для наших данных (берем из матрицы парных коэффициентов
корреляции):
0.823 = β1 + 0.944β2 + 0.998β3 + 0.945β4 +
0.991β5
0.699 = 0.944β1 + β2 + 0.942β3 + 0.999β4 +
0.977β5
0.826 = 0.998β1 + 0.942β2 + β3 + 0.945β4 +
0.992β5 (31)
0.704 = 0.945β1 + 0.999β2 +
0.945β3 + β4 + 0.979β5
0.789 = 0.991β1 + 0.977β2 +
0.992β3 + 0.979β4 + β5
Данную систему линейных уравнений решаем методом Гаусса: β1 = -3.721; β2 = 2.953; β3 = -9.603;
β4 = -13.135; β5 = 23.975;
Стандартизированная форма уравнения регрессии имеет вид:
0 = -3.721x1 + 2.953x2
-9.603x3 -13.135x4 + 23.975x5 (32)
Найденные из данной системы β-коэффициенты позволяют
определить значения коэффициентов в регрессии в естественном масштабе по
формулам:
(33)
(34)
Анализ параметров уравнения регрессии.Перейдем к статистическому
анализу полученного уравнения регрессии: проверке значимости уравнения и его коэффициентов,
исследованию абсолютных и относительных ошибок аппроксимации.
Для несмещенной оценки дисперсии проделаем следующие
вычисления:
Несмещенная ошибка ε = Y
- Y(x) = Y - X*s (абсолютная ошибка аппроксимации).Результаты данной операции
представлены в таблице 21.
Таблица 21 - Несмещенная ошибка ε
|
Y
|
Y(x)
|
ε = Y - Y(x)
|
ε2
|
(Y-Yср)2
|
|ε: Y|
|
|
427
|
444.87
|
-17.87
|
319.51
|
210156.76
|
0.0419
|
|
817
|
591.22
|
225.78
|
50978.52
|
4682.47
|
0.28
|
|
1270
|
1039.33
|
230.67
|
53207.83
|
147895.18
|
0.18
|
|
773
|
684.87
|
88.13
|
7767.71
|
12640.18
|
0.11
|
|
763
|
915.05
|
-152.05
|
23120.18
|
14988.76
|
0.2
|
|
709
|
903.78
|
-194.78
|
37940.99
|
31127.04
|
0.27
|
|
764
|
781.44
|
-17.44
|
304.09
|
14744.9
|
0.0228
|
|
1216
|
1261.66
|
-45.66
|
2084.4
|
109277.47
|
0.0375
|
|
1018
|
943.52
|
74.48
|
5547.66
|
17575.18
|
0.0732
|
|
1315
|
1405.99
|
-90.99
|
8279.46
|
184531.61
|
0.0692
|
|
1178
|
933.11
|
244.89
|
59969.93
|
85598.04
|
0.21
|
|
1437
|
1374.35
|
62.65
|
3924.54
|
304231.04
|
0.0436
|
|
301
|
718.57
|
-417.57
|
174363.7
|
341556.76
|
1.39
|
|
|
0
|
427904.26
|
1706943.43
|
2.95
|
Средняя ошибка аппроксимации
(35)
Оценка дисперсии равна:
se2 = (Y - X*Y(X))T(Y
- X*Y(X)) = 427904.26 (36)
Несмещенная оценка дисперсии равна:
(37)
Оценка среднеквадратичного отклонения равна (стандартная
ошибка для оценки Y):
(36)
Найдем оценку ковариационной матрицы вектора k = S • (XTX)-1..
Результаты данной операции представлены в таблице 22.
Таблица 22 -Матрица ковариационных значений
|
1284953.2
|
304683.89
|
-663172.42
|
24743.43
|
90300.49
|
-90085.45
|
|
304683.89
|
114814.25
|
-194034.03
|
12030.2
|
31640.54
|
-38521.14
|
|
-663172.42
|
-194034.03
|
374145.16
|
-18078.46
|
-55458.04
|
61307.73
|
|
24743.43
|
12030.2
|
-18078.46
|
2334.86
|
3935.67
|
-5888.84
|
|
90300.49
|
31640.54
|
-55458.04
|
3935.67
|
9345.06
|
-11699.06
|
|
-90085.45
|
-38521.14
|
61307.73
|
-5888.84
|
-11699.06
|
16124.96
|
Дисперсии параметров модели определяются соотношением S2i
= Kii, т.е. это элементы, лежащие на главной диагонали
Множественный коэффициент корреляции (Индекс множественной
корреляции).
Тесноту совместного влияния факторов на результат оценивает
индекс множественной корреляции.
В отличии от парного коэффициента корреляции, который может
принимать отрицательные значения, он принимает значения от 0 до 1.
Поэтому R не может быть использован для интерпретации
направления связи. Чем плотнее фактические значения yi располагаются
относительно линии регрессии, тем меньше остаточная дисперсия и, следовательно,
больше величина Ry(x1,...,xm).
Таким образом, при значении R близком к 1, уравнение
регрессии лучше описывает фактические данные и факторы сильнее влияют на
результат. При значении R близком к 0 уравнение регрессии плохо описывает фактические
данные и факторы оказывают слабое воздействие на результат.
(38)
Связь между признаком Y факторами X сильная
Коэффициент детерминации.
R2= 0.872 = 0.75 (39)
Проверка гипотез относительно коэффициентов уравнения
регрессии.
Проверка значимости параметров множественного уравнения
регрессии.
Число v = n - m - 1 называется числом степеней
свободы. Считается, что при оценивании множественной линейной регрессии для
обеспечения статистической надежности требуется, чтобы число наблюдений, по
крайней мере, в 3 раза превосходило число оцениваемых параметров.
) t-статистика
Tтабл
(n-m-1;α/2) = (8;0.025) = 2.306 (40)
(41)
Находим стандартную ошибку коэффициента регрессии b0:
(42)
(43)
Статистическая значимость коэффициента регрессии b0
не подтверждается.
Находим стандартную ошибку коэффициента регрессии b1:
(44)
(45)
Статистическая значимость коэффициента регрессии b1
подтверждается.
Находим стандартную ошибку коэффициента регрессии b2:
(46)
(47)
Статистическая значимость коэффициента регрессии b2
подтверждается.
Находим стандартную ошибку коэффициента регрессии b3:
(48)
(49)
Статистическая значимость коэффициента регрессии b3
подтверждается.
Находим стандартную ошибку коэффициента регрессии b4:
(50)
(51)
Статистическая значимость коэффициента регрессии b4
подтверждается.
Находим стандартную ошибку коэффициента регрессии b5:
(52)
(53)
Статистическая значимость коэффициента регрессии b5
подтверждается.
Доверительный интервал для коэффициентов
уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии,
которые с надежность 95% будут следующими:
(bi - ti Sbi; bi
+ ti Sbi) (54)
0: (-695.09 -2.306•1133.56;-695.09 + 2.306 •
1133.56) = (-3309.08;1918.89) 1: (-1668.76 - 2.306 •338.84;
-1668.76+2.306 • 338.84) = (-2450.13;-887.39) 2: (1774.46 - 2.306 •
611.67; 1774.46 + 2.306 • 611.67) = (363.94;3184.98) 3: (-378.76 -
2.306 • 48.32; -378.76 + 2.306 • 48.32) = (-490.19;-267.33) 4:
(-606.67 - 2.306 • 96.67; -606.67 + 2.306 • 96.67) = (-829.59;-383.75) 5:
(1013.4 - 2.306 • 126.98; 1013.4 + 2.306 • 126.98) = (720.57;1306.23)
Проверка общего качества уравнения множественной регрессии.
Оценка значимости уравнения множественной регрессии
осуществляется путем проверки гипотезы о равенстве нулю коэффициент
детерминации рассчитанного по данным генеральной совокупности: R2
или b1 = b2 =... = bm = 0 (гипотеза о
незначимости уравнения регрессии, рассчитанного по данным генеральной
совокупности).
Для ее проверки используют F-критерий Фишера.
При этом вычисляют фактическое (наблюдаемое) значение
F-критерия, через коэффициент детерминации R2, рассчитанный по
данным конкретного наблюдения.
По таблицам распределения Фишера-Снедоккора находят
критическое значение F-критерия (Fкр). Для этого задаются уровнем значимости α (обычно его берут равным 0,05) и двумя числами степеней свободы k1=m
и k2=n-m-1.
) F-статистика. Критерий Фишера
(55)
Чем ближе этот коэффициент к единице, тем больше уравнение
регрессии объясняет поведение Y.
Более объективной оценкой является скорректированный
коэффициент детерминации:
(56)
Добавление в модель новых объясняющих переменных
осуществляется до тех пор, пока растет скорректированный коэффициент
детерминации.
Проверим гипотезу об общей значимости - гипотезу об
одновременном равенстве нулю всех коэффициентов регрессии при объясняющих
переменных:
H0: β1 = β2 =... = βm = 0. (57)
Проверка этой гипотезы осуществляется с помощью F-статистики
распределения Фишера.
Если F < Fkp = Fα; n-m-1, то нет оснований для отклонения гипотезы H0.
(58)
Табличное значение при степенях свободы k1 = 5 и k2
= n-m-1 = 14 - 5 - 1 = 8, Fkp(5;8) = 3.69
Поскольку фактическое значение F > Fkp, то коэффициент
детерминации статистически значим и уравнение регрессии статистически надежно
Оценка значимости дополнительного включения фактора (частный
F-критерий).
Необходимость такой оценки связана с тем, что не каждый
фактор, вошедший в модель, может существенно увеличить долю объясненной
вариации результативного признака. Это может быть связано с последовательностью
вводимых факторов (т. к. существует корреляция между самими факторами).
Мерой оценки значимости улучшения качества модели, после
включения в нее фактора хj, служит частный F-критерий - Fxj:
(58)
где m - число оцениваемых параметров.
В числителе - прирост доли вариации у за счет дополнительно
включенного в модель фактора хj.
Если наблюдаемое значение Fxj больше Fkp,
то дополнительное введение фактора xj в модель статистически
оправдано.
Частный F-критерий оценивает значимость коэффициентов
«чистой» регрессии (bj). Существует взаимосвязь между частным
F-критерием - Fxj и t-критерием, используемым для оценки значимости
коэффициента регрессии при j-м факторе:
(59)
Проверка других полиномов Проведя аналогичные вычисления для
полинома первой и третьей степени получили коэффициенты детерминации в
переделах от 0.7 до 0.86.Атак же провели проверку по Критерию Фишера.
4.
Математическая модель
4.1
Понятие имитационной модели, цель моделирования
Объект - некоторая часть окружающего нас мира, которая может
быть рассмотрена как единое целое [11].
Свойства объекта - совокупность признаков объекта, по которым
его можно отличить от других объектов.
Модель - это упрощенное представление о реальном объекте,
процессе или явлении [12].
Моделирование - построение моделей для изучения объектов,
процессов, явлений.
Компьютерное моделирование - это метод решения задачи анализа
или синтеза сложной системы на основе использования ее компьютерной модели.
Суть компьютерного моделирования заключена в получении количественных и
качественных результатов на основе имеющейся модели.
Под компьютерной моделью понимают [13]:
- Условный образ объекта или некоторой системы, описанный с
помощью взаимосвязанных компьютерных таблиц, блок-схем, диаграмм, графиков,
рисунков, анимационных фрагментов, гипертекстов и т.д. и отображающий структуру
и взаимосвязи между элементами объекта - структурно-функциональная модель;
- Отдельная программа, совокупность программ,
программный комплекс, позволяющий с помощью последовательности вычислений и графического
отображения их результатов воспроизводить (имитировать) процессы
функционирования объекта при условии воздействия на него различных (включая
случайные) факторов - имитационные модели.
Имитационная модель воспроизводит поведение сложной системы взаимодействующих
элементов. Для имитационного моделирования характерно наличие следующих
обстоятельств (одновременно всех или некоторых из них):
- объект моделирования - сложная неоднородная система;
- в моделируемой системе присутствуют факторы
случайного поведения;
- требуется получить описание процесса,
развивающегося во времени;
- принципиально невозможно получить результаты
моделирования без использования компьютера.
Имитационная модель основана на подражании реальному процессу
(имитации) [14].
4.2
Входная информация
Входной информацией для модели будет матрица состоящая из
двух столбцов.В первом столбце содержится натуральный логарифм числа людей
выезжающих из города на постоянное жительство. Во втором столбце содержится
натуральный логарифм числа людей приезжающих в город на постоянное жительство.
Эти показатели поступают из модели прогнозирования депопуляции города. Эта
модель имеет три варианта развития. Первый показывает, что будет происходит с
численностью населения в случае,если не принимать никаких мер препятствующих
вырождению города. Вторая моделирует изменение численности населения в
результате резкого увеличения числа иммигрантов, привлеченных извне, благодаря
большому количеству новых рабочих мест,в частности, за счет строительства крупного
производственного многопрофильного кластера. Третий вариант предусматривает
постепенное уменьшение числа эмигрантов, благодаря процессу создания
предприятий малого и среднего бизнеса.
4.3
Построение модели
Используя средства математического пакета MathCad, построим регрессионную
модель на основе имеющихся данных.начальные сведения возьмем из собранной и
проанализированной информации. Коэффициенты регрессионного уравнения найдем с
помощью встроенной функция для обеспечения полиномиальной регрессии при
произвольной степени полинома регрессии - regress(VX,VY, n) Рисунок 4.
есть m-мерный вектор или матрица m*k, содержащий координаты
x. VY есть m-мерный вектор, содержащий координаты y соответствующие m точкам,
определенным в VX.А n-положительное целое число, определяющее порядок
многочлена, которые нужно использовать для размещения данных. Порядок
многочлена, не может превышать число точек данных. Если вы хотите, многочлен
4-го порядка от одной переменной, вы должны иметь не менее 4 точек данных


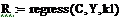

Рисунок 4 - Задание начальный данных,нахождение коэффициентов
и формирования функции интерполяции
На практике не рекомендуется делать степень аппроксимирующего
полинома выше четвертой - шестой, поскольку погрешности реализации регрессии
сильно возрастают
Эта функция возвращает вектор VS, запрашиваемый функцией
interp(VS,VX,VY,x), содержащий коэффициенты многочлена n-й степени, который
наилучшим образом приближает “облако” точек с координатами, хранящимися в
векторах VX и VY.. Функция interp(VS,VX,VY,x) возвращает интерполируемое
значение y, соответствующее x
Статистическая значимость такого подхода была доказана в третьей
части данной поясняющей записки.
4.4
Результаты моделирования
Для модели депопуляции в которой населении города убывает на
всем протяжении времени график представлен на рисунке.

График убывание населения в городе при депопуляции
На всем протяжении периода количество убывающего населения
превышает количество прибывающего, тогда при моделировании количество сделок
постепенно падает рисунок.
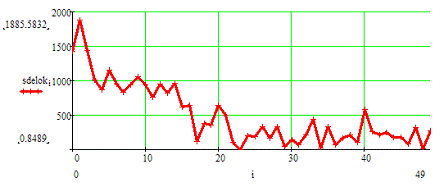
График количества сделок за год при депопуляции города
Этот график объясняется тем что даже миграция населения становится
меньше из-за того что некому становится уезжать из города.
Для модели предполагающей резкое увеличения числа иммигрантов,
привлеченных извне благодаря большому количеству новых рабочих мест,в
частности, за счет строительства крупного производственного многопрофильного
кластера через 25 лет после начала моделирования движение населения представлено
на рисунке.

График изменения численности населения в городе при строительстве
крупного производственного
При таком развитии событий число приезжий после строительства
растет, соответственно растет и число сделок с недвижимостью.
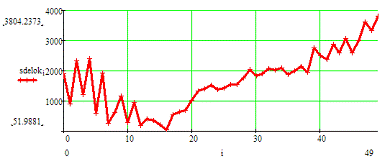
График количества сделок за год при строительстве крупного
производственного кластера
Для модели предполагающей уменьшение числа эмигрантов благодаря
процессу создания предприятий малого и среднего бизнеса население будет вначале
убывать, но не так быстро как в других моделях. А потом начинает постепенно
расти.

График изменения численности населения в городе при создания
предприятий малого и среднего бизнеса
При создании предприятий малого бизнеса поток людей уезжающих из
города будет уменьшаться за счет людей, которые останутся в городе на созданных
рабочих местах.

График количества сделок при создания предприятий малого и
среднего бизнес
Заключение
В ходе выполнения работы мной были проанализированы данные о
сделках с недвижимостью в городе Камышине с июня 2006 по февраль 3013 года. Для
каждого года были найдены основные статистические показатели цен за квадратный
метр жилой недвижимости. Таблица с данными расположена в приложении на странице
48-49.
Были сведены в таблицу средние годовые цены за квадратный
метр недвижимости и другие сведения отражающие основные социально-экономические
показатели города. Сводная таблица расположена в приложении на странице 50.На
основе корреляционного анализа сводной таблицы были выделены два показателя,
описывающих миграционные потоки, которые имеют наибольшее влияние на количество
сделок заключенных за год.
Для формализации связи на основе регрессионного анализа были
подобранны коэффициенты для полиноминального уравнения, описывающего
зависимость между миграционными потоками и количество сделок с жилплощадью
заключенных за год.
Используя прогноз депопуляции, выполненный на кафедре по
проекту р-Поволжье-а №13-07-97033. Было смоделировано три варианта развития
событий. По результатам моделирования негативного варианта событий можно
сделать следующие выводы:
- Неизбежная депопуляция города при сохранения
прежних тенденций социально экономического развития
- Повышение доступности жилья из-за большого оттока
населения.
- При этом возможно увеличение населения за счет
того, что цена на недвижимость станет более низкой, чем в других регионах.
При моделирование вариантов развития предполагающих принятие
контрмер к депопуляции населения количество сделок с недвижимость растет либо
скачкообразно -при строительстве крупного производственного кластера, либо
постепенно - при развитии малого и среднего бизнеса.
Список
литературы
1)
Кулешова Л.В. Ипотечное кредитование как способ решения жилищной проблемы в
России[Текст] / Л.В. Кулешова, Е.Н. Лапина // Политематический сетевой
электронный научный журнал Кубанского государственного аграрного университета
(Научный журнал КубГАУ) [Электронный ресурс]. - Краснодар: КубГАУ, 2012. -
№05(079). С. 648 - 659. - Режим доступа:
http://ej.kubagro.ru/2012/05/pdf/47.pdf
)Население
России 2007: Пятнадцатый ежегодный демографический доклад / отв. ред. А. Г.
Вишневский; Гос. ун-т -- Высшая школа экономики. -- М.: М.: Изд. дом Гос. ун-та
-- Высшей школы экономики, 2009. -- с.240-246
)Корреляция
- Википедия) [Электронный ресурс]// wikipedia.org Режим доступа: http://ru.wikipedia.org/wiki/%D0%9A%D0%BE% D1%80%D1% 80%D0%B5% D0%BB%D1%8F%D1%86%D0%B8%D1%8F
)Орлов
А.И. Прикладная статистика. Учебник. / А.И.Орлов.- М.: Издательство «Экзамен»,
2004. - 656 с.
)
Федеральная служба государственной регистрации, кадастра и картографии
(Росреестр) [Электронный ресурс]:Система предназначена для автоматизации
деятельности Росреестра, обеспечивающей информационную поддержку решаемых
Росреестром государственных задач и всех предоставляемых Росреестром
государственных услуг по исполнению государственной функции «Организация
проведения государственной кадастровой оценки», в том числе для обеспечения
участников рынка недвижимости, органов государственной власти и местного
самоуправления, граждан и юридических. - Режим доступа https://portal.rosreestr.ru /wps/portal/!ut/p/5с/... Загл. с экрана.
)
Единая межведомственная информационно-статистическая система [Электронный
ресурс] / www.fedstat.ru Электрон. дан. [2014] Режим доступа:
http://www.fedstat.ru/indicator/data.do Загл. с экрана. - Яз. рус.
)
Камышин - Официальный сайт Администрации городского округа [Электронный
ресурс]:/www.admkamyshin.info ru Электрон. дан. [2014] Режим доступа: http://www.admkamyshin.info ru /2014/03/28/otchet-glavy-gorodskogo-okruga.html Загл. с экрана. - Яз.
рус.
)Экономико-математические
методы и прикладные модели: Учеб. пособие для вузов/ В.В. Федосеев, А.Н.
Гармаш, Д.М. Дайитбегов и др.; Под ред. В.В. Федосеева. - М.: ЮНИТИ, 1999. -
391 с.
)
Курс социально-экономической статистики: Учебник для вузов / Под ред. проф.
М.Г. Назарова. - М.: Финстатинформ, ЮНИТИ-ДАНА, 2000. - 771 с.
)Mathcad[Электронный
ресурс]/ wikipedia.org Электрон. дан. [2013] Режим доступа:
http://ru.wikipedia.org/wiki/Mathcad,свободный.- Загл. с экрана. - Яз. рус.
)Энциклопедия
учителя информатики[Электронный ресурс] /http://inf.1september.ru
Электрон.дан.[2013] - Режим доступа http://inf.1september.ru/2007/13/01.htm
свободный - Загл.с экрана. - Яз.рус.
)
Компьютерное моделирование [Электронный ресурс]/ Электрон. дан.[2013] - Режим
доступа http://www.mista.ru/ gorod/ diplom/2_3.htm, свободный - Загл.с экрана.
- Яз.рус.
)Лычкина
Н.Н. Современные тенденции в имитационном моделировании. - Вестник
университета, серия Информационные системы управления №2 - М., ГУУ., 2000г.;
)Мир
ПК [Электронный ресурс] / Открытые системы. Имитационное моделирование.
Электрон.дан [2004] - Режим доступа
http://www.osp.ru/os/2004/12/184891/_p2.html, свободный - Загл. с экрана -
Яз.рус.
)Нименья
И. Н. Эконометрика: Экзамен без проблем / И. Н. Нименья. - СПб.:Нева, 2003. -
224с.