Лінійні стохастичні моделі еволюції фінансових індексів
Львівський
національний університет імені Івана Франка
Кафедра
економічної кібернетики
КУРСОВА
РОБОТА
з
дисципліни «Математичні методи і моделі ринкової економіки»
на
тему:
Лінійні
стохастичні моделі еволюції фінансових індексів
м.
Львів - 2014 рік
ЗМІСТ
ВСТУП
РОЗДІЛ
1. ТЕОРЕТИЧНІ ОСНОВИ МЕТОДІВ І МОДЕЛЕЙ ФІНАНСОВИХ ІНДЕКСІВ
1.1
Теорія часових рядів як метод аналізу фінансових даних
.2
Огляд стану моделювання часових рядів за допомогою моделей авторегресії та
проінтегрованого ковзного середнього
РОЗДІЛ
2. МАТЕМАТИЧНІ МЕТОДИ ЛІНІЙНИХ СТОХАСТИЧНИХ МОДЕЛЕЙ ФІНАНСОВИХ РИНКІВ
2.1
Модель ковзного середнього MA(q)як метод згладжування даних вибіркового
характеру
.2
Авторегресійна модель AR(p) як лінійна комбінація незалежних складових попередніх
періодів
.3
Модель авторегресії та ковзного середнього ARMA(p,q) та інтегральна модель
ARIMA(p,d,q)
РОЗДІЛ
3. МОДЕЛЬ ЕВОЛЮЦІЇ ФІНАНСОВИХ РИНКІВ НА ПРИКЛАДІ МОДЕЛІ АВТОРЕГРЕСІЇ ТА
КОВЗНОГО СЕРЕДНЬОГО ARMA(p,q)
ВИСНОВКИ
Список використаних джерел
ВСТУП
Побудова та дослідження математичних
моделей, що адекватно описують динаміку таких фінансових інструментів як акції,
облігації, опціони, котирування валют та ін., в даний час є актуальним
напрямком фінансової математики. У зв'язку з чим, стає необхідним вивчення
статистичних характеристик і особливостей структури фінансових часових рядів,
обчислення параметрів моделей, що описують еволюцію фінансових інструментів і
визначення виду розподілу стохастичного процесу, що лежить в основі ринкових
флуктуацій.
Об’єкт дослідження - процеси, що
можуть бути описані часовими рядами.
Предметом дослідження є побудова
ARMA-моделей. В роботі використовувались математичні методи аналізу моделей,
експериментальні дослідження з застосуванням сучасної електронно-обчислювальної
техніки та програмного забезпечення.
Метою дослідження є виявлення та
формалізований опис емпіричних закономірностей фінансових часових рядів,
розробка алгоритмів і комплексу стохастичних моделей і прогнозування фінансових
індексів.
Для досягнення поставленої мети
потрібно було вирішити такі завдання:
. Виявити і проаналізувати
особливості структури і динаміки фінансових часових рядів.
. Розробити алгоритм оцінювання
параметрів волатильності на основі узагальненої авторегресійної моделі;
. Розробити алгоритм оцінювання
параметрів волатильності на основі моделі ковзного середнього.
. Реалізувати на конкретному
прикладі лінійну стохастичну модель за реальними фінансовими даними.
Наукове значення математичного
моделювання в теорії фінансів обумовлене революційними перетвореннями
фінансового ринку - зміною його структури, зростанням мінливості в цінах,
появою нових фінансових інструментів, використанням сучасних інформаційних
технологій для аналізу цін, що пред'являє до фінансової теорії відповідно нові
вимоги і ставить нові проблеми, для вирішення яких необхідне проведення
глибоких наукових досліджень в галузі математичного моделювання фінансових
процесів. Утворюючи велику і складну систему з величезною кількістю змінних,
різних факторів і зв'язків, фінансові ринки вимагають для свого аналізу досить
складних математичних методів, методів статистичної обробки даних, чисельних
методів і комп'ютерних засобів.
Робота складається з трьох частин.
Перший розділ описує дослідження
часових рядів за допомого лінійних моделей. Розкриваються причини популярності
цих моделей.
У другому розділі безпосередньо
наводиться та досліджується кожна модель зокрема, обґрунтовується доцільність
використання кожної з них. Описуються моделі:
MA(q),AR(p),ARMA(p,q),ARIMA(p,d,q), для кожної з яких, будується алгоритм
застосування.
У третьому розділі описується
практична реалізація моделі ARIMA(p,d,q), для реальних фінансових даних.
Проводиться аналіз за допомогою програмного продукту Matrixer та аналізуються
результати.
РОЗДІЛ 1. ТЕОРЕТИЧНІ ОСНОВИ МЕТОДІВ
І МОДЕЛЕЙ ФІНАНСОВИХ ІНДЕКСІВ
1.1 Теорія
часових рядів як метод аналізу фінансових даних
Під часовим рядом (time
series) розуміють послідовність спостережуваних значень деякої змінної,
відтворених через рівні проміжки часу. Якщо прийняти довжину такого проміжку за
одиницю часу (рік, квартал, день), то можна вважати що послідовність
спостережень  відтворені
в моменти
відтворені
в моменти  .
.
Основна відмінна особливість
статистичного аналізу часових рядів полягає в тому, що послідовність
спостережень  розглядається
як реалізація послідовностей, статистично залежних випадкових величин
розглядається
як реалізація послідовностей, статистично залежних випадкових величин  , що мають
деякий спільний розподіл з функцією розподілу [14,c.84].
, що мають
деякий спільний розподіл з функцією розподілу [14,c.84].

Щоб зробити задачу
стохастичного аналізу часових рядів доступною для практичного застосування,
необхідно так чи інакше обмежувати клас розглянутих моделей часових рядів,
вводячи припущення щодо структури ряду і його ймовірнісних характеристик. Одне
з таких обмежень розглядає стаціонарність часового ряду.
Ряд 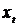 ,
,  , називають
строго стаціонарним якщо для будь-якого
, називають
строго стаціонарним якщо для будь-якого  спільний розподіл ймовірностей
випадкових величин
спільний розподіл ймовірностей
випадкових величин 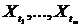 таке ж, як
і для
таке ж, як
і для 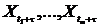 при
будь-яких
при
будь-яких 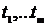 і
і  , таких, що
, таких, що 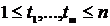 і
і  .
.
Іншими словами, властивості
строго стаціонарного часового ряду не змінюються при зміні початку відліку
часу. Зокрема, при m = 1 з припущення про строгу стаціонарність часового ряду 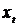 випливає,
що закон розподілу ймовірностей випадкової величини
випливає,
що закон розподілу ймовірностей випадкової величини  не залежить
від t, а значить, не залежать від t і всі його основні числові характеристики,
у тому числі: математичне сподівання
не залежить
від t, а значить, не залежать від t і всі його основні числові характеристики,
у тому числі: математичне сподівання  і дисперсія
і дисперсія  .
.
Значення μ визначає
постійний рівень, щодо якого коливається аналізований часовий ряд 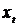 , а σ характеризує
розмах цих коливань [15, c.186].
, а σ характеризує
розмах цих коливань [15, c.186].
Ступінь тісноти статистичної
зв'язку між випадковими величинами  і
і  може бути виміряна парним
коефіцієнтом кореляції
може бути виміряна парним
коефіцієнтом кореляції


Практична перевірка строгої
стаціонарності ряду 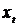 на підставі
спостереження значень
на підставі
спостереження значень  в загальному
випадку скрутна. У зв'язку з цим під стаціонарним на практиці часто мають на
увазі часовий ряд
в загальному
випадку скрутна. У зв'язку з цим під стаціонарним на практиці часто мають на
увазі часовий ряд 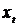 , у якого
, у якого

 ,
,
 для будь яких t і
для будь яких t і  .
.
Ряд, для якого виконані
зазначені три умови, називають стаціонарним у широкому сенсі (слабо
стаціонарним, стаціонарним другого порядку або коваріаційно стаціонарним).
Якщо ряд є стаціонарним у
широкому сенсі, то він не обов'язково є строго стаціонарним. У той же час, і
строго стаціонарний ряд може не бути стаціонарним у широкому сенсі просто тому,
що у нього можуть не існувати математичне очікування і / або дисперсія.
Однак, далеко не всі
тимчасові "економетричні" ряди є стаціонарними. Аналіз показує, що
часто в статистичних даних дуже рельєфно вимальовуються наступні три складові:
• повільно мінливий
(наприклад, "інфляційний") тренд (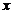 ),
),
• періодичні чи неперіодичні
цикли ( ),
),
•нерегулярна, флуктуіруюча
("стохастична" або "хаотична") компонента ( ) [7,
c.254].
) [7,
c.254].
При цьому в спостережувальні
дані ( ) вони
можуть входити вельми різноманітними засобами, що умовно можна представити як
) вони
можуть входити вельми різноманітними засобами, що умовно можна представити як

Для стаціонарного часового
ряду характерним є процес білого шуму. «Білим шумом» ("чисто випадковим
тимчасовим рядом ") називають стаціонарний часовий ряд  , для якого
, для якого  ,
,  і ρ
(τ) = 0 при
τ
≠ 0.
і ρ
(τ) = 0 при
τ
≠ 0.
Останнє означає, що при t ≠
s випадкові величини  і
і 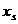 , відповідні
спостереженнями процесу білого шуму в моменти t і s, некорреліровані.
, відповідні
спостереженнями процесу білого шуму в моменти t і s, некорреліровані.
У випадку, коли  має
нормальний розподіл, випадкові величини
має
нормальний розподіл, випадкові величини взаємно незалежні і мають однакове
нормальний розподіл
взаємно незалежні і мають однакове
нормальний розподіл  ,утворюючи
випадкову вибірку з цього розподілу, тобто
,утворюючи
випадкову вибірку з цього розподілу, тобто  ~
~  ,такий ряд називають гауссовским
білим шумом.
,такий ряд називають гауссовским
білим шумом.
В той же час, в загальному
випадку, навіть якщо деякі випадкові величини  взаємно незалежні і мають однаковий
розподіл, то це ще не означає, що вони утворюють процес білого шуму, тому
випадкова величина
взаємно незалежні і мають однаковий
розподіл, то це ще не означає, що вони утворюють процес білого шуму, тому
випадкова величина  може просто
не мати математичного очікування і / або дисперсії (як приклад ми знову можемо
вказати на розподіл Коші) [10, c. 324].
може просто
не мати математичного очікування і / або дисперсії (як приклад ми знову можемо
вказати на розподіл Коші) [10, c. 324].
Часовий ряд, відповідний
процесу білого шуму, веде себе вкрай нерегулярним чином через некорельованість
при t ≠ s випадкових величин  і
і 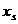 . Це ілюструє наведений нижче графік
змодельованої реалізації гауссовского процесу білого шуму (Рис. 1.1) (NOISE) з
D (
. Це ілюструє наведений нижче графік
змодельованої реалізації гауссовского процесу білого шуму (Рис. 1.1) (NOISE) з
D ( ) ≡
0.04.
) ≡
0.04.
У зв'язку з цим процес білого
шуму не годиться для безпосереднього моделювання еволюції більшості часових
рядів, що зустрічаються в економіці. У той же час, як ми побачимо нижче, такий
процес є базою для побудови більш реалістичних моделей часових рядів, що
породжують "більш гладкі" траєкторії ряду. У зв'язку з частим
використанням процесу білого шуму в подальшому викладі, ми будемо відрізняти
цей процес від інших моделей часових рядів, використовуючи для нього позначення
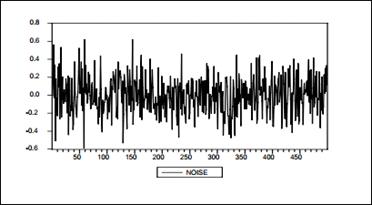
Рис. 1.1 Реалізація
гаусівського процесу білого шуму
Як приклад ряду, траєкторія
якого схожа на реалізацію процесу білого шуму, можна вказати, на прикладі ряду,
утвореного значеннями темпів зміни (приросту) індексу Доу-Джонса протягом
1984року (Рис. 1.2).
Зауважимо, однак, що тут
спостерігається деяка асиметрія розподілу ймовірностей значень  (скошенность
цього розподілу в бік позитивних значень), що виключає опис моделі цього ряду
як гауссовского білого шуму.
(скошенность
цього розподілу в бік позитивних значень), що виключає опис моделі цього ряду
як гауссовского білого шуму.

Рис. 1.2 Процес білого шуму на
основі індексу Доу-Джонса
Аналіз часових рядів - сукупність
математико-статистичних методів аналізу, призначених для виявлення структури
часових рядів і для їх прогнозування. Виявлення структури часового ряду
необхідно для того, щоб побудувати математичну модель того явища, яке є
джерелом аналізованого часового ряду. Прогноз майбутніх значень часового ряду
використовується для ефективного прийняття рішень [15, с.241].
Тут доречно сказати, що в кінцевому
рахунку, одна з важливих цілей емпіричного аналізу статистичних даних з
фінансових індексам полягає в прогнозуванні, передбаченні "майбутнього
руху цін" (Рис1.3):

Рис. 1.3 Прогнозування «майбутнього
руху цін»
Практично єдиним підходом до
дослідження складних систем для випадку, коли невідома, або надто складна їх
структура та модель їхньої динаміки полягає в аналізі часових рядів деяких
вихідних характеристик системи, на підставі чого намагаються зробити висновки
щодо стану, структури та еволюції системи. Традиційним статистичним підходом в
аналізі часових рядів є подання їх за допомогою лінійних моделей у вигляді, що
використовується в прикладній статистиці.
Причини популярності цих моделей
криються, з одного боку, в їх простоті і, з іншого боку, в тому, що вже з
невеликим числом параметрів ними можна добре апроксимувати вельми широкий клас
стаціонарних послідовностей.
Одним із найбільш перспективних
напрямків досліджень є побудова моделей з „довгою пам’яттю”. Такі ряди
характеризуються функцією автокореляції, що повільно спадає зі зростанням
часового ряду. Наявність пам’яті дозволяє прогнозувати майбутні значення ряду.
На протязі багатьох років дослідниками активно використовувались моделі
Бокса-Дженкінса.(процеси з „короткою пам’яттю”), в яких передбачається
експоненційний темп спадання коефіцієнтів у функції релаксації на зовнішні
імпульси. Базовим видом цих моделей є моделі рухомого середнього (moving
average, MA), та авторегресійний процес (autoregressive process, AR) при якому
наступне значення y є лінійною комбінацією попередніх значень.
Поєднання двох типів моделей утворює
модель авто регресійного рухомого середнього (ARMA (p, q)), яка є лінійною
комбінацією осциляцій AR-моделі з керованим кореляціями та шумом MA-моделі. Всі
ARMA- моделі є слабко стаціонарними і тому для застосування їх до
нестаціонарних даних необхідні перетворення, що зроблять їх стаціонарними.
Найбільш загальним перетворенням є диференціювання, тобто знаходження перших
різниць. На основі диференційованих відповідну кількість разів даних будується
авторегресійна інтегрована модель рухомого середнього (autoregressive
integrated moving average), ARIMA [5, с.141].
Модель ARCH (autoregressive
conditional heteroskedasticity) була запропонована Робертом Енглом (Engle,
Robert) [18] для аналізу економічних часових рядів зі змінною дисперсією, за
яку він одержав Нобелівську премію з економіки за 2003 рік (разом з Клайвом
Гренджером).
Загальне припущення цієї
моделі полягає в тому, що математичне сподівання (Е) випадкових збурень
(інновацій) ( ) дорівнює
нулю.
) дорівнює
нулю.
Сутність моделі ARCH полягає
у тому, що якщо абсолютна величина велика, то це призводить до
збільшення умовної дисперсії у наступні періоди. В свою чергу, при значній
умовній дисперсії поява великих (за абсолютною величиною) значень
велика, то це призводить до
збільшення умовної дисперсії у наступні періоди. В свою чергу, при значній
умовній дисперсії поява великих (за абсолютною величиною) значень  стає більш
ймовірною. Навпаки, якщо значення
стає більш
ймовірною. Навпаки, якщо значення  протягом декількох періодів близькі
до нуля, то це призводить до зниження умовної дисперсії у наступні періоди
практично до рівня k. У свою чергу, при низькому рівні умовної дисперсії більш
ймовірна поява малих (за абсолютною величиною) значень
протягом декількох періодів близькі
до нуля, то це призводить до зниження умовної дисперсії у наступні періоди
практично до рівня k. У свою чергу, при низькому рівні умовної дисперсії більш
ймовірна поява малих (за абсолютною величиною) значень  .
.
Таким чином, ARCH-процес
характеризується інерційністю умовної дисперсії (кластеризацією волатильності).
Узагальнення цієї моделі  модель
GARCH (generalized ARCH), яке було здійснене Т. Болерслевим [18], дозволяє
отримати більш довгі кластери при невеликій кількості параметрів. Обидві моделі
та їх модифікації виходять з припущення про короткострокову пам’ять в
досліджуваних процесах, а також про ринкову ефективність.
модель
GARCH (generalized ARCH), яке було здійснене Т. Болерслевим [18], дозволяє
отримати більш довгі кластери при невеликій кількості параметрів. Обидві моделі
та їх модифікації виходять з припущення про короткострокову пам’ять в
досліджуваних процесах, а також про ринкову ефективність.
Модель ARMA часто дозволяє
одержати більш „компактний” опис часових залежностей для умовного математичного
сподівання, ніж модель AR. Подібним чином модель GARCH дає можливість обійтися
меншою кількістю параметрів порівняно з моделлю ARCH, якщо мова йде про умовну
дисперсію.моделі широко використовуються для моделювання особливостей
фінансових часових рядів, пов’язаних, зокрема з: - „важкими хвостами”
розподілів;
кластеризацією волатильності.
Як вже було зазначено,
розподіли ймовірності для фінансово-економічних часових рядів часто демонструють
хвости, які значно довші (іноді кажуть „важчі”) за нормальний розподіл. Важкий
хвіст відомий як завищений ексцес, або лептокуртозис. Феномен кластеризації
волатильності передбачає, що волатильність коливається, почергово зростаючи та
спадаючи. За періодами високої волатильності слідує період з низькою
волатильністю і навпаки.
Моделі ARCH і GARCH мають
спільний недолік: вони не відображають той факт, що має місце на практиці ефект
асиметрії, тобто волатильність реагує по-різному на падіння та підвищення цін.
Це відбувається тому, що волатильність залежить від квадрату , а тому
нечутлива до його знаку. Цей недолік долається в рамках так званої
експоненціальної моделі GARCH, або EGARCH, яка була запропонована Д. Нельсоном
[13].
, а тому
нечутлива до його знаку. Цей недолік долається в рамках так званої
експоненціальної моделі GARCH, або EGARCH, яка була запропонована Д. Нельсоном
[13].
Зауважимо, що припущення про
нормальний закон розподілу цінових флуктуацій ставилися під сумнів ще до
остаточного формування гіпотези ефективного ринку. Зокрема, Б. Мандельброт [17]
показав, що прибутки можуть належати сімейству стійких розподілів Парето, які
характеризуються невизначеною, або нескінченною дисперсією.
Таким чином, лінійна
парадигма в своїй основі припускає, що інвестори раціонально реагують на
інформацію, тобто використовують її відразу після отримання, а не чекають її
накопичення в майбутньому.
Концепція раціонального
інвестора стверджує, що минула інформація вже дисконтована, знайшовши
віддзеркалення у вартості цінних паперів. Отже,лінійна парадигма має на увазі,
що прибутки повинні мати приблизно нормальний розподіл і бути незалежними.
В роботах по аналізу часових
рядів першим кроком є, як правило, визначення порядку інтегрованості ряду (мова
йде про значення параметру d процесу ARIMA (p, d, q)). Як правило, автори
обмежуються вибором d, що дорівнює 0 або 1. Випадок d=0 відповідає короткій
пам’яті ряду, тоді як при d=1 можна зробити висновок про нескінченість пам’яті.
Нескінченість пам’яті означає, що кожен шок впливає на поведінку ряду
нескінченно довго. З іншого боку, існування короткої пам’яті означає, що
наслідки шоку зникнуть досить швидко, але при цьому поза зором дослідників
залишається проміжна ситуація, коли наслідки шоку виявляються хоча і обмеженими
в часі, але тривалими (тобто, випадок довгої пам’яті, або персистентності) [11,
с.123].
Для вирішення цієї проблеми
Грейнджер і Джойо [18] запропонували новий клас моделей ARIMA (p, d, q), що
допускає можливість використання дробового параметру d, а саме
дробово-інтерговані процеси (ARFIMA) процеси з довгою пам’яттю, які можуть
розглядатись в якості альтернативи традиційним варіантам короткої та
нескінченої пам’яті ряду.
Процеси ARMA (p, q) та ARIMA
(p, d, q) є частковими випадками цього процесу при d=0 та d=1 відповідно.
Моделювання довгої пам’яті на
основі використання традиційних процесів ARMA з включенням великої кількості лагів
також можливе (автокореляція буде являти собою у цьому випадку суму експонент),
однак таке моделювання не дозволяє оцінити ступінь персистентності ряду, і,
крім того, в цьому випадку для персистентного ряду ми отримуємо корні поліномів
авторегресії ковзного середнього близькими до одиниці, внаслідок чого
асимптотичні розподіли виявляються поганими апроксимаціями розподілу на
скінчені вибірки [5, c.124].
Наявність довгої пам’яті
означає, що інформація, яка міститься в минулій поведінці ряду, виявляється корисною
для прогнозування його майбутніх значень і дає можливість здійснити більш
точний прогноз, ніж прогноз, зроблений за допомогою моделі „випадкового
блукання”.
РОЗДІЛ 2. МАТЕМАТИЧНІ МЕТОДИ
ЛІНІЙНИХ СТОХАСТИЧНИХ МОДЕЛЕЙ ФІНАНСОВИХ РИНКІВ
.1 Модель ковзного середнього MA(q)
як метод згладжування даних вибіркового характеру
Ще однією простою моделлю породження
часового ряду є процес ковзного середнього порядку q (MA (q)). Відповідно до
цієї моделі,

де  - процес
білого шуму.
- процес
білого шуму.
Такий процес має нульове
математичне очікування. Модель можна узагальнити до процесу, що має ненульове
математичне очікування μ, вважаючи
 тобто
тобто

Для процесу змінного
середнього порядку q використовується позначення MA (q) (ковзне середнє -
moving average).
При q = 0 і μ =
0 отримуємо
процес білого шуму. Якщо q = 1, то
 - ковзне середнє першого порядку. В
останньому випадку
- ковзне середнє першого порядку. В
останньому випадку
 , k> 1,
, k> 1,
Так, що процес  являється
стаціонарним з
являється
стаціонарним з


Автокореляції цього процесу
рівні

тобто коррелограмм процесу
має вельми специфічний вид. Корельованими виявляються тільки сусідні
спостереження. кореляція між ними позитивна, якщо b> 0, і негативна при b
<0. Відповідно, процес MA (1) з b> 0 має більш гладкі, в порівнянні з
білим шумом, реалізації, а процес MA (1) з b <0 має менш гладкі, в
порівнянні з білим шумом, реалізації. Зауважимо, що для будь-якого процесу MA
(1)  тобто
кореляційний зв'язок між сусідніми спостереженнями невелика, тоді як у процесу
AR (1) такий зв'язок може бути як завгодно сильною (при значеннях
тобто
кореляційний зв'язок між сусідніми спостереженнями невелика, тоді як у процесу
AR (1) такий зв'язок може бути як завгодно сильною (при значеннях 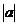 , близьких
до 1). Модель MA (q) коротко можна записати у вигляді
, близьких
до 1). Модель MA (q) коротко можна записати у вигляді
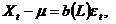 де
де

для неї
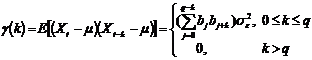
так що MA (q) є стаціонарним
процесом з нульовим математичним очікуванням, дисперсією
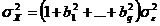
і автокореляції

Тут статистичний зв'язок між
спостереженнями зберігається протягом q одиниць часу (тобто "тривалість
пам'яті" процесу дорівнює q) [3, c. 290].
Подібного роду часові ряди
відповідають ситуації, коли деякий економічний показник знаходиться в рівновазі,
але відхиляється від положенняя рівноваги в силу послідовно виникаючих
непередбачуваних подій, причому система така, що вплив таких подій
відзначається протягом деякого періоду часу.
Якщо вплив минулих подій
слабшає з часом показовим чином, так що 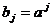 , 0 <a <1, то штучне
припущення про те, що ряд
, 0 <a <1, то штучне
припущення про те, що ряд  починається
в "нескінченному минулому", призводить до моделі нескінченного
ковзного середнього MA (∞)
починається
в "нескінченному минулому", призводить до моделі нескінченного
ковзного середнього MA (∞)

Раніше ми бачили, що таке ж
подання допускає стаціонарний процес авторегресії першого порядку AR (1)

тобто в даному випадку процес
MA (∞) еквівалентний процесу AR (1).
Взагалі, всякий стаціонарний
процес AR (p) можна записати у формі процесу
(∞):

Де 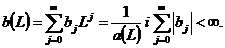
.2 Авторегресійна модель
AR(p) як лінійна комбінація незалежних складових попередніх періодів
Однією з широко
використовуваних моделей часових рядів є процес авторегресії (модель
авторегресії). У своїй простій формі модель авторегресії описує механізм породження
ряду таким чином:

де  - процес
білого шуму, що має нульове математичне очікування і дисперсію
- процес
білого шуму, що має нульове математичне очікування і дисперсію  - деяка
випадкова величина, а a ≠ 0 - деякий постійний коефіцієнт. При цьому E (
- деяка
випадкова величина, а a ≠ 0 - деякий постійний коефіцієнт. При цьому E ( ) = aE(
) = aE( ) так що
розглянутий процес може бути стаціонарним тільки якщо E (
) так що
розглянутий процес може бути стаціонарним тільки якщо E ( ) = 0 для
всіх t = 0, 1,..., n.
) = 0 для
всіх t = 0, 1,..., n.
Далі,

Якщо випадкова величина  не
корельована з випадковими величинами
не
корельована з випадковими величинами  ,
,  ...,
..., 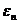 , то звідси випливає, що
, то звідси випливає, що
( ,
, ) = 0, Cov (
) = 0, Cov (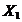 ,
, ) = 0,...,
Cov (
) = 0,...,
Cov ( ,
,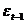 ) = 0, Cov (
) = 0, Cov ( ,
, ) = 0
) = 0
Припускаючи, нарешті, що
( ) = D (
) = D ( ) =
) =  для всіх t
= 1,..., n,
для всіх t
= 1,..., n,
знаходимо:

Останнє може виконуватися
тільки при виконанні умови  <1, тобто
<1, тобто 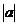 <1.
<1.
При цьому отримуємо вираз для


Що стосується автоковаріацій
і автокореляцій, то


тобто при зроблених
припущеннях автоковаріаціі і автокорреляции залежать тільки від того, наскільки
рознесені за часом відповідні спостереження [6,c.126].
Таким чином, механізм
породження послідовних спостережень, заданий співвідношеннями

породжує стаціонарний часовий
ряд, якщо 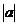 <1;
<1;
випадкова величина  не
корельована з випадковими
не
корельована з випадковими  ,
,  ...,
..., 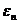 ;
;
( ) = 0;(
) = 0;( ) =
) =  .
.
При цьому
 .
.
Розглянута модель породжує
(при зазначених умовах) стаціонарний ряд, що має нульове математичне
очікування. Однак її можна легко поширити і на тимчасові ряди  з
ненульовим математичним очікуванням E (
з
ненульовим математичним очікуванням E ( ) = μ, вважаючи, що
зазначена модель відноситься до центрованої ряду
) = μ, вважаючи, що
зазначена модель відноситься до центрованої ряду :
:
 , t = 1,..., n,
, t = 1,..., n,
так що
 t = 1,..., n,
t = 1,..., n,
Де δ = μ
(1- a).
Тому без обмеження спільності
можна обійтися в поточному розгляді моделями авторегресії, що породжують
стаціонарний процес з нульовим середнім.
Продовжуючи розгляд для
раніше визначеного процесу  (з нульовим математичним
очікуванням), зауважимо, що для нього
(з нульовим математичним
очікуванням), зауважимо, що для нього
 так що
так що
ρ (1) = γ (1) / γ
(0) = a,
і при значеннях a> 0,
близьких до 1, між сусідніми спостереженнями мається сильна позитивна
кореляція, що забезпечує більш гладкий характер поведінки траєкторій ряду в
порівнянні з процесом білого шуму. При a <0 процес авторегресії, навпаки,
має менш гладкі реалізації, оскільки в цьому випадку проявляється тенденція
чергування знаків послідовних спостережень. Наступні два графіки демонструють
поведінку змодельованих реалізацій часових рядів, породжених моделями авто
регресії
 = a
= a  і a = - 0.8
(Рис. 2.1)
і a = - 0.8
(Рис. 2.1)
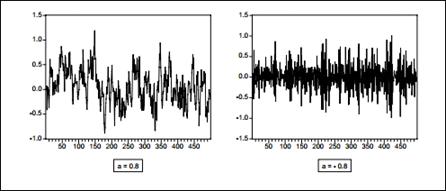
Рис. 2.1 Змодельована
реалізація часового ряду
Тепер ми повинні звернути
увагу на наступну важливу обставину. В практичних ситуаціях стартове"
значення  , на основі
якого в відповідно до співвідношення
, на основі
якого в відповідно до співвідношення  = a
= a  +
+  будуються подальші значення ряду
будуються подальші значення ряду  , може
відноситися до кінця попереднього періоду, на якому просто в силу інших
економічних умов еволюція відповідного економічного показника слід іншої
моделі, наприклад, моделі
, може
відноситися до кінця попереднього періоду, на якому просто в силу інших
економічних умов еволюція відповідного економічного показника слід іншої
моделі, наприклад, моделі  = a
= a  +
+  з іншими
значеннями
з іншими
значеннями  Більш того,
статистичні дані про поведінку ряду до моменту t = 0 можуть бути відсутнім
зовсім, так що значення
Більш того,
статистичні дані про поведінку ряду до моменту t = 0 можуть бути відсутнім
зовсім, так що значення  є просто
деякою спостережуваної числовий величиною. В обох випадках ряд
є просто
деякою спостережуваної числовий величиною. В обох випадках ряд  вже не буде
стаціонарним навіть при
вже не буде
стаціонарним навіть при 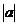 <1. Розглянемо
докладніше характеристики і поведінку ряду в таких ситуаціях [8,c.183].
<1. Розглянемо
докладніше характеристики і поведінку ряду в таких ситуаціях [8,c.183].
Якщо не конкретизувати
модель, відповідно до якої породжувалися спостереження до моменту t = 1, то
значення  можна
розглядати як фіксоване. при цьому
можна
розглядати як фіксоване. при цьому

так що і математичне
очікування і дисперсія випадкової величини  , а також ковариации
, а також ковариации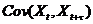 залежать від
t.
залежать від
t.
У той же час, якщо 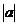 <1, то
при t → ∞ отримуємо
<1, то
при t → ∞ отримуємо
( ) → 0,
D(
) → 0,
D( ) →
) →  ,
, 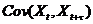 →
→  ,
,
тобто при t → ∞
значення математичного очікування і дисперсії випадкової величини  , а також
автоковаріаціі
, а також
автоковаріаціі 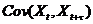 стабілізуються,
наближаючись до своїх граничних значень.
стабілізуються,
наближаючись до своїх граничних значень.
З цієї точки зору, умова 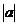 <1 можна
трактувати як умова стабільності ряду, що породжується моделлю
<1 можна
трактувати як умова стабільності ряду, що породжується моделлю  при
фіксованому значенні
при
фіксованому значенні  .
.
Розглянемо в цій ситуації
поряд із щойно дослідженим ряду  ,
,
формалізований
стохастичний фінансовий індекс
 ,
, 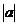 <1
<1
ряд, породжуваний моделлю

 ;
;
маємо:
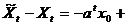
 ;
;
при t → ∞
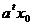 → 0 і
→ 0 і 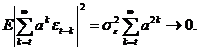
Таким чином, ряд  є граничним
для
є граничним
для  ; ряд
; ряд  "виходить
на режим"
"виходить
на режим"  при t →
∞. При цьому вихід ряду
при t →
∞. При цьому вихід ряду  на режим
на режим  відбувається
тим швидше, чим ближче
відбувається
тим швидше, чим ближче 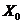 і a до
нуля.
і a до
нуля.
Для ряду 
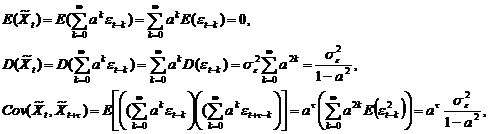
так що  -
стаціонарний ряд (в широкому сенсі). Крім того,
-
стаціонарний ряд (в широкому сенсі). Крім того,


так що 
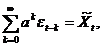
тобто  задовольняє
співвідношенню
задовольняє
співвідношенню

Оскільки  не входить
в праву частину виразів для
не входить
в праву частину виразів для  то випадкова величина
то випадкова величина  не
корельована з
не
корельована з  тобто
тобто  є
інновацією (оновленням). У підсумку отримуємо, що
є
інновацією (оновленням). У підсумку отримуємо, що  -
стаціонарний процес авто регресії першого порядку, і фактично саме цей процес
мається на увазі, коли говорять про стаціонарному процесі AR (1).
-
стаціонарний процес авто регресії першого порядку, і фактично саме цей процес
мається на увазі, коли говорять про стаціонарному процесі AR (1).
Проілюструємо сказане вище за
допомогою змодельованих реалізацій ряду  , породжених моделлю
, породжених моделлю  з
з  = 0.2 і
різними значеннями коефіцієнта a і стартового значення
= 0.2 і
різними значеннями коефіцієнта a і стартового значення Рис. (2.2).
Рис. (2.2).
Розглянуту щойно модель  називають
процесом авторегресії першого порядку. Процес авторегресії порядку p (в
короткому позначенні - AR (p)) визначається співвідношеннями
називають
процесом авторегресії першого порядку. Процес авторегресії порядку p (в
короткому позначенні - AR (p)) визначається співвідношеннями

де  - процес
білого шуму з D (
- процес
білого шуму з D ( ) =
) =  . Для
простоти ми будемо тепер відразу вважати, що
. Для
простоти ми будемо тепер відразу вважати, що 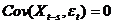 для всіх
s> 0; при цьому говорять, що випадкові величини
для всіх
s> 0; при цьому говорять, що випадкові величини  утворюють
інноваційну (обновляющую) послідовність, а випадкова величина
утворюють
інноваційну (обновляющую) послідовність, а випадкова величина  називається
інновацією для спостереження в момент t.
називається
інновацією для спостереження в момент t.

Рис. 2.2 Змодельовані
ситуації ряду
Така термінологія пояснюється
тим, що спостережуване значення ряду в момент t виходить тут як лінійна
комбінація p попередніх значень цього ряду плюс не корелювали з цими
попередніми значеннями випадкова складова  , відображає оновлену інформацію,
скажімо, про стан економіки, на момент t, впливає на спостережуване значення
, відображає оновлену інформацію,
скажімо, про стан економіки, на момент t, впливає на спостережуване значення  . При
розгляді процесів авторегресії і деяких інших моделей зручно використовувати
оператор запізнювання L (lag operator), який впливає на часовий ряд і
визначається співвідношенням
. При
розгляді процесів авторегресії і деяких інших моделей зручно використовувати
оператор запізнювання L (lag operator), який впливає на часовий ряд і
визначається співвідношенням

в деяких посібниках його
називають оператором зворотного зсуву та використовують для нього позначення B
(backshift operator).
Якщо оператор запізнювання
застосовується k разів, що позначається як 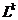 , то це дає в результаті
, то це дає в результаті

Вираз

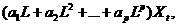
а співвідношення, що процес
авторегресії p-го порядку, у вигляді

Де 
Для того, щоб такий процес
був стаціонарним, всі корені алгебраїчного рівняння a (z) = 0 (речові і
комплексні) повинні лежати поза одиничного кола . (Зокрема, для процесу AR (1) маємо
a(z)=1- az, рівняння a (z) = 0 має корінь z= 1/a, і умова стаціонарності
. (Зокрема, для процесу AR (1) маємо
a(z)=1- az, рівняння a (z) = 0 має корінь z= 1/a, і умова стаціонарності  рівносильно
вже знайомому нам умові
рівносильно
вже знайомому нам умові  .) При цьому
рішення рівняння
.) При цьому
рішення рівняння  можна
представити у вигляді
можна
представити у вигляді
 де
де 
звідки, зокрема, випливає, що

Стаціонарний процес AR (p) з
ненульовим математичним очікуванням μ задовольняє
співвідношенню

або
 де
де

При цьому рішення рівняння a  має вигляд
має вигляд

Таким чином, якщо
стаціонарний процес AR (p) заданий у вигляді
 то
то
слід пам'ятати про те, що в
цьому випадку математичне очікування цього процесу рівне не δ, а

Для процесу AR (1) маємо 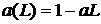 , так що
(незалежно від того, рівне μ нулю чи ні)
, так що
(незалежно від того, рівне μ нулю чи ні)
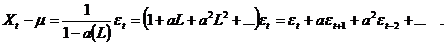
З останнього виразу відразу
видно, що
 , k = 0, 1, 2,....
, k = 0, 1, 2,....
При 0 <a <1
коррелограмм (графік функції ρ (k) для k = 0,
1, 2,...) відображає показове спадання кореляцій зі зростанням інтервалу між
спостереженнями;
при -1 <a <0
коррелограм має характер загасаючої косинусоид.
Порівняємо поведінку
коррелограм стаціонарного процесу AR (1) при a = ± 0.8 (Рис. 2.3):

Рис. 2.3 Поведінка
коррелограм
Коррелограммa процесу AR (p)
при p> 1 має більш складну форму, залежну від розташування (на комплексній
площині) коренів рівняння a (z) = 0. Однак для великих значень k автокорреляция
ρ
(k) добре
апроксимується значенням  , де
, де  - найменший
за абсолютною величиною корінь рівняння a(z) = 0, якщо цей корінь є речовим і
позитивним, або
- найменший
за абсолютною величиною корінь рівняння a(z) = 0, якщо цей корінь є речовим і
позитивним, або
укладена в інтервалі  в іншому
випадку. Тут A> 0 - деяка постійна, обумовлена коефіцієнтами
в іншому
випадку. Тут A> 0 - деяка постійна, обумовлена коефіцієнтами 
Якщо помножити на (k> 0)
обидві частини співвідношення, що визначає процесс AR (p), і після цього взяти
від обох частин математичне очікування, то отримаємо співвідношення
(k> 0)
обидві частини співвідношення, що визначає процесс AR (p), і після цього взяти
від обох частин математичне очікування, то отримаємо співвідношення
 k> 0.
k> 0.
Розділивши обидві частини
останнього на  , приходимо
до системи рівнянь Юла-Уокера
, приходимо
до системи рівнянь Юла-Уокера
 , k> 0.
, k> 0.
Ця система дозволяє
послідовно знаходити значення автокореляцій і дає можливість, використовуючи
перші p рівнянь, висловити коефіцієнти 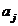 через значення перших p
автокореляцій, що можна безпосередньо використовувати при підборі моделі
авторегресії до реальних статистичними даними.
через значення перших p
автокореляцій, що можна безпосередньо використовувати при підборі моделі
авторегресії до реальних статистичними даними.
.3. Модель авторегресії та
ковзного середнього ARMA(p, q) та інтегральна модель ARIMA(p, d, q)
Процес  з нульовим
математичним сподіванням, належить такому класу процесів, що характеризуються
порядками p i q його AR і MA cкладових і визначається як процесс ARMA(p, q)
(autoregressive moving average, mixed autoregressive moving average). Більш
того, процес
з нульовим
математичним сподіванням, належить такому класу процесів, що характеризуються
порядками p i q його AR і MA cкладових і визначається як процесс ARMA(p, q)
(autoregressive moving average, mixed autoregressive moving average). Більш
того, процес  з нульовим
математичним сподіванням належить класу ARMA(p, q), якщо
з нульовим
математичним сподіванням належить класу ARMA(p, q), якщо
 ,
, 
де 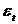 - процесс
білого шуму і
- процесс
білого шуму і  . В
оперативній формі останнє відношення має вигляд
. В
оперативній формі останнє відношення має вигляд 
 ,
,
де 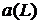 і
і  має то й же
вигляд, що і в попередніх моделях AR(p) i MA(q). Якщо процесс має стале
математичне сподівання µ, то він є просом типу ARMA(p, q), якщо
має то й же
вигляд, що і в попередніх моделях AR(p) i MA(q). Якщо процесс має стале
математичне сподівання µ, то він є просом типу ARMA(p, q), якщо
 ,
,
Виділимо наступні властивості
ARMA(p, q) з 
Якщо процес стаціонарний, то
існує еквівалентний йому процес МА(∞)
 ,
,
або
 ,
,
де 
Якщо всі корені рівняння 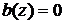 лежать поза
одиничним колом
лежать поза
одиничним колом  , то існує
еквівалентне представлення процесу
, то існує
еквівалентне представлення процесу  у вигляді процесу авто регресії
нескінченного порядку AR(∞)
у вигляді процесу авто регресії
нескінченного порядку AR(∞)
 ,
,
або  ,
,

Звідси випливає, що
стаціонарний процес ARMA (p, q) завжди можна апроксимувати процесом змінного
середнього достатньо високого порядку, а при виконанні умови оборотності його
можна також апроксимувати процесом авторегресії досить високого порядку.
Специфіку форми корелограми
процесу ARMA (p, q) в загальному випадку вказати важче, ніж для моделей AR (p)
і MA (q). Зазначимо лише, що для значень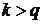 корелограм процессу
корелограм процессу  виглядає
так само, як і коррелограмм процесу авторегресії
виглядає
так само, як і коррелограмм процесу авторегресії  . Так, для процесу ARMA (1, 1)
. Так, для процесу ARMA (1, 1)
 для
для 
як і у процесі  . При цьому,
однак
. При цьому,
однак  .
.
Передумовою для обґрунтування
використання моделей ARMA є наступний факт. Якщо ARMA  ряд
ряд  і ARMA
і ARMA  ряд
ряд  статистично
незалежні між собою, і
статистично
незалежні між собою, і 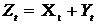 , то типовим
є положення, коли
, то типовим
є положення, коли  є ARMA (p,
q) поруч, у якого
є ARMA (p,
q) поруч, у якого

 якщо
якщо 
 якщо
якщо  .
.
Можливі також ситуації, коли
значення p і 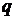 є меншими
зазначених значень. (Такі ситуації виникають у випадках, коли многочлени
є меншими
зазначених значень. (Такі ситуації виникають у випадках, коли многочлени  і
і  , відповідні
авторегресійним частинам процесів
, відповідні
авторегресійним частинам процесів  і
і  , мають
спільні корені.)
, мають
спільні корені.)
В окремому випадку, коли
обидва ряди мають тип AR (1), але з різними параметрами, їх сума має тип ARMA
(2, 1).
В економіці багато часові
ряди є агрегованими. Із зазначеного вище факту випливає, що якщо кожна з
компонент відповідає простій моделі AR, то при незалежності цих компонент їх
сума буде ARMA процесом. Такого ж роду процес ми отримаємо, якщо частина
компонент має тип AR, а інші компоненти мають тип MA. Єдиним винятком є
випадок, коли всі компоненти є MA процесами - в цьому випадку в результаті
отримуємо MA процес.
Припустимо, нарешті, що
"істинний" економічний ряд відповідає AR (p)моделі, але значення
цього ряду вимірюються з випадковими помилками, що утворюють процес білого шуму
(тобто MA (0)). Тоді спостережуваний ряд має тип ARMA (p, p).
Зауваження
Раніше ми вже говорили про
те, що якщо ARMA (p, q) процес  задовольняє умові оборотності, то
його можна представити у вигляді стаціонарного процесу AR (∞). Останній,
у свою чергу, можна апроксимувати стаціонарним процесом AR (p), бути може,
досить високого порядку.
задовольняє умові оборотності, то
його можна представити у вигляді стаціонарного процесу AR (∞). Останній,
у свою чергу, можна апроксимувати стаціонарним процесом AR (p), бути може,
досить високого порядку.
Таким чином, в практичних
завданнях можна було б і зовсім обійтися без використання моделей ARMA,
обмежуючись небудь AR або MA моделями. При цьому, однак, кількість
коефіцієнтів, які підлягають оцінюванню, може виявитися занадто великим (що
знижує точність оцінювання) і навіть перевершувати кількість наявних
спостережень. У цьому сенсі моделі ARMA можуть бути "більш економними
".
РОЗДІЛ 3. МОДЕЛЬ ЕВОЛЮЦІЇ ФІНАНСОВИХ
РИНКІВ НА ПРИКЛАДІ МОДЕЛІ АВТОРЕГРЕСІЇ ТА КОВЗНОГО СЕРЕДНЬОГО ARMA (p, q)
Вихідні дані:
- Дані обсяги випуску акцій по місяцях 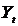 подані в
таблиці 1
подані в
таблиці 1
- Рівень значущості 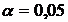
Обсяг випуску акцій

Побудуємо задачу
нестаціонарного ряду Y. Побудуємо автокореляцію і часткову автокореляцію
функції. Для цього ми вводимо ми використовуємо програмний пакет Matrixer.
Використовуємо значення вектора 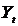 і за допомогою функції «acfіY
&pacf» отримаємо результати:
і за допомогою функції «acfіY
&pacf» отримаємо результати:

Рис. 3.1 Оцінки і статистика
функції
Також ми отримали результат у
вигляді графіків:


Рис. 3.2 Автокореляційна (а)
і часткова автокореляційна (б) функції
Так як, згідно рис.3.2 значно
відрізняються від нуля тільки коефіцієнти часткової автокореляції  для величини лагу 1, то робимо висновок про те, що ряд
для величини лагу 1, то робимо висновок про те, що ряд 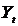 є
реалізацією стохастичногo процесу ARMA(1,0).
є
реалізацією стохастичногo процесу ARMA(1,0).

Для побудови моделі ARMA(1,0)
використовуємо формулу «boxjen! (1,0) Y». З’являється вікно (рис.3) у якому ми
обираємо метод.

Рис. 3.3 Вибір методу оптимізації
Побудова ARMA здійснюється за
допомогою методу найменших квадратів. Відповідні процедури мають ітераційний
характер і можуть продовжуватись безкінечно, якщо не досягаються умови
завершення процесу за точністю отриманих результатів. В цьому випадку слід
задавати кінчеве число кроків ітераційного процесу, або римусово зупинити
процес рішення за допомогою кнопки «Результати» у вікні процесу рішень.
Результати розрахунку моделі
ARMA(1,0) на рис.3.4.

Рис. 3.4 Результати розрахунку
моделі ARMA(1,0)
Значущим є тільки коефіцієнт
при  .
.
Для перевірки оптимальності
моделі ARMA(1,0) розрахуємо параметри моделей ARMA(2,0) i ARMA(2,1). За
допомогою функції «boxjen!(2,0) Y» та «boxjen!(2,1) Y» отримаємо:

Рис. 3.5 Результати
розрахунку моделі ARMA(2,0)

Рис. 3.6 Результати
розрахунку моделі ARMA(2,1)
Значущим в обох моделях є
тільки коефіцієнт при  .
.
Зведемо результати
разрахунків за трьома моделями ARMA(1,0), ARMA(,0) та ARMA(2,1) в таблицю 3.2.
Таблица
3.2
Результати розрахунків параметрів
моделей ARMA(1,0), ARMA(2,0) і ARMA(2,1)
|
Параметр
|
Модель ARMA
|
|
(1,0)
|
(2,0)
|
(2,1)
|
|
Значення
|
Значущість
|
Значення
|
Значущість
|
Значення
|
Значущість
|
|
α0
|
-10,553
|
0,844
|
-16,63
|
0,763
|
-14,17
|
0,548
|
|
α1
|
1,0049
|
0
|
0,93
|
0
|
1,548
|
0,025
|
|
α2
|
|
|
0,077
|
0,597
|
-0,541
|
0,426
|
|
β1
|
|
|
|
|
-0,663
|
0,277
|
|
R2
|
0,906
|
|
0,907
|
|
0,908
|
|
|
Σε^2
|
80,82
|
|
81,41
|
|
81,69
|
|
|
AIC
|
|
11,73
|
|
11,76
|
|
Значення критеріїв
відрізняються несуттєво, при тому для ARMA(1,0) значення критерії  , AIC
мінімальні, що говорить про оптимальність моделі ARMA(1,0). Результати
розрахунків по моделі ARMA(1,0) на рис. 3.7.
, AIC
мінімальні, що говорить про оптимальність моделі ARMA(1,0). Результати
розрахунків по моделі ARMA(1,0) на рис. 3.7.

Рис. 3.7 Фактичні і
розрахункові результати моделі ARMA
ВИСНОВКИ
Задачі оцінювання, моделювання і
прогнозування поведінки систем, що відносяться до галузі економіки та
економетрики зокрема, давно обговорюються на міждисциплінарному рівні.
Дослідники все частіше намагаються застосувати методи з областей фізики і математики
для вивчення динамічних характеристик фінансових інструментів.
Однак при цьому ігнорується той
факт, що застосовувані методи і вигадувані алгоритми стають корисними лише
тоді, коли вони орієнтовані на розуміння динаміки цінового руху. Питання, відповідь
на який шукає кожен практичний учасник фінансового ринку, говорить: що може
впливати на передбачуваність цінового руху? Модель, шум? Якщо шум, то як його
позбутися, модель - на основі чого?
Відомі алгоритми та їх програмні
реалізації, орієнтовані здебільшого на рішення приватних завдань і
характеризуються наявністю суб'єктивних факторів. Існують загальні Емпіричний
аналіз еволюції фінансових індексів, як, зрозуміло, і багатьох інших -
економічних, соціологічних, - повинен починатися, перш за все, з побудови
відповідної ймовірно-статистичної (або який-небудь інший) моделі, правильний
вибір якої є справою досить непростим
У загальній теорії часових
рядів є цілий арсенал різноманітних "стандартних" лінійних моделей,
серед яких в першу чергу треба назвати такі, як 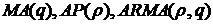 .
.
У зв'язку з цим не можна
створити універсальний алгоритм, який поєднує в собі оцінювання, моделювання та
прогнозування вартості фінансових інструментів, використовуючи який можна було
б без участі суб'єктивних факторів передбачити з достатньою точністю ціну
обраних фінансових інструментів на наступний день, місяць чи рік, не вимагаючи
при цьому ніяких даних крім минулих значень цін.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
1. Айвазян
С.А., Прикладная статистика и основы эконометрики. / Айвазян С.А., Мхитарян
B.C.- М.: ЮНИТИ, 1998. - 1022 с.
2. Бабчук
В.Г. Инвариантные множества системы линейных стохастических диффузионных
уравнений с постоянными коэффициентами / Бабчук В.Г - Киев: ИК АН УССР, 1980.-
452с.
. Вовк
В.М. Моделювання економічних процесів підприємства: монографія / В.М. Вовк,
Н.І. Камінська, С.С. Прийма. - Дрогобич: Коло, 2011. - 448 с.
. Вовк
В.М. Оптимізаційні методи і моделі: навч. посібник / В.М. Вовк, Л.М. Зомчак. -
Львів: ЛНУ імені Івана Франка, 2014. - 360 с.
. Здрок
В.В. Моделювання економічної динаміки: Практикум / В.В. Здрок, Т.Я. Лагоцький,
І.М. Паславська. - Львів: "Магнолія 2006", 2013. - 256 с.
. Истигечева
Е.В. Прогнозирование изменений котировок финансовых инструментов на основе
модели стохастической волатильности // Истигечева Е.В - Томск:. Известия ТПУ,
2006.-Т.7. - 420 с.
. Истигечева
Е.В., Оценивание параметров волатильности // Истигечева Е.В., Мицель А.А. -
Томск, 2006. -422 с.
. Макаров
А. Исследование устойчивости параметрически возмущенных линейных стохастических
систем с убывающими коэффициентами. / Макаров А.П., Самохин Ю.А., Фомин В.Н. -
Ижевск, 1984. - 360 с.
. Вовк
В.М. Макроекономічна політика в Україні: проблеми науки та практики.
Актуальність оптимізації управління в економіко-виробничих системах: монографія
/ В.М. Вовк - Харків: ВД «ІНЖЕК», 2007. - 350 с.
10. Мандельброт
Б., (Не) послушне рынки. Фрактальная революция в финансах / Бенуа Мандельброт,
Хадсон Р.Л., 2006.-Киев.: Диалектика. -400 с. [243]
. Мокін,
Б.І. М Математичні методи ідентифікації динамічних систем навчальний посібник /
Б.І. Мокін, В.Б. Мокін, О.Б. Мокін. - Вінниця:ВНТУ, 2010. - 260 с.
12. Пугачев
В.С. Теория стохастических систем. / Пугачев В.С., Синицын И.Н. М.: Логос,
2004, - 1000 с.
. Суслов
В.И., Эконометрия: Учебник. Новосибирск / Суслов В.И., Ибрагимов Н.М., Талышева
Л.П., Цыплаков А.А. Изд-во СО РАН, 2005 - 744 с.
. Тихомиров
Н.П., Дорохииа Е.Ю. Эконометрика. М.: Изд.-во Рос. экон. акад., 2002. - 640 с.
. Ширяев,.
Вероятность: [В 2-х кн.] Элементарная теория вероятностей. Математические
основания. Предельные теоремы / А.Н. Ширяев. Москва: МЦНМО, 2004. [Кн. 1] -
Издание 3-е, переработанное и дополненное.- 2004. - 520 с.
. Ширяев,.
Задачи по теории вероятностей: учеб. пособие / А. Н. Ширяев. - Москва: Изд-во
МЦНМО, 2006. - 416с.; 22. - Предм Библиогр.: 2000. - 604 с.
17. Boltzmann
L. Weitere Studien über das Wärmegleichgewicht unter
18. Grassberger
P., Procaccia I. Characterization of strange attractors. Phys. Rev. Lett. 50,
346-349 (1983).
. Gasmolekülen
// Sitzber. Acad. Wiss. Wien. 1872, Bd. 66.- S. 275-376.
20. Engle
R.F. Autoregressive conditional heteroscedasticity with estimates of the
variance of United Kingdom inflation // Econometrica, 1982. -V.50. pp.