Адекватность модели энерговооруженности предприятия
Федеральное
агентство по образованию
Государственное
образовательное учреждение
высшего
профессионального образования
«Южно-Уральский
государственный университет»
Кафедра
Экономической теории и мировой экономики
Контрольная
работа
по
курсу «Эконометрика»
Выполнил:
Студент группы: ЗЭУ-342
Шостак Наталья
Николаевна
Проверил преподаватель:
Сергей Алексеевич
Никифоров
Челябинск
Задача
Имеются выборочные данные по
однородным предприятиям: энерговооруженность труда одного рабочего (кВт /час) и
выпуск готовой продукции (шт).
Определить
. Факторные и результативные
признаки.
. Провести исследование взаимосвязи
энерговооруженности и выпуска готовой продукции.
. Построить уравнение регрессии и
вычислить коэффициент регрессии.
. Построить графики практической и
теоретической линии регрессии.
. Определить форму связи и измерить
тесноту связи.
. Провести оценку адекватности.
Решение
. (Х) - факторным признаком является
энерговооруженность.
(Y)- результативным признаком
является выпуск готовой продукции.
. Исходные данные поместим в
следующую таблицу.
|
Номер анализа
|
X
|
Y
|
(X -X̄)
|
(X - X̄)²
|
X²
|
Y²
|
(XY)
|
|
1
|
1,5
|
11
|
-1
|
1
|
2,25
|
121
|
16,5
|
|
2
|
2
|
6
|
-0,5
|
0,25
|
4
|
36
|
12
|
|
3
|
2,5
|
16
|
0
|
0
|
6,25
|
256
|
40
|
|
4
|
3
|
21
|
0,5
|
0,25
|
9
|
441
|
63
|
|
5
|
3,5
|
26
|
1
|
12,25
|
676
|
91
|
|
Итого:
|
12,5
|
80
|
0
|
2,5
|
33,75
|
1530
|
222,5
|
3. Первичная информация проверяется
на однородность по признаку-фактору с помощью коэффициента вариации
адекватность модель
энерговооруженность регрессия

. Проверка первичной
информации на нормальность распределения с помощью правила «трех сигм».
Сущность правила заключается в том, что в интервал «трех сигм» должны попасть
факторные признаки. Те показатели, которые больше или меньше интервала «трех
сигм», удаляются из таблицы.
|
Интервалы X̄ ± Ģ
|
Число единиц входящих в интервал
|
Удельный вес единиц
|
Удельный вес при нормальном распределении
|
|
X̄ ± 1Ģ (X̄
-1Ģ) - (X̄ + 1Ģ) (2,5 - 0,707) - (2,5 + 0,707)
1,793 - 3,207
|
5
|
50
|
68,3
|
|
X̄ ± 2Ģ (X̄
-2Ģ) - (X̄ + 2Ģ) 1,086 - 3,914
|
5
|
50
|
95,4
|
|
X̄ ± 3Ģ (X̄
-3Ģ) - (X̄ + 3Ģ) 0,379 - 4,621
|
5
|
50
|
99,7
|
. Исключить из первичной информации
резко выделяющиеся единицы, которые по признаку-фактору не попадают в интервал
«трех сигм».
Вывод: Резко выделяющихся единиц в
первичной информации нет.
. Для установления факта наличия
связи производится аналитическая группировка по признаку-фактору. Построить
интервальный ряд распределения.
|
№
|
интервалы
|
Номер
|
Число
|
Y
|
∑Y
|
Ȳ
|
|
X
|
анализа
|
анализов
|
|
|
|
|
1
|
1,5 - 2
|
1
|
1
|
11
|
11
|
11
|
|
2
|
2 - 2,5
|
2
|
1
|
6
|
6
|
6
|
|
3
|
2,5 - 3
|
3
|
1
|
16
|
16
|
16
|
|
4
|
3 -3,5
|
4,5
|
2
|
21, 26
|
23,5
|
|
ИТОГО
|
_
|
_
|
5
|
_
|
80
|
_
|
. Построить эмпирическую линию
связи. По оси абсцисс откладываются значения интервалов факторного признака -
(X). По оси ординат откладываются значения средней величины результативного
признак - (Ȳ).
Эмпирическая линия связи
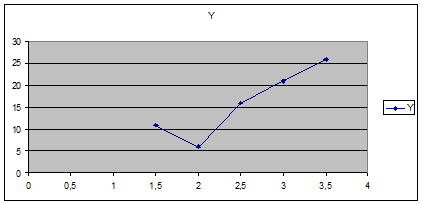
. Для измерения степени тесноты
связи используется линейный коэффициент связи:
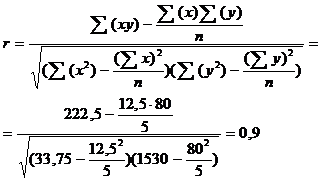
Т.о. связь высокая. r =
0,9 а интервал связи (0,7 - 0,99).
. Предположим, что между
энерговооруженности труда и выпуском готовой продукции существует линейная
корреляционная связь которую можно выразить уравнением прямой.
Для этого составим новую
таблицу.
|
№
|
X
|
Y
|
XY
|
X²
|
Y²
|
(Y - Ȳ)
|
(Y - Ȳ)²
|
Yx
|
(Y - Yx)
|
(Y - Yx)²
|
|
1
|
1,5
|
11
|
16,5
|
2,25
|
121
|
-5
|
25
|
7
|
4
|
16
|
|
2
|
2
|
6
|
12
|
4
|
36
|
-10
|
100
|
11,5
|
-5,5
|
30,25
|
|
3
|
2,5
|
16
|
40
|
6,25
|
256
|
0
|
0
|
16
|
0
|
0
|
|
4
|
3
|
21
|
63
|
9
|
441
|
5
|
25
|
20,5
|
0,5
|
|
5
|
3,5
|
26
|
91
|
12,25
|
676
|
10
|
100
|
25
|
1
|
1
|
|
∑
|
12,5
|
80
|
222,5
|
33,75
|
1530
|
0
|
2,5
|
80
|
0
|
47,5
|
Вычислим параметры прямой с помощью
системы двух нормальных уравнений:
= a₀ + a1X₀ + a1 Σ(X) = Σ(Y)₀∑(X) + a1∑(X²)
= ∑(XY)
a₀ + 12,5a1 = 80
,5a₀ + 33,75a1 = 222,5
a₀ + 12,5a1 = 80 х { (-2,5)}
,5a₀ + 33,75a1 = 222,5
,5a₀ - 31,25a1 = -200
+12,5a₀ + 33,75a1 = 222,5
,5a1 = 22,5
a1 = 9₀ = - 6,5
Конечное уравнение следующее.
= - 6,5 + 9(X)
В уравнении регрессии коэффициент a1
показывает, что с увеличением энерговооруженности труда одного рабочего на 1
(квт/час) выпуск готовой продукции возрастает на 9 шт.
Построим графики практической и
теоретической линии регрессии. По оси абсцисс отложим значения факторного
признака (x), по оси ординат (Yx) и (Y). Чтобы определить (Yx) в уравнение
регрессии подставить значения (x) и занести в таблицу.
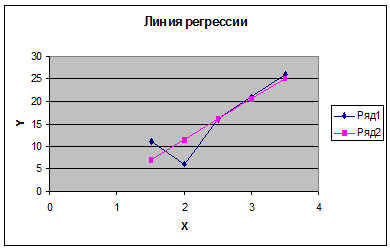
. Одним из важнейших этапов
исследования является измерение тесноты связи. Для этого применяют линейный
коэффициент корреляции (r) и индекс корреляции (R). Индекс корреляции
применяется для измерения тесноты связи между признаками при любой форме связи,
как линейной, так и нелинейной.
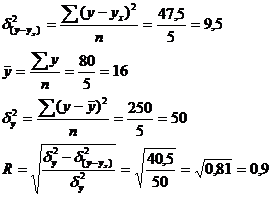
Индекс корреляции
измеряется от 0 до 1. Чем ближе индекс к 1, тем теснее связь между признаками.
Частным случаем индекса корреляции является коэффициент корреляции, который
применяется только при линейной форме связи. В отличии от индекса корреляции
линейный коэффициент корреляции показывает не только тесноту связи, но и
направление связи (прямая или обратная) и измеряется от -1 до +1.
Все показатели тесноты
корреляционной связи показывают тесную связь между производительностью труда и
энерговооруженностью труда. Т.к. R=r=0,9 то можно сделать заключение, что
гипотеза о линейной форме связи подтверждена.
Адекватность модели
Проведем оценку адекватности
регрессионной модели с помощью критерия Фишера.
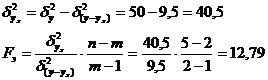
Выводы
Табличное значение
критерия Фишера равно (Fт = 10,13). Эмпирическое значение критерия Фишера (Fэ =
12,79) сравниваем с табличным.
Если Fэ < Fт, то
уравнение регрессии можно признать неадекватным.
Если Fэ > Fт, то
уравнение регрессии признается значимым. (12,79 > 10,13)
Т.о. данная модель
является адекватной.