Оценка погрешностей измерений
Федеральное
государственное бюджетное образовательное учреждение
Высшего
профессионального образования
Саратовский
государственный технический университет имени Гагарина Ю.А.
Кафедра
«Электронные приборы и устройства»
Курсовая
работа на тему:
«Оценка
погрешностей измерений»
Выполнил студент
группы ЭПУ-41
Оруджев Р.Ф.
1. Задание к курсовой работе
Выборка случайных величин
|
1
|
50,95
|
11
|
50,99
|
21
|
50,72
|
31
|
50,86
|
41
|
50
|
|
2
|
49,99
|
12
|
50,48
|
22
|
50
|
32
|
50,48
|
42
|
50,07
|
|
3
|
49,99
|
13
|
50,41
|
23
|
50,39
|
33
|
50,61
|
43
|
49,87
|
|
4
|
51,19
|
14
|
50,54
|
24
|
50,13
|
34
|
50
|
44
|
49,47
|
|
5
|
51,27
|
15
|
49,97
|
25
|
50,26
|
35
|
51,13
|
45
|
50
|
|
6
|
50,74
|
16
|
50
|
26
|
50,31
|
36
|
50,34
|
46
|
|
7
|
49,72
|
17
|
50,17
|
27
|
51,28
|
37
|
49,98
|
47
|
49,6
|
|
8
|
49,81
|
18
|
49,85
|
28
|
49,75
|
38
|
49,23
|
48
|
49,48
|
|
9
|
50,82
|
19
|
50,35
|
29
|
49,58
|
39
|
50,15
|
49
|
50,91
|
|
10
|
49,89
|
20
|
50,22
|
30
|
49,44
|
40
|
50
|
50
|
49,64
|
2. Расчетная часть
.1 Объем выборки
В математической статистике исходная исследуемая
случайная величина называется генеральной совокупностью, а полученный из нее
набор экспериментальных данных - выборочной совокупностью (выборкой).
Число объектов (наблюдений) в
совокупности, генеральной или выборочной, называется ее объемом (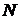 и
и 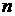 соответственно).
соответственно).
Согласно исходным данным, 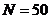 .
.
.2 Интервальные статические ряды
Числа 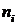 , показывающие сколько раз
встречаются варианты
, показывающие сколько раз
встречаются варианты  в ряде
наблюдений, называются частотами, а отношение их к объему выборки - частостями
в ряде
наблюдений, называются частотами, а отношение их к объему выборки - частостями :
:
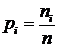 ,
,
где 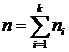 .
.
Для определения оптимального
значения интервала в первом приближении используем формулу Стерджеса:
 ,
,
По формуле (2) получаем следующий
результат: 
Составим интервальный статический
ряд, воспользовавшись формулами (1-2).
Таблица 1. Интервальный статический
ряд (5 интервалов)
|
Интервал
|
49.076-49.693
|
49.693-50.31
|
50.31-50.927
|
50.927-51.544
|
51.544-52.161
|
|
№
интервала
|
1
|
2
|
3
|
4
|
5
|
|
Частота,
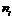 6251360 6251360
|
|
|
|
|
|
|
Частость,
 0.120.50.260.120 0.120.50.260.120
|
|
|
|
|
|
Таблица 2. Интервальный статический ряд (10
интервалов)
|
Интервал
|
49.384-49.693
|
49.693-50.001
|
50.001-50.31
|
50.31-50.618
|
50.618-50.927
|
50.927-51.236
|
51.236-51.544
|
51.544-51.853
|
51.853-52.161
|
|
№
интервала
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Частота,
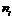 15187945100 15187945100
|
|
|
|
|
|
|
|
|
|
|
|
Частость,
 0.213.61.41.80.810.200 0.213.61.41.80.810.200
|
|
|
|
|
|
|
|
|
|
|
Таблица 3. Интервальный статический ряд (15
интервалов)
|
Интервал
|
49.076-49.281
|
49.281-49.487
|
49.487-49.693
|
49.693-49.899
|
49.899-50.104
|
50.104-50.31
|
50.31-50.516
|
50.516-50.721
|
50.721-50.927
|
50.927-51.133
|
51.133-51.338
|
51.338-51.544
|
51.544-51.75
|
51.75-51.956
|
51.956-52.161
|
|
№
интервала
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
|
Частота,
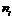 1236126634330000 1236126634330000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частость,
 0.020.040.060.120.240.120.120.060.080.060.060000 0.020.040.060.120.240.120.120.060.080.060.060000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4. Интервальный статический ряд (20
интервалов)
|
Интервал
|
49.076-49.23
|
49.23-49.384
|
49.384-49.539
|
49.539-49.693
|
49.693-49.847
|
49.847-50.001
|
50.001-50.156
|
50.156-50.31
|
50.31-50.464
|
50.464-50.618
|
50.618-50.773
|
50.927-51.081
|
51.081-51.236
|
51.236-51.39
|
51.39-51.544
|
51.544-51.698
|
51.698-51.853
|
51.853-52.007
|
52.007-52.161
|
|
№
интервала
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
|
Частота,
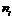 01
2331534542223200000 01
2331534542223200000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частость,
 00.020.040.060.060.30.060.080.10.080.040.040.040.060.0200000 00.020.040.060.060.30.060.080.10.080.040.040.040.060.0200000
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
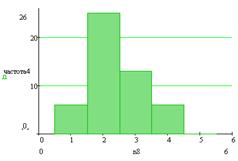
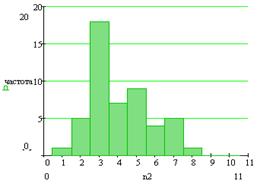
а б
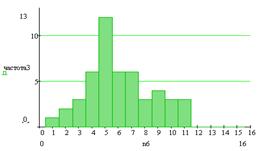
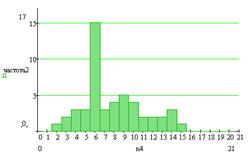
в г
Рис. 4. Диаграммы частоты в выбранных
интервалах: а - для 5 интервалов, б - для 10 интервалов, в - для 15 интервалов,
г - для 20 интервалов
2.3 Медиана вариационного ряда
Медиана 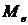 вариационного
ряда - это значение признака, приходящееся на середину ряда. Получаем:
вариационного
ряда - это значение признака, приходящееся на середину ряда. Получаем:
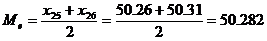

Значение медианы не зависит от
выбора количества интервалов (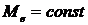 ).
).
.4 Размах вариации
Размах вариации называется число 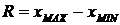 , где
, где  -
наибольший,
-
наибольший, 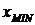 -
наименьший вариант ряда.
-
наименьший вариант ряда.


Размах вариации не зависит от выбора
количества интервалов ( ).
).
.5 Выборочное среднее
Выборочным средним 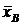 называется
среднее арифметическое всех значений выборки:
называется
среднее арифметическое всех значений выборки:
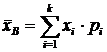 ,
,
Для интервального статистического
ряда в качестве  берут
середины интервалов, а
берут
середины интервалов, а  -
соответствующие им частости.
-
соответствующие им частости.
Для 5 интервалов 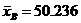 ; для 10
; для 10 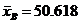 , для 15
интервалов
, для 15
интервалов  , для 20
, для 20 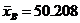 .
.
.6 Выборочная дисперсия
Выборочная дисперсия 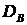 - это
среднее арифметическое квадратов отклонений значений выборки от выборочной
средней:
- это
среднее арифметическое квадратов отклонений значений выборки от выборочной
средней:
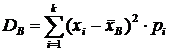 ,
,
Для 5 интервалов 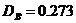 , для 10
, для 10 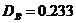 , для 15
интервалов
, для 15
интервалов 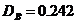 , для 20
, для 20 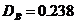 .
.
.7 Выборочное среднеквадратическое
отклонение выборки
Этот параметр определяется как:
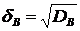 ,
,
Для 5 интервалов 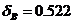 , для 10
, для 10  , для 15
интервалов
, для 15
интервалов 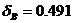 , для 20
, для 20 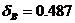 .
.
2.8 Эмпирическая (статистическая)
функция распределения
Эта функция 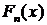 , определяет
для каждого значения
, определяет
для каждого значения  частость
события
частость
события 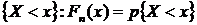 . Для
нахождения эмпирической функции ее записывают в виде:
. Для
нахождения эмпирической функции ее записывают в виде:
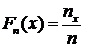 ,
,
где 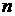 - объем выборки,
- объем выборки,  - число
наблюдений, меньших
- число
наблюдений, меньших . Найдем по
(8) значения эмпирической функции распределения с 5, 10, 15, 20 интервалами:
. Найдем по
(8) значения эмпирической функции распределения с 5, 10, 15, 20 интервалами:
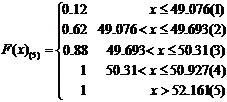
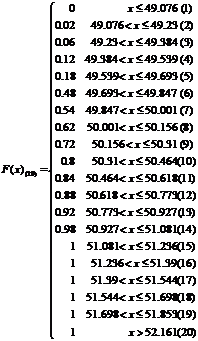
* в скобках обозначен номер
интервала
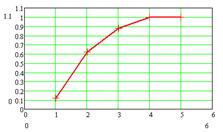
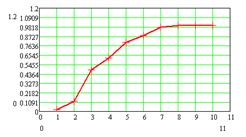
а б
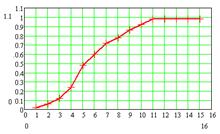
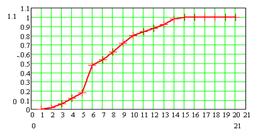
в г
Рис. 5. График эмпирической функции
распределения: а - для 5 интервалов, б - для 10 интервалов, в - для 15
интервалов, г - для 20 интервалов
Мода - значение во множестве
наблюдений, которое встречается наиболее часто. По следующей формуле вычислим
значение моды:
 ,
,
где 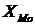 - минимальная граница модульного
интервала;
- минимальная граница модульного
интервала;
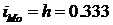 - величина модального интервала;
- величина модального интервала;
 - частота модального интервала;
- частота модального интервала;
 - частота интервала, предшествующего
модальному;
- частота интервала, предшествующего
модальному;
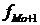 - частота интервала, следующего за
модальным.
- частота интервала, следующего за
модальным.
Таблица 5. Параметры для вычисления
моды и значения моды
|
Количество
интервалов
|
5
|
10
|
15
|
20
|
|
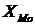 50.3150.00150.10450.001 50.3150.00150.10450.001
|
|
|
|
|
|
 25181215 25181215
|
|
|
|
|
|
 6563 6563
|
|
|
|
|
|
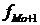 13763 13763
|
|
|
|
|
|
 50.49950.16950.25950.156 50.49950.16950.25950.156
|
|
|
|
|
.10 Медиана
Медиана интервального статистического ряда
вычисляется по следующей формуле:
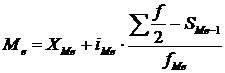 ,
,
где 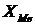 - начальное значение медианного
интервала;
- начальное значение медианного
интервала;
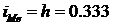 - величина медианного интервала;
- величина медианного интервала;
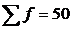 - сумма частот ряда;
- сумма частот ряда;
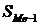 - сумма накопленных частот в
интервалах, предшествующих медианному;
- сумма накопленных частот в
интервалах, предшествующих медианному;
 - частота медианного интервала.
- частота медианного интервала.
Таблица 6. Параметры для вычисления
медианы и значения медианы
|
Количество
интервалов
|
5
|
10
|
15
|
20
|
|
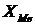 50.92750.3149.89949.847 50.92750.3149.89949.847
|
|
|
|
|
|
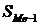 312463 312463
|
|
|
|
|
|
 13766 13766
|
|
|
|
|
|
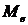 50.78550.35450.8551.804 50.78550.35450.8551.804
|
|
|
|
|
.11 Кривая распределения
Кривая распределения (считаем, что закон
распределения нормальный) для упорядоченных значений случайных величин выглядит
следующим образом:
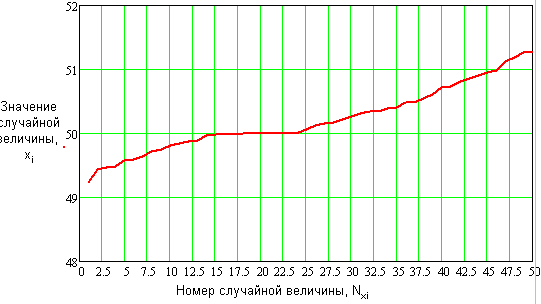
Рис. 6. Кривая распределения для упорядоченных
значений случайных величин
.12 Степень сродства к нормальному распределению
Степень сродства к нормальному распределению
(здесь - для диаграммы частоты) - отношение числа точек, для которых отклонение
от гауссовой функции составляет менее 0.05 по модулю к числу интервалов.
Для определения этого параметра воспользуемся
формулами (11).
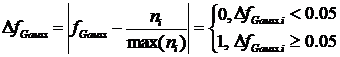 ,
,
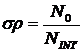 погрешность
вариационный выборочный распределение
погрешность
вариационный выборочный распределение
где 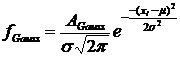 ;
;
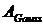 - множитель амплитуды гауссовой
функции (подбираемая для ее сравнения с диаграммой частот);
- множитель амплитуды гауссовой
функции (подбираемая для ее сравнения с диаграммой частот); 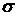 -
дисперсия;
-
дисперсия; 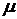 -
математическое ожидание;
-
математическое ожидание;  -
нормированное к максимуму значения частот в каждом интервале;
-
нормированное к максимуму значения частот в каждом интервале; 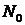 - число
точек, для которых отклонение от гауссовой функции составляет менее 0.05;
- число
точек, для которых отклонение от гауссовой функции составляет менее 0.05; 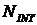 - число
интервалов,
- число
интервалов, 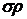 - степень
сродства к нормальному распределению (%).
- степень
сродства к нормальному распределению (%).
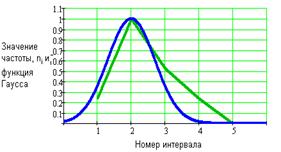
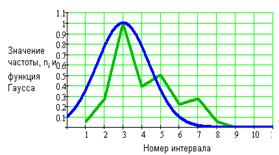
а б
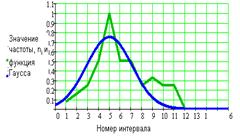

в г
Рис. 7. Сравнение функции Гаусса с
диаграммой частоты: а - для 5 интервалов (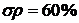 ), б - для 10 интервалов (
), б - для 10 интервалов (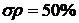 ), в - для
15 интервалов (
), в - для
15 интервалов ( ), г - для
20 интервалов (
), г - для
20 интервалов (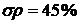 )
)
.13 Сравнение параметров случайных
величин
Сравним с помощью таблиц и графиков
найденные параметры случайных величин.
Таблица 7. Параметры случайных
величин
|
Количество интервалов Параметр
|
5
|
10
|
15
|
20
|
|
Выборочное
среднее, 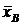 50.23650.61849.22450.208 50.23650.61849.22450.208
|
|
|
|
|
|
Выборочная
дисперсия, 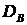 0.2730.2330.2420.238 0.2730.2330.2420.238
|
|
|
|
|
|
Выборочное
среднеквадратическое отклонение, 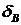 0.5220.4830.4910.487 0.5220.4830.4910.487
|
|
|
|
|
|
Мода,
 50.49950.16950.25650.156 50.49950.16950.25650.156
|
|
|
|
|
|
Медиана
интервального статистического ряда, 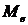 50.78450.35450.82551.804 50.78450.35450.82551.804
|
|
|
|
|
|
Степень
сродства к нормальному распределению, 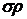 , %60504745 , %60504745
|
|
|
|
|
Вывод
В ходе выполнения данной курсовой работы были
изучены методы статистической оценки распределения случайной величины. Были
осуществлены расчеты по представленной выборке, рассмотрены основные числовые
характеристики случайной величины: объем выборки, медиана вариационного и
статистического ряда, размах вариации, выборочное среднее, выборочная
дисперсия, среднеквадратическое отклонение, мода, медиана. Выявлено, что
выборочная дисперсия и выборочное среднеквадратическое отклонение выборки имеет
максимальное значение при 5 интервалах. Обнаружено, что медиана интервального
статистического ряда растет при увеличении числа интервалов.
Построены диаграммы частоты в
выбранных интервалах, кривая распределения, эмпирическая функция распределения,
определяющая частость события для каждого значения случайной величины , а также
графики сравнения функции Гаусса с диаграммой частоты. Диаграммы частоты при
увеличении числа интервалов становятся неравномерными, а эмпирическая функция
распределения, наоборот, становится более гладкой.
, а также
графики сравнения функции Гаусса с диаграммой частоты. Диаграммы частоты при
увеличении числа интервалов становятся неравномерными, а эмпирическая функция
распределения, наоборот, становится более гладкой.
Был установлен теоретический закон
распределения случайной величины - данная случайная величина имеет нормальное
распределение со степенью сродства к нормальному распределению не менее 45% в
выбранных интервалах. Замечено, что при увеличении числа интервалов степень
сродства уменьшается вследствие большей неравномерности диаграммы частоты.