Побудова регресійної залежності хімічного складу і механічних властивостей сталі, оптимізація властивостей з використанням отриманої математичної моделі

Побудова регресійної залежності хімічного складу і механічних властивостей сталі, оптимізація властивостей з використанням отриманої математичної моделі

Вступ

Математична модель - це наближений опис якого-небудь класу явищ або об'єктів реального світу на мові математики. Основна мета моделювання - дослідити ці об'єкти і передбачити результати майбутніх спостережень. Математичне моделювання і пов'язаний з ним комп'ютерний експеримент незамінні в тих випадках, коли натурний експеримент неможливий з тих чи інших причин. Математична модель дозволяє одержати визначену інформацію про процеси, що протікають в об’єкті, розрахувати характеристики об’єкту і дати рекомендації з його оптимізації.

Основні етапи математичного моделювання включають в себе:

А) Побудова моделі. На цьому етапі задається деякий "нематематичний" об'єкт - конструкція, виробничий процес . При цьому, як правило, чіткий опис ситуації неможливий. Спочатку виявляються основні особливості явища і зв'язки між ними на якісному рівні. Потім знайдені якісні залежності формулюються мовою математики, тобто будується математична модель. Це найважча стадія моделювання.

Б) Розв’язання математичної задачі, до якої приводить модель. На цьому етапі велика увага приділяється розробці алгоритмів і чисельних методів рішення задачі на ЕОМ, за допомогою яких результат може бути знайдений з необхідною точністю.

В) Інтерпретація отриманих результатів з математичної моделі. Результати, виведені з моделі на мові математики, інтерпретуються мовою, прийнятою в даній області.

Г) Перевірка адекватності моделі. На цьому етапі з'ясовується, чи узгоджуються результати експерименту з теоретичними наслідками з моделі в межах певної точності.

Д) Модифікація моделі. На цьому етапі відбувається або ускладнення моделі, щоб вона була більш адекватною дійсності, або її спрощення заради досягнення практично прийнятного рішення.

У даній курсовій роботі передбачається побудова регресійної залежності хімічного складу і механічних властивостей сталі, оптимізація властивостей з використанням отриманої математичної моделі. Відповідно до індивідуального завдання необхідно виконати попередню обробку даних; побудувати регресійну модель першого і другого порядку, перевірити їх адекватність; перевірити значимість коефіцієнтів рівняння; дати рекомендації щодо підвищення рівня властивостей; вибрати й обґрунтувати оптимальний вид рівняння для визначення очікуваних значень властивостей.

. Попередня обробка результатів

Попередню обробку виконують для кожного фактора, у даному випадку для C, Mn, Si, S, Al, Ti, T, 𝛹. Для проведення попередньої обробки використовуємо програму "Statistica".

Рекомендується наступний порядок проведення попередньої обробки:

обчислення вибіркових характеристик;

перевірка на грубі випади;

перевірка закону розподілу;

перевірка незалежності факторів між собою (кореляційний аналіз).

При обчисленні вибіркових характеристик визначають:

а) вибіркове середнє - Хср

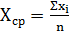 (1.1)

Де

хі - значення фактора в і-ом досліді;- число дослідів.

б) мінімальне та максимальне відхилення

 (1.2)

 (1.3)

в) коефіцієнт варіації

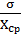=  (1.4)

Коефіцієнт варіації характеризує відносний розкид результатів, і значення Хср і COV використовують надалі у аналізі.

Всі значення статичних характеристик приведені у таблиці 1.1.

Таблиця 1.1 - Попередня статистична обробка даних

Визначимо коефіцієнт варіації для кожного фактору:

(C) = 20,5%(Mn) = 13.3%(Si) = 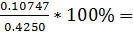25.3%

cov(S) = 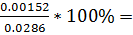5.3%(Al) = 89.5%(Ti) = 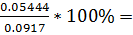59.4%(T) = 14%(𝛹) = 10.5%

Перевірку вибірки на наявність випадів можна здійснювати за різними методиками і вибір методу залежить від числа дослідів. Найбільше поширений метод полягає в обчисленні критерію відносного максимального відхилення і порівняння його з табличним значенням. У цьому методі для максимального і мінімального значень вибірки обчислюють по формулам (1.2) та (1.3).

Для невеликого числа дослідів (n<25 ) знайдене значення t порівнюють з табличним значенням критерію максимального відхилення С для обраного рівня надійності Р і числа ступенів волі f=n.

Якщо С > t, даний результат є випадом і відповідний результат можна виключити з вибірки.

Для більшого числа дослідів t (в нашому випадку ми маємо 30 дослідів) можна порівнювати з критерієм Ст’юдента tтабл для числа ступенів волі f=n і вважати результат випадом, якщо t > t.

У нашому випадку для n=30 і f = 28 tтабл=2,045.

Визначимо нормоване відхилення по мінімальному значенню за формулою (1.2):

τmin(C)= =0.812459

τmin(Mn)=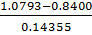 =1.667254

τmin(Si)= =0.977008

τmin(S)=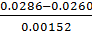 =1.707999

τmin(Al)= =0.626301

τmin(Ti)=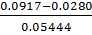 =1.169558

τmin(T)= =1.560579

τmin(𝛹)=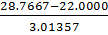 =2.245399

Визначимо нормоване відхилення по максимальному значенню за формулою (1.3):

𝜏max(C)=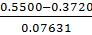 = 2.332544

𝜏max(Mn)= =1.119243

𝜏max(Si)= =1.256154

𝜏max(S)= =0.919692

𝜏max(Al)=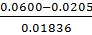 =2.0151207

𝜏max(Ti)=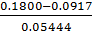 =1.622686

𝜏max(T)=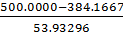 =2.147728

𝜏max(𝛹)= =2.068421

Обчислені дані приведені в таблиці 1.2

Таблиця 1.2 - Результати перевірки вихідних даних на наявність випадів

Оцінка виду розподілу і можливості перетворення його до нормального може бути виконана за різними критеріями (графічно - по виду кривої розподілу, по співвідношенню коефіцієнтів асиметрії й ексцесу і за критерієм Пірсона - c2). При виконанні цього етапу спочатку необхідно переглянути гістограму частотного розподілу по кожному фактору. Для відповіді на питання про закон розподілу в цьому випадку необхідно порівняти за критерієм Пірсона - c2 одержуваний розподіл результатів з теоретичним для даного закону.

Для цього необхідно порівняти розрахований критерій Пірсона з табличним для обраної надійності Р і числа ступенів волі f =n - 3. Якщо c2 таб л≥ c2експ, дані розподілені за цим законом. Чим менше c2експ, тим менше відхилення від теоретичного закону.

Регресійний аналіз припускає, що результати експериментів розподілені по нормальному закону, тобто у вибірці однаково часто зустрічаються результати більші і менші середнього значення. При розробці регресійної моделі необхідно перевірити закон розподілу значень факторів. Оцінку виду розподілу виконаємо за різними критеріями (графічно - по виду кривої розподілу і за критерієм Пірсона - c2). Спочатку переглянемо гістограми частотного розподілу по кожному фактору. Потім порівняємо одержуваний розподіл результатів з теоретичним для даного закону. Чим менше c2експ, тим менше відхилення від теоретичного закону. В таблиці 1.3 приведені розраховані критерії Пірсона для нормального розподілу. Закон розподілу вибирають по меншому c2.

Таблиця 1.3 - Результати перевірки вихідних факторів на відповідність закону розподілу

На рисунку 1.1 приведені криві розподілу факторів. Ми приймаємо, що всі ці закони розподілу нормальні, але криві нагадують криві бімодального закону розподілу.

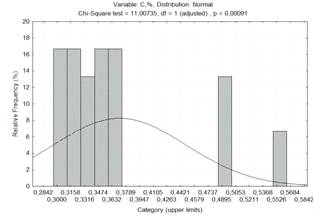
Рисунок 1.1 - Діаграма частотного розподілу вмісту вуглецю

Рисунок 1.2 - Діаграма частотного розподілу вмісту марганцю

Рисунок 1.3 - Діаграма частотного розподілу вмісту кремнію

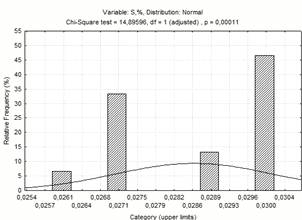
Рисунок 1.4 - Діаграма частотного розподілу вмісту сірки

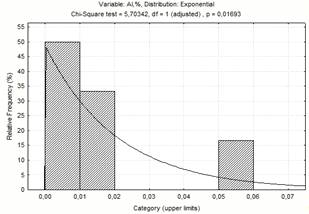
Рисунок 1.5 - Діаграма частотного розподілу вмісту алюмінію

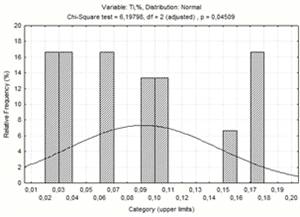
Рисунок 1.6 - Діаграма частотного розподілу вмісту титану

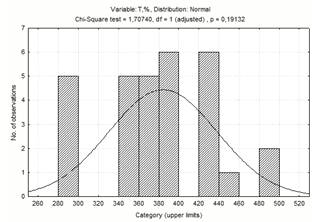
Рисунок 1.7 - Діаграма частотного розподілу температури

Рисунок 1.8 - Діаграма частотного розподілу відносного звуження

2. Кореляційний аналіз

Кореляційний аналіз на етапі попередньої обробки застосовують для визначення ступеня зв’язку факторів між собою і з властивістю. Оцінка коефіцієнтів у рівнянні регресії методом найменших квадратів вимагає незалежність факторів. У матеріалознавстві фактори досить часто зв’язані між собою (наприклад, спільне введення легуючих добавок у сталь у виді феросплавів). Сильна кореляція між факторами може привести до перекручених оцінок впливу факторів на властивість (за рахунок взаємної позитивної кореляції не впливові фактори можуть бути оцінені як впливові, негативна кореляція взаємно компенсує вплив факторів на властивість). Тому для вирішення питання про включення того чи іншого фактора в модель необхідно виконати аналіз даних за допомогою програми кореляційного аналізу. Кількісною характеристикою ступеня зв’язку в методі кореляційного аналізу с коефіцієнт парної кореляції r

де r - коефіцієнт парної кореляції;ср, xср - середні значення по відповідним перемінним.

Спочатку підготуємо таблицю кореляційного аналізу, у яку в процесі обчислень занесемо значення коефіцієнтів парної кореляції (таблиця 2.1). Значимі коефіцієнти позначимо *.

Таблиця 2.1 - Таблиця кореляційного аналізу

Після розрахунку коефіцієнта парної кореляції необхідно перевірити його статистичну значимість. Для цього по таблиці критичних значень коефіцієнтів парної кореляції для обраного рівня надійності Р=0,95 і числа ступенів волі f=30-2=28 знаходять значення rтабл=0,30. Якщо |rрозр| ≥ rтабл, лінійний зв’язок між цими величинами є статистично значимий. Значимість коефіцієнта парної кореляції можна також перевірити по t - критерію Ст’юдента. Для цього обчислюють і порівнюють з табличним значенням критерію Ст’юдента для обраної надійності Р=0,95 і числа ступенів волі f=30-1=29. Маємо tтабл= 2,04.

Значення r лежать в інтервалі -1...+1.Чим ближче r до ±1, тим сильніше ступінь лінійного зв'язку між перемінними. Знак "-" (негативна кореляція) означає, що зі збільшенням однієї перемінної інша буде зменшуватися. Знак "+" - зі збільшенням однієї перемінної інша буде також зростати. При r = 1 між перемінними існує функціональний зв'язок.

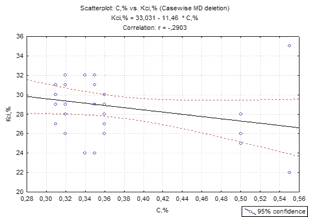
Рисунок 2.1 - Графік зв’язку між вуглецем та відносного звуження

Рисунок 2.2 - Графік зв’язку між марганцем та відносним звуженням

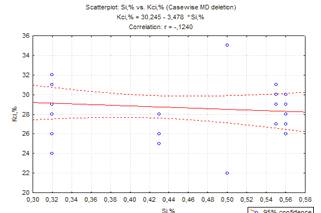
Рисунок 2.3 - Графік зв’язку між кремнієм та відносним звуженням

Рисунок 2.4 - Графік зв’язку між сіркою та відносним звуженням

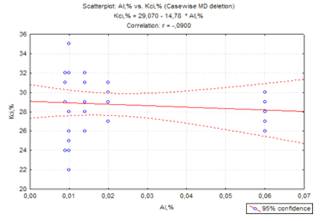
Рисунок 2.5 - Графік зв’язку між алюмінієм та відносним звуженням

Рисунок 2.6 - Графік зв’язку між титаном та відносним звуженням

Рисунок 2.7 - Графік зв’язку між температурою та відносним звуженням

Після перевірки значимості за даними таблиці кореляційного аналізу будуємо граф кореляційних зв'язків (рисунок 2.8). Для цього наносимо вершини графа - досліджувані фактори і властивість, потім з’єднуємо відрізками ті вершини, між якими існує статистично значимий зв'язок.

Рисунок 2.8 - Граф кореляційних зв’язків

3. Розробка регресійної моделі першого порядку

Розробку регресійної моделі завжди починають з побудови лінійної моделі, що включає усі фактори (крім виключених через взаємну кореляцію). Таку математичну модель називають повною. Під повною регресійною моделлю першого порядку розуміють залежність виду:

у= bo + b1x1 + b2x2 + …… + bkxk ± ε (2.1)

де к - число факторів;

ε - помилка пророкування моделі.

Задача регресійного аналізу полягає в розрахунку за результатами експериментів значень коефіцієнтів bi. Коефіцієнти розраховують на ЕОМ і одночасно зі значеннями коефіцієнтів одержують ряд статистичних характеристик, що описують рівняння в цілому, а також характеризують вплив факторів.

Статичні характеристики, що описують рівняння в цілому:- залишкова сума квадратів;

ε - стандартне відхилення моделі (інтервал відхилення від площини регресії,у якому з заданою надійністю лежать експериментальні значення властивості);- коефіцієнт детермінації, що показує, яка частина варіації властивості пояснюється моделлю (0-100%);- коефіцієнт множинної кореляції,що показує ступінь зв’язку факторів із властивістю. Його значення лежать в інтервалі 0-1,0;- критерій Фішеру моделі;- критерій Ст’юдента моделі, що лежить від R;

залишки - різниця експериментальних і розрахованих по рівнянню значень властивості.

Статичні характеристики, зв’язані з факторами:

∆bi - довірчий інтервал визначення і-го коефіцієнта;- коефіцієнт часткової кореляції.

Регресійний аналіз проводять у визначеній послідовності:

1 перевірка адекватності моделі;

2 перевірка статистичної значимості коефіцієнтів;

3 аналіз моделі і видача рекомендацій з оптимізації властивості.

Адекватність моделі перевіряють по F і t. Якщо Fpозр ≥ Fтабл, то модель є адекватною і її можна використовувати для подальшого аналізу. При аналізі адекватності перевагу варто віддавати F- критерію як більш чуттєвому.

Це означає, що, якщо модель адекватна по t і неадекватна по F, модель варто вважати неадекватною. У нашому випадку модель э адекватною, тому що 3.5595>2.6

Таблиця 3.1 - Модель першого порядку при N = 30Summary for Dependent Variable:= 0 ,72875340 R2 = 0,53108151R2 =0,38188018 F(7,22) = 3,5595<01038 Std.Error of estimate: 2,3693

Рівняння повної моделі першого порядку має вигляд:

𝛹 = 139,00 - 151,46C - 41.12Mn + 87.06Si - 2217.26S -704.93Al +175.32Ti+ 0.04T ± 2.3693

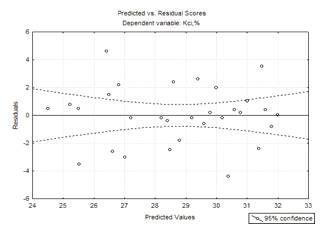
Рисунок 3.1 - Графік експериментальних значень та залишків для початкової моделі

Рисунок 1.2 - Графік експериментальних та отриманих значень для початкової моделі

Для підвищення якості і вiрогiдностi розробленої моделi необхiдно проаналiзувати залишки - рiзницю мiж експериментальними i розрахованими по моделi значеннями властивостi.

Значення залишкiв повиннi задовольняти наступним вимогам:

-        сума залишків повинна дорівнювати нулю. За знаком і величиною відхилення суми від нуля можна визначити розташування поверхні відгуку об'єкта щодо площини регресії. Якщо сума залишків більше нуля, поверхня лежить вище площини регресії, якщо менше нуля - то нижче. Це задовольняє визначити вид перетворення для значень властивості;

-        значення 𝛹ехсп - 𝛹розр повинні корелювати між собою. Чим більше коефіцієнт парної кореляції між ними, тим точніше модель відображає результати експерименту;

-        значення залишків повинні мати нормальний закон розподілу.

Далі з моделі першого порядку виключили 12й дослід, отримали модель для 29 дослідів. Після чого статистичні характеристики моделі підвищились:Summary for Dependent Variable:= 0,79661372 R2=0 ,63459342R2= 0,51279123 F(7,21)=5,2100<,00147 Std.Error of estimate: 2,1196

Потім видалили 7 дослід, отримали модель для 28 дослідів. Статистичні характеристики моделі також підвищились:Summary for Dependent Variable= 0,83521759 R2= 0,697588 42R2= 0,59174437 F(7,20)=6,5907<,00041 Std.Error of estimate: 1,9320

Далі видалили 9й дослід, отримали модель для 27 дослідів. Статистичні характеристики моделі значно підвищились:Summary for Dependent Variable=0 ,86101418 R2=0 ,74134542R2=0 ,64605162 F(7,19)=7,7796<,00017 Std.Error of estimate: 1,8075

Після цього видалили 5й дослід, отримали модель для 26 дослідів. Внаслідок послідовного виключення деяких дослідів модель стала ще кращою, її статистичні характеристики значно підвищилися. А саме вона має більший критерій Фішеру 10,074 >3.5595 і коефіцієнт множинної кореляції 0,89254985>0.79661372.

Таблиця 3.2 - Статистичні характеристики покращеної моделі першого порядку N=26Summary for Dependent Variable:= 0,89254985 R2= 0,79664523R2=0 ,71756282 F(7,18)=10,074<,00004 Std.Error of estimate: 1,6462

Після виключення деяких дослідів повна модель першого порядку має вигляд:

𝛹 = -13.4691+3.5087C+20.1562Mn - 26.0696Si + 272.3130S + 121.6505Al - 30.8925 + 0.0582 ± 1.6462

Рисунок 3.3 - Графік експериментальних значень та залишків кінцевої моделі першого порядку

Рисунок 3.4 - Графік експериментальних та отриманих значень для кінцевої моделі першого порядку

Проранжуємо фактори, розташувавши їх у порядку зменшення ступеня впливу на властивість. Для цього побудуємо гістограми ранжирування, на яких розташуємо фактори у порядку зменшення коефіцієнтів у кодовому масштабі b, які характеризують ступінь впливу фактора на властивість, і коефіцієнтів часткової кореляції rxy, що характеризують ступінь зв’язку фактора та властивості і у деякій мірі доповнюють коефіцієнти у кодовому масштабі. Гістограми ранжирування представлені на рисунках 2.5 і 2.6.

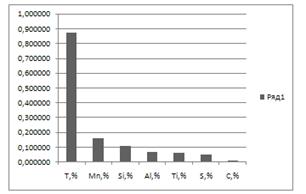
Рисунок 2.5 - Гістограма ранжирування факторів за коефіцієнтом часткової кореляції для покращеної моделі першого порядку.

. Розробка регресійної моделі другого порядку

У матеріалознавстві в більшості випадків більш точно результати експерименту описують нелінійні моделі. Обмежимося неповною моделлю другого порядку.

Ефекти взаємодії вибирають на пiдставi знань про об’єкт дослідження, з урахуванням графа кореляційних зв'язків обираємо ефект взаємодії між та Т і С. При перемноженні модель адекватна (Fрозр>Fтабл).

Таблиця 4.1 - Статистичні характеристики вихідної моделі другого порядку

Regression Summary for Dependent Variable:=0 ,77979743 R2=0 ,60808403R2=0 ,45878271 F(8,21)=4,0729<,00462 Std.Error of estimate: 2,2170

Рівняння вихідної моделі другого порядку має вигляд:

сталь регресійний математичний випад

𝛹 = 172.38 - 235.09C - 40.82Mn + 86.21Si - 2270.19S - 703.34Al + 176.99Ti - 0.04T + 0.20T-C ± 2.2170

Рисунок 4.1 - Графік експериментальних значень та залишків для вихідної моделі другого порядку

Рисунок 4.2 - Графік експериментальних та отриманих значень для вихідної моделі другого порядку

При аналізі залишків був виключений 12й дослід, після чого статистичні характеристики почали збільшуватись. Модель з 29 дослідами має такі характеристики:Summary for Dependent Variable:= 0,82201429 R2=0,67570749R2= 0,54599048 F(8,20)=5,2091<,00130 Std.Error of estimate: 2,0352

Далі виключили 7й дослід. Модель із 28 дослідами має такі статистичні характеристики:Summary for Dependent Variable:= 0,86957487 R2= 0,75616045R2= 0,65349116 F(8,19)=7,3650<,00018 Std.Error of estimate: 1,7803

Потім виключили 9й дослід. Модель із 27 дослідами має такі характеристики:Summary for Dependent Variable:= 0,89935793 R2= 0,80884468R2= 0,72388676 F(8,18)=9,5205<,00004 Std.Error of estimate: 1,5334

Після виключення 5го досліду статистичні характеристики значно збільшилися, а саме вона має більший критерій Фішеру 9,5205>4.0729 і коефіцієнт множинної кореляції 0.89935793> А саме вона має більший критерій Фішеру 10,074 >3.5595 і коефіцієнт множинної кореляції 0,892549 >0.796613.

Таблиця 4.2 - Статистичні характеристики кінцевої моделі другого порядкуSummary for Dependent Variable:= 0,93016718 R2=0 ,86521098R2= 0,80178085 F(8,17)=13,640<,00001 Std.Error of estimate: 1,2399

Оптимальна модель другого порядку має наступний вигляд:

𝛹 = 147.43 - 238.72C - 23.44Mn + 47.97Si - 1312.38S - 767.54Al + 122.68Ti - 0.09T + 0.32T-C ± 1.2399

Рисунок 4.3 - Залишки оптимальної моделі другого порядку після виключення дослідів

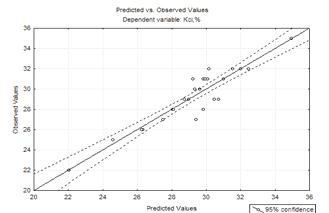
Рисунок 4.4 - Залишки оптимальної моделі другого порядку після виключення дослідів

Визначимо оптимальний вид рівняння для розрахунку очікуваного значення властивості.

Для цього порівняємо статистичні характеристики, що описують рівняння в цілому.

Чим менше залишкова сума квадратів, чим більше коефіцієнти детермінації, множинної кореляції і критерій Фішеру, тим точніше модель описує результати експерименту. Для порівняння статистичних характеристик складемо таблицю 4.3.

Таблиця 4.3 - Порівняння статистичних характеристик моделей першого і другого порядків

Виходячи з таблиці 4.3 можна зробити висновок, що модель другого порядку набагато точніше описує результати експерименту, так як вона має значно більші коефіцієнти детермінації та множинної кореляції, а також помітно більший критерій Фішеру.

Тому для розрахунку очікуваного значення властивості краще використовувати модель другого порядку.