Кристаллический анализ структуры и потенциальных свойств диоксида титана

Введение. Описание и применение кристаллических
модификаций кварца
диоксид
титан дифрактограмма кристаллический
Кварц - один из самых распространённых минералов
в земной коре. Химическая формула: SiO2,
природный диоксид кремния. Кремнезём, наиболее распространённой формой
нахождения которого в природе является кварц, обладает развитым полиморфизмом.
Две основные полиморфные кристаллические
модификации кварца: кристаллы a- кварца (низкотемпературная
модификация кварца) относятся к тригонально-трапецоэдрическому классу 3:2
тригональной системы, кристаллы b- кварца
(высокотемпературная модификация кварца) - к гексагонально-трапецоэдрическому
классу 6:2 гексагональной системы. Кристаллическая структура a-
кварца - каскадного типа, построена из кремне-кислородных тетраэдров,
расположенных винтообразно ( с правым или левым ходом винта) по отношению к
главной оси кристалла. В зависимости от этого различают правые и левые
структурно-морфологические формы кристаллов кварца, отличимые внешне по
симметрии расположения некоторых граней. Отсутствие плоскостей и центра
симметрии у кристаллов a- кварца обуславливает наличие у
него пьезоэлектрических и пироэлектрических свойств. Твердость кварца - 7
баллов по шкале Мооса - принята за нижнюю границу твердости ювелирных камней.
Кварц имеет среднюю плотность (2,65), заметную спайность по ромбоэдру,
стеклянный блеск. Окраска его разнообразна и обусловлена либо пигментирующими
включениями, либо дефектами кристаллической структуры. В последнем случае
окраска может изменяться от нагревания, яркого света, облучения рентгеновскими
и гамма-лучами.
Среди всех полезных свойств кварца это является
едва ли не самым важным: оно открыло кварцу обширные применения в радиотехнике
и электронике. Кварц хорошо пропускает ультрафиолетовые лучи и используется в
специальной оптике. Высококачественные кристаллы кварца представляют собой
весьма дорогое «пьезооптическое сырье»; его технические применения обусловлены
также тугоплавкостью, высокой теплопроводностью, малым тепловым расширением.
Таблица 1
Характеристики кристаллической решетки
|
Модификация/
параметр
|
a- кварца
|
b- кварца
|
|
Параметры
элементарной решетки, Å
|
a
|
4.9133
|
-
|
|
b
|
-
|
-
|
|
c
|
5.4053
|
-
|
|
a
|
90
|
90
|
|
b
|
90
|
90
|
|
g
|
120
|
120
|
|
Элементы
симметрии
|
32
- тригональный- трапецоэдр
|
622-гексакональный-трапецоэдр
|
|
Ступень
|
аксиальная
|
аксиальная
|
|
Обозначение
вида симметрии
|
32,
L33L2, D3
|
622,
L66L2
|
|
Сингония
|
тригональная
|
гексагональная
|
В кристаллах кварца, получаемых в щелочных
средах, преобладающим типом электрически активных точечных дефектов являются
примесные щелочные ионы, входящие в структуру кварца при гетеровалентном
изоморфизме. В кварце основными механизмами внутреннего трения являются потери,
связанные с точечными дефектами, а также с рассеянием на границах неоднородностей
и включений и, наконец, потери, связанные с диффузией междоузельных (щелочных)
ионов.
Часть 1.
. Стереографические проекции элементов симметрии
и общей простой формы рутильной модификации диоксида титана
Исходные элементы симметрии планаксиальной
ступени тетрагональной сингонии представлены на рис. 3, это вертикальная
поворотная ось 4 порядка, горизонтальная поворотная ось второго порядка и
перпендикулярна ей вертикальная плоскость.

Рис. 3.
Стереографическая проекция элементов симметрии и общей простой формы
Данные элементы симметрии порождают другие
элементы симметрии. Новые элементы симметрии можно получить с помощью теорем о
сочетании элементов симметрии.
Теорема 1. Точка пересечения четной
оси симметрии с перпендикулярной ей плоскостью симметрии есть центр симметрии: 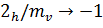
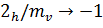 .
.
Теорема 2 (обратная теореме 1). Если
есть четная ось симметрии и на ней центр симметрии, то перпендикулярно этой оси
проходит плоскость симметрии: 
 .
.
Теорема 3. Если есть ось симметрии
порядка 
 и перпендикулярно этой оси проходит
ось второго порядка, то всего имеется
и перпендикулярно этой оси проходит
ось второго порядка, то всего имеется 
 осей второго порядка,
перпендикулярных оси -го порядка:
осей второго порядка,
перпендикулярных оси -го порядка: 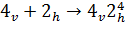
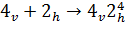 .
.
Теорема 4. Если есть ось симметрии
-го порядка и вдоль нее проходит плоскость симметрии, то таких плоскостей
имеется 
 :
: 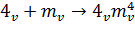
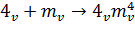 .
.
Таким образом, исходя из приведенных
выше теорем, можно записать: 
 . Соответственно
кристаллографическая формула выглядит следующим образом:
. Соответственно
кристаллографическая формула выглядит следующим образом: 
 .
.
. Стандартная установка
кристаллографических и кристаллофизических осей координат. Изображение проекции
заданной грани на сетке Вульфа
На рис. 4 приведена стандартная
установка кристаллографических и кристаллофизических осей координат для класса 
 тетрагональной сингонии. Из рисунка
видно, что оси кристаллофизической системы координат (X1, X2, X3) совпадают
с осями кристаллографической системы координат (X, Y, Z).
тетрагональной сингонии. Из рисунка
видно, что оси кристаллофизической системы координат (X1, X2, X3) совпадают
с осями кристаллографической системы координат (X, Y, Z).
Для решения количественных задач с
помощью стереографической и гномостереографической проекции пользуются обычно
градусными сетками. Наиболее употребительна сетка Вульфа. Сетка Вульфа - это
стереографическая проекция всей системы меридианов и параллелей, нанесенных на
поверхность сферы.

Рис. 4. Кристаллографическая и
кристаллофизическая установки осей координат
Плоскостью проекций является
плоскость одного из меридианов. Положение любой точки на сетке Вульфа
определяется ее сферическими координатами 
 и
и 
 .
.
Угол 
 между плоскостями
между плоскостями 
 и
и 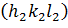
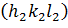 находится как угол между их
обратными векторами. Косинус угла между этими плоскостями в тетрагональной
сингонии определяется следующим образом:
находится как угол между их
обратными векторами. Косинус угла между этими плоскостями в тетрагональной
сингонии определяется следующим образом:
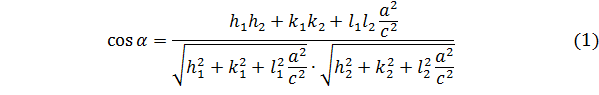
Рассчитаем угол 
 . В качестве грани
. В качестве грани 
 выбирается грань
выбирается грань 
 , а грани
, а грани 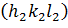
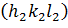 соответствует грань
соответствует грань 
 . Соответственно:
. Соответственно:
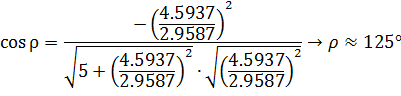
Рассчитаем угол 
 с проекцией в экваториальной
плоскости. В качестве грани
с проекцией в экваториальной
плоскости. В качестве грани 
 выбирается грань
выбирается грань 
 , а грани
, а грани 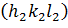
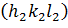 соответствует грань
соответствует грань 
 . Соответственно:
. Соответственно:

Изобразим проекцию грани 
 и проекции других граней общей
простой формы на сетке Вульфа, исходя из рассчитанных сферических координат
(рис. 5).
и проекции других граней общей
простой формы на сетке Вульфа, исходя из рассчитанных сферических координат
(рис. 5).

Рис. 5. Проекция грани 
 и простой формы на ее основе на
сетке Вульфа
и простой формы на ее основе на
сетке Вульфа
Часть 2. Стереографические проекции частных
простых форм рутильной модификации диоксида титана
Таблица 2
Частные простые формы рутильной модификации
диоксида титана
|
Частная
простая форма
|
Стереографическая
проекция
|
Название
простой формы
|
Собственная
симметрия грани
|
Форма
фигур травления
|
|

|
|
Пинакоид
|

|
Квадрат
|
|

|
|
Тетрагональная
бипризма
|

|
Ромб
|
|

|
|
Дитетрагональная
призма
|

|
Равнобедренный
треугольник
|
|

|
|
Тетрагональная
бипирамида
|

|
Равнобедренный
треугольник
|
Часть 3. Матричные представления преобразований
симметрии
Преобразования симметрии в
кристаллическом пространстве можно описать аналитически как соответствующие
преобразования координат. Для этого выбираем в пространстве прямоугольную
систему координат 
 . Точка с координатами
. Точка с координатами 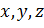
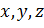 после преобразования симметрии
займет новое положение с координатами
после преобразования симметрии
займет новое положение с координатами 
 , которые определяются уравнениями
преобразования:
, которые определяются уравнениями
преобразования:




где 
 косинусы углов между осями старой и
новой системы координат. Любому преобразованию симметрии можно поставить в
соответствие определитель преобразования
косинусы углов между осями старой и
новой системы координат. Любому преобразованию симметрии можно поставить в
соответствие определитель преобразования 
 .
.
Представим исходные элементы
симметрии в матричном виде.
Таблица 3
Матричные представления исходных
элементов симметрии
|
Элемент
симметрии
|
Преобразование
кристаллофизических осей
|
Матричное
представление
|
|
Вертикальная
поворотная ось четвертого порядка    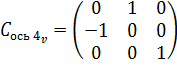
|
|
|
|
Элемент
симметрии
|
Преобразование
кристаллофизических осей
|
Матричное
представление
|
|
Горизонтальная
поворотная ось второго порядка    
|
|
|
|
Вертикальная
плоскость симметрии    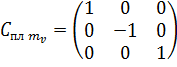
|
|
|
Получим новые элементы симметрии путем
перемножения матриц:
. Получение центра инверсии:


2. Получение горизонтальной плоскости
симметрии:

. Получение горизонтальных осей симметрии
второго порядка:



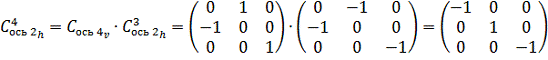
получили исходный элемент 
 .
.
4. Получение вертикальных плоскостей
симметрии:




получили исходный элемент симметрии 

Сведем все новые элементы симметрии,
полученные матричным методом в таблицу:
Таблица 4
Новые элементы симметрии, полученные
матричным методом
|
Элемент
симметрии
|
Преобразование
кристаллофизических осей
|
Матричное
представление
|
|
Центр
инверсии
|
 
|
|
|
Горизонтальная
плоскость симметрии 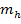 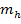  
|
|
|
|
Горизонтальная
поворотная ось второго порядка    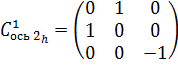
|
|
|
Горизонтальная поворотная ось
второго порядка 

Горизонтальная поворотная ось
второго порядка 

Часть 4. Оценка возможности возникновения
эффектов
При оценке возможности возникновения тех или
иных эффектов будем пользоваться принципом Кюри:
) В присутствии внешнего воздействия кристалл
изменяет свою симметрию;
) Результирующая симметрия кристалла
содержит те элементы симметрии, которые идентичны для воздействия и для
кристалла (включая направления).
. Пироэлектрический эффект
Пироэлектричество - это свойство некоторых
диэлектрических кристаллов изменять величину электрической поляризации при
изменении температуры. В результате нагревания или охлаждения
пироэлектрического кристалла на его гранях появляются электрические заряды.
Если в кристалле нет единичных
полярных направлений, то пироэлектрического эффекта наблюдаться не будет. Из 32
классов симметрии полярные единичные направления могут существовать лишь в 10
классах симметрии, а именно в тех, где есть либо одна-единственная ось
симметрии, либо одна ось и продольные плоскости симметрии. Пироэлектрический
эффект может проявляться только в диэлектрических кристаллах, принадлежащих к
одному из десяти полярных классов симметрии: 1, 2, 3, 4, 6, m, mm2, 3m, 4mm, 6mm
 Класс симметрии 4/mmm не содержит
полярных направлений, поэтому пироэлектрический эффект наблюдаться не будет.
Класс симметрии 4/mmm не содержит
полярных направлений, поэтому пироэлектрический эффект наблюдаться не будет.
2. Пьезоэлектрический эффект
Пьезоэффект - эффект возникновения
поляризации диэлектрика
<#"821708.files/image076.gif"> , где
, где 
 и
и 
 - компоненты вектора поляризации и
тензора механических напряжений соответственно, а
- компоненты вектора поляризации и
тензора механических напряжений соответственно, а 
 - компоненты тензора
пьезоэлектрических модулей.
- компоненты тензора
пьезоэлектрических модулей.
Пьезоэлектрическому эффекту
соответствует предельная группа симметрии 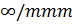
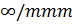 , которая представлена элементами:
, которая представлена элементами: 
 . Группа изображается покоящимся
цилиндром.
. Группа изображается покоящимся
цилиндром.
Таблица 5
Оценка возникновения пьезоэффекта
|
Неэквивалентные
направления в кристалле
|
Общие
элементы симметрии
|
Результирующая
симметрия кристалла
|
Вероятность
возникновения эффекта
|
|
[001]
|

|

|
эффект
невозможен
|
|
[100] или [110]
|

|

|
эффект
невозможен
|
|
[hk0]
|

|

|
эффект
невозможен
|
|
[hkl] или [h0l]
|

|

|
эффект
невозможен
|
|
[hkl]
|

|

|
эффект
невозможен
|
. Эффект поляризации в электрическом поле
Поляризация кристалла в
электрическом поле можно описать при помощи тензоров 2-го ранга -
диэлектрической проницаемости 
 или диэлектрической восприимчивости
или диэлектрической восприимчивости

 . Уравнение, описывающее данный
эффект:
. Уравнение, описывающее данный
эффект: 
 , где
, где 
 вектор электрического смещения,
вектор электрического смещения, 
 вектор электрического поля.
вектор электрического поля.
Эффекту поляризации в электрическом
поле соответствует предельная группа симметрии 
 , которая представлена элементами:
, которая представлена элементами: 
 Группа изображается покоящимся
конусом.
Группа изображается покоящимся
конусом.
Таблица 6
Оценка возникновения эффекта
поляризации в электрическом поле
|
Направление,
параллельное оси бесконечного порядка
|
Общие
элементы симметрии
|
Результирующая
симметрия кристалла
|
Вероятность
возникновения эффекта
|
|
[001]
|

|

|
возможен продольный эффект
|
|
[100] или [110]
|

|

|
возможен
продольный эффект
|
|
[hk0]
|
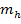
|

|
возможен
поперечный и продольный эффект
|
|
[hhl] или [h0l]
|

|

|
возможен
поперечный и продольный эффект
|
|
[hkl]
|

|

|
эффект
невозможен
|
. Эффект электропроводности
Электропроводность описывается тензором второго
ранга - тензором удельной проводимости или обратным ему тензором удельного
электрического сопротивления.
Уравнение, описывающее явление
электропроводности, связывает между собой два вектора - вектор плотности тока и
напряжённости электрического поля: 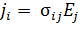
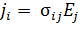 . Принципиальное отличие между
явлением электропроводности и поляризации в электрическом поле отсутствует. В
обоих случаях явление и воздействие являются векторными, симметрия воздействия
совпадает. Поэтому все результаты, полученные для предыдущего случая,
распространяются и на данный эффект.
. Принципиальное отличие между
явлением электропроводности и поляризации в электрическом поле отсутствует. В
обоих случаях явление и воздействие являются векторными, симметрия воздействия
совпадает. Поэтому все результаты, полученные для предыдущего случая,
распространяются и на данный эффект.
Часть 5. Расчет дифрактограммы кварца
Для расчета рентгенограммы поликристаллического
вещества необходимо определить положение дифракционных пиков и вычислить
относительную интегральную интенсивность.
. Расчет межплоскостных расстояний
Исходными данными для расчета являются периоды
решетки, находимые в литературе, и индексы интерференции, определяемые из
пространственной группы по законам погасаний.
Расчет следует проводить до тех пор,
пока вычисленные межплоскостные расстояния не станут меньше половины длины
волны того излучения, для которого рассчитывается диаграмма, так как на
рентгенограмме получаются отражения от плоскостей, для которых 

Расчет брэгговских углов
производится по данным о межплоскостных расстояниях по формуле Вульфа-Брэгга: 
 .
.
Заданный материал относится к тригональной
сингонии. Расчёт межплоскостных расстояний производится по формуле для
гексагональной системы координат:
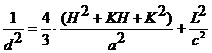
. Вычисление относительной
интегральной интенсивности
Вычисление относительной
интегральной интенсивности производится не только при расчете рентгенограмм,
часто оно представляет собой основную цель исследования, например при
определении структуры вещества, искажений кристаллической решетки,
характеристической температуры, изучении сверхструктуры и др. Интегральная
интенсивность линий рентгенограммы является функцией ряда факторов. Эта
зависимость выражается уравнением:

где 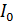
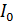 - интенсивность первичных лучей;
- интенсивность первичных лучей; 
 - постоянная для данного вещества и
данных условий съемки величина;
- постоянная для данного вещества и
данных условий съемки величина; 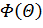
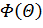 - угловой множитель интенсивности;
- угловой множитель интенсивности; 
 - множитель повторяемости;
- множитель повторяемости; 
 - абсорбционный множитель;
- абсорбционный множитель; 
 - температурный множитель
интенсивности;
- температурный множитель
интенсивности; 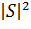
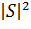 - структурный множитель
интенсивности.
- структурный множитель
интенсивности.
Угловой множитель 
 учитывает поляризацию, происходящую
при рассеянии рентгеновых лучей, а также конечную величину пучка рассеянных
лучей и геометрию съемки рентгенограммы:
учитывает поляризацию, происходящую
при рассеянии рентгеновых лучей, а также конечную величину пучка рассеянных
лучей и геометрию съемки рентгенограммы:

Множитель повторяемости 
 равен числу семейств плоскостей в
их совокупности, имеющих одинаковое межплоскостное расстояние и одинаковый
структурный множитель. В нашем случае граням (0001) отвечает множитель 2,
граням (100), (110) и (h0l) - 6, для
остальных граней (hki0), (hhl) и (hkil) множитель
равен 12.
равен числу семейств плоскостей в
их совокупности, имеющих одинаковое межплоскостное расстояние и одинаковый
структурный множитель. В нашем случае граням (0001) отвечает множитель 2,
граням (100), (110) и (h0l) - 6, для
остальных граней (hki0), (hhl) и (hkil) множитель
равен 12.
Абсорбционный множитель 
 учитывает ослабление лучей в
образце при данной геометрии съемки.
учитывает ослабление лучей в
образце при данной геометрии съемки.
Температурный множитель 
 учитывает разность фаз рассеянных
лучей, возникшую вследствие тепловых колебаний.
учитывает разность фаз рассеянных
лучей, возникшую вследствие тепловых колебаний.
Расчёт интенсивности в данной работе
производится в рамках приближения Брэдли, согласно которому можно без потери
точности принять произведение абсорбционного и температурного множителей равным
единице (для материалов с достаточно сильным поглощением рентгеновского
излучения).
Структурный множитель 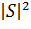
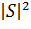 учитывает зависимость интенсивности
рентгеновых лучей от расположения атомов в элементарной ячейке и определяется
базисом решетки:
учитывает зависимость интенсивности
рентгеновых лучей от расположения атомов в элементарной ячейке и определяется
базисом решетки:

Структурный множитель представляет
собой, таким образом, взятую по всем атомам базиса сумму произведений атомного
множителя 
 на комплексную экспоненту, в
аргумент которого входит сумма парных произведений индексов интерференции
на комплексную экспоненту, в
аргумент которого входит сумма парных произведений индексов интерференции 
 на одноименные координаты базиса
на одноименные координаты базиса 
 и
и 

Обращение структурного множителя в нуль
свидетельствует о погасании соответствующего отражения, поэтому при отсутствии
данных о пространственной группе выражение структурного множителя можно
использовать для определения индексов наблюдаемых интерференций.
fj- атомный множитель (или фактор)
рассеяния рентгеновских лучей, его значения были получены эмпирическим путём, с
помощью справочных данным был построен график зависимости атомного множителя от

 , с помощью его полиномиальной
аппроксимации был получен полином 4-го порядка= 0,0018x4 - 0,0594x3 + 0,5761x2
- 3,1976x + 14,047, с помощью полиномы были рассчитаны значения
, с помощью его полиномиальной
аппроксимации был получен полином 4-го порядка= 0,0018x4 - 0,0594x3 + 0,5761x2
- 3,1976x + 14,047, с помощью полиномы были рассчитаны значения 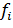
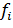 .
.
Кварц характеризуется следующим атомным базисом:
[(0.4699 0 0.6667), (0 0.4699 0.3334), (0.5301
0.5301 0) - Si (0.4141
0.2681 0.1188), (0.7319 0.146 0.7855), (0.854 0.5859 0.4522), (0.2681 0.4141
0.8812), (0.146 0.7319 0.2145), (0.5859 0.854 0.5478 ) - O].
Рассчитаем структурный множитель 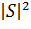
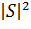 :
:
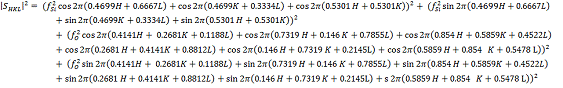
Таблица 7
Расчет интенсивности рентгеновских
рефлексов на излучении меди для кварца
|
Индексы
|
  , нм , нм   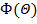    
|
|
|
|
|
|
|
|
|
|
|
H
|
K
|
L
|
|
|
|
|
|
|
|
|
|
|
|
1
|
0
|
0
|
0,181
|
6
|
10,438
|
1,175
|
60,94
|
11,49
|
192,581
|
70415,19
|
0,194
|
|
|
1
|
0
|
2
|
0,077
|
12
|
16,089
|
1,797
|
26,06
|
10,33
|
1162,521
|
363569,11
|
1,000
|
|
|
0
|
0
|
3
|
0,060
|
2
|
18,335
|
2,040
|
20,24
|
9,95
|
2261,554
|
91545,56
|
0,252
|
|
|
1
|
1
|
1
|
0,054
|
12
|
19,321
|
2,146
|
18,30
|
9,79
|
1093,954
|
240248,75
|
0,661
|
|
|
2
|
0
|
0
|
0,045
|
12
|
21,244
|
2,350
|
15,27
|
9,50
|
947,405
|
173609,41
|
0,478
|
|
|
0
|
2
|
1
|
0,042
|
12
|
22,161
|
2,447
|
14,10
|
9,37
|
464,229
|
78532,29
|
0,216
|
|
|
1
|
1
|
2
|
0,042
|
12
|
22,174
|
2,448
|
14,08
|
9,36
|
1318,263
|
222758,18
|
0,613
|
|
|
2
|
0
|
2
|
0,034
|
12
|
24,750
|
2,715
|
11,46
|
9,02
|
121,121
|
16661,98
|
0,046
|
|
2
|
1
|
0
|
0,026
|
12
|
28,642
|
3,109
|
8,56
|
691,972
|
72895,86
|
0,201
|
|
1
|
2
|
1
|
0,025
|
12
|
29,385
|
3,182
|
8,39
|
8,48
|
843,947
|
84927,04
|
0,234
|
|
1
|
2
|
2
|
0,022
|
12
|
31,548
|
3,393
|
7,40
|
8,25
|
529,212
|
46992,26
|
0,129
|
|
3
|
0
|
0
|
0,020
|
12
|
32,924
|
3,525
|
6,87
|
8,11
|
108,324
|
8935,65
|
0,025
|
|
3
|
0
|
1
|
0,019
|
6
|
33,610
|
3,590
|
6,64
|
8,04
|
54,125
|
2155,28
|
0,006
|
|
1
|
2
|
3
|
0,018
|
12
|
34,983
|
3,719
|
6,21
|
7,91
|
371,339
|
27652,01
|
0,076
|
|
3
|
0
|
2
|
0,018
|
12
|
35,632
|
3,779
|
6,02
|
7,85
|
1032,238
|
74568,38
|
0,205
|
|
2
|
2
|
0
|
0,015
|
12
|
38,873
|
4,071
|
5,24
|
7,56
|
584,251
|
36720,67
|
0,101
|
|
0
|
3
|
3
|
0,015
|
12
|
38,902
|
4,073
|
5,23
|
7,56
|
584,692
|
36707,23
|
0,101
|
|
2
|
2
|
1
|
0,015
|
12
|
39,517
|
4,127
|
5,11
|
7,51
|
593,826
|
36391,96
|
0,100
|
|
3
|
1
|
0
|
0,014
|
12
|
40,786
|
4,237
|
4,87
|
7,40
|
658,455
|
38476,62
|
0,106
|
|
3
|
1
|
1
|
0,014
|
12
|
41,421
|
4,291
|
4,76
|
7,35
|
329,104
|
18798,13
|
0,052
|
|
2
|
2
|
2
|
0,014
|
12
|
41,431
|
4,292
|
4,76
|
7,35
|
153,757
|
8779,61
|
0,024
|
|
3
|
1
|
2
|
0,013
|
12
|
43,320
|
4,450
|
4,47
|
7,20
|
678,157
|
36342,87
|
0,100
|
|
4
|
0
|
0
|
0,011
|
12
|
46,443
|
4,700
|
4,08
|
6,96
|
343,848
|
16815,67
|
0,046
|
|
1
|
3
|
3
|
0,011
|
12
|
46,471
|
4,702
|
4,07
|
6,95
|
249,423
|
12188,94
|
0,034
|
|
4
|
0
|
1
|
0,011
|
12
|
47,074
|
4,749
|
4,01
|
6,91
|
1430,349
|
68806,45
|
0,189
|
|
4
|
0
|
2
|
0,010
|
12
|
48,975
|
4,893
|
3,83
|
6,77
|
39,220
|
1802,57
|
0,005
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Рис. 6. Штрихдиаграмма для кварца на излучении
меди
Таблица 8
Расчет интенсивности рентгеновских рефлексов на
излучении хрома для кварца
|
Индексы
|
  , нм , нм   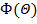    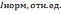
|
|
|
|
|
|
|
|
|
|
H
|
K
|
L
|
|
|
|
|
|
|
|
|
|
|
1
|
0
|
0
|
0,181
|
6
|
20,570
|
3,182474
|
16,24
|
11,49
|
192,581
|
18761,23
|
0,191
|
|
1
|
0
|
2
|
0,077
|
12
|
32,509
|
3,182474
|
7,03
|
10,33
|
1162,521
|
98001,13
|
1,000
|
|
0
|
0
|
3
|
0,060
|
2
|
37,592
|
3,182474
|
5,52
|
9,95
|
2261,554
|
24969,94
|
0,255
|
|
1
|
1
|
1
|
0,054
|
12
|
39,913
|
3,182474
|
5,03
|
9,79
|
1093,954
|
66030,91
|
0,674
|
|
2
|
0
|
0
|
0,045
|
12
|
44,644
|
3,182474
|
4,29
|
9,50
|
947,405
|
48741,77
|
0,497
|
|
0
|
2
|
1
|
0,042
|
12
|
47,014
|
3,182474
|
4,01
|
9,37
|
464,229
|
22365,96
|
0,228
|
|
1
|
1
|
2
|
0,042
|
12
|
47,049
|
3,182474
|
4,01
|
9,36
|
1318,263
|
63455,99
|
0,648
|
|
2
|
0
|
2
|
0,034
|
12
|
54,282
|
3,182474
|
3,48
|
9,02
|
121,121
|
5064,12
|
0,052
|
|
2
|
1
|
0
|
0,026
|
12
|
68,369
|
3,182474
|
2,31
|
8,56
|
691,972
|
19218,84
|
0,196
|
|
1
|
2
|
1
|
0,025
|
12
|
72,094
|
3,182474
|
2,21
|
8,48
|
843,947
|
22369,39
|
0,228
|

. Выбор излучения для прецизионной
рентгеносъемки
Точность рентгеновского определения периодов
идентичности резко возрастает с увеличением брэгговских углов. В самом деле,
показано, что точность измерения межплоскостного расстояния определяется
величиной

Отсюда следует, что чем больше 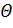
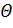 , тем меньше относительное изменение
межплоскостного расстояния, которое может быть обнаружено.
, тем меньше относительное изменение
межплоскостного расстояния, которое может быть обнаружено.
Итак, при прецизионной съемке
следует выбирать излучение, прежде всего исходя из возможно больших реализуемых
значений 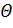
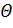 .
.
Таблица 9
Выбор излучения для прецизионной рентгеносъемки
|
Исследуемый
материал
|
Материал
анода
|
Фильтр
|
Плоскости
|
Θ,
град.
|
Cu
|
Ni
|
(2 3 3)
|
81.849
|
|
Cr
|
V
|
(4 0 0)
|
87.145
|
Из указанной таблицы следует, что для наиболее
точного определения межплоскостных расстояний рекомендуется применение анода из
хрома.
Заключение
В ходе курсового проекта была изучена
кристаллическая структура диоксида титана. Проведённый анализ позволил
установить отсутствие в кристаллах диоксида титана пиролитического и
пьезоэлектрического эффектов, что связано с присутствием центра симметрии в его
кристаллической структуре. Также в данной работе были рассчитаны рентгенограммы
исследуемого материала для двух типов излучения. Также было выяснено, что для
прецизионной рентгеносъёмки лучше выбирать анод из хрома, а не из меди, так как
его излучение, как показали расчёты, способно рождать рефлексы при больших
значениях угла дифракции.
Список использованной литературы
1. Интернетный
ресурс <http://ruschemical.com>;
. Интернетный
ресурс <http://wiki.web.ru>;
. Интернетный
ресурс <http://tio-2.ru>;
. Шаскольская
М. П. Кристаллография. Учебник для втузов. М., «Высш. школа», 1976. 391 с. с
ил:
. Миркин
Л. И. Справочник по рентгеноструктурному анализу поликристаллов под редакцией
проф. Я. С. Уманского, Государственной издательство физико-математической
литературы, М.: 1961.