ЭВМ-эксперимент и машинная обработка информации
Контрольная
работа
по
дисциплине «ЭВМ-эксперимент и машинная обработка информации»
Тема:
Численное интегрирование
Аннотация
В данной работе будут рассмотрены три метода
приближённого интегрирования определённого интеграла: метод прямоугольников,
метод трапеций и метод Симпсона. Все эти методы будут подробно выведены с
оценкой погрешности каждого из них. В работу включено наглядное применение
нахождения определенного интеграла методом прямоугольников и трапеций. В
материале имеются иллюстрации, с помощью которых, можно более глубоко вникнуть
в суть рассматриваемой темы.
Введение
Основная цель этой работы заключается в
ознакомлении с численным интегрированием. Суть численного интегрирования
заключается в том, что подынтегральную функцию заменяют другой приближенной
функцией, так, чтобы, во-первых, она была близка к первоначальной функции и, во
вторых, интеграл от нее легко вычислялся. Методы численного интегрирования,
основаны на замене подынтегральной функции интерполяционным многочленом. Это позволяет
приближенно заменить определенный интеграл интерполяционной суммой. В
зависимости от способа ее вычисления получаются разные методы численного
интегрирования, такие как:
метод прямоугольников;
метод трапеций;
метод Симпсона.
В частности при выполнении данной работы
использовался метод трапеций.
1. Математическая модель
.1 Определение интеграла и его
геометрический смысл
В начале узнаем, что такое
определённый интеграл. Возможны два различных подхода к определению
определённого интеграла. Приращение  любой из преобразованных функций
любой из преобразованных функций 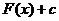 при
изменении аргумента от
при
изменении аргумента от 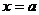 до
до 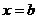 называют
определённым интегралом от a до b функции f и обозначается
называют
определённым интегралом от a до b функции f и обозначается 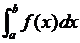 . Причём
функция
. Причём
функция 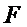 является
первообразной для функции f на некотором промежутке D, а числа а и b
принадлежат этому промежутку. Это можно записать следующим образом:
является
первообразной для функции f на некотором промежутке D, а числа а и b
принадлежат этому промежутку. Это можно записать следующим образом:
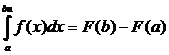 (1)
(1)
это формула Ньютона-Лейбница.

Рис. 1
Если при любой последовательности
разбиений отрезка [a;b] таких, что 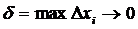 (n→∞) и при любом
выборе точек
(n→∞) и при любом
выборе точек 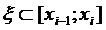 интегральная
сумма
интегральная
сумма  стремится к
одному и тому же конечному пределу А, то это число А и есть определённый
интеграл, т.е.
стремится к
одному и тому же конечному пределу А, то это число А и есть определённый
интеграл, т.е. 
 (2)
(2)
Где 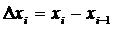
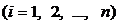
 - начало разбиения
- начало разбиения 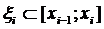 произвольная
точка из отрезка
произвольная
точка из отрезка 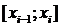 сумма всех
произведений
сумма всех
произведений 
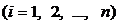 . Простыми
словами, определенный интеграл есть предел интегральной суммы, число членов
которой неограниченно возрастает, а каждое слагаемое стремится к нулю.
. Простыми
словами, определенный интеграл есть предел интегральной суммы, число членов
которой неограниченно возрастает, а каждое слагаемое стремится к нулю.
1.2 Геометрический смысл

Рис. 2
Всякая непрерывная на отрезке [a,b]
функция f интегрируема на отрезке [a,b], функция f неотрицательна, но
определённый интеграл  численно
равен S криволинейной трапеции, ограниченной графиком функции f, осью абсцисс и
прямыми
численно
равен S криволинейной трапеции, ограниченной графиком функции f, осью абсцисс и
прямыми
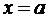 и
и 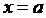 ,
,  .
.
1.3 Приближённые методы вычисления
Как мы уже отметили, если функция f
непрерывна на промежутке, то на этом промежутке существует функция  такая, что
такая, что 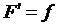 , то есть
существует первообразная для функции
, то есть
существует первообразная для функции 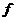 , но не всякая элементарная функция
, но не всякая элементарная функция 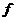 имеет
элементарную первообразную
имеет
элементарную первообразную  . Объясним понятие элементарной
функции.
. Объясним понятие элементарной
функции.
Функции: степенная, показательная,
тригонометрическая, логарифмическая, обратные тригонометрическим называются
основными элементарными функциями. Элементарной функцией называется функция,
которая может быть задана с помощью формулы, содержащей лишь конечное число
арифметических операций и суперпозиций основных элементарных.
Бывает, что на практике сталкиваются
с вычислением интегралов от функций, которые заданы табличными и графическими
способами, или интегралы от функций, первообразные которых выражаются через
элементарные функции очень сложно, что неудобно, долго и не рационально. В этих
случаях вычисление определённого интеграла по формуле Ньютона-Лейбница (1)
сводит вычисление определённого интеграла от какой-либо функции к нахождению её
первообразной. Значит, если первообразная не элементарна, надо вычислить
определённый интеграл как-то по другому, поэтому прибегают к различным методам
приближённого интегрирования.
В основе приближённых методов
интегрирования лежит геометрический смысл определённого интеграла, который
рассмотрен выше.
Формул приближённого интегрирования
существует много. В данной курсовой работе будет рассмотрено три метода
приближённого интегрирования: метод трапеций, метод прямоугольников и метод
Симпсона.
Формула прямоугольников
Теперь рассмотрим первый вид
приближённого вычисления:
требуется вычислить определённый интеграл: 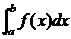 .
.
Пусть на отрезке [a,b] задана
непрерывная функция  . Разделим
отрезок [a,b], аналогично как в формуле трапеций: точками
. Разделим
отрезок [a,b], аналогично как в формуле трапеций: точками 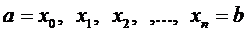 на n равных
частей длины
на n равных
частей длины 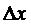 , где
, где 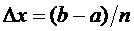 .
.

Рис. 3
Обозначим через y0,y1,y2,…,yn-1,yn
значение функции  в точках
в точках  то есть,
если записать в наглядной формуле:
то есть,
если записать в наглядной формуле:
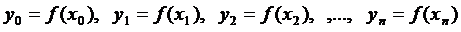
В данном способе подынтегральную
функцию заменяем функцией, которая имеет ступенчатый вид (на рис. выделена).
Составим суммы:
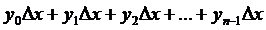 ;
; 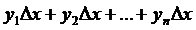 .
.
Каждое слагаемое этих сумм выражает
площадь, полученных прямоугольников с основанием 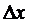 .
.
Каждая из этих сумм является
интегральной суммой для  на отрезке
[a,b], и равна площади ступенчатых фигур, а значит приближённо выражает
интеграл. Вынесем
на отрезке
[a,b], и равна площади ступенчатых фигур, а значит приближённо выражает
интеграл. Вынесем 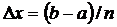 из каждой
суммы, получим:
из каждой
суммы, получим:
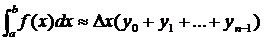

Выразив x, получим окончательно:
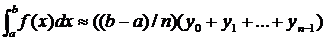 (3)
(3)
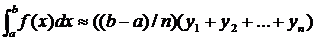 (3*)
(3*)
Это и есть формулы прямоугольников.
Их две, так как можно использовать два способа замены подынтегральной функции.
Если  -
положительная и возрастающая функция, то формула (3) выражает S фигуры,
расположенной под графиком, составленной из входящих прямоугольников, а формула
(3*) - площадь ступенчатой фигуры, расположенной под графиком функции
составленной из выходящих треугольников.
-
положительная и возрастающая функция, то формула (3) выражает S фигуры,
расположенной под графиком, составленной из входящих прямоугольников, а формула
(3*) - площадь ступенчатой фигуры, расположенной под графиком функции
составленной из выходящих треугольников.
Ошибка, совершаемая при вычислении
интегралов по формуле прямоугольников, будет тем меньше, чем больше число n (то
есть чем меньше шаг деления)

Для вычисления погрешности этого
метода используется формула:
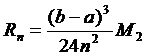 , где
, где 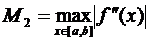
Результат полученный по формуле (3)
заведомо даёт большую площадь прямоугольника, так же по формуле (3*) даёт
заведомо меньшую площадь, для получения среднего результата используется
формула средних прямоугольников:
 (3**)
(3**)
Формула трапеций.

Рис. 4
Возьмём определённый интеграл
 ,
,
где  - непрерывная подынтегральная
функция, которую мы для наглядности будем предполагать положительной. При
вычислении интеграла с помощью формулы трапеций подынтегральная функция
- непрерывная подынтегральная
функция, которую мы для наглядности будем предполагать положительной. При
вычислении интеграла с помощью формулы трапеций подынтегральная функция 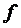 заменяется
функцией, график которой представляет собой ломанную линию (на рис. 1 красным
цветом), звенья которой соединяют концы ординат
заменяется
функцией, график которой представляет собой ломанную линию (на рис. 1 красным
цветом), звенья которой соединяют концы ординат  и
и 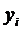
 Тогда площадь криволинейной
трапеции, ограниченной линиями x=a,
Тогда площадь криволинейной
трапеции, ограниченной линиями x=a,  ,
,  ,
, 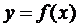 , а значит (следуя из
геометрического смысла), и значение нужного нам интеграла, приблизительно равна
сумме площадей обычных трапеций с основаниями
, а значит (следуя из
геометрического смысла), и значение нужного нам интеграла, приблизительно равна
сумме площадей обычных трапеций с основаниями  и
и 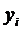 , и высотой
, и высотой 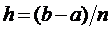 , так как
(если более привычно выражать для нас)
, так как
(если более привычно выражать для нас) 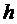 это
это 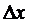 ,a
,a 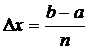 при делении отрезка на n равных
отрезков при помощи точек
при делении отрезка на n равных
отрезков при помощи точек 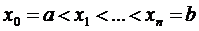 . Прямые
. Прямые 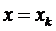 разбивают
криволинейную трапецию на n полосок. Принимая каждую из этих полосок за
обыкновенную трапецию, получаем, что площадь криволинейной трапеции
приблизительно равна сумме обыкновенных трапеций.
разбивают
криволинейную трапецию на n полосок. Принимая каждую из этих полосок за
обыкновенную трапецию, получаем, что площадь криволинейной трапеции
приблизительно равна сумме обыкновенных трапеций.

Рис. 5
Площадь крайней полоски слева, как помниться из
школьного курса геометрии, равна произведению полусуммы основания на высоту.


Итак, запишем сказанное выше в
математическом виде:

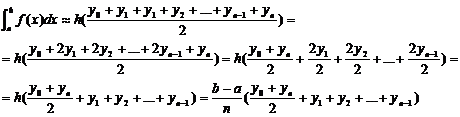 (4)
(4)
Формула (4) и есть формула трапеций
Для определения погрешности
интеграла вычисленного с помощью формулы трапеций используется формула:
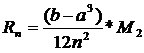 , где
, где 
Формула Симпсона (формула парабол).
Существует два подхода к формуле
Симпсона. В одном используется парабола в другом нет.
А) с использованием параболы.
Разделим отрезок [a;b] на чётное
число равных частей 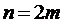 . Площадь
криволинейной трапеции, соответствующей первым двум отрезкам [x0,x1], [x1,x2] и
ограниченной заданной кривой
. Площадь
криволинейной трапеции, соответствующей первым двум отрезкам [x0,x1], [x1,x2] и
ограниченной заданной кривой 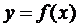 , заменим площадью криволинейной
трапеции, которая ограничена параболой второй степени, проходящей через три
точки M0[x0,y0], M1[x1,y1], M2[x2,y2] и имеющей ось, параллельную оси Oy. Такую
криволинейную трапецию называют параболической трапецией.
, заменим площадью криволинейной
трапеции, которая ограничена параболой второй степени, проходящей через три
точки M0[x0,y0], M1[x1,y1], M2[x2,y2] и имеющей ось, параллельную оси Oy. Такую
криволинейную трапецию называют параболической трапецией.
Уравнение параболы с осью,
параллельной оси Oy, имеет вид:
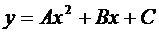 .
.

Рис. 6
Коэффициенты A, B и C однозначно определяются из
условия, что парабола проходит через три заданные точки. Аналогичные параболы
строятся и для других пар отрезков. Сумма параболических трапеций и даст
приближённое значение интеграла. Сначала вычислим площадь одной параболической
трапеции. Для этого докажем лемму.
Лемма: если криволинейная трапеция
ограничена параболой 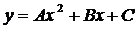 , осью Ox и
двумя ординатами, расстояние между которыми равно 2h, то её площадь равна:
, осью Ox и
двумя ординатами, расстояние между которыми равно 2h, то её площадь равна:
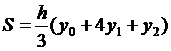 (5)
(5)
где  и
и 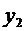 - крайние ординаты, а
- крайние ординаты, а 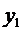 - ордината
кривой в середине отрезка.
- ордината
кривой в середине отрезка.

Рис. 7
Доказательство:
Расположим вспомогательную систему
координат так, как показано на рис. Коэффициент в уравнение параболы  определяются
из следующих уравнений:
определяются
из следующих уравнений:
Если 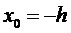 , то
, то 
Если 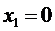 , то
, то  (6)
(6)
Если 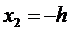 , то
, то 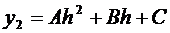
Считая коэффициенты A, B, C
известными определим площадь параболической трапеции с помощью определённого
интеграла:

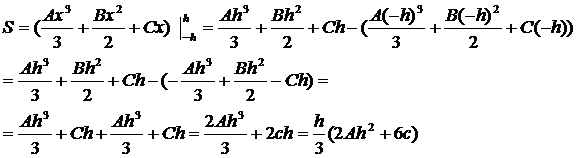
из равенства (6) следует, что
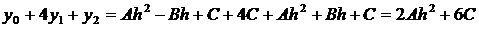
следовательно:
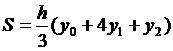
ч.т.д. пользуясь формулой (5), можно
написать приближённые равенства, учитывая, что
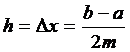


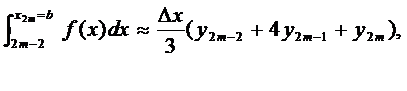
складывая левые и правые части,
получим слева искомый интеграл, справа его приближённое значение:
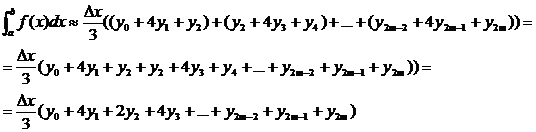
или
 (7)
(7)
Это и есть формула Симпсона. Здесь
число точек деления произвольно, но чем это число больше, тем точнее сумма в
правой части равенства (6) даёт значение интеграла. Формула Симпсона даёт самое
точное значение интеграла (из классических формул приближённого
интегрирования), погрешность для этого метода находится по формуле:
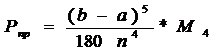 где
где 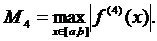
Б) Без использования парабол

Рис. 8
В тех случаях, когда линия 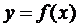 между
между 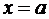 и
и  мало
изогнута, интеграл
мало
изогнута, интеграл 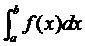 приближенно
выражается достаточно простой формулой. Будем считать
приближенно
выражается достаточно простой формулой. Будем считать  положительной
и искать площадь криволинейной трапеции aABb. Для этого разделим отрезок [a;b]
точкой
положительной
и искать площадь криволинейной трапеции aABb. Для этого разделим отрезок [a;b]
точкой
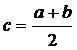
пополам и в точке 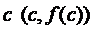 проведём
касательную к линии
проведём
касательную к линии 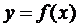 . После
этого разделим [a,b] точками p и g на 3 равные части и проведём через них
прямые
. После
этого разделим [a,b] точками p и g на 3 равные части и проведём через них
прямые 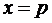 и
и 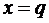 . P и Q -
точки пересечения прямых с касательной. Соединив AP и BQ, получим 3
прямолинейные трапеции aAPp, pPQq, qQBb. Сумма площадей этих трапеций равна
будет примерно равна площади криволинейной трапеции aABb:
. P и Q -
точки пересечения прямых с касательной. Соединив AP и BQ, получим 3
прямолинейные трапеции aAPp, pPQq, qQBb. Сумма площадей этих трапеций равна
будет примерно равна площади криволинейной трапеции aABb:
Обозначим: Aa, Pp, qQ, bB -
основания трапеций;
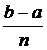 - высота трапеций, в данном случае
число n строго задано n=3
- высота трапеций, в данном случае
число n строго задано n=3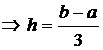
Получаем:
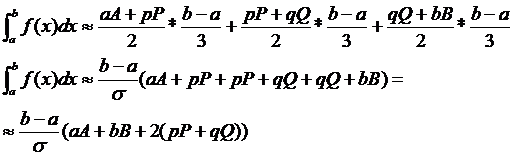 (8)
(8)
Обозначим, что: 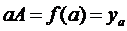 ,
, 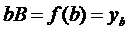 . Отрезки pP
и qQ не являются ординатами точек линии
. Отрезки pP
и qQ не являются ординатами точек линии 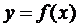 , так как P и Q лежат на
касательной. Но нам нужна сумма этих отрезков, которая выражается через среднюю
линию трапеции и равна полусумме её оснований, откуда
, так как P и Q лежат на
касательной. Но нам нужна сумма этих отрезков, которая выражается через среднюю
линию трапеции и равна полусумме её оснований, откуда
 .
.
Значит 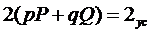 . Формула
(8) принимает вид:
. Формула
(8) принимает вид:
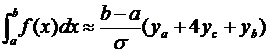 (9)
(9)
Эта формула называется малой
формулой Симпсона.

Рис. 9
Малая формула Симпсона пригодна, когда график
подынтегральной функции мало изогнут, например, для случая, изображённого на
рисунке, применять малую формулу уже нельзя, так как она даёт значение 0 на
[a,b]. Но если отрезок [a,b] разбить на части [a,c] и [c,b] и к каждому из них
применить формулу (9), то получится приемлемый результат.
Эта идея лежит в основе вывода «большой» формулы
Симпсона.
Для вычисления интеграла 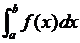 выберем
какое-либо чётное число и разложим [a,b] на n равных частей точками
выберем
какое-либо чётное число и разложим [a,b] на n равных частей точками
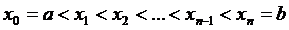
Интеграл представим в виде суммы
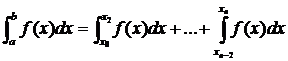
К каждому слагаемому справа применим
малую формулу Симпсона. Учитывая, что в каждом интеграле длина промежутка
интегрирования 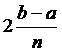 , и положить
, и положить
 , то
получим:
, то
получим:

Раскроем скобки:
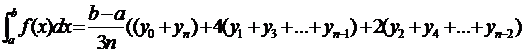
Это и есть «большая формула
Симпсона». Её точность, также как и у всех формул рассмотренных выше, тем выше,
чем больше n. Эта формула совпадает с формулой (7), выведенной с помощью
парабол. Для оценки погрешности формулы Симпсона используется формула:
метод парабола интеграл
мatlab

Качество этой формулы лучше, чем
формулы трапеции и прямоугольников, так как при одном и том же n она даёт
большую точность.
Общий вид интеграла, решение которого, будет
рассмотрено:

Заданные значения:
 ,
, 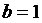 ,
, 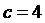 ,
, 
Подставив заданные значения,
получаем:
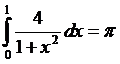
Т.е. получаем интегральное представление
числа Пи.
2.1 Программа для вычисления
интеграла
Программа для вычисления значения
интеграла методом трапеций в среде пакета Matlab:
function
y=int_trapezoidal(n,a,b)(mod(n,2)~=1)=(b-a)/n;=a:h:b;=0;i=1:n/2=s+f(x(2*i-1))+2*f(x(2*i))+f(x(2*i+1));=s*h/2;=3.051757810013100e-005;
disp ('Количество элементарных
отрезков: '), disp(n)('Результат: '), disp (y)('Погрешность: '), disp (erf)disp
('Введите четное число!')
endy=f(x)
y=4/(1+x^2);
Цикл if отвечает за то, что если
пользователь введет число n элементарных отрезков не кратных двум, программа
выведет на экран сообщение:
Введите четное число!

Рис. 10
Цикл for - это основная составляющая
программы для данного метода. Здесь суммируется площади трапеций, на которые
разбивается наша площадь под кривой.
Погрешность erf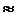 3.0517e-005
была получена как разность результатов с n = 64 и n = 128 элементарными
отрезками.
3.0517e-005
была получена как разность результатов с n = 64 и n = 128 элементарными
отрезками.
Таблица полученных результатов
|
n,
коли-во эл. отрезков
|
Значение
интеграла
|
|
2
|
3.100000000000000
|
|
4
|
3.131176470588235
|
|
8
|
3.138988494491089
|
|
16
|
3.140941612041389
|
|
32
|
3.141429893174975
|
|
64
|
3.141551963485653
|
|
128
|
3.141582481063753
|
Даже при n = 128 ответ является
точным лишь до пятого знака после запятой (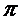 =3,141592653589793 - точное значение
числа пи для 15 знаков после запятой).
=3,141592653589793 - точное значение
числа пи для 15 знаков после запятой).
Только при n = 700000 значение числа
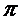 совпадает с
точным значением до 13 знака после запятой.
совпадает с
точным значением до 13 знака после запятой.
2.2 Определение значения интеграла с
помощью метода прямоугольников. Сравнение результатов
Программа для вычисления значения
интеграла методом прямоугольников в среде пакета Matlab:
function s =
int_rectangle(n,a,b)= (b-a)/n;= 0;= a:h:b;i = 1:n= s+f(x(i))*h;y = f(x)
y = 4/(1+x^2);
Таблица полученных результатов
|
n,
коли-во эл. отрезков
|
Значение
интеграла
|
|
2
|
3.600000000000000
|
|
4
|
3.381176470588235
|
|
8
|
3.263988494491089
|
|
16
|
3.203441612041389
|
|
32
|
3.172679893174975
|
|
64
|
3.157176963485654
|
|
128
|
3.149394981063753
|
Очевидно, что метод прямоугольников значительно
уступает точностью методу трапеций с одинаковым количеством элементарных
отрезков n.
Погрешность данного метода составляет
7.781982421901e-003, что на два порядка больше, чем погрешность метода
трапеций.
Использование для вычисления одновременно двух
методов (трапеций и прямоугольников) позволило исследовать зависимость точности
вычислений при применении обоих методов.
Следовательно, при понижении численного значения
точности, вычислений результаты расчетов по обеим методам стремятся друг к
другу и оба к точному результату.
Заключение
В завершении работы, хочется отметить ряд
особенностей применения рассмотренных выше методов. Каждый способ приближённого
решения определённого интеграла имеет свои преимущества и недостатки, в
зависимости от поставленной задачи следует использовать конкретные методы. Если
необходимо быстро получить решение, но нет необходимости в большой точности
ответа, следует воспользоваться методом прямоугольников. Если же необходимо
получить наиболее точный результат, идеально подходит метод Симпсона. Метод
трапеций даёт ответ более точный, чем метод прямоугольников, но методу Симпсона
он сильно уступает, этот метод можно назвать «золотой серединой» между двумя
другими.
Список литературы
1. Каханер
Д., Моулер К., Нэш С. Численные методы и программное обеспечение. - М.: Мир,
2011. - 575 с.
2. Форсайт
Дж., Малькольм М., Моулер Машинные методы математических вычислений. - М.: Мир
2009. - 277 с.
. Зализняк
В.Е. Основы научных вычислений. Введение в численные методы для физиков. - М.:
Едиториал УРСС, 2012. - 296 с.