Численное решение обыкновенных дифференциальных уравнений
Содержание
Введение
1. Численное
интегрирование
1.1 Правило трапеций
1.2 Правило Симпсона
.3 Метод Гаусса
1.4 Численные
примеры и сравнение методов
2. Численное
решение обыкновенных дифференциальных уравнений. Решение систем линейных
алгебраических уравнений
3. Решение
систем линейных алгебраических уравнений
. Численное
решение уравнений
Заключение
Библиографический
список
Приложение 1
Приложение 2
Приложение 3
Приложение 4
Введение
Курсовая работа посвящена комплексной визуализации результатов решения
ряда научных и инженерных задач. Рассматриваются такие проблемы как
табулирование функций, решение нелинейных уравнений, поиск оптимальных решений,
решение задач Коши, численное интегрирование и другие задачи в системе
компьютерного программного обеспечения - пакета универсальных интегрированных
программ MATLAB. Средствами MATLAB могут быть успешно решены и довольно сложные
инженерные проблемы, такие, как поиск спектра частот собственных колебаний и
критических сил потери устойчивости стержневых, пластинчатых и оболочечных
систем, решение краевых задач для упругих систем и задач сейсмостойкости
сооружений и др. Численные результаты таких задач должны сопровождаться
соответствующими эпюрами и формами, т. е. визуализацией расчетов. Кроме MATLAB существуют и другие, довольно мощные
среды программирования и визуализации, такие как Visual Digital Fortran, Delphi, Visual C++ и т. п.
Однако, в системе MATLAB получаются
наиболее простые и в то же время эффективные программы.
Слово MATLAB состоит из начальных букв слов МАТrix LABoratory - матричная лаборатория. Название
системы полностью отражает ее суть. Это действительно матричная лаборатория,
где начальным кирпичиком является не простая переменная или константа, а
матрица и ее частные случаи - вектор-строка, вектор-столбец.
Систему MATLAB разработал Молер (С.В. Moler) в 70-х г. г. ХХ века, которая
использовалась на больших ЭВМ. В начале 80-х г. г. Джон Литл (John Little) из фирмы Math Works, Inс. Модернизировал эту систему для
персональных компьютеров типа IBM PC, VAX и Macintosh. Далее к расширению системы были
привлечены крупнейшие ученые и научные школы в математике, программировании и
естествознании. Это позволило MATLAB
стать признанным лидером в решении различных проблем науки и техники среди
других подобных систем. Этому способствовало создание языка программирования,
который вобрал в себя преимущества традиционных языков (Fortran, Pascal, Basic,
C++) и достаточно
Система MATLAB,
обладает большими возможностями программирования и комплексной визуализации результатов
инженерных расчетов и научных исследований. В этой связи покажем применение
богатых возможностей MATLAB
в решении задач вычислительной математики. Развитие многих наук привело
исследователей к необходимости численного решения различных проблем, т. е.
применению численных методов.
1. Численное интегрирование
Задачи, в которых требуется вычисление интегралов, возникают почти во
всех областях прикладной математики. Иногда удается найти аналитическую
формулу, т. е. выразить неопределенный интеграл в виде комбинации
алгебраических и трансцедентных функций, после чего остается вычислить значение
определенного интеграла, подставляя в формулу пределы интегрирования. Во многих
случаях, однако, не удается найти никакой аналитической формулы или же она
получается настолько сложной, что вычислять интеграл с ее помощью труднее, чем
другими способами. В таких ситуациях приходится применять различные методы численного
интегрирования, которые основаны на том, что интеграл представляется в виде
предела суммы площадей, и позволяют вычислить эту сумму с достаточной
точностью.
Обращаясь к содержанию этой главы, поставим задачу и сделаем необходимые
предположения. Требуется вычислить определенный интеграл
|
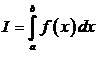
|
(1.1)
|
при
условии, что а и b конечны и f(х) является непрерывной функцией х
во всем интервале 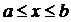 .
.
Общий
подход к решению задачи будет следующим. Определенный интеграл I
представляет собой площадь, ограниченную кривой f(х), осью х и
прямыми х = а и х = b. Мы будем
пытаться вычислить I, разбивая интервал от a до b
на множество меньших интервалов, находя приблизительно площадь каждой полоски,
получающейся при таком разбиении, и суммируя площади этих полосок. При этом
придется рассмотреть два способа разбиения исходного интервала на меньшие.
.
Разбиение на интервалы производится заранее; обычно интервалы выбираются
равными. Кроме того, если вычисление интеграла предполагается производить
«вручную», то интервалы выбираются так, чтобы значения х,
соответствующие концу каждого интервала, было возможно легче вычислять. Из этой
категории методов будут рассмотрены правило трапеций и метод парабол
(Симпсона).
.
Местоположение и длина интервалов определяются путем анализа; сначала ставится
требование достичь наивысшей точности с заданным числом интервалов, а затем в
соответствии с этим определяются их границы. Примером такого подхода является
метод Гаусса.
.1
Правило трапеций
Рассмотрим
интеграл (1.1), который представляет собой заштрихованную площадь на рис. 1.
Разобьем интервал интегрирования на n равных частей, каждая длиной h=(b
- a)/n.
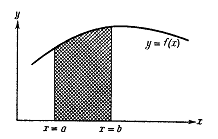
Рис.
1. Геометрическое представление задачи о численном интегрировании.
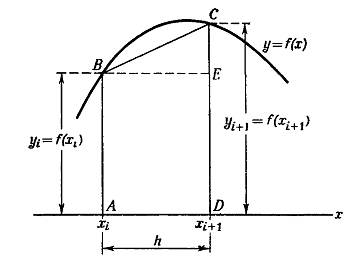
Рис.
2. Один интервал из заштрихованной области, изображенной на рис.1. Масштаб по
оси х увеличен.
Рассмотрим
теперь один из этих интервалов, как изображено на рис. 2, где масштаб по оси х
сильно увеличен. Площадь, лежащая под кривой у = f(х) между хi, и xi+1,
равна
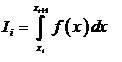
Но
если h достаточно мало, то эту площадь без большой ошибки можно
приравнять к площади трапеции ABCD. Если написать yi
= f(хi), то
площадь прямоугольника ABED будет равна yih, а площадь
треугольника ВЕС будет равна  , так что
, так что
|
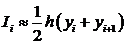
|
(1.2)
|
Но поскольку
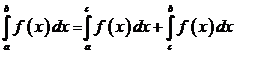
получаем
|
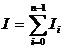 (1.3) (1.3)
|
|
где x0=a и xn=b.
Теперь, подставляя (1.2) в (1.3), окончательно получаем
|
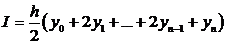 (1.4) (1.4)
|
|
Эта формула описывает хорошо известное правило трапеций для численного
интегрирования; согласно этому правилу, приближенное значение интеграла (1.1)
получается в виде суммы площадей n трапеций. Правило трапеций - один из
простейших методов численного интегрирования. Сущность его состоит в том, что
интервал интегрирования разбивается на множество меньших отрезков, внутри
которых подынтегральная кривая у = f(х) заменяется с некоторой
степенью точности более простыми функциями; интегралы от них можно вычислить,
используя только ординаты на концах отрезков.
1.2 Правило Симпсона
Этот метод аналогичен правилу трапеций в той части, что интегрирование
производится путем разбиения общего интервала интегрирования на множество более
мелких отрезков; однако теперь для вычисления площади над каждым из них через
три последовательных ординаты разбиения проводится квадратичная парабола. Можно
было бы ожидать, что аналогично тому, как правило трапеций дает точный
результат при интегрировании линейных функций, правило Симпсона даст точный
результат при интегрировании многочленов второго порядка; в действительности же
получается несколько парадоксальный результат: формула Симпсона дает точные
значения интеграла при интегрировании многочленов до третьего порядка
включительно. Поэтому при всей своей простоте этот метод весьма точен, хотя
формула для численного интегрирования получается ненамного сложней, чем для
правила трапеций. Простота и точность правила Симпсона сильно способствуют его
широкому применению при вычислениях на ЭВМ.
Вспомним, что количество отрезков n в случае правила трапеций
определялось формулой
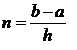
Предположим теперь, что число n является четным и что
|
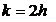
|
(1.5)
|
Тогда
|
 (1.6) (1.6)
|
|
|
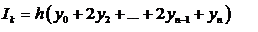
|
(1.7)
|
Уравнения (1.5), (1.6) и (1.7) можно подставить . При этом получим
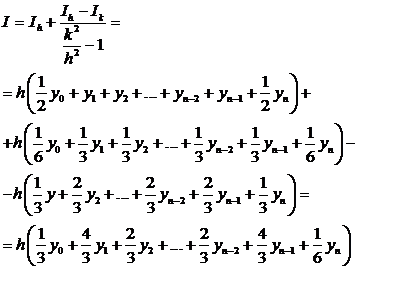
и окончательно:
|
 (1.8) (1.8)
|
|
Формула (1.8) называется формулой Симпсона. Ее можно было вывести другим
путем, а именно проводя параболу через три ординаты на концах двух соседних
интервалов и потом складывая получившиеся при этом площади.
1.3 Метод Гаусса
Погрешность метода тем меньше, чем выше порядок многочлена, при численном
интегрировании которого получается точный результат. Чтобы упростить выкладки,
изменим пределы интегрирования так, чтобы они стали равными (+1, -1). Для этого
введем новую переменную
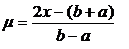
так что
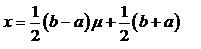
Интеграл (1) после такой подстановки запишется в виде
|
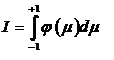
|
(1.9)
|
где
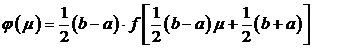
Это означает, что соответствующей заменой переменных можно свести все
интегралы к виду (1.9).
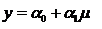
для которой
|

|
(1.10)
|
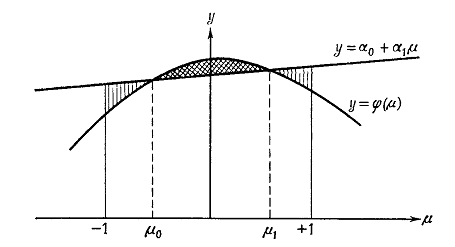
Рис. 3. Геометрическое представление метода Гаусса с двумя ординатами.
Интеграл, стоящий в левой части этого уравнения, представляет собой
площадь трапеции на рис.3. Пусть сумма площадей вертикально заштрихованных
участков (между -1 и μ0 и от μ1 до + 1) равна площади зачерненного
участка (между μ0 и μ1). Тогда площадь трапеции в точности
равна площади под кривой у = φ(μ). Задача заключается в нахождении
такой прямой линии, для которой достигается это равенство.
Положим
|
 (1.11) (1.11)
|
|
где необходимо определить А0, А1, μ0, μ1. Так как в формуле имеются четыре
параметра, то естественно предположить, что формула даст точный результат при
интегрировании кубической параболы
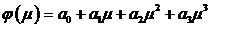
Перепишем эту функцию в виде
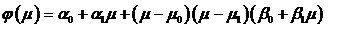
Если α0 и α1 должны удовлетворять уравнению
(1.10), то μ0 и μ1 определяются из условия
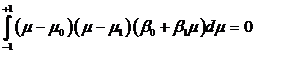
Так как это равенство должно быть справедливо для любых β0 и β1 то необходимо потребовать выполнения
двух следующих равенств:
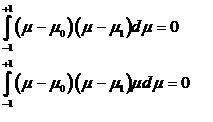
Выполнив интегрирование, можно записать два последних равенства в виде
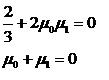
откуда следует, что
|
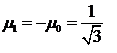 (1.12) (1.12)
|
|
Теперь остается только найти А0 и А1
в формуле (1.11). Заметим, что
|
 (1.13) (1.13)
|
|
И из формул (11) и (12) следует, что
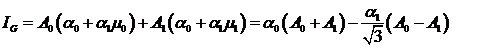
Так как значение выражения в правой части последней формулы должно быть
равно значению интеграла в формуле (1.13) при всех α0 и α1, то для А0 и А1
получаем систему уравнений
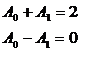
из которой находим
|
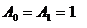 (1.14) (1.14)
|
|
Уравнение (1.11) окончательно запишется в виде
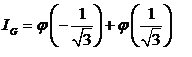
Это и есть формула численного интегрирования Гаусса для случая двух
ординат. Ошибка ограничения равна нулю при интегрировании многочленов до
третьего порядка включительно. Естественно ожидать, что при интегрировании многочленов
высших степеней и прочих функций ошибка ограничения будет определяться формулой

где
|
 (1.15) (1.15)
|
|
Чтобы найти К, предположим, что
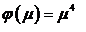
При этом
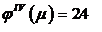
так что
|
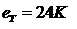 (1.16) (1.16)
|
|
Точное значение интеграла легко вычислить:
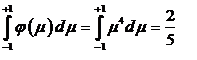
С другой стороны, из формул (1.15) и (1.16)

Поэтому
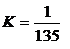
и окончательная формула для ошибки ограничения запишется в следующем
виде:
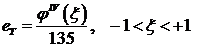
Можно вывести гауссовы формулы численного интегрирования более высоких
порядков, предусматривая большее количество ординат и вводя различные весовые
коэффициенты Ai:
|
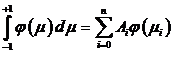 (1.17) (1.17)
|
|
В общем случае, при (n
+ 1) ординате, получается точная формула для нахождения интеграла от многочлена
степени 2n + 1.
Оказывается, что значения μi в уравнении (1.17) являются корнями
полиномов Лежандра степени n.
По этой причине вышеописанный метод численного интегрирования часто называют
методом Лежандра - Гaycca. Полиномы Лежандра Рn (μ) можно найти с помощью рекуррентных
формул
|
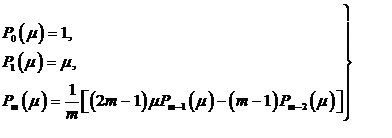 (1.18) (1.18)
|
|
Например, для m
= 2
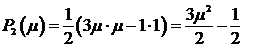
Заметим,
что корни Р2(μ) равны 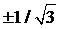 , как мы уже определили ранее.
, как мы уже определили ранее.
Весовые
коэффициенты в формуле (18) можно найти из следующего соотношения:

В
качестве примера возьмем n = 2, так что 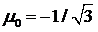 ,
, 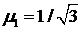 и
и 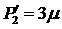 . При
этом
. При
этом
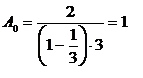
и
совершенно аналогично А1 = 1.
В
общем случае ошибка ограничения определяется формулой

Итак, метод Гаусса позволяет достичь большей точности, нежели формула
Симпсона при том же количестве ординат, но зато точки, где следует определять
эти ординаты, полностью определены и совершенно не зависят от произвола
программиста. Как и во многих других случаях, при численном интегрировании
приходится делать выбор между простотой формулы Симпсона и возможной экономией
машинного времени при использовании метода Гаусса. На практике чаще
используется метод Симпсона.
.4 Численные примеры и сравнение методов
Рассмотрим следующий интеграл:
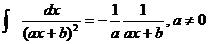
Программа вычисления в системе Matlab приведена в Приложении
1. Результат решения:
a = 1; b =
1; x0 = 1; xn = 3; n = 100; h = 0.020000000000000;
аналитические
решения: s = 0.250000000000000
метод
Симпсона: s = 0.250000000645597
квадратурные
формулы Гаусса: s = 0.249997523978987
метод
Чебышева: s = 0.249974640808074
Выводы
имеют общий характер.
.
Формула Симпсона при n ординатах дает примерно ту же степень точности, что и
формула трапеций при 2n ординатах.
.
Метод Гaycca при n ординатах дает примерно ту же степень точности, что и
формула Симпсона при 2n ординатах.
.
Для достижения той же степени точности при использовании формулы Симпсона
приходится производить примерно вдвое меньше вычислений, чем по формуле
трапеций, которая требует вдвое большего количества ординат.
.
Для достижения той же степени точности при использовании метода Гаусса
приходится производить примерно вдвое меньше вычислений, чем по формуле
Симпсона благодаря вдвое меньшему количеству ординат.
Экономия
времени при использовании метода Гаусса имеет свою оборотную сторону. Дело в
том, что если приходится заново вычислять тот же интеграл с большим количеством
точек, то нельзя использовать ранее вычисленные ординаты, так как они находятся
в неподходящих местах.
2. Численное решение обыкновенных дифференциальных уравнений
Многие задачи физики, химии, экологии, механики и других разделов науки и
техники при их математическом моделировании сводятся к дифференциальным
уравнениям. Поэтому решение дифференциальных уравнений является одной из
важнейших математических задач. В вычислительной математике изучаются численные
методы решения дифференциальных уравнений, которые особенно эффективны в
сочетании с использованием персональных компьютеров.
Среди множества численных методов решения дифференциальных уравнений
наиболее простые - это явные одношаговые методы. К ним относятся различные
модификации метода Рунге-Кутта.
Постановка задачи: Требуется найти функцию у = у(х),
удовлетворяющую уравнению
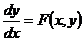 (2.3)
(2.3)
и
принимающую при х = х0 заданное значение у0:
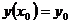 . (2.4)
. (2.4)
При
этом решение необходимо получить в интервале х0 £ х £ хк.
Из теории дифференциальных уравнений известно, что решение у(х)
задачи Коши (2.3), (2.4) существует, единственно и является гладкой функцией, если
правая часть F(x, y) удовлетворяет некоторым
условиям гладкости. Численное решение задачи Коши методом Рунге-Кутта 4-го
порядка заключается в следующем. На заданном интервале [х0, хк]
выбираются узловые точки. Значение решения в нулевой точке известно у(х0)
= у0. В следующей точке у(х1)
определяется по формуле
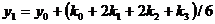 , (2.5)
, (2.5)
Здесь
 (2.6)
(2.6)
т.
е. данный вариант метода Рунге-Кутта требует на каждом шаге четырехкратного
вычисления правой части уравнения (2.3). Этот алгоритм реализован в программе ode45.
Кроме этой программы MATLAB располагает обширным набором аналогичных программ,
позволяющих успешно решать обыкновенные дифференциальные уравнения.
Решить
задачу Коши
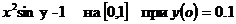 . (2.7)
. (2.7)
Выполним
решение данной задачи с помощью программы ode45. Вначале в
М-файл записываем правую часть уравнения (2.7), сам М-файл оформляется как файл
- функция, даем ему имя :
function f=odddde(x,y)
f=x^2*sin(y-1);
Для численного решения задачи Коши в окне команд набираются следующие
операторы.
Протокол программы.
>>[X Y] = ode45 ( @ F , [0
1] , [1] ) ;
% Дескриптор @ обеспечивает связь с файлом - функцией правой части
% [0 1] - интервал на котором необходимо получить решение
% [0,1] - начальное значение решения
>> рlot (X,Y) ;
>> % Последняя команда выводит таблицу численного решения задачи.
Программа вычисления в системе Matlab приведена в Приложении 2. Результат решения:
График решения задачи Коши (2.7) показан на рис. 4.. В программе ode45 по умолчанию интервал разбивается
на 40 точек с шагом h
= 1/40 = 0.025; xend =1.
Рис. 4. График решения задачи Коши.
3. Решение систем линейных алгебраических уравнений
Системы уравнений появляются почти в каждой области прикладной
математики. В некоторых случаях эти системы уравнений непосредственно составляют
ту задачу, которую необходимо решать, в других случаях задача сводится к такой
системе. Если задана некоторая произвольная система уравнений, то без
предварительного исследования нельзя сказать, имеет ли она какое-либо решение
и, в случае если решение существует, является ли оно единственным. На этот
вопрос существуют три и только три ответа.
. Решение системы уравнений существует и является единственным.
Например,
|
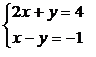
|
(3.1)
|
Решение этой системы х = 1 и у = 2. никакие другие значения
х и у не способны одновременно удовлетворить этим двум
уравнениям. В этой главе мы будем в основном рассматривать именно такие системы
уравнений, т. е. имеющие единственное решение. Геометрически эта система
уравнений представлена на рис. 5, где видно, что две прямые линии,
соответствующие двум уравнениям, пересекаются в одной и только в одной точке.
Координаты этой точки как раз и представляют собой искомое решение.
. Система уравнений вообще не имеет решения. Например,
|
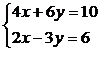 (3.2) (3.2)
|
|
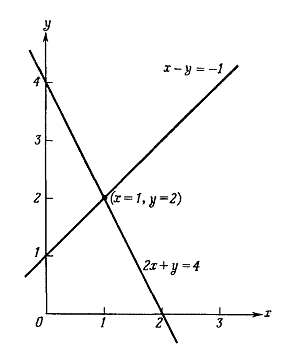
Рис. 5. Геометрическое представление системы двух линейных уравнений,
имеющей единственное решение. Прямые линии, соответствующие уравнениям системы
образуют между собой довольно большой угол.
На рис. 6 показаны прямые линии, соответствующие этим двум уравнениям.
Две прямые параллельны, они нигде не пересекаются, и система уравнений не имеет
решения.
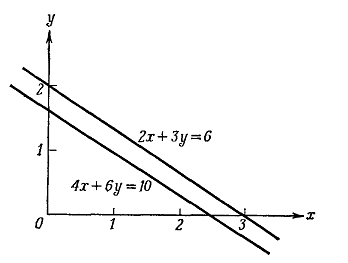
Рис. 6. Геометрическое представление системы двух линейных уравнений, не
имеющей решения. Прямые линии параллельны.
. Система уравнений имеет бесконечное множество решений. Например,
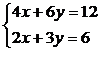
Как видно из рис. 7, эти два уравнения описывают одну и ту же прямую
линию. Любая точка, лежащая на этой линии, является решением такой системы
уравнений, например: (х = 0, у = 2), (х = 1, у =
4/3) и т. д.
Системы уравнений типа 2 и 3 называются вырожденными. Иногда
непосредственно из поставленной задачи бывает ясно, что система уравнений не может
быть вырожденной. Если же, как это бывает в большинстве случаев,
соответствующая информация отсутствует, то приходится или проверять
вырожденность системы уравнений в процессе решения, или исследовать такую
возможность непосредственно непосредственная проверка состояла бы в вычислении
определителя системы, тогда равенство определителя нулю прямо указывало бы на
вырожденность.
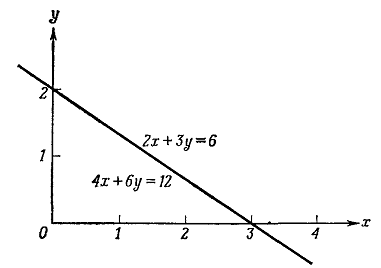
Рис. 7. Геометрическое представление системы двух линейных уравнений,
имеющей бесконечное множество решений. Оба уравнения изображаются одной и той
же прямой линией.
С точки зрения обычной математики система линейных уравнений всегда
является или вырожденной, или невырожденной. С точки же зрения практических
вычислений могут существовать почти вырожденные системы, при решении
которых получаются недостоверные значения неизвестных. Рассмотрим систему
уравнений:
|
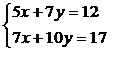
|
(3.3)
|
Эта система имеет единственное решение х = 1; у = 1. Теперь
рассмотрим пару значений неизвестных х = 2,415; у = 0. При
подстановке этих значений в исходные уравнения получаем
|
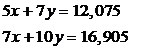 (3.4) (3.4)
|
|
После округления до двух значащих цифр правые части равенств (3.4)
совпадают с правыми частями исходных уравнений. А так как исходные уравнения
были заданы только с точностью до двух значащих цифр, то решение (3.4) так же
хорошо отвечает условиям поставленной задачи, как и решение х = 1; у =
1.
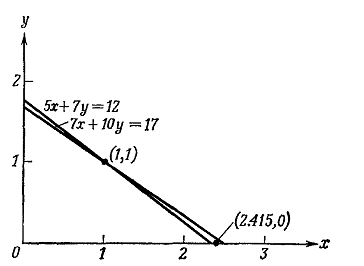
Рис. 8. Геометрическое представление системы двух линейных уравнений,
которая является почти вырожденной. Прямые, соответствующие двум уравнениям,
почти совпадают.
Дело в том, что две прямые линии, описываемые двумя уравнениями этой
системы, почти параллельны, как это показано на рис. 8.. Точка х
= 2,415; у = 0 хотя и не лежит ни на одной из этих прямых линий, но
очень близка к ним.
Системы типа (3.3) называются плохо обусловленными. В любом
случае, когда две линии (либо плоскости и гиперплоскости) почти параллельны,
система уравнений становится плохо обусловленной. В этом случае найти численное
решение системы трудно, а точность его весьма сомнительна. Более того, система
из трех и более уравнений может оказаться плохо обусловленной, даже если
никакие плоскости не являются параллельными или почти параллельными 1). Вне
зависимости от геометрической интерпретации обусловленность системы можно
исследовать при ее решении методом Гаусса или с помощью специальной проверки.
. Методы численного решения системы линейных уравнений подразделяются на
два типа, прямые (конечные) и итерационные (бесконечные). Естественно,
никакой практический метод решения системы уравнений не может быть бесконечным.
Имеется в виду только то, что прямые методы могут в принципе (с точностью до
ошибок округления) дать точное решение, если оно существует, с помощью
конечного числа арифметических операций. С другой стороны, итерационный метод
требует бесконечного числа арифметических операций, приводящих к точному
решению. Иными словами, при использовании итерационного метода появляется
ошибка ограничения, отсутствующая в прямых методах.
К решению систем линейных уравнений сводятся многочисленные практические
задачи, например различные краевые задачи для обыкновенных и в частных
производных дифференциальных уравнений. Можно с полным основанием утверждать,
что данная проблема является одной из самых распространенных и важных задач
вычислительной математики.
 . (3.5)
. (3.5)
Система уравнений (3.5) в матричной форме представляется следующим
образом:
АХ = В, (3.6)
где А - квадратная матрица коэффициентов, размером п ´ п строк и столбцов;
Х - вектор-столбец неизвестных;
В - вектор-столбец правых частей.
Систему уравнений (3.5) можно решить различными методами. Один из
наиболее простых и эффективных методов является метод исключения Гаусса и его
модификации. Алгоритм метода основан на приведении матрицы А к треугольному
виду (прямой ход) и последовательном вычислении неизвестных (обратный ход). Эти
процедуры можно выполнять над невыраженными матрицами, в противном случае метод
Гаусса неприменим.
Недостатком метода является накапливание погрешностей в процессе
округления, поэтому метод Гаусса без выбора главных элементов используется
обычно для решения сравнительно небольших (п £ 100) систем уравнений с плотно
заполненной матрицей и не близким к нулю определителем. Если матрица А сильно
разрежена, а ее определитель не близок к нулю, то метод Гаусса пригоден для
решения больших систем уравнений. В MATLAB имеется обширный арсенал методов решения систем уравнений (3.5) методом
исключения Гаусса. Для этого применяются следующие операторы дают решения ряда
систем линейных уравнений АХ = В, где А - матрица размером m ´ n, В - матрица размером п ´ к.
Решить систему линейных уравнений:

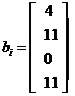
Программа вычисления в системе Matlab приведена в Приложении
3. Результат решения:
x = 1.000000000000000
2.000000000000001
3.000000000000001
4.000000000000000= 1.000000000000000 2.000000000000001 3.000000000000001
4.000000000000000= 1.000000000000000 2.000000000000000 3.000000000000000
4.000000000000000= 1.000000000000000 2.000000000000000 3.000000000000000
4.000000000000000
4. Численное решение уравнений
Нахождение корней уравнения - это одна из древнейших математических
проблем, которая не потеряла своей остроты и в наши дни: она часто встречается
в самых разнообразных областях науки и техники.
Рассмотрим общеизвестное квадратное уравнение:
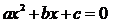
говорят, что значения
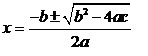
являются корнями этого уравнения, потому что для этих значений х
уравнение удовлетворяется. В более общем случае, если имеется некоторая функция
F(х), то бывает необходимо найти такие значения аргумента х,
для которых
|
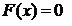
|
(4.1)
|
Функция F(х) может быть алгебраической или
трансцендентной; мы обычно будем предполагать, что она дифференцируема.
В общем случае функции, которые мы будем рассматривать, не имеют
аналитических формул для своих корней в противоположность, например,
квадратному уравнению. Поэтому приходится пользоваться приближенными методами
нахождения корней, которые в основном состоят из двух этапов:
. Отыскание приближенного значения корня.
. Уточнение приближенного значения до некоторой заданной степени
точности. численное интегрирование уравнение
Очень часто приближенное значение корня бывает известно из физических
соображений, в других случаях можно использовать графические методы. Кроме
того, существуют специальные методы нахождения приближенного корня для того
практически важного случая, когда F(x) является полиномом.
Численный метод, в котором производится последовательное, шаг за шагом,
уточнение первоначального грубого приближения, называется методом итераций.
Каждый шаг в таком методе называется итерацией. Если при
последовательных итерациях получаются значения, которые все ближе и ближе
приближаются к истинному значению корня, то говорят, что метод итераций сходится.
Предположим, что для простоты вычислений выбраем ξ = xn. Тогда приобретает следующий вид:
|
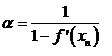
|
(4.2)
|
xn+1 находим из. Формулы
|

|
(4.3)
|
Нетрудно видеть, что (4.3) эквивалентно простому методу последовательных
приближений

Где
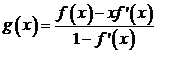
Вспомним
также, что если 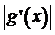 < 1, то метод сходится. Для g'(х) имеем
< 1, то метод сходится. Для g'(х) имеем
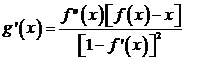
Но поскольку f(х) подчиняется соотношению , то для х,
достаточно близких к а, выражение в скобках становится малым. Поэтому
итерационный метод, описываемый формулой (4.3), сходится, если
. х0 выбрано достаточно близко к решению х = f(х).
2.
Производная 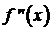 не становится слишком большой.
не становится слишком большой.
.
Производная 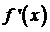 не слишком близка к 1.
не слишком близка к 1.
Это
и есть знаменитый метод Ньютона-Рафсона. Обычно его записывают в более
привычной форме:
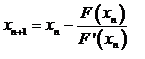
Где
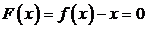
Таким образом, мы возвращаемся к уравнению в форме (4.1), и условия
сходимости принимают следующий вид:
. х0 выбрано достаточно близко к корню уравнения F(х) = 0.
. Производная F"(х) не
становится очень большой.
. Производная F'(х) не слишком близка к нулю.
Последнее условие означает, что никакие два корня не находятся слишком
близко один к другому.
Рассмотрим геометрическое толкование метода Ньютона-Рафсона. В формуле
(4.3) мы выбрали точку ξ совпадающей с хn . На рис.9 это соответствует тому,
что угол θ равен углу наклона касательной к у = f(х) в точке х
= хn.
Нахождение следующего приближения сводится при этом к тому, что проводится
касательная к кривой у = f(х) в точке х = хn и отыскивается точка ее пересечения
с прямой у = х. Эта точка и будет новым приближением хn+1. Чтобы найти f(хn+1),
через значение xn +1 проводится вертикальная линия. После
этого проводится новая касательная, точка пересечения которой с прямой у = х
даст значение xn+2.
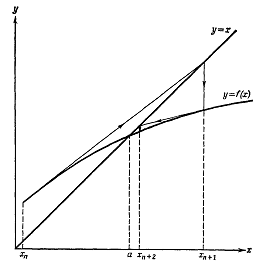
Рис.9. Геометрическое представление метода Ньютона-Рафсона для f(х) = x.
Если уравнение задано в форме (4.1) и используется итерационная формула ,
то геометрически можно представить себе ход вычислений по рис.10. В этом случае
отыскивается точка пересечения кривой у = F(х) с осью х.
Исходя из некоторого начального приближения хn , находим соответствующее ему
значение F(хn)
, проводим касательную к кривой у = F(x) и ищем точку пересечения этой
касательной с осью х. Легко видеть, что эта точка и будет значением хn+1 из формулы, так как там и требуется
провести через точку с координатами хn , F(хn) прямую с угловым коэффициентом F'(хn) и затем найти ее пересечение с осью х.
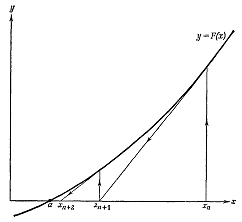
Рис.10. геометрическое представление метода Ньютона-Рафсона для F(х) =
0.
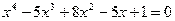
Программа вычисления в системе Matlab приведена в Приложении 4. Результат решения:
0 1 2 3 4 5 6 7
1 0 -1 4 45 176 475 1044
1
0
Заключение
Система MATLAB представляет собой уникальный сплав универсальных
программных и алгоритмических средств с широкой гаммой специализированных
приложений. Входной язык и среда программирования MATLAB очень близки к
современным системам визуального программирования на базе универсальных алгоритмических
языков типа Basic, C++, Java, Object Pascal. По ряду аспектов MATLAB уступает
указанным системам (режим интерпретации, небольшой запас визуальных
компонентов). Однако с его библиотекой численных методов ни по объему, ни по
качеству не может сравниться ни одна из систем программирования. Кроме того, в
пакете MATLAB тщательно отработаны средства визуализации результатов вычислений
и отображения различных графических объектов. На базе ядра MATLAB созданы
многочисленные расширения, обеспечивающие моделирование и анализ систем в
разнообразных сферах человеческой деятельности.
Библиографический список
1. Дьяконов
В.П. MATLAB 6. Учебный курс. - СПб.: Питер,
2001. - 592 с.
. Баженов
В.А., Дащенко А.Ф., Коломиец Л.В., Оробей В.Ф. Строительная механика.
Специальный курс. Применение метода граничных элементов. - Одесса: Астропринт,
2001. - 288 с.
.
Строительная механика. Динамика и устойчивость сооружений / Под ред. А.Ф.
Смирнова. - М. : Стройиздат, 1984. - 415 с.
. Турчак Л.И.
Основы численных методов. - М.: Наука, 1987. - 320 с.
. Мэтьюз
Дж.Г., Финк К.Д. Численные методы. Использование MATLAB. Пер. с англ. - М.: Изд. Дом «Вильямс», 2001. - 720
с.
. Дьяконов
В., Круглов В. Математические пакеты расширения MATLAB. Специальный справочник. - СПб.: Питер, 2001. - 480
с.
. Сборник
задач для курсовых работ по теоретической механике: Учебное пособие для
технических вузов / Яблонский А.А. и др. М.: Высш. шк., 1985. - 367 с.
. Кириллов
В.Х., Лещенко Д.Д. Курс теоретической механики. Учебное пособие для студентов
технических вузов. - Одесса: ОГАСА, 2002. - 263 с.
. Даффи Д.А.,
Бекман У.А. Тепловые процессы с использованием солнечной энергии. - М.: Мир,
1977. - 305 с.
. Кириллов
В.Х. Гидродинамика и тепломассообмен в двухфазных потоках плёночных аппаратов
для холодильной техники: Дис…док. техн. наук. - Одесса, 1993. - 342 с.
. Капустин
В.Ф. Практические занятия по курсу математического программирования. - Л.: Изд.
Ленинград. ун-та, 1976. - 192 с.
. Дьяконов В.
SIMULINK 4. Специальный справочник. - СПб.:
Питер, 2002. - 528 с.
Приложение 1
Протокол программы (в М-файле)
format long
% метод трапеции=1=1=1=3=100=abs(xn-x0)/n=int(x0,a,b);i=1:n-1
x(i)=x0+i*h;
s=s+2*int(x(i),a,b);('метод трапеций')=(s+int(xn,a,b))*h/2
disp('аналитические решения')=intt(xn,a,b)-intt(x0,a,b)
% метод симсона
j=0;=int(x0,a,b);j<n-1=j+1;=s+4*int(x0+j*h,a,b);j==n-1
continue=j+1;=s+2*int(x0+j*h,a,b);('метод симсона')=h*(s+int(xn,a,b))/3
t=[0.06943184 0.33000984 0.66999052 0.93056816];=[0.17392742
0.32607258 0.32607258 0.17392742];=0;i=1:4
s=s+w(i)*int(x0+(xn-x0)*t(i),a,b);
end('квадратурные формулы Гаусса')
s=(xn-x0)*s
tch=[0.083751 0.312730 0.5 0.68727 0.916249];=0;i=1:5
s=s+0.2*int(x0+(xn-x0)*tch(i),a,b);('метод Чебышева')=(xn-x0)*s
function y=int(x,a,b)=1/((a*x+b)^2);y=intt(x,a,b)=-1/(a*(a*x+b));
Приложение 2
Протокол программы (в М-файле)long=1
% количество шагов=1000;
% обнулениемассив=zeros(1,n);
y=zeros(1,n);
% н.у
x(1)=0;(1)=0.1;
% шаг решения
h=(xend-x(1))/n;i=2:n
k1=odddde(x(i-1),y(i-1));
k2=odddde(x(i-1)+h/2,y(i-1)+h*k1/2);
k3=odddde(x(i-1)+h/2,y(i-1)+h*k2/2);
k4=odddde(x(i-1)+h,y(i-1)+h*k3);
y(i)=y(i-1)+h*(k1+2*k2+2*k3+k4)/6;
x(i)=x(i-1)+h;
%plot(x,y)=0.1;
[xm,ym]=ode45(@odddde,[0:0.001:1],y0);(x,y,xm,ym)
Приложение 3
Протокол программы (в М-файле)
%Ввод строками=[2 -4 3 1;
-1 5 -7 -3;
10 -2 4 4;
-1 1 -1 -1];=[7;-24;34;-6];=a\b
%Ввод столбцами=[2 -1 10 -1;
-4 5 -2 1;
3 -7 4 -1;
1 -3 4 -1];=[7 -24 34 -6];=b/a=b*a^-1=b*inv(a)
Приложение 4
Протокол программы (в М-файле)
%начальное значение корня=1;
%счетчик интераций
n=0;abs(ur(x)/dur(x))>1e-7
x=x-ur(x)/dur(x);
n=n+1;
if n>=1000
disp('решения
нет')
break
end(x)(n)y=ur(x)=x^4-5*x^3+8*x^2-5*x+1;y=dur(x)long=1;=7;(1)=x-h;(1)=ur(x(1));i=1:n;(i+1)=x(1)+i*h;(i+1)=ur(x(i+1));(x)(y)i=1:n-1(i)=y(i+1)-y(i);i=1:n-2y(i)=dy(i+1)-dy(i);i=1:n-3y(i)=d2y(i+1)-d2y(i);i=1:n-4y(i)=d3y(i+1)-d3y(i);=(dy(1)+0.5*d2y(1)-d3y(1)/6+d4y(1)/12)/h;