Теория игр

ЗАДАНИЕ 1

Каждый из игроков А и В записывает одно из чисел 3, 6, 7 или 8, затем они одновременно показывают написанное. Если оба числа оказались одинаковой четности, то игрок А выигрывает столько очков, какова сумма этих чисел, если разной четности - выигрывает игрок В. Составить платежную матрицу, найти нижнюю и верхнюю чистые цены игры, максиминную и минимаксную стратегии игроков. Указать наличие седловой точки (если она есть).

Решение:

. Составим платежную матрицу

Пусть А₁ - стратегия первого игрока, он записывает число 3, А₂ - стратегия первого игрока, он записывает число 6, А₃ - стратегия первого игрока, он называет записывает число 7, А₄ - стратегия первого игрока, он называет записывает число 8.

В₁ - стратегия второго игрока, он записывает число 3, В₂ - стратегия второго игрока, он записывает число 6, В₃ - стратегия второго игрока, он записывает число 7, В₄ - стратегия второго игрока, он записывает число 8.

Если 1-й игрок применит первую стратегию и второй игрок тоже (оба запишут 3), то оба числа оказываются равной четности, игрок А выигрывает 3 + 3 = 6.

Если 1-й игрок применит первую стратегию (напишет 3), а второй игрок использует вторую стратегию (напишет 6), то оба числа оказываются разной четности, игрок В выигрывает 3 + 6 = 9.

Если 1-й игрок применит первую стратегию (напишет 3), а второй игрок использует третью стратегию (напишет 7), то оба числа оказываются равной четности, игрок А выигрывает 3 + 7 = 10.

Если 1-й игрок применит первую стратегию (напишет 3), а второй игрок использует 4-ю стратегию (напишет 8), то оба числа оказываются разной четности, игрок В выигрывает 3 + 8 = -11.

Если 1-й игрок применит вторую стратегию (напишет 6), а второй игрок использует первую стратегию (напишет 3), то оба числа оказываются разной четности, игрок В выигрывает 3 + 6 = 9.

Если 1-й игрок применит вторую стратегию (напишет 6) и второй игрок использует вторую стратегию (напишет 6), то оба числа оказываются одинаковой четности, игрок А выигрывает 6 + 6 = 12.

Если 1-й игрок применит вторую стратегию (напишет 6), а второй игрок использует третью стратегию (напишет 7), то оба числа оказываются разной четности, игрок В выигрывает 6 + 7 = 13.

Если 1-й игрок применит вторую стратегию (напишет 6), а второй игрок использует четвертую стратегию (напишет 8), то оба числа оказываются одинаковой четности, игрок А выигрывает 6 + 8 = 14.

Если 1-й игрок применит третью стратегию (напишет 7), а второй игрок использует первую стратегию (напишет 3), то оба числа оказываются одинаковой четности, игрок А выигрывает 7 + 3 = 10.

Если 1-й игрок применит третью стратегию (напишет 7), а второй игрок использует вторую стратегию (напишет 6), то оба числа оказываются разной четности, игрок В выигрывает 7 + 6 = 13.

Если 1-й игрок применит третью стратегию (напишет 7), и второй игрок использует третью стратегию (напишет 7), то оба числа оказываются одинаковой четности, игрок А выигрывает 7 + 7 = 14.

Если 1-й игрок применит третью стратегию (напишет 7), а второй игрок использует четвертую стратегию (напишет 8), то оба числа оказываются разной четности, игрок В выигрывает 7 + 8 = 15.

Если 1-й игрок применит четвертую стратегию (напишет 8), а второй игрок использует первую стратегию (напишет 3), то оба числа оказываются разной четности, игрок В выигрывает 8 + 3 = 11.

Если 1-й игрок применит четвертую стратегию (напишет 8), а второй игрок использует вторую стратегию (напишет 6), то оба числа оказываются одинаковой четности, игрок А выигрывает 8 + 6 = 14.

Если 1-й игрок применит четвертую стратегию (напишет 8), а второй игрок использует третью стратегию (напишет 7), то оба числа оказываются разной четности, игрок В выигрывает 8 + 7 = 15.

Если 1-й игрок применит четвертую стратегию (напишет 8) и второй игрок использует четвертую стратегию (напишет 8), то оба числа оказываются одинаковой четности, игрок А выигрывает 8 + 8 = 16.

Таким образом, получаем матрицу выигрышей игрока А:

Величина α - гарантированный выигрыш игрока А называется нижней ценой игры. Стратегия, обеспечивающая получение выигрыша α, называется максиминной. Если первый игрок будет придерживаться своей максиминной стратегии, то у него есть гарантия, что он в любом случае выиграет не меньше α.

Величина β - гарантированный проигрыш игрока В называется верхней ценой игры. Стратегия, обеспечивающая получение проигрыша β, называется минимаксной. Если второй игрок будет придерживаться своей минимаксной стратегии, то у него есть гарантия, что он в любом случае проиграет не больше β.

Поскольку , то платежная матрица не имеет седловую точку, т.е. она решается в смешенных стратегиях.

Цена игры находится в пределах:

ЗАДАНИЕ 2

Упростить платежную матрицу:

Решение:

Если все элементы i-й строки платежной матрицы больше соответствующих элементов k-й строки, то i-я строка игрока А называется доминирующей над k-й строкой.

Все элементы 1-й строки меньше или равны элементам 3-й строки. Следовательно, игроку А не выгодно использовать 1-ю стратегию, вероятность, что он будет ее использовать равна нулю х₁ = 0. Третья стратегия доминирует над первой. Первую строку удаляем.

Все элементы 5-й строки меньше или равны элементам 2-й строки. Следовательно, игроку А не выгодно использовать 5-ю стратегию, вероятность, что он будет ее использовать равна нулю х₅ = 0. Вторая строка доминирует над пятой. пятую строку удаляем.

Все элементы 3-й строки меньше или равны элементам 4-й строки. Следовательно, игроку А не выгодно использовать 4-ю стратегию, вероятность, что он будет ее использовать равна нулю х₄ = 0. Третья строка доминирует над четвертой. Четвертую строку удаляем. Получаем матрицу:

Если все элементы j-го столбца платежной матрицы меньше соответствующих элементов k-го столбца, то j-я строка игрока В называется доминирующей над k-й строкой. Все элементы 1-го столбца больше или равны элементам 4-го столбца. Игроку В не выгодно использовать 1-ю стратегию, вероятность ее применения равна нулю у₁ = 0. 4-й столбец доминирует над 1-м столбцом. 1 столбец удаляем. Все элементы 5-го столбца больше элементов 4-го столбца. Игроку В не выгодно использовать 5-ю стратегию, вероятность ее применения равна нулю у₅ = 0. 4-й столбец доминирует над 5-м столбцом. 5 столбец удаляем. Все элементы 2-го столбца больше элементов 3-го столбца. Игроку В не выгодно использовать 2-ю стратегию, вероятность ее применения равна нулю у₂ = 0. 3-й столбец доминирует над 2-м столбцом. 2 столбец удаляем. Получаем платежную матрицу:

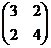
ЗАДАНИЕ 3

платежный матрица игра программирование

Решить матричную игру с помощью сведения к задаче линейного программирования и надстройки "Поиск решения":

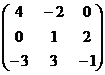
. Сведение матричной игры к задаче линейного программирования

Теория игр находится в тесной связи с линейным программированием, так как каждая конечная игра двух лиц с нулевой суммой может быть представлена как задача линейного программирования.

Находим нижнюю цену игры:

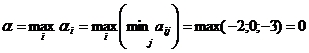
Находим верхнюю цену игры:

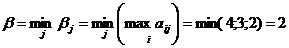
Поскольку 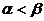, то платежная матрица не имеет седловой точки.

Цена игры находится в пределах:

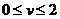
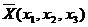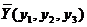Решением игры являются смешенные стратегии игроков  и , где х₁ - вероятность применения 1-м игроком 1-й стратегии, х₂ - вероятность применения 1-м игроком второй стратегии, х₃ - вероятность применения 1-м игроком третьей стратегии, у₁ - вероятность применения 2-м игроком 1-й стратегии, у₂ - вероятность применения 2-м игроком второй стратегии, у₃ - вероятность применения 2-м игроком третьей стратегии.

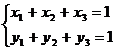
Применение первым игроком оптимальной стратегии должно обеспечивать ему при любых действиях второго игрока выигрыш не меньше цены игры v:

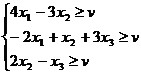
Величина v неизвестна, однако можно считать, что цена игры v > 0. Преобразуем систему ограничений, разделив все челны на неравенств на v:

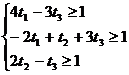, где

.

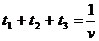
Оптимальная стратегия игрока А должна максимизировать величину v, следовательно, функция должна принимать минимальное значение:

.

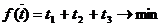Таким образом, имеем задачу линейного программирования.

Аналогично для второго игрока составим задачу линейного программирования (двойственная задача):

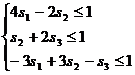, где

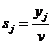
Оптимальная стратегия игрока В должна минимизировать величину v, следовательно, функция:

Таким образом, для нахождения решения игры имеем пару двойственных задач линейного программирования.

. Решение задачи линейного программирования

Найдем решение с помощью надстройки Excel Поиск решения.

Представим рабочий лист Excel с занесенными исходными данными (рисунок 1):

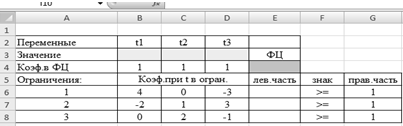
Рисунок 1 - Фрагмент листа Excel с исходными данными

В ячейках В3:D3 будут значения переменных t₁, t₂, t₃.

Далее в ячейку E4 заносим значение целевой функции. Для этого используем встроенную математическую функцию СУММПРОИЗВ.

Порядок вычисления:

) Активируем Мастер функции (в главном меню выбираем Вставка/Функция)

) в окне Категория выбираем Математические, в окне Функция - СУММПРОИЗВ. Щелкаем на кнопку ОК.

3) Заполняем аргументы функции (рисунок 2)

Массив_1 - ячейки содержащий набор прибыли на изделия (В4:D4)

Массив_2 - ячейки, содержащие в будущем значения переменных (В3:D3). Щелкаем на клавишу F4, чтобы аргумент функции в этом массиве остался постоянным ($В$3:$D$3).

) Нажимаем клавишу ОК

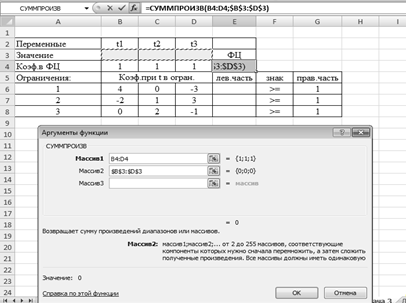
Рисунок 2 - Использование функции СУММПРОИЗВ

Далее ячейку с функцией Е4 копируем в левые части ограничений, т.е. в ячейки Е6, Е7 и Е8.

Теперь можно использовать надстройку Поиск решения. Порядок вычисления:

) В главном меню выбираем Сервис, в надстройках Поиск решения

) Заполняем аргументы Поиска решения

Установить целевую ячейку - заносим ячейку с функцией цели Е4.

Равной минимальному.

Изменяя ячейки - заносим диапазон ячеек со значением переменных (В3:D3)

Ограничения:

Рисунок 3 - Ввод ограничений

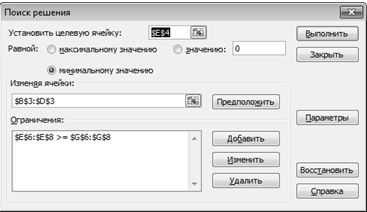
Рисунок 4 - Заполнение аргументов "Поиск решения"

В Параметрах отмечаем Линейная модель и Неотрицательные значения.

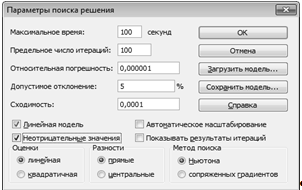
Рисунок 5 - Ввод параметров поиска решения

Нажимаем кнопку ОК и в меню Поиск решения Выполнить.

Рисунок 6 - Сообщение о выполнении задачи

Выделяем все виды отчетов и нажимаем ОК. Получаем:

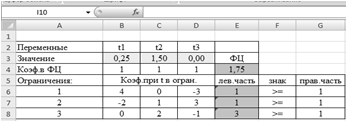
Рисунок 7 - Результаты решения задачи

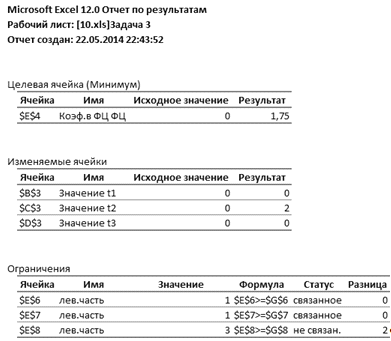
Рисунок 8 - Отчет по результатам

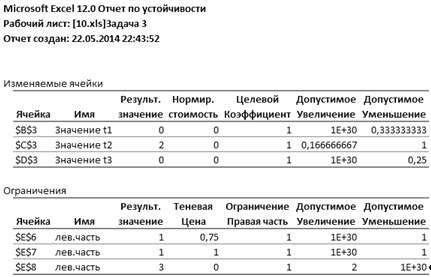
Рисунок 9 - Отчет по устойчивости

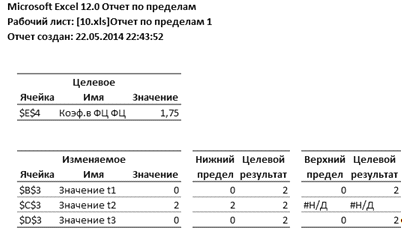
Рисунок 10 - Отчет по пределам

Находим значение седловой точки (цена игры):

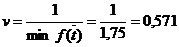
Находим оптимальные стратегии первого игрока:

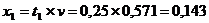
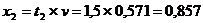
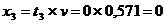
Если первый игрок с вероятностью 0,143 будет применять первую стратегию, с вероятностью 0,857 - вторую стратегию, а третью не применять совсем, то при достаточно большом количестве игр с данной матрицей его выигрыш в среднем составит не менее 0,571.

Решение двойственной задачи получаем из отчета по устойчивости (рисунок 9). Оптимальные стратегии второго игрока:

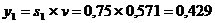
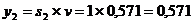
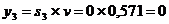
Если второй игрок с вероятностью 0,429 будет применять первую стратегию, с вероятностью 0,571 - вторую стратегию, а третью стратегию не применять совсем, то при достаточно большом количестве игр с данной матрицей его проигрыш в среднем составит не более 0,571.

ЗАДАНИЕ 4

Произвести возможные упрощения платежной матрицы и найти решение игры, используя графический метод решения.

Решение:

. Упростим платежную матрицу

Стратегия A₃ доминирует над стратегией A₄ (все элементы строки 3 больше или равны значениям 4-ой строки), следовательно исключаем 4-ую строку матрицы. Вероятность х₄ = 0.

С позиции проигрышей игрока В стратегия B₃ доминирует над стратегией B₂ (все элементы столбца 3 больше элементов столбца 2), следовательно исключаем 3-й столбец матрицы. Вероятность у₃ = 0.

. Решим игру графически

Графический метод применяется к играм, в которых хотя бы один игрок имеет только две стратегии.

Находим нижнюю цену игры:

Находим верхнюю цену игры:

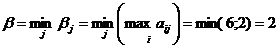
Поскольку 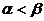, то платежная матрица не имеет седловой точки.

Цена игры находится в пределах:

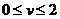
Оптимальное решение следует искать в области смешенных стратегий. Построим на плоскости отрезки, соответствующие стратегиям первого игрока (рисунок 11).

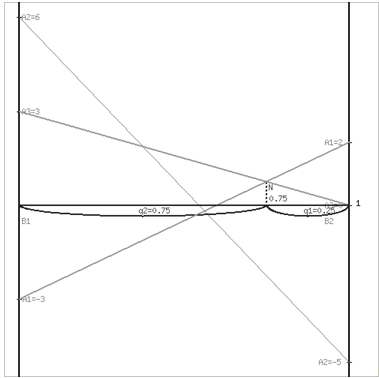
Рисунок 11 - Решение игры графическим методом

Максиминной оптимальной стратегии игрока B соответствует точка N, лежащая на пересечении прямых A₁A₁ и A₃A₃, для которых можно записать следующую систему уравнений:

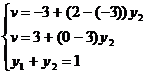
Получаем y₂ = 0,75. Тогда y₁ = 1 - у₂ = 1 - 0,75 = 0,25.

Цена игры: v = 0,75.

Если второй игрок с вероятностью 0,25 будет применять первую стратегию, с вероятностью 0,75 - вторую стратегию, а третью стратегию не применять совсем, то при достаточно большом количестве игр с данной матрицей его проигрыш в среднем составит не более 0,75.

Теперь можно найти минимаксную стратегию игрока A, записав соответствующую систему уравнений, исключив стратегию A₂, которая дает явно больший проигрыш игроку A, и, следовательно, х₂ = 0.

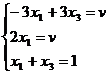
Получаем, х₁ = 0,375, х₃ = 0,625.

Если первый игрок с вероятностью 0,375 будет применять первую стратегию, с вероятностью 0,625 - третью стратегию, а вторую и четвертую не применять совсем, то при достаточно большом количестве игр с данной матрицей его выигрыш в среднем составит не менее 0,75.

ЗАДАНИЕ 5

Фирма может принять решение о строительстве среднего или малого предприятия. Малое предприятие впоследствии можно расширить. Решение определяется будущим спросом на продукцию, которую предполагается выпускать на сооружаемом предприятии. Строительство среднего предприятия экономически оправданно при высоком спросе. С другой стороны, можно построить малое предприятие и через 2 года его расширить.

Фирма рассматривает данную задачу на 10-летний период. Анализ рыночной ситуации показывает, что вероятности высокого и низкого уровней спроса равны 0,75 и 0,25 соответственно. Строительство среднего предприятия обойдется в 5 млн. р., малого - в 1 млн. р. Затраты на расширение через 2 года малого предприятия оцениваются в 4,2 млн. р.

Ожидаемые ежегодные доходы для каждой из возможных альтернатив:

ü  Среднее предприятие при высоком (низком) спросе дает 1 (0,3) млн. р.;

ü  Малое предприятие при низком спросе - 0,2 млн. р.;

ü  Малое предприятие при высоком спросе - 0,25 млн. р в течение 10 лет;

ü  Расширенное предприятие при высоком (низком) спросе - 0,9 (0,2) млн. р.;

ü  Малое предприятие без расширения при высоком спросе в течение первых 2 лет и последующем низком спросе - 0,2 млн. р. в год за остальные 8 лет.

Определить оптимальную стратегию фирмы в строительстве предприятий.

Решение:

Рассматриваем доход за 10-тилетний период.

Среднее предприятие (стратегия А₁).

. При высоком спросе доход составит: 1 × 10 - 5 = 5 (млн. руб.)

. При низком спросе прибыль будет равна: 0,3 × 10 - 5 = -2 (млн. руб.)

Малое предприятие без расширения (стратегия А₂).

. При высоком спросе доход составит: 0,25 × 10 - 1 = 1,5 (млн. руб.)

. При низком спросе прибыль будет равна: 0,2 × 10 - 1 = 1 (млн. руб.)

Малое предприятие с расширением (стратегия А₃).

. При высоком спросе доход составит:

0,25 × 2 - 1 + 0,9 × 8 - 4,2 = 2,5 (млн. руб.)

2. При низком спросе прибыль будет равна:

0,2 × 2 - 1 + 0,2 × 8 - 4,2 = -3,2 (млн. руб.)

Поскольку анализ рыночной ситуации показывает, что вероятности высокого и низкого уровней спроса равны 0,75 и 0,25 соответственно, то вероятность что в первые 2 года спрос будет высокий, а последующие 8 лет низкий равна 1 - 0,75 - 0,25 = 0. Соответственно ситуацию, что малое предприятие без расширения при высоком спросе в течение первых 2 лет и последующем низком спросе в остальные 8 лет, не рассматриваем.

Таким образом, поучили матрицу прибылей фирмы (таблица 1).

Таблица 1 Матрица прибылей фирмы

Для выбора оптимальной стратегии фирмы используем различные критерии.

а) Решение игры с природой по критерию Гурвица, α = 0,4;

Критерий Гурвица устанавливает баланс между случаями крайнего пессимизма и крайнего оптимизма путем взвешивания обоих способов поведения соответствующими весами (1 - α) и α, где 0< α <1. Значение α от 0 до 1 может определяться в зависимости от склонности лица, принимающего решение, к пессимизму или к оптимизму.

Критерий Гурвица записывается следующим образом:

Находим минимальные значения по стокам: (-2; 1; -3,2)

Находим максимальные значения по строкам: (5; 1,5; 2,5)

Вероятность, что спрос будет высокий составляет α = 0,75.

Находим сумму произведений по каждой строке:

Находим значение критерия:

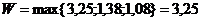
По критерию Гурвица, оптимальной является первая стратегия (строительство среднего предприятия).

б) Решение игры с природой по критерию Лапласа

Принцип Лапласа предполагает, что наступления различных состояний природы, равновероятны .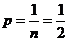

Ожидаемый доход при различных действиях составляют:

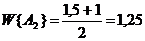
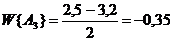
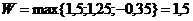
По критерию Лалпаса, оптимальной является первая стратегия (строительство среднего предприятия).

в) Решение игры с природой по критерию Вальда

Этот критерий опирается на принцип наибольшей осторожности, поскоку он основан на выборке наилучшей из наихудших стратегий.

При выборе оптимальной стратегии используется максиминный критерий:

По критерию Вальда, оптимальной является вторая стратегия (строительство малого предприятия без расширения).

Список использованных источников

1.      Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб. пособие. - 2 изд., испр. - М.: Дело, 2002 - 440 с.

.        Экономико-математические методы и модели в управлении производством / А.С. Пелих, Л.Л. Терехов, Л.А. Терехова. - ростов нД: "Феникс", 2005. - 248 с.

.        Экономико-математические методы и модели: учебное пособие / колю авторов; под ред. С.И. Макарова. - М.: КНОРУС, 2007 - 232 с.