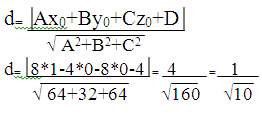Решение уравнений системы матриц

Решение уравнений системы матриц

АЛТАЙСКАЯ АКАДЕМИЯ ЭКОНОМИКИ И ПРАВА

Контрольная работа

по дисциплине Линейная алгебра

Вариант № 5

Решение уравнений системы матриц

совместимость алгебраическое уравнение матрица гаусс

Барнаул, 2014г.

.Предприятие выпускает 3 вида изделий, используя 2 вида сырья, нормы расхода сырья на одно изделие задаются матрицей А. Количество выпускаемого товара, каждого вида, задается матрицей выпуска В. Определить денежные расходы предприятия на выпуск изделий, если стоимость единицы каждого вида сырья выражается матрицей С.

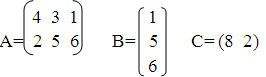
Решение. Найдем матрицу суммарных расходов сырья двух видов на всю выпускаемую продукцию:

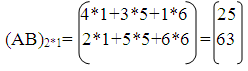
Денежные расходы предприятия на выпуск изделий равны (AB)_2*1 =(8*25+63*2)=326.

2. Для матрицы A найти А^-1, сделать проверку A^-1A

Для матрицы А найдем обратную матрицу А^-1 . Определитель матрицы А равен detA=-10, А₁₁=6, А₁₂=-10, А₁₃=7, А₂₁=2, А₂₂=-8, А₂₃=7, А₃₁=-8, А₃₂=4, А₃=-7. Тогда:

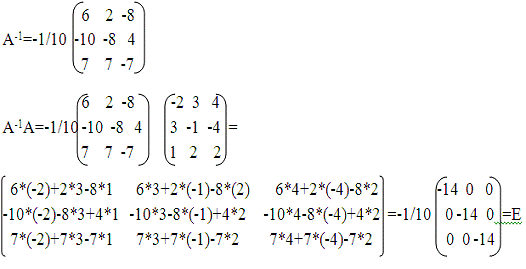
3. Проверить совместность системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) с помощью обратной матрицы (матричным методом).

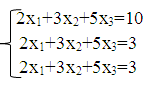
Решение:

а)Вычислим значение определитель функции

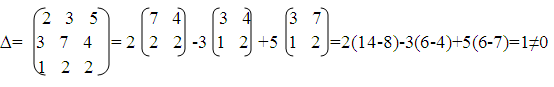
Так как главный определитель отличен от нуля, то система совместна, найдем дополнительные определители:

x₁=∆₁/∆=3/1=3

x₂=∆₂/∆=-2/1=-2

x₃=∆₃/∆=2/1=2

Проверка. Подставив найденные значения неизвестных в исходную систему, получим три тождества.

2*3+3*(-2)+5*2=10

*3+7*(-2)+4*2=3

*3+2*(-2)+2*2=3

б) Решим матричным способом систему уравнений:

А*Х=В следовательно Х=А^-1*В

Найдем А^-1:

Определим миноры матрицы:

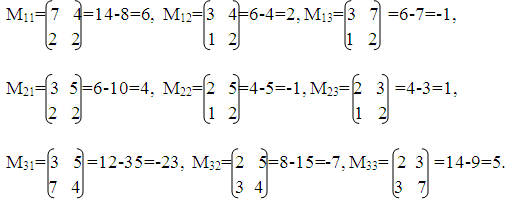
Матрица миноров:

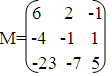
Матрица алгебраических дополнений:

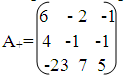
Матрица алгебраических дополнений транспонированная:

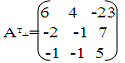
Обратная матрица:

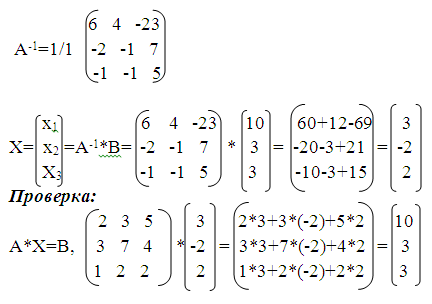
4. Решить систему линейных уравнений методом Гаусса

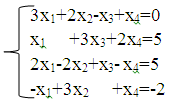
Решение. Составим расширенную матрицу А и приведем ее с помощью элементарных преобразований строк к трапециевидному виду.

rang (A)=rang (A)=4, следовательно, система совместна. Последней матрице со-ответствует система (равносильная исходной), которую можно представить в виде:

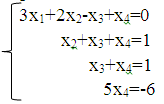
Из системы, обратным ходом метода Гаусса (двигаясь снизу вверх), последовательно находим:

5х₄=-6, х₄=-6/5

х₃-6/5=1, х₃=11/5

х₂+11/5-6/5=1, х₂=1-11/5+6/5, х₂=0

х₁+2*0-11/5-6/5=0, 3х₁=17/5, х₁=12/15.

5. Решить матричное уравнение модели Леонтьева “затраты-выпуск”

X-AX=Y где X-вектор совокупного продукта, А данная матрица коэффициентов прямых затрат и Y -вектор конечного продукта:

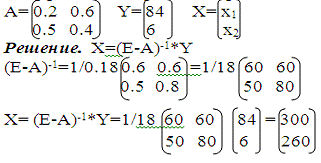
6. Даны координаты вершин пирамиды ABCD. Требуется найти: 1). Длину ребра AB. 2).Угол между ребрами AB и AD. 3). Проекцию ребра AD на AB. 4). Площадь грани ABC. 5). Объем пирамиды.

A(1, 1, 0), B(-1, 3, 3), C(1, -3, -2), D(1, 0, 0).

Решение. 1) Найдем координаты вектора AB -2, 2, 3 и его длину

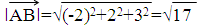
2) Найдем косинус угла между найденным вектором и вектором AD= 0, -1, 0 через скалярное произведение

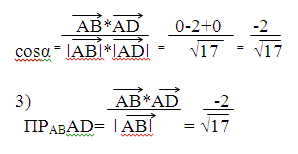
4) Площадь грани АВС, S=1/2 AB*AC

Найдем координаты АС= 0, -4, -2

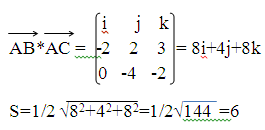
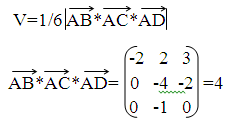
Следовательно V=4/6=2/3.

7. Даны координаты вершин треугольника ABC. Требуется найти:

). Уравнение стороны AB. 2). Уравнение высоты, проведенной из точки B. 3). Длину высоты. 4). Уравнение медианы, проведенной из точки С.

А(0;-2), В(-2;-2), С(1;1)

Решение:

) Воспользуемся уравнением прямой , проходящей через две заданные точки:

2) Найдем вектор, перпендикулярный искомой прямой:

АС 1;3

Тогда из общего уравнения х+3у+С=0 находим С из условия принадлежности точки В этой прямой:  -2-6+С=0

Следовательно С=8 и уравнение искомой прямой х+3у+8=0

) Длину высоты найдем как расстояние d от точки В(х₀;у₀) до прямой

Ах + Ву + С = 0 по формуле:

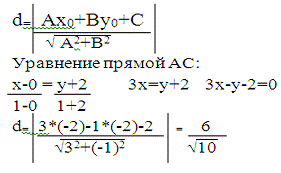
4) Найдем середину отрезка АВ:

х=(0-2)/2=-1 у=(-2-2)/2=2

Уравнение прямой через найденную точку и точку С имеет вид:

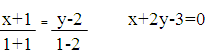
8. Для пирамиды ABCD, координаты которой даны в задаче 6, найти: 1). Уравне-ние ребра AD. 2). Уравнение грани ABC. 3). Длину высоты, опущенной из вершины D на грань ABC.

A(1, 1, 0), B(-1, 3, 3), C(1, -3, -2), D(1, 0, 0).

Решение:

1.Найдем направляющий вектор

AD=(1-1; 0-1; 0-0)=(0;-1;0)

Уравнения прямой составим по точке А(1;1;0) и направляющему вектору AD(0;-1;0): х-1=0, у-1=0, z=0.

. Cоставим уравнение плоскости по трём точкам

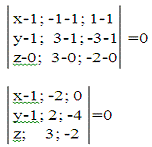
Раскрываем определитель по первому столбцу, находим уравнение плоскости:

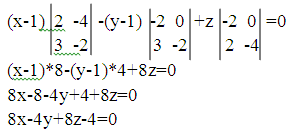
3. Длину высоты, опущенной из вершины D на грань ABC это расстояния от точки D(1; 0; 0) до плоскости 8x-4y+8z-4=0.Найдем по формуле