Понятия выборочной теории. Ряды распределения. Корреляционный и регрессионный анализ
Содержание
Введение
Постановка
задачи на выполнение курсовой работы (рабочая легенда)
. Основные
понятия выборочной теории (тема 7)
.1 Выборочный
метод
.2 Построение
статистических рядов распределения
.3
Графическое представление рядов распределения
. Теория
статистического оценивание параметров распределения (тема 8)
.1 Точечные
оценки характеристик положения и мер изменчивости
.2
Интервальные оценки и доверительные интервалы
. Проверка
статистических гипотез (тема 9)
.1 Гипотезы о
параметрах распределения
.2 Гипотеза о
законе распределения
.
Корреляционный и регрессионный анализ (тема 10)
.1
Корреляционная зависимость
.2 Уравнение
регрессии
Заключение
Список
литературы
Приложения
Введение
В данной курсовой работе отрабатываются выборочный метод математической
статистики, точечное и доверительное оценивание и проверка статистических
гипотез.
Цели выполнения курсовой работы:
· подготовить курсантов к практическому применению методов математической
статистики последующих дисциплин; профессионального и математического цикла
(фундаментальное изложение которых предполагает использование понятий и методов
математической статистики);
· привить необходимые в профессиональной деятельности навыки
использования методов математической статистики для обработки и анализа
статистической информации, изучить методы построения точечных и интервальных
оценок, критерии согласия;
· развить аналитические способности курсантов, логику,
интуицию, умение оперировать строгими определениями и проводить строгие
доказательства.
В результате выполнения курсовой работы курсант должен приобрести
практические навыки решения следующих задач:
· построения точечных и интервальных статистических рядов;
· нахождения точечных и интервальных оценок параметров
распределения;
· проверки гипотезы о законе распределения с помощью критериев
Пирсона и Колмогорова;
· проверки параметрических гипотез.
При выполнении курсовой работы необходимо провести обработку
статистических данных соответствующей таблицы и получить необходимые
результаты.
По данным таблиц наблюдения для каждого ряда распределения необходимо:
· вычислить статистики среднего значения, вариации, асимметрии и эксцесса;
· построить гистограмму и полигон частот;
· подобрать гипотетические кривые распределения;
· найти точечные оценки для параметров гипотетических
распределений;
· построить доверительные интервалы для параметров нормального
распределения;
Постановка задачи на выполнение курсовой работы (рабочая
легенда)
В ходе выполнения курсовой работы (КР) необходимо провести исследование
конкретной генеральной совокупности, которая представляет собой результаты
тестирования 401 курсанта. Тестирование проводилось в целях получения оценки
способностей курсантов к восприятию гуманитарных (признак Х) и
военно-технических (признак Y)
дисциплин.
В результате выполнения заданий КР курсант должен сформулировать
конкретные выводы о законе распределения исследуемых признаков, а также о
наличии и характере статистической связи между численными оценками способностей
курсантов к восприятию гуманитарных и военно-технических дисциплин данной
группы обучаемых.
Исследование генеральной совокупности проводится на материале парной
выборки объемом n = 20. Такой
объем выборки позволяет, с одной стороны, оценить подразделение в составе
взвода (учебной группы), с другой стороны, обеспечивает объем вычислений,
достаточный для приобретения курсантами необходимых практических навыков. Чтобы
выполнить условие репрезентативности выборки, когда все объекты генеральной
совокупности имеют одинаковую вероятность попасть в нее, необходимо обеспечить
случайность выбора. Поэтому выборку курсанты получают (по заданию
преподавателя) с помощью таблицы случайных чисел (см. приложения).
Из генеральной совокупности (Приложение 1), содержащей 401 пару значений
признаков Х и Y, выбираются пары с номерами,
соответствующими случайным числам, взятым из таблицы Приложения 2.
1.
Основные понятия выборочной теории (тема 7)
1.1
Выборочный метод
Изучить:
а) понятия генеральной и выборочной совокупностей-
б) определение состава выборки:
- репрезентативность
выборки-
- способы отбора-
- определение достаточного объема выборки.
в) устройство таблицы случайных чисел и правило ее использования при
составлении выборки определенного объема.
Математическая статистика - раздел математики, разрабатывающий методы
регистрации, описания и анализа данных наблюдений и экспериментов с целью
построения вероятностных моделей массовых случайных явлений.
Генеральная совокупность (ГС) - множество всех объектов,
подлежащих изучению.
Выборочная совокупность (ВС) - совокупность случайно выбранных
объектов.
Определение состава выборки: поскольку ГС представляет собой всю
изучаемую совокупность, то ее называют основной выборкой. Отбор единиц в ВС
может быть повторным и бесповторным.
Для того, чтобы получить наиболее правильные ответы необходимо, чтобы
выборка была представительной (репрезентативной), то есть правильно
представлять совокупности.
Способы отбора:
1. Случайная выборка - отбор единиц из генеральной совокупности в целом без
разделения на группы.
2. Механическая выборка - применяется в тех случаях, когда
генеральная совокупность каким - то образом упорядочена.
3. Типическая выборка - используется в тех случаях, когда все единицы
генеральной совокупности объединены в нескольких типических групп.
4. Серийная выборка. Сущность: В собственно случайной, либо механической
выборке групп элементов проводится сплошная выборка.
Для определения объёма выборки можно воспользоваться таблицей достаточно
больших чисел. При неограниченном увеличение число n независимых опытов, частность события А сходится по
вероятности к его вероятности в отдельном опыте.
5. 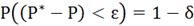
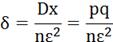
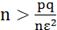 где
где  - величина допустимой ошибки, которую мы можем себе
позволить. P- показатель надежности.
- величина допустимой ошибки, которую мы можем себе
позволить. P- показатель надежности.
Задание 1
1.1 Из генеральной совокупности данных, состоящей из N = 401 пары
значений признаков X и Y, имеющих вполне определенное смысловое содержание,
выделить систему двух выборок - выборка признака X и выборка признака Y -
объемом n = 20.
|
Случайные числа по 19
варианту
|
145
|
144
|
183
|
159
|
194
|
240
|
243
|
348
|
361
|
363
|
|
354
|
355
|
270
|
260
|
219
|
51
|
49
|
299
|
296
|
333
|
|
X
|
59
|
56
|
63
|
60
|
60
|
63
|
62
|
60
|
62
|
64
|
58
|
59
|
63
|
62
|
64
|
64
|
61
|
62
|
61
|
62
|
|
Y
|
83
|
82
|
79
|
76
|
76
|
84
|
84
|
83
|
81
|
79
|
81
|
83
|
80
|
81
|
84
|
80
|
78
|
81
|
83
|
81
|
1.2
Построение статистических рядов распределения
Изучить:
а) понятия варианта, вариационного и статистического рядов распределения
и методику их построения-
б) понятия размаха выборки, частоты, относительной частоты (частости),
накопленной частоты (частости) признака-
в) понятия интервального ряда, величины (шага) интервала, шкалы
интервалов, методику их расчета и построения.
Каждое
значение 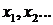 называется вариантом, а изменение этого значения -
варьированием.
называется вариантом, а изменение этого значения -
варьированием.
Различные
значения признака являются вариантами, а их последовательность, записанная в
возрастающем или убывающем порядке, называется вариационным рядом. Для
построения вариационного ряда необходимо упорядочить значения данных 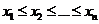 .
.
Статистический
ряд - это перечень вариантов и
соответствующих им частотам или относительных частот. Для построения необходимо
записать значение признаков 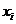 в
возрастающем порядке, частоту признака
в
возрастающем порядке, частоту признака 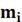 (кол-во
повторений), и относительную частоту.
(кол-во
повторений), и относительную частоту.
Частота
варианта - число 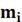 , показывающие сколько раз повториться значение
вариант
, показывающие сколько раз повториться значение
вариант 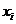 в ряде наблюдений, а его отношение к объему выборки -
относительная частота варианта (частость) (
в ряде наблюдений, а его отношение к объему выборки -
относительная частота варианта (частость) (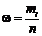 ). Сумма частостей равна единице или 100 %.
). Сумма частостей равна единице или 100 %.
Накопленная
частота - сумма частот, накопленная с
1- ого варианта до данного.
Для
построения интервального ряда необходимо определить величину, шаг, интервал,
рассчитать шкалу интервалов, произвести расчёт интервальных частот.
Вариационные
ряды строятся на основе количественного группировочного признака и состоят из
двух элементов: вариант и частот.
Вариационные
ряды в зависимости от характера вариации подразделяются на дискретные
(прерывные) и интервальные (непрерывные). Дискретные ряды распределения
основаны на дискретных (прерывных) признаках, имеющих только целые значения.
Интервальные
ряды распределения базируются на непрерывно изменяющемся значении признака,
принимающем любые (в том числе и дробные) количественные выражения, поэтому
значение признаков таких рядах задается в виде интервала.
Для
построения ряда распределения непрерывно изменяющихся признаков, либо
дискретных, представленных в виде интервалов, необходимо установить оптимальное
число групп (интервалов), на которые следует разбить все единицы изучаемой
совокупности.
Задание 2
2.1 Для выборок признаков X и Y построить вариационный и статистический ряды распределения.
Таблица 1
Вариационный ряд
|
X
|
59
|
56
|
63
|
60
|
60
|
63
|
62
|
60
|
62
|
64
|
58
|
59
|
63
|
62
|
64
|
64
|
61
|
62
|
61
|
62
|
Таблица 2
Статистический ряд
|
Xi
|
56
|
58
|
59
|
60
|
61
|
62
|
63
|
64
|
|
mi
|
1
|
1
|
2
|
3
|
2
|
5
|
3
|
3
|
|
miнк
|
1
|
2
|
4
|
7
|
9
|
14
|
17
|
20
|
|
ωi
|
0,05
|
0,05
|
0,1
|
0,15
|
0,1
|
0,25
|
0,15
|
0,15
|
|
ωiнк
|
0,05
|
0,1
|
0,2
|
0,35
|
0,45
|
0,7
|
0,85
|
1
|
Таблица 3
Вариационный ряд
|
Y
|
83
|
82
|
79
|
76
|
76
|
84
|
84
|
83
|
81
|
79
|
81
|
83
|
80
|
81
|
84
|
80
|
78
|
81
|
83
|
81
|
Таблица 4
Статистический ряд
|
Yi
|
76
|
78
|
79
|
80
|
81
|
82
|
83
|
84
|
|
mi
|
2
|
1
|
2
|
2
|
5
|
1
|
4
|
3
|
|
miнк
|
2
|
3
|
5
|
7
|
12
|
13
|
17
|
20
|
|
ωi
|
0,1
|
0,05
|
0,1
|
0,1
|
0,25
|
0,05
|
0,2
|
0,15
|
|
ωiнк
|
0,1
|
0,15
|
0,25
|
0,35
|
0,6
|
0,65
|
0,85
|
1
|
m1нк =m1
mi+1нк = miнк + mi
ωi 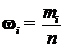
ω1нк =ω1
ωi+1нк = ωiнк +ωi
.2
Для выборки признака X построить интервальный ряд распределения.
Составляем
ряд распределения X используя статистический ряд распределения X по
формулам:
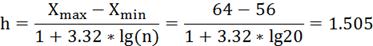
где
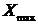 максимальное значение X,
максимальное значение X,
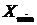 -
минимальное значение X,
-
минимальное значение X,
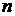 - объем
выборки.
- объем
выборки.
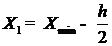
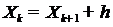
Таблица 5
Интервальный ряд для X
|
Интервалы
|
(55,25-56,75]
|
(56,75-58,25]
|
(58,25-59,75]
|
(59,75-61,25]
|
(61,25-62,75]
|
(62,75-64,25)
|
|
Xинт
|
56
|
57,5
|
59
|
60,5
|
62
|
63,5
|
|
mi
|
1
|
1
|
2
|
5
|
5
|
6
|
|
miнк
|
1
|
2
|
4
|
9
|
14
|
20
|
|
ωi
|
0,05
|
0,05
|
0,1
|
0,25
|
0,25
|
0,3
|
|
ωiнк
|
0,05
|
0,1
|
0,2
|
0,45
|
0,7
|
1
|
.3 Для выборки признака Y
построить интервальный ряд распределения
Составляем ряд распределения Y используя статистический ряд распределения Y по формулам:
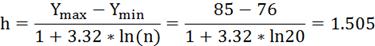
где
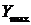 максимальное значение Y,
максимальное значение Y,
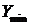 -
минимальное значение Y,
-
минимальное значение Y,
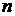 - объем
выборки.
- объем
выборки.
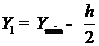
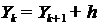
Таблица 6
Интервальный ряд
|
для Y
|
|
|
|
|
|
|
Интервалы
|
(75,25-76,75]
|
(78,25-79,75]
|
(79,75-81,25]
|
(81,25-82,75]
|
(82,75-84,25)
|
|
Yинт
|
76
|
77,5
|
79
|
80,5
|
82
|
83,5
|
|
mi
|
2
|
1
|
2
|
7
|
1
|
7
|
|
miнк
|
2
|
3
|
5
|
12
|
13
|
20
|
|
ωi
|
0,1
|
0,05
|
0,1
|
0,35
|
0,05
|
0,35
|
|
ωiнк
|
0,1
|
0,15
|
0,25
|
0,6
|
0,65
|
1
|
1.3
Графическое представление рядов распределения
Изучить:
а) понятие полигона распределения и методику его построения;
б) понятие гистограммы и методику ее построения;
в) понятие эмпирической функции распределения и методику ее построения
для дискретного и интервального рядов.
Полигон распределения дискретного ряда - ломанная линия последовательно
соединяющая в прямоугольной системе координат точки с координатами
Гистограммой частот (частостей) называют ступенчатую фигуру,
состоящую из прямоугольников, основаниями которых служат частичные интервалы
длины h, а высоты равны плотности частоты
или плотность частости.
Для построения гистограммы по оси абсцисс указывают значения границ
интервалов и на их основании строят прямоугольники, высота которых
пропорциональна частотам (или частостям).
Эмпирической (выборочной) функцией распределения (или функцией распределения выборки)
называется функция F*(x), задающая для каждого значения х
относительную частоту события Х<х.
Кумулятивная кривая - это график выборочной функции F*(x), дающий
приближенное представление о графике теоретической функции F(x)(Кумулята - это сумма накопленных частностей)
Ряд распределения - представляет собой упорядоченное распределение
единиц изучаемой совокупности на группы по определенному варьирующему признаку.
Задание 3
3.1 Для выборки признака X построить полигон и эмпирическую функцию
распределения для статистического ряда. (По таблице 2)
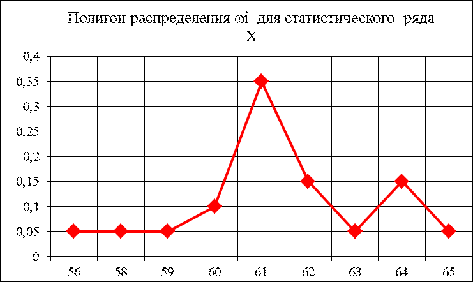
Рисунок 1
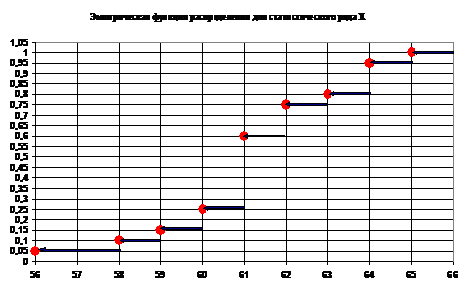
Рисунок 2
.2 Для выборки признака Y построить полигон, гистограмму и эмпирическую
функцию распределения для интервального ряда. (По таблице 6.)
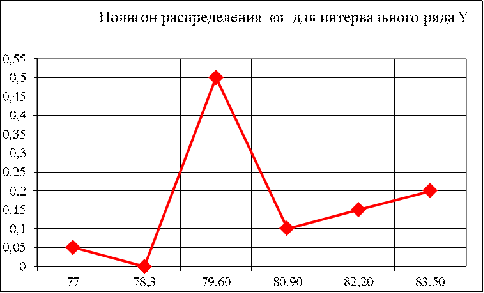
Рисунок 3
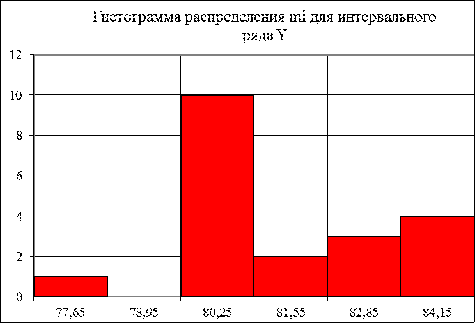
Рисунок 3
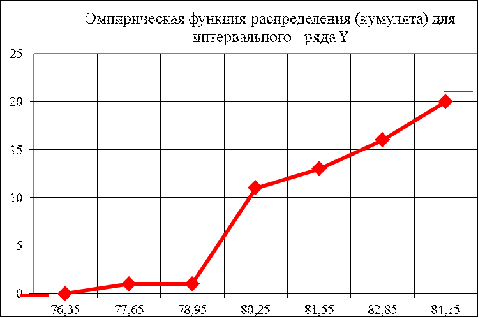
Рисунок 4
2. Теория статистического оценивание параметров распределения
(тема 8)
.1
Точечные оценки характеристик положения и мер изменчивости
Изучить:
а) числовые характеристики, описывающие центр распределения (среднее
арифметическое, выборочные мода и медиана);
б) нахождение средней арифметической наблюденных значений случайной
величины;
в) нахождение моды выборочной совокупности;
г) нахождение медианы выборочной совокупности.
д) понятие и формулы для нахождения выборочных начальных моментов;
е) понятие и формулы для нахождения выборочных центральных моментов;
ж) понятия и формулы для нахождения выборочной дисперсии, исправленной
дисперсии, эмпирических коэффициентов асимметрии и эксцесса.
Среднее арифметическое значение выборочной совокупности рассчитывается по
формуле:
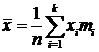
Мода
(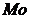 ) - значение
признака, которое наблюдалось наибольшее число раз.
) - значение
признака, которое наблюдалось наибольшее число раз.
Модальный
интервал - интервал которому
соответствует наибольшая частота(mi ).
Медиана
(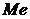 )(Вариационного ряда)- значение варианта соответствует середине
вариационного ряда.
)(Вариационного ряда)- значение варианта соответствует середине
вариационного ряда.
Медиана
(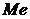 )(Интервального ряда) - значение признака, приходящегося на середину
интервального ряда наблюдений.
)(Интервального ряда) - значение признака, приходящегося на середину
интервального ряда наблюдений.
Если
объем выборки равен 2k-1 (нечетное число), тогда медианой является то
значение признака которое приходится на середину интервального ряда наблюдений:
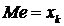
Если
n=2k, тогда за медиану мы принимаем половину между 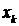 и
и 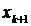 :
:
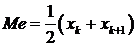
Для
нашей задачи:
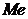 :
: 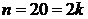
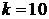 ;
; 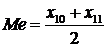
Аналогично статистическому ряду среднее арифметическое значение
интервального ряда распределения рассчитываем по формуле:
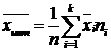
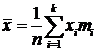
Мода
для интервального ряда рассчитывается по формуле:
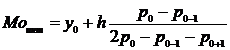
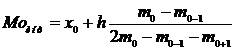
где
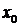 - начало модального интервала;
- начало модального интервала;
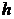 - длина
интервала (шаг);
- длина
интервала (шаг);
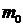 - частота
модального интервала;
- частота
модального интервала;
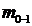 - частота
домодального интервала;
- частота
домодального интервала;
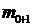 - частота
следующего за модальным интервала.
- частота
следующего за модальным интервала.
Начальный выборочный момент первого порядка:
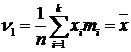
Центральный выборочный момент второго порядка:
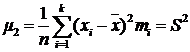
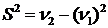
Эмпирической
(выборочной) дисперсией (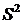 ) называют среднюю арифметическую квадратов отклонений
результатов наблюдений от их средней арифметической:
) называют среднюю арифметическую квадратов отклонений
результатов наблюдений от их средней арифметической:
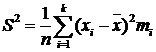
Исправленной
эмпирической дисперсией называется
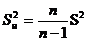
Эмпирический
коэффициент асимметрии:
Асимметрия - характеризует скошенность распределения вероятности
случайной величины относительно математического ожидания.
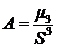
Эксцесс
(коэффициент крутости)- мера остроты
пика распределения случайной величины.
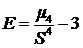
Задание 4
4.1 Для выборки признака X:
по статистическому ряду (Таблица 2.) найти среднюю арифметическую,
выборочные моду и медиану.
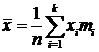
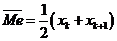
Для
статистического ряда X
|
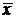 61,25 61,25
|
|
|
Mo
|
62
|
|
Mе
|
62
|
.1 Для выборки признака X:
по интервальному ряду (Таблица 5.) найти среднюю арифметическую,
выборочные моду и медиану.
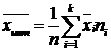
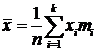
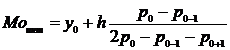
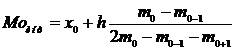
Для
выборки признака Y:
по
статистическому ряду (Таблица 4.) найти среднюю арифметическую, выборочные моду
и медиану.

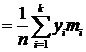
Для
статистического ряда Y
|

|
80,95
|
|
Mo
|
80,43
|
|
Mе
|
80,82
|
Задание 5
5.1
Найти выборочную дисперсию 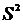 ,
исправленную выборочную дисперсию
,
исправленную выборочную дисперсию 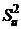 ,
среднеквадратическое отклонение
,
среднеквадратическое отклонение 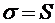 ,
эмпирические коэффициенты асимметрии
,
эмпирические коэффициенты асимметрии 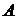 и
эксцесса
и
эксцесса 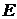 для статистического ряда признака X.
для статистического ряда признака X.
Таблица 7
|
Xi
|
mi
|
Xi-Xср
|
(Xi-Xср)2·mi
|
(Xi-Xср)3·mi
|
(Xi-Xср)4·mi
|
|
56
|
1
|
-5,25
|
27,56
|
-144,7
|
759,69
|
|
58
|
1
|
-3,25
|
10,56
|
-34,32
|
111,56
|
|
59
|
2
|
-2,25
|
10,12
|
-22,78
|
51,25
|
|
60
|
3
|
-1,25
|
4,68
|
-5,85
|
7,32
|
|
61
|
2
|
-0,25
|
0,12
|
-0,03
|
0,007
|
|
62
|
5
|
0,75
|
2,81
|
2,1
|
1,58
|
|
63
|
3
|
1,75
|
9,18
|
16,07
|
28,13
|
|
64
|
3
|
2,75
|
22,68
|
62,39
|
171,57
|
|
S2
|
4,38
|
|
S2и
|
4,61
|
|
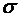 и=Sи2,14 и=Sи2,14
|
|
|
S3и
|
9,92
|
|
S4и
|
21,32
|
|
Aи
|
-0,64
|
|
Eи
|
-0,34
|
5.5
Найти выборочную дисперсию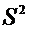 , исправленную выборочную дисперсию
, исправленную выборочную дисперсию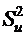 , среднеквадратическое отклонение
, среднеквадратическое отклонение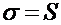 , эмпирические коэффициенты асимметрии
, эмпирические коэффициенты асимметрии 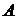 и эксцесса
и эксцесса 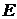 для
статистического ряда признакаY.
для
статистического ряда признакаY.
Таблица 8
|
Yi
|
mi
|
Yi - Yср
|
(Yi - Yср)2· mi
|
(Yi - Yср)3· mi
|
(Yi - Yср)4· mi
|
|
76
|
2
|
-4,95
|
49,005
|
-242,57
|
1200,74
|
|
78
|
1
|
-2,95
|
8,7
|
-25,67
|
75,73
|
|
79
|
2
|
-1,95
|
7,6
|
-14,82
|
28,91
|
|
80
|
2
|
-0,95
|
1,8
|
-1,7
|
1,62
|
|
81
|
5
|
0,05
|
0,01
|
0,006
|
0,000
|
|
82
|
1
|
1,05
|
1,1
|
1,51
|
1,21
|
|
83
|
4
|
2,05
|
16,81
|
34,46
|
70,64
|
|
84
|
3
|
3,05
|
27,9
|
85,11
|
259,6
|
|
S2
|
5,64
|
|
S2и
|
5,94
|
|
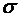 и=Sи1,96 и=Sи1,96
|
|
|
S3и
|
14,49
|
|
S4и
|
35,33
|
|
Aи
|
-0,5
|
|
Eи
|
-0,6
|
2.2
Интервальные оценки и доверительные интервалы
Изучить:
а) понятия интервальной оценки и доверительного интервала;
б) построение интервальных оценок;
в) интервальные оценки числовых характеристик;
г) как влияет на величину интервала объем выборки и доверительная
вероятность γ;
д) интервальная оценка вероятности события.
Оценки неизвестных параметров бывают двух видов - точечные и
интервальные.
Точечная оценка - оценка имеющая конкретное числовое значение. Например,
среднее арифметическое:
= (x1+x2+…+xn)/n,
где: X - среднее арифметическое;1,x2,…xn
- выборочные значения;- объем выборки.
Интервальная оценка - оценка, определяемая двумя числами, которые являются
концами доверительного интервала.
Доверительный интервал - интервал, который с заданной точностью покрывает
исследуемый параметр.
Задание 6
6.1
Рассчитать доверительные интервалы для оценки математического ожидания
признаков Х и Y по выборочным средним и 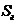 . Если
. Если 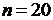 ,
,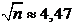 , а надежность ᵞ=0,9
, а надежность ᵞ=0,9
Используя
таблицу распределения Стьюдента, находим 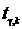
в
зависимости от числа степеней свободы 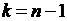
Для
X
|
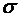 и=Sи2,14 и=Sи2,14
|
|
|
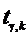 1,73 1,73
|
|
|
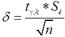 0,831 0,831
|
|
|
xср-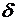 <M(x)<xср+ <M(x)<xср+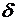 60,4186< M(x)<<62,0814 60,4186< M(x)<<62,0814
|
|
Для Y
|
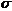 и=Sи2,43 и=Sи2,43
|
|
|
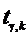 1,73 1,73
|
|
|
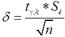 0,943 0,943
|
|
|
yср-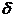 <M(x)<yср+ <M(x)<yср+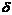 80,0068< M(x)<<81,8932 80,0068< M(x)<<81,8932
|
|
6.1
Рассчитать доверительные интервалы для оценки математического ожидания
признаков Х и Y по выборочным средним и 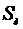 .
.
Если
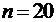 ,
,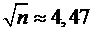 , а надежность ᵞ=0,9
, а надежность ᵞ=0,9
Найдем
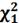 и
и 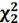 по
таблице Пирсона:
по
таблице Пирсона:
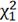 (0,9;19)= 11,65091;
(0,9;19)= 11,65091;
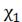 (
(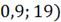 =
=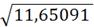 =3,413
=3,413
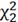 (0,1;19)= 27,20357;
(0,1;19)= 27,20357;
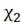 (0,1;19)=
(0,1;19)=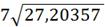 =5,216
=5,216
Доверительный интервал для СКО:
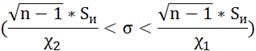
Для распределения X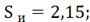
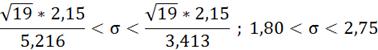
Для распределения Y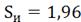 ;
;
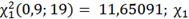 (
(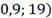 =
=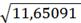 =3,413
=3,413
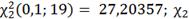 (0,1;19)=
(0,1;19)=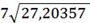 =5,216
=5,216
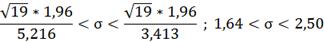
статистический выборочный точечный
корреляционный
3.
Проверка статистических гипотез (тема 9)
3.1
Гипотезы о параметрах распределения
Изучить:
а) понятие статистической гипотезы. Классификация гипотез
(параметрическая, непараметрическая, нулевая, альтернативная, простая,
сложная);
б) понятия ошибок первого и второго рода;
в) статистический критерий проверки нулевой гипотезы;
г) уровень значимости статистического критерия и его связь с ошибками
первого и второго рода. Критическая область и критические точки;
д) методика проверки статистических гипотез;
е) проверка гипотезы о генеральной средней при известной и неизвестной
генеральной дисперсии;
ж) проверка гипотезы о генеральной дисперсии.
Статистическая гипотеза представляет собой некоторое предположение о
законе распределения случайной величины или о параметрах этого закона,
формулируемое на основе выборки. Гипотезы, в основе которых нет никаких
допущений о конкретном виде закона распределения, называют непараметрическими,
в противном случае - параметрическими.
Статистическая гипотеза называется непараметрической, если в ней
сформированы предположения относительно вида функции распределения или закона
распределения.
Статистическая гипотеза называется параметрической, если в ней
сформулированы предположения относительно значений параметров функции
распределения известного вида.
Нулевой
гипотезой называют основную
выдвинутую гипотезу и обозначают 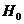 .
.
Альтернативной (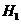 )
называют гипотезу, конкурирующую с основной в том смысле, что если нулевая
гипотеза отвергается, то принимается альтернативная.
)
называют гипотезу, конкурирующую с основной в том смысле, что если нулевая
гипотеза отвергается, то принимается альтернативная.
Статистическая
гипотеза называется простой, если она имеет вид: 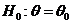 .
.
Сложной называют гипотезу, которая состоит из конечного или
бесконечного числа простых гипотез.
Статистический
критерий проверки нулевой гипотезы:
)
Если выборка принадлежит критическому множеству 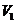 , то
отвергают основную гипотезу.
, то
отвергают основную гипотезу.
)
Если выборка не принадлежит критическому множеству 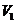 , то нет оснований отвергать основную гипотезу.
, то нет оснований отвергать основную гипотезу.
Критическая
точка - точка раздела между
критической областью 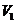 и областью допустимых значений. Критической
областью называют совокупность значений критерия, при которых нулевую
гипотезу отвергают.
и областью допустимых значений. Критической
областью называют совокупность значений критерия, при которых нулевую
гипотезу отвергают.
Задание 7
7.1 Предположив, что признак X распределен по нормальному закону с
известным стандартным отклонением sг
= 2,003, по имеющейся выборке проверить гипотезу о том, что генеральная средняя
равна числу a0 = 61,27. Проверку провести для трех основных видов
альтернативных гипотез при уровне значимости a = 0,05.
1)
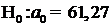 ,
,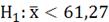 ;
;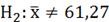 ;
;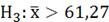 ;
;
)
a = 0,05
)
U - нормальный закон распределения
)
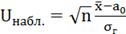 ;
;
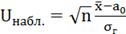 = 0,067
= 0,067
)
Вычислим 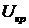 :
:
5.1:
Для двусторонней области:
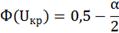
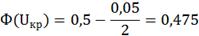
находим
по таблице Лапласа:
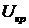 : ±1,96
: ±1,96
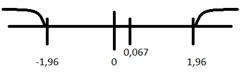
Вывод:
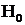 не отвергается
не отвергается
5.2:
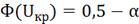
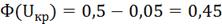
находим по таблице Лапласа:
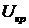 : 1,65
: 1,65
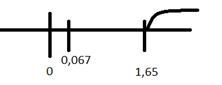
Вывод: Н0 не отвергается
5.3:
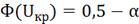
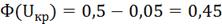
 : -1,65
: -1,65
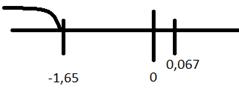
Вывод: Н0 не отвергается
7.2
Предположив, что признак X распределен по нормальному закону, по имеющейся
выборке проверить гипотезу о том, что генеральная дисперсия равна числу 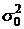 = 4,2. Проверку провести для трех основных видов
альтернативных гипотез при уровне значимости a = 0,05.
= 4,2. Проверку провести для трех основных видов
альтернативных гипотез при уровне значимости a = 0,05.
1)
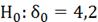
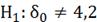
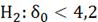
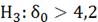
)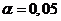
)
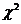 -распределение
-распределение
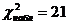
По
критерию Пирсона:
Правосторонняя
область:
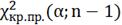
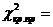 30,1
30,1
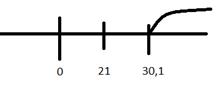
Гипотеза
не отвергается, т.к.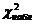 не лежит в области
не лежит в области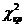
Левостороння
область:
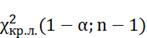
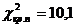
Гипотеза
не отвергается, т.к.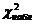 не лежит в области
не лежит в области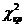
Двустороння
область:
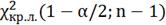
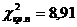
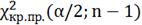
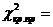 32,9
32,9

Гипотеза не отвергается
.2
Гипотеза о законе распределения
Изучить:
а) формулировку задачи, решаемой с помощью критериев согласия;
б) критерий Пирсона проверки гипотезы о нормальном распределении
генеральной совокупности;
в) критерий Колмогорова и схему его применения.
Критерий
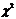 К. Пирсона
К. Пирсона
Использование
этого критерия основано на применении такой меры (статистики) расхождения между
теоретическим F(x) и эмпирическим распределением Fп(x), которая
приближенно подчиняется закону распределения  .
Гипотеза Н0 о согласованности распределений проверяется путем
анализа распределения этой статистики. Применение критерия требует построения
статистического ряда.
.
Гипотеза Н0 о согласованности распределений проверяется путем
анализа распределения этой статистики. Применение критерия требует построения
статистического ряда.
Критерий
Пирсона сконструирован так, что чем ближе нулевое значение статистики, то
вероятнее, что нулевая гипотеза справедлива. Критерий Пирсона имеет только
правостороннюю критическую область.
Примечание.
Использование критерия Пирсона можно считать правомерным при объемах выборки не
менее 50 наблюдений. Однако такой объем исходных данных значительно усложнил бы
выполнение курсовой работы. Поэтому применение критерия Пирсона при выполнении
задания 8 носит более иллюстративный характер.
Задание 8
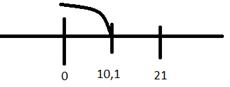
8.1 Используя критерий Пирсона, при уровне значимости a = 0,05 проверить, согласуется ли
гипотеза о нормальном распределении признака X, представленного в виде
интервального ряда.
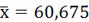 =61,25и = 2,14
=61,25и = 2,14
1) Нулевая гипотеза: ГС распределена по нормальному закону
) a = 0,05
Таблица 9
|
Итервалы
|
(55,25-6,75]
|
(56,75-8,25]
|
(58,25-9,75]
|
(59,75-1,25]
|
(61,25-2,75]
|
(62,75-4,25)
|
|
Xср
|
56
|
57,5
|
59
|
60,5
|
62
|
63,5
|
|
mi
|
1
|
1
|
2
|
5
|
5
|
6
|
|
Xинт-Xср инт
|
-5,25
|
-3,75
|
-2,25
|
-0,75
|
0,75
|
2,25
|
|
(Xинт-Xср инт)/Sи
|
-2,44
|
-1,74
|
-1,05
|
-0,35
|
0,35
|
1,05
|
|
F((Xинт-Xср инт)/Sи)
|
0,0167
|
0,0878
|
0,2541
|
0,3939
|
0,3271
|
0,1456
|
|
miтеор
|
0,26
|
1,39
|
4,02
|
6,23
|
5,17
|
2,30
|
4)
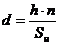
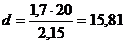
)
Найдем по таблице Пирсона
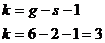
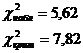
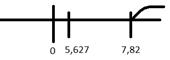
Вывод:
Гипотезу не отвергаем, т.к. не выходит за пределы
8.2 Используя критерий Пирсона, при уровне значимости a = 0,05 проверить, согласуется ли
гипотеза о нормальном распределении признака Y, представленного интервальным
рядом.
 инт = 80,77и = 1,95
инт = 80,77и = 1,95
1) Нулевая гипотеза: ГС распределена по нормальному закону
) a = 0,05
Таблица 10
|
Интервалы
|
(75,25-76,75]
|
(76,75-78,25]
|
(78,25-79,75]
|
(79,75-81,25]
|
(81,25-82,75]
|
(82,75-84,25)
|
|
Yинт
|
76
|
77,5
|
79
|
80,5
|
82
|
83,5
|
|
mi
|
2
|
1
|
2
|
7
|
1
|
7
|
|
Yинт-Yср инт
|
-4,87
|
-3,37
|
-1,87
|
-0,37
|
1,12
|
2,62
|
|
((Yинт-Yср инт)/Sи
|
-2
|
-1,38
|
-0,77
|
-0,15
|
0,46
|
1,08
|
|
F((Yинт-Yср инт)/Sи)
|
0,062
|
0,1804
|
0,3332
|
0,398
|
0,3056
|
0,1518
|
|
miтеор
|
0,82
|
2,39
|
4,42
|
5,28
|
4,05
|
2,01
|
4)
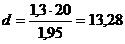
)
Найдем по таблице Пирсона
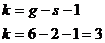
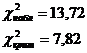
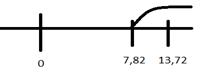
Вывод:
Гипотезу отвергаем, т.к. входит в пределы
4.
Корреляционный и регрессионный анализ (тема 10)
4.1
Корреляционная зависимость
Изучить:
а) виды зависимостей между признаками (функциональная, статистическая,
корреляционная);
б) двумерная случайная величина и ее числовые характеристики;
в) момент связи (ковариация) между составляющими X и Y двумерной
случайной величины;
г) коэффициент корреляции и его свойства;
д) выборочный коэффициент корреляции;
е) проверка гипотезы о значимости коэффициента корреляции генеральной
совокупности.
Корреляционный анализ (correlation analysis) [лат. correlatio -
соотношение] - раздел математической статистики, объединяющий практические
методы исследования корреляционной связи между двумя и более случайными
признаками или факторами.
Цель корреляционного анализа - обеспечить получение некоторой информации
об одной переменной с помощью другой переменной. В случаях, когда возможно
достижение цели, говорят, что переменные коррелируют. В самом общем виде
принятие гипотезы о наличии корреляции означает что изменение значения
переменной X, произойдет одновременно с пропорциональным изменением значения Y.
Если
зависимость между признаками на графике указывает на линейную корреляцию,
рассчитывают коэффициент корреляции 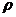 , который
позволяет оценить тесноту связи переменных величин, а также выяснить, какая
доля изменений признака обусловлена влиянием основного признака, какая -
влиянием других факторов. Коэффициент варьирует в пределах от -1 до +1. Если
, который
позволяет оценить тесноту связи переменных величин, а также выяснить, какая
доля изменений признака обусловлена влиянием основного признака, какая -
влиянием других факторов. Коэффициент варьирует в пределах от -1 до +1. Если 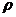 =0, то связь между признаками отсутствует. Равенство
=0, то связь между признаками отсутствует. Равенство 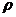 =0 говорит лишь об отсутствии линейной корреляционной
зависимости, но не вообще об отсутствии корреляционной, а тем более
статистической зависимости. Если
=0 говорит лишь об отсутствии линейной корреляционной
зависимости, но не вообще об отсутствии корреляционной, а тем более
статистической зависимости. Если 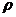 = ±1, то
это означает наличие полной (функциональной) связи. При этом все наблюдаемые значения
располагаются на линии регрессии, которая представляет собой прямую.
= ±1, то
это означает наличие полной (функциональной) связи. При этом все наблюдаемые значения
располагаются на линии регрессии, которая представляет собой прямую.
Практическая
значимость коэффициента корреляции определяется его величиной, возведенной в
квадрат, получившая название коэффициента детерминации.
Задание
9
.1
По выборке X и Y построить поле корреляции и выдвинуть предположение о
существовании (или не существовании) зависимости между признаками X и Y.
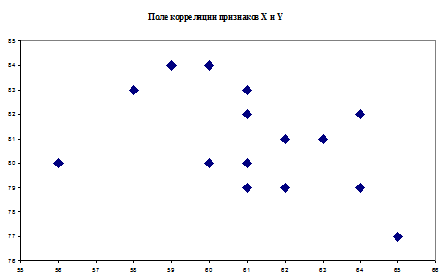
Рисунок
5
Из
рисунка 5 видно, что точки на графике расположены беспорядочно, соответственно
можно сделать такой вывод, что корреляционной зависимости между признаками X и Y
нет.
.2
Найти выборочный коэффициент корреляции и подтвердить (опровергнуть) вывод,
сделанный в пункте 9.1.
Данные
в корреляционной таблице представляют случайную выборку. Статистические
числовые характеристики (Sх,Sy), полученные по этой выборке, являются оценками параметров генеральной
совокупности, поэтому о тесноте зависимости между признаками X и Y мы
судим по величине оценки коэффициента корреляции 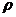 . Следует
проверить его значимость, т.е. установить - достаточна ли его величина при
данном объеме выборки (n=20) для вывода о наличии корреляционной зависимости
между признаками X и Y.
. Следует
проверить его значимость, т.е. установить - достаточна ли его величина при
данном объеме выборки (n=20) для вывода о наличии корреляционной зависимости
между признаками X и Y.
Выборочный
коэффициент корреляции рассчитывается по формуле:
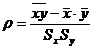
Таблица 11
|
№
|
X
|
Y
|
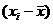 ( (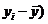 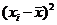 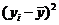 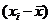 ( (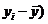
|
|
|
|
|
|
1
|
56
|
77
|
-5,3
|
-3,6
|
28,09
|
12,96
|
19,08
|
|
2
|
58
|
79
|
-3,3
|
-1,6
|
10,89
|
2,56
|
5,28
|
|
3
|
59
|
79
|
-2,3
|
-1,6
|
5,29
|
2,56
|
3,68
|
|
4
|
60
|
79
|
-1,3
|
-1,6
|
1,69
|
2,56
|
2,08
|
|
5
|
60
|
79
|
-1,3
|
-1,6
|
1,69
|
2,56
|
2,08
|
|
6
|
61
|
79
|
-0,3
|
-1,6
|
0,09
|
2,56
|
0,48
|
|
7
|
61
|
79
|
-0,3
|
-1,6
|
0,09
|
2,56
|
0,48
|
|
8
|
61
|
79
|
-0,3
|
-1,6
|
0,09
|
2,56
|
0,48
|
|
9
|
61
|
80
|
-0,3
|
-0,6
|
0,09
|
0,36
|
0,18
|
|
10
|
61
|
80
|
-0,3
|
-0,6
|
0,09
|
0,36
|
0,18
|
|
11
|
61
|
80
|
-0,3
|
-0,6
|
0,09
|
0,36
|
0,18
|
|
12
|
61
|
81
|
-0,3
|
0,4
|
0,09
|
0,16
|
-0,12
|
|
13
|
62
|
81
|
0,7
|
0,4
|
0,49
|
0,16
|
0,28
|
|
14
|
62
|
82
|
0,7
|
1,4
|
0,49
|
1,96
|
0,98
|
|
15
|
62
|
82
|
0,7
|
1,4
|
0,49
|
1,96
|
0,98
|
|
16
|
63
|
82
|
1,7
|
1,4
|
2,89
|
1,96
|
2,38
|
|
17
|
64
|
83
|
2,7
|
2,4
|
7,29
|
5,76
|
6,48
|
|
18
|
64
|
83
|
2,7
|
2,4
|
7,29
|
5,76
|
6,48
|
|
19
|
64
|
84
|
2,7
|
3,4
|
7,29
|
11,56
|
9,18
|
|
20
|
65
|
84
|
3,7
|
3,4
|
13,69
|
11,56
|
12,58
|
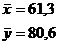
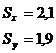
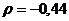
Так
как значение коэффициента корреляции очень мало, то можно подтвердить
предположение, сделанное в п. 9.1 и сказать, что связь слабая.
.3
Проверить гипотезу о значимости выборочного коэффициента корреляции
Проверим
значимость выборочного коэффициента корреляции 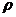 , т.е.
установим достаточна ли его величина при данном объеме выборки для
обоснованного вывода о наличии корреляционной связи.
, т.е.
установим достаточна ли его величина при данном объеме выборки для
обоснованного вывода о наличии корреляционной связи.
)
H0: 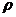 =0;
=0;
H1: 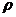
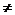 0
0
)
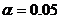 - уровень значимости.
- уровень значимости.
)
По распределению Стьюдента:
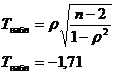
)
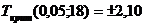 (двусторонняя критическая область)
(двусторонняя критическая область)
Вывод: Нулевая гипотеза не отвергается, т.е. между признаками X и Y отсутствует корреляционная зависимость.
4.2
Уравнение регрессии
Изучить:
а) понятие парной линейной регрессии;
б) составление системы нормальных уравнений;
в) свойства оценок по методу наименьших квадратов;
г) методику нахождения уравнения линейной регрессии.
Предположим, что между двумя признаками Х и У существует некоторая
взаимосвязь (корреляционная зависимость), при которой с изменением одного
признака изменяется и другой, но каждому значению признака Х могут
соответствовать разные, заранее непредсказуемые значения признака У, и
наоборот.
Основная задача корреляционного анализа состоит в выявлении связи между
случайными переменными путем точечной и интервальной оценок различных (парных,
множественных, частных) коэффициентов корреляции Дополнительная задача
корреляционного анализа (являющаяся основной в регрессионном анализе) заключается
в оценке уравнений регрессии одной переменной по другой.
Связь между признаками бывает положительной и отрицательной.
Если с увеличением (уменьшением) одного признака в основном увеличиваются
(уменьшаются) значения другого, то такая корреляционная связь называется прямой
или положительной.
Если с увеличением (уменьшением) одного признака в основном уменьшаются
(увеличиваются) значения другого, то такая корреляционная связь называется
обратной или отрицательной.
Задание 10
10.1 Предположив, что между признаками X и Y существует линейная
зависимость, найти коэффициенты уравнения регрессии Y на X и записать уравнение
в виде y = b0 + b1x.
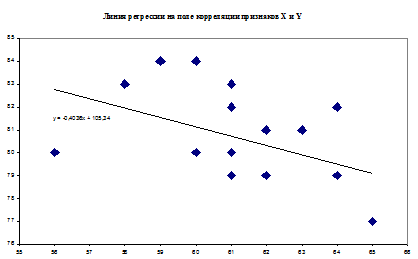
Рисунок 6.
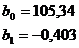
Заключение
Итак, статистические ряды распределения представляют собой один из
наиболее важных элементов статистического исследования.
Статистические ряды распределения являются базисным методом для любого
статистического анализа.
Статистический ряд распределения представляет собой упорядоченное
распределение единиц изучаемой совокупности на группы по определенному
варьирующему признаку, характеризует структуру изучаемого явления. Анализируя
рассчитанные показатели статистического ряда распределения, можно делать выводы
об однородности или неоднородности совокупности, закономерности распределения и
границах варьирования единиц совокупности. Изучив основные приемы исследования
и практики применения рядов распределения, а также методику вычисления наиболее
важных статистических величин, необходимо отметить, что конечная цель изучения
статистики в целом - анализ изучаемого явления - крайне важен для всех сфер
человеческой жизни. Анализ отображает явления в целом и вместе с этим учитывает
влияние каждого фактора в отдельности. На основании проведенного анализа можно
учитывать и прогнозировать факторы, негативно влияющие на развитие событий.
Социально-экономическая статистика обеспечивает предоставление важной
цифровой информации об уровне и возможностях развития страны: ее экономическом
положении, уровне жизни населения, его составе и численности, рентабельности
предприятий, динамике безработице и т.д. Статистическая информация является
одним из решающих ориентиров государственной экономической политики.
Список литературы
1. Гмурман
В.Е. Теория вероятностей и математическая статистика. - М.: Высшая школа, 2011.
- 479 с.
2. Гмурман
В.Е. Руководство к решению задач по теории вероятностей и математической
статистике. - М.: Высшая школа, 2004. - 400 с.
3. Вентцель
Е.С. Теория вероятностей. - М.: Издательский центр «Академия», 2010. - 576 с.
4. Вентцель
Е.С. Задачи и упражнения по теории вероятностей. - М.: Издательский центр
«Академия», 2005. - 448 с.
5. Бочаров
П.П., Печинкин А.В. Теория вероятностей и математическая статистика: Учебное пособие.
- М.: ФИЗМАТЛИТ 2005. - 296 с
. Вентцель
Е.С. Теория вероятностей и её инженерные приложения: Учебное пособие для вузов.
- М.: «Академия», 2009. - 432 с.
. Кибзун
А.И., Горяинова Е.Р., Наумов А.В. Теория вероятностей и математическая
статистика: Базовый курс с примерами и задачами. - М.: ФИЗМАТЛИТ, 2012. - 232
с.
. Гнеденко
Б.В. Курс теории вероятностей: Классический университетский учебник. - М.: ЛКИ,
2007. - 448 с.
. Кремер
Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. - М.:
ЮНИТИ ДАНА, 2009. - 551 с.
Приложение 1
Генеральная совокупность статистических данных по результатам
тестирования курсантов
|
№ п/п
|
X
|
Y
|
№ п/п
|
X
|
Y
|
№ п/п
|
X
|
Y
|
№ п/п
|
X
|
Y
|
№ п/п
|
X
|
Y
|
|
61
|
80
|
|
64
|
81
|
|
61
|
82
|
|
64
|
79
|
|
58
|
82
|
|
62
|
81
|
|
62
|
83
|
|
62
|
83
|
|
65
|
77
|
|
57
|
81
|
|
63
|
84
|
|
61
|
82
|
|
64
|
82
|
|
60
|
79
|
|
61
|
81
|
|
62
|
82
|
|
60
|
83
|
|
63
|
83
|
|
61
|
80
|
|
62
|
82
|
|
63
|
79
|
|
61
|
79
|
|
59
|
80
|
|
62
|
79
|
|
63
|
83
|
|
62
|
76
|
|
59
|
79
|
|
61
|
81
|
|
63
|
81
|
|
64
|
84
|
|
61
|
80
|
|
61
|
78
|
|
60
|
82
|
|
61
|
80
|
|
59
|
82
|
|
62
|
81
|
|
62
|
77
|
|
61
|
83
|
|
63
|
79
|
|
58
|
81
|
|
60
|
80
|
|
64
|
80
|
|
62
|
82
|
|
62
|
79
|
|
57
|
80
|
|
63
|
82
|
|
59
|
81
|
|
63
|
83
|
|
62
|
80
|
|
58
|
79
|
|
61
|
79
|
|
58
|
82
|
|
59
|
76
|
|
63
|
81
|
|
59
|
79
|
|
60
|
76
|
|
60
|
81
|
|
58
|
77
|
|
64
|
82
|
|
61
|
80
|
|
59
|
80
|
|
60
|
82
|
|
57
|
79
|
|
61
|
83
|
|
63
|
81
|
|
60
|
81
|
|
61
|
80
|
|
56
|
80
|
|
59
|
84
|
|
64
|
79
|
|
61
|
80
|
|
62
|
83
|
|
55
|
81
|
|
57
|
82
|
|
63
|
79
|
|
62
|
79
|
|
63
|
84
|
|
59
|
82
|
|
58
|
79
|
|
62
|
79
|
|
63
|
78
|
|
61
|
80
|
|
61
|
83
|
|
59
|
81
|
|
63
|
81
|
|
64
|
79
|
|
63
|
79
|
|
62
|
80
|
|
56
|
82
|
|
60
|
81
|
|
62
|
77
|
|
64
|
80
|
|
64
|
81
|
|
59
|
83
|
|
61
|
80
|
|
63
|
80
|
|
60
|
78
|
|
63
|
80
|
|
57
|
82
|
|
62
|
81
|
|
62
|
82
|
|
59
|
76
|
|
64
|
79
|
|
58
|
80
|
|
61
|
75
|
|
61
|
81
|
|
58
|
79
|
|
59
|
80
|
|
57
|
82
|
|
62
|
76
|
|
62
|
80
|
|
56
|
80
|
|
58
|
81
|
|
58
|
83
|
|
63
|
77
|
|
63
|
82
|
|
59
|
82
|
|
56
|
82
|
|
60
|
82
|
|
60
|
79
|
|
60
|
83
|
|
59
|
84
|
|
56
|
83
|
|
61
|
79
|
|
59
|
78
|
|
64
|
84
|
|
58
|
81
|
|
57
|
80
|
|
62
|
81
|
|
60
|
76
|
|
61
|
81
|
|
59
|
82
|
|
58
|
79
|
|
60
|
80
|
|
61
|
78
|
|
59
|
82
|
|
60
|
80
|
|
59
|
80
|
|
61
|
79
|
|
62
|
79
|
|
58
|
80
|
|
61
|
84
|
|
60
|
81
|
|
62
|
81
|
|
63
|
75
|
|
59
|
82
|
|
62
|
83
|
|
61
|
83
|
|
61
|
80
|
|
62
|
81
|
|
61
|
80
|
|
59
|
84
|
81
|
|
60
|
79
|
|
63
|
82
|
|
63
|
82
|
|
58
|
81
|
|
59
|
82
|
|
59
|
78
|
|
61
|
80
|
|
62
|
82
|
|
60
|
82
|
|
59
|
78
|
|
60
|
76
|
|
60
|
81
|
|
61
|
82
|
|
62
|
80
|
|
61
|
76
|
|
61
|
81
|
|
61
|
83
|
|
62
|
83
|
|
63
|
78
|
|
62
|
81
|
|
59
|
82
|
|
61
|
85
|
|
63
|
81
|
|
64
|
79
|
|
63
|
82
|
|
60
|
83
|
|
62
|
84
|
|
64
|
80
|
|
62
|
77
|
|
59
|
80
|
|
61
|
82
|
|
63
|
83
|
|
64
|
79
|
|
63
|
79
|
|
60
|
81
|
|
59
|
81
|
|
60
|
82
|
|
63
|
81
|
|
59
|
81
|
|
59
|
81
|
|
60
|
80
|
|
61
|
81
|
|
61
|
82
|
|
58
|
83
|
|
61
|
80
|
|
59
|
81
|
|
62
|
80
|
|
62
|
80
|
|
57
|
82
|
|
62
|
81
|
|
58
|
82
|
|
63
|
78
|
|
63
|
79
|
|
60
|
84
|
|
63
|
81
|
|
59
|
83
|
|
64
|
79
|
|
№ п/п
|
X
|
Y
|
№ п/п
|
X
|
Y
|
№ п/п
|
X
|
Y
|
№ п/п
|
X
|
Y
|
№ п/п
|
X
|
Y
|
|
61
|
81
|
|
61
|
84
|
|
60
|
81
|
|
63
|
83
|
|
63
|
83
|
|
62
|
83
|
|
62
|
80
|
|
61
|
80
|
|
62
|
82
|
|
59
|
81
|
|
63
|
82
|
|
63
|
78
|
|
62
|
81
|
|
60
|
83
|
|
60
|
80
|
|
64
|
79
|
|
64
|
79
|
|
61
|
79
|
|
58
|
82
|
|
62
|
81
|
|
62
|
80
|
|
62
|
81
|
|
60
|
78
|
|
61
|
79
|
|
64
|
82
|
|
63
|
79
|
|
61
|
79
|
|
63
|
77
|
|
63
|
78
|
|
63
|
79
|
|
64
|
82
|
|
59
|
80
|
|
59
|
79
|
|
62
|
81
|
|
64
|
82
|
|
63
|
83
|
|
62
|
78
|
|
58
|
82
|
|
59
|
80
|
|
64
|
83
|
|
64
|
84
|
|
59
|
77
|
|
57
|
81
|
|
58
|
81
|
|
63
|
81
|
|
61
|
82
|
|
58
|
79
|
|
59
|
83
|
|
59
|
83
|
|
61
|
79
|
|
62
|
80
|
|
58
|
80
|
|
62
|
85
|
|
62
|
82
|
401
|
60
|
77
|
|
63
|
79
|
|
59
|
82
|
|
63
|
84
|
|
63
|
83
|
|
|
|
|
64
|
77
|
|
60
|
83
|
|
62
|
82
|
|
64
|
84
|
|
|
|
|
60
|
76
|
|
62
|
84
|
|
61
|
79
|
|
62
|
83
|
|
|
|
|
61
|
77
|
|
63
|
80
|
|
62
|
78
|
|
61
|
82
|
|
|
|
|
62
|
76
|
|
61
|
79
|
|
63
|
80
|
|
62
|
81
|
|
|
|
|
63
|
75
|
|
62
|
78
|
|
64
|
83
|
|
63
|
81
|
|
|
|
|
60
|
76
|
|
63
|
79
|
|
61
|
84
|
|
64
|
79
|
|
|
|
|
61
|
79
|
|
64
|
82
|
|
62
|
83
|
|
63
|
83
|
|
|
|
|
62
|
81
|
|
62
|
81
|
|
63
|
84
|
|
62
|
82
|
|
|
|
|
63
|
83
|
|
63
|
82
|
|
64
|
83
|
|
59
|
77
|
|
|
|
|
60
|
82
|
|
62
|
81
|
|
63
|
82
|
|
58
|
78
|
|
|
|
|
61
|
83
|
|
63
|
82
|
|
64
|
81
|
|
59
|
79
|
|
|
|
|
62
|
81
|
|
62
|
83
|
|
65
|
80
|
|
61
|
82
|
|
|
|
|
63
|
80
|
|
61
|
83
|
|
62
|
|
63
|
83
|
|
|
|
|
64
|
81
|
|
60
|
84
|
|
63
|
78
|
|
65
|
81
|
|
|
|
|
60
|
80
|
|
62
|
84
|
|
61
|
79
|
|
64
|
80
|
|
|
|
|
61
|
81
|
|
61
|
85
|
|
60
|
82
|
|
63
|
81
|
|
|
|
|
62
|
83
|
|
62
|
81
|
|
58
|
83
|
|
62
|
83
|
|
|
|
|
63
|
84
|
|
63
|
80
|
|
59
|
84
|
|
61
|
80
|
|
|
|
|
64
|
85
|
|
64
|
83
|
|
60
|
85
|
|
62
|
79
|
|
|
|
|
60
|
85
|
|
60
|
82
|
|
61
|
82
|
|
64
|
80
|
|
|
|
|
62
|
84
|
|
61
|
81
|
|
62
|
81
|
|
60
|
78
|
|
|
|
|
60
|
83
|
|
62
|
80
|
|
64
|
79
|
|
59
|
76
|
|
|
|
|
63
|
82
|
|
63
|
81
|
|
63
|
76
|
|
58
|
77
|
|
|
|
|
64
|
83
|
|
64
|
79
|
|
64
|
76
|
|
57
|
78
|
|
|
|
|
61
|
82
|
|
65
|
78
|
|
60
|
78
|
|
59
|
79
|
|
|
|
|
63
|
76
|
|
64
|
77
|
|
62
|
79
|
|
62
|
81
|
|
|
|
|
62
|
78
|
|
62
|
79
|
|
64
|
82
|
|
63
|
83
|
|
|
|
|
61
|
79
|
|
63
|
81
|
|
65
|
81
|
|
64
|
85
|
|
|
|
|
63
|
80
|
|
61
|
83
|
|
61
|
80
|
|
63
|
84
|
|
|
|
|
64
|
81
|
|
62
|
84
|
|
62
|
79
|
|
64
|
85
|
|
|
|
|
65
|
83
|
|
61
|
82
|
|
63
|
79
|
|
60
|
85
|
|
|
|
|
64
|
82
|
|
62
|
81
|
|
64
|
81
|
|
61
|
82
|
|
|
|
|
62
|
85
|
|
61
|
80
|
|
64
|
82
|
|
62
|
84
|
|
|
|
Приложение 2
Значения случайных чисел для различных вариантов исходных
данных
|
№1
|
073
|
211
|
052
|
378
|
096
|
057
|
078
|
064
|
139
|
082
|
|
058
|
389
|
043
|
369
|
046
|
076
|
223
|
002
|
087
|
056
|
|
№2
|
268
|
070
|
329
|
128
|
002
|
083
|
341
|
265
|
074
|
052
|
|
094
|
053
|
212
|
096
|
043
|
089
|
333
|
008
|
039
|
077
|
|
№3
|
076
|
265
|
196
|
093
|
080
|
135
|
074
|
303
|
070
|
361
|
|
340
|
045
|
020
|
053
|
035
|
085
|
149
|
065
|
047
|
077
|
|
№4
|
100
|
375
|
084
|
099
|
128
|
325
|
048
|
068
|
025
|
097
|
|
076
|
064
|
196
|
313
|
080
|
135
|
074
|
303
|
070
|
361
|
|
№5
|
346
|
248
|
232
|
383
|
064
|
054
|
240
|
256
|
311
|
264
|
|
367
|
353
|
068
|
090
|
358
|
094
|
042
|
074
|
057
|
342
|
|
№6
|
174
|
177
|
066
|
142
|
050
|
080
|
077
|
214
|
291
|
068
|
|
058
|
045
|
043
|
369
|
046
|
076
|
223
|
002
|
087
|
056
|
|
№7
|
005
|
052
|
068
|
296
|
234
|
073
|
077
|
067
|
110
|
341
|
|
065
|
080
|
074
|
069
|
098
|
176
|
356
|
099
|
268
|
205
|
|
№8
|
073
|
211
|
045
|
076
|
096
|
057
|
078
|
064
|
139
|
082
|
|
002
|
143
|
268
|
094
|
054
|
165
|
053
|
026
|
056
|
145
|
|
№9
|
068
|
269
|
085
|
111
|
165
|
276
|
368
|
047
|
020
|
344
|
|
046
|
070
|
329
|
128
|
040
|
083
|
341
|
074
|
052
|
|
№10
|
291
|
128
|
087
|
259
|
341
|
085
|
135
|
151
|
065
|
165
|
|
125
|
376
|
092
|
362
|
281
|
047
|
073
|
220
|
149
|
304
|
|
№11
|
382
|
067
|
008
|
313
|
250
|
285
|
034
|
163
|
124
|
093
|
|
274
|
118
|
191
|
307
|
136
|
322
|
266
|
274
|
076
|
401
|
|
№12
|
221
|
050
|
137
|
367
|
291
|
158
|
045
|
043
|
369
|
046
|
|
040
|
268
|
170
|
067
|
089
|
076
|
203
|
102
|
187
|
156
|
|
№13
|
340
|
245
|
020
|
053
|
135
|
076
|
182
|
065
|
147
|
064
|
|
366
|
353
|
168
|
090
|
358
|
361
|
242
|
057
|
074
|
342
|
|
№14
|
198
|
118
|
045
|
068
|
099
|
177
|
254
|
163
|
040
|
167
|
|
111
|
234
|
186
|
083
|
352
|
291
|
097
|
88
|
256
|
243
|
|
№15
|
221
|
150
|
137
|
367
|
091
|
248
|
170
|
167
|
353
|
089
|
|
260
|
294
|
184
|
090
|
293
|
143
|
242
|
061
|
276
|
368
|
|
№16
|
186
|
273
|
284
|
260
|
398
|
143
|
085
|
165
|
287
|
203
|
|
366
|
353
|
068
|
190
|
358
|
361
|
242
|
257
|
074
|
342
|
|
№17
|
145
|
296
|
333
|
183
|
299
|
051
|
363
|
354
|
049
|
144
|
|
355
|
159
|
240
|
243
|
348
|
270
|
260
|
219
|
194
|
381
|
|
№18
|
346
|
248
|
232
|
383
|
032
|
054
|
240
|
125
|
311
|
366
|
|
076
|
064
|
196
|
093
|
080
|
135
|
074
|
303
|
070
|
361
|
|
№19
|
273
|
211
|
245
|
176
|
096
|
194
|
253
|
157
|
097
|
143
|
|
058
|
178
|
064
|
139
|
279
|
089
|
333
|
240
|
188
|
077
|
|
№20
|
366
|
353
|
068
|
290
|
358
|
361
|
042
|
157
|
074
|
342
|
|
221
|
050
|
137
|
367
|
091
|
340
|
170
|
167
|
268
|
189
|
|
№21
|
055
|
159
|
400
|
143
|
348
|
070
|
206
|
215
|
094
|
281
|
|
344
|
289
|
201
|
269
|
310
|
188
|
148
|
233
|
205
|
246
|
|
№22
|
080
|
206
|
159
|
088
|
198
|
091
|
104
|
347
|
174
|
168
|
|
065
|
186
|
073
|
284
|
060
|
398
|
074
|
085
|
287
|
203
|
|
№23
|
073
|
211
|
052
|
378
|
096
|
057
|
078
|
064
|
139
|
082
|
|
058
|
389
|
043
|
369
|
046
|
076
|
223
|
002
|
087
|
056
|
Приложение 3
Приложение 4
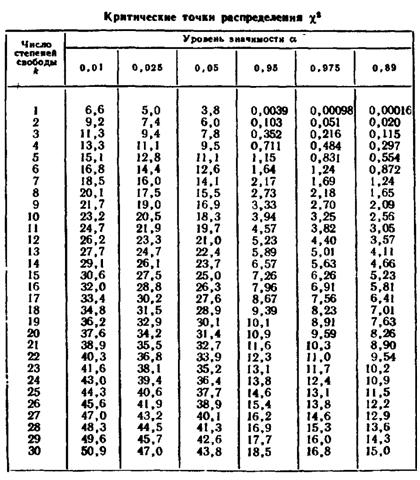
Приложение 5
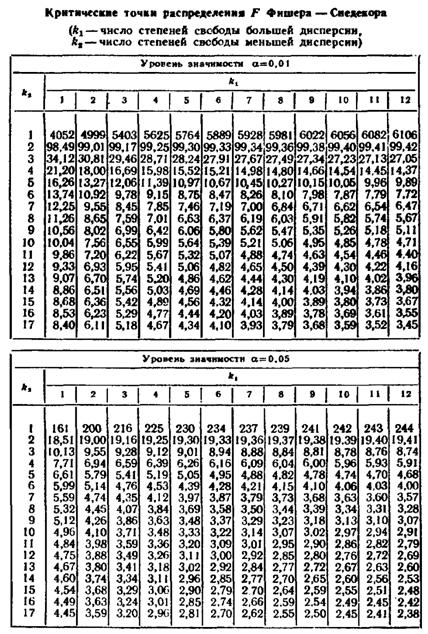
Приложение 6