Понятие предиката. Множество истинности предиката. Классификация предикатов
Курсовая работа
Понятие предиката.
Множество истинности предиката. Классификация предикатов
Введение
тьюринг вычислительный предикат
Алан Тьюринг (Turing) в 1936 году опубликовал в трудах
Лондонского математического общества статью «О вычислимых числах в приложении к
проблеме разрешения», которая наравне с работами Поста и Черча лежит в основе
современной теории алгоритмов.
Предыстория создания этой работы связана с формулировкой
Давидом Гильбертом на Международном математическом конгрессе в Париже в 1900
году неразрешенных математических проблем. Одной из них была задача
доказательства непротиворечивости системы аксиом обычной арифметики, которую
Гильберт в дальнейшем уточнил как «проблему разрешимости» - нахождение общего
метода, для определения выполнимости данного высказывания на языке формальной
логики.
Статья Тьюринга как раз и давала ответ на эту проблему -
вторая проблема Гильберта оказалась неразрешимой. Но значение статьи Тьюринга
выходило далеко за рамки той задачи, по поводу которой она была написана.
Приведем характеристику этой работы, принадлежащую Джону
Хопкрофту: «Работая над проблемой Гильберта, Тьюрингу пришлось дать четкое
определение самого понятия метода. Отталкиваясь от интуитивного представления о
методе как о некоем алгоритме, т.е. процедуре, которая может быть выполнена
механически, без творческого вмешательства, он показал, как эту идею можно
воплотить в виде подробной модели вычислительного процесса. Полученная модель
вычислений, в которой каждый алгоритм разбивался на последовательность простых,
элементарных шагов, и была логической конструкцией, названной впоследствии
машиной Тьюринга».
Алан Тьюринг высказал предположение, что любой алгоритм в
интуитивном смысле этого слова может быть представлен эквивалентной машиной
Тьюринга. Это предположение известно как тезис Черча-Тьюринга. Каждый компьютер
может моделировать машину Тьюринга (операции перезаписи ячеек, сравнения и
перехода к другой соседней ячейке с учетом изменения состояния машины).
Следовательно, он может моделировать алгоритмы в любом формализме, и из этого
тезиса следует, что все компьютеры (независимо от мощности, архитектуры и т.д.)
эквивалентны с точки зрения принципиальной возможности решения алгоритмических
задач.
За время своего существования человечество придумало
множество алгоритмов для решения разнообразных практических и научных проблем.
Утверждение о существовании алгоритмически неразрешимых проблем является весьма
сильным - мы констатируем, что мы не только сейчас не знаем соответствующего
алгоритма, но мы не можем принципиально никогда его найти.
Успехи математики к концу XIX века привели к формированию
мнения, которое выразил Д. Гильберт - «в математике не может быть неразрешимых
проблем», в связи с этим формулировка проблем Гильбертом на конгрессе 1900 года
в Париже была руководством к действию, констатацией отсутствия решений в данный
момент.
Первой фундаментальной теоретической работой, связанной с
доказательством алгоритмической неразрешимости, была работа Курта Гёделя - его
известная теорема о неполноте символических логик. Это была строго
формулированная математическая проблема, для которой не существует решающего ее
алгоритма. Усилиями различных исследователей список алгоритмически неразрешимых
проблем был значительно расширен. В частности, не существует алгоритма (машины
Тьюринга), позволяющего по описанию произвольного алгоритма и его исходных
данных (и алгоритм и данные заданы символами на ленте машины Тьюринга)
определить, останавливается ли этот алгоритм на этих данных или работает бесконечно.
Фундаментально алгоритмическая неразрешимость связана с
бесконечностью выполняемых алгоритмом действий, т.е. невозможностью
предсказать, что для любых исходных данных решение будет получено за конечное
количество шагов.
Раскрытие вопроса - что такое машина Тьюринга, какие задачи
можно решать с ее помощью и каким образом, является целью данной курсовой
работы. Работа состоит введения, заключения, списка использованных источников и
двух глав. В первой - теоретической, вводится понятие машины Тьюринга, подробно
рассматривается принципы ее работы, раскрываются все основные моменты,
сопутствующие данному понятию: функций, вычислимых по Тьюрингу, эквивалентности
машины Тьюринга понятию «алгоритм», правила конструирования машин Тьюринга,
композиций машин Тьюринга и др. Во второй главе приведены решения задач,
реализованных на машинах Тьюринга.
1.
Машины Тьюринга
1.1
Определение машины Тьюринга
Введение понятия машины Тьюринга явилось одной из первых и
весьма удачных попыток дать точный математический эквивалент для общего
интуитивного представления об алгоритме. Это понятие названо по имени
английского математика, сформулировавшего его в 1937 г., за 9 лет до появления
первой электронно-вычислительной машины.
Машина Тьюринга есть математическая (воображаемая) машина, а
не машина физическая. Она есть такой же математический объект, как функция,
производная, интеграл, группа и. т.д. И, так же как и другие математические
понятия, понятие машины Тьюринга отражает объективную реальность, моделирует
некие реальные процессы. Именно Тьюринг предпринял попытку смоделировать
действия математика (или другого человека), осуществляющего некую умственную
созидательную деятельность. Такой человек, находясь в определенном
«умонастроении» («состоянии»), просматривает некоторый текст. Затем он вносит в
этот текст какие-то изменения, проникается новым «умонастроением» и переходит к
просмотру последующих записей.
Машина Тьюринга действует примерно так же. Ее удобно
представлять в виде автоматически работающего устройства. В каждый дискретный
момент времени устройство, находясь в некотором состоянии, обозревает
содержимое одной ячейки, протягиваемой через устройство ленты и делает шаг,
заключающийся в том, что устройство переходит в новое состояние, изменяет (или
оставляет без изменения) содержимое обозреваемой ячейки и переходит к обозрению
следующей ячейки - справа или слева. Причем шаг осуществляется на основании
предписанной команды. Совокупность всех команд представляет собой программу
машины Тьюринга.
Опишем теперь машину Тьюринга более тщательно. Машина
располагает конечным числом знаков (символов, букв), образующих так называемый
внешний алфавит А = {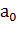 ,
,  , …,
, …, 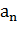 }. В каждую ячейку
обозреваемой ленты в каждый дискретный момент времени может быть записан только
один символ из алфавита А. Ради единообразия удобно считать, что среди букв
внешнего алфавита А имеется «пустая буква», и именно она записана в пустую
ячейку ленты. Условимся, что «пустой буквой» или символом пустой ячейки
является буква
}. В каждую ячейку
обозреваемой ленты в каждый дискретный момент времени может быть записан только
один символ из алфавита А. Ради единообразия удобно считать, что среди букв
внешнего алфавита А имеется «пустая буква», и именно она записана в пустую
ячейку ленты. Условимся, что «пустой буквой» или символом пустой ячейки
является буква 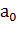 . Лента предполагается неограниченной в обе
стороны, но в каждый момент времени на ней записано конечное число непустых
букв.
. Лента предполагается неограниченной в обе
стороны, но в каждый момент времени на ней записано конечное число непустых
букв.
Далее, в каждый момент времени машина способна находиться в
одном состоянии из конечного числа внутренних состояний, совокупность которых Q = { ,
,  , …,
, …, 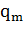 }. Среди состояний выделяются
два - начальное
}. Среди состояний выделяются
два - начальное  и заключительное (или состояние остановки)
и заключительное (или состояние остановки)  . Находясь в состоянии
. Находясь в состоянии  , машина начинает
работать. Попав в состояние
, машина начинает
работать. Попав в состояние  , машина останавливается.
, машина останавливается.
Работа машины определяется программой (функциональной схемой).
Программа состоит из команд. Каждая команда Т (i, j) (i=1,2,…, m; j=0,1, …, n) представляет собой
выражение одного из следующих видов:
 >
>  С;
С;  >
>  П;
П;  >
>  Л,
Л,
где 0 ≤ k ≤ m; 0≤ λ ≤ n. В выражениях первого
вида символ С будем часто опускать.
Как же работает машина Тьюринга? Находясь в какой-либо момент
времени в незаключительном состоянии (т.е. в состоянии, отличном от  ), машина совершает шаг,
который полностью определяется ее текущим состоянием
), машина совершает шаг,
который полностью определяется ее текущим состоянием  и символом
и символом 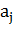 , воспринимаемым ею в
данный момент на ленте. При этом содержание шага регламентировано
соответствующей командой Т (i, j):
, воспринимаемым ею в
данный момент на ленте. При этом содержание шага регламентировано
соответствующей командой Т (i, j):  >
>  X, где Х
X, где Х  {С, П, Л}. Шаг
заключается в том, что:
{С, П, Л}. Шаг
заключается в том, что:
) содержимое 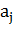 обозреваемой на ленте ячейки стирается и на его
место записывается символ
обозреваемой на ленте ячейки стирается и на его
место записывается символ 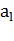 (который может совпадать с
(который может совпадать с 
) машина переходит в новое состояние 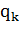 (оно также может
совпадать с предыдущем состоянием
(оно также может
совпадать с предыдущем состоянием  );
);
) машина переходит к обозрению следующей правой ячейки от
той, которая обозревалась только что, если Х=П, или к обозрению следующей левой
ячейки, если Х=Л, или же продолжает обозревать ту же ячейку ленты, если Х = С.
В следующий момент времени (если 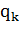 ≠
≠  ) машина делает шаг,
регламентированный командой Т (k, l):
) машина делает шаг,
регламентированный командой Т (k, l):  →
→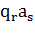 Х и т.д.
Х и т.д.
Поскольку работа машины, по условию, полностью определяется
ее состоянием  в данный момент и содержимым
в данный момент и содержимым 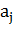 обозреваемой в этот
момент ячейки, то для каждых
обозреваемой в этот
момент ячейки, то для каждых  и
и 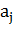 (i=1, 2, …, m; j=0, 1, …, n) программа машины должна
содержать одну и только одну команду, начинающуюся символами
(i=1, 2, …, m; j=0, 1, …, n) программа машины должна
содержать одну и только одну команду, начинающуюся символами  . Поэтому программа
машины Тьюринга с внешним алфавитом А={
. Поэтому программа
машины Тьюринга с внешним алфавитом А={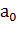 ,
,  , …,
, …, 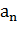 } и алфавитом внутренних
состояний Q
={
} и алфавитом внутренних
состояний Q
={ ,
,  , …,
, …, 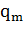 } содержит m (n+1) команд.
} содержит m (n+1) команд.
Словом в алфавите А или в алфавите Q, или в алфавите A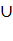 Q называется любая
последовательность букв соответствующего алфавита. Под k-й конфигурацией будем
понимать изображение ленты машины с информацией, сложившейся на ней к началу k-го шага (или слово в
алфавите А, записанное на ленту к началу k-го шага), с указанием
того, какая ячейка обозревается в этот шаг и в каком состоянии находится
машина. Имеют смысл лишь конечные конфигурации, т.е. такие, в которых все
ячейки ленты, за исключением, быть может, конечного числа, пусты. Конфигурация
называется заключительной, если состояние, в котором при этом находится машина,
заключительное.
Q называется любая
последовательность букв соответствующего алфавита. Под k-й конфигурацией будем
понимать изображение ленты машины с информацией, сложившейся на ней к началу k-го шага (или слово в
алфавите А, записанное на ленту к началу k-го шага), с указанием
того, какая ячейка обозревается в этот шаг и в каком состоянии находится
машина. Имеют смысл лишь конечные конфигурации, т.е. такие, в которых все
ячейки ленты, за исключением, быть может, конечного числа, пусты. Конфигурация
называется заключительной, если состояние, в котором при этом находится машина,
заключительное.
Если выбрать какую-либо незаключительную конфигурацию машины
Тьюринга в качестве исходной, то работа машины будет состоять в том, чтобы
последовательно (шаг за шагом) преобразовывать исходную конфигурацию в
соответствии с программой машины до тех пор, пока не будет достигнута
заключительная конфигурация. После этого работа машины Тьюринга считается
закончившейся, а результатом работы считается достигнутая заключительная
конфигурация.
Будем говорить, что непустое слово ɑ в алфавите А\ {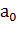 }=
}= , …,
, …, 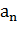 } воспринимается машиной
в стандартном положении, если оно записано в последовательных ячейках ленты,
все другие ячейки пусты, и машина обозревает крайнюю справа ячейку из тех, в
которых записано слово ɑ. Стандартное положение называется начальным
(заключительным), если машина, воспринимающая слово в стандартном положении,
находится в начальном состоянии
} воспринимается машиной
в стандартном положении, если оно записано в последовательных ячейках ленты,
все другие ячейки пусты, и машина обозревает крайнюю справа ячейку из тех, в
которых записано слово ɑ. Стандартное положение называется начальным
(заключительным), если машина, воспринимающая слово в стандартном положении,
находится в начальном состоянии  (соответственно в состоянии остановки
(соответственно в состоянии остановки  ). Наконец, будем
говорить, что слово ɑ перерабатывается машиной в слово b, если от слова ɑ,
воспринимаемого в начальном стандартном положении, машина после выполнения
конечного числа команд приходит к слову b, воспринимаемому в
положении остановки.
). Наконец, будем
говорить, что слово ɑ перерабатывается машиной в слово b, если от слова ɑ,
воспринимаемого в начальном стандартном положении, машина после выполнения
конечного числа команд приходит к слову b, воспринимаемому в
положении остановки.
1.2
Применение машин Тьюринга к словам
Проиллюстрируем на примерах все введенные понятия, связанные
с машинами Тьюринга.
Пример 2.1. Дана машина Тьюринга с внешним алфавитом
А={0,1} (здесь 0-символ пустой ячейки), алфавитом внутренних состояний Q={ ,
,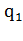 ,
,  } и со следующей
функциональной схемой (программой):
} и со следующей
функциональной схемой (программой):
 0→
0→ 0П;
0П;  0→
0→ 1;
1;  1→
1→ 1П;
1П;  1→
1→ 1→
1→ 1П.
1П.
Посмотрим, в какое слово переработает эта машина слово 101,
исходя из стандартного начального положения. Будем последовательно выписывать
конфигурации машины при переработке ею этого слова. Имеем стандартное начальное
положение.
Таким образом, исходное слово 101 переработано машиной в
слово 10101.
Полученную последовательность конфигураций можно записать
более коротким способом. Конфигурация (1) записывается в виде следующего слова
в алфавите А Q: 10
Q: 10 1 (содержимое обозреваемой ячейки записано справа
от состояния, в котором находится в данный момент машина). Далее, конфигурация
(2) записывается так: 101
1 (содержимое обозреваемой ячейки записано справа
от состояния, в котором находится в данный момент машина). Далее, конфигурация
(2) записывается так: 101 0, конфигурация (3) - 1010
0, конфигурация (3) - 1010 0 и, наконец, (4) - 1010
0 и, наконец, (4) - 1010 1. Вся последовательность
записывается так:
1. Вся последовательность
записывается так:
 1 => 101
1 => 101 0 => 1010
0 => 1010 0 => 1010
0 => 1010 1.
1.
Приведем последовательность конфигураций при переработке этой
машиной слова 11011, исходя из начального положения, при котором в состоянии  обозревается крайняя
левая ячейка, в которой содержится символ этого слова (самостоятельно
проанализируйте каждый шаг работы машины, указывая, какая команда обусловила
его).
обозревается крайняя
левая ячейка, в которой содержится символ этого слова (самостоятельно
проанализируйте каждый шаг работы машины, указывая, какая команда обусловила
его).
Более короткая запись этой последовательности конфигураций,
т.е. процесса работы машины, будет
 11011=>1
11011=>1 1011=>11
1011=>11 011=>110
011=>110 11=>1101
11=>1101 1=>11011
1=>11011 0=>11011
0=>11011 1.
1.
Таким образом, слово 11011 переработано машиной в слово
110111.
Пример 2.2. Машина Тьюринга задается внешним
алфавитом А={0,1, *} (как и в предыдущем примере 0 - символ пустой ячейки),
алфавитом внутренних состояний Q={ ,
,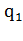 ,
,  ,
,  } и программой:
} и программой:
 0→
0→ 0Л,
0Л,  0→
0→ 1П,
1П,  0→
0→ 0Л,
0Л,  1→
1→ 0Л,
0Л,  1→
1→ 1Л,
1Л,  1→
1→ 1П,
1П,  *→
*→ 0,
0,  *→
*→ *Л,
*Л,  *→
*→ *П.
*П.
Посмотрим, как эта машина перерабатывает некоторые слова, и
постараемся обнаружить закономерность в ее работе.
Предварительно заметим, что программа машины может быть
записана также в виде следующей таблицы:
Чтобы определить по таблице, что будет делать машина,
находясь, например, в состоянии  и наблюдая в обозреваемой ячейке символ 1, нужно
найти в таблице клетку, находящуюся на пересечении столбца
и наблюдая в обозреваемой ячейке символ 1, нужно
найти в таблице клетку, находящуюся на пересечении столбца  и строки, содержащей 1.
В этой клетке записано
и строки, содержащей 1.
В этой клетке записано  1Л. Это означает, что на следующем шаге машина
останется в прежнем состоянии
1Л. Это означает, что на следующем шаге машина
останется в прежнем состоянии  , сохранит содержимое обозреваемой ячейки 1 и
перейдет к обозрению следующей левой ячейки на ленте.
, сохранит содержимое обозреваемой ячейки 1 и
перейдет к обозрению следующей левой ячейки на ленте.
Применим эту машину к слову 11*11. Вот последовательность
конфигураций, возникающих в процессе работы машины (исходная конфигурация -
стандартная начальная):
*1 1=> 11*
1=> 11* 10=> 11
10=> 11 *10=> 1
*10=> 1 1*10=>
1*10=>  11*10=>
11*10=>  011*10=>
011*10=>  11*10=> 11
11*10=> 11 1*10=> 111
1*10=> 111 *10=> 111*
*10=> 111* 10=> 111*1
10=> 111*1 0=> 111*
0=> 111* 10=> 111
10=> 111 *00=> 11
*00=> 11 1*0=> 1
1*0=> 1 11*0=>
11*0=>  111*0=>
111*0=>  0111*0=> 1
0111*0=> 1 111*0=> 11
111*0=> 11 11*0=> 111
11*0=> 111 1*0=> 1111
1*0=> 1111 *0=> 1111*
*0=> 1111* 0=> 1111
0=> 1111 *0=> 1111
*0=> 1111 00.
00.
Предлагается проверить самостоятельно, что данная машина
Тьюринга осуществляет следующие преобразования конфигураций:
* 1=> 111
1=> 111 0; 1*111
0; 1*111 1=> 11111
1=> 11111 0; 11*11
0; 11*11 1=> 11111
1=> 11111 0; 11111*1
0; 11111*1 1=> 1111111
1=> 1111111 0.
0.
Нетрудно заметить, что данная машина Тьюринга реализует
операцию сложения: в результате ее работы на ленте записано подряд столько
единиц, сколько их было всего записано по обе стороны от звездочки перед
началом работы машины.
Этот маленький опыт работы с машинами Тьюринга позволяет
сделать некоторые выводы. Так тщательно описанное устройство этой машины
(разбитая на ячейки лента, считывающая головка) по существу не имеет никакого
значения. Машина Тьюринга - не что иное, как некоторое правило (алгоритм) для
преобразования слов алфавита A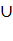 Q, т.е. конфигураций. Таким образом, для определения машины
Тьюринга нужно задать ее внешний и внутренний алфавиты, программу и указать,
какие из символов обозначают пустую ячейку и заключительное состояние.
Q, т.е. конфигураций. Таким образом, для определения машины
Тьюринга нужно задать ее внешний и внутренний алфавиты, программу и указать,
какие из символов обозначают пустую ячейку и заключительное состояние.
.3
Конструирование машин Тьюринга
Создание (синтез) машин Тьюринга (т.е. написание
соответствующих программ) является задачей значительно более сложной, нежели
процесс применения данной машины к данным словам.
Пример 3.1. Построим такую машину Тьюринга, которая
из n записанных подряд единиц
оставляла бы на ленте n-2 единицы, также записанные подряд, если n ≥ 2, и работала бы
вечно, если n=0
или n=1.
В качестве внешнего алфавита возьмем двухэлементное множество
A={0, 1}. Количество
необходимых внутренних состояний будет определено в процессе составления
программы. Считаем, что машина начинает работать из стандартного начального
положения, т.е. когда в состоянии  обозревается крайняя
правая единица из n, записанных на ленте.
обозревается крайняя
правая единица из n, записанных на ленте.
Начнем с того, что сотрем первую единицу, если она имеется,
перейдем к обозрению следующей левой ячейки и сотрем там единицу, если она в этой
ячейке записана. На каждом таком переходе машина должна переходить в новое
внутреннее состояние, ибо в противном случае будут стерты вообще все единицы,
записанные подряд. Вот команды, осуществляющие описанные действия:
 1 →
1 →  0Л;
0Л;  1 →
1 →  0Л.
0Л.
Машина находится в состоянии  и обозревает третью
справа ячейку из тех, в которых записано данное слово (n единиц). Не меняя
содержимого обозреваемой ячейки, машина должна остановиться, т.е. перейти в
заключительное состояние
и обозревает третью
справа ячейку из тех, в которых записано данное слово (n единиц). Не меняя
содержимого обозреваемой ячейки, машина должна остановиться, т.е. перейти в
заключительное состояние  , независимо от содержимого ячейки. Вот эти
команды:
, независимо от содержимого ячейки. Вот эти
команды:
 0 →
0 →  0;
0;  1 →
1 →  1.
1.
Теперь остается рассмотреть ситуации, когда на ленте записана
всего одна единица или не записано ни одной. Если на ленте записана одна
единица, то после первого шага (выполнив команду  1 →
1 →  0Л) машина будет
находиться в состоянии
0Л) машина будет
находиться в состоянии  и будет обозревать вторую справа ячейку, в
которой записан 0. По условию, в таком случае машина должна работать вечно. Это
можно обеспечить, например, такой командой:
и будет обозревать вторую справа ячейку, в
которой записан 0. По условию, в таком случае машина должна работать вечно. Это
можно обеспечить, например, такой командой:
 0 →
0 → 0П,
0П,
выполняя которую шаг за шагом, машина будет двигаться по
ленте неограниченно вправо (или протягивать ленту через считывающую головку
справа налево). Наконец, если на ленте не записано ни одной единицы, то машина,
по условию, также должна работать вечно. В этом случае в начальном состоянии  обозревается ячейка с
содержимым 0, и вечная работа машины обеспечивается следующей командой:
обозревается ячейка с
содержимым 0, и вечная работа машины обеспечивается следующей командой:
 0 →
0 →  0П.
0П.
В заключение отметим следующее. Созданная нами машина
Тьюринга может применяться не только к словам в алфавите А={0,1},
представляющим собой записанные подряд n единиц (n ≥ 2). Она применима
и ко многим другим словам в этом алфавите, например к словам: 1011, 10011,
111011, 11011, 1100111, 1001111, 10111, 10110111, 10010111 и т.д. (исходя из
стандартного начального положения). С другой стороны, построенная машина не
применима (т.е. при подаче этих слов на вход машины она работает вечно) не
только к слову «1» или к слову, состоящему из одних нулей. Она не применима и к
следующим словам: 101, 1001, 11101, 101101, 1100101101 и т.д.
1.4
Вычислимые по Тьюрингу функции
Определение 4.1: Функция называется
вычислимой по Тьюрингу, если существует машина Тьюринга, вычисляющая ее, т.е.
такая машина Тьюринга, которая вычисляет ее значения для тех наборов значений
аргументов, для которых функция определена, и работающая вечно, если функция
для данного набора значений аргументов не определена.
Остается договориться о некоторых условностях для того, чтобы
это определение стало до конца точным. Во-первых, напомним, что речь идет о
функциях (или возможно о частичных функциях, т.е. не всюду определенных),
заданных на множестве натуральных чисел и принимающих также натуральные
значения. Во-вторых, нужно условиться, как записывать на ленте машины Тьюринга
значения 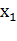 ,
, 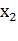 , …,
, …,  аргументов функции f (
аргументов функции f ( ,
, 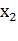 , …,
, …,  ), из какого положения
начинать переработку исходного слова и, наконец, в каком положении получать
значение функции. Это можно делать, например, следующим образом. Значения
), из какого положения
начинать переработку исходного слова и, наконец, в каком положении получать
значение функции. Это можно делать, например, следующим образом. Значения 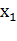 ,
, 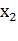 , …,
, …,  аргументов будем
располагать на ленте в виде следующего слова:
аргументов будем
располагать на ленте в виде следующего слова:
 0
0 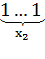 0 … 0
0 … 0  0.
0.
Здесь полезно ввести следующие обозначения. Для натурального x обозначаем:
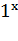 =
= 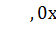 =
=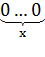 .
.
Дополнительно полагаем 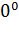 =
=  = Ʌ - пустое слово.
Так что на слова
= Ʌ - пустое слово.
Так что на слова  = Ʌ,
= Ʌ, 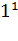 =1,
=1,  = 11,
= 11,  = 111, … будем смотреть
как на «изображения» натуральных чисел 0, 1, 2, 3, … соответственно. Таким
образом, предыдущее слово можно представить следующим образом:
= 111, … будем смотреть
как на «изображения» натуральных чисел 0, 1, 2, 3, … соответственно. Таким
образом, предыдущее слово можно представить следующим образом: 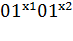 0…
0… 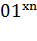 0. Далее, начинать
переработку данного слова будем из стандартного начального положения, т.е. из
положения, при котором в состоянии
0. Далее, начинать
переработку данного слова будем из стандартного начального положения, т.е. из
положения, при котором в состоянии  обозревается крайняя
правая единица записанного слова. Если функция f (
обозревается крайняя
правая единица записанного слова. Если функция f ( ,
, 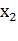 , …,
, …,  ) определена на данном
наборе значений аргументов, то в результате на ленте должно быть записано
подряд f
(
) определена на данном
наборе значений аргументов, то в результате на ленте должно быть записано
подряд f
( ,
, 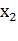 , …,
, …,  ) единиц; в противном
случае машина должна работать бесконечно. При выполнении всех перечисленных
условий будем говорить, что машина Тьюринга вычисляет данную функцию. Таким
образом, сформулированное определение становиться абсолютно строгим.
) единиц; в противном
случае машина должна работать бесконечно. При выполнении всех перечисленных
условий будем говорить, что машина Тьюринга вычисляет данную функцию. Таким
образом, сформулированное определение становиться абсолютно строгим.
Пример 4.1. Построим машину Тьюринга, вычисляющую
функцию f(x)= x/2. Эта функция не всюду
определена: областью ее определения является лишь множество всех четных чисел.
Поэтому, учитывая определение 4.1, нужно сконструировать такую машину Тьюринга,
которая при подаче на ее вход четного числа давала бы на входе половину этого
числа, а при подаче нечетного - работала бы неограниченно долго.
Сконструировать машину Тьюринга - значит написать (составить)
ее программу. В этом процессе два этапа: сначала создается алгоритм вычисления
значений функции, а затем он записывается на языке машины Тьюринга
(программируется).
В качестве внешнего алфавита возьмем двухэлементное множество
A={0,1}. В этом алфавите
натуральное число x изображается словом 11…1, состоящим из x единиц, которое на ленте
машины Тьюринга записывается в виде х единиц, состоящих в ячейках подряд.
Работа машины начинается из стандартного начального положения: 01…1 10 (число единиц равно
х).
10 (число единиц равно
х).
Сделаем начало вычислительного процесса таким: машина
обозревает ячейки, двигаясь справа налево, и каждую вторую единицу превращает в
0. Такое начало обеспечивается следующими командами:
(1):  1 →
1 →  1Л;
1Л;
(2):  1 →
1 →  0Л;
0Л;
(3):  0 →
0 →  0Л.
0Л.
Если число х единиц нечетно, то машина продолжит движение по
ленте влево неограниченно, т.е. будет работать бесконечно. Если же число х
единиц четно, то в результате выполнения команд создается конфигурация  0010101…01010, в которой
число единиц равно х/2. Остается сдвинуть единицы так, чтобы между ними не
стояли нули. Для осуществления этой процедуры предлагается следующий алгоритм.
Будем двигаться по ленте вправо, ничего на ней не меняя, до первой единицы и
перейдем за единицу. Передвижение осуществляется с помощью следующих команд:
0010101…01010, в которой
число единиц равно х/2. Остается сдвинуть единицы так, чтобы между ними не
стояли нули. Для осуществления этой процедуры предлагается следующий алгоритм.
Будем двигаться по ленте вправо, ничего на ней не меняя, до первой единицы и
перейдем за единицу. Передвижение осуществляется с помощью следующих команд:
(4):  0 →
0 →  0П;
0П;
(5):  0 →
0 →  0П;
0П;
(6):  1 →
1 → 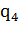 1П.
1П.
В результате их выполнения получим конфигурацию
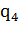 010101…010100. (*)
010101…010100. (*)
Заметим 0, перед которым остановились, на 1 и продвинемся
вправо до ближайшего 0:
(7): 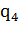 0 →
0 → 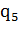 1П;
1П;
(8): 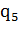 1 →
1 → 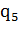 1П.
1П.
Получим конфигурацию 00111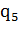 0101…010100, в которой
правее обозреваемой ячейки записаны «пары» 01, …, 01. Кроме того, на ленте одна
единица записана лишняя. Продвинемся по ленте вправо до последней «пары» 01.
Это можно сделать с помощью своеобразного цикла:
0101…010100, в которой
правее обозреваемой ячейки записаны «пары» 01, …, 01. Кроме того, на ленте одна
единица записана лишняя. Продвинемся по ленте вправо до последней «пары» 01.
Это можно сделать с помощью своеобразного цикла:
(9): 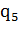 0 →
0 → 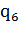 0П;
0П;
(10): 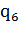 1 →
1 → 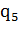 1П.
1П.
Получим конфигурацию 001110101…01010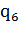 00. Двигаться дальше
вправо бессмысленно. Вернемся на две ячейки назад и заменим единицу из
последней «пары» 01 на ноль:
00. Двигаться дальше
вправо бессмысленно. Вернемся на две ячейки назад и заменим единицу из
последней «пары» 01 на ноль:
(11): 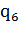 0 →
0 →  0Л;
0Л;
(12):  0 →
0 →  0Л;
0Л;
(13):  1 →
1 → 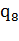 0Л.
0Л.
Получим конфигурацию 001110101…01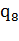 00. Число единиц на ленте
снова равно х/2. Продвинемся влево на одну ячейку с помощью команды
00. Число единиц на ленте
снова равно х/2. Продвинемся влево на одну ячейку с помощью команды
(14): 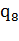 0 →
0 → 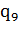 0Л.
0Л.
В результате чего получим конфигурацию 001110101…010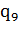 100. Теперь уничтожим
самую правую единицу и продвинемся по ленте влево до следующей единицы:
100. Теперь уничтожим
самую правую единицу и продвинемся по ленте влево до следующей единицы:
(15): 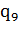 1 →
1 →  0Л;
0Л;
(16):  0 →
0 →  0Л.
0Л.
Получим конфигурацию
…0 100, (**)
100, (**)
в которой левее обозреваемой ячейки записана серия пар 10,
10, …, 10 (если читать справа налево). Теперь на ленте недостает одной единицы,
т.е. число единиц равно (х/2) - 1. Продвинемся по ленте влево до последней
«пары» 10. Это можно сделать с помощью цикла
(17):  1 →
1 → 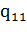 1Л;
1Л;
(18): 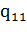 0 →
0 →  0Л,
0Л,
выполнив который, придем к следующей конфигурации: 001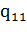 110101…0100. Вернемся
вправо к ближайшему нулю и превратим его в единицу:
110101…0100. Вернемся
вправо к ближайшему нулю и превратим его в единицу:
(19): 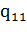 1 →
1 → 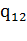 1П;
1П;
(20): 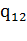 1 →
1 → 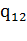 1П;
1П;
(21): 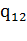 0 →
0 →  1П.
1П.
Получим конфигурацию 001111 101…0100, в которой число
единиц снова равно х/2.
101…0100, в которой число
единиц снова равно х/2.
Если теперь перешагнем вправо по ленте через обозреваемую
единицу и переведем машину в состояние 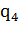 с помощью команды
с помощью команды
(22):  1 →
1 → 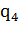 1П,
1П,
то придем к следующей конфигурации: 0011111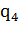 01…0100, которая по
существу аналогична конфигурации (*). В результате программа зацикливается
(становится циклической): снова ближайший 0 превращается в 1, а самая правая 1
- в 0, затем машина возвращается к самому левому нулю, оказываясь в начале
следующего цикла, и т.д.
01…0100, которая по
существу аналогична конфигурации (*). В результате программа зацикливается
(становится циклической): снова ближайший 0 превращается в 1, а самая правая 1
- в 0, затем машина возвращается к самому левому нулю, оказываясь в начале
следующего цикла, и т.д.
Как же завершается работа программы? В некоторый момент
конфигурация будет иметь вид 00111…1110 100. Выполнив команды
(17), (18), придем к конфигурации 00111…1
100. Выполнив команды
(17), (18), придем к конфигурации 00111…1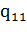 110100. Далее выполняются
команды (19), (20), (21), что приводит к конфигурации: 00111…111111
110100. Далее выполняются
команды (19), (20), (21), что приводит к конфигурации: 00111…111111 00. Остается остановить
машину. Это делается с помощью команды
00. Остается остановить
машину. Это делается с помощью команды
(23):  0 →
0 →  0Л.
0Л.
Заключительная конфигурация имеет вид: 00111…1111 100.
100.
1.5
Правильная вычислимость функций на машине Тьюринга
В предыдущем параграфе мы рассмотрели, каким образом «данная
машина Тьюринга вычисляет функцию f ( ,
, 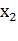 , …,
, …,  )». Для этого нужно,
чтобы каждое из чисел
)». Для этого нужно,
чтобы каждое из чисел 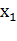 ,
, 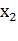 , …,
, …,  было записано на ленту
машины непрерывным массивом из соответствующего числа единиц, а сами массивы
были разделены символом 0. Если функция f (
было записано на ленту
машины непрерывным массивом из соответствующего числа единиц, а сами массивы
были разделены символом 0. Если функция f ( ,
, 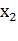 , …,
, …, 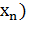 определена на данном
наборе значений аргументов, то в результате на ленте должно быть записано
подряд f
(
определена на данном
наборе значений аргументов, то в результате на ленте должно быть записано
подряд f
( ,
, 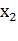 , …,
, …,  ) единиц. При этом мы не
очень строго относились к тому, в каком начальном положении машина начинает
работать (часто это было стандартное начальное положение), в каком завершает
работу и как эта работа протекает.
) единиц. При этом мы не
очень строго относились к тому, в каком начальном положении машина начинает
работать (часто это было стандартное начальное положение), в каком завершает
работу и как эта работа протекает.
В дальнейшем нам понадобится более сильное понятие
вычислимости функции на машине Тьюринга - понятие правильной вычислимости.
Определение 5.1: Будем говорить, что
машина Тьюринга правильно вычисляет функцию f ( ,
, 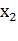 , …,
, …,  ), если начальное слово
), если начальное слово  0…
0…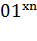 0 она переводит в слово
0 она переводит в слово  0…0 и при этом в процессе
работы не пристраивает к начальному слову новых ячеек на ленте ни слева, ни
справа. Если же функция f не определена на данном наборе значений аргументов, то,
начав работать из указанного положения, она никогда в процессе работы не будет
надстраивать ленту слева.
0…0 и при этом в процессе
работы не пристраивает к начальному слову новых ячеек на ленте ни слева, ни
справа. Если же функция f не определена на данном наборе значений аргументов, то,
начав работать из указанного положения, она никогда в процессе работы не будет
надстраивать ленту слева.
Пример 5.1. Приведем программы машин Тьюринга,
правильно вычисляющих функции S(x) = x+1 и O(x)
= 0. Функция S(x) = x+1 осуществляет перевод:  0 =>
0 => 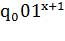 . Ее программа:
. Ее программа:  0 →
0 →  П,
П,  1 →
1 →  1П,
1П,  0 →
0 →  1,
1,  1 →
1 →  1Л,
1Л,  0 →
0 →  0. Функция O(x) = 0 осуществляет
перевод:
0. Функция O(x) = 0 осуществляет
перевод:  0 =>
0 =>  . Ее программа:
. Ее программа:  0 →
0 →  0П,
0П,  1 →
1 →  1П,
1П,  0 →
0 →  0Л,
0Л,  1 →
1 → 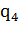 0,
0, 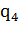 0 →
0 →  0Л,
0Л,  0 →
0 →  0. Соответствующую машину
Тьюринга обозначили О.
0. Соответствующую машину
Тьюринга обозначили О.
Пример 5.2. Построить две машины «левый сдвиг»  и «правый сдвиг»
и «правый сдвиг» 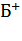 . Первая из начального
стандартного положения перерабатывает слово
. Первая из начального
стандартного положения перерабатывает слово  0 в то же самое слово и
останавливается, обозревая самую левую ячейку с нулем. Вторая машина из
начального состояния, в котором обозревается левая ячейка с нулем, слово
0 в то же самое слово и
останавливается, обозревая самую левую ячейку с нулем. Вторая машина из
начального состояния, в котором обозревается левая ячейка с нулем, слово  0 перерабатывает в то же
самое слово и останавливается, обозревая самую правую ячейку с нулем.
0 перерабатывает в то же
самое слово и останавливается, обозревая самую правую ячейку с нулем.
Программа машины  :
:  0 →
0 →  0Л,
0Л,  1 →
1 →  1Л,
1Л,  0 →
0 →  0. Ясно, что программа
машины
0. Ясно, что программа
машины 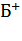 получается из программы
предыдущей машины заменой символа «Л» символом «П».
получается из программы
предыдущей машины заменой символа «Л» символом «П».
1.6
Композиция машин Тьюринга
Определение 6.1: Пусть заданы машины
Тьюринга 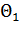 и
и 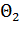 , имеющие общий внешний
алфавит {
, имеющие общий внешний
алфавит {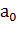 ,
,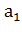 , …,
, …,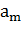 } и алфавиты внутренних
состояний {
} и алфавиты внутренних
состояний { ,
,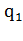 , …,
, …,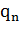 } и {
} и { ,
, 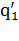 , …,
, …, 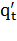 } соответственно.
Композицией (или произведением) машины
} соответственно.
Композицией (или произведением) машины 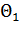 на машину
на машину 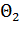 называется новая машина
называется новая машина  с тем же внешним
алфавитом {
с тем же внешним
алфавитом {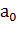 ,
,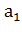 , …,
, …,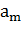 }, внутренним алфавитом {
}, внутренним алфавитом { ,
,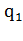 , …,
, …,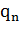 ,
,  , …,
, …, 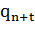 } и программой,
получающейся следующим образом. Во всех командах из
} и программой,
получающейся следующим образом. Во всех командах из 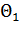 , содержащих символ
остановки
, содержащих символ
остановки  , заменяем последний на
, заменяем последний на  . Все остальные символы в
командах из
. Все остальные символы в
командах из 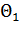 остаются неизменными. В командах из
остаются неизменными. В командах из 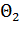 символ
символ  остается неизменным, а
все остальные состояния
остается неизменным, а
все остальные состояния  (i = 1, …, t) заменяем соответственно на
(i = 1, …, t) заменяем соответственно на 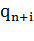 . Совокупность всех так
полученных команд образует программу машины-композиции
. Совокупность всех так
полученных команд образует программу машины-композиции  .
.
Введенное понятие является удобным инструментом для
конструирования машин Тьюринга. Покажем это на примере.
Пример 6.1. Сконструируем машины Тьюринга, правильно
вычисляющие функции-проекторы 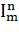 (
(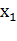 ,
, 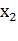 , …,
, …,  ) =
) = 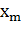 (1≤ m ≤ n).
(1≤ m ≤ n).
Рассмотрим сначала конкретный случай n=3, m=2, т.е. функцию 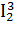 (
(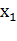 ,
, 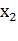 ,
, 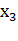 ) =
) = 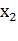 . Мы должны переработать
слово
. Мы должны переработать
слово 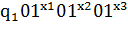 0 в слово
0 в слово  0. Будем применять к
начальной конфигурации последовательно сконструированные ранее машины Тьюринга
0. Будем применять к
начальной конфигурации последовательно сконструированные ранее машины Тьюринга 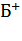 , В,
, В,  , О:
, О:
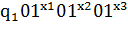 0
0
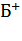 :
:  0;
0;
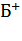 :
: 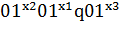 0;
0;
О: 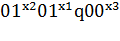 0;
0;
 :
: 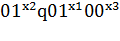 0;
0;
О:  0;
0;
 :
: 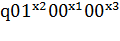 0.
0.
Таким образом, функция 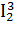 (
(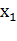 ,
, 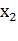 ,
, 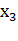 ) =
) = 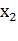 вычисляется следующей
композицией машин:
вычисляется следующей
композицией машин: 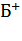 В
В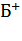 О
О О
О =
= 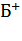 В
В .
.
Теперь мы можем представить себе алгоритм построения
композиции машин 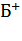 , В,
, В,  , О для вычисления любой
функции вида
, О для вычисления любой
функции вида 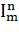 (
(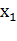 ,
, 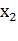 , …,
, …,  ) =
) = 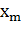 . С помощью правого
сдвига
. С помощью правого
сдвига 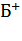 , применив его m-1 раз, нужно сначала
достичь массива
, применив его m-1 раз, нужно сначала
достичь массива 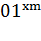 :
:
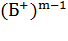 :
: 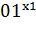 0…
0… 0…
0…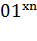 0.
0.
Затем, двигаясь влево, транспонировать (с помощью В) массив 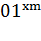 с каждым соседним слева
массивом, пока массив
с каждым соседним слева
массивом, пока массив 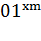 не выйдет на первое место:
не выйдет на первое место:
 :
: 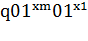 0…
0… 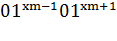 0…
0…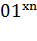 0.
0.
Теперь нужно дойти до крайнего правого массива с помощью (n-1) - кратного применения
правого сдвига 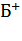 :
:
 :
: 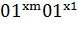 0…
0…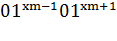 0…
0… 0.
0.
Наконец, нужно стирать последовательно справа налево все
массивы единиц, кроме первого:
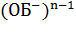 :
: 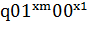 0…
0… 0…
0…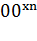 0.
0.
Итак, данную функцию (правильно) вычисляет следующая машина
Тьюринга:
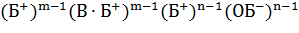 .
.
1.7
Тезис Тьюринга (основная гипотеза теории алгоритмов)
Напомним, одно из свойств алгоритма заключается в том, что он
представляет собой единый способ, позволяющий для каждой задачи из некоего
бесконечного множества задач за конечное число шагов найти ее решение.
На понятие алгоритма можно взглянуть и с несколько иной точки
зрения. Каждую задачу из бесконечного множества задач можно выразить
(закодировать) некоторым словом некоторого алфавита, а решение задачи - каким-то
другим словом того же алфавита. В результате получим функцию, заданную на
некотором подмножестве множества всех слов выбранного алфавита и принимающую
значения в множестве всех слов того же алфавита. Решить какую-либо задачу -
значит найти значение этой функции на слове, кодирующем данную задачу. А иметь
алгоритм для решения всех задач данного класса - значит иметь единый способ,
позволяющий в конечное число шагов «вычислять» значения построенной функции для
любых значений аргумента из ее области определения. Таким образом,
алгоритмическая проблема - по существу, проблема о вычислении значений функции,
заданной в некотором алфавите.
Остается уточнить, что значит уметь вычислять значения
функции. Это значит вычислять значения функции с помощью подходящей машины
Тьюринга. Для каких же функций возможно их тьюрингово вычисление?
Многочисленные исследования ученых, обширный опыт показали, что такой класс
функций чрезвычайно широк. Каждая функция, для вычисления значений которой
существует какой-нибудь алгоритм, оказывалась вычислимой посредством некоторой
машины Тьюринга. Это дало повод Тьюрингу высказать следующую гипотезу,
называемой основной гипотезой теории алгоритмов, или тезисом Тьюринга:
Для нахождения значений функции, заданной в некотором
алфавите, тогда и только тогда существует какой-нибудь алгоритм, когда функция
является вычислимой по Тьюрингу, т.е. когда она может вычисляться на подходящей
машине Тьюринга.
Это означает, что строго математическое понятие вычислимой
(по Тьюрингу) функции является по существу идеальной моделью взятого из опыта
понятия алгоритма. Данный тезис есть не что иное, как аксиома, постулат,
выдвигаемый нами, о взаимосвязях нашего опыта с той математической теорией,
которую мы под этот опыт хотим подвести. Конечно же данный тезис в принципе не
может быть доказан методами математики, потому что он не имеет
внутриматематического характера (одна сторона в тезисе - понятие алгоритма - не
является точным математическим понятием). Он выдвинут исходя из опыта, и именно
опыт подтверждает его состоятельность. Точно так же, например, не могут быть
доказаны и математические законы механики; они открыты Ньютоном и многократно
подтверждены опытом.
Впрочем, не исключается принципиальная возможность того, что
тезис Тьюринга будет опровергнут. Для этого должна быть указана функция,
которая вычислима с помощью какого-нибудь алгоритма, но невычислима ни на какой
машине Тьюринга. Но такая возможность представляется маловероятной (в этом одно
из значений гипотезы): всякий алгоритм, который будет открыт, может быть
реализован на машине Тьюринга.
1.8
Машины Тьюринга и современные электронно-вычислительные машины
Изучение машин Тьюринга и практика составления программ для
них закладывают фундамент алгоритмического мышления, сущность которого состоит
в том, что нужно уметь разделять тот или иной процесс вычисления или какой-либо
другой деятельности на простые составляющие шаги. В машине Тьюринга расчленение
(анализ) вычислительного процесса на простейшие операции доведено до предельной
возможности: распознавание единичного рассмотренного вхождения символа,
перемещение точки наблюдения данного ряда символов в соседнюю точку и изменение
имеющейся в памяти информации. Конечно, такое мелкое дробление вычислительного
процесса, реализуемого в машине Тьюринга, значительно его удлиняет. Но вместе с
тем логическая структура процесса, расчлененного, образно выражаясь, до
атомарного состояния, значительно упрощается и предстает в некотором
стандартном виде, весьма удобном для теоретических исследований. (Именно такое расчленение
на простейшие составляющие вычислительного процесса на машине Тьюринга дает еще
один косвенный аргумент в пользу тезиса Тьюринга, обсуждавшегося в предыдущем
параграфе: всякая функция, вычисляемая с помощью какого-либо алгоритма, может
быть вычислена на машине Тьюринга, потому что каждый шаг данного алгоритма
можно расчленить на еще более мелкие операции, которые реализуются в машине
Тьюринга.) Таким образом, понятие машины Тьюринга есть теоретический инструмент
анализа алгоритмического процесса, а значит, анализа существа алгоритмического
мышления.
В современных ЭВМ алгоритмический процесс расчленен не на
столь мелкие составляющие, как в машинах Тьюринга. Наоборот, создатели ЭВМ
стремятся к известному укрупнению выполняемых машиной процедур (на этом пути,
конечно, есть свои ограничения). Так, для выполнения операции сложения на
машине Тьюринга составляет целая программа, а в современной ЭВМ такая операция
является простейшей.
Далее, машина Тьюринга обладает бесконечной внешней памятью
(неограниченная в обе стороны лента, разбитая на ячейки). Но ни в одной реально
существующей машине бесконечной памяти быть не может. Это говорит о том, что
машины Тьюринга отображают потенциальную возможность неограниченного увеличения
объема памяти современных ЭВМ.
Наконец, можно провести более подробный сравнительный анализ
работы современной ЭВМ и машины Тьюринга. В большинстве ЭВМ принята
трехадресная система команд, обусловленная необходимостью выполнения бинарных
операций, в которых участвует содержимое сразу трех ячеек памяти. Например,
число из ячейки a умножается на число из ячейки b, и результат отправляется в
ячейку с. Существуют ЭВМ двухадресные и одноадресные. Так, одноадресная ЭВМ
работает следующим образом: вызывается (в сумматор) число из ячейки а; в сумматоре
происходит, например, умножение этого числа на число из ячейки b; результат
отправляется из сумматора в ячейку с. Машину Тьюринга можно считать
одноадресной машиной, в которой система одноадресных команд упрощена еще
больше: на каждом шаге работы машины команда предписывает замену лишь
единственного знака, хранящегося в обозреваемой ячейке, а адрес обозреваемой
ячейки при переходе к следующему такту может меняться лишь на единицу
(обозрение соседней справа или слева ячейки ленты) или не меняться вовсе. Это
удлиняет процесс, но в то же время резко унифицирует его, делает стандартным.
Подводя итоги, можно сказать, что современные ЭВМ есть некие
реальные физические модели машин Тьюринга, огрубленные с точки зрения теории,
но созданные в целях реализации конкретных вычислительных процессов. В свою
очередь, понятие машины Тьюринга и теория машин есть теоретический фундамент и
обоснование современных ЭВМ.
2.
Реализация алгоритмов в машине Тьюринга
Пример 1. Реализация в машине Тьюринга алгоритма перехода
от n к n+1 в десятичной системе
счисления.
Пусть дана десятичная запись натурального числа n и требуется указать
десятичную запись числа n+1, т.е. вычислить функцию f(n)=n+1.
Ясно, что здесь внешний алфавит машины должен содержать все
цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и символ пустой клетки 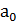 . Число n будем записывать в
десятичной системе на ленте, причем цифры будут помещаться по одной в каждой
клетке подряд без пропусков.
. Число n будем записывать в
десятичной системе на ленте, причем цифры будут помещаться по одной в каждой
клетке подряд без пропусков.
Чтобы решить поставленную задачу, машина должна в первом
такте работы стереть последнюю цифру числа n, заменить ее цифрой на
единицу большей и перейти в стоп - состояние, если последняя цифра была меньше
цифры 9.
Если же последняя цифра числа n была 9, то машина
должна, стерев цифру 9, записать в освободившуюся клетку цифру 0 и произвести
сдвиг влево к соседнему более высокому разряду, оставаясь в том же начальном
состоянии. Здесь во втором такте работы машина должна прибавить единицу к цифре
более высокого разряда. Очевидно, что в случае сдвига влево, управляющая
головка машины может выйти на пустую клетку в случае, в случае когда цифры
более высокого разряда нет. При этом машина вписывает в пустую клетку цифру 1.
При реализации алгоритма вычисления функции f(n)=n+1 машина может прибывать
лишь в двух состояниях 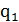 и
и 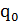 .
.
Таким образом, машина Тьюринга, реализующая алгоритм перехода
от n к n+1 в десятичной системе
счисления будет иметь вид:
|
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|

|
1н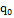
|
1н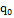
|
2н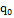
|
3н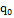
|
4н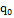
|
5н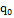
|
6н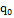
|
7н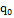
|
8н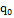
|
9н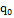
|
0^
|
Пример 2. Алгоритм сложения натуральных чисел.
Пусть на ленту подается два числа, заданных наборами палочек;
например, 2 и 3. Нужно сложить эти числа.
Будем обозначать символ сложения звездочкой. Таким образом,
на ленте машины будет записано слово
 ||*|||
||*|||  . (1)
. (1)
Требуется предложить функциональную схему, которая будучи
примененной к слову (1), давала бы в результате сумму чисел 2 и 3, то есть
слово
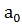 |||||
|||||  . (2)
. (2)
Опишем процесс работы машины для решения задачи. Пусть в
начальный момент обозревается самая левая палочка. Ее нужно сдвинуть вправо,
минуя все палочки и звездочку до тех пор, пока не будет достигнута первая
пустая клетка. В эту пустую клетку вписывается первая палочка. Затем нужно
вернуться за второй палочкой и ее перенести вправо так же, как это делалось с
первой палочкой. После этой процедуры нужно вернуться к звездочке, стереть ее и
остановиться. Изобразим все такты работы машины в виде соответствующих
конфигураций:
1)  ||*|||
||*|||  11)
11)  |*||||
|*||||  21)
21)  *||||
*|||| 

1)  |*|||
|*|||  12)
12)  |*||||
|*||||  22)
22)  *|||||
*||||| 
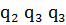
3)  |*|||
|*|||  13)
13) 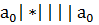 23)
23) 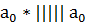
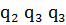
4)  |*|||
|*|||  14)
14)  |*||||
|*||||  24)
24)  *|||||
*||||| 
5)  |*|||
|*|||  15)
15)  |*||||
|*||||  25)
25)  *|||||
*||||| 
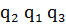
6)  |*|||
|*|||  16)
16) 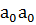 *||||
*||||  26)
26)  *|||||
*||||| 

7)  |*|||
|*|||  17)
17)  *||||
*||||  27)
27)  *|||||
*||||| 

8)  |*||||
|*||||  18)
18)  *||||
*||||  28)
28)  *|||||
*||||| 
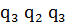
9)  |*||||
|*||||  19)
19)  *||||
*||||  29)
29)  *|||||
*||||| 

10)  |*||||
|*||||  20)
20)  *||||
*||||  30)
30) 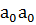 |||||
||||| 
Этот процесс позволяет записать алгоритм в виде двумерной
таблицы:
|
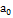
|
*
|
|
|
|

|
|
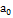 н н 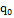
|
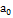 п п 
|
|

|
| н 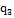
|
*п 
|
| п 
|
|
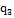
|
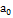 п п 
|
*^ 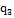
|
| ^ 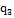
|
Таким образом, здесь использован внешний алфавит 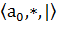 и состояния машины
и состояния машины 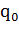 ,
, 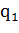 ,
, 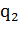 ,
, 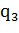 .
.
Заключение
Таким образом, машина Тьюринга представляет собой простейшую
вычислительную машину с линейной памятью, которая согласно формальным правилам
преобразует входные данные с помощью последовательности элементарных действий.
С математической точки зрения машина Тьюринга - просто определенный алгоритм
для переработки слов. Несмотря на простоту машины Тьюринга, на ней можно
вычислить всё, что можно вычислить на любой другой машине, осуществляющей
вычисления с помощью последовательности элементарных действий. Машина Тьюринга
может выполнять все возможные преобразования слов, реализуя тем самым все
возможные алгоритмы.
Один из естественных способов доказательства того, что
алгоритмы вычисления, которые можно реализовать на одной машине, можно
реализовать и на другой, - это имитация первой машины на второй. На машине
Тьюринга можно имитировать машину Поста, нормальные алгоритмы Маркова и любую
программу для обычных компьютеров, преобразующую входные данные в выходные по
какому-либо алгоритму. В свою очередь, на различных абстрактных исполнителях
можно имитировать Машину Тьюринга. Исполнители, для которых это, возможно,
называются полными по Тьюрингу.
Богатство возможностей машины Тьюринга проявляется в том, что
если какие-то алгоритмы реализуются машинами Тьюринга, то можно построить
машины Тьюринга, реализующие различные композиции этих алгоритмов. Очевидно,
что такие композиции также являются алгоритмами, поэтому их реализация
посредством машины Тьюринга подтверждает, что конструкция Тьюринга является
универсальным исполнителем. На машинах Тьюринга оказалось возможным осуществить
или имитировать все алгоритмические процессы, которые когда-либо описывались
математиками.
Список
использованной литературы
1. Ершов С.С. Элементы теории алгоритмов:
учебное пособие [Текст] / С.С. Ершов. - Челябинск: Издательский центр ЮУрГУ,
2009. - 64 с.
2. Игошин В.И. Математическая логика и
теория алгоритмов: Учеб. пособие для студ. высш. учеб. заведений [Текст] /
Владимир Иванович Игошин. - М.: Издательский центр «Академия», 2012. - 448 с.
. Клини С. Машины Тьюринга и рекурсивные
функции [Текст] / С. Клини. - М., 2010.
. Успенский В.А. Теория алгоритмов: основные
открытия и приложения [Текст] / В.А. Успенский, А.Л. Семенов. - М.: Наука,
2012. - 288 с.