Полиномы Жегалкина для логических операций
Введение
На сегодняшний день практически каждый человек в
мире ежедневно пользуется такими благами цивилизации, как компьютеры, мобильные
телефоны, калькуляторы и пр. Люди стали остро зависеть от сетевого общения и от
Интернет-ресурсов, позволяющих найти нужную нам информацию гораздо быстрее, чем
при поиске ее традиционными способами в книгах, газетах, журналах. Однако мало
кто задумывается о том, каким образом работают наши электронные «помощники».
Математической основой цифровой техники является
алгебра логики, разработанная в середине XIX
века английским математиком Джорджем Булем. В честь своего «отца» алгебру
логики также называют булевой алгеброй. Возможность её применения в технике
заметил впервые в 1910 году известный физик П. Эренфест. Доказательство такой
возможности привёл и обосновал в своих работах советский физик В. И. Шестаков.
Булева алгебра оперирует с переменными, которые
принимают только лишь два значения - 0 и 1, то есть с двоичными переменными.
Функция двоичных переменных, принимающая те же два значения, называется
логической функцией или булевой функцией.
Теория булевых функций, начиная с прошлого века
и продолжая сегодняшним днем, является теоретической базой современных ЭВМ.
Возникло понятие алгоритма, и это очень помогает решать многие доселе
неразрешимые проблемы. Именно через математическую логику и теорию алгоритмов
сейчас математические методы проникают в экономику, биологию, лингвистику и
многие другие науки.
Целью моей курсовой работы является рассмотрение
и изучение одного из способов приведения логических функций к более короткому
виду, точнее - приведение логических функций к многочлену (полиному) Жегалкина.
Разработанный в начале ХХ века русским
математиком Иваном Ивановичем Жегалкиным вид логического многочлена сейчас
широко применяется в самых различных сферах человеческой деятельности - начиная
от криптографии (шифрования данных для их сбережения от посторонних глаз) и
заканчивая применением в сумматорах - аналого-цифровых устройствах, которые
реализуют логическую операцию «исключающее ИЛИ», которую также называют суммой
по модулю 2. К слову, сумматоры являются обязательной частью любого
аналого-цифрового устройства, любого без исключений процессора.
ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Высказывание - повествовательное предложение. О
нём можно сказать либо, что оно истинно, либо, что оно ложно, но ни в коем
случае не истинно и ложно одновременно. В логике главенствующее значение в
высказывании имеет не его значение, а истинность его или ложность. Истинное
значение высказывания принимают за «1», а ложное - за «0». То есть существует
множество {1;0}, которое называется множеством истинных значений.
Алгебру высказываний также называют булевой
алгеброй, а переменные, принимающие значения 1 и 0 называют булевыми
переменными.
Логическая операция (оператор, связка) -
операция над высказываниями, которая позволяет составлять новые высказывания,
соединяя высказывания более простые.
Простейшие связки
. Дизъюнкция - операция «ИЛИ», называемая
также логической суммой. Дизъюнкцией высказываний Х и Y
называют высказывание, обозначаемое как Х⋁Y
(или Х+Y) и представляющее
собой ложное высказывание в том случае, когда Х и Y
ложны, и истинное высказывание во всех остальных случаях.
Таблица истинности для дизъюнкции
|
Х
|
Y
|
Х⋁Y
|
|
0
|
0
|
0
|
|
0
|
1
|
1
|
|
1
|
0
|
1
|
|
1
|
1
|
1
|
2. Конъюнкция - операция «И», которую также
называют логическим произведением. Конъюнкцией высказываний Х и Y называют
высказывание, обозначаемое как Х⋀Y
(или Х∙Y) и представляющее собой истинное высказывание в том случае,
когда Х и Y истинны, и ложное высказывание во всех остальных случаях.
Таблица истинности для конъюнкции
. Отрицание, называемое также инверсией,
высказывания Х называют высказывание, обозначаемое как 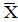 ,
которое является ложным при истинном Х и истинным при ложном Х.
,
которое является ложным при истинном Х и истинным при ложном Х.
Таблица истинности для отрицания
|

|
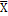
|
|
0
|
1
|
|
1
|
0
|
. Импликацией (логическое следование)
высказываний Х и Y называется
высказывание, обозначаемое Х→Y,
которое является ложным только в том случае, когда Х истинно, а Y
- ложно. В остальных случаях импликация является истинной.
Логическое следование представляет собой оборот
речи «если Х, то Y». Например,
«если я сдам курсовую по дискретной математике вовремя, то у меня ее примут».
Таблица истинности для импликации:
Импликация - не симметричная логическая
операция, то есть высказывания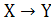 и
и  не
являются эквивалентными (равными).
не
являются эквивалентными (равными).
Высказывание  называется
конверсией высказывания
называется
конверсией высказывания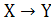 .
.
. Эквивалентностью высказываний 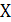 и
и
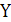 называется
высказывание вида
называется
высказывание вида 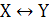 , которое принимает
истинные значения лишь в тех случаях, когда оба высказывания (
, которое принимает
истинные значения лишь в тех случаях, когда оба высказывания (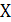 и
и 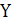 )
либо одновременно истинны, либо одновременно ложны.
)
либо одновременно истинны, либо одновременно ложны.
Таблица истинности для эквивалентности:
Выше мной были перечислены основные логические
операции, которые, в случае отсутствия скобок, выполняются в следующем порядке:
1. Конъюнкция (⋀)
2. Дизъюнкция (⋁)
. Импликация (→)
. Эквивалентность (↔)
. Отрицание (¬)
Помимо элементарных или, как их иначе называют,
простейших связок существует еще несколько логических операций.
. Штрих Шеффера (антиконъюнкция)
обозначается как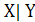 (или
(или  )
)
Таблица истинности
2. Стрелка Пирса (антидизъюнкция) обозначается
как 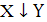 (или
(или
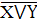 )
)
Таблица истинности
. Сумма по модулю 2 (антиэквивалентность)
обозначается как  (или
(или 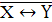 )
)
Таблица истинности:
СВОЙСТВА ЛОГИЧЕСКИХ ОПЕРАЦИЙ
1. Коммутативность дизъюнкции и конъюнкции

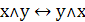
2. Ассоциативность дизъюнкции и конъюнкции


3. Дистрибутивность дизъюнкции и конъюнкции
относительно друг друга


4. Идемпотентность дизъюнкции и конъюнкции
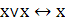

5. Двойное отрицание
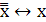
. Закон Моргана
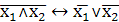
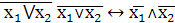
7. Склеивание
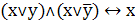
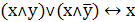
8. Поглощение

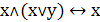
. Закон исключения третьего

10. Отрицание противоречия
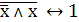
11. Контрапозиция
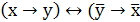 )
)
12. Ценное заключение
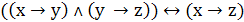
13. Модус поненс
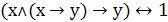
14. Противоположность
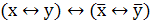
Действия с логическими константами (нулём и
единицей)
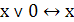

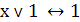
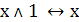

БУЛЕВЫ ФУНКЦИИ
Булевой функцией называется функция f
(x1,x2,…,xn),
которая принимает значение либо 1, либо 0. Число булевых функций переменной
определяется по формуле  .
.
Функция f зависит от переменной xi фиктивно,
если для любых двух наборов значений переменных, которые отличаются только лишь
значением переменной xi, значения функции совпадают.
Фиктивные переменные функции можно добавлять к
функции и исключать из нее.
Две булевы функции называют рaвными
или рaвносильными, если
одну можно получить из другой путем добавления и/или изъятия фиктивных
переменных.
Все функции от двух аргументов в булевой алгебре
называют элементарными булевыми функциями. Основные элементарные булевы функции
- это конъюнкция, дизъюнкция и отрицание. Они удовлетворяют всем аксиомам
булевой алгебры.
Рассмотрим функции одной переменной:
|
х
|
f1(x)
|
f2(x)
|
f3(x)
|
f4(x)
|
|
0
|
0
|
0
|
1
|
1
|
|
1
|
0
|
1
|
0
|
1
|
Функции f1(x)
и f4(x)
называются константами нуля и единицы соответственно. Функция f2(x)
совпадает по своим значениям с переменной х и называется тождественной
переменной х. Функция f3(x)
совпадает с инвертированной переменной х. Исходя из этого, можно построить
таблицу истинности, которая будет более краткой в написании (это совершенно
необязательно, однако подобное представление таблиц истинности часто
используется в литературе):
|
х
|
0
|
х
|
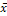
|
1
|
|
0
|
0
|
0
|
1
|
1
|
|
1
|
0
|
1
|
0
|
1
|
Рассмотрим функции двух переменных (считать f(x))
:
|
х1
|
х2
|
f1
|
f2
|
f3
|
f4
|
f5
|
f6
|
f7
|
f8
|
f9
|
f10
|
f11
|
f12
|
f13
|
f14
|
f15
|
f16
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
Функции f1
и f16 называют
константами 0 и 1 соответственно. Функции f4
= х1, f6= х2, f11=
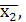 f13
f13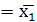 ,
то есть f4, f6, f11, f13 зависят лишь от одной переменной, в отличие от
остальных функций
,
то есть f4, f6, f11, f13 зависят лишь от одной переменной, в отличие от
остальных функций
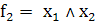



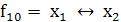
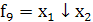


Функции f3
и f5 называются
функциями запрета.
алгебра булевый логический таблица
СВОЙСТВА ЭЛЕМЕНТАРНЫХ БУЛЕВЫХ ФУНКЦИЙ,
ЗАДАВАЕМЫХ ЛОГИЧЕСКИМИ ОПЕРАЦИЯМИ
. Дизъюнкция, конъюнкция,
эквивалентность, сумма по модулю 2, штрих Шеффера, стрелка Пирса обладают
свойством коммутативности, то есть замена переменных местами в выражении не
играет роли.
. Дизъюнкция, конъюнкция, сумма по модулю
2 имеют свойства ассоциативности (когда результат вычисления не зависит от
порядка выполнения операций между несколькими переменными (расстановки скобок),
потому позволительно опускать скобки в записи), которую также называют
сочетательным законом, и дистрибутивности, называемую также распределительным законом.
. Закон ДеМоргана
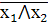 =
=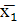 ⋁
⋁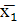
 =
=
4. Закон двойного отрицания
 =х
=х
5. Выражение дизъюнкции через конъюнкцию и
сумму по модулю 2
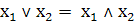 ⊕
⊕
 ⊕
⊕

. Выражение конъюнкции через импликацию
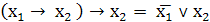
. Выражение отрицания через штрих
Шеффера, стрелку Пирса, сумму по модулю 2 и эквивалентность
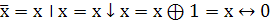
8. Выражение конъюнкции через штрих Шеффера
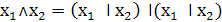
. Выражение дизъюнкции через стрелку
Пирса

10. Закон поглощения

11. Закон склеивания
Для конъюнкции, дизъюнкции и суммы по модулю 2
существует несколько справедливых тождеств
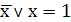

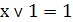
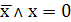
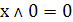
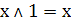
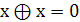
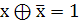
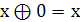
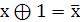
ПОЛИНОМЫ ЖЕГАЛКИНА ДЛЯ ЛОГИЧЕСКИХ ОПЕРАЦИЙ
Полином (многочлен) Жегалкина от n
переменных - это функция вида
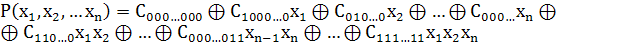 (1)
(1)
где 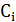 -
коэффициенты, принимающие значение либо нуля, либо единицы, или в более общем
виде
-
коэффициенты, принимающие значение либо нуля, либо единицы, или в более общем
виде
 (2)
(2)
где 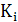 -
элементарная конъюнкция, то есть полином Жегалкина есть многочлен, представляющий
собой сумму по модулю 2 n
элементарных конъюнкций.
-
элементарная конъюнкция, то есть полином Жегалкина есть многочлен, представляющий
собой сумму по модулю 2 n
элементарных конъюнкций.
Любую булеву функцию возможно представить в виде
многочлена Жегалкина, и при том только единственным образом. Это утверждение
также называют теоремой Жегалкина.
По сути, операция приведения логической функции
представляет собой выражение логических операций через конъюнкцию и сумму по
модулю 2.
СВОЙСТВА АЛГЕБРЫ ЖЕГАЛКИНА
Множество булевых функций, в которых могут быть
задействованы только операции конъюнкции и суммы по модулю 2 и единица (также
говорят, что эти булевы функции заданы в базисе Жегалкина S ={⊕,
⋀,
1}), называется алгеброй Жегалкина.
Основные свойства алгебры Жегалкина
. Коммутативность
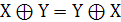

. Ассоциативность
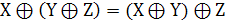

. Дистрибутивность
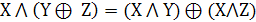
. Свойства констант
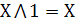

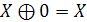
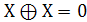
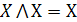
Утверждение: через операции алгебры Жегалкина
можно выразить все другие булевы функции
 ⊕
X
⊕
X

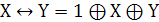
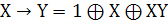
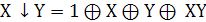
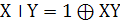
СПОСОБЫ ПОСТРОЕНИЯ ПОЛИНОМОВ ЖЕГАЛКИНА
Существует несколько способов построения
полиномов Жегалкина, каждый из которых удобен по-своему в определенных случаях.
ПОСТРОЕНИЕ ПОЛИНОМОВ ЖЕГАЛКИНА С ПОМОЩЬЮ ТАБЛИЦ
ИСТИННОСТИ (МЕТОД НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ)
Построение полиномов Жегалкина с помощью таблиц
истинности или, как еще говорят, методом неопределенных коэффициентов - процесс
кропотливый, требующий внимания и определенной сноровки, а также полного
осознания того, что надо делать.
Этот способ можно применять и тогда, когда
функция задана таблицей истинности, и тогда, когда функция представлена логической
формулой.
Пример 1: построить полином Жегалкина для
функции

Составим
таблицу истинности для функции

|

|
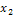
|

|

|
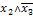
|
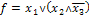
|
|
0
|
0
|
0
|
1
|
0
|
0
|
|
0
|
0
|
1
|
0
|
0
|
0
|
|
0
|
1
|
0
|
1
|
1
|
1
|
|
0
|
1
|
1
|
0
|
0
|
0
|
|
1
|
0
|
0
|
1
|
0
|
1
|
|
1
|
0
|
1
|
0
|
0
|
1
|
|
1
|
1
|
0
|
1
|
1
|
1
|
|
1
|
1
|
1
|
0
|
0
|
1
|
1. Теперь, используя формулу (1), построим полином
Жегалкина для нашей функции в общем виде (для трёх переменных):

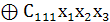 . (3)
. (3)
2. Найдем значения коэффициентов 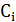
Так как 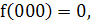 то
то
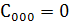 .
.
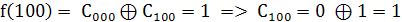


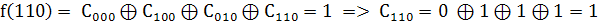
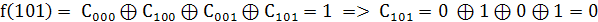
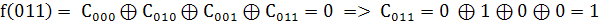

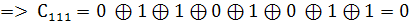
3. Составим полином Жегалкина, подставив
полученные значения коэффициентов в формулу (3)
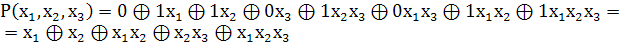
Ответ: полином Жегалкина, построенный для
функции ,
будет равен
,
будет равен

Пример 2: построить многочлен Жегалкина,
используя данную таблицу истинности
|

|
|

|

|
|
0
|
0
|
0
|
1
|
|
0
|
0
|
1
|
1
|
|
0
|
1
|
0
|
1
|
|
0
|
1
|
1
|
1
|
|
1
|
0
|
0
|
1
|
|
1
|
0
|
1
|
1
|
|
1
|
1
|
0
|
1
|
|
1
|
1
|
1
|
0
|
Решение:
. Запишем общий вид полинома Жегалкина (с
неопределенными коэффициентами), то есть формулу (1) для 3 переменных
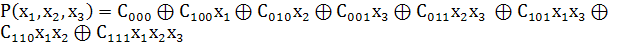
. Найдём коэффициенты
Так как 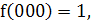 то
то
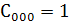 .
.
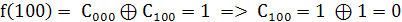
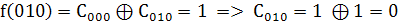

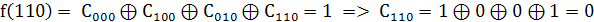
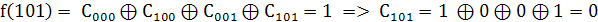


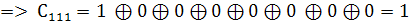
. Подставим найденные коэффициенты в
формулу (3) и найдем таким образом многочлен Жегалкина
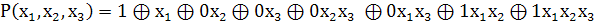
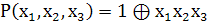
Ответ: полином Жегалкина для данной таблицы
истинности имеет следующее значение: 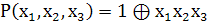 .
.
ПОСТРОЕНИЕ ПОЛИНОМОВ ЖЕГАЛКИНА С ПОМОЩЬЮ
ЭКВИВАЛЕНТНЫХ ПРЕОБРАЗОВАНИЙ ДНФ И КНФ, СДНФ И СКНФ
В тех случаях, когда функция задана логической
формулой, иногда удобнее использовать не громоздкий метод неопределенных
коэффициентов, а компактный метод эквивалентных преобразований. Для этого
необходимо уметь привести функцию в ДНФ или СДНФ, не прибегая к использованию
таблиц истинности. Чаще всего используются следующие тождества
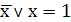

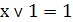
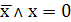
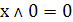
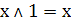
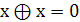
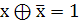
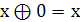
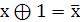
а также закон ДеМоргана. Далее следует раскрыть
скобки по самым обычным правилам.
Пример 1: построить полином Жегалкина для
функции, заданной в виде СДНФ -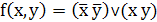
Решение:
. Избавимся от дизъюнкции с помощью
закона ДеМоргана
 =
= 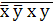
2. Избавимся от отрицаний
 =
= 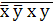 =
=
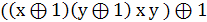 =
=


Ответ: полином Жегалкина имеет вид  )
=
)
= 
 .
.
Пример 2: построить полином Жегалкина для
функции, представленной в ДНФ - 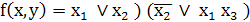
Решение:
. Заменим дизъюнкцию конъюнкцией и суммой
по модулю два
( ∨
∨ ) (
) ( ∨
∨
 )
= (
)
= ( ⊕
⊕
 ⊕
⊕ ) (
) ( ⊕
⊕ ⊕
⊕
 )
)
. Избавимся от отрицаний
( ∨
∨ ) (
) ( ∨
∨
 )
= (
)
= ( ⊕
⊕
 ⊕
⊕ ) (
) ( ⊕
⊕ ⊕
⊕
 )
=
)
= 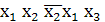 ⊕
⊕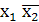
 ⊕
⊕
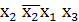 ⊕
⊕ ⊕
⊕
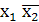 ⊕
⊕ ⊕
⊕
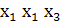 ⊕
⊕ = 0 ⊕
= 0 ⊕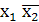
 ⊕
0 ⊕
0 ⊕
⊕
0 ⊕
0 ⊕
 ⊕
0⊕
⊕
0⊕
 ⊕
⊕
 ⊕
⊕
 =
=
 ⊕
⊕
 ⊕
⊕
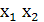 ⊕
⊕
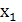 ⊕
⊕ =
=  ⊕
⊕
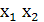 ⊕
⊕

Ответ: полином Жегалкина имеет вид
 ) =
) =  ⊕
⊕
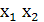 ⊕
⊕

МЕТОД ТРЕУГОЛЬНИКА
Метод треугольника позволяет преобразовать
таблицу истинности в полином Жегалкина с помощью построения вспомогательной
треугольной таблицы в соответствии со следующими правилами:
. Строится полная таблица истинности, в
которой строки идут в порядке возрастания двоичных кодов от 000…00 до 111…11.
. Строится вспомогательная треугольная
таблица, в которой первый столбец совпадает со столбцом значений функции в
таблице истинности.
. Ячейка в каждом последующем столбце
получается путём суммирования по модулю 2 двух ячеек предыдущего столбца -
стоящей в той же строке и строкой ниже.
. Столбцы вспомогательной таблицы
нумеруются двоичными кодами в том же порядке, что и строки таблицы истинности.
. Каждому двоичному коду ставится в
соответствие один из членов полинома Жегалкина в зависимости от позиций кода, в
которых стоят единицы. Например, ячейке 111 соответствует член ABC, ячейке 101
- член AC, ячейке 010 - член B, ячейке 000 - член 1 и т. д.
. Если в верхней строке какого-либо
столбца стоит единица, то соответствующий член присутствует в полиноме
Жегалкина.
Заключение
Математика - наука очень точная, однако в ней
можно проявить фантазию, решая задачи различными способами. Дискретная
математика не является в этом исключением.
В своей курсовой работе я рассмотрела несколько
самых распространенных способов решения поставленной мне задачи: приведения
логических функций к полиномам Жегалкина. Каждый из рассмотренных мной способов
имеет свои особенности применения, но все они требуют безусловной
внимательности и сосредоточенности.
В заключение хочется сказать, что Иван Иванович
Жегалкин оказал большую услугу человечеству, когда вывел полином, названный
впоследствии его именем. Полином, члены которого связываются только двумя
операциями и единицей, оказался невероятно полезен и очень широко применяется
человеком в процессе его жизни и деятельности.
Список использованной
литературы
1. Яблонский
С. В. Введение в дискретную математику: Учеб. пособие для вуов . - 2-е изд.,
перераб. и доп. - М.: Наука. Гл. ред. физ.-мат. лит. - 1986.- 384 с.
2. Марченков
С. С. Замкнутые классы булевых функций. - М.: Физ.-мат. лит. - 2000. - 126 с.
. Дунаев
С. Д., Золотарев С. Н. Цифровая схемотехника: Учебное пособие для техникумов и
колледжей ж.-д. транспорта. - М.: ГОУ «Учебно-методический центр по образованию
на железнодорожном транспорте», 2007. - 238 с.
4. Супрун В.П. Табличный метод
полиномиального разложения булевых функций - М.: Кибернетика. - 1987. - № 1
5. Логачёв О.А, Сальников А.А., Ященко В.В.
Булевы функции в теории кодирования и криптологии - МЦНМО, 2004. - 470с.
. Е.Л Рабкин, Ю.Б. Фарфоровская,
дискретная математика - электронное издание.