Плоскость и прямая в пространстве
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
Глава 1.
Плоскость в пространстве
.1 Точка
пересечения прямой с плоскостью
.2 Угол между
прямой и плоскостью
Глава 2.
Прямая в пространстве
.1 Различные
случаи положения прямой в пространстве
.2 Угол между
прямой и плоскостью
ЗАКЛЮЧЕНИЕ
СПИСОК
ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
ВВЕДЕНИЕ
Всякое уравнение первой степени относительно координат x, y, z
+ By + Cz +D = 0
задает плоскость, и наоборот: всякая плоскость может быть представлена
уравнением, которое называется уравнением плоскости.
Вектор n (A, B, C), ортогональный плоскости, называется нормальным
вектором плоскости. В уравнении коэффициенты A, B, C одновременно не равны 0.
Особые случаи уравнения
. D = 0, Ax+By+Cz = 0 - плоскость проходит через начало координат.
. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz.
. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz.
. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz.
Уравнения координатных плоскостей: x = 0, y = 0, z = 0.
Прямая в пространстве может быть задана:
) как линия пересечения двух плоскостей,т.е. системой уравнений:
A1 x + B1 y + C1 z + D1
= 0, A2 x + B2 y + C2 z + D2 = 0;
) двумя своими точками M1(x1, y1, z1)
и M2(x2, y2, z2), тогда прямая,
через них проходящая, задается уравнениями:
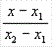 =
=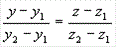 ;
;
) точкой M1(x1, y1, z1), ей
принадлежащей, и вектором a (m, n, р), ей коллинеарным. Тогда прямая
определяется уравнениями:

Уравнения называются каноническими уравнениями прямой.
Вектор a называется направляющим вектором прямой.
Параметрические уравнения прямой получим, приравняв каждое из отношений
параметру t:
= x1 +mt, y = y1 + nt, z = z1 + рt.
Решая систему как систему линейных уравнений относительно неизвестных x и
y, приходим к уравнениям прямой в проекциях или к приведенным уравнениям
прямой:
= mz + a, y = nz + b
От уравнений можно перейти к каноническим уравнениям, находя z из каждого
уравнения и приравнивая полученные значения:

От общих уравнений (3.2) можно переходить к каноническим и другим
способом, если найти какую-либо точку этой прямой и ее направляющий вектор n =
[n1, n2], где n1(A1, B1,
C1) и n2(A2, B2, C2) -
нормальные векторы заданных плоскостей. Если один из знаменателей m, n или р в
уравнениях (3.4) окажется равным нулю, то числитель соответствующей дроби надо
положить равным нулю, т.е. система
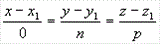
равносильна системе 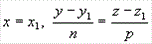 ; такая прямая перпендикулярна к оси Ох.
; такая прямая перпендикулярна к оси Ох.
Система 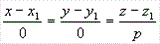 равносильна системе x = x1, y = y1;
прямая параллельна оси Oz.
равносильна системе x = x1, y = y1;
прямая параллельна оси Oz.
Цель курсовой работы: изучить прямую и плоскость в пространстве.
Задачи курсовой работы: рассмотреть плоскость в пространстве, её уравнение, а
также рассмотреть плоскость в пространстве.
Структура курсовой работы: введение, 2 главы, заключение, список использованных
источников.
Глава 1. Плоскость в пространстве
.1 Точка
пересечения прямой с плоскостью
Пусть плоскость Q задана уравнением общего типа: Ax+By+Cz+D=0, а прямая L
в параметрическом виде: x=x1+mt, y=y1+nt, z=z1+pt,
тогда чтобы найти точку пересечения прямой L и плоскости Q, нужно найти
значение параметра t, при котором точка прямой будет лежать на плоскости.
Подставив значение x, y, z, в уравнение плоскости и выразив t, получим

Значение t будет единственным, если прямая и плоскость не параллельны.
Условия
параллельности и перпендикулярности прямой и плоскости
Рассмотрим прямую L:

и плоскость α:
+By+Cz+D=0.
Прямая L и плоскость α:
а) перпендикулярны друг другу тогда и только тогда, когда направляющий
вектор прямой 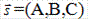 и нормальный вектор
и нормальный вектор 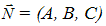 плоскости коллинеарны, т. е.
плоскости коллинеарны, т. е.
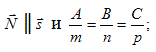
б) параллельны друг другу тогда и только тогда, когда векторы  и
и 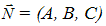 перпендикулярны, т. е.
перпендикулярны, т. е.
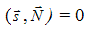 и Am + Bn + Ср = 0.
и Am + Bn + Ср = 0.
.2 Угол
между прямой и плоскостью
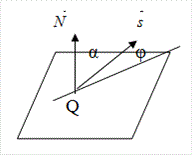
Угол α между нормальным вектором плоскости 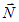 и направляющим вектором прямой
и направляющим вектором прямой 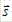 вычисляется по формуле:
вычисляется по формуле:
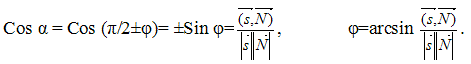
Пучок
плоскостей
Совокупность всех плоскостей, проходящих через заданную прямую L,
называется пучком плоскостей, а прямая L - осью пучка. Пусть ось пучка задана
уравнениями

Почленно умножим второе уравнение системы на постоянную и сложим с первым
уравнением:
A1x+B1y+C1z+D1+ λ(A2x+B2y+C2z+D2)=0.
Это уравнение имеет первую степень относительно х, у, z и, следовательно,
при любом численном значении λ определяет плоскость. Так как данное
уравнение есть следствие двух уравнений, то координаты точки, удовлетворяющие
этим уравнениям будут удовлетворять и данному уравнению. Следовательно, при
любом численном значении λ данное уравнение есть уравнение плоскости, проходящей
через заданную прямую. Полученное уравнение есть уравнение пучка плоскостей.
Пример. Написать уравнение плоскости, проходящей через точку M1(2,
-3, 4) параллельно прямым
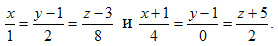
Решение. Запишем уравнение связки плоскостей, проходящих через данную точку M1:
А (х - 2) + В (у + 3) + C(z - 4) = 0.
Так как искомая плоскость должна быть параллельна данным прямым, то ее
нормальный вектор должен быть перпендикулярен направляющим векторам 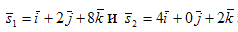 этих прямых. Поэтому в качестве
вектора N можно взять векторное произведение векторов
этих прямых. Поэтому в качестве
вектора N можно взять векторное произведение векторов 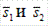 :
:
Следовательно, А = 4, В = 30, С = - 8. Подставляя найденные значения А,
В, С в уравнение связки плоскостей, получим
4(x-2)+30(y + 3) -8(z-4) =0 или 2x + 15у - 4z + 57 = 0.
Решение. Запишем уравнения данной прямой в параметрическом виде:
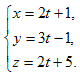
Подставим эти выражения для х, у, z в уравнение плоскости:
(2t+1)+3(3t-1)-2(2t+5)+2=0 Þ t=1.
Подставим t = 1 в параметрические уравнения прямой. Получим
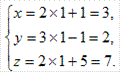
Итак, прямая и плоскость пересекаются в точке М(3, 2, 7).
Пример. Найти угол φ между прямой  и плоскостью 4x-2y-2z+7=0.Решение.
Применяем формулу (3.20). Так как
и плоскостью 4x-2y-2z+7=0.Решение.
Применяем формулу (3.20). Так как
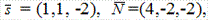 то
то
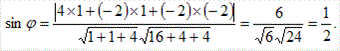
Следовательно,φ = 30°.
Глава 2. Прямая в пространстве
Прямая линия в пространстве бесконечна, поэтому задавать ее удобнее
отрезком. Из школьного курса Евклидовой геометрии известна аксиома, «через две
точки в пространстве можно провести прямую и, притом, только одну».
Следовательно, на эпюре прямая может быть задана двумя фронтальными и двумя
горизонтальными проекциями точек. Но так как прямая - это прямая (а не кривая),
то с полным основанием мы можем соединить эти точки отрезком прямой и получить
фронтальную и горизонтальную проекции прямой (рис. 13).

Доказательство от обратного: в плоскостях проекций V и Н заданы две
проекции а' b' и ab (рис.14). Проведем через них плоскости, перпендикулярные к
плоскостям проекций V и Н (рис.14), линией пересечения плоскостей будет прямая
АВ.
.1 Различные
случаи положения прямой в пространстве
В рассмотренных нами случаях прямые не были ни параллельными, ни
перпендикулярными к плоскостям проекций V, Н, W. Большинство прямых занимает
именно такое положение в пространстве и их называют прямыми общего положения.
Они могут быть восходящими или нисходящими (разобраться самостоятельно).
На рис. 17 показана прямая общего положения, заданная тремя проекциями.
Рассмотрим семейство прямых, обладающих важными свойствами - прямые,
параллельные какой-либо плоскости проекци.
На рис. 17 показана прямая общего положения, заданная тремя проекциями.
Рассмотрим семейство прямых, обладающих важными свойствами - прямые,
параллельные какой-либо плоскости проекций.
а) Горизонтальная прямая (иначе - горизонталь, прямая горизонтальною
уровня). Так называется прямая, параллельная горизонтальной плоскости проекций.
Ее изображение в пространстве и на эпюре показано на рис. 18.

Горизонталь легко узнать на эпюре «в лицо»: ее фронтальная проекция всегда
параллельна оси ОХ. Полностью важнейшее свойство горизонтали формулируются так:
У горизонтали - фронтальная проекция параллельна оси ОХ, а горизонтальная
отражает натуральную величину. Попутно горизонтальная проекция горизонтали на
эпюре позволяет определить угол ее наклона к плоскости V (угол b) и к плоскости
W (у) - рис.18.
б) Фронтальная прямая (фронталь, прямая фронтального уровня) - это
прямая, параллельная фронтальной плоскости проекций. Мы не иллюстрируем ее
наглядным изображением, а показываем ее эпюр (рис. 19).
Эпюр фронтали характерен тем, что горизонтальная и профильная ее проекции
параллельны соответственно осям X и Z, а фронтальная проекция располагается
произвольно и показывает натуральную величину фронтали. Попутно на эпюре
имеются углы наклона прямой к горизонтальной (а) и профильной (у) плоскостям
проекций. Итак, еще раз:
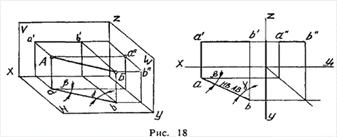
У фронтали - горизонтальная проекция параллельна оси ОХ, а фронтальная
отражает натуральную величину
в) Профильная прямая. Очевидно, что это прямая, параллельная профильной
плоскости проекций (рис. 20). Очевидно также, что натуральная величина
профильной прямой имеется на профильной плоскости проекций (проекция
а"b" - рис. 20) и здесь же можно видеть углы ее наклона к плоскостям
Н (a) и V (b).

Следующее семейство прямых, хотя и не столь важных, как прямые уровня -
это проецирующие прямые.
Прямые, перпендикулярные к плоскостям проекций, называются проецирующими
(по аналогии с проецирующими лучами - рис. 21).
АВ пл. Н - прямая горизонтально-проецирующая;пл. V - прямая
фронтально-проецирующая;пл. W - прямая профильно-проецирующая.

2.2 Угол
между прямой и плоскостью
плоскость прямая угол треугольник
Метод прямоугольного треугольника
Прямая общего положения, как мы уже говорили, наклонена к плоскостям
проекций под некоторым произвольным углом.
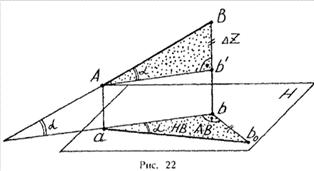
Угол между прямой и плоскостью определяется углом, составленным прямой и
ее проекцией на эту плоскость (рис. 22). Угол a определяет угол наклона отрезка
АВ к пл. Н. Из рис. 22: Ab1 |1пл. Н; Вb1 = ВЬ - Аа = Z Рис. 22
В прямоугольном треугольнике AВb1 катет Ab1 равен горизонтальной проекции
ab; а другой катет Вb1 равен разности расстояний точек А и В от пл. Н. Если из
точки В на горизонтальной проекции прямой ab проведем перпендикуляр и отложим
на нем величину Z,то, соединив точку а с полученной точкой b0, получим
гипотенузу аb0, равную натуральной величине отрезка АВ. На эпюре это выглядит так
(рис. 23):
Аналогично определяется угол наклона прямой к фронтальной плоскости
проекций (b) - рис. 24.
Обратите внимание: при построениях на горизонтальной проекции прямой мы
откладываем на вспомогательной прямой величину Z; при построениях на фронтальной
проекции - величину Y.

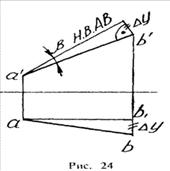
Рассмотренный метод носит название прямоугольного треугольника. С его
помощью можно определить натуральную величину любого интересующего нас отрезка,
а также углы его наклона к плоскостям проекций.
Взаимное
положение прямых
Ранее мы рассмотрели вопрос принадлежности точки прямой: если точка
принадлежит прямой, то ее проекции лежат на одноименных проекциях прямой
(правило принадлежности, см. рис. 14). Из школьного курса геометрии вспомним:
две прямые пересекаются в одной точке (или: если две прямые имеют одну общую
точку, то они пересекаются в этой точке).
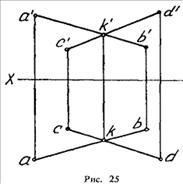
Проекции пересекающихся прямых на эпюре имеют ярко выраженный признак:
проекции точки пересечения лежат на одной линии связи (рис. 25). Действительно:
точка К принадлежит и АВ, и CD; на эпюре точка k' лежит на одной линии связи с
точкой k.
Прямые АВ
и CD - пересекаются
Следующее из возможных взаимных расположении двух прямых в пространстве -
прямые скрещиваются. Это возможно в случае, когда прямые не параллельны, но и
не пересекаются. Такие прямые всегда можно заключить в две параллельные
плоскости (рис. 26). Это отнюдь не означает, что две скрещивающиеся прямые
обязательно лежат в двух параллельных плоскостях; а лишь то, что через них
можно провести две параллельные плоскости.
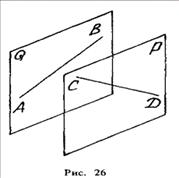
Проекции двух скрещивающихся прямых могут пересекаться, но точки их
пересечения не лежат на одной линии связи (рис. 27).
Попутно решим вопрос о конкурирующих точках (рис. 27). На горизонтальной
проекции мы видим две точки (е,f), а на фронтальной они сливаются в одну
(e'f'), причем не ясно, какая из точек видна, а какая не видна (конкурирующие
точки).
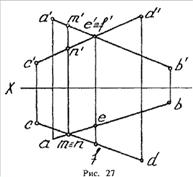
Две точки, фронтальные проекции которых совпадают, называются
фронтально-конкурирующими.
Подобный случай мы рассматривали ранее (рис. 11), при изучении темы
«взаимное расположение двух точек». Поэтому применим правило:
Из двух конкурирующих точек считается видимой та, координата которой
больше.
Из рис. 27 видно, что горизонтальная проекция точки Е (е) отстоит от оси
ОХ дальше, чем точка f. Следовательно, координата «Y» точки «е» больше, чем у
точки f; следовательно, видимой будет точка Е. На фронтальной проекции точка f'
заключена в скобки как невидимая.
Еще одно следствие: точка е принадлежит проекции прямой ab, а это значит,
что на фронтальной проекции прямая а'Ь' расположена «поверх» прямой c'd'.
Параллельные
прямые

Параллельные прямые на эпюре легко распознать «в лицо», ибо одноименные
проекции двух параллельных прямых - параллельны.
Обратите внимание: одноименные! Т.е. фронтальные проекции параллельны
между собой, а горизонтальные - между собой (рис. 29).
Доказательство: на рисунке 28 в пространстве даны две параллельные прямые
АВ и CD. Проведем через них проецирующие плоскости Q и Т - они окажутся
параллельными (ибо если две пересекающиеся прямые одной плоскости параллельны
двум пересекающимся прямым другой плоскости, то такие плоскости параллельны).
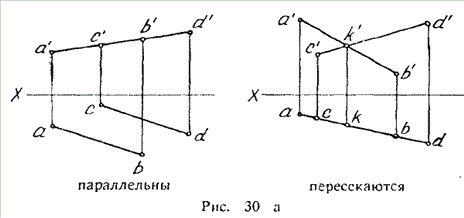
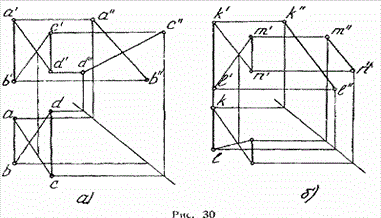
На эпюре З0а заданы параллельные прямые, на эпюре 30б прямые
скрещивающиеся, хотя и в том, и в другом случае фронтальные и горизонтальные
проекции взаимно параллельны.

Существует, однако, прием, с помощью которого можно определить взаимное
положение двух профильных прямых, не прибегая к построению третьих проекции.
Для этого достаточно соединить концы проекций вспомогательными прямыми, как по
казано на рис 30. Если окажется, что точки пересечения этих прямых лежат на
одной линии связи - профильные прямые параллельны между собой - рис. З0а. Если
нет - профильные прямые скрещивающиеся (рис. 306).
Особые
случаи положения прямых:
Проекции
прямого угла
Если две прямые общего положения пересекаются пол прямым углом, то их
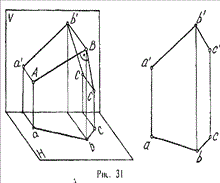
проекции образуют угол, не равный 90° (рис. 31).
А так как при пересечении двух параллельных плоскостей третьей в
пересечении получаются параллельные прямые, то горизонтальные проекции ab и cd
- параллельны.
Если повторить операцию и спроецировать прямые АВ и CD на фронтальную
плоскость проекций, мы получим тот же результат.
Особый случай представляют собой две профильные прямые, заданные
фронтальными и горизонтальными проекциями (рис.30). Как было сказано, у
профильных прямых фронтальные и горизонтальные проекции взаимно параллельны,
однако, по этому признаку нельзя судить о параллельности двух профильных
прямых, не построив третьей проекции.

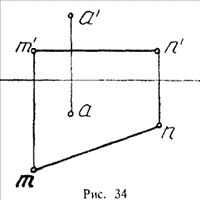
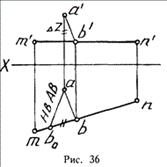
Задача. Постройте равнобедренный прямоугольный треугольник ABC, катет ВС
которою лежит на прямой MN (рис. 34).
Воспользуемся свойством проекции прямого угла и опустим из точки «а»
перпендикуляр HА проекцию mn (на пл. Н наш прямой угол проецируется без
искажении) - рис. 35.
В качестве вспомогательной прямой, проводимой из конца отрезка под прямым
углом к данному, мы используем часть горизонтальной проекции прямой, а именно
bm (рис. 36). Отложим на ней величину разности координат Z, взятую с
фронтальной проекции, и соединим точку «а» с концом полученного отрезка. Мы
получим натуральную величину катета АВ (a’b’; ab).
На рисунках 31 и 32 показаны две прямые общего положения, образующие
между собой угол 90° (на рис. 32 эти прямые лежат в одной плоскости Р). Как
видим, на эпюрах угол, образованный проекциями прямых, не равен 90°.
Отдельным вопросом мы рассматриваем проекции прямою угла по следующей
причине:
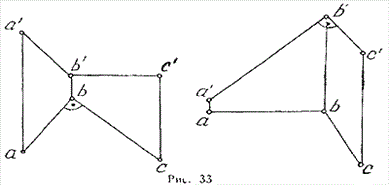
Если одна из сторон прямого угла параллельна какой-либо плоскости
проекций, то на эту плоскость прямой угол проецируется без искажений (рис. 33).
Мы не станем доказывать это положение (проработайте это самостоятельно),
а рассмотрим преимущества, которые можно извлечь из этого правила.
Прежде всего, отметим, что по условию одна из сторон прямого угла
параллельна какой-либо плоскости проекций, следовательно, одна из сторон будет
либо фронталью, либо горизонталью (может быть и профильной прямой) - рис. 33.
А фронталь и горизонталь на эпюре легко узнать «в лицо» (одна из проекции
обязательно параллельна оси ОХ), или ее можно легко построить при
необходимости. Кроме того, у фронили и горизонтали есть важнейшее свойство:
одна из их проекции обязательно отражает
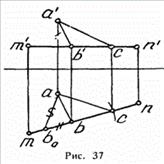
Пользуясь правилом принадлежности, найдем фронтальную проекцию точки b' с
помощью линии связи. У нас появился катет АВ (a'b';ab).
Чтобы отложить катет ВС на стороне MN, нужно сначала определить
натуральную величину отрезка АВ (a’d’; ab). Для этого воспользуемся уже
изученным правилом прямоугольного треугольника.

ЗАКЛЮЧЕНИЕ
Общие уравнения прямой в пространстве
Уравнение прямой может быть рассмотрено как уравнение линии пересечения
двух плоскостей. Как было рассмотрено выше, плоскость в векторной форме может
быть задана уравнением:
 ×
× + D = 0, где
+ D = 0, где
 - нормаль плоскости;
- нормаль плоскости;  - радиус- вектор произвольной точки
плоскости.
- радиус- вектор произвольной точки
плоскости.
Пусть в пространстве заданы две плоскости: 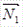 ×
×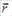 + D1 = 0 и
+ D1 = 0 и 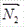 ×
×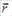 + D2 = 0, векторы нормали
имеют координаты:
+ D2 = 0, векторы нормали
имеют координаты: 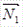 (A1, B1, C1),
(A1, B1, C1), 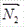 (A2, B2, C2);
(A2, B2, C2);
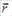 (x, y, z). Тогда общие уравнения
прямой в векторной форме:
(x, y, z). Тогда общие уравнения
прямой в векторной форме:

Общие уравнения прямой в координатной форме:

Для этого надо найти произвольную точку прямой и числа m, n, p.При этом
направляющий вектор прямой может быть найден как векторное произведение
векторов нормали к заданным плоскостям.
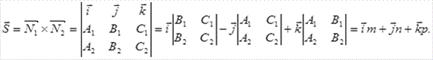
Уравнение плоскости в пространстве
Пусть даны точка 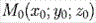 и ненулевой вектор
и ненулевой вектор 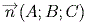 (
(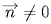 то есть
то есть 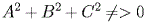 ). Тогда векторное уравнение
плоскости
). Тогда векторное уравнение
плоскости 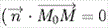 , где
, где  - произвольная точка плоскости) принимает вид
- произвольная точка плоскости) принимает вид  - уравнение плоскости по точке и
вектору нормали.
- уравнение плоскости по точке и
вектору нормали.
Каждое уравнение первой степени 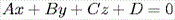 при условии
при условии задает в прямоугольной системе
координат
задает в прямоугольной системе
координат  единственную плоскость, для которой вектор
единственную плоскость, для которой вектор 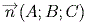 является вектором нормали.
является вектором нормали.
Если 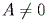 ,
, 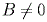 ,
, 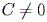 ,
, 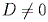 ..., то уравнение
..., то уравнение  можно преобразовать к виду
можно преобразовать к виду . Числа
. Числа  ,
,  и
и 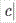 равны длинам отрезков, которые
отсекает плоскость на осях
равны длинам отрезков, которые
отсекает плоскость на осях  ,
, 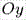 и
и 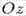 соответственно. Поэтому уравнение
соответственно. Поэтому уравнение  называется уравнением плоскости
"в отрезках".
называется уравнением плоскости
"в отрезках".
Пусть  - какая-нибудь точка плоскости,
- какая-нибудь точка плоскости,  - вектор перпендикулярный плоскости.
Тогда уравнение
- вектор перпендикулярный плоскости.
Тогда уравнение есть уравнение этой плоскости.
есть уравнение этой плоскости.
Коэффициенты  ,
,  ;
;  в уравнении плоскости
в уравнении плоскости 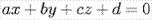 являются координатами вектора,
перпендикулярного плоскости.
являются координатами вектора,
перпендикулярного плоскости.
Если уравнение плоскости разделить на число, равное длине вектора 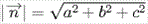 , то получим уравнение плоскости в
нормальной форме.
, то получим уравнение плоскости в
нормальной форме.
Уравнение плоскости, которая проходит через точку 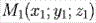 и перпендикулярна ненулевому вектору
и перпендикулярна ненулевому вектору  , имеет вид
, имеет вид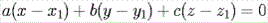 .
.
Всякое уравнение первой степени 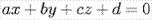 задает в координатном пространстве
единственную плоскость, которая перпендикулярна вектору с координатами
задает в координатном пространстве
единственную плоскость, которая перпендикулярна вектору с координатами 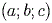 .
.
Уравнение  является уравнением плоскости, проходящей через точку
является уравнением плоскости, проходящей через точку 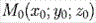 и перпендикулярной ненулевому вектору
и перпендикулярной ненулевому вектору
 .
.
Каждая плоскость 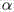 задается в системе прямоугольных координат
задается в системе прямоугольных координат  ,
, 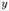 ,
,  уравнением вида
уравнением вида 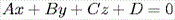 .
.
Верно и обратное утверждение: уравнение вида 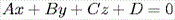 при условии, что среди коэффициентов
при условии, что среди коэффициентов 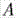 ,
, 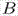 ,
, 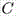 есть ненулевые, задает в пространстве
плоскость в системе прямоугольных координат. Плоскость в пространстве задается
в системе прямоугольных координат
есть ненулевые, задает в пространстве
плоскость в системе прямоугольных координат. Плоскость в пространстве задается
в системе прямоугольных координат  ,
,  ,
,  уравнением вида
уравнением вида 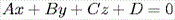 , при условии, что
, при условии, что  .
.
Верно и обратное утверждение: уравнение вида 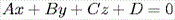 при условии
при условии  задает в пространстве плоскость в
системе прямоугольных координат.
задает в пространстве плоскость в
системе прямоугольных координат.
Плоскость в пространстве задается уравнением 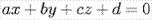 , где
, где  ,
,  ,
,  ,
, 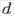 - действительные числа, причем
- действительные числа, причем  ,
,  ,
,  одновременно не равны 0 и составляют
координаты вектора
одновременно не равны 0 и составляют
координаты вектора 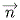 , перпендикулярного этой плоскости и называемого вектором
нормали.
, перпендикулярного этой плоскости и называемого вектором
нормали.
Плоскость в пространстве задается уравнением 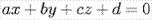 , где
, где  ,
,  ,
,  ,
, 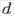 - действительные числа, причем
- действительные числа, причем  ,
,  ,
,  одновременно не равны 0 и составляют
координаты вектора
одновременно не равны 0 и составляют
координаты вектора 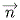 , перпендикулярного этой плоскости и называемого вектором
нормали.
, перпендикулярного этой плоскости и называемого вектором
нормали.
Пусть даны точка 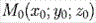 и ненулевой вектор
и ненулевой вектор 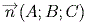 (
(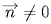 то есть
то есть 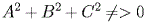 ). Тогда векторное уравнение
плоскости
). Тогда векторное уравнение
плоскости 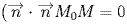 , где
, где  - произвольная точка плоскости) принимает вид
- произвольная точка плоскости) принимает вид  - уравнение плоскости по точке и
вектору нормали.
- уравнение плоскости по точке и
вектору нормали.
Каждое уравнение первой степени 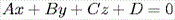 при условии
при условии задает в прямоугольной системе
координат
задает в прямоугольной системе
координат  единственную плоскость, для которой вектор
единственную плоскость, для которой вектор 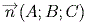 является вектором нормали.
является вектором нормали.
Если 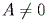 ,
, 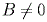 ,
, 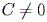 ,
, 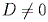 , то уравнение
, то уравнение  можно преобразовать к виду
можно преобразовать к виду . Числа
. Числа  ,
,  и
и 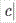 равны длинам отрезков, которые
отсекает плоскость на осях
равны длинам отрезков, которые
отсекает плоскость на осях  ,
, 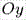 и
и 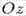 соответственно. Поэтому уравнение
соответственно. Поэтому уравнение  называется уравнением плоскости
"в отрезках".
называется уравнением плоскости
"в отрезках".
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Стереометрия.
Геометрия в пространстве. Александров А.Д., Вернер А.Л., Рыжик В.И.
2. Александров
П. С. Курс аналитической геометрии и линейной алгебры. - Главная редакция
физико-математической литературы, 2000.- 512 с.
. Беклемишев
Д.В. Курс аналитической геометрии и линейной алгебры, 2005. - 304 с.
. Ильин
В. А., Позняк Э. Г. Аналитическая геометрия: Учеб. для вузов. - 7-е изд.,
стер., 2004. - 224 с. - (Курс высшей математики и математической физики.)
. Ефимов
Н. В. Краткий курс аналитической геометрии: Учебн. пособие. - 13-е изд.,
стереот. -, 2005. - 240 с.
. Канатников
А.Н., Крищенко А.П. Аналитическая геометрия. -2-е изд. -, 2000, 388 с
(Сер.Математика в техническом университете
. Кадомцев
СБ. Аналитическая геометрия и линейная алгебра , 2003. - 160 с.
. Федорчук
В. В. Курс аналитической геометрии и линейной алгебры: Учеб. пособие, 2000. -
328 с.
. Аналитическая
геометрия (конспект лекций Троицкого Е.В., 1 курс, 1999/2000)- 118 с.
. Бортаковский,
А.С. Аналитическая геометрия в примерах и задачах: Учеб. Пособие / А.С.
Бортаковский, А.В. Пантелеев. - Высш. шк., 2005. - 496 с: ил. - (Серия
«Прикладная математика»).
. Морозова
Е.А., Скляренко Е.Г. Аналитическая геометрия. Методическое пособие 2004. - 103
с.
. Методические
указания и рабочая программа по курсу «Высшая математика» - 55 с.