Максимумы, минимумы в геометрии
Районная
научно-практическая конференция
«К
вершинам науки»
Тема:
«Минимумы, максимумы в геометрии»
Ученица МОУ СЭЛ № 11Б
класс
Руководитель: Валентина
Ивановна
Ижевск
2010
Введение
«В мире не происходит
ничего, в чем бы не был виден смысл какого-нибудь максимума или минимума»
Леонард Эйлер
(1707-1783)
На уроках математике мы решали
задачи на нахождение наибольшего или наименьшего значения величин, которые
всегда решали с помощью нахождения производной. Эта тема показалась мне довольно
интересной. Я знала, что с подобными задачами люди сталкивались в повседневной
жизни еще в древние века. Причем и по сей день, они не утратили своей
актуальности, поскольку пригождаются не только в математике, но и других
науках, таких как естествознание, экономике, архитектуре, физике. Решая
задания, связанные с максимумами и минимумами у меня возник ряд вопросов: как
человек в древние времена справлялся с решением этих задач, не зная при этом
математического анализа? Значит, существовали и какие-то другие методы решения,
и если да, то какие именно? Эти вопросы побудили меня написать
исследовательскую работу на тему: « Максимумы, минимумы в геометрии», целью
которой было отыскать другие способы решения геометрических задач..
Так же, немаловажным при выборе темы
оказалось и то, что эти задачи очень интересны, ведь они похожи на наши
повседневные проблемы. Мы стараемся приобрести вещи наилучшего качества по
возможности за наименьшую цену; пытаемся максимально увеличить свои доходы,
прилагая при этом минимум усилий и т.д.
В преддверии Единого
Государственного экзамена (ЕГЭ) необходимо повторить стереометрические задачи,
которые встречаются в части С и найти наиболее оптимальные способы их решения.
Цель работы: найти методы решения
задач на нахождение наибольших и наименьших величин, не используя
дифференцирование и применить их для решения геометрических задач.
Задачи.
1. Изучить имеющуюся
литературу по данному вопросу.
2. Описать методы решения
геометрических задач на нахождение наибольших и наименьших величин, не
используя производные
. Решить задачи, использую
данные методы.
максимум минимум геометрическая
задача
1.
Историческая справка
Большой интерес к проблемам
экстремума математики проявляли еще в глубокой древности, а философское
осмысление этих проблем можно найти уже у Аристотеля (384-322 г. до н.э.).
Однако достаточно глубокие математические исследования этих проблем начались
лишь в XVII в. Еще до открытия дифференциального исчисления знаменитый
французский ученый Пьер Ферма (1601 - 1665) в 1638 г. дал формулировку
необходимых условий экстремума.
Мощный толчок развитию исследований
экстремальных задач математики дало создание математического анализа
(дифференциального и интегрального исчисления) великими учеными Исааком
Ньютоном (1642-1727) и Готфридом Вильгельмом Лейбницем (1646-1716).
Примечательно, что первая статья по дифференциальному исчислению была
опубликована Лейбницем в 1684 г. под названием «Новый метод для максимумов и
минимумов, а также для касательных, для которого не является препятствием
дробные и иррациональные количества, и особый вид исчисления для этого».
Если в дифференциальном исчислении
рассматриваются вопросы нахождения экстремумов функций, в которых в качестве
аргументов выступают конечномерные векторы, то в вариационном исчислении
изучаются проблемы определения экстремумов функционалов, для которых
аргументами служат функции.
Подлинным творцом вариационного
исчисления выступил великий математик Леонард Эйлер (1707-1783), основной
период научной деятельности которого был связан с Петербургской академией наук.
Основы вариационного исчисления были заложены Эйлером в его работе «Метод
нахождения кривых, обладающих свойствами максимума или минимума» (1744 г)
.
Основная часть
Максимум - это то, к
чему постоянно стремится минимум, а минимум - это то, чего максимуму всегда не
хватает.
Ф. Кривин
В повседневной жизни человек
постоянно употребляет слова максимум и минимум: увеличить до максимума -
сократить до минимума. Приложить максимум усилий - приложить минимум усилий и
т.д. Но что же значат слова «максимум» и «минимум»?
- Я прошу минимум, -
проговорил Доронин.
А ты максимум проси, -
усмехнулся Костюков.
Страна большая, казна
богатая. Просил бы вдвое, глядишь - своё и получишь…
(«У нас уже утро»
Александр Борисович Чаковский)
Слова maximum и minimum латинские,
они обозначают «наибольшее» и «наименьшее» значение. Термин «экстремум»- от
латинского extremum, что означает «крайнее»- объединяет понятия максимум и
минимум. Впервые этот термин был упомянут французским ученым Дюбуа Раймоном.
Задачи на максимум и минимум во все
времена привлекали внимание ученых. Из попыток решить ту или иную задачу
возникали и развивались новые теории, а иногда и целые направления математики.
Следует поставить перед
собой цель изыскать способ решения всех задач…одним и притом простым способом
Даламбер
Единого метода решения всех
геометрических задач на максимумы и минимумы нет. Выделим одни из главных
методов:
· С использованием
замечательных неравенств.
· Методы исследования
функций классического анализа
· Элементарные методы
решения задач(исследование квадратичной функции)
I. Замечательные неравенства.
Среднее арифметическое и среднее геометрическое в геометрии
Впервые понятие о среднем
арифметическим и среднем геометрическим чисел a и b древнегреческий математик
Папп Александрийский еще в III веке н.э. Он считал, что:
Среднее арифметическое (А) чисел a и
b- это число, удовлетворяющее условию:
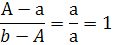
Среднее геометрическое(G) чисел a и
b- это число, удовлетворяющее условию:

Среднее гармоническое (H)- это
число, удовлетворяющее условию
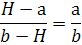
Существуют и более современные
определения этих величин
Определения средних величин:
В математике среднее арифметическое
набора чисел - это сумма всех чисел в этом наборе делённая на их количество.
Среднее геометрическое положительных
чисел x1, x2,..., xn - число, равное
арифметическому корню n-й степени из их произведения
Средним гармоническим
действительных положительных чисел 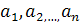
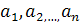
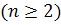
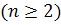 называют положительное
число H=H(
называют положительное
число H=H(

Средним квадратическим
(квадратичным) действительных чисел 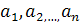
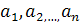
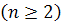
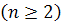 называют действительное
неотрицательное число
называют действительное
неотрицательное число
=Q(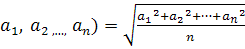
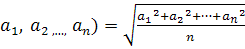
Очень часто
геометрические задачи на экстремумы можно решить, применив неравенство Огюстен
Луи Коши(французский математик) (неравенство о среднем арифметическим и средним
геометрическим 1821г):
Теорема: Среднее
арифметическое положительных чисел не меньше их среднего геометрического.
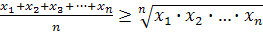
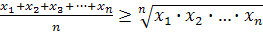 обобщенная теорема или
обобщенная теорема или
) 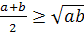
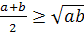
) 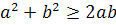
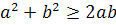
) 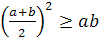
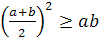
) 

Доказательство:
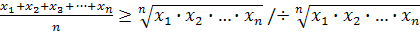
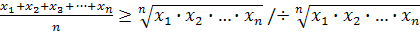 ;
;
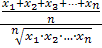
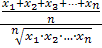
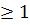
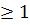 ;
;

Обозначим
1=
 ,…, yn=
,…, yn=
 , отсюда
, отсюда
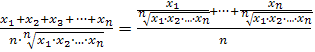
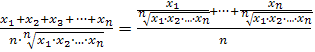 =
=

Применим метод
математической индукции
)Проверим верно ли
неравенство 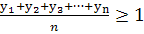
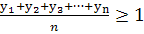 при n=1
при n=1

 значит
значит 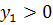
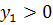
(утверждение верно)
) Предположим, что для
n=k утверждение верно
) Докажем, что
утверждение верно и для n=k+1
Докажем, что если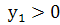
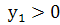 ,…
,…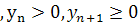
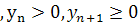 ;
; 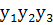
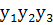 …
…
 =1,то
=1,то
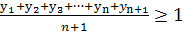
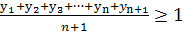 ;
;
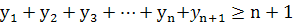
Пусть 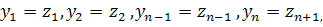
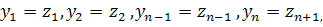
Так как 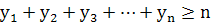
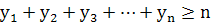 , то
, то
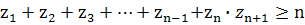
Если все числа 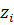
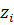 одновременно не равны
1, то существуют два таких числа, для которых выполняется:
одновременно не равны
1, то существуют два таких числа, для которых выполняется:
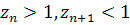
Заменим произведение 
 на сумму
на сумму 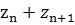
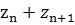
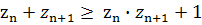
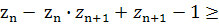
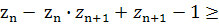 0
0
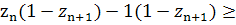
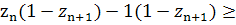 0
0

Так как

 то
то

 верно q.e.d.
верно q.e.d.
способ

) 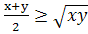
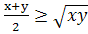
Пусть a = 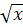
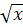 , b=
, b=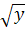
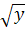
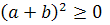
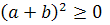 отсюда
отсюда

 +
+
 a
a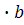
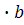 +y
+y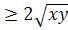
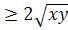

)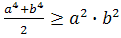
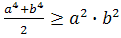
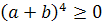
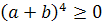
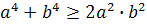
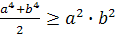
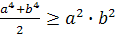 аналогично
аналогично
) 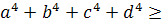
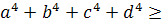 2(
2(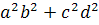
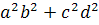 )
)
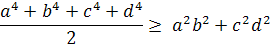
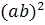
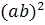 +
+ 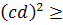
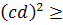 2a
2a
 b
b
 c
c
 d
d

 a
a
 b
b
 c
c
 d, отсюда
d, отсюда
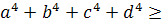
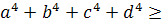 4 a
4 a
 b
b
 c
c
 d
d

 a
a
 b
b
 c
c
 d
d





Теорема: Для любых
положительных чисел a и b справедливы следующие соотношения:
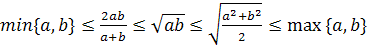
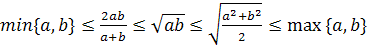 , где символом
, где символом 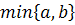
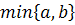 обозначено наименьшее из
чисел a и b, символом обозначено
обозначено наименьшее из
чисел a и b, символом обозначено 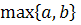
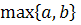 наибольшее из этих
чисел, причем равенство между любыми из этих «средних» чисел имеет место при
a=b,
наибольшее из этих
чисел, причем равенство между любыми из этих «средних» чисел имеет место при
a=b, 


Доказательство:
Возьмем полуокружность с
центром О. А- произвольная точка на продолжении диаметра СB
Опустим перпендикуляра
из точек D и E
┴BC┴BC
Проедем прямые: AE-
касательная, АD - секущая
) Пусть AB=a, AC=b (a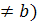
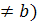 , тогда
, тогда
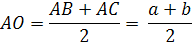
)Так как OE-радиус, то 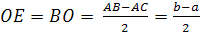
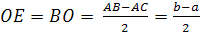
) Т.к AE- касательная,
то OЕ┴АЕ (по свойству касательной), треугольник ОЕА -прямоугольный
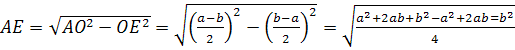
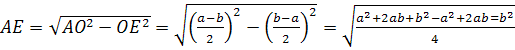
=

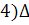 AOD- прямоугольный,
поэтому:
AOD- прямоугольный,
поэтому:

Из прямоугольного
треугольника ОЕА по свойству высоты, проведенной из прямого угла

Так как: >
AO>AE>AF(так как в прямоугольном треугольнике гипотенузы всегда больше
катетов), то можно составить неравенства:

Задачи с использованием
замечательных неравенств
Задача 1
Докажите, что из всех
треугольников данной площади равносторонний имеет наименьший периметр.

Дано: 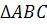
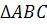 ABC=S
ABC=S
Р- наименьший
Доказать:

Решение:
По формуле Герона:
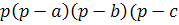
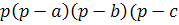 )=
)=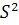
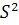
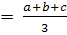
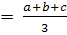
По теореме Коши для
четырех чисел:
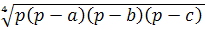
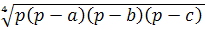 =
=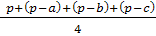
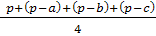 =
=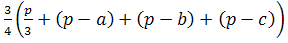
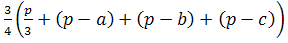
Произведение четырех
сомножителей постоянно 
 =
=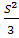
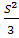
То их сумма минимальна,
если они все равны между собой, то есть

 отсюда=b=c=
отсюда=b=c= 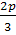
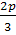 то есть треугольник
равносторонний. Q.e.d.
то есть треугольник
равносторонний. Q.e.d.
Задача 2
Докажите, что
максимальная полная поверхность прямоугольного параллелепипеда равна 
 , где L -сумма всех
ребер параллелепипеда.
, где L -сумма всех
ребер параллелепипеда.
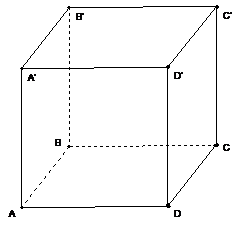
ABCDA1B1C1D1-прямоугольный
параллелепипед 1=a=c=b
Доказать: Sполн.пов=

Доказательство:
)Sполн.пов=
2SAA1D1D+2SAA1B1B+2SABCD=2ab+2ac+2bc=2(ab+bc+ac)
)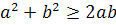
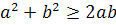
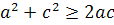
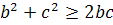
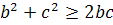 сложим эти неравенства
сложим эти неравенства
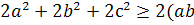
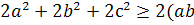 +bc+ac)
+bc+ac)

 +bc+ac, при a=b=c
+bc+ac, при a=b=c
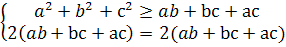
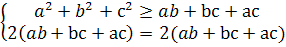 сложим эти два
неравенства
сложим эти два
неравенства

 /
/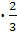
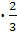
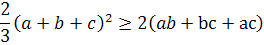 =
=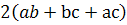
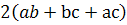 , отсюда
, отсюда 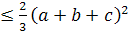
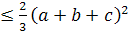
Так как L-сумма всех
ребер, то+b+c = 

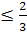
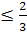


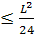
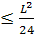 значит
значит
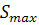
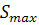 =
=
 q.e.d.
q.e.d.
Задача 3
Найдите наибольший
периметр параллелограмма, диагонали которого 6 см и 8 см.
Решение.
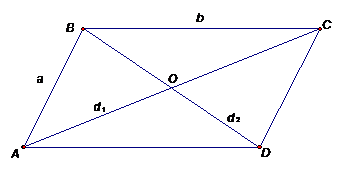
1. Пусть а и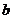 -- длины соседних сторон параллелограмма, а
-- длины соседних сторон параллелограмма, а 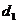 и
и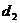 --
длины диагоналей параллелограмма. Тогда периметр параллелограмма
--
длины диагоналей параллелограмма. Тогда периметр параллелограмма 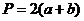 .
.
. Докажем, что из
всех параллелограммов с данными диагоналями наибольший периметр имеет ромб.
По теореме о сумме квадратов
диагоналей параллелограмма 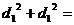
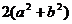 значит, сумма квадратов
сторон есть величина постоянная.
значит, сумма квадратов
сторон есть величина постоянная.
По неравенству между
средним арифметическим и средним квадратичным



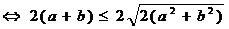 ,
,
причем равенство
достигается тогда и только тогда, когда  . Значит, параллелограмм
с наибольшим периметром является ромб.
. Значит, параллелограмм
с наибольшим периметром является ромб.
Имеем 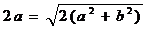
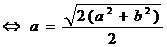
С учетом 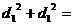
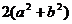

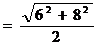
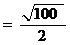 =5
=5
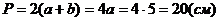
Ответ: 20 см.
Задача 4
Из гранита нужно
вырубить постамент в форме прямоугольного параллелепипеда, высота которого
должна быть равна диагонали основания, а площадь основания должна быть равна 4 
 . При каких длинах
сторон основания площадь поверхности постамента будет наименьшей.
. При каких длинах
сторон основания площадь поверхности постамента будет наименьшей.

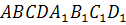
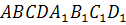 -прямоугольный
параллелепипед
-прямоугольный
параллелепипед

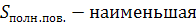 =x, BC=y,
=x, BC=y, 

Найти: x, y
Решение:
)По теореме Пифагора:
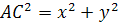
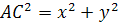 отсюда
отсюда
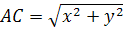
По условию AC=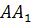
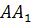 =
=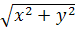
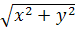
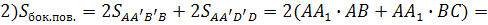
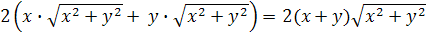
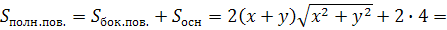

)xy=4
 (по условию)
(по условию)
По формулам
замечательных неравенств:
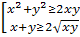
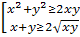
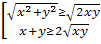
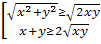
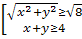
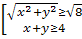
)Площадь полной
поверхности прямоугольного параллелепипеда будет наименьшей, если его высота и
сумма сторон основания будет наименьшими,
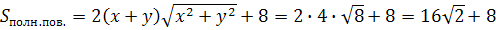
Ответ: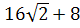
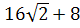
II. Аналитический
метод(исследование функции)
Большинство стереометрических задач
на отыскание наибольшего и наименьшего значения решаются аналитически. Чаще
всего используется соответствующая формула, выбирается независимая переменная,
которую обычно обозначают буквой х, получают функцию, выражающую величину,
наибольшее или наименьшее значение которой требуется найти, определяют границы
измерения аргумента х. Полученная функция исследуется элементарными методами.
Задача 1
Через вершину конуса провести
плоскость так, чтобы площадь ее сечения была максимальной

Найти Sсеч
Решение:
SCDE=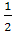
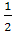 CD
CD
 CE
CE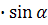
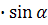 =
=


 , где
, где 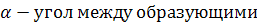
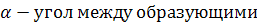 , l- длина образующей.
, l- длина образующей.
Площадь треугольника
будет наибольшей, если треугольник прямоугольный, то есть в нашем случае угол
между образующими должен быть равен 90
 , тогдаCDE =
, тогдаCDE =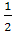
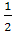

 =
=

Ответ: 

Задача 2
Найти наименьший из всех
объемов конусов, описанных около шара радиуса r.

радиус конусарадиус шара
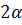
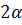 -угол между образующей и
плоскостью основания
-угол между образующей и
плоскостью основания
Найти: Vнаим
Решение:осевая линия
конуса, значит┴AB
∠OAD=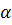
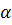 =R= r
=R= r
 =AD
=AD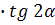
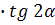 =
=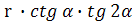
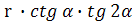 =
=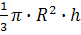
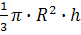 =
=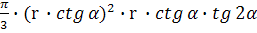
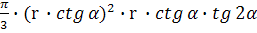 =
=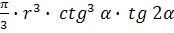
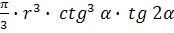 =
=
=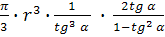
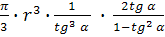 =
= 
 =
=

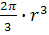
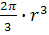 -постоянная величина
-постоянная величина
Значит необходимо найти
при каком значении 
 наименьшая
наименьшая
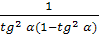
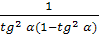 имеет наименьшее
значение, значит
имеет наименьшее
значение, значит
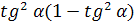
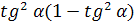 - должна иметь
наибольшее значение
- должна иметь
наибольшее значение
Так как 
 =1 величина постоянная,
то функция
=1 величина постоянная,
то функция
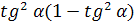
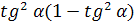 принимает наибольшее
значение при
принимает наибольшее
значение при 
 =
= 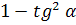
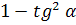
То есть 2
 =1
=1
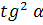
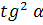 =
= 
 min =
min =
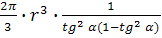
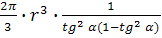 =
= 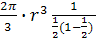
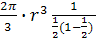 =
= 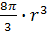
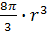
Ответ:

Задача 3
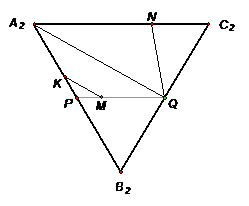
Площадь основания правильной
треугольной призмы 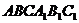 равна
равна
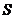 .
Точки
.
Точки  и
и
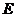 -
середины ребер ВС и
-
середины ребер ВС и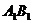 соответственно. Рассматриваются треугольники, вершинами которых служат точки
пересечения плоскостей, параллельных основаниям призмы, с отрезками
соответственно. Рассматриваются треугольники, вершинами которых служат точки
пересечения плоскостей, параллельных основаниям призмы, с отрезками  ,
,
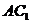 ,
и
,
и 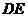 .
Найти наименьшее значение площади рассматриваемых треугольников
.
Найти наименьшее значение площади рассматриваемых треугольников
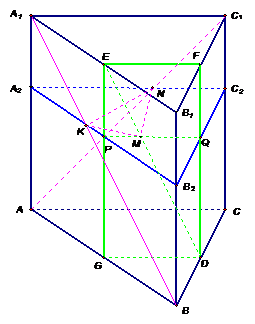
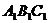
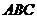
. Т.к 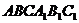 правильная
треугольная призма, значит
правильная
треугольная призма, значит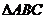 равносторонний,
равносторонний, 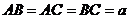 ;
По формуле площади правильного треугольника
;
По формуле площади правильного треугольника 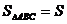 .
.
. Построим
плоскость 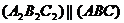 .
.
а. Тогда 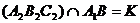 ;
;
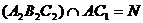 .
.
б. Пусть 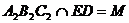 .
.
Проведем 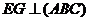 и
и
 ,
где
,
где  ;
;
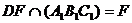
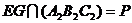 ,
,  ,
значит
,
значит 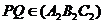 и
и
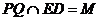
. Пусть 
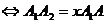 ,
тогда
,
тогда 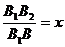
 и
и
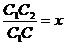
 ,
причем по условию задачи
,
причем по условию задачи
. Т.к. 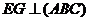 (по
построению),
(по
построению),  (как
боковое ребро правильной призмы), то
(как
боковое ребро правильной призмы), то 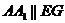 (по признаку).
Аналогично
(по признаку).
Аналогично 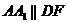 .
.
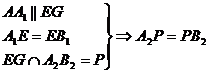 (по теореме Фалеса).
Аналогично
(по теореме Фалеса).
Аналогично  .
.
 -средняя линия
-средняя линия 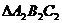 (по
определению), отсюда
(по
определению), отсюда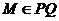 .
.
5. Рассмотрим подобные
треугольники.

Из  (по
двум углам):
(по
двум углам): 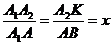 ,
отсюда
,
отсюда  .
Т.к.
.
Т.к.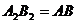 ,
то
,
то 
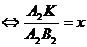 , а
, а 
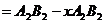
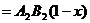
а. Аналогично из  и
и
 получаем
получаем
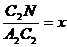 и
и
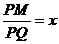 соответственно.
соответственно.
б. Из  (по
двум углам):
(по
двум углам): 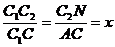 ,
отсюда
,
отсюда 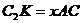 .
Т.к.
.
Т.к.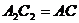 ,
то
,
то 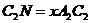
 , а
, а 

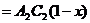
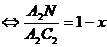
в. Из 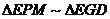 (по
двум углам):
(по
двум углам): 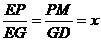 ,
отсюда
,
отсюда  .
Т.к.
.
Т.к. ,
то
,
то 
 , а
, а 

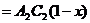
г. Получили 

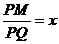 .
.
. Найдем площадь 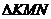 .
.

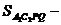


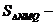

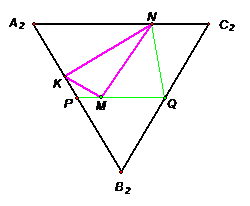
а. Поскольку 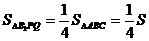 (по
свойству средней линии), тогда
(по
свойству средней линии), тогда 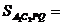
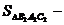
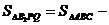
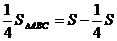
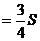 .
.
б. Поскольку  медиана
медиана
 ,
то
,
то 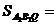
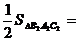
 . Тогда
. Тогда 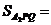
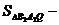
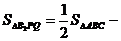

 .
.
в.  и
и 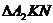 имеют
общий угол, это
имеют
общий угол, это  ,
то по теореме о соотношении площадей треугольников, имеющих общий угол, имеем
,
то по теореме о соотношении площадей треугольников, имеющих общий угол, имеем 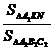
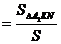
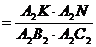
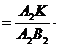
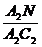 =
=

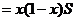
Аналогично,  и
и
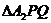 имеют
общий угол, это
имеют
общий угол, это 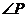 ,
значит
,
значит
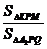
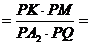
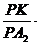
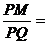
=
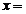

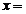
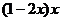
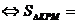

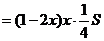
г. Аналогично  и
и
 имеют
общий угол, это
имеют
общий угол, это  ,
значит
,
значит 
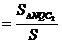
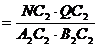
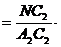
 =
=

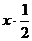



д.

 (как треугольники с
одним и тем же основанием и равными высотами)
(как треугольники с
одним и тем же основанием и равными высотами) 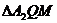 и
и 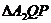 имеют
общий угол, это
имеют
общий угол, это 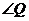 ,
значит
,
значит
е. 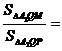
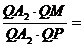
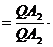
 =
=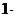

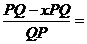

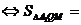
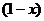

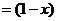

Следовательно, 
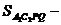


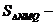
 =
=
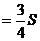
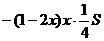
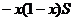
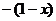

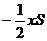 =
=
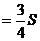
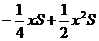
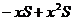
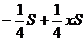
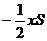 =
=
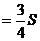
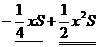
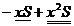

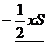 =
=

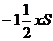


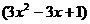
. Поскольку  -
величина постоянная, то наименьшее значение функции
-
величина постоянная, то наименьшее значение функции 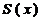 зависит
зависит
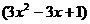 при
при .
Исследуем функцию
.
Исследуем функцию 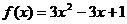 на
минимум. Квадратный трехчлен
на
минимум. Квадратный трехчлен 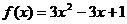 принимает свое
наименьшее значение на указанном отрезке в точке
принимает свое
наименьшее значение на указанном отрезке в точке 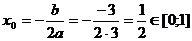 . Следовательно,
наименьшее возможное значение функции достигается также при
. Следовательно,
наименьшее возможное значение функции достигается также при 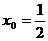 и
равно
и
равно 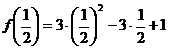
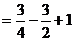


 . Тогда
. Тогда 
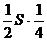
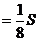
Ответ: 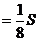
III.
Мат анализ. Решение задач с помощью производной
Определение:
Производная - основное понятие
дифференциального исчисления, характеризующее скорость изменения функции.
Определяется как предел отношения приращения функции к приращению ее аргумента
при стремлении приращения аргумента к нулю, если таковой предел существует.
Термин «производная» был введен
французским математиком Лагранжем(1736 - 1813).
Далее я рассмотрела задачу, в
которой наибольшее значение находиться тремя способами.
Задача. В прямоугольном
параллелепипеде ABCDA1B1C1D1 с
ребрами CD = 24, AD= 6 и DD1 =4 проведена плоскость через центр
симметрии грани A1B1C1D1, вершину А
и точку Р, лежащую на ребре DC. Какую наименьшую площадь может иметь сечение
параллелепипеда этой плоскостью? На какие части делит точка P ребро DC в этом
случае?
Решим задачу тремя способами и
решим, который из них быстрее и проще
В правильную четырехугольную
пирамиду, сторона основания которой равна а, а высота пирамиды h, вписана
правильная четырехугольная призма. Найдите площадь боковой поверхности призмы
через a и h.
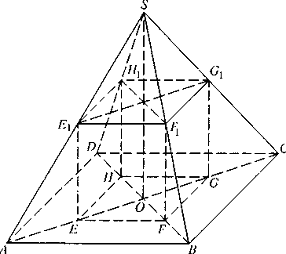
Дано: Пусть 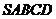 -
правильная четырехугольная пирамида,
-
правильная четырехугольная пирамида, 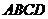 - квадрат,
- квадрат,  ,
тогда диагонали
,
тогда диагонали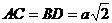 .
.
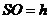 -высота
пирамиды, где
-высота
пирамиды, где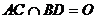 .
.
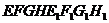 - вписанная правильная
четырехугольная призма, так что
- вписанная правильная
четырехугольная призма, так что 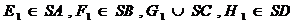 .
.
 , значит
, значит 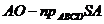 .
т.к.
.
т.к.
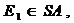 то
то  аналогично
аналогично
 .
.
Найти: 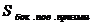 -
наибольшую
-
наибольшую
Решение:пр AS(ASO)
Так как призма
правильная, то Sбок. пов.= 4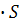
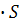 EE1F1F=4
EE1F1F=4
 EE1
EE1
 EF
EF
)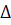
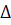 SOA
SOA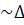
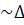 E1EA
E1EA
Пусть 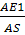
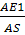 =
=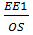
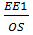 =
=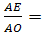
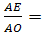 x, отсюда так как OS=h1=x
x, отсюда так как OS=h1=x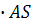
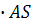 ; 1=
; 1=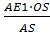
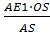 =
= 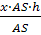
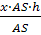 = x
= x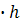
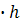 =x
=x
)ABCD-квадрат, так как
SABCD-правильная пирамида, значит =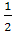
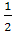 AC =
AC = 


 =
= 


 =
= 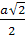
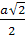 (по Т. Пифагора)=x
(по Т. Пифагора)=x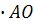
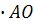 =
=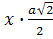
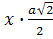 =AO-AE=
=AO-AE=
 -
- 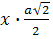
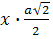 =
= 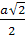
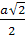 (1-x)
(1-x)
)так как EFGH E1F1G1H1
-правильная пирамида
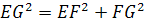
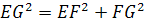 = 2
= 2
 , отсюда
, отсюда
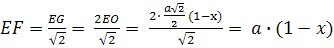
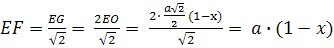
) Sбок. пов.=
4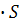
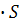 EE1F1F=4
EE1F1F=4
 EE1
EE1
 EF
EF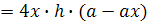
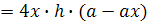
Так как x и h-постоянные
величины, то будем исследовать функцию x(1-x)
1. Элементарный
способ(исследование квадратичной функции):
f(x)= x-

Это квадратичная
функция. Ее графиком является парабола, ветви которой направлены вниз, значит
наибольшее значение данной функции будет в точке х0
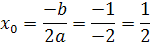 бок. пов.=
4
бок. пов.=
4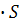
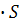 EE1F1F =
EE1F1F =
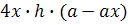
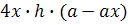 = 4
= 4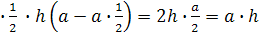
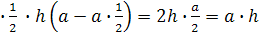
Ответ: 

2. С применением производной:
f(x)= x-

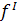
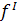 (x)=
(x)= 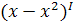
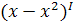 =1-2x
=1-2x
-2x=0= 

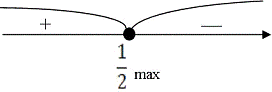
(2)=2-4<0бок.
пов.= 4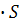
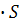 EE1F1F =
EE1F1F =
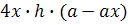
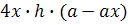 = 4
= 4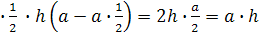
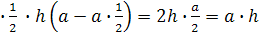
Ответ: 

3. С помощью среднего
арифметического и среднего геометрического
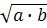
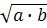 <
<
 то есть
то есть
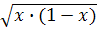
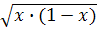 <
<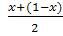
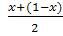 ;
;
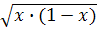
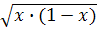 <
<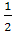
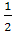
. f(x) = 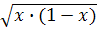
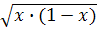 -
-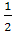
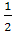
. ОДЗ: x-
 >0
>0
. Нули: 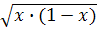
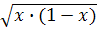 -
-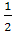
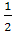 = 0
= 0
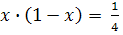
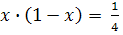 /
/ 

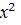
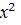 - 4х+1=0
- 4х+1=0
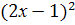
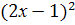 =0
=0
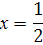 бок. пов.=
4
бок. пов.=
4
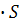 EE1F1F =
EE1F1F =
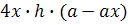
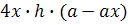 = 4
= 4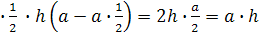
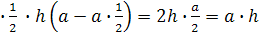
Ответ: 

Вывод
Выбирая тему для
исследовательской работы, я поставила для себя цель найти новые способы решения
геометрических задач на нахождение наибольших и наименьших значений функции и выяснить,
какой из них удобнее применять при решении задач. В ходе работы над проектом я
освоила аналитические методы задач и решение задач при помощи замечательных
неравенств. Геометрический подход к экстремальным задачам обычно приводит к
кратким и изящным решениям. Зачастую эти решения опираются на нестандартную
идею, придумать которую довольно трудно.
Замечание. Функцию
>'(л:) =х(1 -л) можно исследовать на наибольшее значение по-другому. Так как
х е (О, 1), ю и (1 - х) 6 (О, 1). В силу нера-
/-г- а +6 венства \аЬ
< -г- о среднем геометрическом и среднем арифметическом
., /Х + (\-Х)\1 1
„
двух положительных чисел
х (х - 1) < I-----\ --. Равенство в этом неравенстве достигается в точке х0,
удовлетворяющей условию х0 = 1 - х0. г. е. в точке.х0 = - Значит, наибольшее
значение функции у (х) на (0,1) равно-.
Отметим, что неравенство
л/ай~< -;- удобно использовать при нахождении наибольшего значения функции
вида /(.х) (А - /(х)), где 0«г/(.х) < А. А = соп51, или при нахождении
наименьшего значения функции вида
/(х) + -!-, где /(х)
> О, А = сопз!, А > 0.
Аналогично можно
использовать и другие неравенства о средних:
аЬ а+Ь
где а > О, Ь > 0.
Равенства в этих неравенствах достигаются тогда и только тогда, когда а = Ь.
Список используемой
литературы
4. «Элементарная геометрия» том 2 Стереометрия Понарин Я. П.
«МЦНМО» 2006г
5. «Стереометрические задачи и методы их решения» Э.Г. Готман
«МЦНМО» 2006г
6. «Пособие по математике для поступающих в ВУЗы» 5-е издание
Дорофеев, Потапов, Розов 1976г
. «Рассказы о максимумах и минимумах» В.М. Тихомиров
«Наука» Москва 1986г
. «Задачи на максимум и минимум» Сергей Ахтыршев
«БХВ-Петербург» Санкт-Петербург 2004
. «Неравенства в задачах» И.Х. Сивашинский 1967г
. Журнал «Квант»