Геометричні екстремуми

Геометричні екстремуми

НАЦІОНАЛЬНИЙ ПЕДАГОГІЧНИЙ УНІВЕРСИТЕТ

ІМЕНІ М.П.ДРАГОМАНОВА

Кафедра вищої математики

КУРСОВА РОБОТА

з геометрії

на тему: Геометричні екстремуми

Студента 2 курсу 21 МІА групи

напряму підготовки: Математика

спеціальності математика, інформатика та

адміністрування комп`ютерних систем

Мар’янчик Анастасії Вікторівни

Керівник проф.. фіз.-мат. наук

Працьовитий М. В.

м. Київ - 2013 р.

Вступ

З давніх часів перед людиною виникають практичні проблеми вибору оптимального значення деякої величини при певних умовах.

Як правило, в задачах подібного роду досягнення деякого результату може бути здійснено не єдиним способом і доводиться відшукувати найкращий спосіб досягнення результату.

Однак в одній і тій же задачі в різних ситуаціях найкращими можуть бути зовсім різні рішення. Тут все залежить від обраного або заданого критерію. Наприклад, які повинні бути найкращі обриси судна? Відповіді будуть різними в залежності від того, для яких цілей призначене судно. Для різних цілей різні будуть і головні критерії. Критерії можуть бути наступними:

. Необхідно, щоб при русі у воді судно відчувало найменший опір (це головний критерій швидкохідного судна)

. Необхідно, щоб судно було максимально стійким при сильному хвилюванні і сильному вітрі.

. Необхідно, щоб судно мало найменшу осадку (у разі коли судно призначається для експлуатації на дрібних водоймах).

Завдання такого характеру, отримали назву задачі на екстремуми або завдання на оптимізацію, виникають у самих різних областях людської діяльності. І їх роль в житті людей дійсно дуже важлива. Вирішенням таких завдань займалися найбільші математики минулих епох - Евклід, Архімед, Аполлоній, Герон, Тарталья, Торрічеллі, Ньютон та багато інших. Адже, незважаючи на все різноманіття, їх об'єднує одна особливість - пошук найбільш вигідного, у певному відносинах, найбільш економного, найменш трудомісткого, найбільш продуктивного рішення. Цей пошук коротко можна назвати пошуком кращого.

Метою курсової роботи є вивчення різних методів розв'язання задач на екстремуми.

Завданням курсової роботи є: розглянути стародавні задачі на максимум і мінімум, зрозуміти навіщо розв’язують задачі на максимум і мінімум, розглянути найдавнішу задачу - задачу Дідони, задача Евкліда, задача Архімеда, задача Фаньяно, задача Ферма-Торрічеллі-Штейнера, задача Штейнера.

Стародавні задачі на максимум і мінімум

Навіщо розв’язують задачі на максимум і мінімум.

Про максимуми і мінімуми ми дізнаємося в школі. Ось одна старовинна задача, яку ми могли розв’язувати на уроці геометрії.

Дано дві точки А і В які лежать по одну сторону прямої l. Потрібно знайти на l таку точку D, щоб сума відстаней від А до D і від В до D була найменша (мал.1).

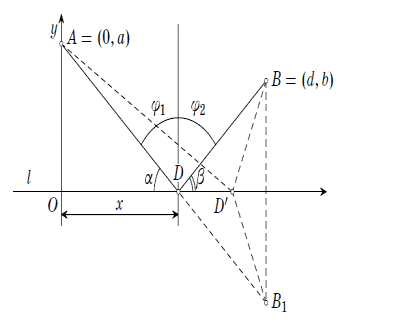
Мал. 1

Тут потрібно знайти найменше значення, тобто мінімум. В більшості задач потрібно знайти максимум, тобто найбільше значення чого не будь. Обоє понять - максимум і мінімум - об’єднані одним терміном - «екстремум», що на латині означає «крайнє». Задачі на відшукання максимуму і мінімуму називаються екстремальними задачами. Методи розв’язання і дослідження різних видів екстремальних задач складають розділи математичного аналізу. Вони об’єднані в загальний розділ, який називається теорія екстремальних задач.

Тут наша мета - розглянути два запитання: навіщо розв’язують задачі на максимум і мінімум та із яких компонентів складається теорія екстремальних задач.

Вище була поставлена геометрична задача. Її можна зустріти в кожній книжці із геометрії. Коли ж вона з’явилася вперше? І навіщо?

Вважають, що автором цієї задачі являється відомий математик античності Герон Олександрійський. Про Герона ми багато дізналися завдяки формулі площі трикутника, яка носить його ім’я. Книга, де знаходиться ця задача, називається «Про дзеркала» . Про дату її написання є спори., але більшість дослідників сходяться в тому. Що вона написана і столітті до н. е. Сама робота Герона не збереглася, і про неї відомо лише із коментарів, написаних пізніше.

Розв’язання задачі Герона.

Нехай В1 - точка, симетрична в відносно прямої l. З’єднаємо А і В1. АВ1 перетинається із прямою l і дає шукану точку D (див. мал. 1).

Дійсно, для будь-якої точки D`, відмінної від D, має місце рівність

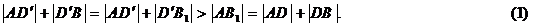
Тут і далі ми будемо використовувати наступні позначення: - відрізок, з’єднуючий точки А і В, 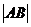 - довжина відрізка , АВǁCD - пряма АВ паралельна CD.

В нерівності (1) ми використовували властивості симетрії, із якої слідує рівність 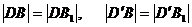 і нерівність трикутника 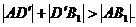 задача розв’язана.

Відповідь: шукана D володіє властивістю, що кут α дорівнює куту β (див. мал. 1), а також кут φ1 дорівнює куту φ2, або можна сказати так, кут падіння рівний куту відбиття.

Попробуємо тепер, використати ідею, закладену у щойно проведеному міркуванні, розв’язати наступні задачі.

Задача 1. Даний кут і точка С всередині нього. Знайти точки А і В на сторонах кута, так щоб периметр трикутника АВС був найбільшим.

Задача 2. Даний кут і дві точки С і D всередині нього. Знайти точки А і В на сторонах кута так, щоб сума довжин  була найменшою.

Повернемося до задачі Герона. Герон досліджує у своїй книзі закони відбиття світла і пропонує свої домисли до запитань, зв’язаних із властивостями дзеркал. Зокрема. Він доводить, що параболічне дзеркало фокусує пучок променів, паралельних оси параболи.

В ту пору закони природи старалися осягнути умоглядно, з допомогою логічних роздумів, не звертаючись до експерименту. У нас ще буде привід поговорити про зародження сучасної науки, що спирається на досвід. Першим експериментатором в історії був Г. Галілей, який жив у XVII столітті, Герон при пояснені законів відображення шукав для них логічну підставу. Він висловив пропозицію, що природа діє найкоротшим шляхом. Ось як пише про це один із його коментаторів Доміанос: «Герон …показав, що прямі, наклонені під рівними кутами, є самими меншими із усіх проміжних, які утворюють нахили з однієї і тієї ж сторони і від однієї і тієї ж прямої. Доводячи це, він говорить, що якщо природа не хоче попросту обводити промінь зору, то вона зламає їх під рівними кутами».

Дослідники історії науки припускають, що тут вперше прозвучала думка про те, що природа керує екстремальними принципами. Ідею Герона розвив Ферма. Ферма вивів відомий до того часу закон заломлення світла від одної точки до іншої в неоднорідному середовищі характеризується тим, що уздовж неї тратиться найменше часу. Починаючи з того моменту, ідея екстремальності проявів природи стає провідною зіркою всього природознавства. На підтвердження і були наведені як епіграф слова Ейлера. Відкладемо поки що обговорення дивовижності цього феномену, але факт залишається фактом: траєкторії світла і радіохвиль, рух маятників і планет, течії рідин і газів і багато інших рухи виділяються з різноманіття всіх можливих рухів тим, що вони є рішеннями деяких завдань на максимум або мінімум. Ця обставина виявляється плідним засобом математичного опису природи.

Ось у чому полягає перша причина, що спонукає вирішувати завдання на максимум і мінімум і розвиватися теорії екстремальний завдань. Вона привела в ХВІ столітті до створення спеціального розділу цієї теорії, який був названий варіаційним обчисленням.

Друга причина криється в нас самих. Людям властиво прагнення до кращого, і тому їм завжди хочеться вибрати оптимальну з наявних можливостей. Трапляється, що математика може тут допомогти.

Обговоримо це, і нехай знову завдання Герона послужить нам прикладом. Іноді в підручниках їй надають вид проблеми, що виникає на практиці. Тоді пряма l стає, скажімо, прямолінійним ділянкою залізниці, точки A і B - містами, точка D - залізничною платформою. І постає питання: де слід поставити платформу, щоб з'єднують її з містами прямолінійні шосейні ділянки мали найменшу сумарну довжину?

Ось ще кілька геометричних задач, які можуть мати прикладне значення.

Задача 3. Нехай є три міста - A, B і C. Потрібно вказати таке місце D, щоб сумарна довжина прямолінійних ділянок шосе, що з'єднують D з A, B і C, була мінімальною.

Задача 4. Те ж саме, що і в задачі 3, але для чотирьох міст.

Задача 5. Чи зміниться рішення попередньої задачі, якщо поставити питання про найменшій довжині шосейної дороги,з'єднує 4 міста, і при цьому не уточнено, що всі шляхи повинні з'єднуватися в одній точці?

Звичайно, такого роду завдання являють собою лише моделі реальних життєвих ситуацій. На практиці все йде набагато складніше: і ділянки залізної дороги не бувають прямолінійними,і шосе не будують суворо за прямими, і «сума відстаней» в чистому вигляді рідко буває «критерієм оптимальності». Але без сумніву, що і при будівництві залізних, шосейних або інших доріг, так само як і при будівництві газо- і нафтопроводів,і при чому іншому, зазвичай виникає питання про те, як це здійснити найбільш доцільно, скажімо, найбільш дешево.

Такі проблеми постійно виникають у господарській діяльності. Весь час доводиться вишукувати або най дешевший, або найшвидший, або самий короткий, або самий економічний спосіб досягнення мети.

Наведемо приклад проблеми оптимізації економічного утримання. Нехай є бази з деяким продуктом, магазини та автопарк. Як випливає диспетчеру автопарку організувати доставку необхідного продукту в магазини найбільш економічно? (Такого типу задачі називаються «транспортними». У наслідку ми уточнимо їх постановку.) При вирішенні подібних питань доводиться звертатися до математики. Методи, розроблені для вирішення завдань на максимум і мінімум до сере-діне XX століття, виявилися недостатніми для вирішення подібних проблем.

З'ясувалося, зокрема, що в багатьох завданнях економічного змісту велику роль відіграє поняття опуклості - там часто зустрічаються опуклі і навіть лінійні функції множини. Довелося істотно розвинути теорію опуклих множин і функцій. Ця теорія отримала навіть спеціальну назву - опуклий аналіз. Були створені і нові напрямки в теорії екстремальних задач - лінійне і опукле програмування. Почала цих напрямків були закладені в 1930-тіроки радянським математиком Л. В. Канторовичем.

Велике число завдань оптимізації виникає в техніці. Це завдання управління технологічними процесами, приладами,системами. Ось приклад. Нехай є візок, що рухається прямолінійно без тертя по горизонтальних рейках. Візок управляється зовнішньою силою, яку можна змінювати в заданих межах. Потрібен зупинити візок в певному положенні в найкоротший час. Ця задача називається найпростішої завданням про швидкодію в автоматичному регулюванні. Дуже багато завдань виникло в хімічній промисловості,в космонавтиці і т. п. При цьому з'ясувалося також, що методи варіаційного обчислення недостатні для вирішення цих завдань. Довелося створювати нову главу, що доповнює варіаційне числення. Вона отримала назву оптимального управління.

Ось і друга причина, що змушує нас вирішувати задачі оптимізації і розвивати теорію екстремальних завдань, - бажання «задовольнити вимогам практики», про який говорив Чебишев.

Але цими двома причинами не можна пояснити всього.

У наступному оповіданні мова піде про найдавніші завдання на максимум і мінімум - про класичну ізоперемитричну задачу. Близько двадцяти п'яти століть тому в Стародавній Греції було відкрито чудова властивість кола - серед замкнутих кривих заданої довжини охоплювати найбільшу площу. Ви,напевно, вирішували в школі завдання, що описують аналогічні властивості багатокутників. Згадаймо дві з них.

Задача 6. Знайти трикутник заданого периметра, що має найбільшу площу.

Задача 7. Довести, що квадрат має найбільшу площу серед усіх прямокутників з заданим периметром.

Питання, рівносильний останньої задачі, розглядався ще в "Засадах" Евкліда; рішенням цієї ж завдання Ферма проілюстрував свій метод знаходження максимумів і мінімумів,відомий нам як теорема Ферма.

Навіщо ж ставилися і для чого вирішувалися такі завдання? Що приваблює в них? Чому в більшості книг з геометрії автори так люблять обговорювати завдання на максимум і мінімум?

Це не так легко пояснити, але факт залишається фактом, що протягом всієї історії математики завдання на екстремум викликали інтерес і бажання вирішувати їх. Може бути, вся справа в тому, що людині властиве прагнення до досконалості, в тому,що є якийсь таємничий стимул осягнення «самої суті »? А може бути, в екстремальних задачах завжди або, принаймні, часто присутнє щось витончене, привабливе, щось від тієї краси, про яку говорить Рассел? І саме це спонукає нас вирішувати завдання на максимум і мінімум?

Сказаного досить, щоб зрозуміти важливість і захопливість обраного нами предмета.

Але, може бути, не зайве сказати про тимчасових кордонах наших оповідань. Перші завдання на максимум і мінімум були поставлені в дуже далекі часи: класичні ізопериметричні завдання обговорювалася в V столітті до н. е.. Про неї ми поговоримо в наступній розповіді. А в передостанньому, чотирнадцятому, оповіданні ми обговоримо проблеми, які виникають в наші дні.

Довгий час кожна задача на екстремум вирішувалася індивідуально. У XVII столітті виразно стала відчуватися необхідність створення якихось спільних методів. Такі методи були розроблені Ферма, Ньютоном, Лейбніцем і іншими - спочатку для однієї, потім для декількох, а потім і нескінченного числа змінних. У підсумку сформувалися основні розділи теорії екстремальних задач: математичне програмування, тобто теорія скінчено вимірних завдань оптимізації, опукле (у тому числі лінійне) програмування (де вивчають опуклі задачі оптимізації), варіаційне числення та теорія оптимального управління.

У першій частині обговорюються завдання, пов'язані з іменами найбільших математиків різних часів - Евкліда, Архімеда,Ферма, Кеплера, Гюйгенса, І. Бернуллі, Ньютона, Лейбніца. Я не відмовив собі в задоволенні «слідувати за думками» цих великих людей.

У другій же частині ... Але про це поки ще рано говорити.

Найдавніша задача-задача Дідони

Епіграфом до нашої розповіді поставлені «з Енеїди два вірші »одного з найбільших поетів Стародавнього Риму - Публія Вергілія Марона. Як і всяке безсмертне творіння, «Енеїда» оповідає про пристрасті людських, про добро і зло,про рок і стражданні, про підступність і кохання, про життя і смерть. Наведені рядки відносяться до події, що сталася, якщо вірити переказу, в IX столітті до н. е.. Згадаймо легенду, відтворену в «Енеїді».

Фінікійська царівна Дідона, рятуючись від переслідувань свого брата, вирушила на захід уздовж берегів Середземного моря шукати собі притулок. Їй сподобалося одне місце на узбережжі нинішнього Туніської затоки. Дідона повела переговори з місцевим ватажком Ярбом про продаж землі. Запросила вона зовсім небагато - стільки, скільки можна «оточити бичачою шкурою ». Дідоні вдалося умовити Ярбай. Угода відбулася,і тоді Дідона порізала шкуру бика на дрібні тасьми, зв'язала їх воєдино і оточила велику територію, на якій заснувала фортеця, а поблизу від неї - місто Карфаген. Там чекали її згодом нерозділена любов і мученицька смерть. Цей епізод дає привід задуматися над питанням: скільки ж землі можна оточити бичачої шкурою?

Чому ми починаємо саме з цього завдання? Адже рішення її досить складно. Здавалося б, слід було починати з простіших речей. Але я все-таки вибираю інший шлях. Тут, у цій частини, я буду вести вас не від простого до складного, а від далекого минулого до наших днів і тому почати хочу «з самого початку ». Хіба не дивно, що в ті «нечувані року» ставилися і вирішувалися такі важкі і глибокі проблеми? Як мало знали наші попередники в порівнянні з тим, що знаємо ми з вами! Але вони йшли до мети і досягали її!

Отже, скільки ж землі можна оточити бичачої шкурою?Для того щоб відповісти на це питання, потрібно правильно математично поставити завдання. Сучасний математик скаже так:

Серед замкнутих плоских кривих, що мають задану довжину, знайти криву, що охоплює максимальну площу.

Це завдання і називають завданням Дідони або класичною ізопериметричною задачою. (Ізопериметричні фігури - це фігури, що мають однаковий периметр.)

Ми поки обійшлися тільки словами, і людини з достатнім рівнем математичної культури таке формулювання цілком задовольнить, бо він знає, що таке крива, довжина і площа. На подання ж точного сенсу цих слів пішло понад дві тисячі років. Щоб як слід пояснити ці терміни, слід було б написати окрему книгу. Не будемо надмірно заглиблюватися в це і підійдемо до нашого завдання «наївно», як підходили до неї древні (і як повинна була на практиці підійти до неї сама царівна Дідона).

Спробуємо тільки обійтися без шкури бика. Відмотаємо від котушки шматочок нитки. Відріжемо його і зв'яжемо кінцями. Покладемо цю пов'язану нитку на аркуш паперу. Вийшла плоска замкнута крива. Якщо тепер вирізати шматок паперу по контуру нитки, вийде образ площі, охоплюваній цією кривою. Цю площу можна виміряти. Вимірювання можна справити досить точно, якщо наш лист був листом міліметрівки. Тепер вже можна зрозуміти і питання завдання: потрібно з'ясувати, як слід покласти нашу нитку, щоб вона охоплювала найбільшу площу. Ми доведемо трохи пізніше, що крива, вирішальна класичну ізопериметричну задачу, - це коло. Вергілій при описі дії Дідони вжив дієслово «circumdare» (оточувати), що містить корінь «circus» (коло),що дозволяє думати, що класичну ізопериметричну задачу сама Дідона вирішила правильно.

Із історії класичної ізопериметричної задачі. Багато істориків вважають, що це - перша екстремальна задача, що обговорювалася в науковій літературі. Разом з ізопериметричною властивістю кола (тобто властивістю окружності охоплювати найбільшу площу серед ізопериметричних фігур) античні геометри відзначали ізопіфанову властивість кулі (тобто властивість сфери охоплювати найбільший обсяг серед ізопіфанних фігур - фігур, що мають рівну площу поверхні). З цією властивістю - найбільшої місткості - пов'язані уявлення про коло і кулі як втіленні геометричного досконалості (згадаймо слова Піфагора, взяті епіграфом до цієї розповіді). Ось ще одне підтвердження тієї ж думки. Велика книга М. Коперника починається зі слів: «Перш за все ми повинні помітити, що світ є кулястим або тому, що ця форма цілковита з усіх і не потребує ніяких скріпить, і вся представляє цілісність, або тому, що ця форма серед всіх інших володіє найбільшою місткістю, що найбільше личить того, що має охопити і зберегти все ».

Зараз неможливо сказати, коли вперше була висловлена думка про найбільшої місткості кола і кулі. У всякому разі, Аристотель (IV століття до н. е.) - один з найвидатніших мислителів в історії людства - користується цими фактами, як відомими. А хто ж (не рахуючи Дідони) насправді вирішив класичну ізопериметричну задачу? Література, присвячена ізопериметричними властивостями кола і ізопіфанновим властивостям кулі, величезна. З неозорого числа робіт назвемо одну книгу - монографію німецького геометра В. Бляшке. Там є і вказівки історичного характеру. Серед тих, хто дав рішення ізопериметричною і ізопіфаних завдань, стародавні автори називали і Архімеда. Вважається, що перші суворі докази максимального властивості кола і кулі дав Г. А. Шварц. Якщо вам захочеться простежити «історію" ізопериметричних завдань ", яка почалася в сиву давнину легендою про карфагенську царицю Дідони, до пана таємного радника Германа Амандусом Шварца з Берліна », ви можете звернутися до статті Бляшке (слова, укладені вище в лапки, взяті з).

Але насправді Шварцу, а до нього Вейерштрасу і після нього - самому Бляшке, як і багатьом іншим математикам XIX і XX століть, належить (щодо класичної ізопериметричних завдань) лише про оформлення ідей своїх далеких попередників, оформлення, здатне задовольнити сучасні вимоги суворості. Основні ж шляхи вирішення ізопериметричних завдань були абсолютно правильно намічені ще в античні часи. Зараз ми розповімо про один з таких шляхів, що належить Зенодор - математику, що жив, як вважають, десь між III століттям до н. е. і I століттям н. е.

Зенодор абсолютно строго, на сучасному рівні цього поняття, доводить наступне твердження.

Якщо існує плоский n-кутник, що має найбільшу площу серед усіх n-кутників із заданим периметром,то він повинен бути рівностороннім і прямокутним.

Плоский n-кутник, що має найбільшу площу серед всіх ізопериметричних з ним n-кутників, будемо називати(для стислості) максимальним n-кутником. Використовуючи цей термін, теорему Зенодора можна сформулювати коротше.

Максимальний n-кутник (якщо він існує) повинен бути правильним.

Теорема Зенодор є наслідком двох лем.

Лема 1. Максимальний n-кутник повинен бути рівностороннім.

Лема 2. Максимальний n-кутник повинен бути прямокутним.

Викладаючи роботи наших далеких попередників, я не буду, як правило, відтворювати їх буквально, не стану зберігати позначення і стиль авторів чи прагнути приводити саме авторські докази. Мені хотілося б відтворити лише про основні напрямлені думки і загальний дух міркувань, змінюючи і модернізуючи формулювання і докази. Так і тут я наведу обробки доказів лем 1і 2. При цьому дворазово буде використано вирішення завдання Герона.

Перш ніж приступити до доказів, потрібно зробити одне зауваження.

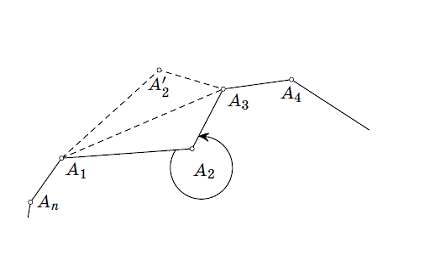
Мал. 2

Слід згадати про обставину, що не обумовленому Зенодору. Покажемо, що не опуклий багатокутник не може бути максимальним. Дійсно, якщо, скажімо, кут A1A2A3 більше 180о (Мал. 2), то, відобразивши вершину A2 відносно прямої A1A3 і розглянувши багатокутник A1A’2A3 ... An, де A’2 - образ A2, ми отримаємо ізопериметричний багатокутник більшої площі, ніж площа A1A2 ... An. Тепер вже можна навести докази.

Доведення леми 1. Нехай A1A2 ... An - максимальний n-кутник. Тоді він, як було зазначено, є опуклим. Припустимо, що не всі його сторони мають однакові довжини, і прийдемо до протиріччя. Нехай дві які-небудь суміжні сторони, скажімо, A1A2 і A2A3, не рівні між собою по довжині. Через вершину A2 проведемо пряму l, паралельнуA1A3 (мал. 3). Розглянемо завдання Герона для прямої l і точок A1 і A3 про визначення точки D на l, для якої сума відстаней |A1D|+ |A3D| була б мінімальною. У попередньому пункті було доведено, що в шуканої точці D кут α дорівнює куту β. Але кут α дорівнює куту DA1A3, а кут β дорівнює куту DA3A1 по властивості навхрест лежачих кутів при паралельних.

Мал. 3

Таким чином, трикутник A1DA3 - рівнобедрений і, значить, точка D відмінна від точки A2. Разом з тим:

а) площа ∆A1DA3 дорівнює площі ∆A1A2A3, бо у них однакові висоти і підстави;

б) сума бічних сторін трикутника A1DA3 менше суми сторін A1A2 і A2A3, або D (≠A2) є рішення задачі Герона. Побудуємо тепер рівнобедрений трикутник A1A’2A3, у якого |A1A’2|+|A’2A3| = |A1A2|+ |A2A3|. Його площа, зрозуміло, більше площі ∆A1A2A3, оскільки висота |A’2C| більше висоти |DC| (в силу того, що похила |A1A’2| довша похилої |A1D|), значить, площа багатокутника A1A’2 ... An більша площі ізопериметричного з ним багатокутника A1A2 ... An,що суперечить максимальності останнього багатокутника.

Лема 1 доведена.

Наслідок. З леми 1 випливає, що максимальним трикутником є рівносторонній і що максимальний чотирикутник повинен бути ромбом. З останнього ув'язнення і з мал. 4 негайно можна вивести, що максимальний чотирикутник насправді - квадрат.

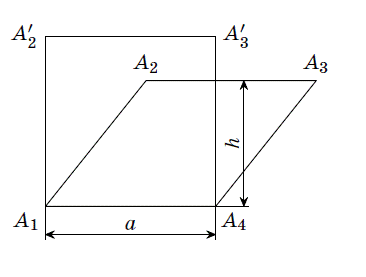
Мал. 4

Доведення леми 2.Нехай знову A1A2 ... An - максимальний n-кутник. Ми вже знаємо (лема 1), що всі сторони його рівні, і пам'ятаємо, що він опуклий. Припустимо тепер, що не всі його кути однакові,і прийдемо до протиріччя. Якщо не всі кути рівні, то існують два нерівних суміжних кута α≠β. Доведемо, що тоді існують і два нерівних несуміжних кута. Розглянемо послідовно розташовані кути багатокутника α, β, γ, δ, ε, ...(Їх не менше п'яти). Якщо γ≠ α або δ ≠ β, то ми досягли мети, так як кути γ і α (або δ і β) - несуміжні. Залишається розглянути випадок α = γ, δ = β, α≠β, коли послідовність має вигляд: α, β, α, β, ε ... Але тут не рівні один одному два несуміжних кута - перший і четвертий.

Таким чином, при зробленому припущенні можна вважати, що існують два непересічні внутрішніми частинами трикутника DEF і PQR (мал. 5), кожен з який утворений поспіль йдуть вершинами нашого n-кутника, причому кут E менше кута Q. У силу того,що |DE| = |EF| = |PQ| = |QR|, і через нерівності між кутами, отримуємо, що |DF| <|PR|. Опустимо з E і Q перпендикуляри EG на DF і QT на PR. До продовження відрізка EG докладемо трикутник ET’P’,рівний (конгруентний) трикутнику QTP (точка T переходить в T’, P - у P’, Q - в E). І знову розглянемо завдання Герона для прямої T’G і точок P’ і F. Нехай S - рішення задачі Герона, тобто точка на T’G, для якої сума відстаней від P’ до S і від S до F мінімальна. У силу того, що кут P’ET’(рівний половині кута Q) більше кута FEG (рівного половині кута E), точка S не співпадає з точкою E (бо кути P’ST’ і FSG рівні) і,більше того, S лежить на відрізку EG. Відкладемо тепер на прямий QT відрізок TU, рівний по довжині відрізку T’S, і розглянемо трикутники DSF і PUR. Сума бічних сторін цих трикутників менше суми бічних сторін вихідних трикутників DEF і PQR.

Мал. 5

Дійсно,

|DS|+ |SF|+ |PU|+ |UR|= 2(|SF|+ |SP’|) <2(|FE|+ |EP’|)= |DE|+ |EF|+ |PQ|+ |QR|.

Ми користувалися тим, що наші трикутники рівнобедрені, і тим, що S - рішення задачі Герона. З іншого боку,площа ∆P’ES більше площі ∆ESF, бо у першого висота дорівнює |P’T’| = |PR|, у другого висота дорівнює |FG| = |DF|, а по доведеному вже |DF| <|PR|. Звідси випливає, що сума площ трикутників DSF і PUR більше суми площ первинних трикутників DEF і PQR. Дійсно,

∆DSF + S∆PUR = S∆DEF - 2S∆ESF + S∆PQR+ S∆ESP’> S∆DEF+ S∆PQR

Значить, n-кутник DSF ... PUR ... має менший периметрі більшу площу, ніж наш початковий n-кутник DEF ...... PQR ... Тепер можна з будь-яким з трикутників (DSF або POR) вчинити точно так само, як ми вчинили з ∆A1DA3 при доказі леми 1, тобто надбудувати його, зрівнявши периметри багатокутників і зробивши площа нового багатокутника ще більшою, ніж площа багатокутника DEF ... PQP ... , Отже, цей багатокутник - не максимальний. Лема 2повністю доведена, а з нею доведена і теорема Зенодора. Залишилось вивести з неї рішення класичної ізопериметричної задачі.

Лема про існування максимального n -кутника. Ми довели, що якщо максимальний n-кутник існує, то він правильний. Але чи існує максимальний n-кутник? А раптом ні? Тоді все піде прахом. Адже не всяка функція має максимум. Наприклад, функція f(x) =-(1+ x2)-1 не досягає свого найбільшого значення .

Запитання існування рішень не були предметом розгляду давніх авторів. Значення проблем існування і методи доведення теорем існування були зрозумілі приблизно сто років тому. Надалі нам доведеться не раз торкатися цих питань. Тут же ми наведемо без доведення наступне твердження (яке Зенодор, мабуть вважав само собою зрозумілим).

Лема 3. Максимальний n-кутник існує.

Звідси з лем 1 і 2 слідує

Теорема 1. Максимальний n-кутник є правильним n-кутником.

Тепер залишилося вже зовсім небагато.

Завершення доведення.

Нехай P - периметр правильного n-кутника, a S - його площа. Ми знаємо з геометрії, що P = 2nRsin (π / n), де R - радіус описаного кола

S =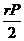

де r - радіус вписаного кола. При цьому r = Rcos(π/ n). Зіставляючи все це, приходимо до формули, яка зв'язує S і P:

- 4n tg π/n·S = 0.

Теорема 1 означає, що якщо P - периметр деякого довільного n-кутника, а S - його площа, то має місце нерівність

- 4n tg π/n·S ≥0.

З нерівності tg α≥α (вірного для 0≤α<π/1) і з (2)отримаємо нерівність

- 4πS≥ 0

справедливе для будь-якого n-кутника і будь-якого n. Зазначимо, що для будь-якого кола має місце очевидне рівність

- 4πS = 0

де P - довжина кола, а S - площа кола.

Тепер сформулюємо лему, що зв'язує всі поняття,беруть участь у формулюванні класичної ізопериметричної задачі, з поняттям n-кутника. Вона означає, що довжину кривої площа, охоплювану нею, можна з будь-яким ступенем точності наблизити периметром і площею n-кутника.

Лема 4. Для будь-якої замкнутої плоскої кривої довжини P *,охоплює площу S *, і для будь-якого ε> 0 можна знайти деякий n-кутник, периметр P і площа S якого задовольняють нерівностям

|P-P*|≤ε, |S-S*|≤ε

З леми 4 і співвідношення (3) отримуємо, що за будь ε знайдеться такий багатокутник з периметром P і площею S,що виконані нерівності

πS*≤4πS+4πε ≤ P2 +4 πε≤(P*+ε)2+ 4 πε = P*2+ε(2P*+ 4 π+ε).

У силу того, що e довільно, приходимо до остаточного нерівності

πS*≤P*2,

Підсумуємо сказане у вигляді наступного твердження.

Теорема 2. Площа, охоплювана будь-якої замкнутої кривої даної довжини, вбирається площі кола, окружність якого має таку ж довжину.

Ми знайшли повне рішення ізопериметричної проблеми.

Коментарі. 1. Повне рішення нашої задачі вийшло з'єднанням двох геометричних лем Зенодора і двох сучасних, але, по суті справи, технічних лем 3 і 4. Все необхідне для доказу леми 3 було заготовлено в працях Вейерштраса; поняттями довжини кривої і площі, охоплюваній кривої, було надано точне значення Жорданом, і тим самим їм були зроблені основні заготовки для доказу леми 4.

. Детальний проведення доказів лем 3 і 4 можна прочитати в цитованій книзі Бляшке [4].Але перш ніж закінчити цю розповідь - ще один відступ.

Доведення Штейнера. Важко втриматися і поряд з доказом, висхідним до ідей древніх, що не запропонувати схему ще одного доказу, основна думка якого належить Якобу Штейнеру, математику, збагатив геометрію багатьма чудовими ідеями. Доказ Штейнера неявно передбачає, що шукана крива, вирішальна ізопериметричне завдання, існує. (А ми ж уже знаємо, що це дійсно так.) Залишається довести, що ця екстремальна крива - коло.

Твердження 1. Екстремальна крива опукла.

Що таке опукла крива? Це така крива, що якщо взяти будь-які дві точки, що лежать в області, обмеженою цією кривою, то і весь відрізок, що з'єднує дві точки, буде лежати всередині кривої.

Зауважимо до речі, що опуклість відіграє велику роль в задачах на максимум і мінімум. Про неї у нас ще піде мова далі. Опуклості присвячено багато чудових книг, розрахованих на школярів, наприклад: Люстерник [14], Ягломі Болтянский [24] та ін.

Повернемося до доказу Штейнера і доведемо твердження 1.

Якщо крива не опуклі, то на ній знайшлися б дві точки A і A’ такі, що обидві дуги ABA’ і AB’A, що з'єднують точки A і A’, лежать по одну сторону від прямої AA’ (мал. 6). Замінивши одну з цих дуг її дзеркальним відображенням відносно AA’,отримаємо нову криву більшої площі при тій же довжині.

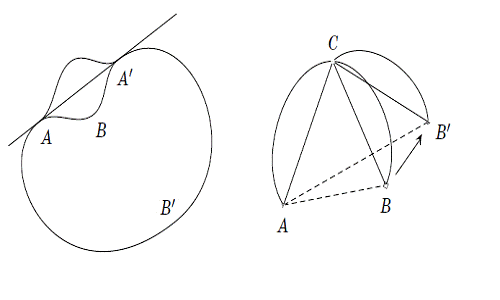
Мал. 6

Твердження 2. Якщо точки A і B ділять довжину екстремальної лінії навпіл, то хорда [AB] ділить площу фігури навпіл.

Дійсно, якби хорда [AB] ділила площу на дві нерівні частини, то більшу частину слід було б відобразити щодо діаметра, і фігура, що складається з більшої частини та її відображення, мала б ту ж довжину і велику площу.

Твердження 3. Нехай знову точки A і B ділять довжину екстремальної лінії навпіл і C - будь-яка точка кривої. Тоді кут ACB - прямий.

Це центральне місце. Метод, застосовуваний далі, носить назву чотирьохшарнірного методу Штейнера.

Нехай є точка C така, що кут ACB не є прямим. Площа, обмежена дугою ACB і діаметром AB, розбивається на три частини: трикутник ABC і сегменти, прилеглі до сторін AC і CB. Так от, уявімо тепер собі, що в точці C у нас шарнір, з'єднує ці два сегменти. «Розсунемо» сегменти так, щоб кут ACB’ став прямим (мал. 7). Тоді площа, обмежена дугою ACB’ збільшиться, бо з всіх трикутників із заданими бічними сторонами найбільшу площу має прямокутний трикутник (так як S∆ABC = 0,5·|AC|·|BC|·sin C≤0,5|AC|·|BC| і рівність досягається,якщо кут дорівнює 90о). А тепер відобразимо отриману фігуру щодо AB’. У підсумку приходимо до фігури з тим же периметром і більшою площею. Затвердження доведено.

Ми прийшли до наступного: екстремальна крива - це безліч точок C, з яких хорда AB, що ділить довжину екстремальної лінії навпіл, видно під кутом 90о, тобто ця крива - коло.

Людина захоплений вигукне: «Прекрасно!» Скептик почне чіплятися: «То не доведено, це треба обгрунтувати ...Спробуй доведи існування ... Чому при шарнірному розсуванні частини сегментів у точки C не стануть перетинатися? »...Чи не станемо відповідати на його бурчання. Визнаємо: приголомшливо, але вимагає обгрунтування!

Максимуми і мінімуми в природі (оптика)

Карл Зігель - видатний математик XX століття. Йому належать фундаментальні результати в багатьох областях математики і механіки. Слова, поставлені нами вище за епіграф, - це, звичайно, жарт, але в ній міститься частка істини. У нас вже був привід при обговоренні завдання Герона відзначити, що природа «керується» екстремальними принципами. У першому оповіданні йшлося, що при відображенні від плоскої поверхні вона «обирає» траєкторію найменшої довжини.

У словах Герона, процитованих нами в першому оповіданні,можна побачити зародок фундаментального принципу, остаточно сформульованого в XVII-XIX століттях. Тоді було з'ясовано, що природі властиво «діяти» оптимально і в оптиці, і в механіці, і в термодинаміки - взагалі всюди.

Екстремальний принцип, що стосується явищ природи, був вперше чітко сформульований в оптиці при спробі теоретичного осмислення законів заломлення світла. Різноманітним питань оптики, зокрема історії закону про заломлення світла, присвячена книга Тарасова та Тарасової .

Якщо опустити жердину в нерухому гладь прозорого озера,він здасться нам як би зламаним. Це відбувається через заломлення світла.

Ще древні намагалися знайти закон заломлення. Зокрема, в II столітті до н. е.. Птолемей намагався знайти цей закон дослідним шляхом. Але він не дійшов до правильної відповіді.

Вперше його знайшов голландський учений Снелліус. Зараз ім'я Снелліуса не так широко відомо, як імена його великих сучасників - Декарта, Гюйгенса і Ферма, про які нам далі доведеться говорити. Найвідомішим фактом, пов'язують з ім'ям Снелліуса, так і залишився відкритий ним експериментально (і не опублікований за життя) закон заломлення світла. Але свого часу Снелліус був дуже знаменитий: для Кеплера він був «гордістю геометрів нашого століття». Тут, мабуть, доречно нагадати, що в XVII столітті математиків називали геометрами. Повернемося, однак, до переломлення світла.

Мал. 7 Закон Снелліуса полягає в наступному

Нехай два промені A1OB1 і A2OB2 (що йдуть «зверху вниз») переломлюються в точці O (мал. 7). Кути α1і α2, утворені прямими A1Oі A2O з вертикаллю OC, називаються, як ми вже знаємо, кутами падіння. Кути β1 і β2, утворені прямими B1O і B2Oз вертикаллю OD, називаються кутами заломлення. Снелліус встановив, що

,

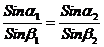тобто, що ставлення синуса кута падіння до синуса кута заломлення є величина постійна, не залежна від кута падіння.

До того ж самого закону незалежно від Снелліуса прийшов Декарт - один з найвидатніших мислителів і вчених Франції. У нас ще буде привід (в останньому оповіданні цієї частини) поміркувати на тему про те, «помиляються чи генії?». Так от, Декарт був з тих геніїв, хто «помилявся». З його «помилок», розкиданих по ниві науки, виросли згодом численні життєдайні пагони.

Так і тут, Декарт вивів закон заломлення, спираючись на свою концепцію поширення світлових променів. Сама ця концепція не витримала випробування часом, але з неї викристалізувався згодом закон збереження кількості руху.

З теорії Декарта випливало, що в більш щільному середовищі, наприклад у воді, швидкість поширення світла більше, ніж у менш щільною, наприклад у повітрі.

Цей факт багатьом видався сумнівним. Інше пояснення закону заломлення, виходячи з в точності протилежній посилці (у більш щільному середовищі світло поширюється повільніше), дав Ферма. Ім'я Ферма знайоме всім завдяки його «великої теореми ». Ферма і Декарт були співвітчизниками і сучасниками. Вони часто сперечалися один з одним у пошуках наукової істини. Так було і тут. У даному випадку Ферма виявився прав - експериментально було доведено, що в більш щільному середовищі світло поширюється повільніше.

Для пояснення закону заломлення світла Ферма і висунув екстремальний принцип для оптичних явищ. Згодом він був названий його ім'ям. Принцип Ферма говорить: у неоднорідному середовищі світло обирає таку траєкторію, уздовж якої час, що витрачається їм на подолання шляху від однієї точки до іншої, мінімально.

Принцип Ферма дозволяє точно поставити і вирішити завдання на мінімум, приводить до висновку закону Снелліуса. А саме, цей принцип призводить до необхідності знайти мінімум функції одного змінного (мал. 9):

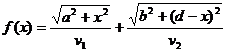
Треба сказати, що до моменту, коли Ферма висунув свій екстремальний принцип (а це відбулося близько 1660 р.), він вже володів алгоритмом знаходження максимумів і мінімумів функцій, що складається, як тепер ми знаємо, в прирівнювання нулю похідної. За допомогою похідних закон Снеллиуса виводиться настільки просто, що його зараз проходять навіть у школі. Митеж повторимо цей висновок в тринадцятому оповіданні. Ферма ж отримав потрібний результат набагато більш складним шляхом. Може виникнути питання: чому ж він не скористався своїм алгоритмом? Відповідь дуже проста: у той час похідних ще було! Лейбніц не було опубліковано ще своєї роботи, де він ввів це поняття. Ферма міг застосовувати свій прийом тільки для поліномів, де він фактично передбачив поняття похідної,а диференціювати радикали він не вмів. І той висновок закону Снеллиуса, який зараз входить в шкільний курс алгебри та аналізу, був знайдений Лейбніцем, причому в тій же самій роботі 1684, в якій закладено фундамент всього грандіозного будови - математичного аналізу.

Отже, Ферма вивів закон Снеллиуса зі свого екстремального принципу, але його рішення було вельми складним. Набагато більш просте рішення, що грунтується на принципі Ферма, дав Гюйгенс - ще один геніальний вчений XVII століття, автор хвильової теорії світла.

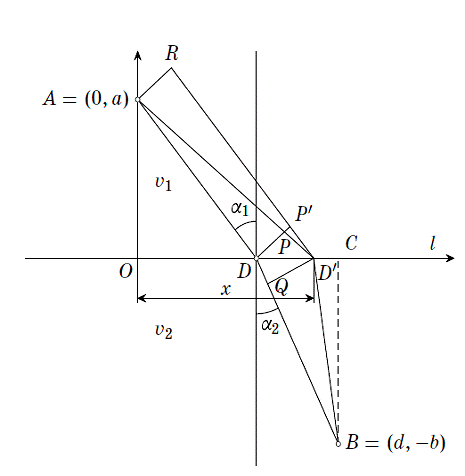
Мал. 8

Рішення Гюйгенса ми і наведемо зараз. Спочатку необхідно точно поставити задачу. Вона ставиться так.

Дано дві точки A і B по різні сторони від горизонтальної прямої l, що розділяє два середовища. Потрібно знайти таку точку D, щоб час подолання шляху ADB було мінімальним за умови, що швидкість поширення світла у верхній середовищі v1, а в нижній - v2 (мал. 8). Зазначимо, що (1) є математичне пере формулювання завдання. Звернемо увагу на схожість цього завдання із завданням Герона. Рішеня Гюїренса. Нехай точка D (див. мал. 9) така,що в ній виконано співвідношення

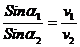
Покажемо, що для будь-якої іншої точки D’≠ D час, витрачений на подолання шляху AD’B, буде більше часу,витраченого на шлях ADB. Для цього оживимо перпендикуляри в точках A і D до прямої AD. Точку перетину з AD’ перпендикуляра, проведеного з точки D, позначимо через P. Проведемо пряму, паралельну AD, через точку D’, і точку перетину цієї прямої і перпендикуляра DP позначимо P’, а точку перетину її з перпендикуляром, проведеним з A, - через R. Нарешті, опустимо перпендикуляр D’Q з D’ на DB. З мал. 9видно, що величина кута PDD’ дорівнює α1, а величина кута D’DQ дорівнює π/2- α2. Значить,

|D’P’| = |D’D| sin α1, |DQ| = |DD’| sin α2

Тепер проведемо порівняння часів проходження ламаних ADB і AD’B.

Внаслідок того, що

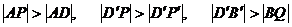
(похилі більше перпендикулярів), а також з (3) отримуємо

,

.

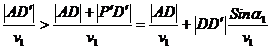Складаючи ці нерівності, отримуємо з урахуванням (2)

.

Отже, точка, заломлюючись в якій світло витратить найменшу час на проходження шляху від A до B, характеризується тим, що відношення синуса кута падіння до синуса кута відбиття одно v1/v2, тобто постійному числу. Але саме в цьому і полягає закон Снелліуса.

В основу принципу Ферма покладено допущення про те, що світло поширюється по деяких лініях. Це подання найлегше пов'язати з корпускулярної теорією світла, згідно якої світло - це потік частинок. Гюйгенсу належить ще одне пояснення законів поширення і заломлення світла, засноване на уявленні про світло як про хвилі, фронт якої рухається з часом.

Хвильовий фронт St - це безліч точок, яких світло, розповсюджуваний деяким джерелом, може досягти за заданий час t. Наприклад, якщо в нульовий момент часу джерело - це точка, а середовище однорідна, то через час t фронт St буде сферою радіуса vt з центром у джерелі світла. У міру видалення від джерела сферична хвиля стає все більш плоскою, і якщо ми уявимо джерело нескінченно віддаленим, то в межі хвильовий фронт виявиться площиною, рівномірно рухається зі швидкістю v.

Для визначення руху хвильового фронту в більш складних ситуаціях Гюйгенс користується наступним правилом, отримавши назву «принцип Гюйгенса»: кожна точка хвильового фронту St сама стає вторинним джерелом, і через час ∆t ми отримуємо сімейство хвильових фронтів від усіх цих вторинних джерел, а істинний хвильовий фронт St+∆t в момент t+∆t є обвідна цього сімейства (тобто поверхня, що стосується всіх вторинних хвильових фронтів) (див. мал. 9).

Мал. 9

Застосуємо принцип Гюйгенса для виведення закону Снелліуса. Нехай паралельний пучок світлових променів падає на плоску межу розділу двох однорідних середовищ. Як і раніше, будемо уявляти собі, що l горизонтальна, а світло падає зверху (мал. 11). Через v1 і v2 (як і раніше) позначимо швидкості поширення світла над і під l і через α1 і α2 - кути падіння і заломлення відповідно. Хвильовий фронт A1A’Aрухається зі швидкістю v1, і в деякий момент t хвильовий фронт AA1 досягає межі l в точці D. Після цього D становиться вторинним джерелом хвиль, що поширюються в нижній середовищі зі швидкістю v2. В точку D1 світло прийде в момент t+|B1D1|/ v1 = t+(|DD1|sinα1)/v1 = t1, а в проміжну крапку D’ на відрізку DD1 - у момент t’=t+(|DD’|sinα1)/v1. До моменту t1 сферична хвиля від вторинного джерела D буде мати радіус r1=v2(t1-t)=|DD1|(v2/v1)sinα1, а хвиля від D’ - радіус r’=v2(t1-t’) = =|D1D’|(v2/v1)sinα1. Дотичні D1C і D1C’ до цих сфер збігаються, оскільки кути DD1C і D’D1C дорівнюють (так як їх синуси рівні відповідно r1/|DD1| і r’/| D’D1| і обидва числа рівні (v2/v1) sinα1). Але точка D’ була взята на DD1 довільно, і значить, вторинні хвилі в момент t1 всі стосуються прямий CD1, що утворює з l кут α2 такий, що sinα2= (v2/v1) sinα1. Ми знову прийшли до закону Снелліуса.

Ідея «хвильового фронту» може бути проілюстрована не тільки на прикладі оптичних завдань. Ось інший випадок. Нехай подорожній починає свій шлях з точки A, лежачої на прямолінійній шосе, обмежуючим луг. На цьому лузі є точка B,куди подорожній намагається потрапити як можливо швидше. Швидкість по лузі v в два рази менше швидкості по шосе. Якщо подорожній відразу піде по лузі, то за одиницю часу він може потрапити в будь-яку точку кола радіуса v. Якщо ж він весь цей час буде йти по шосе, то він пройде відстань 2v. Нехай він частину шляху пройде по шосе, а частину - по луці. Тоді безліч точок, де він зможе виявитися через одиницю часу, утворює «Хвильовий фронт», що складається з двох відрізків, з'єднаних дугою кола. Звідси дуже легко відповісти на питання, як оптимально рухатися подорожньому.

Тут мені видається доречним ще раз торкнутися питання про екстремальні принципах.

У цьому оповіданні були дані два висновки закону заломлення світла. Між ними є принципова відмінність. При підході Ферма ніяк не прояснюється істинна сутність що відбувається явища. Тут постулюється деякий властивість траєкторій і показується, що це допущення узгоджується з експериментом. Підхід Гюйгенса відштовхується від опису фізичної природи явища. Така подвійність опису типова в природознавстві. Закони природи, з одного боку, допускають тлумачення, що базуються на деяких фізичних моделях, з іншого - виводяться з екстремальних принципів.

Обговорення причин завело б нас надто далеко, але у зв'язку з цим хочу зазначити, що описані в нашій розповіді два підходу зіграли найважливішу роль в історії варіаційного обчислення і всієї теорії екстремальних задач. Насправді будь-яка задача варіаційного числення та оптимального управління може бути досліджена двома шляхами. Можна вивчати її екстремальні траєкторії (подібно Ферма), і це веде до теорії Ейлера-Лагранжа (якої ми торкнемося в чотирнадцятому оповіданні). А крім того, є й інший шлях (Гюйгенса): вивчати пучки екстремальних траєкторій, що призводить до аналогів хвильових фронтів, до теорії, розробленої Гамільтоном і Якобів XIX столітті, і дослідженню задач оптимального управління методами динамічного програмування, які в порівняно недавні часи почав розвивати американський вчений Беллман.

Найбільш відомі екстремальні задачі в геометрії

Задача Евкліда

Задача. У даний трикутник АВС вписати паралелограм ADEF (EFǁAB, DEAC) найбільшою площі.

Геометричне рішення задачі. Доведемо, що шуканий паралелограм характеризується тим, що D, E, F - середини відповідних сторін. Розглянемо паралелограм AD1E1F1 відмінний від паралелограма ADEF. Нехай G - точка перетину прямих DE і F1E1, а G1 - точка перетину прямих D1E1 і FE. Доведемо, що площа паралелограма AD1E1F1 менше площі паралелограма ADEF на величину площі паралелограма GEG1E1. З подоби трикутників EE1G1 і BDE, а також рівностей BD=EF, EG=E1G1 укладаємо, що

З цих рівностей випливає, що EG1*DE=EG*EF, тобто твір суміжних сторін паралелограма DD1G1E дорівнює твору суміжних сторін паралелограма F1GEF. Оскільки площа паралелограма дорівнює добутку його суміжних сторін і синуса кута між цими сторонами, укладаємо, що 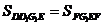. Таким чином

і площа паралелограма AD1E1F1 виявляється менше площі паралелограма ADEF на величину 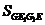. Аналітичне рішення задачі. Нехай Н - висота трикутника АВС, b - довжина відрізка АС, x - довжина відрізка AF. Тоді площа паралелограма, вписаного в трикутник АВС, виражається через x функцією

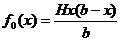
а вирішувану завдання можна сформулювати наступним чином:

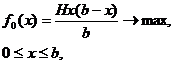
Для її вирішення використовуємо необхідна умова 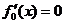. Знаходимо критичні точки

Отже, мінімум функції 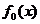 досягається в точці 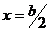, що якраз відповідає випадку, коли точка F є серединою відрізка АС.

Задача Архімеда.

Серед усіх пошарових сегментів кулі фіксованого радіуса, мають задану площу сферичної поверхні, знайти той, який має найбільший об’єм.

Аналітичний розв’язок цієї задачі. Нехай R - радіус кулі, h - висота кульового сегменту, S - площа бокової поверхності.

1.      Формулювання задачі:

.        Необхідна умова екстремуму функцій: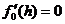

.        Знаходження критичних точок функції. Оскільки , функція має лише одну критичну точку 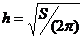. Так як 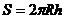, то . Шуканий кульовий сегмент являється півкульою і його висота рівна радіусу.

Задача Фаняьно

На початку XVIII століття італійський інженер і математик Фаньяно деї Тоски (1682-1766) поставив таку задачу:

Мал.11

Вписати в даний гострокутний трикутник ABC трикутник найменшого периметра так, щоб на кожній стороні трикутника ABC лежала одна вершина трикутника.

Скористаємося тим же прийомом: за допомогою рухів площині спробуємо вибудувати боку вписаного трикутника в ламану лінію. Тоді периметр буде не менше відрізка, що з'єднує кінці цієї ламаної. А найменший периметр буде відповідати випадку, коли сторони ламаної лежать на одній прямій.

Отже, нехай точки A1, B1, C1 лежать на сторонах трикутника ABC (A1 -на боці BC і т. д.). Відобразимо точку A1 симетрично відносно сторін AB і AC, отримавши точки A2і A3 відповідно (мал. 11). Довжина три ланкової ламаної A3B1C1A2 дорівнює периметру трикутника A1B1C1. Для того, щоб периметр був найменшим (рівним відрізку A2A3), потрібно, щоб вершини B1 і C1 лежали в точках перетину відрізка A2A3 зі сторонами трикутника AB і AC. Залишилось зрозуміти, як вибрати точку A1 на стороні BC таким чином, щоб довжина відрізка A2A3 була найменшою. Для цього зауважимо, що трикутник A2AA3 - рівнобедрений (A3A = A2A = A1A), а кут при його вершині A дорівнює 2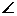BAC і тому не залежить від вибору точки A1 (мал. 12).

Отже, при русі точки A1 по стороні BC кути трикутника A2AA3 не змінюються. А його лінійні розміри будуть найменшими, коли найменшою буде сторона A2A, яка дорівнює A1A.Значить, A1A - висота, опущена на сторону BC.

Ми бачимо, що існує єдиний вписаний трикутник найменшого периметра, його вершина A1 - основа висоти. Якщо провести ті ж міркування c вершинами B1 і C1, отримаємо,що вони також є підставами висот (оскільки трикутник мінімального периметра - єдиний!)

Мал.. 12

Теорема Фаньяно. Серед усіх трикутників, вписаних в даний гострокутний трикутник, найменший периметр має ортотрикутник (тобто трикутник з вершинами в підставах висот).

. Дві суміжні сторони ортотрикутника утворюють рівні кути з відповідною стороною вихідного трикутника. Серед всіх трикутників, вписаних в даний трикутник, тільки ортотрикутник володіє зазначеним властивістю .

. Висоти трикутника є бісектрисами ортотрикутника.

Промінь світла, пущений вздовж однієї зі сторін ортотрикутника, відіб'ється послідовно від усіх сторін трикутника ABC і повернеться у вихідну точку. Таким чином, контур ортотрикутника являє собою замкнуту траєкторію променя світла. Якщо зрушити три дзеркала так, щоб вони утворили гострокутийтрикутник, то промінь світла, що йде по сторонам ортотрикутник замкнеться і ніколи не вийде назовні. Математики кажуть, що сторони ортотрикутника утворюють більярд для даного трикутника.

. Периметр ортотрикутника дорівнює подвоєному добутку висоти трикутника на синус кута, з якого вона виходить.

Отримуємо, що три таких утвореня в трикутнику рівні між собою. Доведіть, що насправді вони рівні подвоєною площі, поділеній на радіус описаного кола.

. Досліджуйте задачу Фаньяно для тупокутного трикутника.

. Досліджуйте завдання Фаньяно для чотирикутника. Для яких чотирикутників вписаний чотирикутник мінімального периметра існує? Чи буде він єдиним?

Задача Ферма-Торрічеллі-Штейнера

Історія цього завдання налічує понад три з половиною століть. Вона була поміщена в книзі італійського фізика і механіка Вівіані «Про максимальних і мінімальних значеннях» в 1659 році. Вінченті Вівіані (1622-1703) був учнем великого Галілео Галілея. Нам він більш відомий як винахідник ртутного барометра (приладу для вимірювання атмосферного тиску), а своїм сучасникам - як один з кращих фахівців по задачах на максимум і мінімум, а також з теорії конічних перетинів. Свій твір Вівіані, дотримуючись традицій того часу, забезпечив довгою назвою: «П'ята книга творів Аполлонія Пергського про конічних перетинах, містить в собі перші дослідження про найбільших і найменших величинахі визнається самим чудовим пам'ятником цього великого геометра» («De maximis et minimis geometrica divinatio in quintumconicorum Apollonii Pergoei nunc desideratum»). Серед безлічі задач на максимум і мінімум, поміщених в цій книзі, є така:

. На площині дано три точки A, B, C, що не лежать на одній прямій. Для якої точки T площині сума відстаней AT + BT + CT найменша?

Ще до книги Вівіані цим завданням цікавився італійський математик Бенавентура Кавальєрі (1598-1647), автор знаменитого «принципу Кавальєрі» для обчислення площ і обсягів, що передбачив інтегральне числення, а також математик і фізик Еванджеліста Торрічеллі (1608-1647). Кажуть,що саме Торрічеллі отримав перше рішення цього завдання (швидше за все, засноване на фізичних міркуваннях). Торрічеллі,як і Вівіані, був учнем Галілея. Саме ним наприкінці свого життя вже осліпнув Галілей диктував глави зі своєї книги «Бесіди про механіку». Подібно багатьом вченим пізнього Відродження, Торрічеллі був різнобічною людиною. Будучи професором математики Флорентійського університету, він багато займався завданнями фізики (його закон розподілу тиску рідини відомий тепер кожному школяреві), а також механіки, балістики і оптики, і навіть написав кілька робіт з конструювання оптичних приладів та шліфовці лінз. Згідно з іншими джерелами, незалежно від Торрічеллі, це завдання вирішив і найбільший французький математик П'єр Ферма(1601-1665). А перше чисто геометричне рішення належить, мабуть, швейцарському геометру Якобу Штейнеру(1796-1863), про якого мова ще попереду.

Мал.13

Розв’язання. Знову скористаємося тим же прийомом: вибудуємо відрізки AT, BT і CT в ламану лінію. Тепер, однак, замість симетрії застосуємо поворот. Повернемо площину на 60◦ навколо точки A, при цьому точка C перейде в деяку точку D, а точка T - в точку N. Трикутник AND дорівнює трикутнику ATC, оскільки переходить у нього при повороті на 60◦, значить TC=ND. Трикутник ANT - рівносторонній, так як AT=AN і 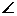TAN = 60◦, тому TA=TN. Отже, сума AT+BT+CT дорівнює довжині ламаної BTND, а значить, вона не менше довжини відрізка BD (мал. 13). Рівність досягається, коли точки B, T, N, і D лежать на одній прямій (у зазначеній послідовності). Це означає, що 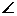BTA+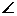ATN=180◦ і, отже, 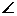BTA=120◦; а також 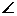AND + 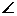ANT = 180◦, значить, 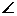AND = 120◦, тому 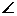ATC=120◦. Таким чином, промені TA, TB і TC утворюють два кута в 120◦, тому і третій кут між ними також дорівнює 120 ◦ (мал. 13). Точка T, з якої всі сторони трикутника видно під кутами 120 ◦, має кілька назв. Іноді її називають точкою Ферма, іноді - точкою Торрічеллі, іноді - точкою Штейнера. Доказ, яке ми привели, з поворотом площини на 60 ◦, належить Якобу Штейнеру. З його чудовими результатами ми ще не раз зустрінемося в цій книзі. А першим за часом з цих трьох математиків був Торрічеллі. Тому ми будемо називати цю точку, по праву першості, точкою Торрічеллі (ми і позначили її буквою T). Це ще одна чудова точка трикутника, поряд з центром ваги (точкою перетину медіан), ортоцентром (точкою перетину висот), центрами вписаного і описаного кіл. Правда, на відміну від чотирьох чудових точок, точка Торрічеллі існує не у будь-якого трикутника. Однак ми вже довели, що

Якщо у трикутника є точка Торрічеллі, то вона є єдиною точкою мінімуму суми відстаней до вершин трикутника.

Коли ж точка Торрічеллі існує? Нехай з трьох кутів трикутника кут при вершині A є найбільшим. Побудуємо на сторонах AC і AB всередину трикутника ABC дуги кіл, що містять по 120 ◦. Ці дуги перетинаються в точці A. Якщо ж кут A менше 120 ◦, то ці дуги мають ще і другу точку перетину (доведіть це!), Яку ми позначимо через T. Це і є точка Торрічеллі. Справді, так як кути ATC і ATB з побудови рівні 120 ◦, то й третій кут BTC також виходить дорівнює 360◦-120◦·2=120◦. І навпаки, якщо точка Торрічеллі існує, то вона будується саме таким чином, оскільки повинна лежати на перетині дуг кіл величиною в 120 ◦, побудованих на сторонах трикутника. Отже,

Трикутник має точку Торрічеллі тоді і тільки тоді, коли всі його кути менше 120 ◦.

А якщо один з кутів трикутника більше або дорівнює 120◦ (наприклад, кут A), то в якій точці сума відстаней до вершин буде мінімальна? Відповідь: в вершині цього кута. Довести це просто. Нехай 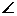A ≥ 120 ◦, а M - довільна точка площини. Якщо M не лежить всередині кута A, то один з кутів MAC або MAB - тупий (нехай це кут MAC), а значить, MC> AC, з іншого боку, за нерівністю трикутника, MA + MB> AB, тому MA + MB + MC> AB + AC.

Якщо ж M лежить всередині кута A, то знову повернемо площину на 60 ◦ (мал. 14), і отримаємо, що трикутник BAD лежить всередині чотирикутника BMND, тому периметр трикутника менше периметра чотирикутника. Отже,

+ AC = AB + AD <BM + MN + ND = BM + AM + CM.

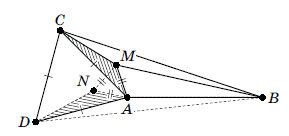
Мал. 14

Теорема Торрічеллі-Ферма-Штейнера. Якщо всі кути трикутника менше 120 ◦, то точкою мінімуму суми відстаней до його вершин є точка Торрічеллі. Якщо ж один з кутів більше або дорівнює 120 ◦, то такою точкою є вершина цього кута.

. Всі кути трикутника ABC менше 120◦. На його сторонах у зовнішню сторону побудовані рівносторонні трикутники ABC', BCA' і CAB'. Тоді описані окружності цих трикутників і відрізки AA', BB' і CC' перетинаються в одній точці - точці Торрічеллі. Крім того, AA '= BB' = CC '.

(теорема Наполеона). Центри описаних кіл трикутників ABC', BCA' і CAB' є вершинами рівностороннього трикутника (трикутника Наполеона). Чому дорівнює сторона трикутника Наполеона, якщо AA'= c?

Це твердження приписують Наполеону, хоча невідомо, чи має він до нього якесь відношення. Наполеон трохи захоплювався геометрією і цілком шанобливо ставився до математики і математикам. Його оточувало багато видатних математиків того часу - Лаплас, Монж, Фур'є. Однак багато історики вважають, що його авторство твердження про рівносторонньому трикутнику - не більше ніж міф, створений придворними підлесниками.

. Якщо на сторонах даного трикутника побудувати у внутрішню сторону рівносторонні трикутники, то їх центри також є вершинами рівностороннього трикутника (внутрішнього трикутника Наполеона). Різниця площ зовнішнього і внутрішнього трикутників Наполеона дорівнює площі вихідного трикутника.

(теорема Помпею). Навколо рівностороннього трикутника ABC описана окружність. Якщо точка M лежить на меншій дузі AB цієї окружності, то MC=MA+MB. Для всіх інших точок M площині виконано нерівність MC<MA + MB.

. Доведіть, що сума відстаней від довільної точки всередині рівностороннього трикутника до його сторін - величина постійна. За допомогою цього твердження отримаєте інший доказ теореми Ферма-Торрічеллі-Штейнера.

Підказка. Через кожну вершину трикутника проведіть пряму,перпендикулярну відрізку, що з'єднує цю вершину з точкою Торрічеллі.Ці прямі утворюють рівносторонній трикутник.

. На площині дано дві точки і пряма. Знайдіть точку,сума відстаней від якої до даних точок і до прямої мінімальна.

. Дано опуклий чотирикутник ABCD. Для якої точки площини сума відстаней до його вершин буде найменшою? Відповідь ясна: для точки перетину діагоналей. Нехай трикутник ABC - гострокутний. Уявімо, що вершина D наближається до вершини C. Тоді чотирикутник ABCD прагне до трикутника ABC, а точка мінімуму суми відстаней - точка перетину діагоналей - прагне до вершини C. У межі отримаємо, що вершина C - точка мінімуму суми відстаней для трикутника ABC. Але ж насправді, як ми знаємо,мінімум суми відстаней до вершин трикутника ABC досягається в його точці Торрічеллі, а не у вершині C. Протиріччя?

. Для трьох точок A, B і C на площині знайдіть таку точку M, для якої значення виразу а) AM +BM+ 2CM; б) AM+ BM-CM досягає найменшого значення.

Задача Штейнера

У просторі дано k точок. З'єднати їх системою кривих найменшою сумарної довжини. Це завдання було вперше поставлено великим геометром Якобом Штейнером (1796-1863). Народжений у Швейцарії в селянській родині Штейнер був в математиці самоучкою. У віці двадцяти років він переїхав до Німеччини, де і працював до кінця життя, спочатку в університеті Гейдельберга, а потім - Берліна. Вклад Штейнера в геометрію величезний. Йому належить безліч нових ідей і красивих, іноді дуже важких теорем. Він вперше довів, що трикутник з двома рівними бісектрисами - рівнобедрений, що всі геометричні побудови, здійснимі за допомогою циркуля і лінійки, можуть бути здійснені за допомогою однієї лінійки, якщо тільки нам дана хоча бодна окружність і її центр. Так званий поризм Штейнера, або «намисто Штейнера», теорема про ланцюжок стосуються кіл, по праву вважається одним з найкрасивіших тверджень геометрії. Як представник «чистої геометрії», він був переконаний, що геометрію треба вивчати умоглядно, без залучення обчислень. Він говорив, що «розрахунок замінює мислення, а геометрія, навпаки, це мислення зміцнює». На його переконання,кожна геометрична задача повинна мати чисто геометричне рішення. Якщо Штейнеру не вдавалося знайти геометричне рішення, він вважав задачу не вирішеною зовсім і не публікував рішення. З цієї причини багато теореми Штейнера дійшли до нас без доказів.

Розв’язання. Ми вирішимо завдання Штейнера для k точок на площині. З незначними змінами цей же доказ годиться і для k точок у просторі, і навіть у просторі R3 довільної розмірності. У цьому сенсі рішення задачі Штейнера універсально!

Рішення розіб'ємо на кілька етапів. Отже, нехай на площині дано k точок, A2, ..., Ak. Подивимося, якими властивостями повинна володіти найкоротша система доріг, що з'єднує ці точки. Перше властивість досить очевидно, і випливає з того, що найкоротшим шляхом з однієї точки в іншу є відрізок прямої:

а) найкоротша система складається з відрізків.

Таким чином, найкоротша система доріг є плоским графом - об'єднанням кінцевого числа відрізків. Кінці цих відрізків - вершини графа, а самі відрізки - його ребра. Дані точки A1,. . ., Ak ми будемо називати справжніми вершинами цього графа, всі інші його вершини (перехрестя доріг) - додатковими. За умовою цей граф зв'язний, тобто з будь-якої його вершини можна дістатися по ребрах в будь-яку іншу. Більше того,цей граф однозв'язний, тобто для будь-якої пари вершин існує єдиний шлях по ребрах, їх зв'язує (при цьому завжди вважаємо, що ніякий шлях не проходить двічі по одному ребру). Зв'язний граф є однозв'язний тоді і тільки тоді, коли він не містить замкнутих шляхів (доказ цього факту - проста вправа). Якби найкоротша система доріг не була однозв'язною, то існував би замкнутий шлях. Прибравши будь-яке ребро з цього шляху, ми отримали б зв'язний граф меншої довжини.

б) будь-які два ребра, виходячи з одної вершини, утворюють кут не менше 120о.

Справді, якщо з вершини A виходять ребра AB і AC,і кут між ними менше 120◦, то ми можемо замінити цю пару ребер іншими, також зв'язують точки A, B і C, але мають меншу сумарну довжину. Якщо в трикутнику ABC всі кути менше 120 ◦, то поставимо одну додаткову вершину T - точку Торрічеллі цього трикутника, з'єднаємо її з вершинами A, B і C, а ребра AB і AC приберемо. Отримаємо зв'язний граф меншою довжини. А якщо у трикутнику ABC, скажімо, кут при вершині B більше або дорівнює 120 ◦, то прибираємо ребро AC, а замість нього ставимо BC. Знову отримаємо зв'язний граф меншої довжини (мал. 15).

Мал.15

З цієї властивості безпосередньо випливає, що

в) із справжньої вершини може виходити одне, два або три ребра; якщо виходить два ребра, то кут між ними більший або рівний 120о; якщо три, то вони утворюють між собою кути в 120о.

Більше трьох ребер виходити не може, інакше один з кутів буде менше 120 ◦.

Таким чином, справжні вершини бувають трьох типів. З додатковими вершинами справа йде простіше - всі вони одного типу:

г) із кожної додаткової вершини виходять три ребра під кутами 120о.

Дійсно, перший тип для додаткової вершини неможливий (якщо з додатковою вершини виходить тільки одне ребро, то ця вершина не потрібна, тому що її можна прибрати разом з ребром), другий - також неможливий (якщо додаткова вершина M з'єднана ребрами тільки з двома вершинами B і C,то приберемо ці ребра разом із самою вершиною M, а точки B і C з'єднаємо ребром; отримаємо зв'язний граф меншої довжини).

Варіаційні методи розв’язання екстремальних задач

Отже, ми розібрали безліч завдань, і кожна з них мала своє елегантне геометричне рішення. На практиці, на жаль,так виходить далеко не завжди. Багато геометричні задачі на мінімум і максимум або зовсім не мають геометричного рішення, або їх геометричні рішення істотно складніше аналітичних. Таким є стан речей, і ставитися до нього можна по-різному. З одного боку, це погано. З іншого боку, ця обставина завжди змушувало математиків шукати нові шляхи вирішення. У таких пошуках до кінця XVII століття народилося і оформилося новий напрямок математики, вставши в рівень з алгеброю і геометрією - математичний аналіз. Саме задачах на максимум і мінімум, поряд із завданнями механіки і оптики, математичний аналіз зобов'язаний своєю появою. Принцип рішення багатьох екстремальних задач зводиться до простого і разом з тим універсальному фактом:

У точці максимуму або мінімуму функції її похідна дорівнює нулю.

Це твердження часто називають теоремою Ферма (не плутати з великої теоремою Ферма і з малою теоремою Ферма в теорії чисел!), оскільки саме П'єр Ферма вперше сформулював його в 1629 році в роботі «Метод відшукання найбільших і найменших значень». Свій метод Ферма назвав «De maximis et minimis» (нагадаємо, що наукові роботи в той час писалися на латині) і продемонстрував, як з його допомогою можна вирішити завдання Евкліда: з усіх прямокутників з даними периметром знайти той, який має найбільшу площу. Треба сказати, що ідея варіаційного методу в той час, що називається, витала в повітрі. Багато вчених розвивали цей метод. Наприклад, Йоганн Кеплер, слова якого з трактату «Стереометрія винних бочок» ми винесли в епіграф, або Ісаак Ньютон, що говорив що «коли величина є максимальною або мінімальною, в цей момент вона не тече ні вперед, ні назад». Нагадаємо, що похідної функції f(x) в точці x називається число a таке, що Мал..16

f(x+h)=f(x)+a·h+α(h) | h |,

де величина α(h) прагне до нуля при h → 0. Похідну позначають символом f', таким чином, f'(x)=a.

Для досить малих збільшень h функція f(x+h) наближено дорівнює лінійної функції f(x)+ah, причому чим менше h, тим це наближення точніше.

. Через дану точку всередині кута провести відрізок з кінцями на сторонах кута, що має найменшу довжину.

Дивно, що ця чисто геометрична задача не має на стільки ж ясного геометричного рішення. Все більш-менш короткі її рішення використовують похідну. Цікаво й те,що багато схожі на неї завдання-близнюки, які, на перший погляд, навіть складніше її, мають прості геометричні рішення. Наприклад, провести відрізок через дану точку всередині кута,відтинаючий від кута трикутник мінімальної площі або мінімального периметра.

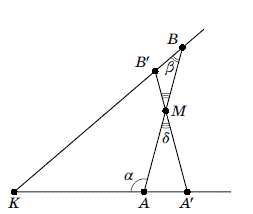
Розв’язання. Позначимо найкоротший відрізок через AB, а дану фіксовану точку всередині кута - через M. Проведемо через M інший відрізок A'B' з вершинами на сторонах кута. Нехай δ - кут між A'B' і AB. Функція f(δ)=A'B' досягає свого мінімуму в точці δ = 0, тому f '(0) = 0. Застосувавши теорему синусів до трикутниками MBB 'і MAA', отримаємо

;

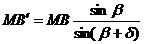
отже,

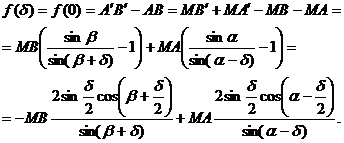
Отже

.

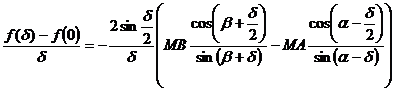Оскільки  при δ → 0, і при цьому

,

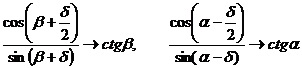отримуємо остаточно f '(0) =-MB ctg β +MA ctg α.

Але так як f'(0) = 0, для найкоротшого відрізка AB отримуємо таку умову:ctg β = MA ctg α.

Що це означає геометрично? Нехай K - вершина кута. Опустимо перпендикуляр KH на AB. Неважко перевірити, що

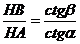. З боку, 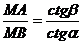, тому MA=HB і MB=HA. Отже, мал.. 17

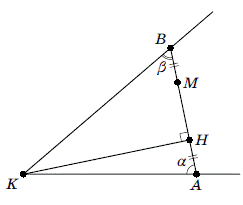
Мал.. 18

Найкоротший відрізок AB характеризується наступним властивістю: проекція вершини кута на AB симетрична точці M відносно середини відрізка AB.

Чому ми лише охарактеризували положення відрізка AB, а не дали способу його побудови? Справа в тому, що для довільного кута цей відрізок не може бути побудований за допомогою циркуля і лінійки. Саме тому ця «проста» геометрична задача має настільки громіздке рішення. Якби існувала така побудова, яке знаходило б найкоротший відрізок для будь-якого кута, то воно годилося б і для прямого кута (мал. 28). Якщо кут K - прямий, то

.

З іншого боку

де γ - кут між KM і KA (ми скористалися подібністю трикутників APM і AKB). Отже, 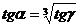. Побудувати відрізок AB означає знайти кубічний корінь з числа tg γ. Останнє, як відомо, не здійснимо за допомогою циркуля і лінійки.

У екстремальних задачах досить частою є ситуація,коли можливо тільки охарактеризувати положення точки мінімуму (максимуму), але не знайти її конструктивно.

Варіаційний метод можна застосовувати і до завдань з декількома змінними, коли функція f(x) задана не так на прямий, а, скажімо,на площині. При цьому x - точка на площині з координатами (х1, x2). Похідна визначається за тим же принципом: похідної в даній точці x називається вектор a = f '(x) такий, що

(x + h) = f (x) + a · h + α (h) | h |,

де h = (h1, h2) - довільний вектор, званий приростом аргументу x, число |h|=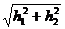 - його довжина, а величина α(h) прагне до нуля при |h| → 0. Різниця тільки в тому, що замість звичайного твори чисел тепер береться скалярний добуток векторів a·h, рівне добутку їх довжин на косинус кута між ними. У координатах скалярний твір виражається як a·h=a1h1+a2h2. У точці мінімуму або максимуму функції f її похідна (якщо вона існує) дорівнює нулю .

Доведення. Справді, нехай f'(x)=a≠0. Тоді розглянемо прирощення h=ta, де t - позитивне число. Враховуючи, що a·ta =t|a|2, отримуємо

(x+ta) = f(x)+t|a|2 + t|a|α (ta) = f(x)+t|a|(|a|+α(ta)).

При t → 0 величина α(ta) прагне до нуля, тому при малих t величина |a|+α(ta) - позитивна, значить f(x+ta)>f(x). Таким чином, точка x не є точкою максимуму. Точно так само,взявши прирощення h =-ta, доводимо, що x не є і точкою мінімуму.

Як приклад знайдемо похідну функції довжини вектора f(x)=|x|. Ця похідна знадобиться нам у багатьох завданнях. Користуючись тим, що |x|2= x·x, отримуємо

.

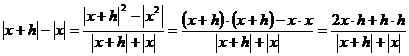Звідси

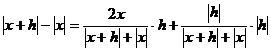
Якщо x≠0, то при h → 0 величина |x+h|+|x| прагне до 2|x|,а величина 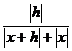 прагне до нуля. Тому

.

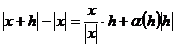Де α(h) → 0 при h → 0. Звідси випливає, що . Отже, функція f(x)=|x| має похідну в будь-якій точці x, крім точки x=0. Ця похідна є вектором одиничної довжини, співаправленнимі з вектором x.

. Задача про найменшою сумою відстаней до k точок. На площині дано k точок. Знайти точку, сума відстаней від якої до цих точок мінімальна.

Розв’язання. Позначимо через x1,. . ., хk дані точки, а через x - довільну точку площини. Нехай також fi(x) =|x-xi| для i = 1,. . ., k. Потрібно знайти точку x, для якої сума f1(x)+. . . + Fk(x) буде найменшою. Похідна функції fi(x) є одиничним вектором, співнаправленимі вектору x-xi. Якщо x - точка мінімуму, то або сума таких векторів дорівнює нулю, або одна з функцій fi не має похідної в точці x, а це означає, що x збігається з точкою xi. Таким чином,

Точка мінімуму суми відстаней або збігається з одного з даних точок, або характеризується наступним властивістю:сума k векторів одиничної довжини, направлених з цієї точки до даних k точкам, дорівнює нулю.

При k = 3 отримуємо точку Торрічеллі або одну з вершин трикутника (як ми знаємо, вершину з кутом ≥ 120◦), при k = 4 - точку перетину діагоналей чотирикутника, якщо чотирикутник опуклий, а якщо не опуклий - то його вершину,лежачу всередині трикутника з вершинами в трьох, що залишилися точках. При k ≥ 5 ця точка, взагалі кажучи, не будується за допомогою циркуля і лінійки.

Виходить досить дивна ситуація. Якщо на площині дано, скажімо, 10 точок, то існує спосіб побудови найкоротшою системи доріг, їх зв'язує (мережа Штейнера). Причому це побудова - точний, його можна зробити за допомогою циркуля і лінійки і знайти точну довжину. Якщо ж нам потрібно вирішити більше,здавалося б, просте завдання - знайти точку, сума відстаней від якої до даних 10 точок мінімальна (тобто знайти найкоротшу не з усіх систем доріг, а тільки з тих, які сходяться в одному перехресті), то ця задача в загальному випадку вирішується лише наближено, а не точно. Про точку мінімуму ми нічого не знаємо, крім того, що вона існує, і того, що сума 10 одиничних векторів з неї в дані точки дорівнює нулю. За допомогою циркуля і лінійки ми рішення побудувати не можемо.

Висновок

Головним засобом розвитку творчого мислення учнів є розв’язування нестандартних задач або задач стандартного вигляду, які розв’язуються

Нестандартними методами.

Розв’язування будь-якої задачі - це дуже складний комплекс дій. Учень повинен мати глибокі математичні знання, вміти оперувати математичними поняттями володіти сукупністю сформованих властивостей мислення.

Завжди під час розв’язування задач перед учнями постає проблема перетворення умови задачі з метою пошуку її розв’язання .

Активний пошук способів розв’язування задач - це процес творчого мислення, що є необхідною умовою творчої діяльності.

Екстремальні задачі розв’язують в два етапи:

1.        Розглядається невизначена задача, текст якої зводиться до рівняння ( або функції).

2.      За даними ознаками чи властивостями наявної функції визначають, який з розв’язків задачі є найбільш корисним.

Існують багато методів розв’язку задач на максимум і мінімум, та серед них можна виділити три основні:

1)       метод оцінки;

2)      метод перетворення площини;

)        метод опорної функції;

)        метод перебору.

В моїй роботі використані деякі теореми, на основі яких розв’язуються складні геометричні задачі :

Теорема 1: Добуто двох додатніх множників, сума яких стала, має найбільше значення при рівності множників ( якщо множники можуть приймати однакові значення).

Теорема 2: Сума двох додатніх чисел, добуток яких сталий, має найменше значення при рівності доданків.

Теорема 3: Середнє геометричне декількох величин не більше їх середнього арифметичного.

Нестандартні задачі корисні й тим, що не містять алгоритмічних підходів, завжди потребують пошуків нових підходів, що стимулюють пізнавальні інтереси учнів, формують навички проведення аналізу систематизації висування гіпотез, допомагають оволодіти дедуктивним методом, активізують самостійну пошукову діяльність.

архімед максимум мінімум штейнер

Список використаної літератури

1. Тихомиров В. М. Рассказы о максимумах и минимумах. - М.: Наука, 1986.

.Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. - М.: Наука, 1978.

. Бляшке В. Круг и Шар. - М.: Наука, 1967.

. Болтянский В. Г., Яглом И. М. Геометрические задачи на максимум и минимум. // Энциклопедия элементарной математики: кн. 5. - М.: Наука, 1966. - с. 270-348.

. Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Геометрические неравенства и задачи на максимум и минимум. - М.: Наука, 1970.

6. Рудин У. Основы математического анализа. - М.: Мир, 1976.