Гармонійні функції
ЗМІСТ
Вступ
1. Збіжність
ряду в нормованому просторі
2. Збіжність
ортогонального ряду в гільбертовому просторі
. Ортонормована
система. Ряд Фур’є за ортонормованою системою
. Базиси
в нормованому просторі
5. Тригонометричний
ряд Фур'є в 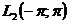
. Деякі
властивості біортогональних систем
. Біортогональні
системи в деяких бананових просторах
. Деякі
властивості базисів бананових просторів
. Деякі
застосування рядів в бананових просторах
Висновки
Список
використаних джерел
ВСТУП
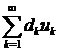 ,
,
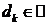 ,
, 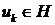 ,
(0)
,
(0)
Ряд називається ортогональним в евклідовому просторі 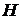 зі скалярним добутком
зі скалярним добутком 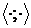 ,
якщо
,
якщо 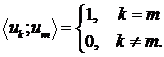 . Якщо ортогональний ряд є збіжним в евклідовому
просторі
. Якщо ортогональний ряд є збіжним в евклідовому
просторі 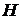 до елемента
до елемента 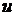 ,
то його коефіцієнти
,
то його коефіцієнти 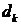 знаходяться за формулою
знаходяться за формулою 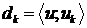 . Система
. Система 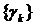 елементів
евклідового простору
елементів
евклідового простору 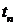
 називається біортогональною
до системи
називається біортогональною
до системи 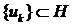 , якщо
, якщо 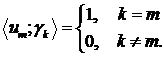 .
Якщо система
.
Якщо система 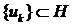 є ортогональною, то вона має біортогональну систему
є ортогональною, то вона має біортогональну систему 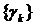 і
і 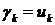 .
Якщо ряд
.
Якщо ряд 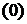 є збіжним в евклідовому просторі
є збіжним в евклідовому просторі 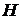 до елемента
до елемента 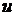 ,
і система
,
і система 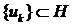 має біортогональну систему
має біортогональну систему 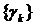 , то коефіцієнти
, то коефіцієнти 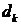 знаходяться
за формулою
знаходяться
за формулою 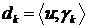 .
.
Метою курсової роботи є вивчення біортогональних систем в банановому
просторі.
1.
Збіжність ряду в нормованому просторі
Нехай 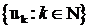 - зліченна підмножина нормованого простору. Ряд
- зліченна підмножина нормованого простору. Ряд
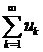 (1)
(1)
називається збіжним в  ,
якщо такий існує елемент
,
якщо такий існує елемент 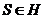 , що
, що
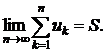 (2)
(2)
При цьому 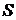 називається сумою ряду (1) і цей факт записується
так:
називається сумою ряду (1) і цей факт записується
так:
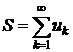 .(3)
.(3)
Теорема 1. Якщо (1) є збіжним в нормованому просторі  , то його загальний член прямує до нуля в
, то його загальний член прямує до нуля в 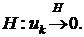
Доведення. Справді, 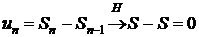 .
.
Теорема 1. Для того, щоб ряд (1) був збіжний в банаховому просторі 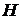 , необхідно і достатньо, щоб
, необхідно і достатньо, щоб
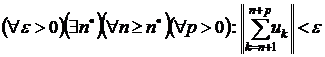 .(4)
.(4)
Доведення. Справді, збіжність ряду (1) рівносильна збіжності
послідовності 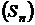 . Але
. Але 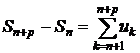 .
Звідси і повноти
.
Звідси і повноти 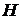 випливає твердження теореми.
випливає твердження теореми.
Ряд (1) називається нормально збіжним або абсолютно збіжним в топології
простору 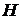 , якщо збіжним в
, якщо збіжним в 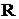 є
ряд
є
ряд
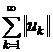 .(6)
.(6)
Теорема
2. Якщо ряд (1) є нормально збіжним в банаховому просторі 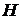 , то він є збіжним в
, то він є збіжним в 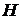 .
.
Доведення. Справді, це випливає із теореми 1 і нерівності
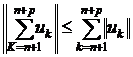 .
.
Приклад 1. Ряд 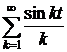 є нормально збіжним в
є нормально збіжним в 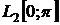 , оскільки
, оскільки 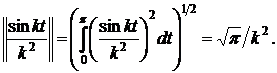
Приклад 2. Оскільки 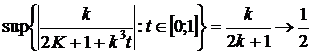 , то ряд
, то ряд 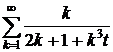 є
розбіжним в просторі
є
розбіжним в просторі 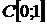 .
.
2.
Збіжність ортогонального ряду в гільбертовому просторі
Система 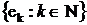 елементів евклідового простору
елементів евклідового простору 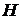 називається ортонормованою якщо
називається ортонормованою якщо
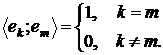
Теорема 1. Нехай 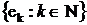 - ортонормована система гільбертового простору
- ортонормована система гільбертового простору 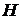 . Для того, щоб ряд
. Для того, щоб ряд
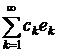 ,
,
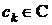 .
.
був збіжним в 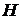 ,
необхідно і достатньо, щоб
,
необхідно і достатньо, щоб 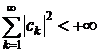 .
.
Доведення. Справді, це випливає із рівностей
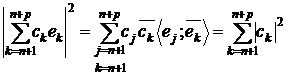
і теореми 1 попереднього пункту.
Приклад 1. Ряд 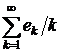 , де
, де 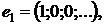
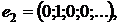
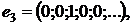 …,
є збіжним в
…,
є збіжним в 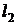 , оскільки система
, оскільки система 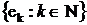 є
ортонормованою в
є
ортонормованою в 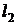 і ряд
і ряд 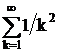 є
збіжним в
є
збіжним в 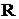 .
.
3.
Ортонормована система. Ряд Фур’є за ортонормованою системою
В курсі алгебри і геометрії показується, що якщо 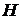 -
-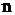 -мірний евклідовий простір,
-мірний евклідовий простір, 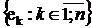 - його базис,
- його базис, 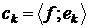 -
координатори вектора
-
координатори вектора 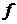 в цьому базисі, то
в цьому базисі, то 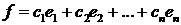 і
і 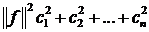 .
Ми розглядаємо аналог цього твердження для нескінченно вимірних просторів і
числа
.
Ми розглядаємо аналог цього твердження для нескінченно вимірних просторів і
числа 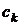 будемо називати не координаторами вектора
будемо називати не координаторами вектора 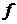 , а коефіцієнтами Фур’є. Нехай
, а коефіцієнтами Фур’є. Нехай 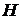 - евклідовий простір,
- евклідовий простір, 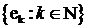 -
зліченна система елементів простору
-
зліченна система елементів простору 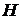 .
Система
.
Система 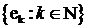 називається ортонормованою, якщо
називається ортонормованою, якщо
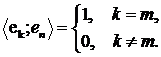
Числа 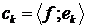 називається коефіцієнтами Фур'є
елемента
називається коефіцієнтами Фур'є
елемента 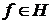 за ортонормованою системою
за ортонормованою системою 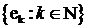 , а ряд
, а ряд
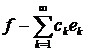 (1)
(1)
рядом Фур'є елемента 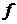 за
цією системою. Елемент
за
цією системою. Елемент
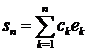 (2)
(2)
називають 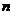 -им поліномом Фур'є або
-им поліномом Фур'є або 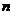 -ю
частинною сумою ряду Фур'є, а елемент
-ю
частинною сумою ряду Фур'є, а елемент
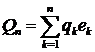 ,
(3)
,
(3)
де 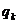 - довільні сталі (дійсні, якщо
- довільні сталі (дійсні, якщо 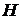 - дійсний, комплексні, якщо
- дійсний, комплексні, якщо  - комплексний), називають поліномом порядку
- комплексний), називають поліномом порядку 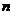 за системою
за системою 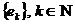 .
Відхиленням полінома
.
Відхиленням полінома 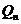 від елемента
від елемента 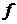 називається
число
називається
число 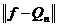 , тобто відхилення - це відстань в
, тобто відхилення - це відстань в  між
між 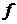 і
і
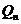 .
.
Теорема 1. Нехай 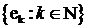 - ортонормована система евклідового (дійсного або
комплексного) простору
- ортонормована система евклідового (дійсного або
комплексного) простору 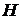 .
Тоді серед всіх поліномів порядку
.
Тоді серед всіх поліномів порядку 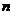 найменше
відхилення від елемента
найменше
відхилення від елемента 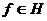 має
має
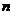 -ий поліном Фур'є елемента
-ий поліном Фур'є елемента 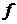 .
.
Доведення. Будемо розглядати тільки дійсний евклідовий простір.
Тоді, використовуючи властивості скалярного добутку і ортонормованість системи 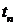
 ,
маємо
,
маємо
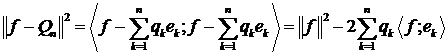
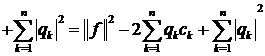
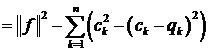 .(4)
.(4)
Звідси видно, що мінімум правої частини (4) досягається при 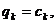
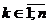 (під сумою стоїть квадратний тричлен як функція
(під сумою стоїть квадратний тричлен як функція 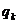 ).
).
Теорема 2. Якщо 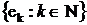 - ортонормована система в евклідовому просторі
- ортонормована система в евклідовому просторі  , то при будь-якому
, то при будь-якому 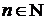 і
для кожного
і
для кожного 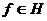 виконується
виконується
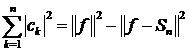 (5)
(5)
і справедлива нерівність Бесселя 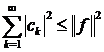 , тобто
, тобто
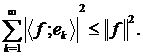
Доведення. Справді, (5) випливає із (4), а остання нерівність є
наслідком (5).4
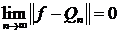 .
(6)
.
(6)
Теорема 3. Якщо ортонормована система 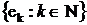 в
евклідовому просторі
в
евклідовому просторі  є повною в
є повною в  ,
то для кожного елемента
,
то для кожного елемента 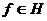 справедлива
рівність Парсеваля (аналог теореми Піфагора)
справедлива
рівність Парсеваля (аналог теореми Піфагора)
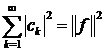 .(7)
.(7)
Доведення. Це випливає із (5) та (6), бо
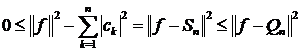 .
.
Теорема 4. Якщо ортонормована система 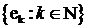 є повною в евклідовому просторі
є повною в евклідовому просторі  , то для кожного елемента
, то для кожного елемента 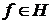 його ряд Фур'є (1) збігається в
його ряд Фур'є (1) збігається в  до
до 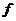 ,
тобто
,
тобто
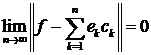 . (8)
. (8)
Доведення. Ця теорема випливає із (5) і
попередньої теореми, бо
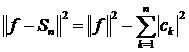 .
.
Теорема 5. Якщо 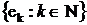 -
ортонормована система в евклідовому просторі
-
ортонормована система в евклідовому просторі  ,
і для деякого
,
і для деякого 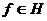 існує послідовність поліномів
існує послідовність поліномів 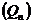 вигляду (3) така, що виконується (6), то для цього
елемента
вигляду (3) така, що виконується (6), то для цього
елемента 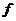 справедливі рівності (7) і (8).
справедливі рівності (7) і (8).
Доведення. Це випливає із (5) та (6).
Система 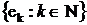 називається ортогональною, якщо
називається ортогональною, якщо
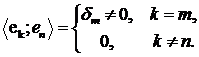
Вивчення ортогональної системи  зводиться
до вивчення ортонормованої системи
зводиться
до вивчення ортонормованої системи 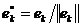 .
.
Теорема 6 (Рісса-Фішера). Якщо 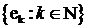 -
ортонормована система гільбертового простору
-
ортонормована система гільбертового простору  і
і
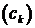 - послідовністиь комплексних (дійсних, якщо
- послідовністиь комплексних (дійсних, якщо  дійсний) чисел таких, що
дійсний) чисел таких, що 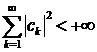 , то існує такий елемент
, то існує такий елемент 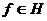 , що
, що 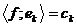 і
справедлива рівність Парсеваля
і
справедлива рівність Парсеваля 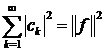 .
.
Доведення. Маємо 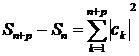 .
Із збіжності ряду (2) і повноти
.
Із збіжності ряду (2) і повноти  випливає
збіжність в
випливає
збіжність в  послідовності
послідовності 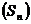 до
деякого елемента
до
деякого елемента 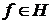 і за теоремою 4 справедлива рівність Парсеваля.
і за теоремою 4 справедлива рівність Парсеваля.
4.
Базиси в нормованому просторі
Система елементів 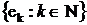 банахового простоу
банахового простоу  називається
базисом цього простору, якщо кожний елемент
називається
базисом цього простору, якщо кожний елемент 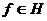 єдиним
чином розвивається в збіжний в
єдиним
чином розвивається в збіжний в  ряд
ряд
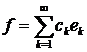 .
(1)
.
(1)
Безпосередньо із означення випливає, що кожний базис є повною системою,
але не навпаки. Наприклад, за теоремою Вейєрштрасса система 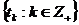 є повною в
є повною в 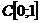 ,
але не є базисом в цьому просторі, бо не кожна функція, неперервна (і навіть не
кожна нескінченно диференційовна функція
,
але не є базисом в цьому просторі, бо не кожна функція, неперервна (і навіть не
кожна нескінченно диференційовна функція 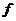 )
подається у вигляді суми рівномірно збіжного на
)
подається у вигляді суми рівномірно збіжного на 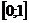 ряду
ряду
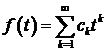 .
.
Теорема 1. Якщо 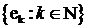 - ортонормована система гільбертового простору
- ортонормована система гільбертового простору  , ряд (1) є збіжним в
, ряд (1) є збіжним в  до
до 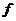 ,
то його коефіцієнти
,
то його коефіцієнти 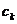 знаходяться за формулою
знаходяться за формулою 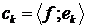 .
.
Доведення. Справді,
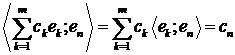 ,
,
якщо 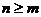 . Тому, враховуючи, що ряд (1) є збіжним в
. Тому, враховуючи, що ряд (1) є збіжним в  і скалярний добуток є неперервною функцією, отримуємо
і скалярний добуток є неперервною функцією, отримуємо
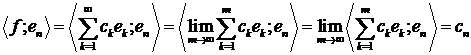 ,
,
звідки випливає потрібний висновок.
Теорема 2. Нехай 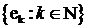 - ортонормована система гільбертового простору
- ортонормована система гільбертового простору  . Тоді наступні умови є еквівалентними: 1) система
. Тоді наступні умови є еквівалентними: 1) система 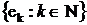 є повною в просторі
є повною в просторі  ; 2) система
; 2) система 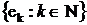 є
базисом простору
є
базисом простору  ; 3) для кожного
; 3) для кожного 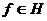 справедлива
рівність Парсеваля
справедлива
рівність Парсеваля 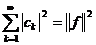 .
.
Доведення. Ця теорема є безпосереднім наслідком теореми 1 і
теорем попереднього пункту.
Приклад 1. Система елементів
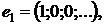
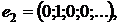
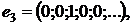 …,
…,
є ортонормованою в 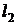 і
є базисом цього простору. Справді, ортонормованість цієї системи встановлюється
безпосередньою перевіркою. Далі, для елемента
і
є базисом цього простору. Справді, ортонормованість цієї системи встановлюється
безпосередньою перевіркою. Далі, для елемента 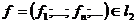 маємо
маємо 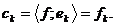 Тому
ряд
Тому
ряд 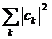 є збіжним. Отже, ряд
є збіжним. Отже, ряд 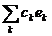 також є збіжним в
також є збіжним в  до
деякого елемента
до
деякого елемента 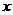 . Покажемо, що
. Покажемо, що 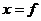 .
Справді,
.
Справді,
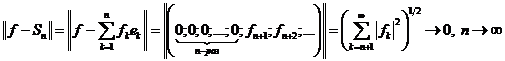
5. Тригонометричний ряд Фур'є
в 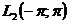
Теорема 1 . Тригонометрична система
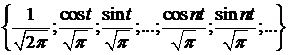 (1)
(1)
є ортонормованим базисом простору 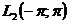 і, отже, кожна функція
і, отже, кожна функція 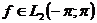 єдиним чином розвивається в збіжний в
єдиним чином розвивається в збіжний в 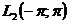 тригонометричний ряд Фур'є
тригонометричний ряд Фур'є
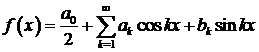 ,
,
і при цьому коефіцієнти 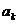 і
і 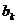 знаходяться
за формулами
знаходяться
за формулами
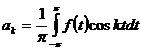 ,
,
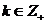 ,
,
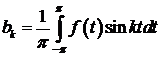 ,
,
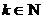 ,
,
і справедлива рівність Парсеваля
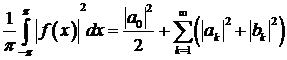 .
.
Доведення. Множина всіх неперервних функцій 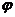 таких,
що
таких,
що 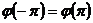 є скрізь щільною в
є скрізь щільною в 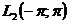 .
З іншого боку за теоремою Вейєрштрасса кожну таку
.
З іншого боку за теоремою Вейєрштрасса кожну таку  можна як завгодно точно в
можна як завгодно точно в 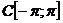 , а тому і в
, а тому і в 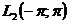 наблизити
скінченними лінійними комбінаціями системи (1). Звідси випливає, що
тригонометрична система є повною в
наблизити
скінченними лінійними комбінаціями системи (1). Звідси випливає, що
тригонометрична система є повною в 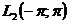 .
Оскільки вона є також ортонормованою, то вона і є базисом.
.
Оскільки вона є також ортонормованою, то вона і є базисом.
Теорема 2. Тригонометрична система
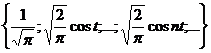 (2)
(2)
є ортонормованим базисом простору 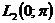 і, отже, кожна функція
і, отже, кожна функція 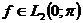 єдиним чином розвивається в збіжний в
єдиним чином розвивається в збіжний в 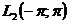 тригонометричний ряд Фур'є.
тригонометричний ряд Фур'є.
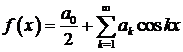 ,
,
і при цьому коефіцієнти 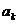 знаходяться за формулами
знаходяться за формулами
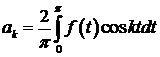 ,
,
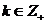 ,
,
базис ортонормований біортогональний банановий
і справедлива рівність Парсеваля
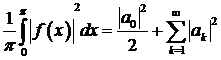 .
.
Доведення. Ця теорема є наслідком теореми 1, оскільки можна
вважати, що 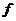 - парна функція і
- парна функція і 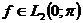 .
.
Теорема 1. Тригонометрична система
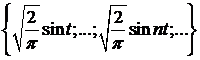 (3)
(3)
є ортонормованим базисом простору 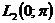 і, отже, кожна функція
і, отже, кожна функція 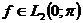 єдиним чином розвивається в збіжний в
єдиним чином розвивається в збіжний в 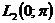 тригонометричний ряд Фур'є
тригонометричний ряд Фур'є
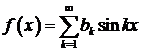 ,
,
і при цьому коефіцієнти 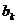 знаходяться за формулами
знаходяться за формулами
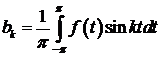 ,
,
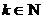 ,
,
і справедлива рівність Парсеваля
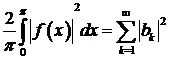 .
.
Доведення. Ця теорема є наслідком теореми 1, оскільки можна
вважати, що 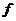 - непарна функція і
- непарна функція і 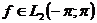 .
.
Теорема 4. Комплексна тригонометрична система
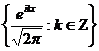 (4)
(4)
є ортонормованою базою простору 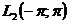 і, таким чином, кожна функція
і, таким чином, кожна функція 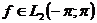 єдиним чином розвивається в збіжний в
єдиним чином розвивається в збіжний в 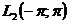 комплексний ряд Фур'є
комплексний ряд Фур'є
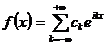 , і при цьому коефіцієнти цього ряду знаходяться за
формулою
, і при цьому коефіцієнти цього ряду знаходяться за
формулою
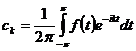
і справедлива рівність Парсеваля 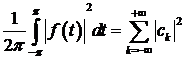 .
.
Доведення. Ця теорема є наслідком теореми 1.
Зауваження 1. Довгий час залишалось відкритим питання про поточкову збіжність
ряду Фур'є із 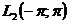 .
Це питання розв'язав Карлесон, який довів, що ряд Фур'є кожної функції
.
Це питання розв'язав Карлесон, який довів, що ряд Фур'є кожної функції 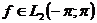 збігається майже скрізь.
збігається майже скрізь.
Доведемо тепер твердження, яке використане при доведенні теореми 1.
Теорема 5. Для кожного 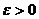 і
кожного проміжка
і
кожного проміжка  і кожної східчастої на
і кожної східчастої на 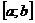 функції
функції 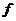 існує
неперервна на
існує
неперервна на 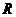 функція
функція 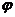 ,
рівна нулеві поза
,
рівна нулеві поза 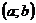 така, що
така, що 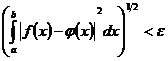 .
.
Доведення. Досить провести функції
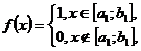
де 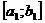 - довільний проміжок, який міститься в
- довільний проміжок, який міститься в 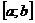 , бо кожна східчаста на
, бо кожна східчаста на 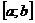 функція
є скінченною лінійною комбінацією таких функцій
функція
є скінченною лінійною комбінацією таких функцій 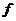 .
Підберемо
.
Підберемо 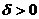 так, щоб
так, щоб 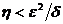 і
і
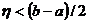 . Безпосередньою перевіркою встановлюємо, що шуканою є
функція
. Безпосередньою перевіркою встановлюємо, що шуканою є
функція
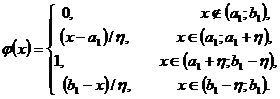
6.
Деякі властивості біортогональних систем
Нехай 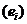 -послідовність
елементів евклідового простору
-послідовність
елементів евклідового простору  зі
скалярним добутком
зі
скалярним добутком 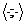 . Послідовність
. Послідовність 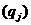 елементів
простору
елементів
простору  називається біортогональною до системи
називається біортогональною до системи 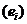 , якщо
, якщо
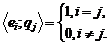 (1)
(1)
Якщо система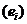 має біортогональну систему
має біортогональну систему 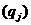 , то ряд Коли
, то ряд Коли 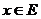 -
будь-який елемент, то ряд
-
будь-який елемент, то ряд
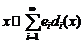 (2)
(2)
називається рядом Фур’є елемента 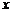 за
системою
за
системою 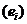 . Ряд (2) може бути збіжним, може бути розбіжним, може
бути збіжним, але його сума може не дорівнювати
. Ряд (2) може бути збіжним, може бути розбіжним, може
бути збіжним, але його сума може не дорівнювати 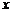 .
.
Приклад 1.
Коли послідовність 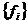 утворює
тотальну множину функціоналів і ряд (2) для деякого елемента
утворює
тотальну множину функціоналів і ряд (2) для деякого елемента 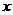 збіжний, то
збіжний, то 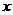 є
сумою цього ряду; справді, для
є
сумою цього ряду; справді, для 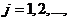 маємо:
маємо:
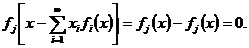
Теорема 1. Якщо ряд (2) для кожного 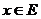 - збіжний, то ряд
- збіжний, то ряд
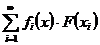
є також збіжний у кожній точці 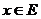 для всякого лінійного функціонала
для всякого лінійного функціонала 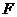 .
.
Доведення. Покладаючи
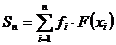 ,
(3)
,
(3)
маємо 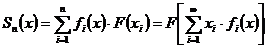 , так що збіжність послідовності
, так що збіжність послідовності 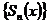 в кожній точці
в кожній точці 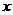 є
очевидна.
є
очевидна.
Теорема 2. Якщо норми частинних сум (3) ряду
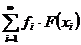 (4)
(4)
в своїй сукупності є обмежені для всякого лінійного
функціонала 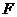 , то ряд (2) є збіжний для кожного елемента
, то ряд (2) є збіжний для кожного елемента 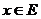 , який є границею будь-якої послідовності лінійних
комбінацій, утворених з членів послідовності
, який є границею будь-якої послідовності лінійних
комбінацій, утворених з членів послідовності 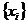 .
.
Доведення. Покладаючи
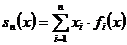 ,
(5)
,
(5)
маємо 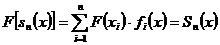 (див. (3)); а тому що за умовою
(див. (3)); а тому що за умовою 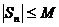 , де
, де 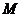 є
незалежне від
є
незалежне від 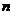 число, то на підставі теореми (якщо послідовність
число, то на підставі теореми (якщо послідовність 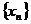 елементів простору
елементів простору 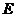 має
таку властивість, що для кожного лінійного функціонала
має
таку властивість, що для кожного лінійного функціонала 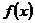 , означеного в
, означеного в 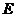 ,
маємо
,
маємо 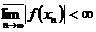 , то послідовність норм
, то послідовність норм 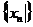 є обмежена), для кожного
є обмежена), для кожного 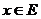 маємо
маємо 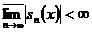 .
Отже, на основі теореми (якщо для даної послідовності
.
Отже, на основі теореми (якщо для даної послідовності 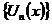 лінійних операцій, означених в
лінійних операцій, означених в 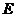 , справедлива нерівність
, справедлива нерівність 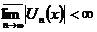 для кожного
для кожного 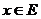 ,
то послідовність норм
,
то послідовність норм 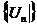 є обмежена) існує таке число
є обмежена) існує таке число 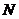 ,
незалежне від
,
незалежне від 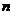 і від
і від 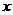 ,
що
,
що 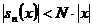 .
.
А тому що для 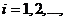 маємо
маємо 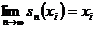 ,
то прості міркування приводять до висновку, що існує
,
то прості міркування приводять до висновку, що існує 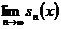 для кожного елемента
для кожного елемента 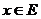 ,
який задовольняє умови теореми.
,
який задовольняє умови теореми.
Теорема 3. Якщо норми частинних сум (5) ряду (2) в своїй
сукупності є обмежені для кожного 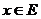 ,
то ряд (4) збіжний для кожного функціонала
,
то ряд (4) збіжний для кожного функціонала 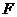 ,
який є границею довільної послідовності лінійних комбінацій, утворених з членів
послідовності
,
який є границею довільної послідовності лінійних комбінацій, утворених з членів
послідовності 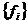 .
.
Доведення аналогічне доведенню теореми 2.
Теорема 4. Якщо виконуються умови попередньої теореми і крім того
послідовність 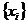 є фундаментальна, то ряд (2) збігається для всякого
елемента
є фундаментальна, то ряд (2) збігається для всякого
елемента 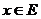 .
.
Доведення. На
підставі (5) для кожного 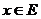 маємо
маємо 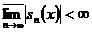 і,
крім того,
і,
крім того, 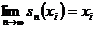 для
для 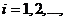 а
звідси випливає збіжність ряду (2) для кожного
а
звідси випливає збіжність ряду (2) для кожного 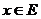 .
.
7.
Біортогональні системи в деяких бананових просторах
Розгляньмо тепер властивості біортогональних послідовностей в
просторах, які нас особливо цікавлять.
Покладемо
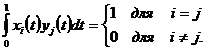 (6)
(6)
Припустимо далі, що 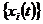 є
послідовність функцій у просторі
є
послідовність функцій у просторі 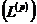 ,
де
,
де 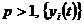 - послідовність функцій в
- послідовність функцій в 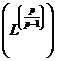 і, крім того, ці послідовності в даних просторах
повні (або замкнені).
і, крім того, ці послідовності в даних просторах
повні (або замкнені).
Теорема 5. Якщо при заданих умовах ряд
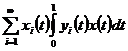
Збігається в середньому з 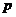 -тим степенем для всякої функції
-тим степенем для всякої функції 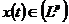 , то ряд
, то ряд
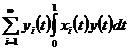
Збігається в середньому з 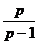 -им степенем для всякої функції
-им степенем для всякої функції 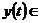
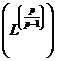 .
.
Доведення. Нехай
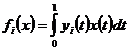 для
для
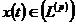 . (7)
. (7)
Отже, за умовою ряд 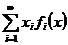 для
всякого
для
всякого 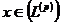 є збіжний в середньому (тобто за нормою) з
є збіжний в середньому (тобто за нормою) з 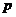 -тим степенем. Тим самим на основі теореми 3, ряд
-тим степенем. Тим самим на основі теореми 3, ряд
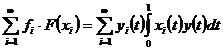 ,
де
,
де 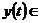
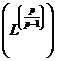
є збіжний за нормою (тобто, в середньому з 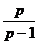 -им степенем) для всякого лінійного функціонала
-им степенем) для всякого лінійного функціонала 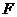 , означеного в просторі
, означеного в просторі 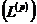 ,
а так само ряд (7) буде збіжний для всякої функції
,
а так само ряд (7) буде збіжний для всякої функції 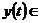
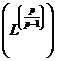 ,
що треба було довести.
,
що треба було довести.
Зокрема, якщо 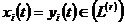 , де
, де 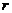 найбільше
з чисел
найбільше
з чисел 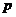 і
і 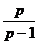 ,
то висновком з попередньої теореми буде така теорема:
,
то висновком з попередньої теореми буде така теорема:
Якщо ряд
для кожного 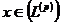 збіжний в середньому з
збіжний в середньому з 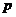 -тим
степенем, то він є також збіжний в середньому з
-тим
степенем, то він є також збіжний в середньому з 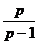 -им
степенем для кожної функції
-им
степенем для кожної функції 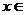
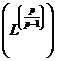 .
.
Тут можна припустити, наприклад, що 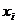 ,
де
,
де 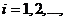 є обмежені функції.
є обмежені функції.
Розглянемо тепер випадок, коли при умові (6), 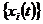 є послідовність інтегровних функцій, а
є послідовність інтегровних функцій, а  є послідовність обмежених функцій у проміжку
є послідовність обмежених функцій у проміжку 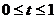 . Припустимо, крім того, що послідовність
. Припустимо, крім того, що послідовність 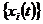 є повна в просторі
є повна в просторі 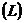 .
.
Теорема 6. Якщо при цих умовах ряд
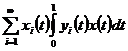
є збіжний у середньому для 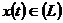 , то ряд
, то ряд
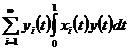
для кожного 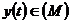 є
майже всюди обмежений і навпаки.
є
майже всюди обмежений і навпаки.
Доведення аналогічне доведенню теореми 5: 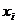 розглядають як елементи області
розглядають як елементи області 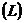 , а
, а 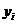 як
лінійні функціонали; нарешті, беруть на увагу теореми 3 і 4.
як
лінійні функціонали; нарешті, беруть на увагу теореми 3 і 4.
Зокрема, коли 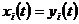 , то маємо висновки:
, то маємо висновки:
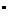 .
Якщо ряд (8), де
.
Якщо ряд (8), де 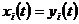
 в
середньому збіжний для кожного
в
середньому збіжний для кожного 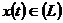 ,
то він для кожного
,
то він для кожного 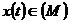 обмежений і навпаки.
обмежений і навпаки.
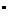 .
Якщо ряд (8), де
.
Якщо ряд (8), де 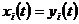
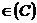 ,
а
,
а 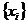 повна послідовність у просторі
повна послідовність у просторі 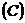 , рівномірно збіжний для кожного
, рівномірно збіжний для кожного 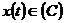 , то він у середньому збіжний для кожного
, то він у середньому збіжний для кожного 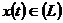 і навпаки.
і навпаки.
Доведення одержимо так: в першій частині теореми 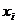 розглядаємо як елементи області
розглядаємо як елементи області 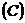 , а
, а 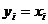 як
представників функціоналів; а в другій частині
як
представників функціоналів; а в другій частині 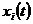 розглядаємо
як елементи області
розглядаємо
як елементи області 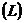 , а
, а 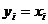 як
представників лінійних функціоналів, означених у просторі
як
представників лінійних функціоналів, означених у просторі 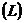 .
.
8.
Деякі властивості базисів бананових просторів
Послідовність 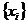 елементів простору
елементів простору 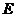 називаємо
базисом (це поняття запровадив у загальному випадку Ю.Шаудер), якщо для
кожного елемента
називаємо
базисом (це поняття запровадив у загальному випадку Ю.Шаудер), якщо для
кожного елемента 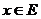 існує точно така одна послідовність чисел
існує точно така одна послідовність чисел 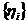 , що
, що
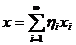 .
.
Коли дано базис 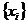 , то нехай
, то нехай 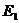 буде
множина послідовностей
буде
множина послідовностей 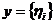 , для яких ряд
, для яких ряд 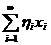 є збіжний. Покладаючи
є збіжний. Покладаючи 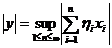 , легко довести, що так нормована множина
, легко довести, що так нормована множина 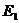 утворює простір типу
утворює простір типу 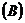 .
.
Покладемо далі
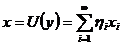 для
кожної послідовності
для
кожної послідовності 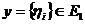 .
.
Так означена операція 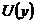 є
лінійна, бо
є
лінійна, бо 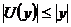 , а тому що вона перетворює множину
, а тому що вона перетворює множину 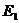 на
на 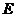 взаємно
одночасно, то обернена операція
взаємно
одночасно, то обернена операція 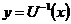 є
також лінійна.
є
також лінійна.
Нарешті, функціонал:
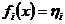 ,
де
,
де 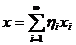
також лінійний, бо
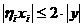 і
і
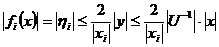 .
.
Отже, маємо
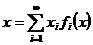 для
кожного
для
кожного 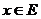 ,
,
а тому що цей розклад єдиний, то одержуємо рівність (1), тобто
послідовність 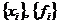 є біортогональна.
є біортогональна.
Зауважимо, що для кожного лінійного функціонала 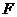 , означеного в просторі
, означеного в просторі 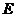 ,
ряд
,
ряд 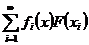 збігається до
збігається до 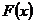 тому,
що для кожного
тому,
що для кожного 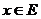 маємо рівність:
маємо рівність:
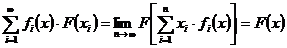 .
.
Невідомо, чи кожний сепарабельний простір типу 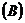 має базис.
має базис.
Ця проблема розв'язана тільки в деяких окремих просторах. Так,
наприклад, у просторі 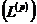 , де
, де 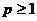 ,
базисом є ортогональна система Haar'a. В просторі
,
базисом є ортогональна система Haar'a. В просторі 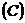 базис
побудував Ю.Шаудер. В просторі
базис
побудував Ю.Шаудер. В просторі 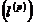 ,
де
,
де 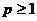 , базис утворює послідовність
, базис утворює послідовність 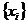 , де
, де 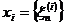
і 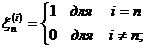
тоді для 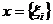 маємо
маємо 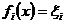 .
Нарешті, в просторі
.
Нарешті, в просторі 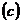 базисом є ця сама послідовність з приєднанням до неї
елемента
базисом є ця сама послідовність з приєднанням до неї
елемента 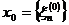 , де
, де 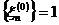 для
для
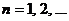 Отже, для елемента
Отже, для елемента 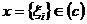 маємо
маємо
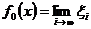 .
.
9.
Деякі застосування рядів в бананових просторах
Теорема 7. Якщо послідовності 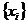 ,
,
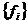 і
і 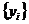 ,
,
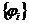 є біортогональні, а рівняння
є біортогональні, а рівняння 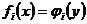 , де
, де 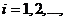 для
кожного
для
кожного 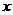 мають точно один розв'язок
мають точно один розв'язок 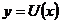 , то із збіжності ряду
, то із збіжності ряду 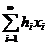 випливає збіжність ряду
випливає збіжність ряду 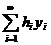 для кожної послідовності чисел
для кожної послідовності чисел 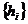 .
.
Доведення. Як легко бачити, з рівностей:  і
і 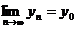 ,
де
,
де 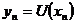 , випливає рівність
, випливає рівність 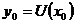 .
Отже, на підставі теореми 7 (Кожна адитивна операція
.
Отже, на підставі теореми 7 (Кожна адитивна операція 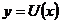 , що задовольняє умову: з
, що задовольняє умову: з 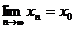 і
і 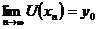 випливає
випливає
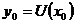 , є лінійна), операція
, є лінійна), операція 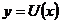 є лінійна. Тим самим, покладаючи
є лінійна. Тим самим, покладаючи 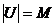 , маємо
, маємо 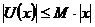 ,
а тому що за означенням
,
а тому що за означенням 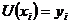 для
для 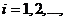 одержуємо
одержуємо
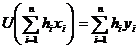 для всяких дійсних
для всяких дійсних 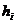 ,
звідки випливає безпосередньо твердження нашої теореми.
,
звідки випливає безпосередньо твердження нашої теореми.
Висновок. Якщо 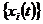 і
і  -
ортогональні, нормовані послідовності неперервних функцій і для кожної
неперервної функції
-
ортогональні, нормовані послідовності неперервних функцій і для кожної
неперервної функції 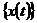 існує тільки одна неперервна функція
існує тільки одна неперервна функція 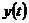 така, що
така, що 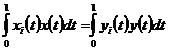 ,
то з рівномірної збіжності ряду
,
то з рівномірної збіжності ряду 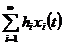 випливає
рівномірна збіжність ряду
випливає
рівномірна збіжність ряду 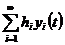 .
.
Аналогічні висновки одержуємо для інших функціональних просторів.
Теорема 8. Нехай 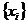 ,
, 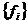 -
біортогональна послідовність, де
-
біортогональна послідовність, де 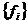 -
тотальна послідовність, а послідовність чисел
-
тотальна послідовність, а послідовність чисел 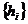 така, що тоді, коли
така, що тоді, коли 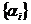 є послідовність коефіцієнтів елемента
є послідовність коефіцієнтів елемента 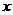 (тобто
(тобто 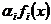 для
для
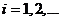 ), то
), то 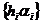 є
послідовність коефіцієнтів елемента
є
послідовність коефіцієнтів елемента 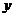 .
.
Коли при цих умовах 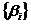 є
послідовність коефіцієнтів деякого лінійного функціонала
є
послідовність коефіцієнтів деякого лінійного функціонала 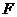 (тобто
(тобто 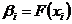 для
для
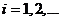 ), то
), то 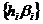 є
послідовність коефіцієнтів деякого лінійного функціонала
є
послідовність коефіцієнтів деякого лінійного функціонала 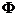 .
.
Доведення. За умовою система рівнянь 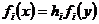 , де
, де 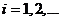 для
кожного
для
кожного 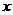 має точно один розв'язок. Позначимо його
через
має точно один розв'язок. Позначимо його
через 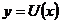 .
.
З рівностей: 
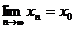 і
і
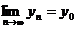 , де
, де 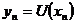 ,
випливає очевидно рівність
,
випливає очевидно рівність 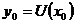 .
Отже, на основі теореми 7 (Кожна адитивна операція
.
Отже, на основі теореми 7 (Кожна адитивна операція 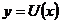 , що задовольняє умову: з
, що задовольняє умову: з 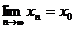 і
і 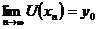 випливає
випливає
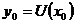 , є лінійна), операція
, є лінійна), операція 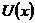 є неперервна.
є неперервна.
Зокрема, легко бачити, що:
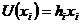 для всіх
для всіх 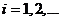 (9)
(9)
Отже, якщо дано такий лінійний функціонал 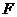 , що
, що 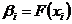 для
для
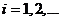 , то за формулою (9) маємо
, то за формулою (9) маємо 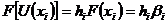 , тобто числа
, тобто числа 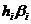 є
коефіцієнтами операції
є
коефіцієнтами операції 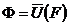 , що й треба було довести.
, що й треба було довести.
Зауважимо, що при  вираз
вираз 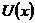 на
основі (9) є границею лінійних комбінацій, утворених з членів послідовності
на
основі (9) є границею лінійних комбінацій, утворених з членів послідовності 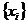 .
.
Як застосування цього зауваження легко одержуємо таку теорему.
Теорема 9. Нехай 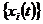 -
ортогональна, нормована і замкнена в просторі
-
ортогональна, нормована і замкнена в просторі 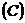 послідовність неперервних функцій.
послідовність неперервних функцій.
Якщо послідовність множників 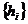 перетворює всяку послідовність
перетворює всяку послідовність 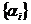 коефіцієнтів обмеженої функції в послідовність
коефіцієнтів
коефіцієнтів обмеженої функції в послідовність
коефіцієнтів 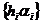 обмеженої функції, то вона перетворює одночасно кожну
послідовність
обмеженої функції, то вона перетворює одночасно кожну
послідовність 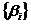 коефіцієнтів довільної неперервної функції також у
послідовність
коефіцієнтів довільної неперервної функції також у
послідовність 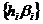 коефіцієнтів якоїсь неперервної функції.
коефіцієнтів якоїсь неперервної функції.
Обернена теорема також справедлива.
Нарешті, маємо:
Теорема 10. Нехай 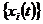 - ортогональна, нормована і повна в просторі
- ортогональна, нормована і повна в просторі 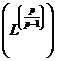 , де
, де 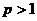 ,
послідовність обмежених функцій.
,
послідовність обмежених функцій.
Якщо послідовність множників 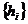 перетворює послідовність коефіцієнтів
перетворює послідовність коефіцієнтів 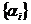 довільної функції
довільної функції 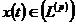 в
послідовність коефіцієнтів
в
послідовність коефіцієнтів 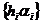 певної
функції
певної
функції 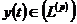 , то вона перетворює також кожну послідовність
коефіцієнтів
, то вона перетворює також кожну послідовність
коефіцієнтів 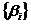 довільної функції
довільної функції 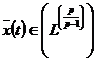 в
послідовність коефіцієнтів
в
послідовність коефіцієнтів 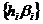 певної
функції
певної
функції 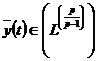 .
.
Коли 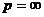 ,
то
,
то 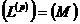 .
.
Негармонійні ряди Фур’є. Нехай 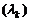 -
довільна послідовність комплексних чисел. Ряд
-
довільна послідовність комплексних чисел. Ряд
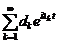
називається узагальненим тригонометричним рядом або рядом Діріхле, або
негармонійним рядом Фур’є. Питання про можливість розкладу довільної функції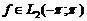 в збіжний в цьому просторі
в збіжний в цьому просторі
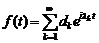 1
1
Вперше розглянув Н.Вінер[.
Він довів наступне твердження.
Теорема. Нехай 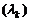 - довільна послідовність різних дійсних чисел таких,
що
- довільна послідовність різних дійсних чисел таких,
що
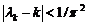 ,
,
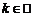 .
.
Тоді система 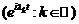 є
базисом простору
є
базисом простору 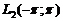 , тобто кожна функція
, тобто кожна функція 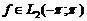 єдиним чином розвивається у збіжний у цьому просторі
().
єдиним чином розвивається у збіжний у цьому просторі
().
ВИСНОВКИ
В цій курсовій роботі ми вивчали властивості систем в
нормованих просторах, властивості базисів, властивості біортогональних систем,
а також деякі застосування рядів в нормованих просторах.
Ця курсова робота допомогла мені зрозуміти і усвідомити, який
великий і ще не повністю вивчений мною світ математики.
СПИСОК
ВИКОРИСТАНИХ ДЖЕРЕЛ
1. Антоневич
А.Б., Князев П.Н., Радыно Я.В. Задачи и упражнения по функциональному
анализу.-Минск:Высшейшая
школа, 1978.-206с.
2. Антоневич
А.Б., Радыно Я.В. Функциональнальный анализ и интегральные уравнения.-Минск:Высшейшая школа, 1978.-206с.
. Ахиезер
Н.И., Глазман Н.М. Теория линейніх операторов в гильбертовом пространстве: В 2т.-Х.:Вища школа, Изд-во. при Харьк. ун-те. 1977.-Т.1.-316с.
. Ахиезер
Н.И., Глазман Н.М. Теория линейніх операторов в гильбертовом пространстве: В 2т.-Х.:Вища школа, Изд-во. при Харьк. ун-те. 1978.-Т.2.-288с.
. Банах
С. Курс функціонального аналізу.-К.: Радянська школа.- 1948.-216с.
. Березанский
Ю.М. Разложения по собственным функциям самосопряженных.-К.: Наукова думка.- 1988.-800с.
. Березанский
Ю.М., Кондратьев Ю. Г. Спектральные метододы в бесконечномерном анализе.-К.: Наукова думка.- 1965. -680с.
. Березанский
Ю.М., Ус Г.Ю., Шефтель Е.Г. Функциональный анализ.-К.:Вища школа.-1990.-600с.