Основные разделы теоретической механики
1. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Теоретическая механика играет важную роль в
подготовке современного инженера. Решение задач по теоретической механике
способствует формированию инженерного мышления студента Теоретическая механика
играет роль своеобразного связующего звена между физикой, математикой и
инженерными дисциплинами. Три раздела теоретической механики: статика,
кинематика и динамика являются научной основой общеинженерных дисциплин.
.1 Статика
Статика - раздел механики, в котором изучаются
правила сложения сил и условия равновесия материальных тел. В статике
рассматриваются абсолютно твердые тела, являющиеся моделями материальных тел.
Материальное тело можно представить как систему, образованную непрерывной
совокупностью материальных точек. Механизм, машина - это механические системы.
А под материальной точкой понимается тело, размерами которого можно пренебречь.
В абсолютно твердых телах расстояние между отдельными точками остается
неизменным. Такое тело не может ни деформироваться, ни изнашиваться.
Мера механического взаимодействия материальных
тел называется силой. Сила характеризуется численным значением (модулем),
направлением и точкой приложения. Таким образом, сила является вектором.
Прямая, по которой направлен вектор, называется линией действия силы.
Совокупность сил, действующих на данное тело, называется системой сил, а силы
входящие в состав данной системы называются составляющими этой системы. Системы
сил, оказывающие на твердое тело одинаковые действия, называются
эквивалентными. Если под действием системы свободное тело не меняет своего
равномерного движения, то такая система называется уравновешенной. Сила,
эквивалентная системе сил называется равнодействующей этой системы.
.1.1 Аксиомы статики
В основе механики, а в частности статики, лежат
аксиомы - законы природы, принятые без доказательства и установленные из опытов
и наблюдений.
Аксиома I.
Две силы, приложенные к твердому телу уравновешиваются тогда и только тогда,
когда они равны по модулю и действуют по одной прямой в противоположных направлениях.
(рис. 6.1.)
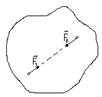
Рис. 1.
Аксиома II.
Не нарушая состояние абсолютно твердого тела силы к нему можно прикладывать
тогда и только тогда, когда они составляют уравновешенную систему.
Из этой аксиомы вытекает следствие:
не нарушая состояния тела, точку приложения силы можно переносить вдоль линии
ее действия (см. рис 6.2.). На рисунке 


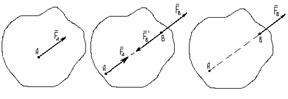
Рис.2.
Другими словами, сила, приложенная к абсолютно
твердому телу, представляет собой скользящий вектор.
Аксиома III.
Равнодействующая двух сил, приложенных к одной точке твердого тела, приложена в
этой же точке и изображается диагональю параллелограмма, построенного на
векторах данных сил  (рис.6.3.)
(рис.6.3.)

Рис.3.
На основании данной аксиомы можно
складывать силы и раскладывать их на составляющие.
Аксиома IV. Силы
взаимодействия двух тел равны по модулю и направлены по одной прямой в
противоположные стороны (3й закон Ньютона), (рис.6.4.)
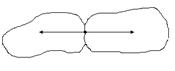
Рис.4.
Аксиома V. Если
твердое тело находится в равновесии, то это равновесие не нарушится, если тело
станет абсолютно твердым. Данная аксиома (принцип отвердевания) используется в
том случае, когда рассматривается равновесие тех тел, которые нельзя считать
твердыми.
.1.2 Связи и реакции связей
Тела, рассматриваемые в механике,
могут быть свободными и несвободными. Свободным называют тело, которое не
испытывает никаких препятствий для перемещения в пространстве в любом
направлении. Если же другие тела ограничивают его движение в одном или
нескольких направлениях, то тело является несвободным. Тела, которые
ограничивают движение рассматриваемого тела, называют связями. Не изменяя
состояния несвободного тела, можно отбросить наложенные на него связи, приложив
их реакции. После этого тело можно рассматривать как свободное. Связи, в
которых отсутствуют силы трения, называют идеальными.
Реакция связи в виде гладкой
поверхности без трения всегда направлена по нормали к опорной поверхности и
называется нормальной. (рис.6.5.)

Рис.5.
Если одна из соприкасающихся
поверхностей является точкой, имеет заострение или ребро, то реакция направлена
по нормали к другой поверхности. (рис 6.6.)

Рис.6.
Реакция шарнирно-подвижной опоры без
трения (рис.6.) направлена перпендикулярно к опорной поверхности.

Рис.
Шарнирно-неподвижная опора без
трения предполагает только поворот тела относительно оси шарнира. Другие
перемещения исключены. Реакция такой опоры проходит через центр шарнира, но
направление реакции заранее неизвестно, поэтому ее обычно представляют в виде
суммы двух составляющих, направленных по координатным осям.  (рис.8.)
(рис.8.)
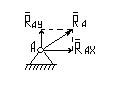
Рис.8.
Определение реакции сводится к
определению каждой из составляющих.
Реакция гибкой нерастяжимой связи
(трос, канат, цепь, нить) направлена вдоль связи к точке подвеса. (рис.6.9.).

Рис.9.
Нити на рис.3.9. без изменения
направления реакций могут быть заменены твердыми стержнями при условии их
невесомости и соединения посредством идеальных шарниров.
.1.3 Система сходящихся сил
Система сил, линии, действия которых
пересекаются в одной точке, называется системой сходящихся сил. Поскольку силы
являются скользящими векторами, их можно перенести в одну точку - точку схода.
Рассмотрим пучок из трех сил, приложенных в одной точке (рис.6.10.).


Рис.10.
На основании аксиомы 3 легко найти
равнодействующую сил 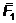 и
и 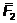
 ,
,
которая также приложена в точке
схода и может быть использована для нахождения равнодействующей трех сил

Этот метод может быть использован
для определения равнодействующей любого числа сходящихся сил, то есть
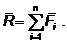
Равнодействующая может быть
определена и построением силового многоугольника (рис.11.).


Рис.11.
Проекция вектора силы на ось - это
скалярная величина, равная произведению модуля вектора на косинус угла,
образованного этим вектором с положительным направлением оси. Если вектор
параллелен оси, то его проекция на ось равна модулю вектора.
.1.4 Теория моментов
Если линии действия сил лежат в
одной плоскости, то такая система сил называется плоской. При изучении плоской
системы сил мы сталкиваемся с понятием момента сил относительно точки и парой
сил. Моментом силы относительно точки называется произведение величины (модуля)
силы на длину перпендикуляра, опущенного из точки на линию действия силы. Длина
опущенного перпендикуляра называется плечом силы. Если бы тело было закреплено
(рис.12.) в точке О, то сила 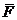 стремилась бы вращать тело относительно
этой точки. На рисунке отрезок ОА - плечо силы
стремилась бы вращать тело относительно
этой точки. На рисунке отрезок ОА - плечо силы 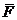 относительно точки О.
относительно точки О.

Момент силы измеряется в
Ньютонометрах (Н∙м)
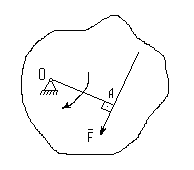
Рис.12.
Принято считать момент
положительным, если сила стремиться вращать тело против часовой стрелки.
Из определения величины момента
следует, что момент силы относительно данной точки не изменится при переносе
силы вдоль линии ее действия, а если линия действия силы проходит через точку,
момент равен нулю.
Парой сил или просто парой
называется система двух равных по модулю и противоположных по направлению
параллельных сил. Кратчайшее расстояние между линиями действия сил пары
называется плечом. Момент пары сил по абсолютной величине равен произведению
одной из сил пары на плечо.
Всякую пару, не изменяя ее действие
на абсолютно твердое тело, можно заменить другой парой, расположенной как
угодно в той же плоскости и имеющей то же направление вращения, при этом можно
изменить как плечо пары, так и соответственно модуль ее сил.
Таким образом, всякую силу можно
переносить параллельно самой себе в любую точку тела, присоединяя при этом
пару, момент которой равен моменту переносимой силы относительно той точки, в
которую переносится сила. А алгебраическая сумма моментов всех данных сил,
расположенных произвольно на плоскости, относительно произвольной точки О
называется главным моментом данной плоской системы сил относительно этой точки
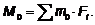
Вектор  , равный
геометрической сумме всех сил данной системы, называется главным вектором этой
системы.
, равный
геометрической сумме всех сил данной системы, называется главным вектором этой
системы.
Момент равнодействующей плоской
системы сил относительно любой точки, лежащей в плоскости действия этих сил,
равен алгебраической сумме моментов составляющих сил относительно той же точки.
На основании вышеизложенного можно
сформулировать условие равновесия рычага. Рычагом называется твердое тело,
вращающееся около неподвижной оси и находящееся под действием сил, лежащих в
плоскости, перпендикулярной и этой оси. Точка пересечения оси рычага с
плоскостью действия сил называется точкой опоры (рис.13.).
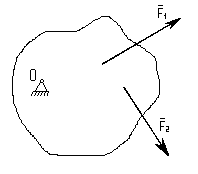
Рис13.
Для равновесия рычага необходимо и
достаточно, чтобы равнялась нулю алгебраическая сумма моментов всех сил, приложенных
к рычагу, относительно точки его опоры.
.1.5 Равновесие системы сил
Для равновесия системы сил,
произвольно расположенных на плоскости, необходимо и достаточно, чтобы и
главный вектор системы и главный момент системы относительного произвольно
выбранного центра равнялись нулю
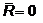 и
и 
Существует три формы уравнений
равновесия плоской системы сил.
Первая форма: для равновесия плоской
системы произвольно расположенных сил необходимо и достаточно, чтобы порознь
равнялись нулю сумма проекций всех сил на каждую из двух любым образом
выбранных осей координат, лежащих в плоскости действия сил, и сумма моментов
всех сил относительно любой точки в той же плоскости.

Первые два уравнения - это уравнения
проекций сил на ось координат, а третье - уравнение моментов.
Вторая форма: для равновесия системы
сил, как угодно расположенной на плоскости, необходимо и достаточно, чтобы
порознь равнялись нулю суммы моментов всех сил относительно каждой из трех,
произвольно выбранных, но не лежащих на одной прямой точек плоскости
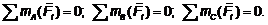
Третья форма: для равновесия системы
сил, произвольно расположенных на плоскости, необходимо и достаточно, чтобы
порознь равнялись нулю сумма проекций всех сил на одну какую-либо ось и суммы
моментов всех сил относительно двух точек плоскости, выбранных произвольно, но
не лежащих на прямой, перпендикулярной к взятой оси проекций.
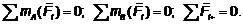
2. КИНЕМАТИКА
Кинематикой называется раздел
теоретической механики, изучающий движение материальных точек и твердых тел без
учета причин, вызывающих это движение. Кинематику часто называют геометрией
движения, так как она в значительной мере основана на геометрических
представлениях. Другими словами, кинематика рассматривает механическое движение
твердого тела без учета сил, вызвавших это движение. Под механическим движением
понимается изменение положения тела в пространстве и во времени относительно
какого-либо другого тела, с которым обычно связывают систему координат,
называемую системой отсчета. Если координаты всех точек тела остаются
неизменными во времени, то тело находится в состоянии покоя. Сама система
координат также может находиться в движении.
Движение тела относительно подвижной
системы координат называется относительным, а относительно неподвижной -
абсолютным. Определить движение тела с точки зрения кинематики - это значит
найти координаты любой его точки в выбранной системе координат отсчета в данный
момент времени.
.1 Уравнения движения точки
Различные точки тела могут совершать
различные движения. Поэтому изучение движения начинают с кинематики точки.
Линия, описываемая движущейся точкой в пространстве называется траекторией этой
точки. Траектории могут быть плоские и пространственные, криволинейные и
прямолинейные. В зависимости от характера изменения скорости движение может
быть равномерным и неравномерным. При равномерном движении точка в равные,
произвольно взятые, промежутки времени проходит пути одинаковой длины.
Движение точки может быть задано
двумя способами: естественным (геометрическим) и координатным.
При естественном способе задания
движения указываются траектория точки и закон ее движения по этой траектории.
Уравнения, определяющие положение движущейся точки в зависимости от времени,
называются уравнениями движения.
Пусть, например, точка М движется по
траектории АВ (рис.14.).

Рис.14.
Примем за начало отсчета точку М0
S - путь, пройденный
точкой с начала отсчета за время t. Величина пути S может
изменяться во времени, оставаясь связанной с ним некоторой функциональной
зависимостью, которую можно выразить уравнением
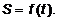
Зная траекторию движения точки и
уравнение движения по этой траектории, можно определить положение точки в любой
момент времени. Таким образом, движение точки вполне определяется заданием
траектории и уравнения движения. При координатном способе движения точки
задается движением ее проекций вдоль осей координат (рис.15).

Рис.15.
Положение точки М в пространстве
определяется координатами x, y, z. При
движении точки изменяются и ее координаты, являющиеся функциями времени
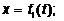
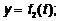
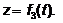
.2 Скорость точки
Скоростью точки называется вектор,
определяющий в каждый данный момент времени быстроту и направление движения
точки.
Скорость равномерного движения определяется
отношением пути, пройденного точкой за некоторый промежуток времени, к величине
этого промежутка времени.
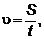 ,
,
где
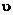 - скорость; S- путь; t- время.
- скорость; S- путь; t- время.
Измеряется скорость в единицах
длины, деленных на единицу времени: м/с; см/с; км/ч и т.д.
В случае прямолинейного движения
вектор скорости направлен вдоль траектории в сторону ее движения.
Если точка за равные промежутки
времени проходит неравные пути, то данное движение называется неравномерным.
Скорость является величиной переменной и является функцией времени.
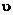

Средней за данный промежуток времени
скоростью точки называется скорость такого равномерного прямолинейного
движения, при котором точка за этот промежуток времени получила бы то же самое
перемещение, как и в рассматриваемом ее движении.
Рассмотрим точку М, которая
перемещается по криволинейной траектории, заданной законом
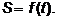 (рис.16.).
(рис.16.).

Рис.716.
За промежуток времени ∆t точка М
переместится в положение М1 по дуге ММ1.Если промежуток
времени ∆t мал, то дугу ММ1 можно
заменить хордой и в первом приближении найти среднюю скорость движения точки



Эта скорость направлена по хорде от
точки М к точке М1. Истинную скорость найдем путем перехода к
пределу при ∆t→ 0

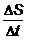
Когда ∆t→ 0,
направление хорды в пределе совпадает c
направлением касательной к траектории в точке М.
Таким образом, величина скорости
точки определяется как предел отношения приращения пути к соответствующему
промежутку времени при стремлении последнего к нулю. Направление скорости
совпадает с касательной к траектории в данной точке.
.3 Ускорение точки
Отметим, что в общем случае, при
движении по криволинейной траектории скорость точки изменяется и по направлению
и по величине. Изменение скорости в единицу времени определяется ускорением.
Другими словами, ускорением точки называется величина, характеризующая быстроту
изменения скорости во времени. Если за интервал времени ∆t скорость
изменяется на величину  ,то среднее
ускорение
,то среднее
ускорение
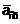

Истинным ускорением точки в данный
момент времени t называется величина, к которой
стремится среднее ускорение при ∆t→ 0,
то есть
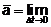
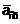
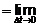

При отрезке времени стремящимся к
нулю вектор ускорения будет меняться и по величине и по направлению, стремясь к
своему пределу  .
.
Размерность ускорения
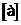 =
= =
= =
= .
.
Ускорение может выражаться в м/с2;
см/с2 и т.д.
В общем случае, когда движение точки
задано естественным способом, вектор ускорения обычно раскладывают на две
составляющие, направленные по касательной и по нормали к траектории точки.
Тогда ускорение точки в момент t можно
представить так
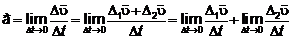
Обозначим составляющие пределы через
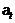 и
и 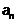 .
.

Направление вектора не зависит от
величины промежутка ∆t времени.
Это ускорение всегда совпадает с
направлением скорости, то есть, направлено по касательной к траектории движения
точки и поэтому называется касательным или тангенциальным ускорением.

Поскольку численное значение вектора
 равно приращению
скорости
равно приращению
скорости 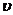 точки за
рассматриваемый промежуток ∆t времени, то
численное значение касательного ускорения
точки за
рассматриваемый промежуток ∆t времени, то
численное значение касательного ускорения

Так как
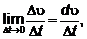 то
то 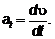
Численное значение касательного
ускорения точки равно производной по времени от численной величины скорости.
Численное значение нормального ускорения точки равно квадрату скорости точки,
деленному на радиус кривизны траектории в соответствующей точке кривой
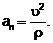
Полное ускорение при неравномерном
криволинейном движении точки складывается геометрически из касательного и
нормального ускорений.

2.4 Сложное движение точки
Движение точки по отношению к
системе отсчета, принимаемой за неподвижную, называется абсолютным движением.
Так, например, движение какой-либо точки М колеса локомотива (рис.1),
совершающееся по отношению к Земле, по кривой называемой циклоидой, можно считать
состоящим из двух простых движений: движение точки по окружности по отношению к
корпусу локомотива и движения этой точки вместе с локомотивом.
Движение же точки по отношению к
подвижной системе отсчета называется относительным движением.
Существует еще один вид движения
точки связанной в данный момент с подвижной системой отсчета по отношению к
неподвижной системе отсчета - переносное движение точки.
В приведенном примере круговое
движение точки М является относительным. Если эту точку мысленно жестко связать
с корпусом локомотива, то ее движение вместе с локомотивом будет переносным, а
движение точки М по циклоиде по отношению к земле является абсолютным.

Рис.1
Еще один пример: движение человека
по палубе движущегося по реке судна есть движение относительное; движение точки
палубы, в которой в данный момент находится человек относительно берега реки -
переносным, а движение человека относительно берега - абсолютным.
Абсолютная скорость точки равна
геометрической сумме ее переносной и относительной скоростей.
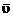 ср =
ср =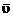 пер +
пер +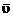 отн.
отн.
Аналогичным образом абсолютное
ускорение точки в случае поступательного движения системы отсчета равно
геометрической сумме переносного и относительного ускорений.
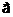 абс =
абс = пер +
пер + отн.
отн.
.5 Простейшие виды движения твердого
тела
Поступательным движением твердого
тела называется такое движение, при котором всякая прямая, неизменно связанная
с этим телом, движется, оставаясь параллельной самой себе. При поступательном
движении твердого тела все его точки движутся по одинаковым и параллельно
расположенным траекториям и имеют в каждый данный момент равные скорости и
равные ускорения. Вращательным движением твердого тела называется такое
движение, при котором плоскость, неизменно связанная с телом и проходящая через
некоторую неподвижную прямую, может лишь поворачиваться вокруг этой прямой,
называемой осью вращения тела. (рис.18.).

Рис.18.
Угол 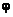 между неподвижной плоскостью,
проходящей через ось вращения, и плоскостью, неизменно связанной с вращающимся
телом и также проходящей через ось вращения, называется углом поворота или
угловым перемещением данного тела. Этот угол является некоторой функцией
времени
между неподвижной плоскостью,
проходящей через ось вращения, и плоскостью, неизменно связанной с вращающимся
телом и также проходящей через ось вращения, называется углом поворота или
угловым перемещением данного тела. Этот угол является некоторой функцией
времени

Это уравнение называется уравнением
вращательного движения тела.
Величина, характеризующая быстроту
вращения твердого тела, называется его угловой скоростью ω.
 =
=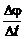 - средняя угловая скорость.
- средняя угловая скорость.
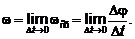
 - угловая скорость тела в данный
момент времени.
- угловая скорость тела в данный
момент времени.
Поскольку  есть
производная по времени функции
есть
производная по времени функции 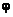 , то
, то 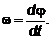
Таким образом, угловая скорость тела
в данный момент времени равна производной от угла поворота тела по времени.
Угловая скорость измеряется в радианах в секунду: 1/с (рад/с).
Один оборот тела соответствует его
повороту на 2π
радиан.
При n оборотах в
минуту
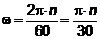 1/с.
1/с.
В данной формуле n выражается
в об/мин.
Величина, характеризующая быстроту
изменения угловой скорости тела, называется угловым ускорением.
Среднее угловое ускорение


Угловое ускорение в данный момент



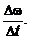
Поскольку 
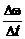 является производной функции ω, то
является производной функции ω, то

То есть угловое ускорение тела в
данный момент времени равно первой производной от угловой скорости по времени или
второй производной от угла поворота. Размерность углового ускорения 1/с2.
Плоскопараллельным или плоским
движением твердого тела называется такое, при котором все точки тела движутся в
плоскостях, параллельных некоторой неподвижной плоскости.
Пусть неизменно связанная с плоской
фигурой произвольная прямая перемещается при движении этой фигуры за некоторый
промежуток времени из положения АВ в положение А′В′ (рис.19).
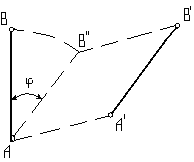
Рис.19.
Это перемещение плоской фигуры можно
представить составленным из поступательного и вращательного перемещений, что
ясно видно из рис.19. Прямая АВ как бы поворачивается на угол 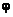 , занимая
положение АВ′′, а затем перемещается параллельно самой
себе в положение А′ В′.
, занимая
положение АВ′′, а затем перемещается параллельно самой
себе в положение А′ В′.
Скорость любой точки плоской фигуры
при плоскопараллельном движении в каждый данный момент равна геометрической
сумме двух скоростей: поступательной скорости произвольной точки фигуры,
выбранной за полюс и вращательной скорости рассматриваемой точки относительно
полюса.
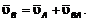
Аналогичным образом, если переносное
движение является поступательным, то ускорение какой-либо точки плоской фигуры
при плоском движении равно векторной сумме ускорений полюса и ускорению этой
точки от вращательного движения плоской фигуры вокруг полюса.

3. ДИНАМИКА
.1 Введение в динамику. Законы
динамики
Динамикой называется раздел
теоретической механики, изучающий зависимость между механическим движением точек
или материальных тел и действующими на них силами. Динамика изучает такие
системы сил, которые не находятся в состоянии равновесия. Система сил,
приложенная к материальной точке, является уравновешенной, если под ее
воздействием точка находится в состоянии относительного покоя или в состоянии
равномерного и прямолинейного движения. Другими словами, под действием
уравновешенной системы сил или при отсутствии силовых воздействий материальная
точка не испытывает ускорений и движется равномерно и прямолинейно.
Сила, действующая на движущуюся
материальную точку равна по модулю произведению массы точки на ее ускорение.
Направление этой силы совпадает с направлением ускорения

Это основной закон динамики. Он
может быть записан и в скалярной форме

Из этого уравнения можно получить
выражение для определения ускорения

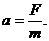
Анализируя выражение, видим, что чем
больше масса, тем больше потребуется сила для сообщения телу определенного
ускорения. Следовательно, масса характеризует «инертность» или «неподатливость»
тела взаимодействию силы.
По определению Ньютона, массой тела
называется количество вещества, содержащееся в этом теле. Из уравнения 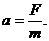 видно, что
масса материальной точки (тела) является мерой ее инертности.
видно, что
масса материальной точки (тела) является мерой ее инертности.
Силы, с которыми действуют друг на
друга две материальные точки (тела) всегда равны по величине и противоположны
по направлению.
Если на материальную точку действует
несколько сил, то ускорение, получаемое точкой будет таким же, как и действие
одной силы, равной геометрической сумме этих сил.
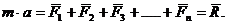
.2 Две основные задачи динамики
точки
Все задачи динамики можно разделить
на две основные группы. Первая задача - это когда известно движение данной
материальной точки или данной системы. Требуется определить силы, действующие
на эту точку или эту систему. Вторая задача - это когда известны силы, действующие
на данную материальную точку или данную систему. Требуется определить движение
этой точки или этой системы. Вторая задача является обратной первой.
Системой материальных точек или
просто системой называется совокупность материальных точек, связанных между
собой определенными условиями. Каждая точка механической системы имеет
определенную массу mi. Сумма этих масс составляет массу
системы mc.

Положение каждой точки по отношению
к системе отсчета Oxyz в данный момент времени
определяется координатами xi; yi; zi.
О распределении масс в теле можно
судить по положению центра масс, координаты которого находятся по формулам


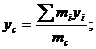
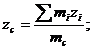
Движение материальной точки
называется свободным, если оно не ограничено в пространстве другими точками и
несвободным, если на нее действует какая-либо другая точка. Ограничения,
налагаемые на движение точек действиями других тел, называются связями.
При изучении движения несвободной
материальной точки применяют принцип освобождаемости точки от связей,
рассматриваемый в статике. Этот принцип позволяет рассматривать движение
несвободной материальной точки, как движение свободной точки под действием
заданных сил и реакций связей.
Все силы, действующие на точки
данной системы можно разделить на два вида: внутренние и внешние. Внутренними
силами называются силы, с которыми действуют друг на друга точки или тела
данной системы.
Геометрическая сумма всех внутренних
сил всякой системы равна нулю. 
Следовательно, алгебраическая сумма
проекций на любую ось всех внутренних сил системы также равна нулю.

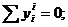
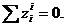
.4 Моменты инерции
Если при поступательном движении
твердого тела (так же как и при движении материальной точки) мерой его
инертности является масса, то при вращательном движении твердого тела мерой
инертности является момент инерции относительно оси вращения.
Моментом инерции твердого тела
относительно оси называется скалярная величина равная сумме произведений массы
каждой точки тела на квадрат расстояния от этой точки до оси. Алгебраическая
сумма моментов всех приложенных к телу сил относительно оси вращения тела
называется вращающим моментом.

где 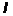 - момент инерции тела относительно
оси;
- момент инерции тела относительно
оси;
 - угловое ускорение.
- угловое ускорение.
Таким образом, вращающий момент Мвр,
приложенный к телу, вращающемуся вокруг неподвижной оси, равен моменту инерции
тела 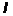 относительно
этой оси, умноженному на угловое ускорение тела. Это уравнение называется
основным уравнением динамики для вращательного движения тела вокруг неподвижной
оси.
относительно
этой оси, умноженному на угловое ускорение тела. Это уравнение называется
основным уравнением динамики для вращательного движения тела вокруг неподвижной
оси.
Момент инерции твердого тела
относительно заданной оси, например оси z, можно
представить в виде произведения массы тела m на квадрат
линейной величины, называемой радиусом инерции тела относительно этой оси
 .
. 
Радиус инерции определяет расстояние
от оси z до точки, в
которой нужно сосредоточить всю массу тела.
Моментом инерции твердого тела
относительно плоскости называется скалярная величина, равная сумме произведений
массы каждой точки тела на квадрат расстояния от этой точки до плоскости.
Для определения моментов инерции
тела относительно координатных плоскостей опустим их каждой точки  перпендикуляры
перпендикуляры

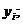
 на
координатные плоскости. Тогда
на
координатные плоскости. Тогда
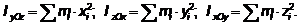
Моментом инерции твердого тела
относительно полюса (полярным моментом инерции) 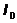 называется скалярная величина, равная
сумме произведений массы каждой точки тела на квадрат расстояния от точки до
полюса
называется скалярная величина, равная
сумме произведений массы каждой точки тела на квадрат расстояния от точки до
полюса
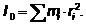
Если через точку О провести
координатные оси  , то по
отношению к этим осям величины
, то по
отношению к этим осям величины  определяются равенствами
определяются равенствами

называемыми центробежными моментами
инерции.
В приведенных формулах  - массы
точек, а
- массы
точек, а 
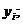
 - их
координаты.
- их
координаты.
.5 Теорема об изменении кинетической
энергии
Движение свободного твердого тела в
общем случае можно разбить на два составляющих движения: на переносное
поступательное движение вместе с центром масс и относительное вращательное
движение по отношению к центру масс. Тогда кинетическая энергия тела
определяется по формуле

 - скорость центра масс тела.
- скорость центра масс тела.
 - момент инерции тела относительно
оси, проходящей через центр масс.
- момент инерции тела относительно
оси, проходящей через центр масс.
Изменение величины 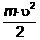 связано с
работой приложенных к телу сил. Работа - это количественная мера превращения
механического движения в какую-либо другую форму движения. Например, работа сил
трения, тормозящих движение тела, работа сил тяжести поднимаемого груза, работа
сил упругости пружины, останавливающей движущееся тело, являются мерами
уничтожимого механического движения, которое превращается в теплоту,
потенциальную энергию, энергию упругого твердого тела.
связано с
работой приложенных к телу сил. Работа - это количественная мера превращения
механического движения в какую-либо другую форму движения. Например, работа сил
трения, тормозящих движение тела, работа сил тяжести поднимаемого груза, работа
сил упругости пружины, останавливающей движущееся тело, являются мерами
уничтожимого механического движения, которое превращается в теплоту,
потенциальную энергию, энергию упругого твердого тела.
Изменение кинетической энергии
механической системы на некотором перемещении равно сумме работ внешних и
внутренних сил, действующих на материальные точки системы на этом перемещении.
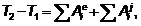
где 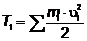 - кинетическая энергия системы в
первом ее положении;
- кинетическая энергия системы в
первом ее положении;
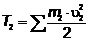 - кинетическая энергия системы во
втором ее положении.
- кинетическая энергия системы во
втором ее положении.
 - работа внешних сил;
- работа внешних сил;
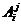 - работа внутренних сил.
- работа внутренних сил.
Поскольку сумма работ внутренних сил
твердого тела на любом перемещении равна нулю  то
то 
то есть изменение кинетической
энергии твердого тела, на некотором перемещении равно сумме работ внешних сил,
действующих на тело на этом перемещении.
Это теорема об изменении кинетической
энергии.
.6 Теорема об изменении количества
движения
Количеством движения механической
системы называется вектор, равный геометрической сумме количеств движения всех
материальных точек этой системы.
Вектор количества движения
механической системы имеет модуль равный произведению массы системы на скорость
ее центра масс и направление этой скорости.
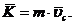
Изменение количества движения
механической системы вызывается только внешними силами.
Из этой теоремы об изменении
количества движения механической системы следует, что если главный вектор
внешних сил все время равен нулю, то количество движения механической системы
остается постоянным.
.7 Теорема о движении центра масс
В ряде случаев для определения
характера движения системы требуется знать закон движения ее центра масс, так
как произведения массы системы на ускорение ее центра масс равно геометрической
сумме всех действующих на систему внешних сил.

где  - масса системы;
- масса системы;
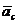 - ускорение центра масс.
- ускорение центра масс.
Это уравнение выражает теорему о
движении центра масс системы.
.8 Теорема об изменении
кинетического момента
Кинетическим моментом или главным
моментом количества движения механической системы относительно данного центра
называют вектор, равный геометрической сумме моментов количеств движения всех
материальных точек системы относительно этого центра.

где 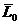 - кинетический момент механической
системы относительно центра О;
- кинетический момент механической
системы относительно центра О;
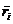 - радиус-вектор точки, проведенный
из центра О;
- радиус-вектор точки, проведенный
из центра О;
 - вектор скорости точки.
- вектор скорости точки.
Производная по времени от кинетического
момента механической системы относительного некоторого центра геометрически
равна главному моменту внешних сил, действующих на эту систему относительно
того же центра.
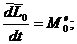
Этому векторному равенству
соответствуют три равенства в проекциях на оси координат:



Приведенные уравнения показывают,
что производная по времени от кинетического момента механической системы
относительно некоторой оси равна главному моменту внешних сил относительно этой
оси.
Отсюда следует, что если главный
момент внешних сил относительно некоторой оси все время равен нулю, то
кинетический момент механической системы относительно этой оси остается
постоянным.
Аналогично, если главный момент
внешних сил относительно некоторого центра все время равен нулю, то
кинетический момент механической системы относительно этого центра остается
постоянным.
.9.1 Дифференциальные уравнения
движения
При поступательном движении твердого
тела все его точки движутся так же, как и его центр масс, поэтому
дифференциальные уравнения движения центра масс являются дифференциальными
уравнениями движения твердого тела. Дифференциальные уравнения движения центра
масс получим, проектируя обе части равенства
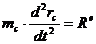
на оси координат 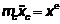 .
.  .
. 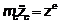 .
.
Здесь  масса тела.
масса тела.
Данные дифференциальные уравнения
используются для решения двух типов задач динамики поступательного движения
тела.
Кинетический момент вращающегося
твердого тела относительно неподвижной оси его вращения равен произведению
момента инерции тела относительно той же оси на угловую скорость тела
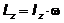
Теорема об изменении кинетического
момента механической системы выражается уравнением
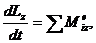
где  - главный момент внешних сил.
- главный момент внешних сил.
так как 
то 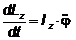
и уравнение принимает вид
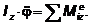
Это уравнение представляет собой
дифференциальное уравнение вращения твердого тела вокруг неподвижной оси. С
помощью рассмотренного дифференциального уравнения можно решать следующие
задачи:
.по заданному уравнению вращения
тела  и его
моменту инерции
и его
моменту инерции 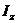 определить
главный момент внешних сил.
определить
главный момент внешних сил.
.по заданным внешним силам и моменту
инерции тела находить уравнение вращения тела.
.определять момент вращения тела 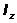 относительно
оси вращения, зная величины
относительно
оси вращения, зная величины 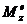 и
и 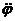 .
.
.9.2 Принцип Даламбера
Если в любой момент времени к
действующим на точку силам и реакции связи присоединить силу инерции, то
полученная система будет уравновешенной. Это положение выражает принцип
Даламбера для материальной точки.
Принцип Даламбера для системы можно
сформулировать так: если в любой момент времени к каждой из точек системы кроме
действующих на нее внешних и внутренних сил присоединить соответствующие силы
инерции, то полученная система сил будет уравновешенной и к ней можно применить
все уравнения статики.
Таким образом, положение
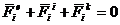
есть математическое выражение
принципа Даламбера для системы.
.9.3 Принцип возможных перемещений
Возможными перемещениями несвободной
механической системы называются воображаемые бесконечно малые перемещения,
допускаемые в данный момент наложенными на систему связями.
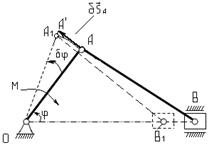
Рис.20.
Возможным перемещением кривошипного
механизма, изображенного на рисунке 20., является перемещение, соответствующее
повороту кривошипа ОА на бесконечно-малый угол  вокруг оси вала. Возможным
перемещением
вокруг оси вала. Возможным
перемещением 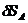 пальца
кривошипа А представляет собой отрезок касательной АА/ к дуге
окружности с центром в точке О, равный по величине
пальца
кривошипа А представляет собой отрезок касательной АА/ к дуге
окружности с центром в точке О, равный по величине 

Возможным перемещением  ползуна В
является бесконечно малый отрезок ВВ1 прямолинейной траектории точки
В.
ползуна В
является бесконечно малый отрезок ВВ1 прямолинейной траектории точки
В.
Если сумма работ реакций связей на
любом возможном перемещении системы равна нулю, то такие связи называются
идеальными.
Принцип возможных перемещений
формулируется так: для равновесия механической системы с идеальными связями
необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее
активных сил при любом возможном перемещении системы была равна нулю. Это
положение устанавливает общее условие равновесия механической системы. Он дает
общий метод решения задач статики. Принцип же Даламбера позволяет использовать
методы статики для решения задач динамики.
.9.4 Общее уравнение динамики
Рассмотрим систему материальных
точек, на которые наложены идеальные связи. Если ко всем точкам системы кроме
действующих активных сил и реакций связей приложить соответствующие силы
инерции, то полученная система сил в соответствии с принципом Даламбера будет
находиться в равновесии. Применяя к этим силам принцип возможных перемещений
получим
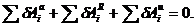
Здесь  - работа активных сил;
- работа активных сил;  - работа
реакций связей;
- работа
реакций связей; 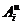 - работа
сил инерции.
- работа
сил инерции.
Поскольку связи идеальны,  , и
окончательно имеем
, и
окончательно имеем

При движении механической системы с
идеальными связями в каждый момент времени сумма элементарных работ всех
приложенных активных сил и всех сил инерции на любом возможном перемещении
системы будут равны нулю. Это уравнение называют общим уравнением динамики. В
аналитической форме это уравнение имеет вид
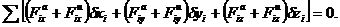
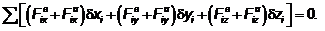
Приведенные уравнения позволяют
составить дифференциальные уравнения движения механической системы.
ЛИТЕРАТУРА
механика статика
кинематика
1. Бать М.И и др. Теоретическая
механика в примерах и задачах. Учеб. пособ. для вузов. В 2-х т./М.И.Бать,
Г.Ю.Джанелидзе, А.С. Кельзон.-9-е изд., перераб. - М.: Наука, 2007.-670 с.
. Бутенин Н.В. и др. Курс
теоретической механики: Учеб.пособие для студ-ов вузов по техн. спец.:В 2-х т./
Н.В.Бутенин, Я.Л.Лунц, Д.Р.Меркин. СПб.:Лань.-5-е изд., испр. 2008.-729 с.
. Мещерский И.В. Задачи по
теоретической механике: Учеб. пособие для студ. вузов, обуч.по техн.
спец./И.В.Мещерский; Под ред.В.А. Пальмова, Д.Д. Меркина.-45-е изд., стер.-
СПб. и др.: Лань, 2009.-447 с. 2.
. Тарг С.М. Краткий курс
теоретической механики: Учеб. для втузов/С.М.Тарг.-15-е изд., стер. - М.: Высш.
шк., 2008.-415 с.
. Сборник заданий для курсовых работ
по теоретической механике: Учеб. пособие для студ.втузов/[А.А. Яблонский, С.
С.Норейко,С.А.Вольфсон и др.];Под общ. ред. А.А. Яблонского.- 11-е
изд.,стер.-М.:Интеграл- Пресс,2008.-382 с.
. Тарг С.М. Краткий курс
теоретической механики: Учеб. для втузов/С.М. Тарг.-15-е
изд.,стер.-М.:Высш.шк.,2007.-415 с.
. Теоретическая механика.
Терминология. Буквенные обозначения величин: Сборник рекомендуемых терминов.
Вып. 102. М.: Наука, 2007. - 48с.
. Яблонский А.А., В.М.Никифорова
Курс теоретической механики. Учеб.пособие для вузов: 13-е изд., исправ.-М.:
Интеграл-Пресс,2009.-603с