Определение параметров механики разрушения в сварных соединениях и композиционных элементах
Определение
параметров механики разрушения в сварных соединениях и композиционных элементах
1. Обзор состояния исследуемой предметной
области
разрушение напряжение
интерферометрия
Использование сварных соединений и
композиционных материалов, позволяющих существенно повысить весовое
совершенство и снизить стоимость создания конструкции, является одним из
наиболее эффективных путей создания перспективных летательных аппаратов. Это
относится, как к истребителю 5-го поколения, так и к новым пассажирским
самолетам, создание которых предусмотрено программой развития гражданской
авиации до 2015 года. В частности, ведущие зарубежные авиационные фирмы, такие
как Boeing, EADS,
Airbus и ряд других, в
последнее время уделяют значительное внимание созданию перспективных
конструкций с помощью сварки трением (Friction
Stir Welding
- FSW). Сварка трением
представляет собой новую технологию, разработанную для соединения твердых тел,
которая обладает значительным потенциалом, особенно при сварке алюминиевых сплавов,
используемых в авиационной и космической промышленности [1-2].
Серьезным препятствием, которое сдерживает
широкое внедрение тонкостенных сварных конструкций, является наличие остаточных
напряжений достаточно высокого уровня [3-6]. Это означает, что анализ процесса
распространения усталостных трещин в поле остаточных напряжений является
необходимым звеном для оптимального проектирования сварных конструкций с учетом
усталости [7]. Отсутствие надежных экспериментальных данных о законах
распространения трещин в поле напряжений сдерживает широкое внедрение
продвинутых сварных конструкций в гражданском авиастроении. То же самое
относится и к высокопрочным композиционным материалам (КМ), которые часто
содержат внутренние напряжения [8]. Можно также утверждать, что для КМ
практически отсутствуют общепринятые, как расчетные, так и экспериментальные
методы определения параметров, относящихся к механике разрушения для дефектов
типа узких разрезов и трещин [9-10].
Учет остаточных или внутренних напряжений
различной природы в процессе конструирования представляет собой очень сложную
задачу. Это связано с тем, что, кроме определения исходного уровня остаточных
напряжений, необходимо оценивать их влияние на процесс распространения
усталостных трещин при циклическом нагружении. Кроме того, в настоящее время,
как в отечественных, так и зарубежных источниках практически отсутствует
количественная информация, описывающая реальное напряженное состояние в
окрестности трещин в сварных соединениях и дефектов типа узких разрезов и
трещин в КМ. Наличие подобных данных необходимо для разработки новых
деформационных критериев разрушения перспективных сварных соединений и
конструкций из КМ. Обе указанные проблемы составляют важнейшее звено в процессе
оценки усталостной прочности сварных соединений и композиционных элементов
конструкций. Подобные задачи не могут быть решены только на основе численного
моделирования. Таким образом, обеспечение оптимального проектирования и
эксплуатационной надежности высокотехнологичных сварных соединений и
перспективных композитных конструкций настоятельно требует значительного объема
новой экспериментальной информации.
Разработка и верификация нового
экспериментального метода определения локального раскрытия трещины и
соответствующих величин коэффициентов интенсивности напряжений, который
обладает способностью описания процесса распространения трещины в сварных
соединениях и изделиях из КМ, является необходимым этапом на этом пути. В НИО-3
ЦАГИ в течение нескольких последних лет создаются новые методы исследования
процессов распространения трещин на основе высокоточных измерений
деформационного отклика, вызванного локальным удалением материала, оптическими
интерференционными методами. Данные подходы не имеет аналогов, как в России,
так и за рубежом по точности и достоверности определения величин параметров,
относящихся к линейной механике разрушения.
Основным средством, которое в настоящее время
используется для описания распространения трещин в поле напряжений, является
традиционная версия метода последовательного наращивания длины трещины (the
crack compliance
method). Первый вариант
данного подхода предложен в работе [11]. В отличие от рассмотренных выше
полевых методов определения величин КИН и T-напряжений,
метод последовательного наращивания длины трещины (ПНДТ) основан на измерении
деформационного отклика на малое приращение длины трещины при постоянной
внешней нагрузке. Исходная версия метода ПНДТ требует весьма сложных
вычислений. Чтобы улучшить ситуацию была разработана потенциально более простая
версия, которая использует соотношения линейной механики разрушения [12-13].
Только такой подход обеспечивает получение величин коэффициента интенсивности
напряжений KI как функцию длины разреза без предварительного
определения величин остаточных напряжений. Кроме того, его реализация основана
на относительно простых вычислениях. Для получения величин остаточных
напряжений требуются дополнительные усилия, связанные с определением весовой
функции. Подробное описание современного состояния традиционной версии метода
ПНДТ представлено в обзоре [14] и книге [15]. В частности, анализ всех
существенных этапов, необходимых для реализации метода ПНДТ, на примере
численного моделирования роста трещины в стандартном компактном образце
выполнен в работе [16]. Представлены величины как коэффициента интенсивности
напряжений (КИН), так и компонент остаточных напряжений (КОН). Полученные
результаты достаточно оптимистичны, но не имеют прямого экспериментального
подтверждения. Определение остаточных напряжений в толстой плите без сварного
шва описано в работе [17]. Имеющийся опыт в получении распределений остаточных
напряжений и определения величин КИН в окрестности сварных соединений на основе
сварки трением методом ПНДТ при статическом нагружении представлен в работах [3,
18-19]. Следует специально отметить, что количество работ, посвященных к
экспериментальному определению величин КИН и КОН на основе метода ПНДТ, весьма
ограничено. Более того, исходная экспериментальная схема сохраняется в
практически неизменном виде до настоящего времени. Конкретно говоря, требуемые
измерения выполняются, в лучшем случае, с помощью набора тензодатчиков, которые
расположены на значительном расстоянии от вершины трещины.
Таким образом, все традиционные варианты метода
ПНДТ основаны на измерении механического отклика с помощью массива
тензодатчиков, расположенного достаточно далеко от вершины трещины. Такой путь
экспериментальной реализации метода ПНДТ не свободен от ряда недостатков.
Во-первых, значительное расстояние между точкой измерения и вершиной трещины
снижает чувствительность метода по отношению к определяемым параметрам механики
разрушения. Главный недостаток традиционного подхода заключается в
необходимости создания сложной численной модели, которая необходима для
корректной интерпретации исходной экспериментальной информации в терминах КИН и
T-напряжений. Такая
модель должна быть создана для каждого конкретного объекта исследования.
Точечный характер измерений не дает возможности надежно установить реальный тип
исследуемого напряженного состояния, что необходимо для верификации
используемой численной модели. Все эти факторы отрицательным образом влияют на
надежность и точность конечного результата.
Рассматриваемый в данной заявке новый способ
«определения коэффициентов интенсивности напряжений и момента остановки трещины
в поле напряжений по данным оптических интерференционных измерений»
представляет собой модифицированную версию метода ПНДТ. Ключевым моментом
модифицированной версии метода ПНДТ является возможность измерения локального
деформационного отклика, вызванного удалением материала между двумя
экспозициями, оптическими интерференционными методами в ограниченном числе
точек. Подобный подход был ранее реализован при совместном применении метода
сверления отверстия и оптических интерференционных измерений деформации контура
зондирующего отверстия в направлении главных деформаций [20-24].
Наличие деформационных компонент перемещений,
измеренных непосредственно на берегах трещины при малом приращении ее длины,
открывает новые метрологические возможности для определения параметров механики
разрушения. Данный факт, во-первых, означает, что необходимость в создании и
верификации численной модели отпадает. Во-вторых, наличие картин
интерференционных полос, зарегистрированных непосредственно в окрестности
вершины трещины, служит надежным индикатором типа напряженного состояния. Это,
в свою очередь, означает, что формулы для перехода от измеряемых величин к
требуемым параметрам механики разрушения, которые не включают суммарную длину трещины,
принимают достаточно простой и наглядный вид. Кроме того, рассматриваемый метод
универсален по отношению, как к геометрической форме и материалу исследуемой
конструкции, так и к этапу циклического нагружения. Таким образом, данный
подход обеспечивает новый качественный уровень получения результатов, которые
необходимы для надежного описания процесса распространения усталостной трещины
в поле напряжений. Наличие подобной информации является необходимым условием
для исследования процесса распространения трещины в перспективных сварных
соединениях и конструкциях из КМ и создания на этой основе деформационных
критериев разрушения. Отсутствие в настоящее время деформационных критериев
разрушения существенно затрудняет применение сварных соединений и конструкций
из КМ в процессе создания перспективных авиационных конструкций.
2. Цель
работы
и
решаемые
в
процессе
ее
выполнения
задачи
.1 Цели
работы
2.1.1
Создание
новых
методов
определения
параметров
линейной механики разрушения на основе измерения локального деформационного
отклика с помощью электронной спектр-интерферометрии. Возможности данных
методов исследования и качество результатов их практического применения
превосходят аналогичные характеристики подходов, используемых в настоящее
время, как в России, так и за рубежом.
.1.2 Повышение уровня надежности обоснования
прочности и ресурса перспективных авиационных конструкций на основе
деформационных критериев разрушения.
.2 Задачи работы
.2.1 Создание специализированных
интерферометров, обеспечивающих применение разработанных уникальных методов
исследования при испытаниях, как малоразмерных образцов, так и реальных
элементов конструкций.
.2.2 Практическое внедрение разработанных
методов и средств исследования с целью получения значительного объема новых
экспериментальных данных, описывающих эволюцию полей внутренних напряжений и
процессы распространения трещин в сварных соединениях и композитных элементах
конструкций, которые используются при создании перспективных ЛА.
.2.3 Формулировка и верификация деформационных и
силовых критериев разрушения сварных соединений и композиционных материалов на
основе уникальных экспериментальных данных, полученных высокоточными
оптическими интерференционными методами.
.2.4 Разработка рекомендаций, необходимых для
оптимального проектирования и повышения эксплуатационной надежности сварных
соединений и конструкций из КМ, используемых при создании перспективных ЛА, в
том числе с учетом наличия внутренних напряжений и их влияния на процесс
распространения трещин.
3. Основные принципы и соотношения используемого
подхода
Экспериментальное определение коэффициента
интенсивности напряжения (КИН) и Т-напряжений для трещины постоянной длинны,
при приращении внешней нагрузки, нашло достаточно широкое распространение
[25-32]. В то же время метод последовательного наращивания длинны трещины
(ПНДТ) обладает способностью получения (КИН), при малом приращении длинны
трещины в условиях постоянной внешней нагрузки [12-13]. В данном реферате
рассматриваются некоторые вопросы, связанные с разработкой и верификацией
нового метода определения КИН и Т-напряжений. Данный подход основан на
совместном применении методов ПНДТ и оптических интерференционных измерений
локального деформационного отклика на приращение длинны трещины. В частности, рассматриваемый
метод обладает способностью оценки влияния радиуса разреза на величины
параметров механики разрушения.
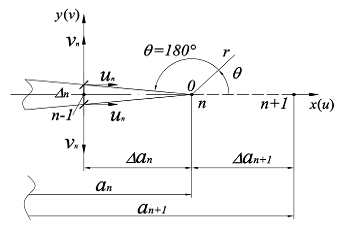
Рис. 1. Полярная система координат с началом в
вершине трещины и принятые обозначения.
Сущность модифицированной версии метода ПНДТ
заключается в регистрации интерференционных полос, которые соответствуют
разнице между двумя полями плоских компонент перемещений. Каждое поле относится
к трещине близкой, но различной длины. Первая экспозиция выполняется для
исходной трещины длиной an-1
(рис. 1). Затем, исходная трещина увеличивается на величину малого приращения Дan
так, что суммарная длина трещины становится равной an
= an-1
+ Дan и
выполняется вторая экспозиция. Необходимые картины интерференционных полос визуализируются
численным вычитанием двух изображений зарегистрированных для двух трещин [33].
Две интероферограммы, которые получены таким способом для тонкой пластины со
сквозной краевой трещины типа I,
показаны на рисунке 2. Положительное направление оси х на рисунке 1 и рисунке 2
совпадает с направлением распространения трещины.

а

b
Рис. 2. Образец #2. Картины интерференционных
полос, полученные в терминах плоской компоненты u
(a) и v
(b).
Исходная длина трещины a14
= 28.5 мм с приращением Дa15
= 1.7 мм.
Разработанная процедура извлечения требуемых
параметров механики разрушения из картины интерференционных полос основана на
формулировке Уильямса [34]. В соответствии с этим подходом компоненты
перемещений в окрестности вершины трещины выражаются в виде бесконечного ряда
для каждой плоской компоненты перемещений. Когда направление оси x
совпадает с линией трещины, выражение для трещины типа I
принимают следующий вид:
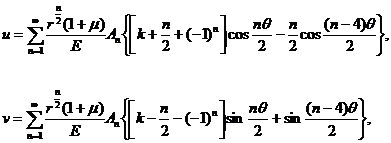 (1)
(1)
где u
и v - плоские
компоненты перемещений в направлении оси x
и y, соответственно; E
- модуль упругости материала; м
- коэффициент Пуассона; k
= (3 - м)/(1 + м)
для условий плоской деформации; k
= (3 - 4м) для плоского напряжённого
состояния; An
-
постоянные коэффициенты, подлежащая определению; r
и и - радиальное и
угловое расстояние от вершины трещины как это показано на рисунке 1.
Асимптотическое разложение (1) даёт следующий
вид упругого поля напряжений в полярной системе координат с центром в вершине
трещины [32]:
 , (2)
, (2)
где KI
-
коэффициент интенсивности напряжений; fij(и)
- угловая функция, определяемая формулой (1); дij
- символ Кронекера. Второй член называется T-напряжения.
Величина Т представляет собой постоянное напряжение, действующее параллельно
плоскости трещины в направлении ее развития трещины с величиной
пропорциональной приложенному номинальному напряжению. Третий член A3
также иногда используется для анализа напряжённого состояния. Несингулярный
член Т представляет собой растягивающее или сжимающее напряжение. Положительные
T-напряжения
усиливают уровень двуосности напряженного состояния и приводят к увеличению
сопротивления развития трещины. Наличие отрицательных по величине T-напряжений
способствует распространению трещины. Величины KI
и T-напряжений
определяются из соотношений (1) и (2) следующим способом [31]:
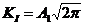 ,
, 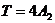 (3)
(3)
В общем случае исходная экспериментальная
информация представляет собой разницу абсолютных величин плоских компонент
перемещений для двух трещин an
и an-1 :
 ,
,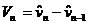 (4)
(4)
Соотношения (4) справедливы для любой точки в
окрестности вершины трещины, расположенной в точке n.
Однако в правой части уравнений (4) содержатся относительные величины компонент
перемещений, которые не могут быть использованы для непосредственного
определения требуемых величин An
из разложения (1). Главная особенность разработанного подхода заключается в
том, что каждая интерференционная картина типа, показанного на рисунке 2,
содержит несколько особых точек, расположенных непосредственно на границе
трещины. Абсолютные величины плоских компонент перемещений и затем величины
коэффициентов An
из формул (1) для трещины длинной an
могут быть определенны в этих точках.
Особые точки, расположены вдоль
линии трещины между точками n-1 и n, где
компоненты перемещений 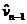 , равны нулю
перед увеличением длинны трещины. Таким образом, картина полос на рисунке 2b
обеспечивает определение абсолютных величин v- компонент
для каждой точки с полярными координатами 0 ≤ r ≤ Дan и и = 180о.
Распределение компоненты перемещений, которая соответствует первому и третьему
членам бесконечного ряда (1), выражается как:
, равны нулю
перед увеличением длинны трещины. Таким образом, картина полос на рисунке 2b
обеспечивает определение абсолютных величин v- компонент
для каждой точки с полярными координатами 0 ≤ r ≤ Дan и и = 180о.
Распределение компоненты перемещений, которая соответствует первому и третьему
членам бесконечного ряда (1), выражается как:
 (5)
(5)
Соотношение (5) показывает, что
определение величины KI из (3)
требует измерения величин компоненты v как минимум
в двух точках интервала 0 ≤ r ≤ Дan, и = 180о.
Первая из них является начальной точкой приращения длины трещины. Подстановка r = Дan и v(Дan, и=180о)
= vn в (5) даёт:
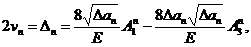 (6)
(6)
где An1 и An3 - коэффициенты
разложения (1) для трещины длинной an. Второе
необходимое уравнение удобно составить для точки с координатами r = Дan/2.
Подстановка r = Дan/2 и v(Дan/2, и=180о)
= v*n в (5) даёт:
 (7)
(7)
Величина КИН вытекает из решения
системы линейных алгебраических уравнений (6) и (7) и подстановки полученного
результата в первое из соотношений (3):
 (8)
(8)
Учёт только первого члена из (1)
приводит к хорошо известным соотношениям Вестергада:
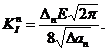 (9)
(9)
Для характеристики величин
Т-напряжений необходимо использовать компоненту перемещений u
направленную вдоль трещины. Распределение компоненты u для точек
лежащих на границе трещины (и = 180о, рис. 1), которое
соответствует второму и четвертому членам бесконечного ряда (1), выражается
как:
 (10)
(10)
Абсолютная величина компоненты u для трещины
длинной Дan опять может
быть получена в точке с полярными координатами r = Дan and и = 180о.
Подстановка r = Дan и u(Дan, и=180о)
= un в (10)
приводит к следующему соотношению:
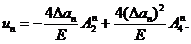 (11)
(11)
Соотношение (11) даёт первое
уравнение необходимое для определения Т-напряжений. Отметим, что все
экспериментальные параметры необходимые для уравнений (6)-(8) и (11) содержатся
на паре картин полос, соответствующих приращению длинны трещины Дan.
Формулировка второго необходимого
уравнения требует привлечения картины интерференционных полос, которая
соответствует увеличению длины трещины от точки n до точки n+1 на
величину Дan+1 (см.
рисунок 1). Абсолютная величина компоненты u в особой
точке n+1 с
координатами r = Дan+1 и и = 0,
обозначенная как un+1, зависит от
первых четырех коэффициентов разложения (1) следующим образом:
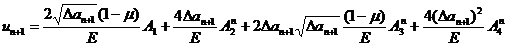 . (12)
. (12)
Соотношение (12) представляет собой
второе уравнение для определения Т-напряжений, так как величины коэффициентов A1 и A3 уже
известны из соотношений (6) и (7). Необходимо отметить, что величина un+1 должна быть извлечена
из картины интерференционных полос типа, показанного на рисунке 2а, которая
зарегистрирована для приращения длины трещины Дan+1. Если для
оценки величины Т-напряжений используется только коэффициент An2 ,
справедлива следующая упрощённая формула:
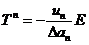 . (13)
. (13)
Величина Т-напряжений (13) может
быть определенна при использовании картины интерференционных полос типа,
показанного на рисунке 2а, которая зарегистрирована только для приращения длины
трещины Дan.
Для экспериментального определения
плоских компонент перемещений служит электронная спектр-интерферометрия [33].
При этом используется широко известная оптическая схема с нормальным по
отношению к плоской поверхности объекта направлением наблюдения и двумя
симметричными направлениями освещения. Когда проекция направления освещения на
плоскую поверхность исследуемого объекта совпадает с направлением оси о, то картина
интерференционных полос описывается следующим образом:
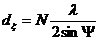 , (14)
, (14)
где dо - плоская
компонента перемещений оси о ; N = ±1; ±2; ±3, …
абсолютные порядки полос; l
= 0.532 мm - длинна
волны лазерного освещения; Y
= 45o - угол
между наклоном направлением освещения и нормальной поверхности направления
наблюдения. Когда направление о совпадает с осью х и осью у,
компоненты перемещений u и v могут быть
получены согласно соотношению (14).
.2 Экспериментальная проверка
Экспериментальная проверка
разработанного подхода проводится с помощью специально сконструированного
образца #2, изготовленного из алюминиевого сплава 2024 (E = 74000
МПа, м = 0.33),
чертеж которого представлен на рисунке 3. Рабочая часть этого образца
представляет собой тонкую пластину размерами 120x48x5 мм3.
Исходная трещина длинной a0 = 20 мм
расположена в центре короткой стороны и направленна вдоль линии симметрии.
Образец нагружается поперечной силой направленной перпендикулярно линии
трещины, как это показано на рисунке 3. Пошаговой процесс увеличения длины
трещины осуществляется с помощью узкого ювелирного лобзика шириной 0.3 мм, что
соответствует радиусу выреза с = 0.15 mm. Данная
процедура сопровождается регистрацией картин интерференционных полос,
описывающих разницу между исходным и конечным состоянием образца с двумя
трещинами для близких значений нагрузки. Схема используемого эксперимента
состоит в следующем. Внешняя поперечная нагрузка Pn1 прикладывается
к образцу. Первая экспозиция выполняется для трещины текущей длины an-1. Затем
длина трещины увеличивается на величину малого приращения Дan и
проводится вторая экспозиция для трещины длинной an = an-1 + Дan . В течение
процесса увеличения длины трещины величина действующего усилия несколько
уменьшается до величины Pn2, вследствие
податливости датчика усилия. Две картины интерференционных полос,
зарегистрированные на 15-м этапе приращении длины трещины, показаны на рисунке
2. Картины интерференционных полос регистрируются для двадцати одного
приращения длины трещины, начиная с исходной трещины a0 = 20 мм до
величины a0+an = 60 мм.
Наиболее надёжные результаты,
которые относятся к одинаковым величинам приращения длины трещины и условиям
нагружения, получены для этапов 15, 16 и 17. Исходная экспериментальная
информация, относящаяся к этим этапам, приведена в таблицах 1 и 2. Величины
коэффициентов An1, An3 и
коэффициентов интенсивности напряжений в таблице 1 соответствуют соотношениям
(5)-(8). Следует специально отметить, что величины КИН полученные по формуле
(9) совпадают с соответствующими данными из таблицы 1 в пределах 3%, так как
величины An3 практически
равны нулю. Последний факт имеет место для всех рассмотренных этапов. Величины
коэффициентов An2, An4 и
Т-напряжений, полученные в соответствии с соотношениями (11)-(12), представлены
в таблице 2. Анализ данных, приведённых в таблицах 1 и 2, приводит к следующим
выводам. Во-первых, величины КИН совпадают с аналогичными данными метода
конечных элементов в пределах 5 %. Во-вторых, экспериментально определённые
величины КИН близки к величинам КИН, представленным в работе [31] для двухконсольной
балки размерами 120x64x5 мм3,
изготовленной из алюминиевого сплава 7010 T7651.
Экспериментальные данные работы [31] получены методом цифровой корреляции
изображений. В частности, для трещины суммарной длиной 40 мм и приращения
нагрузки ДP = 1 kN величины
КИН составляют 7.4 MPa◦m0.5 и не
зависят от количества членов разложения Уильямса (1). Последнее обстоятельство
так же выявлено в наших исследованиях (An3 = 0).

Рис. 3. Чертёж образца #2 и схема
его нагружения.
|
Этап
n
|
Pn1,
[кН]
|
Pn2,
[кН]
|
Дan,
[мм]
|
a0+an,
[мм]
|
Дn,
[мм]
|
Д*n,
[мм]
|
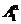 ,
[кгс/мм3/2] ,
[кгс/мм3/2]
|
 ,
[кгс/мм5/2] ,
[кгс/мм5/2]
|
 ,
[МПа◦м1/2] ,
[МПа◦м1/2]
|
|
15
|
0.64
|
0.60
|
1.7
|
50.2
|
11.9
|
8.4
|
8.4
|
0.0
|
6.7
|
|
16
|
0.64
|
0.60
|
1.7
|
51.9
|
12.5
|
8.7
|
8.6
|
-0.1
|
6.8
|
|
17
|
0.64
|
0.60
|
1.7
|
53.6
|
12.3
|
8.7
|
8.7
|
0.0
|
6.9
|
Таблица 2. Исходная экспериментальная информация
и величины Т-напряжений для образца #2
|
Этап
n
|
un,
[мм]
|
un+1,
[мм]
|
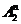 ,[
кгс/мм3/2] ,[
кгс/мм3/2]
|
 ,
[кгс/мм3/2] ,
[кгс/мм3/2]
|
Tn,
[МПа]
|
Tn*,
[МПа]
|
|
15
|
-0.8
|
-2.3
|
-1.7
|
-1.5
|
-68
|
35
|
|
16
|
-0.8
|
-2.8
|
-1.5
|
-1.6
|
-76
|
35
|
Анализ точности определения Т-напряжений
представляется более сложным. Во первых используемая компьютерная программа не
обладает возможностью определения Т-напряжений в пределах приемлемой точности.
Во вторых последний столбец таблицы 2 включает величины Т-напряжений полученные
по соотношению (13) и обозначенные как Tn*.
Различие в знаке и величине Т-напряжений полученных путём решения системы
линейных алгебраических уравнений (11)-(12) и аналогичных данных вытекающих из
соотношения (13) является очевидным. Мы полагаем, что данные, которые
соответствуют членам разложения An2
и An4
являются более надёжными. Однако величины Tn*имеет
тот же самый знак, как аналогичные величины из работы [31]. Данные полученные
методом цифровой корреляции изображения свидетельствует, что Т-напряжения достигают
максимальной величины T2
=
16.5 MПа для второго
члена формулы (1), и затем медленно уменьшаются с увеличением используемых
членов разложения. Таким образом, можно сказать, что выявленные проблемы
относящиеся к определению знака величины Т-напряжений на основе данных
оптических интерференционных методов должны быть более тщательны проверены. Для
этого в настоящее время выполняется широкий набор дополнительных экспериментов.
Ряд экспериментов аналогичных описанным выше выполнен для образца #1, который по
размеру совпадает с образцом #2, при ширине разреза 0.52 мм, что приблизительно
соответствует радиусу выреза с
= 0.26 мм. Величины КИН и Т-напряжений для обоих образцов совпадают в пределах
5% интервала.
4. Влияние радиуса выреза на величины параметров
механики разрушения
Разработанный подход позволяет определить
параметры механики разрушений для трещин, распространяющихся в поле остаточных
напряжений. Так же возможно оценить влияние радиуса разреза на величины КИН и
Т-напряжений полученных при использовании соотношений (6)-(8) и (11)-(12)
соответственно. Для иллюстрации этого факта проведены исследования
распространения трещины в поле остаточных напряжений в окрестности сварного
соединения. Две сварные тонкие пластины размерами 200x100x4
мм3, изготовленные из алюминия, служат объектами исследований. Они
обозначены как образец #015 (ширина разреза b1
= 0.6 мм, радиус разреза с1
~ 0.30 мм) и образец #016 (ширина разреза b1
= 0.3 мм, радиус разреза с2
~ 0.15 мм). Сварной шов длиной 100мм совпадает с одной из двух линий симметрии
каждого образца. Трещины в обоих образцах распространяются от центра шва вдоль
линии симметрии в направлении ортогональном сварному шву. Для оценки
идентичности полей остаточных напряжений в обоих образцах проведено определение
величин максимальных остаточных напряжений уymax
действующих вдоль шва. Эти величины определённые в точках с координатой х=9мм
равны уymax
= 130 и уymax
= 139 MПа соответственно.
Данные получены при совместном применении метода сверления отверстия и
электронной спекл-интерферометрии, причём отверстия выполняются в той части
образца, которая не содержит трещины.
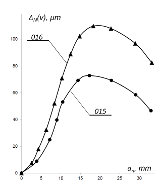
Рис. 4. Зависимость абсолютного раскрытия
трещины от ее суммарной длины.
Техника эксперимента и процедура определения КИН
и Т-напряжений полностью соответствуют описанной выше процедуре. Зависимости
абсолютного раскрытия трещины от её суммарной длины показаны на рис. 4. Эти
кривые построены путём последовательного суммирования величин каждого
отдельного раскрытия трещины Дn,
относящегося к начальной точке приращения длинны трещины. Разница максимальной
величины абсолютного раскрытия трещины для образца #015 (ДN(v)
= 73 мm) и #016 (ДN(v)
= 110 мm) 34%.
Точки, где каждая кривая достигает своего максимального значения, практически
совпадают и соответствуют длине трещине aS
= 16-18 мм. Зависимость величин КИН от суммарной длины трещины показаны на рис.
5a. Эти результаты
показывают, что координаты точек, где KI
= 0 и T = 0 не зависят от
радиуса разреза и вновь соответствуют трещине длинной aS
= 16-18 мм. Максимальные величины КИН для образца #015 (KI
=14.3 MПa◦m1/2)
и #016 (KI
=17.8 MПa◦m1/2)
отличаются на 20%. Различия максимальных величин Т-напряжений для образца #015
(T = -120 MПa)
и образца #016 (T = -188 MПa)
достигает 30%. Т-напряжения, показанные на рис. 5b,
получены на основе соотношений (11)-(12). Необходимо отметить, что формула (13)
даёт Т = 0 для обоих образцов и любого приращения длины трещины.
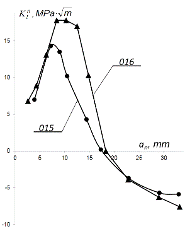
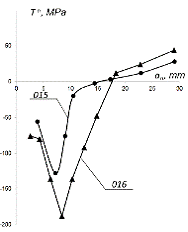 b
b
Рис. 5. Зависимости величин КИН (a)
и T-напряжений (b)
от суммарной длины трещины.
Рассмотрен новый метод для определения
параметров механики разрушения, который будет являться экспериментальной
основой предполагаемой диссертационной работы. Его сущность заключается в
измерении локального деформационного отклика на малое приращение длины трещины
методом электронной спектр-интерферометрии. Полученная таким образом
экспериментальная информация обеспечивает определение первых четырех
коэффициентов разложения Уильямса и дальнейшее вычисление величин коэффициентов
интенсивности напряжений (КИН) и T-напряжений.
Эффективность подхода демонстрируется при оценке влияния реальной ширины и
радиуса закругления U-образного
разреза на величины параметров механики разрушения. Рассматриваются два примера
для разрезов с радиусами закругления с1
~ 0.30 мм и с2
~ 0.15 мм. Первый из них - это образец типа двухконсольной балки. Результаты
определения КИН и T-напряжений,
полученные для двух радиусов закругления, практически совпадают. Второй случай
представляет собой исследование процесса распространения трещины в поле
остаточных напряжений для разрезов двух радиусов с1
~ 0.30 мм и с2
~ 0.15 мм. Различие максимальных величин КИН и T-напряжений
составляет 20 и 30 процентов, соответственно.
Список использованной литературы
1. Mishra, R.S., Friction stir
processing technologies. Advanced Materials & Processing, 2003; 161(10):
43-46.
. Nandan R., DebRoy T.,
Bhadeshia H.K.D.H. Recent advances in friction-stir welding - Process, weldment
structure and properties. Progress in Materials Science, 2008; 53(6): 980-1023.
. Dalle Donna C., Lima E.,
Wegener J., Pyzalla A., Buslaps T. Investigations on residual stresses in
friction stir welds. Proceedings
of the 3rd International Symposium on Friction Stir Welding, Kobe, Japan, TWI
(UK), CD-ROM, 27-28 September 2001.
4.
Lima E. B. F., Wegener J., Dalle Donna C., Goerigk G., Wroblewski T., Buslaps
T., Pyzalla A., Reimers W., Dependence of the microstructure, residual stresses
and texture of AA 6013 friction stir welds on the welding process. Zeitschrift
fьr Metallkunde, 2003; 94: 908-915.
5.
Milan M.T., Bose Filho W.W., Tarpani J.R., Malafaia A.M.S., Silva C.P.O.,
Pellizer B.C. and Pereira L.E. Residual Stress Evaluation of AA2024-T3 Friction
Stir Welded Joints. Journal of Materials Engineering and Performance, 2007;
16(1): 86-92.
6. Martins R.V, Honkimдki V.
Depth resolved strain and phase mapping of dissimilar friction stir welds using
high energy synchrotron radiation. Textures and Microstructures, 2003; 35(3-4):
145-152.
. James M.N., Hughes D.J., Chen
Z., Lombard H., Hattingh D.G., Asquith D., Yates J.R., Webster P.J. Residual
stresses and fatigue performance. Engineering Failure Analysis, 2007; 14(2):
384-395.
. Nairn J.A. Fracture mechanics
of composites with residual stresses, imperfect interfaces, and traction-loaded
cracks. Composites Sciences and Technology, 2000; 61(15): 2159-2167.
. Гольдштейн
Р.В.,
Перельмутер
М.Н.
Моделирование
трещиностойкости
композиционных
материалов.
Вычислительная
механика
сплошных
сред,
2009; 2(2): 22-39.
. Grйdiac M. The use of
full-field measurement methods in composite material characterization: interest
and limitations. Composites: Part A, 2004; 35(7-8): 751-761.
11. Cheng W., Finnie I.
Measurement of residual hoop stresses in cylinders using the compliance method.
ASME Journal of Engineering Materials and Technology, 1986; 108(2): 87-92.
12. Schindler H.-J.
Determination of residual stress distributions from measured stress intensity
factors. International Journal of Fracture, 1995; 74(2): R23-R30.
. Schindler H.-J., Cheng W.,
Finnie I. Experimental determination of stress intensity factors due to
residual stresses. Experimental Mechanics, 1997; 37(3): 272-277.
. Prime M.B. Residual stress
measurement by successive extension of a slot: The crack compliance method.
Applied Mechanics Reviews, 1999; 52(2): 75-96.
. Cheng W., Finie I. (2006)
Residual stress measurement and the slitting method. USA: Springer Mechanical
Engineering Series, 2006.
. Prime M.B. Measuring residual
stress and the resulting stress intensity factor in compact tension specimen.
Fatigue and Fracture of Engineering Materials and Structures, 1999; 22(3),
195-204.
. Prime M.B., Hill M.R.
Residual stress, stress relief, and inhomogeneity in aluminium plate. Scripta
Materialia, 2002; 46(1): 77-82.
. Lima E. B. F., Wegener J.,
Dalle Donna C., Goerigk G., Wroblewski T., Buslaps T., Pyzalla A., Reimers W.,
Dependence of the microstructure, residual stresses and texture of AA 6013
friction stir welds on the welding process. Zeitschrift fьr Metallkunde, 2003;
94: 908-915.
. Milan M.T., Bose Filho W.W.,
Tarpani J.R., Malafaia A.M.S., Silva C.P.O., Pellizer B.C. and Pereira L.E.
Residual Stress Evaluation of AA2024-T3 Friction Stir Welded Joints. Journal of
Materials Engineering and Performance, 2007; 16(1); 86-92.
. Shchepinov V.P., Pisarev V.S.
Novikov S.A., Balalov V.V., Odintsev I.N., Bondarenko M.M. (1996) Strain and
Stress Analysis by Holographic and Speckle Interferometry. John Wiley,
Chichester.
. Pisarev V.S., Balalov V.V.,
Aistov V.S., Bondarenko M.M., Yustus M.G. Reflection hologram interferometry
combined with hole drilling technique as an effective tool for residual
stresses fields investigation in thin-walled structures. Optics & Lasers in
Engineering, 2001; 36(6): 551-597.
. Pisarev V.S., Balalov V.V. A
role of fringe pattern catalogue in the course of interferometrically based
determination of residual stresses by the hole-drilling method. Optics &
Lasers in Engineering, 2004; 41(2): 411-462.
. Pisarev V.S., Grigoriev V.D.,
Balalov V.V., Chumak S.V. Residual stresses deriving from holographic
interferometry data on a base of inverse problem solution. Optics & Lasers
in Engineering, 2004; 42(6): 703-726.
. Pisarev V.S., Bondarenko
M.M., Chernov A.V., Vinogradova A.N. General approach to residual stresses
determination in thin-walled structures by combining the hole drilling method
and reflection hologram interferometry. International
Journal of
Mechanical
Sciences,
2005; 47(9): 1350-1376.
25. Maleski M.J., Kirugulige
M.S., H.V. Tippur H.V. A Method for Measuring Mode I Crack Tip Constraint under
Static and Dynamic Loading Conditions. Experimental Mechanics 2004; 44(5):
522-532.
. Hild F., Roux S. Measuring
stress intensity factors with a camera: Integrated digital image correlation
(I-DIC). Comptes Rendus Mйcanique (C. R. Mecanique), 2006; 334 (1): 8-12.
. Yoneyama S., Morimoto Y.,
Takashi M. Automatic Evaluation of Mixed-mode Stress Intensity Factors
Utilizing Digital Image Correlation. Strain, 2006; 42(1): 21-29.
. Yoneyama S., Ogawa T., Y.
Kobayashi Y. Evaluating mixed-mode stress intensity factors from full-field
displacement fields obtained by optical methods. Engineering Fracture
Mechanics, 2007; 74(9): 1399-1412.
. Rйthorй J., Roux S., Hild F.
Noise-robust stress intensity factor determination from kinematic field
measurements. Engineering Fracture Mechanics, 2008; 75(13): 3763-3781.
. Lуpez-Crespo P., Burguete
R.L., Patterson E.A., Shterenlikht A., Withers P.J., Yates J.R. Study of a
Crack at a Fastener Hole by Digital Image Correlation. Experimental Mechanics,
2009; 49(4): 551-559.
. Yates J.R., Zanganeh M., Tai
Y.H. Quantifying crack tip displacement fields with DIC, Engineering Fracture
Mechanics, 2010; 77(11): 2063-2076.
. Hadj Meliani M., Azari Z.,
Pluvinage G., Matvienko Yu.G. The effective T-stress estimation and crack paths
emanating from U-notches Engineering Fracture Mechanics, 2010; 77(11):
1682-1692.
33.
Rastogi P. (2001) Digital speckle pattern interferometry and related
techniques. Wiley, West Sussex.
. Williams M.L. On the stress
distribution at the base of a stationary crack. ASME Journal of Applied
Mechanics, 1957; 24(1): 109-114.