Моделирование разогрева жала паяльника с учетом потерь тепла на излучение

Моделирование разогрева жала паяльника с учетом потерь тепла на излучение

Моделирование разогрева жала паяльника с учетом потерь тепла на излучение

Введение

В технологии ЭА (электронной аппаратуры) поддержание на заданном уровне температуры жала паяльника является весьма важной задачей, поскольку при формировании электромонтажных соединений на печатных платах с использованием микросхем, полупроводниковых приборов и функциональных элементов, термочувствительных и критичных к нагреву, возможны выход из строя дорогих и дефицитных элементов, снижение надежности изделия. Особенно критична к температурному режиму ручная пайка паяльником, которая имеет следующие параметры: температура жала паяльника 280 - 320°С, время пайки не более 3 с. Однако из-за интенсивной теплоотдачи сначала в припой, набираемый на жало, а затем в паяемые элементы температура рабочей части жала паяльника снижается на 30-110°С и может выйти из оптимального температурного интервала пайки. В связи с этим становится актуальным моделирование разогрева жала паяльника.

Процесс создания математических моделей трудоемок, длителен и требует использования труда специалистов достаточно высокого уровня, имеющих хорошую подготовку как в предметной области, связанной с объектом моделирования, так и в области прикладной математики, современных математических методов, программирования, знающих возможности и специфику современной вычислительной техники. Необходимость построения таких моделей требует разработки системы правил и подходов, позволяющих снизить затраты на разработку модели и уменьшить вероятность появления трудноустранимых впоследствии ошибок.

В связи с этим возникает роль «простого», доступного моделирования, которое смог бы осуществить специалист, студент имеющий не высокий уровень подготовки как в предметной области, связанной с объектом моделирования, так и в области прикладной математики, современных математических методов, программирования.

Решением данной проблемы является среда программирования MathCAD, которая является математическим редактором, позволяющим проводить разнообразные научные и инженерные расчеты, начиная от элементарной арифметики и заканчивая сложными реализациями численных методов. Пользователи Mathcad - это студенты, ученые, инженеры, разнообразные технические специалисты. Благодаря простоте применения, наглядности математических действий, обширной библиотеке встроенных функций и численных методов, возможности символьных вычислений, а также превосходному аппарату представления результатов (графики самых разных типов, мощных средств подготовки печатных документов и Web-страниц), Mathcad стал наиболее популярным математическим приложением.

Таким образом, цель данной работы заключается в моделировании разогрева жала паяльника с учётом потерь тепла на излучение. Для решения данной задачи воспользуемся системой MathCAD.

1. Теоретическое описание разогрева жала паяльника с учётом потерь тепла на излучение

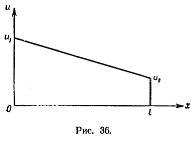
Рассмотрим однородный стержень длины L, теплоизолированный с боков и достаточно тонкий, чтобы в любой момент времени температуру во всех точках поперечного сечения можно было считать одинаковой. Если концы стержня поддерживать при постоянных температурах u₁ и u₂, то, как хорошо известно, вдоль стержня устанавливается линейное распределение температуры (рис. 36)

                                                                (1)

При этом от более нагретого к менее нагретому концу стержня будет перетекает тепло. Количество тепла, протекающего через сечения стержня площади S за единицу времени, даётся экспериментальной формулой:

                                                    (2)

где k - коэффициент теплопроводности, зависящий от материала стержня.

Величина теплового потока считается положительной, если тепло течёт в сторону возрастания х.

Рассмотрим процесс распространения температуры в стержне. Этот процесс может быть описан функцией u (x, t), представляющей температуру в сечении х в момент времени t. Найдём уравнение, которому должна удовлетворять функция u (x, t). Для этого сформулируем физические закономерности, определяющие процессы, связанные с распространением тепла.

. Закон Фурье. Если температура тела неравномерна, то в нём возникают тепловые потоки, направленные из мест с более высокой температурой в места с более низкой температурой.

Количество тепла, протекающего через сечение х за промежуток времени (t, t+dt), равно:

                                                                           (3)    

                                                                           (4)

плотность теплового потока, равная количеству тепла, протекшего в единицу времени через площадь в 1 см². Этот закон представляет обобщение формулы (2). Ему так же можно придать интегральную форму:

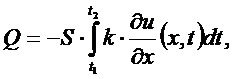                                                                  (5)

где Q - количество тепла, протекающего за промежуток времени (t₁, t₂) через сечение х. Если стержень неоднороден, то k является функцией от х.

. Количество тепла, которое необходимо сообщить однородному телу, чтобы повысить его температуру на ∆u, равно:

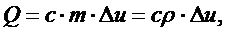                                                 (6)

где с - удельная теплоёмкость, m - маса тела, ρ - его плотность, V - объём.

Если изменение температуры имеет различную величину на разных участках стержня или если стержень неоднороден, то:

                                                (7)

. Внутри стержня может возникать или поглощаться тепло (например, при прохождении тока, вследствие химической реакции и т.д.). Выделение тепла может быть характеризовано плотностью тепловых источников F (x, t) в точке х в момент t¹). В результате действия этих источников на участке стержня (х, х+dx) за промежуток времени (t, t+dt) выделится количество тепла:

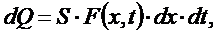                                                           (8)

или в интегральной форме:

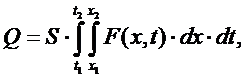                                                      (9)

где Q - количество тепла, выделяющегося на участке стержня (х₁, х₂) за промежуток времени (t₁, t₂).

Уравнение теплопроводности получается при подсчёте баланса тепла на некотором отрезке (х₁, х₂) за некоторый промежуток времени (t₁, t₂). Применяя закон сохранения энергии и пользуясь формулами (5), (7) и (9), можно написать равенство:

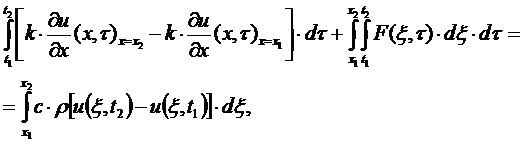 (10)

которое представляет уравнение теплопроводности в интегральной форме.

Чтобы получить уравнение теплопроводности в дифференциальной форме, предположим, что функция u (x, t) имеет непрерывные производные u_xx и u_t²).

Пользуясь теоремой о среднем, получаем равенство:

        (11)

которое при помощи теоремы о конечных приращениях можно преобразовать к виду:

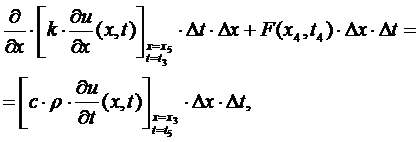(12)

где t₃, t₄, t₅ и х₃, х₄, х₅ - промежуточные точки интервалов (t₁, t₂) и (х₁, х₂).

Отсюда, после сокращения на произведение ∆x∆t, находим:

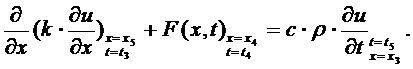                     (13)

Все эти рассуждения относятся к произвольным промежуткам (х₁, х₂) и (t₁, t₂). Переходя к приделу при х₁, х₂→х и t₁, t₂→t, получим уравнение:

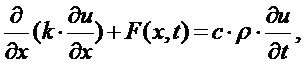                                           (14)

называемое уравнением теплопроводности.

Рассмотрим некоторые частные случаи.

. Если стержень однороден, то k, c, ρ можно считать постоянными, и уравнение обычно записывают в виде:

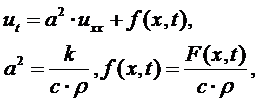
где 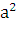 - постоянная, называемая коэффициентом температуропроводности. Если источники отсутствуют, т.е.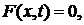

то уравнение теплопроводности принимает простой вид:

                                                                            (14΄)

. Плотность тепловых источников может зависеть от температуры. В случае теплообмена с окружающей средой, подчиняющегося закону Ньютона, количество тепла, теряемого стержнем, рассчитанное на единицу длины и времени, равно:

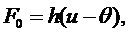
где 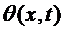 - температура окружающей среды, h - коэффициент теплообмена. Таким образом, плотность тепловых источников в точке x в момент времени t равна:

                                                              (15)

где 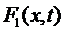- плотность других источников тепла.

Если стержень однороден, то уравнение теплопроводности с боковым теплообменом имеет следующий вид:

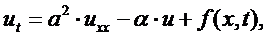
где  - известная функция.

Перепишем последнее уравнение в более привычном для нас виде:

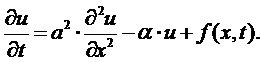                                                   (16)

Будем считать, что температура жала не зависит от координаты х, тогда уравнение (16) примет вид:

                                                              (16΄)

Так как ,

то уравнение будет иметь вид:

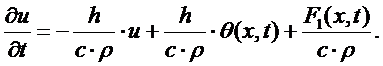
Преобразуя данное уравнение получим:

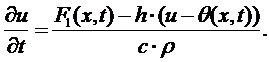                                                  (17)

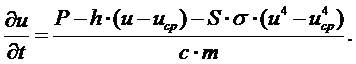
Данное дифференциальное уравнение решим с помощью программы MathCAD. Для решения дифференциальных уравнений программа MathCAD содержит ряд функций таких как: rkfixed, rkadapt, оdesolve и алгоритм Эйлера.

. Средства среды MathCAD для моделирования разогрева жала паяльника с учётом потерь тепла на излучение

Большое количество задач сводится к решению дифференциальных уравнений, однако, лишь небольшая часть их может быть решена аналитически. В связи с этим значительно возрастает роль численного решения дифференциальных уравнений.

Дифференциальным называется уравнение относительно неизвестной функции и её производных различных порядков .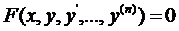

Даже в том случае, когда аналитическое решение данного уравнения все же существует, необходимо представить решение в графическом виде, чтобы понять его характер. В связи с этим, необходимо найти численное решение уравнения.

Для численного интегрирования одного ОДУ у пользователя Mathcad 11 (начиная с версии Mathcad 2000 Pro) имеется выбор-либо использовать вычислительный блок Given/odesoive, либо встроенные функции, как в прежних версиях Mathcad. Первый путь предпочтительнее из соображений наглядности представления задачи и результатов, а второй дает пользователю больше рычагов воздействия на параметры численного метода. Рассмотрим последовательно оба варианта решения.

Вычислительный блок для решения одного ОДУ, реализующий численный метод Рунге-Кутты, состоит из трех частей:

Given - служебное слово;

ОДУ и начальные условия, записанное с помощью логических операторов, причем начальное условие должно быть в форме: y(t0) = b;

Оdesolve (V, t, tmax, N) - встроенная функция для решения ОДУ относительно переменной t на интервале (t0, tmax), N - число шагов. Метод численных вычислений по которому будет работать функция пользователь может выбрать после щелчка по имени функции: фиксированный - метод Рунге-Кутта 4-го порядка с постоянным шагом интегрирования, адаптивный - метод Рунге-Кутта 4-го порядка с переменным шагом интегрирования либо жёсткий - метод Радаус.

Альтернативный метод решения ОДУ перешел из прежних версий Mathcad. Он заключается в использовании одной из встроенных функций: rkfixed (vi, tmin, tmax, n, f), Rkadapt (vi, tmin, tmax, n, f), Bulstoer (vi, tmin, tmax, n, f) и др. Аргументы функций одинаковы: vi - вектор начальных значений, tmin - начальное значение текущей переменной, tmах - конечное значение текущей переменной, n - число шагов, на которые разбит интервал tmах - tmin, f - символьный вектор правых частей уравнений системы. Этот способ несколько проигрывает первому и в простоте, и в наглядности Поэтому предпочтительнее вычислительный блок Given/odesoive.

Так же для нахождения численного решения дифференциального уравнения можно воспользоваться алгоритмом Эйлера.

Применим алгоритмом Эйлера для решения данной задачи.

Алгоритмом Эйлера.

Метод численного решения диф. уравнений включает в себя преобразование дифференциального уравнения в уравнение конечноразностное. Поскольку уравнение:

      (1)

описывает изменение величины u(t), то с известной степенью точности можно записать

,

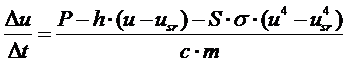где 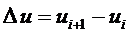, а Dt - конечный интервал, т.е.  (2). С учетом этого из уравнения (1) получим:

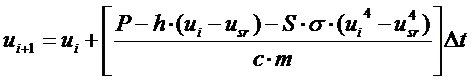 (3)

Это и есть конечноразностное уравнение, соответствующее дифференциальному уравнению (1). В первом приближении предполагается, что правая часть уравнения (1), т.е. скорость изменения u постоянна на отрезке Dt. Это метод касательных или метод Эйлера. Совершенно очевидно, что данный метод будет давать хорошее приближение, если Dt достаточно мало.

При решении такого типа задач часто сталкиваются с необходимостью определить влияние на полученное решение какого либо изменяющегося параметра. Для этого необходимо задать вектор, соответствующий изменению параметра и рассчитывать уже набор векторов решения, т.е. матрицу решения. Принцип реализации таких вычислений приведён ниже в MathCad программе. В которой представлено влияние параметра h (коэффициент теплообмена) на изменение температуры жала паяльника с учётом потерь тепла на излучение.

. Решение задачи в среде MathCAD

Значения констант:

В среде MathCAD программа имеет вид:

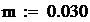
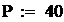
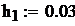
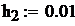
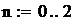
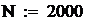
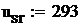
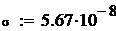
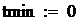
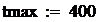
количество шагов интегрирования.

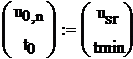 - вектор начальных условий.

решение системы уравнений методом Эйлера.

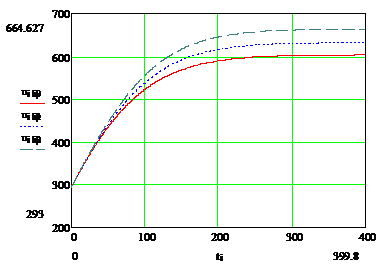
График изменения температуры жала паяльника

паяльник излучение жало

На графике приведены три зависимости температуры жала паяльника, соответствующие трём значениям параметра h (коэффициента теплопроводности). Уменьшение h приводит к увеличению температуры жала паяльника.

Заключение

В процессе выполнения данной работы мы исследовали разогрев жала паяльника с учётом потерь тепла на излучение, а так же определили влияние параметра h (коэффициента теплообмена) на разогрев жала. С помощью графика и программы решения задачи, мы смогли проанализировать изменение температуры жала паяльника. С помощью данной программы мы сможем наблюдать изменение температуры жала паяльника с учётом изменения значений констант, что мы и продемонстрировали на графике.

Данная задача имеет большое применение в технологии производства и ремонта электронной аппаратуры, так как с помощью её мы сможем обеспечить требуемый температурный режим необходимый при пайке дорогих и дефицитных элементов чувствительных к перепаду температуры.

Литература

1. Достанко А.П., Пикуль М.И. Хмыль А.А. Технология производства ЭВМ. Мн.: Высшая школа, 1994.

. Ланин В.Л., Емельянов В.А., Хмыль А.А. Проектирование и оптимизация технологических процессов производства электронной аппаратуры. Мн.:БГУИР, 2008.

. Ланин В.Л. Технология сборки, монтажа и контроля в производстве электронной аппаратуры. Мн.: БГУИР, 2007.

4. Кирьянов Д.В. Самоучитель MathCad 11. - СПб.: БХВ - Петербург, 2003.

. Шушкевич Г.Ч., Шушкевич С.В. Введение в MathCad 2000: Учебное пособие. - Гродно: ГрГУ, 2001. - 140 с.

. А.Н Тиханов, А.А Самарский. Уравнения математической физики.

. М. Херхагер, Х. Партолль MathCad 2000: полное руководство. Пер. с нем. - К.: Издательская группа BHV, 2000, - 416 с.

. Очков В.Ф. Mathcad 7 PRO для студентов и инженеров. - М.: «Компьютер Пресс», 1998 г. - 384 с.

. Бородич Л.И., Герасимович А.И., Кеда Н.П., Мелешко И.Н. Справочное пособие по приближенным методам решения задач высшей математики. - Мн.: Высшая школа, 2010. - 189 с.

. Макаров Е.Г. Инженерные расчеты в MathCad Учебный курс. - СПб.: Питер. 2011. - 448 с.