Расчет системы передачи электрической связи

Расчет системы передачи электрической связи

Курсовая работа

«РАСЧЕТ СИСТЕМЫ ПЕРЕДАЧИ ЭЛЕКТРИЧЕСКОЙ СВЯЗИ»

Введение

Информационно-коммуникационные сети являются технической основой современных информационных технологий, обеспечивающих информатизацию отрасли, региона, страны, всего мирового сообщества. Информатизация все больше и больше охватывает все отрасли народного хозяйства и обеспечивает, прежде всего, автоматизацию и управление как производством, так и другими службами. Для этой цели создаются базы и банки данных, которые с помощью средств связи обеспечивают доступ к любой информации любому пользователю. В современных условиях требуется интенсивное развитие как новых, так и традиционных систем связи, создание локальных и многотерминальных информационно-справочных сетей массового обслуживания.

Информация как совокупность знаний является главнейшим стратегическим ресурсом общества, его основным богатством, определяющим уровень развития общества, его цивилизованность.

Проблемы информатизации предъявляют весьма высокие требования, как к вычислительной технике, так и к технике связи. Для техники связи - это, прежде всего, требования: высоких скоростей (порядка Гигабит и более в секунду); малых коэффициентов ошибок (порядка 10^-10...10^-11); больших дальностей передачи (около 100 млн. км в системах космической связи); малых масс и энергопотребления оборудования.

На основе современной теории связи представляется возможным создать весьма совершенные системы связи, близкие по своим показателям к идеальной шенноновской системе. Однако, даже при использовании современных технологий, в том числе и высокоскоростной микропроцессорной техники, повышение эффективности существующих и вновь создаваемых систем связи с вышеназванными показателями, ставят перед ТЭС ряд новых нерешённых задач и проблем. Теорию электрической связи нельзя считать завершённой, она находится в постоянном движении и обновлении.

1. Структурная схема системы передачи и исходные данные

U(t) z(t) (t) (t_i)  (t)

Рис. 1. Структурная схема ЦСП сообщений

Таблица 1. Исходные данные

. Источник сообщений

. Запишем аналитическое выражение и построим график одномерной плотности вероятности W(a) мгновенных значений сообщения a(t), рис. 2

Из условия нормировки:

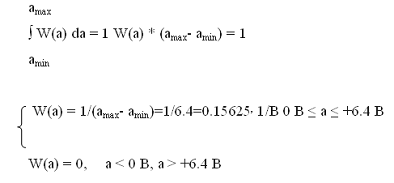
. Найдем интегральную функцию распределения сообщения F(a) и построим её график.

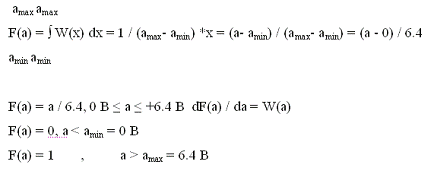
информационный техника модулятор кодовый

3. Рассчитаем значение математического ожидания m_a и дисперсии σ_а² сообщения a(t):

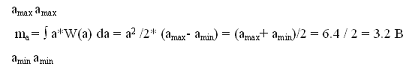
3. Дискретизатор

. Найдём максимально допустимый интервал дискретизации по времени ∆t, пользуясь теоремой Котельникова:

∆t ≤ 1 / 2*Fc, (∆t)_max = 1 / 2*Fc = 1 / (2*10³) = 0.5*10^-3 c = 0.5 мс

. Определим число уровней квантования L и скорость передачи символов на выходе дискретизатора:

= (a_max - a_min) / ∆a = 6.4 / 0.1 = 64= 1 / ∆t = 1/0.5*10^-3 = 2*10³ 1/c

. Среднюю мощность шума квантования рассчитаем пор формуле:

Р_ш.кв = (∆а)² / 12 = 0,01 / 12 = 8.3333*10^-4 В² = 833.3 (мВ)²

4. Отношение средних мощностей сигнала и шума квантования:

Р_а / Р_{ш кв} = σ_а² / σ_{ш кв} = ((a_max - a_min)²*12) / (12* (∆а)²) = L² = 64² = 4096 =

= 10*Lg4096 = 36,12 дБ

. Рассматривая дискретизатор как источник дискретных сообщений с алфавитом L = 64, определим его энтропию Н(А) и производительность Н’(A) при условии, что отсчеты, взятые через интервал ∆t, статистически независимы:

Н(А) = log₂ L = log₂(2)^k = k = 6 (бит/уровень)’(A) = H(A) / ∆t = 2*Fc*H(A) = 2*10³*6 = 12*10³ Бит/с = 12 kБит/с

. Кодер

. Определим число разрядов примитивного кода, необходимое для кодирования всех L = 64 уровней квантованного сообщения.

= H(A) = log₂ 64 = 6

. Запишем комбинацию примитивного двоичного кода, соответствующего передаче уровня j = 54:

→ 0 • 2⁷ + 0 • 2⁶ + 1 • 2⁵ + 1 • 2⁴ + 0 • 2³ + 1 • 2² + 1 • 2¹ + 0 • 2⁰

. Разобьём полученную последовательность на две четырёхразрядные комбинации информационных символов с целью построения для каждой из них корректирующего кода Хэмминга (7,4)

. Построим порождающую матрицу данного кода в соответствии с соотношениями:

информационные символы: c₁ = b₁ c₂ = b₂ c₃ = b₃ c₄ = b₄

проверочные символы: c₅ = b₁х b₂ х b₃ c₆ = b₁х b₃ х b₄ c₇ = b₂х b₃ х b₄

В качестве порождающей матрицы G линейного блокового кода n,K (где n = 7 - общее число символов в кодовой комбинации, К = 4 - количество информационных символов) может служить прямоугольная матрица размера К х n, строками которой являются любые К = 4 ненулевые разрешённые комбинации. Удобно взять комбинации, информационные символы которых образуют единичную матрицу, а проверочные символы γi,j определяются по формулам (4,4), приведенным выше:

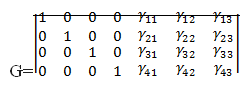
Таким образом, порождающая матрица G кода Хэмминга (7,4) имеет вид:

. Используя порождающую матрицу G, выразим все N_p = 2^k = 2⁴ =16 разрешенных кодовых комбинаций через строки матрицы G. Любую разрешённую кодовую комбинацию получим путём суммирования по модулю 2 двух, трёх или четырёх строк порождающей матрицы G. Нулевая комбинация получается путём суммирования любой строки «сама с собой».

Суммируя поочерёдно 1-ю строку со 2-й, 3-й, 4-й и с «самой собой» получим 4 разрешённые кодовые комбинации:

) 1 1 0 0 0 1 1; 2) 1 0 1 0 0 0 1; 3) 1 0 0 1 1 0 1; 4) 0 0 0 0 0 0 0

Суммируя вторую строку с 3-й и 4-й, получим:

) 0 1 1 0 0 1 0; 6) 0 1 0 1 1 1 0

Суммируя 3-ю строку с 4-й :

) 0 0 1 1 1 0 0

Суммируя 1-ю, 2-ю и 3-ю строки:

Суммируя 1-ю, 2-ю и 4-ю строки:

) 1 1 0 1 0 0 0

Суммируя 1-ю, 3-ю и 4-ю строки:

) 1 0 1 1 0 1 0

Суммируя 2-ю, 3-ю и 4-ю строки:

) 0 1 1 1 0 0 1

Суммируем все четыре строки:

) 1 1 1 1 1 1 1

Кроме того, имеются четыре исходные строки матрицы, которые дают ещё четыре разрешённые кодовые комбинации: 13) 1 0 0 0 1 1 0; 14) 0 1 0 0 1 0 1; 15) 0 0 1 0 1 1 1;

) 0 0 0 1 0 1 1

Таким образом, получены все 2⁴ = 16 разрешённых комбинаций. Остальные N_з = 2⁷-2⁴ = 112 комбинаций кода Хэмминга (7,4) являются запрещенными.

. Используя результаты п.п. (4.3-4.5) закодируем передаваемую информационную последовательность:₁ b₂ b₃ b₄ b₅ b₆ b₇ b₈

1 1 0 0 1 0 1 1 0 0 0 1 1

с₁ с₂ с₃ c₄ с₅ с₆ с₇ c^’₁ c^’₂ c^’₃ c^’₄ с^’₅ с^’₆ с^’₇

В результате 8-ми разрядная последовательность информационных символов, соответствующая передаче уровня j = 54, записывается двумя комбинациями кода Хэмминга (7,4), содержащими 8 информационных и 6 проверочных, всего 14 символов:

. Определим скорость передачи кодовых символов V_c:

V_c = n_L*V/R,

Где R = 4/7 - относительная скорость кода Хэмминга_L - число информационных символов_c = 8*2*10³ /(4/7) = 28*10³ 1/с

. Модулятор

. Изобразим временные диаграммы первичного (модулирующего) сигнала b(t) и соответствующего ему частотно-модулированного (ЧМ) сигнала u(t). Кодовая комбинация b(t) корректирующего кода содержит 14 символов длительностью Т каждый.

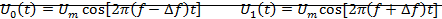
Диаграммы b(t) и u_чм(t) представлены:

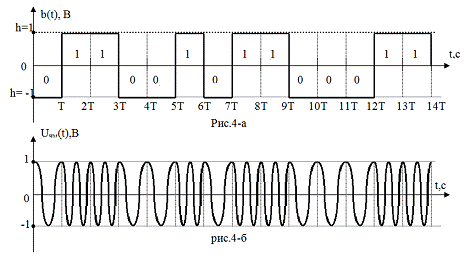
. Запишем аналитическое выражение ЧМ-сигнала, связывающее его с первичным сигналом b(t):

u_чм(t) = U_m*cos 2π [ f₀ + Δf b(t) ] t,

где U_m =1 B - амплитуда сигнала ЧМ,

Δf - девиация частоты;₀ = 100V_c =100/T - несущая частота ЧМ - сигнала;

Т = (∆t)_max/14 = 1/(2*F_c*14) = 1/(2*10³*14) = 35.714*10^-6 с = 35.714 мкс₀ = 100*(2*F_c*14) = 100*2*10³*14 = 2.8*10⁶ Гц = 2.8 МГц

При b(t) = 1 u₁(t) = U_m*cos 2*π [f₀ + Δf ]*t = U_m*cos 2*π *f₁ *t

При b(t) = -1 u₀(t) = U_m*cos 2*π [f₀ - Δf ]*t = U_m*cos 2*π *f₂ *t

Девиацию частоты Δf = (f₁-f₂)/2 выбираем из условия ортогональности ЧМ-сигналов u₁(t) и u₂(t). Это условие заключается в том, что скалярное произведение ЧМ-сигналов равно нулю, т.е. Т           

(u₁* u₂) = ∫ u₁(t) * u₀(t) dt = 0

Ортогональность достигается, если девиация частоты Δf = β / Т (β=1,2,3…-целое число). Выберем β=1, Δf = 1 / Т, тогда разнос частот (f₁-f₂) = 2*Δf = 2/Т получается минимальным и ширина спектра ЧМ-сигнала наименьшая.

. Запишем аналитическое выражение корреляционной функции первичного сигнала В_b(τ) и построим её график. Для случайного синхронного двоичного (телеграфного) сигнала в [1, стр.78] приведена формула:

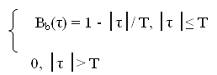
Т = 35.714 мкс; В_b(τ) = 1 - 28*10³ *│ τ │, В²

. Запишем аналитическое выражение спектральной плотности мощности (энергетического спектра) G_B(f) первичного сигнала В(t). Расчёт G_B(f) проведём с использованием теоремы Винера-Хинчина:

_B(f) = 2*∫ В_b(τ)*cos(2* π* f * τ) d τ = T* (sin²[π*f *T])/(π*f *T)²

Результаты расчётов по этой формуле сведём в таблицу 2 и построим график G_B(f):

Таблица 2

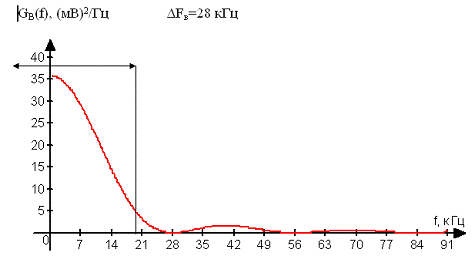
Рис. 1

. Определим ширину ∆F_в энергетического спектра G_B(f):

∆F_в = 1/Т = 1 / 35.714*10^-6 = 28*10³ Гц = 28 кГц

Полученное значение ∆F_в отложим на графике.

. Запишем аналитическое выражение и построим диаграмму энергетического спектра G_u(f) частотно-модулированного сигнала:

_m²           U_m² U_m² * T sin²[π(f-f₁)T]_m² * T sin²[π(f-f₂)T]

Для построения графика G_чм(f-f₀) использованы результаты таблицы 2. Значения G_чм(f-f₀) снижены в 2 раза по сравнению с G_B(f), энергетический спектр смещён вверх по частоте на несущую f₀. Кроме того, появились две дискретные линии (дельта-функции) на частотах f₁=(f₀+∆f) и f₂=(f₀-∆f), вокруг которых размещаются непрерывные спектры боковых колебаний. Мощность перекрывающейся части спектра мала и ею можно пренебречь по сравнению с мощностью двух основных “лепестков” спектра.

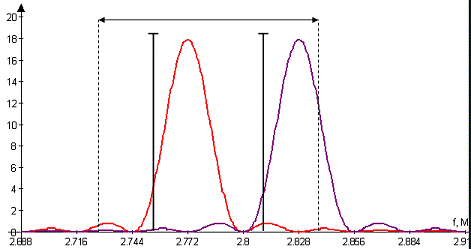
Рис. 2

∆F_чм = 4 / Т = 4 / 35.714*10^-6 = 112 кГц

6. Канал связи

. Запишем аналитическое выражение, связывающее входной и выходной сигналы в канале:

(t) = S(t) + n(t),

где S(t) - полезный сигнал на выходе канала;(t) - аддитивный гауссовский белый шум.

Если задан канал с постоянными параметрами, в котором возможен когерентный приём, то:

(t) = γ *u(t - τ)

Здесь γ = (a+1)/10 +1 - коэффициент передачи канала, (а - последняя цифра номера зачётной книжки);

τ - время задержки при распространении сигнала по каналу связи. При этом форма исходного сигнала u(t) на выходе канала остаётся неизменной, сигнал S(t) только затухает в (1/γ) раз и сдвигается по времени на интервал τ, пропорциональный длине канала связи. Поскольку форма сигнала S(t) на выходе канала известна точно, приём в таком канале - когерентный.

Найдем мощность шума на выходе канала:

Р_ш = N₀ * ∆F_фм = 6.52*10^-6 * 112*10³ = 0.7302 В²

. Рассчитаем отношение мощностей сигнала и шума на выходе канала. Задана ЧМ, это система с активной паузой, поэтому средняя мощность передаваемого сигнала в расчёте на один элемент длительностью Т:

Р_{с пер} = (Р_{С 0}+Р_С1) / 2 = (U_m² / 2 + U_m² / 2) / 2 = U_m² / 2 = 0.5 B²

Коэффициент передачи канала по мощности равен:

γ ² = ((a+1)/10 +1)² = ((1 + 1) / 10+1)² = 1.44

Мощность сигнала на выходе канала:

Р_{с вых} = Р_{с пер} * γ ² = 0.5 * 1.44 = 0.72 В²

Отсюда:

Р_{с вых} / Р_ш = 0.72 / 0.7302 = 0.986 (-0.06 дБ)

В этом канале шум слишком велик и превышает сигнал по мощности. Связь по такому каналу невозможна. Уменьшим шум канала в 2 раз, приняв N₀ = 3.26 *10^-6 В²/Гц, тогда:

Р_ш = N₀ * ∆F_чм = 3.26*10^-6 * 112*10³ = 0.365 В²

Р_{с вых} / Р_ш = 0.72 / 0.365 = 1.972 = 2.95 дБ

При таком отношении сигнал / шум связь по каналу возможна.

. Определим пропускную способность непрерывного канала:

с = ∆F_чм* log₂(1 + Р_{с вых} / Р_ш) = 112 * 10³ * log₂(1 + 1.972) = 1.76*10⁵ бит/с

. Рассчитаем эффективность использования пропускной способности непрерывного канала:

К_с = H’(A) / с = 12 *10³ / 1.76*10⁵ = 0.068

. Демодулятор

В демодуляторе осуществляется оптимальная некогерентная обработка принимаемой с выхода канала связи смеси z(t) ЧМ-сигнала с белым гауссовским шумом.

. Запишем общее решающее правило приёма сигналов m-позиционного кода при условии, что:

(b_i) = 1 / m = const; i = 1,2,3….m,

где p(b_i) - априорная вероятность передачи символа b_i.

Решающее правило, оптимальное по критерию идеального наблюдателя, обеспечивает минимум средней вероятности ошибки и записывается в виде:

где z - совокупность одного или нескольких отсчетов принятой реализации z(t), называемая “выборкой” сигнала;(b_i / z) - апостериорная, т.е. найденная после ”опыта”, заключающегося в наблюдении выборки z вероятность передачи символа b_i.Согласно этому правилу необходимо сравнивать между собой значения апостериорных вероятностей для разных символов b_i (i = 1,2,3….m) и принять решение в пользу того из них, вероятность которого максимальна. При p(b_i) = 1 / m = const, решающее правило сводится к правилу максимального правдоподобия:

где W(z / b_i) - условная плотность вероятности выборки z при передаче символа b_i, называемая функцией правдоподобия этого события.

. Алгоритм некогерентного приёма двоичных сигналов с ЧМ в канале с белым гауссовским шумом записывается в виде :

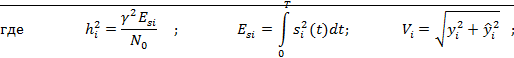
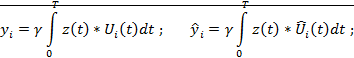
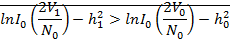
где N₀ - спектральная плотность белого шума в канале;₀ (2V₁ / N₀₎ - функция Бесселя;_i - энергия сигнала S_i(t).

Блок обработки сигнала

Рис. 3

4. Рассчитаем среднюю вероятность ошибки при некогерентном приёме ЧМ по формуле:

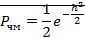
где h² = E_Si / N₀ - отношение энергии элемента сигнала к спектральной плотности белого шума N₀.

² = (U_m² * T * γ ²) / (2*N₀)= (1 * 35.714*10^-6 * 1.44) / (2 * 3.26*10^-6) = 7.887

. При некогерентном приёме АМ:

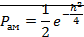
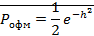
Сравнивая эти формулы, видно, что переход от АМ к ЧМ позволяет при неизменной вероятности ошибки снизить энергию ЧМ-сигнала в 2 раза, что эквивалентно выигрышу в (10*lg2) = 3 дБ. Соответственно, переход от АМ к ОФМ позволит снизить энергию сигнала в 4 раза, т.е. получить выигрыш в 6 дБ. Таким образом, наиболее помехоустойчивой является система ОФМ, затем система с ортогональными сигналами - ЧМ, а наименее помехоустойчивой оказалась АМ - система с пассивной паузой.

8. Декодер

. Построим проверочную матрицу кода кода Хэмминга (7,4):

. Построим таблицу синдромов, соответствующую всем возможным вариантам одиночных ошибок. В качестве i-го синдрома (i = 1,2,3….7) возьмём i-й столбец проверочной матрицы Н:

Таблица 3

. Вычислим синдром первой кодовой комбинаций, определённой в п.4.6

Если комбинация принята безошибочно, её синдром равен:

(b) = b_{5 пр} х b_{5 контр}, b_{6 пр} х b_6контр, b_{7 пр} х b_{7 контр} = (0,0,0)

здесь b_{5 контр} = b_{1 пр} х b_{2 пр} х b_{3 пр} - результат проверки на приёме,_{5 пр} - фактически принятый контрольный символ.

Если ошибок нет, b_{5 контр} = b_{5 пр}, поэтому b_{5 пр} х b_{5 контр} = 0. Тот же результат получится по 6-му и 7-му контрольным символам, поэтому синдром будет нулевым, S = (0,0,0)

. Введём одиночную ошибку в кодовую комбинацию, инвертировав символ с номером i = |N1-7|=|1-7|= 6

. Проделаем аналогичную процедуру, введя дополнительную ошибку в любой кодовый символ, например в 1-й. Получим код (1 1 1 0 0 0 0), найдем синдром ошибки S = (1 0 0), указывающий по таблице синдромов на то, что ошибка произошла в 5-м символе. После её исправления внесём фактически ещё одну, уже третью ошибку и получим кодовую комбинацию вида (1 1 1 0 1 0 0).

. Определим вероятность необнаружения ошибки при использовании кода Хэмминга:

но =C³₇*p³,

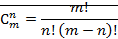
где р - вероятность ошибки на выходе демодулятора.но =35*(6.96*10^-3)³ = 1.18*10^-5

7. Определим вероятность ошибки декодирования в режиме исправления ошибок для кода Хэмминга (7,4):дек = C²₇*p²,дек = 21*(9.69*10^-3)² = 1.97*10^-3

. В итоге можно сделать вывод о том, что двойные ошибки только обнаруживаются кодом Хэмминга (7.4), но не исправляются.

Минимальное кодовое разрешение для этого кода d_min = 3. Кратность исправляемых ошибок q_n = (d_min - 1) / 2 = 1, т.е код исправляет только одиночные ошибки. Кратность обнаруживаемых ошибок q₀ = (d_min - 1) = 2. Если в кодовую комбинацию (п. 4.6) введены 2 ошибки, декодирование произойдёт с ошибкой. Данная запрещённая (с 2-мя ошибками) кодовая комбинация отстоит от истиной на расстоянии d = 2, а от ближайшей разрешённой отличается только в (d_min - 2) = 1 - в одном разряде, т.е отстоит на кодовом расстоянии d = 1. Поэтому происходит ложное исправление и ошибочный приём комбинации (1 1 1 0 1 0 0), отличающейся от переданной на d = 3 разряда. Однако двойные ошибки в коде происходят гораздо реже, чем одиночные, которые исправляются кодом Хэмминга (7.4).

9. Фильтр восстановитель

. Найдём значение частоты среза F_c идеального фильтра нижних частот (ФНЧ), при котором обеспечивается теоретически точное восстановление непрерывного сигнала. Как известно из теории дискретизации сигнала с ограниченным спектром, для его восстановления необходимо и достаточно использовать ФНЧ с F_c = F_в, где F_в - верхняя граничная частота спектра сигнала. В заданном варианте F_в = 10³ Гц, поэтому F_с = 10³ Гц.

. Изобразим АЧХ и ФЧХ идеального ФНЧ:

ФЧХ - φ(f) = - ω* τ_з = -2 * π * f * τ_з,(f) = 0, f > F_с

где τ_з - время задержки сигнала в ФНЧ

ФЧХ фильтра линейна, её наклон зависит от τ_з. Выберем

τ_з = 3 / F_с = 6*∆t=3*10^-3=3 мс,

где ∆t - интервал Котельникова

При этом ФЧХ:

φ(f) = (-6* π / F_с)*f, 0 ≤ f ≤ F_с

. Найдём импульсную характеристику g(t) фильтра - восстановителя:

(t) = ∫ехр[j*ω*(t - τ_з)] df = (2*F_с) * [sin 2 π *F_c*(t - τ_з)] / [2π*F_c*(t - τ_з)] =

= 2*10³ *;

Результаты расчёта g(t) сведём в таблицу 4 и построим график g(t), рис. 10:

Таблица 4

Как видно из таблицы нули импульсной характеристики g(t) отстоят друг от друга на интервал Котельникова ∆t = 1 / (2*Fc) = 0.5 мс. Импульсная характеристика идеального ФНЧ бесконечна по длительности, а сам идеальный ФНЧ физически нереализуем.

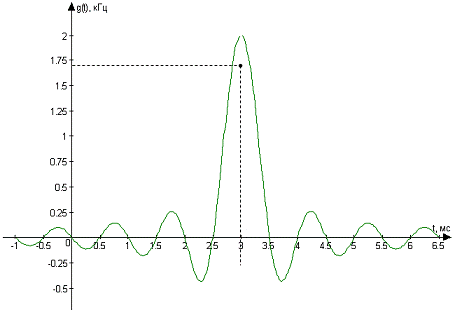
Рисунок 4

Запишем условие физической реализуемости найденной импульсной характеристики g(t). Поскольку отклик реальной цепи не может возникнуть раньше, чем поступило воздействие на вход цепи, а импульс поступает на вход ФНЧ в момент t = 0, то g(t) = 0 при t ≥0 есть условие физической реализуемости. При t < 0 на рис.10 показана g(t) идеального, физически нереализуемого ФНЧ. Выбор достаточно большой задержки в фильтре τ_з = 3 / F_с = 6*∆t позволяет реализовать ФНЧ, близкий к идеальному. При этом погрешность из-за отбрасывания “хвоста” g(t), t < 0 не превышает по максимуму 5% от g_max(τ_з) = 2 * F_с. Дальнейшее увеличение задержки τ_з >3 / F_с нецелесообразно, т.к. его реализация усложняется, а погрешность g(t) снижается незначительно.

Заключение

Современная теория электрической связи использует понятия и методы из различных научных областей. Прежде всего, математики, физики, теории цепей и вычислительной техники. Все понятия и методы из этих областей образуют в курсе ТЭС определенное единство и должны рассматриваться как одно целое в рамках системного подхода, принятого на вооружение современной наукой. Основное понятие, использованное в курсе ТЭС, - понятие математической модели сообщений, сигналов, помех и каналов в системах связи. Все эти модели таковы, что позволяют с той или иной степенью полноты и точности осуществить две взаимосвязанные операции - анализ и синтез устройств преобразования сигналов. ТЭС развивалась так, что методы анализа часто обгоняли методы синтеза. Однако, в последнее время эта ситуация меняется коренным образом под влиянием широкого внедрения ЭВМ в практику научного поиска.

Практическая разработка новых систем сегодня все больше базируется на подходе, включающем следующие этапы: модель, алгоритм, программа. Переход к цифровым методам передачи различных сообщений и цифровой обработке сигналов на большей части тракта передачи при широком использовании микропроцессорной техники обеспечивает интеграцию средств связи и средств вычислительной техники. На этой основе создаются интегральные цифровые сети, в которых достигается не только наиболее полная интеграция по видам связи и услуг, но и интеграция технических средств передачи, обработки, коммутации, управления и контроля. Интегральные сети, объединяющие в единый комплекс вычислительные и информационные системы на базе ЭВМ, включая персональные компьютеры, образуют единую информационно-коммуникационную сеть.

Литература

1. Зюко А.Г., Кловский Д.Д., Коржик В.И., Назаров. М.В. Теория электрической связи / Под ред. Д.Д. Кловского. - М.: Радио и связь, 2008.

2. Кловский Д.Д., Шилкин В.А. Теория электрической связи. - Сб. задач и упражнений. - М.: Радио и связь, 1990.

3. Кловский Д.Д., Шилкин В.А. Теория передачи сигналов в задачах.- М.:Связь, 1978.

4. Зюко А.Г., Кловский Д.Д., Назаров М.В., Финк Л.М. Теория передачи сигналов /. - М.: Радио и связь, 1986.

5. Кловский Д.Д. Теория передачи сигналов.- М.: Связь, 2010.

6. РД ПГАТИ 2.11-2001. Выполнение и оформление курсовых проектов и работ. Правила и рекомендации. // Составители: Сапаров В.Е., Киреев В.Р., Горчакова М.Г.  Самара, ПГАТИ, 2001.

7. Методические разработки к лабораторным работам по 2 части курса «Теория электрической связи». Раздел 1// Составители: Николаев Б.И., Широков С.М. и др.- Самара, ПИИРС, 2007.

8. Дж. Прокис «Цифровая связь» перевод с английского под редакцией Д.Д. ловского.-М.: Радио и связь, 2000.