Интерференция поляризованных волн в случае параллельных и сходящихся пучков
Интерференция
поляризованных волн в случае параллельных и сходящихся пучков
Введение
интерференция физика поляризованный
свет
Интерференция - это взаимодействие двух (или
более) волн, в результате которого в одних точках волнового поля происходит
увеличение, а в других - уменьшение интенсивности по сравнению с суммарной
интенсивностью отдельных волн до их взаимодействия.
Поляризация волн - характеристика волн,
определяющая пространственную направленность векторных волновых полей.
Исторически это понятие было введено в оптике ещё во времена "довекторных
описаний" и первоначально основывалось на свойствах поперечной анизотропии
волновых пучков. Оно распространено на все без исключения типы физических
волновых возмущений, но основная терминология по-прежнему осталась связанной с
электромагнитными полями.
Интерференция поляризованных волн - явление,
возникающее при сложении когерентных поляризованных световых колебаний.
Трудность получения интерференции поляризованных
волн состоит в том, что при наложении двух когерентных лучей, поляризованных во
взаимно перпендикулярных направлениях, никакой интерференционной картины с
максимумами и минимумами интенсивности получиться не может. Интерференция
возникает только в том случае, если колебания во взаимодействующих лучах
совершаются вдоль одного и того же направления. Колебания в двух лучах,
первоначально поляризованных во взаимно перпендикулярных направлениях, можно
свести в одну плоскость, пропустив эти лучи через поляризующую кристаллическую
пластинку.
1.Интерференция при прохождении через кристалл
поляризованного света
интерференция физика поляризованный
свет
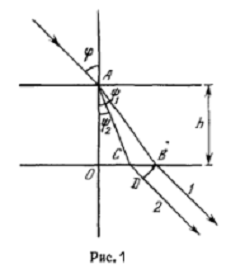
Пусть на плоскопараллельную
кристаллическую пластинку падает волна под углом 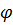
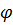 (рис.1). В кристалле она
разделяется на две волны, распространяющиеся в разных направлениях м с
различными скоростями. Пусть АВ и АС - волновые нормали этих волн, а
(рис.1). В кристалле она
разделяется на две волны, распространяющиеся в разных направлениях м с
различными скоростями. Пусть АВ и АС - волновые нормали этих волн, а 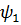
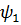 и
и 
 - соответствующие им углы
преломления. В кристалле направления волновых нормалей не совпадают. Вне
кристалла различие между этими направлениями пропадает. Из кристалла выходят
два луча 1 и 2, параллельные падающему и поляризованные в перпендикулярных
плоскостях. Оптическая разность хода между ними представляется выражением:
- соответствующие им углы
преломления. В кристалле направления волновых нормалей не совпадают. Вне
кристалла различие между этими направлениями пропадает. Из кристалла выходят
два луча 1 и 2, параллельные падающему и поляризованные в перпендикулярных
плоскостях. Оптическая разность хода между ними представляется выражением:
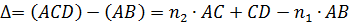
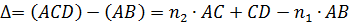 ,
,
где 
 и
и 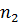
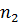 - показатели преломления
рассматриваемых волн, а D - основание перпендикуляра, опущенного из точки В на
луч 2. Если h - толщина пластинки, то
- показатели преломления
рассматриваемых волн, а D - основание перпендикуляра, опущенного из точки В на
луч 2. Если h - толщина пластинки, то
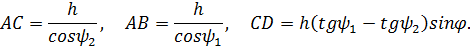
По закону преломления 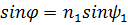
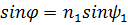 =
=
 . Используя эти выражения, получим:
. Используя эти выражения, получим:

 (1)
(1)
Разность хода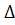
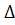 между лучами 1 и 2 обусловлена
двумя обстоятельствами:
между лучами 1 и 2 обусловлена
двумя обстоятельствами:
) различием показателей преломления 
 и
и 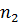
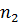 ; 2) различием углов преломления
; 2) различием углов преломления 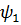
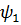 и
и 
 . Второе обстоятельство играет малую
роль. В большинстве случаев им можно пренебречь и пользоваться приближенным
выражением:
. Второе обстоятельство играет малую
роль. В большинстве случаев им можно пренебречь и пользоваться приближенным
выражением:

 (2)
(2)
где угол 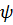
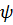 имеет любое промежуточное значение
между углами преломления
имеет любое промежуточное значение
между углами преломления 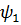
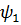 и
и 
 .
.
Разность хода 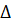
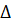 можно использовать для получения
интерференции лучей 1 и 2. Если бы свет, падавший на кристаллическую пластинку,
был естественный, то интерференция была бы невозможна, так как в этом случае
лучи 1 и 2 не были бы коррелированны между собой. Для получения коррелированных
лучей 1 и 2 падающий свет должен быть поляризован - линейно или эллиптически.
Но и в этом случае при наложении лучей 1 и 2 интерференция все же не возникнет,
так как лучи 1 и 2 поляризованы во взаимно перпендикулярных плоскостях. Нужно
свести колебания в этих лучах к одному направлению, т.е. предварительно
пропустить их через николь. В случае плоскопараллельных пластинок лучи сводятся
вместе в фокальной плоскости линзы - получаются полосы равного наклона. В
случае тонких пластинок переменной толщины наблюдаются полосы равной толщины,
локализованные на самих пластинках.
можно использовать для получения
интерференции лучей 1 и 2. Если бы свет, падавший на кристаллическую пластинку,
был естественный, то интерференция была бы невозможна, так как в этом случае
лучи 1 и 2 не были бы коррелированны между собой. Для получения коррелированных
лучей 1 и 2 падающий свет должен быть поляризован - линейно или эллиптически.
Но и в этом случае при наложении лучей 1 и 2 интерференция все же не возникнет,
так как лучи 1 и 2 поляризованы во взаимно перпендикулярных плоскостях. Нужно
свести колебания в этих лучах к одному направлению, т.е. предварительно
пропустить их через николь. В случае плоскопараллельных пластинок лучи сводятся
вместе в фокальной плоскости линзы - получаются полосы равного наклона. В
случае тонких пластинок переменной толщины наблюдаются полосы равной толщины,
локализованные на самих пластинках.
Схема для получения интерференции в
параллельных лучах приведена на рис.2. Кристаллическая пластинка К вводится
между поляризатором Р и анализатором А. Линейно поляризованный свет, выйдя из
поляризатора Р, после прохождения через кристаллическую пластинку К
превращается в поляризованный эллиптически, а затем проходит через анализатор
А, превращаясь снова в линейно поляризованный. Интенсивность проходящего света
зависит от ориентации анализатора. При вращении последнего интенсивность I
будет меняться.
Разность фаз, возникающая при
прохождении света через кристаллическую пластинку, равна 
 , т.е. зависит от длины волны
, т.е. зависит от длины волны 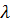
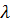 .
.

При неподвижном анализаторе она
различна для разных длин волн. По этой причине интерференционная картина
получается окрашенной. При вращении анализатора краска меняется. При повороте
анализатора на 90
 окраска меняется на дополнительную
- светлые места становятся темными и наоборот. Если главные сечения
поляризатора и пластинки параллельны или перпендикулярны между собой, то через
пластинку проходит только один луч. Ему не с чем интерферировать, и окрашивание
пропадает. Все эти явления получили название хроматической поляризации. Она
была открыта Араго в 1911 г.
окраска меняется на дополнительную
- светлые места становятся темными и наоборот. Если главные сечения
поляризатора и пластинки параллельны или перпендикулярны между собой, то через
пластинку проходит только один луч. Ему не с чем интерферировать, и окрашивание
пропадает. Все эти явления получили название хроматической поляризации. Она
была открыта Араго в 1911 г.
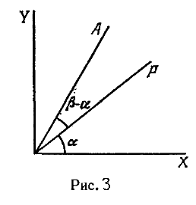
Обычно главные сечения поляризатора
и анализатора устанавливаются параллельно (николи параллельны) или
перпендикулярно (николи скрещены) друг к другу. В последнем случае установка
весьма чувствительна к обнаружению анизотропии. Через два скрещенных николя
свет не проходит (поле зрения темное). Если же между ними ввести какое-либо
анизотропное тело, то даже при наличии слабой анизотропии система начинает
пропускать свет (поле зрения просветляется).
Для количественного расчета примем
главные направления кристаллической пластинки за координатные оси X и Y (рис.3).
Пусть поляризатор пропускает колебания только в направлении Р, а анализатор -
только в направлении А. Углы между этими направлениями и осью X обозначим
соответственно 
 и
и 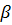
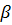 . Амплитуду света, вышедшего из
поляризатора, примем за единицу. Тогда по выходе из пластинки амплитуда
световых колебаний вдоль оси X будет cos
. Амплитуду света, вышедшего из
поляризатора, примем за единицу. Тогда по выходе из пластинки амплитуда
световых колебаний вдоль оси X будет cos
 , а вдоль оси Y - sin
, а вдоль оси Y - sin
 . Из этих колебаний анализатор
пропустит колебания с амплитудами
. Из этих колебаний анализатор
пропустит колебания с амплитудами 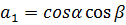
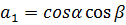 и
и 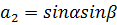
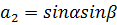 соответственно, причем в результате
прохождения через пластинку между обоими колебаниями возникнет разность фаз
соответственно, причем в результате
прохождения через пластинку между обоими колебаниями возникнет разность фаз 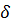
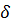 . От сложения обоих колебаний
получится колебание, амплитуда
. От сложения обоих колебаний
получится колебание, амплитуда 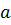
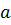 которого определяется отношением
которого определяется отношением

 .
.
После подстановки значений 
 и
и 
 , приведенных выше, для
интенсивности света, проходящего через анализатор, получим
, приведенных выше, для
интенсивности света, проходящего через анализатор, получим

 . (3)
. (3)
В этой формуле в сочетании с
формулой (1) содержится объяснение всех особенностей интерференции поляризованного
света в параллельных лучах. Пока свет монохроматичен, а толщина пластинки всюду
одинакова, все величины в (3) постоянны, так что получается равномерная
освещенность пластинки. При повороте поляризатора или анализатора на 90
 выражение (3) переходит в
выражение (3) переходит в
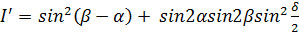
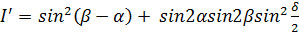 .
.
Следовательно, 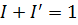
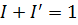 . Это очевидно и из общих
соображений, так как при указанном повороте весь свет, пропускавшийся ранее,
будет задержан, а задержавшийся начнет проходить. В частном случае, когда
николи параллельны (
. Это очевидно и из общих
соображений, так как при указанном повороте весь свет, пропускавшийся ранее,
будет задержан, а задержавшийся начнет проходить. В частном случае, когда
николи параллельны (
 ,
,
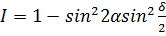
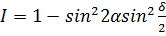 , (4)
, (4)
а когда скрещены -
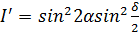
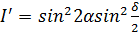 . (5)
. (5)
В белом свете, если его разложить на
спектральные составляющие, первое слагаемое в (3) остается постоянным, а второе
зависит от длины волны и приводит к окрашиванию поля зрения. Если направление Р
совпадает с одним из главных направлений пластинки (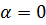
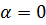 или
или 
 , то
, то 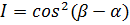
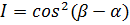 , т.е. интенсивность
, т.е. интенсивность 
 постоянна и не зависит от длины
волны. В этом случае, как было уже отмечено выше, интерференции нет, и в белом
свете получается равномерно освещенное неокрашенное поле. Интенсивность его
можно менять поворотом николя-анализатора А, но оно все время остается белым.
постоянна и не зависит от длины
волны. В этом случае, как было уже отмечено выше, интерференции нет, и в белом
свете получается равномерно освещенное неокрашенное поле. Интенсивность его
можно менять поворотом николя-анализатора А, но оно все время остается белым.
. Интерференция поляризованных волн
в случае сходящихся пучков
Более сложные явления наблюдаются
при интерференции сходящихся поляризованных лучей. Обычно применяемая схема для
наблюдения таких явлений представлена на рис.4. Параллельный пучок линейно
поляризованного света линзой 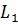
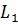 превращается в сходящийся и
концентрируется на кристаллической пластинке К. После прохождения через
пластинку К каждый луч разделяется на два параллельных луча, между которыми
возникает разность хода. При наложении таких лучей свет становится
поляризованным эллиптически, причем разность хода между лучами, а с ней и
характер эллиптической поляризации зависят от угла наклона падающего луча.
Линза
превращается в сходящийся и
концентрируется на кристаллической пластинке К. После прохождения через
пластинку К каждый луч разделяется на два параллельных луча, между которыми
возникает разность хода. При наложении таких лучей свет становится
поляризованным эллиптически, причем разность хода между лучами, а с ней и
характер эллиптической поляризации зависят от угла наклона падающего луча.
Линза 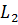
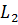 , одинаковая с
, одинаковая с 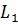
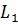 , делает лучи снова параллельными.
Распределение светового поля в фокальной плоскости FF линзы проектируется
объективом О и николем-анализатором А на экран, где и наблюдается интерференционная
картина.
, делает лучи снова параллельными.
Распределение светового поля в фокальной плоскости FF линзы проектируется
объективом О и николем-анализатором А на экран, где и наблюдается интерференционная
картина.

Чтобы составить представление о
форме получающихся интерференционных полос, введем понятие изохроматической
поверхности (поверхности одинакового цвета). Возьмем в неограниченной
кристаллической среде произвольную точку О и представим, что через нее во
всевозможных направлениях и притом в одинаковых фазах проходят плоские волны. В
каждом направлении волновой нормали распространяются две волны, линейно
поляризованные во взаимно перпендикулярных плоскостях. На расстоянии r от точки
О между ними возникает разность хода 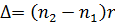
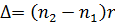 , где
, где 
 и
и 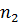
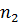 - показатели преломления этих волн.
Фиксировав
- показатели преломления этих волн.
Фиксировав 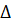
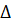 , будем откладывать на волновых
нормалях отрезки с длиной
, будем откладывать на волновых
нормалях отрезки с длиной 
 . Геометрическое место концов таких
отрезков есть поверхность равной разности фаз между волнами, которые могут
распространяться вдоль одной и той же волновой нормали. Она и называется
изохроматической поверхностью. Придавая
. Геометрическое место концов таких
отрезков есть поверхность равной разности фаз между волнами, которые могут
распространяться вдоль одной и той же волновой нормали. Она и называется
изохроматической поверхностью. Придавая 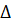
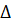 всевозможные значения, получим
семейство изохроматических поверхностей с общим центром О. Линии, получающиеся
от сечения такого семейства плоскостями, называются изохроматическими линиями,
или изохроматами. Очевидно, изохроматы есть линии постоянной разности фаз между
соответствующими волнами, которые могут распространяться вдоль одной и той же
волновой нормали.
всевозможные значения, получим
семейство изохроматических поверхностей с общим центром О. Линии, получающиеся
от сечения такого семейства плоскостями, называются изохроматическими линиями,
или изохроматами. Очевидно, изохроматы есть линии постоянной разности фаз между
соответствующими волнами, которые могут распространяться вдоль одной и той же
волновой нормали.
Для одноосного кристалла
изохроматическая поверхность есть поверхность вращения вокруг оптической оси
(рис.5). В направлении оптической оси она уходит в бесконечность, так как для
этого направления оба показателя преломления 
 и
и 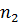
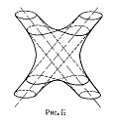
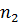 совпадают. В двуосных кристаллах
таких направлений два (рис.6). Это есть оптические оси, точнее - оси нормалей.
Мы рассмотрим качественные изображения.
совпадают. В двуосных кристаллах
таких направлений два (рис.6). Это есть оптические оси, точнее - оси нормалей.
Мы рассмотрим качественные изображения.
Интерферирующие волны возникают при
двойном преломлении одной и той же падающей волны. Волновые нормали
получившихся двух волн внутри кристаллической пластинки несколько отличаются
друг от друга по направлению. Но таким различием можно пренебречь, как при
замене точной формулы (1) приближенной (2). В этом приближении
интерференционные полосы можно отождествить с определенным семейством
изохромат. Представим, что на передней плоскости кристаллической пластинки К
(рис.4) помещена маленькая диафрагма. Примем центр этой диафрагмы за центр О
семейства изохроматических поверхностей. Задняя плоскость пластинки К пересечет
это семейство вдоль изохроматических линий. Эти линии в указанном выше
приближении будут совпадать с интерференционными линиями на задней поверхности
пластинки К. Если оптическая система дает изображение этой поверхности на
экране, то при этом получится и подобное изображение рассматриваемой системы
интерференционных линий. При другой фокусировке, из-за преломления волновых
нормалей при выходе из пластинки К, полного подобия между изохроматами и
интерференционными линиями на экране не будет. Однако существенно это не
сказывается на виде интерференционных полос. Изохроматы практически всегда
качественно верно передают форму интерференционных полос.
Форма изохромат и интерференционных
полос определяется симметрией кристалла и ориентацией его оптических осей. На
рис.7 показаны интерференционные полосы в случае пластинки одноосного
кристалла, вырезанной перпендикулярно к оптической оси. В соответствии с осевой
симметрией они имеют форму концентрических кругов. Картина получена в
скрещенных николях.
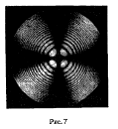
Кольца пересечены темным крестом.
Происхождение его весьма простое. На пластинку К падает линейно поляризованный
свет. Рассмотрим плоскость главного сечения и плоскость, перпендикулярную к
ней. Пусть обе плоскости пересекаются вдоль оси вращения системы. Лучи в этих
плоскостях не испытывают двойного преломления, интерференции в таких случаях не
возникает. После прохождения через пластинку обе системы лучей остаются линейно
поляризованными с сохранением прежнего направления колебаний. Лучи с такими
колебаниями гасятся николем-анализатором. Вокруг прямых, по которым
рассматриваемые плоскости пересекаются с плоскостью экрана, и формируется
темный крест. Если николи перевести в параллельное положение, то вся картина
сменяется дополнительной, в частности, черный крест заменяется белым.

Если в предыдущем опыте пластинку К
заменить двумя сложенными вместе пластинками из правого и левого кварца,
вырезанными перпендикулярно к оптической оси, то получаются спиралеобразные
интерференционные картины, называемые спиралями Эйри (рис.8). Их происхождение
связано с тем, что кварц вращает плоскость поляризации. Для правого кварца это
вращение происходит в одну сторону, а для левого - в противоположную.
Хроматическая поляризация
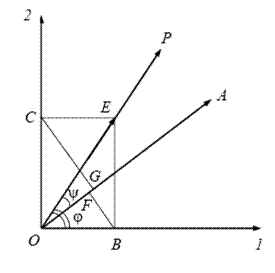
Интерференцию поляризованных волн
так же можно наблюдать на установке, с помощью которой получаются эллиптически
поляризованные волны (рис. 9): необходимо иметь две волны, с взаимно
перпендикулярными плоскостями поляризации и постоянной разностью фаз.
Естественный свет направляется на поляризатор П, потом проходит через
анизотропную пластинку Г, вырезанную параллельно оптической оси. В этой
пластинке образуются две волны: обыкновенная волна (о) с плоскостью
поляризации, перпендикулярной плоскости чертежа, и необыкновенная волна (е) с
плоскостью поляризации, совпадающей с плоскостью чертежа. Разность фаз между
этими волнами 
 (d - толщина
пластинки). Таким образом, после пластинки образуются две волны с постоянной
разностью фаз и с перпендикулярными плоскостями поляризации, т.е. образуется
эллиптически поляризованная волна. Если удалить поляризатор П, то эллиптически
поляризованной волны не образуется. Это объясняется тем, что в естественном
свете цуги волн имеют различные начальные фазы, вследствие чего ориентация
эллипсов от различных цугов будет произвольной. Поляризатор П необходим для
получения поляризованной волны с усредненной начальной фазой.
(d - толщина
пластинки). Таким образом, после пластинки образуются две волны с постоянной
разностью фаз и с перпендикулярными плоскостями поляризации, т.е. образуется
эллиптически поляризованная волна. Если удалить поляризатор П, то эллиптически
поляризованной волны не образуется. Это объясняется тем, что в естественном
свете цуги волн имеют различные начальные фазы, вследствие чего ориентация
эллипсов от различных цугов будет произвольной. Поляризатор П необходим для
получения поляризованной волны с усредненной начальной фазой.
На рис. 10 плоскость чертежа
перпендикулярна падающему пучку света. Обозначим: 1 и 2 - разрешенные
направления колебаний, задаваемые кристаллической пластинкой (оси ох и оу); ОР
и ОА - направления световых колебаний, пропускаемых поляризатором Р и
анализатором А соответственно; ОЕ=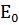
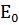 - амплитуда электрического вектора
падающей волны, направленной параллельно ОР; ОВ и ОС - проекции вектора
- амплитуда электрического вектора
падающей волны, направленной параллельно ОР; ОВ и ОС - проекции вектора 
 на главные направления 1 и 2
кристалла; OF и OG -
составляющие колебаний, пропускаемые всей системой;
на главные направления 1 и 2
кристалла; OF и OG -
составляющие колебаний, пропускаемые всей системой; 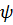
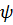 - угол между плоскостями
пропускания поляризатора и анализатора. Амплитуда компонент световой волны в
направлениях 1 и 2 соответственно равна
- угол между плоскостями
пропускания поляризатора и анализатора. Амплитуда компонент световой волны в
направлениях 1 и 2 соответственно равна 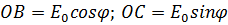
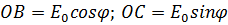 .
.
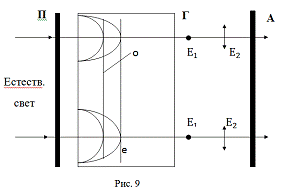
Анализатор пропускает лишь
составляющие, параллельные ОА, амплитуды которых станут меньше и соответственно
будут равны:
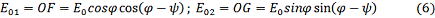
Две волны, вышедшие из анализатора,
имеют одну и ту же плоскость поляризации и получены из одного и того же пучка
первоначального плоскополяризованного света, и могут интерферировать друг с
другом.

Суммарная интенсивность, получаемая
в результате интерференции двух монохроматических волн с разностью фаз 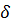
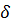 , определяется соотношением
, определяется соотношением

 ,
,

 ,
,
где использовано тождество 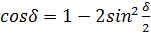
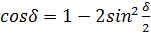 и введено обозначение
и введено обозначение 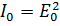
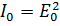 .
.
Рассмотрим пример, когда плоскости
пропускания анализатора А и поляризатора Р взаимно перпендикулярны, т.е. 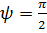
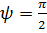 . В этом случае общее выражение для
интенсивности прошедшего света имеет вид
. В этом случае общее выражение для
интенсивности прошедшего света имеет вид

Интенсивность прошедшего света
минимальна (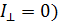
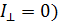 при выполнении следующих условий.
Первое условие минимума:
при выполнении следующих условий.
Первое условие минимума:
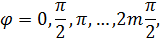
где m - целое
число, т.е. когда направления колебаний, пропущенных поляризатором и
анализатором, совпадают с одним из главных (разрешенных) направлений в
кристаллической пластинке. В этом случае в кристаллической пластинке разложения
света на две компоненты не происходит (вторая волна в ней уже не возникает) и
темнота будет наблюдаться для всех длин волн, поскольку состояние поляризации
света, вышедшего из поляризатора, не изменится в результате прохождения сквозь
пластинку. Интерференция отсутствует, свет вообще не пройдет через систему,
какова бы ни была толщина пластинки (
 .
.
Второе условие минимума
интенсивности для монохроматического света:

 (7)
(7)
Условие (7) не может одновременно выполняться
для всех длин волн. Поэтому при использовании белого света в отличие от первого
случая темнота наблюдается лишь для ряда длин волн, которые укладываются целым
числом волн в данной разности хода.
Интенсивность прошедшего света максимальна при
следующих условиях. Первое условие максимума:

т.е. в том случае, когда пластинка ориентирована
так, что ее главные разрешенные направления делят углы между главными
направлениями поляризатора и анализатора пополам:

 и
и 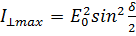
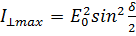 .
.
Вторым условием максимума для
монохроматического света будет
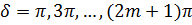
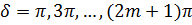 , т.е.
, т.е. 
 .
.
При выполнении этих условий
направление колебаний света, прошедшего через пластинку, повернется на 90
 и будет параллельно анализатору.
Таким образом, весь свет, пропущенный поляризатором, пройдя через анализатор,
окажется наиболее насыщенным. Отсюда следует, что действие кристаллической
пластинки сводится к дополнительному пропусканию или задержке некоторого
окрашенного света.
и будет параллельно анализатору.
Таким образом, весь свет, пропущенный поляризатором, пройдя через анализатор,
окажется наиболее насыщенным. Отсюда следует, что действие кристаллической
пластинки сводится к дополнительному пропусканию или задержке некоторого
окрашенного света.
Заключение
Явления интерференции поляризованных
волн в истории оптики имели большое значение для выяснения фундаментального
вопроса о природе световых колебаний. Они исследовались в классических опытах
Френеля и Араго. Волны, исходящие от независимых источников света,
интерферировать не будут, даже если они предварительно пропущены через
поляризационное приспособление. Для интерференции необходима когерентность. Но
результат интерференции линейно поляризованных волн зависит от угла между
плоскостями световых колебаний. Интерференционные полосы наиболее контрастны,
когда плоскости колебаний параллельны. Интерференция никогда не наблюдается,
если волны поляризованы во взаимно перпендикулярных плоскостях. Это и было
впервые установлено в опытах Френеля и Араго. Отсюда Френель пришел к
заключению о поперечности световых колебаний.
Список литературы
2. Ландсберг Г.С. Оптика, М.,
1976.
. Сивухин Д.В. Общий курс
физики. Оптика, т.4, М., 1985.
. Шерклифф У. Поляризованный
свет, М., 1965.
. Матвеев А.Н. Оптика, М.,
1985.