Гидродинамика. Уравнение Эйлера и Бернулли. Гидродинамическое подобие потоков. Потери напора и энергии в потоке

Гидродинамика. Уравнение Эйлера и Бернулли. Гидродинамическое подобие потоков. Потери напора и энергии в потоке

Министерство сельского хозяйства и продовольствия Республики Беларусь

Учреждение образования

"ГРОДНЕНСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ"

Кафедра технического обеспечения производства и переработки продукции животноводства

Гидродинамика. Уравнение Эйлера и Бернулли. Гидродинамическое подобие потоков. Потери напора и энергии в потоке

Гродно 2014

Содержание

Введение

1 Описание и аналитические исследования гидродинамических процессов

1.1 Дифференциальные уравнения движения Эйлера

1.2 Уравнение Бернулли

1.3 Гидродинамическое подобие потоков

2. Описание и анализ аппаратов гидродинамических процессов

3. Инженерно-технологический расчет

Список использованной литературы и информационных источников

Введение

Гидродинамические аппараты эжекторного типа получили широкое распространение практически во всех отраслях техники. Эжекторы (струйные насосы) распространены во многих отраслях промышленности: энергетике, металлургии, машиностроении, химической и пищевой. Их принципиальной особенностью является повышение давления эжектируемого потока без непосредственной затраты механической энергии при исключительной простоте конструкции (отсутствуют подвижные механические части), что значительно упрощает обслуживание и ремонт.

Эжекторными называются устройства, в которых осуществляется процесс эжекции, заключающийся в передаче кинетической энергии одного потока другому потоку путем непосредственного контакта (смешения). Например, эффективность работы насоса-смесителя оказывается наивысшей, так как с пользой расходуется не только энергия пассивного потока, но и остаточная энергия активного потока.

Смешиваемые потоки могут находиться в одной и той же фазе (жидкой, паровой, газовой) или в разных фазах (например, пар и жидкость, газ и твердое тело и др.). В процессе смешения фазовое состояние смешиваемых потоков может оставаться неизменным или же изменяться (например, пар может превратиться в жидкость). Поток, вступающий в процесс смешения с большей скоростью, называется активным, с меньшей скоростью - пассивным.

Для получения гетерогенных смесей со строго дозируемым количеством добавок можно использовать эжектор, в котором активный поток (высоконапорный) является несущей средой (например, жидкость), а пассивный поток (эжектируемая среда) - необходимые для получения смеси добавки. Применение эжектора в качестве насоса-смесителя позволит получить высококачественные смеси из жидкостей, газов, многофазных сред (газ-жидкость) и твердых сыпучих материалов. При этом если совместить работу эжектора-смесителя с кавитацией в его проточной части, то можно получить наиболее качественные смеси, которые обладают высокой однородностью и стойкостью к расслоению.

В данном проекте рассмотрена и теоретическая база, описывающая и объясняющая принципы гидромеханических и гидродинамических процессов, происходящих в струйных насосах, а также в графической части проекта приведены принципиальные схемы эжекторов и в качестве примера - чертеж пароструйного эжектора типа ЭП-3-600, используемый для откачки пара из паровых турбин ядерных и тепловых электростанций.

1. Описание и аналитические исследования гидродинамических процессов

Движение жидкостей и газов характеризуется скоростями w и ускорениями а частиц в различных точках потока жидкости, а также давлением р в этих точках. Различают установившееся и неустановившееся движение жидкостей. Установившимся движением называют такое, при котором скорость частиц, плотность, температура давление и расход жидкости в каждой фиксированной точке пространства не изменяются во времени.

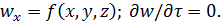
Пусть, например, жидкость движется в трубопроводе переменного сечения. Скорость жидкости при этом то увеличивается, то уменьшается в зависимости от места расположения сечения в трубопроводе, но в каждом фиксированном сечении она неизменна во времени. Такое движение называют стационарным. При неустановившемся, или нестационарном, движении все факторы изменяются во времени, т. е. скорость является функцией не только координаты, но и времени:

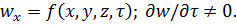
Примером неустановившегося движения может служить истечение жидкости из резервуара при переменном ее уровне в резервуаре.

Установившееся движение потоков характерно для непрерывных процессов, а неустановившееся - для периодических.

Установившееся движение может быть равномерным и неравномерным.

Равномерное движение имеет место, когда скорость, давление, глубина и форма потока не меняются по длине потока. Примером равномерного движения является движение жидкости в трубопроводе постоянного сечения с постоянной скоростью.

Неравномерное движение происходит, например, в конической трубе, когда скорость, давление и глубина потока меняются по длине трубы.

Если рассмотреть поперечное сечение потока жидкости и мысленно представить его состоящим из отдельных элементарных струек, то окажется, что частицы жидкости, находящиеся а струйках, расположенных на различном расстоянии от оси потока, движутся с различными скоростями.

Скорость движения жидкости буден максимальной по оси потока и минимальной в струйках у стенки трубы. Распределение скоростей в потоке зависит от режима движения жидкости.

В технике оперируют не локальными скоростями частиц жидкости, а средней скоростью потока.

Эта скорость представляет собой отношение секундного объемного расхода V_сек к площади поперечного сечения потока F:

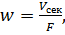 (1.1)

откуда V_сек = wF, а массовый расход (в кг/c)

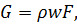
где ρ - плотность жидкости, кг/м³.

Неустановившиеся режимы движения реализуются главным образом в периодических процессах или возникают кратковременно при пусках, остановках, а также изменениях режима работы аппаратов непрерывного действия. Исследование механизма движения вязкой жидкости показало, что имеют место два режима, резко отличающихся один от другого. Это различие подтверждено в 1883 г. опытами английского физика О. Рейнольдса. При малых скоростях струйка чернил 1 (рис.1.1) движется параллельно стенкам трубки 2. Этот режим движения называют ламинарным, или слоистым ("ламина" в переводе с латинского означает слой).

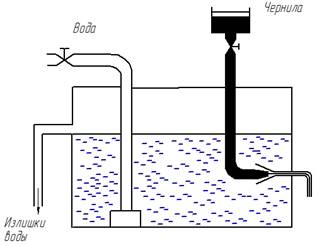
Рис 1.1 Схема опыта Рейнольдса: 1 - струйка чернил; 2 - трубка.

При увеличении скорости движения жидкости линия тока струйки закручивается в виде вихря, а при еще большей скорости движение становится неупорядоченным, частицы движутся по хаотическим траекториям. Линии тока в трубке исчезают в беспорядке бурного турбулентного движения. Этот режим называется турбулентным (от латинского "турбулентус" - беспорядочный). Исходя из опытных данных и некоторых теоретических соображений О. Рейнольдс установил общие условия, при которых возможно существование того или другого режима и переход из одного режима в другой, а именно, что характер движения жидкости зависит от вязкости μ, скорости ее движения w, плотности жидкости ρ и диаметра трубки d. Для характеристики режима движения введен безразмерный комплекс, учитывающий влияние перечисленных факторов. Этот комплекс впоследствии был назван критерием Рейнольдса:

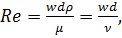 (1.2)

где ν - кинематическая вязкость жидкости.

Границы существования того или иного режима определяются двумя критическими значениями критерия Рейнольдса: нижним Re_кр.н и верхним Re_кр.в. При Rе < Re_кр.н всегда имеет место ламинарный режим; при Rе > Re_кр.в режим устойчиво турбулентный. Для воды Re_кр.н = 2320 и Re_кр.в = 10000.

В диапазоне Re_кр.н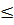Re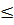Re_кр.в режим движения жидкости чаще всего турбулентный, однако он неустойчивый. Поэтому этот режим называется переходным, хотя точнее этот диапазон значений критерия Рейнольдса следовало бы называть переходной зоной.

В критерий Рейнольдса входит величина d - это определяющий размер канала, по которому течет жидкость.

Для круглой трубы

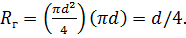
Если труба не круглого сечения, то вводится понятие гидравлического радиуса

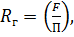
где F - площадь сечения потока; П - смоченный периметр.

Смоченным периметром П называют линию контакта (соприкосновения) живого сечения потока жидкости со стенками, вдоль которых движется поток. Для открытого канала (рис. 1.2)

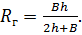
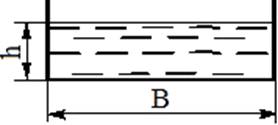
Рис 1.2 Схема открытого канала.

В расчетах часто используют понятие эквивалентного диаметра:

 (1.3)

Дифференциальные уравнения движения Эйлера

Уравнения движения Л. Эйлера устанавливают связь между давлением и скоростью движения жидкости в любой точке потока.

Рассмотрим установившийся поток идеальной жидкости, которая движется без трения, т. е. не обладает вязкостью. Выделим в потоке элементарный параллелепипед объемом dV = dx dy dz, ориентированный относительно осей координат (см. рис. 1.3).

Проекции сил тяжести и давления, действующих на параллелепипед, составляют:

на ось х

,

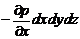на ось у

,

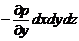на ось z

.

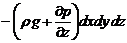Согласно основному принципу динамики, сумма проекций сил, действующих на движущийся элементарный объем жидкости, равна произведению массы жидкости на ее ускорение.

Масса жидкости в объеме параллелепипеда равна

Рис. 1.3. Схема к выводу дифференциальных уравнений равновесия Эйлера

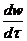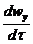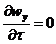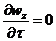Если жидкость движется со скоростью w, то ее ускорение равно , а проекции ускорения на оси координат: ,  и , где w_x, w_y и w_z - составляющие скорости вдоль осей х, у и z. Для установившегося потока в рассматриваемом случае ,  и . Производные же ,  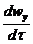и  отвечают изменению во времени значений w_x, w_y и w_z при перемещении частицы жидкости из одной точки пространства в другую. Тогда в соответствии с основным принципом динамики

,

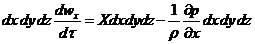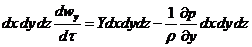, (1.5)

,

или после сокращения

,

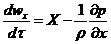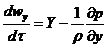, (1.6)

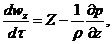
где субстанциональные производные соответствующих составляющих скорости

,

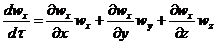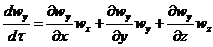, (1.7)

.

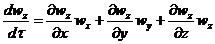Система уравнений (1.6) с учетом выражений (1.7) представляет собой дифференциальные уравнения движения идеальной жидкости Эйлера для установившегося потока.

При неустановившемся движении скорость жидкости изменяется не только при перемещении частицы потока из одной точки пространства в другую, но и с течением времени в каждой точке. Поэтому для неустановившихся условий они принимают вид

,

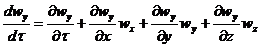, (1.8)

.

Система уравнений (1.6) с учетом выражений (1.8) представляет собой дифференциальные уравнения движения идеальной жидкости Эйлера для неустановившегося потока.

Система уравнений (1.6) является системой дифференциальных уравнений движения идеальной жидкости для установившегося потока. Эти уравнения были получены Л. Эйлером в 1755 г.

Из дифференциальных уравнений Эйлера легко полудить уравнение Бернулли, широко используемое в гидродинамике.

Уравнение Бернулли

Умножим левые и правые части каждого из членов уравнений (1.6) соответственно на dх, dу, dz и сложим почленно с учетом того, что

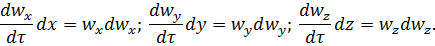
Тогда

 (1.9)

но

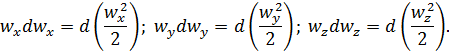
Тогда левую часть уравнения (1.9) можно представить в виде

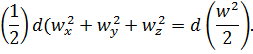
В правой части уравнения примем, что Xdx+Ydy+Zdz=dU. Величина dU является некоторой силовой функцией и 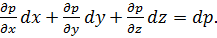 В окончательном виде получим основное уравнение гидродинамики

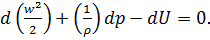 (1.10)

При действии только силы тяжести на поток жидкости силовая функция dU=-gdz и из (1.10) получим

Разделив каждый член этого уравнения на ускорение свободного падения g, будем иметь

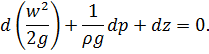
Но сумма дифференциалов есть дифференциал суммы и

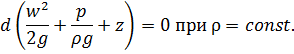
Тогда

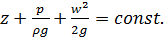 (1.11)

Уравнение (1.11) является уравнением Бернулли для идеальной жидкости.

Для двух поперечных сечений трубопровода 1-1 и 2-2 уравнение (1.11) можно записать так (рис 1.4):

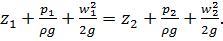 (1.12)

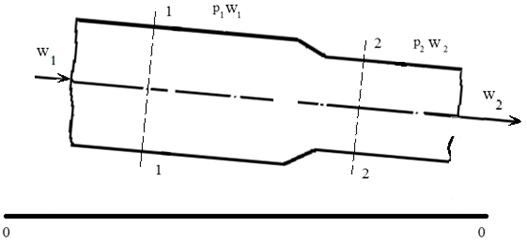
Рис 1.4 - Схема трубопровода

Величина  является полным гидродинамическим напором.

Здесь z, как раньше уже отмечалось, - нивелирная, или геомет-рическая, высота, р/(ρg) - статический пьезометрический напор, скоростной, или динамический, напор, который характеризует удельную кинетическую энергию в данной точке жидкости. Единицы измерения динамического напора, как и остальных членов уравнения Бернулли, 1 м или 1 Н∙м/Н.

Таким образам, из уравнений (1.11) и (1.12) следует, что при установившемся движении идеальной жидкости гидродинамический напор остается постоянным для любого сечения потока. Имея в виду энергетический смысл каждого члена уравнения Бернулли, можно утверждать, что при установившемся движении идеальной жидкости сумма потенциальной 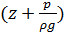 и кинетической  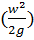энергии жидкости есть величина постоянная для любого поперечного сечения потока.

При изменении поперечного сечения потока происходит переход потенциальной энергии в кинетическую и наоборот. Уравнение Бернулли выражает частный случай закона сохранения энергии и является уравнением энергетического баланса потока идеальной жидкости.

Рассмотрим поток идеальной жидкости, движущейся в трубопро-воде переменного сечения. В сечениях 1-1 и 2-2 (рис. 1.5) нивелирные высоты будут равны соответственно z₁ и z₂, а площади поперечных сечений - f₁ и f₂. Установим в этих сечениях пьезометрические трубки и трубки Пито. Как известно, с помощью пьезомтрических трубок измеряют статический напор (линия Р-Р). 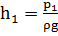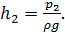Жидкость поднимается в пьезометрических трубках на высоты, соответствующие статическому напору  и  Трубки Пито представляют собой пьезометрические трубки, у которых

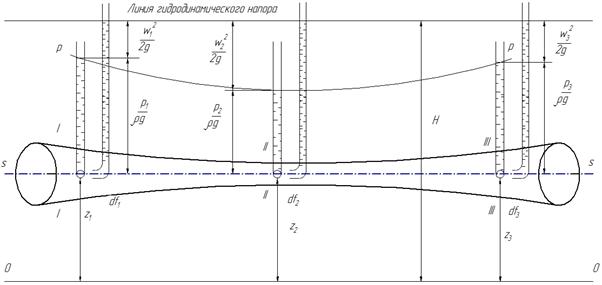
Рис 1.5 - Диаграмма Бернулли для идеальной жидкости

нижний конец загнут навстречу потоку жидкости. Используют трубки Пито для измерения полного гидродинамического напора.

Разность высот, измеряемых трубкой Пито и обычной пьезометрической трубкой, равна , представляет собой высоту, соответствующую скоростному напору.

Так как f₁>f₂, то согласно уравнению неразрывности потока 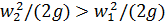. Но полный гидродинамический напор

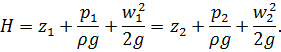
Зная z₁ и z₂, можно определить скоростной напор в каждом сечении по разности уровней жидкости в обычных пьезометрических трубках и трубках Пито.

Измерив высоту, соответствующую скоростному напору, можно найти скорость движения жидкости в той точке, в которой расположен загнутый наконечник трубки Пито:

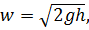
где h - высота, соответствующая скоростному напору.

Уравнение Бернулли для потока идеальной жидкости немного видоизменяется, т.к. реальная жидкость в отличие от идеальной обладает вязкостью. Вязкость обусловливает возникновение в потоке жидкости сил внутреннего трения, которые оказывают гидравлическое сопротивление движению жидкости. На преодоление возникающего сопротивления расходуется часть потенциальной энергии потока (так называемый потерян-ный напор). Поэтому общий гидродинамический напор будет непрерывно уменьшаться по длине потока.

Рассмотрим движение струйки вязкой жидкости в трубопроводе, изображенном на рис. 1.6.

Рис 1.6 - Диаграмма Бернулли для вязкой жидкости

В общем случае баланс энергии при движении вязкой жидкости запишется так:

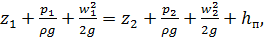 (1.13)

где h_п - потерянный напор, который характеризует энергию, израсходованную на преодоление гидравлического сопротивления.

Из уравнения (1.13) получим

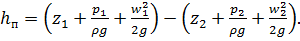 (1.14)

Пьезометрическим уклоном называют падение потенциальной энергии на единицу длины потока:

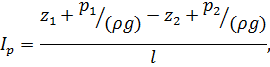
где l - расстояние между сечениями I-I и 2-2 на рис. 1.6.

Гидродинамический (гидравлический) уклон представляет собой падение гидродинамического напора также на единицу длины потока:

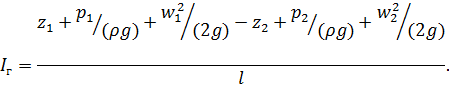
Для горизонтального постоянного сечения трубопровода w₁=w₂; z₁=z₂. В этом случае уравнение (1.14) можно переписать так:

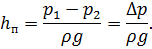
Таким образом, движущая сила - перепад давлений - расходуется на преодоление гидравлического сопротивления, а гидродинамический и пьезометрический уклоны одинаковы по величине и направлению.

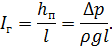
Гидродинамическое подобие потоков

Движение вязкой жидкости, как и любое сложное явление природы, может быть описано чисто теоретически с помощью дифференциальных уравнений. Эти уравнения описывают целый класс однородных по своей сущности явлений, и для применения их к конкретному условию они должны быть ограничены так называемыми условиями однозначности (геометрическими, физическими, граничными и начальными). Сложность основных уравнений гидродинамики, например уравнений Навье-Стокса, приводит к тому, что для многих практических задач не удается найти точное аналитическое решение, или же оно оказывается очень громоздким.

Совокупность параметров, обуславливающих какой-либо гидродинамический процесс, можно рассматривать как конкретное решение дифференциальных уравнений этого процесса. Ему соответствует вполне конкретные начальные и граничные условия. Они представляют собой зависимости или константы, определяющие физические параметры в начальный момент и на границах во время движения. Следовательно, не только уравнения процесса, но также безразмерные формы начальных и граничных условий подобных потоков должны быть одинаковыми. Имея это в виду, запишем уравнения Навье-Стокса для несжимаемой жидкости:

где р - давление; μ - динамическая вязкость; w - скорость; ρ - плотность; τ - время.

В этом уравнении первый член характеризует изменение давления потока в направлении оси абсцисс, второй член - силу трения, третий - силу тяжести, четвертый и пятый - силы инерции. Учитывая физический смысл членов уравнения, запишем

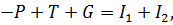
где Р - сила давления; Т - сила трения; G - сила тяжести; I₁ и I₂ - силы инерции.

При расчете трубопроводов представляют интерес соотношения следующих сил: давления и инерции Р/I₁, инерции и трения I₁/Т, тяжести и инерции G/I₁ и, наконец, соотношение инерционных сил I₁/I₂.

Применим метод получения критериев подобия. Из соотношения сил инерции и трения получим безразмерный комплекс w_xρ/μ, который называется критерием Рейнольдса и характеризует гидродинамическое подобие:

Здесь d - диаметр трубопровода; d является характерным линейным размером.

Из соотношения сил давления и инерции получим критерий Эйлера:

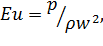
а из соотношения сил тяжести и инерции - критерий Фруда:

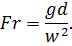
Отношение сил инерции позволяет получить критерий гомохронности Ho=wτ/d, который характеризует временнόе подобие в нестационарных процессах.

Полученные критерии подобия, за исключением критерия Эйлера, состоят только из параметров, входящих в условия однозначности, следовательно, они являются определяющими, а критерии Эйлера - определяемым (давление не входит в условия однозначности и является искомой величиной).

На основании второй теоремы подобия связь между критериями представим в виде критериального уравнения

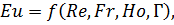
где Г=l/d - параметрический критерий; l - длина трубопровода.

Для стационарного процесса из уравнения следует исключить критерий гомохронности Но:

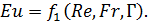В случае развитого турбулентного режима силы тяжести не оказывают влияния на движение жидкости и уравнение имеет вид

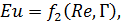 (1.15)

или

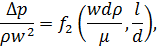
где Δр - потерянный напор в трубопроводе длиной l, H/м².

Умножим и разделим правую часть уравнения на 2.

Тогда Δp=f₃(wdρ/μ; l/d)(ρw²/2).

Вынесем симплекс l/d из-под знака функции:

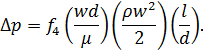
Обозначим f₄(wdρ/μ) через λ и окончательно получим уравнение, которое называется уравнением Дарси - Вейсбаха и является основным при расчете трубопроводов:

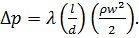 (1.16)

Если разделим левую и правую части уравнения (1.16) на ρg, то получим потерянный напор в трубопроводе (в м)

 (1.17)

Коэффициент гидравлического сопротивления λ в этих уравнениях в общем случае зависит от режима движения жидкости н относительной шероховатости трубы.

Вид расчетной формулы для коэффициента гидравлического сопротивления определяют на основании экспериментальных данных [5].

2. Описание и анализ аппаратов гидродинамических процессов

Эже́ктор - (от éjecter - выбрасывать от лат. ejicio) - устройство, в котором происходит передача кинетической энергии от одной среды, движущейся с большей скоростью, к другой. Эжектор, работая по закону Бернулли, создаёт в сужающемся сечении пониженное давление одной среды, что вызывает подсос в поток другой среды, которая затем переносится и удаляется от места всасывания энергией первой среды.

Эжекторы используются в струйных насосах, например водоструйных, жидкостно-ртутных, паро-ртутных, паромасляных.

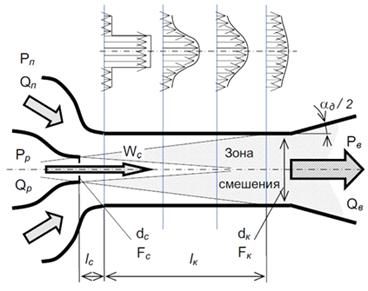
Рис 2.1 - Схема эжектора,

где l_к - длина камеры смешения (КС); l_с - расстояние от КС до сопла; 𝛼_д - угол раскрытия; n_д - угол уширения диффузора; Р_р - давление, подаваемое насосом; Q_p - расход активной струи; Р_n - давление на входе подсасываемой жидкости, Р_в - на выходе из эжектора; F_k и F_c - соответственно площади сечений в конце КС и среза сопла; W_с - скорость истечения струи; d_c - диаметр среза сопла

К газоструйным эжекторам относятся струйные аппараты со степенью сжатия более 2,5. При такой степени сжатии оптимальной является коническая форма камеры смешения. Наибольшее распространение газоструйные эжекторы получили в конденсационных установках паровых турбин, где пароструйные эжекторы служат для создания и поддержания давления в конденсаторе около 3-10 кПа, а также в пароэжекторных холодильных установках, где для охлаждения воды до 4-6 °С необходимо поддерживать давление в испарителе около 1 кПа.

Для увеличения производительности и сохранения большой степени сжатия в газоструйных эжекторах камера смешения в этих аппаратах выполняется из двух частей: развитой конической сужающейся части (конфузора) и последующей цилиндрической части (горловины).

На рис. 2.2 схематически изображен профиль проточной части эжектора этого типа и указаны основные обозначения. Выходное сечение рабочего сопла условно совмещено с входным сечением камеры смешения, состоящей из конической и цилиндрической частей:

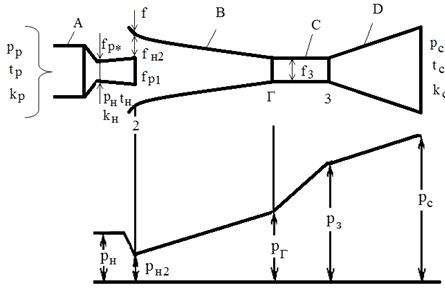
Рис 2.2 - Профиль проточной части и изменение давления по длине эжектора: А - рабочее сопло; В - конический участок камеры смешения; С - цилиндрический участок КС; D - диффузор.

Согласно условиям f_р2=f_р1; w_р2=w_р1 при расчетном режиме р_р2=р_р1=р_н

β = f₂/f₃ - отношение сечений начала и конца конической части камеры смешения;

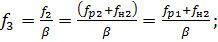 (2.1)

П_3Г=р_Г/р₃ - отношение давлений в начале и в конце цилиндрической части камеры смешения. Угол конусности конфузора на основании многочисленных испытаний, проведенных в основном турбостроительными заводами - изготовителями пароструйных эжекторов конденсационных установок, обычно принимается равным 5-7°, значения β=f₂/f₃ лежат в пределах 2-3. Газоструйные эжектора без диффузора используются в случаях, когда необходимо получить после эжектора сжатый поток, движущийся с большой скоростью. В этом случае давление в конце цилиндрической камеры смешения р₃ устанавливается равным давлению р_с в пространстве, куда вытекает поток. Скорость смешанного потока на выходе из камеры равна λ_сз. Достижимые коэффициенты инжекции и степени сжатия струйных эжекторов без диффузоров меньше, чем для аппаратов с диффузорами. Основной геометрический параметр "бездиффузорного" газоструйного эжектора определяется расчетом.

Пароструйные эжекторы,. служащие для отсоса паровоздушной смеси из конденсатора, при нормальной работе турбины должны обеспечить общую степень повышения давления примерно 20-30 (с 3-5 до 100 кПа). Поэтому они выполняются, как правило, двух- или трехступенчатыми (см. рис. 2.3). В первой ступени давление отсасываемой из конденсатора паровоздушной смеси повышается в 4-5 раз, например с 4 до 20 кПа, после чего она поступает в промежуточный холодильник, а затем во вторую ступень эжектора, где давление ее повышается до атмосферного.

Рис. 2.3 - Принципиальная схема трехступенчатой паровоздушной струйной установки:

Э₁-Э₃ - струйные эжекторы соответственно первой, второй и третьей ступеней; X1 - ХЗ - холодильники соответственно первой, второй и третьей ступеней; К - конденсатор, из которого отсасывается паровоздушная смесь; П - коллектор рабочего пара; Д₁-Д₃ - дренажи конденсата из холодильников соответственно первой, второй и третьей ступеней.

В трехступенчатом эжекторе сжатие смеси протекает аналогично, с той только разницей, что оно распределяется между тремя последовательно включенными ступенями, причем и в этом случае за каждой ступенью эжектора имеются холодильники. Характеристики многоступенчатого эжектора определяются основными размерами проточной части ступеней эжектора и эффективностью работы промежуточных холодильников.

В условиях эксплуатации основными причинами, вызывающими изменения давления всасывания эжектора, являются изменения расхода отсасываемого воздуха и температуры паровоздушной смеси. Вследствие этого наиболее удобными для практических целей являются характеристики эжектора, представленные в форме зависимости давления всасывания р_в перед ступенью эжектора от расхода сухого воздуха G_B при различных температурах отсасываемой паровоздушной смеси t_см (рис. 2.4). Аналогичный характер имеет характеристика эжектора при отсасывании сухого воздуха (рис. 2.5).

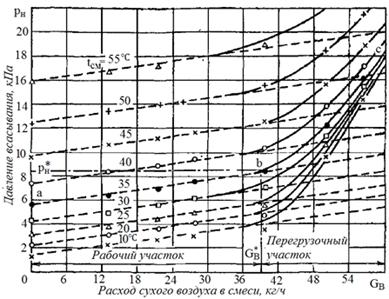
Рис. 2.4. Характеристика эжектора ЭП-2-400 при отсасывании насыщенной паровоздушной смеси:

t_см - температура смеси; пунктирная линия - расчетные характеристики при объемной производительности эжектора V_H = 1400 м³/ч.

Рис.2.5. Характеристики пароструйных эжекторов ЛМЗ при отсасывании сухого воздуха (по заводским данным):

Устройство и принцип действия паростуйного эжектора типа ЭП-3-600: пароструйный эжектор состоит из собранных последовательно на корпусе водяной камеры трёх эжекторов и трёх кожухотрубных конденсаторов. Эжектируемая паровоздушная смесь из конденсатора паровой турбины подводится к всасывающему патрубку первой ступени. Рабочий пар, подаваемый в сопло эжектора, разгоняется в нем до сверхзвуковой скорости, захватывает в приёмной камере паровоздушную смесь и увлекает её в камеру смешения эжектора, при этом давление эжектируемой паровоздушной смеси на выходе из эжектора увеличивается до 5 раз. Далее паровоздушная смесь из эжектора первой ступени подаётся в конденсатор первой ступени, в котором большая часть водяного пара (до 95%) конденсируется. В приёмный патрубок эжектора второй ступени засасываются паровоздушная смесь из конденсатора первой ступени. Процесс повторяется. Конденсат пара сливается через патрубки в нижней части конденсаторов [6]. Чертеж эжектора типа ЭП-3-600 представлен в графической части.

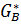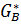Характеристика эжектора при отсасывании им сухого воздуха или паровоздушной смеси определенной температуры состоит из двух различных участков. На первом участке, отвечающем изменению расхода воздуха от нуля до некоторого значения  и называемом рабочим (участок ab, рис. 2.4), характеристики сравнительно пологие, на втором участке, отвечающем G_B> и называемом перегрузочным (участок bc), они значительно более крутые.

Массовая производительность эжект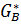ора , превышение которой при данных условиях работы эжектора вызывает его перегрузку, называется максимальной рабочей производительностью эжектора.

Два участка характеристики эжектора соответствуют двум различным режимам работы его первой ступени: предельному и допредельному, а переход от одного из этих режимов к другому зависит от того, является ли действительное противодавление первой ступени большим или меньшим, чем ее предельное противодавление (р_с)_пр. На рис. 2.6 вверху схематически представлена серия характеристик р_с = f (u) при различных давлениях инжектируемого пара р_н и постоянном давлении рабочего пара р_р. Линия ab есть линия предельных противодавлений; она определяет переход от допредельного режима к предельному.

На рис. 2.6 внизу представлена зависимость давления всасывания от коэффициента инжекции. При работе эжектора на предельном режиме существует однозначная зависимость давления всасывания от коэффициента инжекции (cd, рис. 2.6).

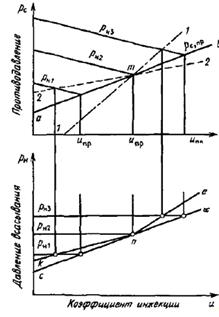
Рис 2.6 - Характеристика первой ступени эжектора

Режим работы каждой последовательно включенной ступени эжектора зависит от фактического противодавления, которое устанавливается после ее диффузора и которое в свою очередь зависит от режима работы эжекционной установки в целом.

На рис. 2.6 представлены для эжектора первой ступени зависимости давления всасывания от коэффициента инжекции для двух характерных случаев:

) наклон линии фактических противодавлений (1-1) больше наклона линии предельных противодавлений (ab). Эжектор при коэффициентах инжекции больших, чем в точке пересечения этих линий (m), работает на допредельном режиме, а при коэффициентах инжекции меньших, чем в точке m,- на предельном. При этом, как видно из рис. 2.6, на участке u<u_m давление всасывания определяется предельным режимом, а при u>u_m давление всасывания оказывается выше, чем при работе на предельном режиме. Характеристика р_н = f (u) представляется ломаной линией сnе;

) наклон линии фактических противодавлений (2-2) меньше наклона линии предельных противодавлений ab. Эжектор работает на допредельном режиме при коэффициентах инжекции меньших, чем в точке пересечения m, а его характеристика р_н = f (u) на этом участке расположена выше предельной характеристики сn (линия kn); при u>u_m характеристика эжектора р_н = f (u) изображается линией nd.

В многоступенчатом эжекторе все ступени, кроме последней, работают в условиях переменного давления всасывания и противодавления. При этом, как правило, имеет место случай 1, т. е. наклон линии фактических противодавлений р_c = f (u) больше наклона линии предельных противодавлений. Последняя ступень работает с постоянным противодавлением, превышающим атмосферное лишь на небольшую величину, равную потере давления в концевом холодильнике и выхлопной линии. Возможны две схемы работы последней ступени (рис. 2.7):

) вся линия предельных противодавлений (ab) лежит выше атмосферной линии. В этом случае при любом коэффициенте инжекции эжектор работает с противодавлением ниже предельного и характеристика р_н = f (u) представлена линией cd (рис. 2.7, а);

) линия предельных противодавлений ab пересекает атмосферную линию в точке m (рис. 2.7, б). В этом случае характеристика р_н = f (u) представлена ломаной линией knd.

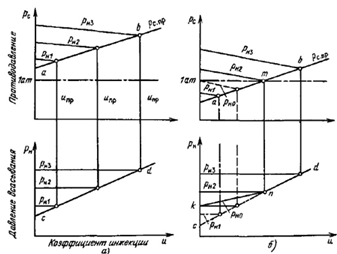
Рис 2.7 - Характеристики последней ступени эжектора:

а - предельное противодавление выше атмосферного; б - предельное противодавление ниже атмосферного (при малых u).

Последняя ступень должна, как правило, работать по схеме 1, т. е. вся линия предельных противодавлений должна лежать выше атмосферной линии. Рабочий участок характеристики определяется работой первой ступени эжектора на предельном режиме, а перегрузочная часть - переходом первой ступени на допредельный режим. При увеличении по какой-либо причине давления всасывания второй ступени (т. е. противодавления первой ступени) пересечение линий фактического и предельного противодавления происходит при меньшем коэффициенте инжекции, т. е. раньше наступает перегрузка эжектора. К такому же результату приводит снижение предельного противодавления первой ступени, например, в результате снижения давления рабочего пара.

По приведенным выше уравнениям может быть построен как рабочий, так и перегрузочный участки характеристики [5].

3. Инженерно-технологический расчет

Рис. 3.1 - Водоструйный насос

Требуется выкачивать G=215 дм³/мин раствора относительной плотности 1,06 из подвального бака водоструйным насосом (рис.1). Высота подъёма H=3,8 м. Давление воды перед насосом р_изб=1,9кгс/см² (~0,19 МПа). КПД насоса η=0,15. Сколько кубометров воды будет расходовать в 1 ч водоструйный насос [4]?

Переведем величины:

G = 215 дм³/мин = 12,9 м³/ч = 0,00618 м³/с; ρ_ж = 1,06×1000 = 1060 кг/м³.

Производимая насосом полезная работа (мощность):

N_пол = Gρ_жg/3600; (3.1)

N_пол = 12,9×1060×9,81×3,8/3600 = 141,6 (Вт).

Затрачиваемая насосом мощность:

гидродинамический бернулли паростуйный эжектор

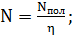 (3.2)

Напор рабочей воды перед насосом H_p:

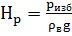; (3.3)

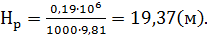
Расход рабочей воды составляет:

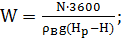 (3.4)

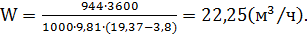
Ответ: 22,25 м³.

Список использованной литературы и информационных источников

1. Плаксин, Ю.М. Процессы и аппараты пищевых производств: учебники и учеб. пособия для студентов высш. учеб. заведений / Ю.М. Плаксин, Н.Н. Малахов, В.А. Ларин - 2-е изд., перераб. и доп. - М.: КолосС, 2007. - 760 с.: ил.

. Кавецкий, Г.Д. Процессы и аппараты пищевой технологии: учебники и учеб. пособия для студентов высших учебных заведений / Г.Д. Кавецкий, Б.В. Васильев - 2-е изд., перераб. и доп. - М.: Колос, 2000 - 551 с.

. Остриков, А.Н. Процессы и аппараты пищевых производств: учеб. для вузов: в 2 кн. / А.Н. Остриков, Ю.В. Красовицкий, А.А. Шевцов и др.; под ред. А.Н. Острикова. - СПб.: ГИОРД, 2006. - Кн. 1. - 632 с.: ил.

. Павлов, К.Ф. Примеры и задачи по курсу процессов и аппартов химической технологии: учебное пособие для вузов / К.Ф. Павлов, П.Г. Романков, А.А. Носков; под ред. чл.-корр АН СССР П.Г. Романкова - 10-е изд., перераб. и доп. - Л.: Химия, 1987. - 576 с.: ил.

. Соколов, Е.Я. Струйные аппараты / Е.Я. Соколов, Н.М. Зингер -3-е изд., перераб. - М: Энергоатомиздат, 1989.- 352 с.: ил.