Применение адаптивных фильтров в идентификации систем

Применение адаптивных фильтров в идентификации систем

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

( ФГБОУ ВПО )

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

ФАКУЛЬТЕТ ПРИКЛАДНОЙ МАТЕМАТИКИ, ИНФОРМАТИКИ И МЕХАНИКИ

КАФЕДРА ТЕХНИЧЕСКОЙ КИБЕРНЕТИКИ И АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

Применение адаптивных фильтров для идентификации систем

Курсовая работа

Выполнил:

студент 5-го курса в/о

Литикова А.С.

Научный руководитель:

д.ф.-м.н. Аверина Л.И.

Воронеж 2014

Содержание

Введение

. Основная идея адаптивной обработки сигнала

2. Алгоритмы адаптивной фильтрации

.1 Оптимальный фильтр Винера

.2 Адаптивный алгоритм LMS

.3 Детерминированная задача оптимальной фильтрации

.4 Адаптивный алгоритм RLS

.5 Алгоритм RLS с экспоненциальным забыванием

3. Адаптивные фильтры в идентификации систем

. Реализация моделей адаптивных фильтров, сравнение результатов

Выводы

Приложения

Библиографический список

Введение

Цифровая обработка сигналов в сложных радиоэлектронных системах характеризуются рядом особенностей, осложняющих решение радиотехнических задач. В высококачественных системах цифровой обработка сигналов часто ведется в условиях неопределенности системных характеристик. Априорная и текущая информация о параметрах системы является неполной. Кроме того, при эксплуатации системы параметры её объектов и среды функционирования могут изменяться непредвиденным заранее образом и тогда нестационарность выступает как один из видов неопределенности. Стохастичность поведения также является важной чертой, характеризующей обработку сигналов в сложных системах. Это обусловлено наличием источников случайных помех и всякого рода второстепенных (с точки зрения решения задачи) процессов с непредсказуемым поведением. Таким образом, стохастичность и нестационарность объектов и условий их функционирования определяют фактор сложности системы.

Одним из наиболее перспективных путей преодоления трудностей, порождаемых этим фактором сложности является применение методов адаптации. При адаптивной цифровой обработки информация об объекте и внешних воздействиях собирается в ходе обработки и используется для изменения параметров блоков обработки. Адаптивные устройства обработки сигнала действуют по принципу замкнутого контура. Входной сигнал фильтруется или взвешивается в программируемом фильтре для получения выходного сигнала, который затем сравнивается с полезным, стандартным или обучающим сигналом для нахождения сигнала ошибки. Затем этот сигнал ошибки используется для корректировки весовых параметров процессора обработки с целью постепенной минимизации ошибки. При этом адаптивной системе требуется минимальный объект исходной информации о поступающем сигнале.

Процессоры радиотехнической обработки можно разделить на два больших класса: адаптивные фильтры и адаптивные антенны. Адаптивные антенны осуществляют пространственную обработку сигнала с помощью антенной решетки, формируя диаграмму направленности таким образом, чтобы в ней создавался главный максимум в направлении прихода сигнала и происходила генерации нулей в направлении источников помех. В адаптивных цифровых фильтрах используется программируемый фильтр, частотная характеристика или передаточная функция которого изменяется, или адаптируется, таким образом, чтобы пропустить без искажения полезные составляющие сигнала и ослабить нежелательные сигналы или помехи, т.е. уменьшить искажения входного полезного сигнала. Адаптивный фильтр действует по принципу оценивания статистических параметров поступающего сигнала и подстройки собственной переходной характеристики таким образом. чтобы минимизировать некоторую функцию стоимости. Такие адаптивные фильтры часто используются для восстановления на выходах каналов сигналов с меняющимися во времени характеристиками.

Цель настоящей курсовой работы - исследовать и изучить научную литературу по рассматриваемой теме, исследовать работу основных алгоритмов адаптации (LMS-алгоритма, RLS-алгоритма и RLS-алгоритма с экспоненциальным забыванием) на примере идентификации фильтра 31-го порядка с импульсной характеристикой в виде экспоненциально затухающей синусоиды. Кроме того, будет рассмотрена реакция алгоритмов на скачкообразные изменения параметров системы.

1. Основная идея адаптивной обработки сигнала

Общая структура адаптивного фильтра показана на рис. 1. Входной дискретный сигнал х(k) обрабатывается дискретным фильтром, в результате чего получается выходной сигнал у(k). Этот выходной сигнал сравнивается с образцовым сигналом d(k), разность между ними образует сигнал ошибки е(k), Задача адаптивного фильтра - минимизировать ошибку воспроизведения образцового сигнала. С этой целью блок адаптации после обработки каждого отсчета анализирует сигнал ошибки и дополнительные данные, поступающие из фильтра, используя результаты этого анализа для подстройки параметров (коэффициентов) фильтра.

Рис. 1. Общая структура адаптивного фильтра.

Возможен и иной вариант адаптации, при котором образцовый сигнал не используется или требуемые параметры сигнала напрямую не могут быть измерены. Такой режим работы называется адаптацией по косвенным данным (blind adaptation) или обучением без учителя (unsupervised learning). Исследование последнего варианта адаптации не входит в рамки данной курсовой работы.

В качестве фильтра в структуре, показанной на рис. 1, чаще всего используется нерекурсивный цифровой фильтр. Одним из главных достоинств этого варианта является то, что нерекурсивный фильтр является устойчивым при любых значениях коэффициентов. Однако следует помнить, что алгоритм адаптации в любом случае вносит в систему обратную связь, вследствие чего адаптивная система в целом может стать неустойчивой.

Далее будут рассмотрены два адаптивных алгоритма с использованием образцового сигнала, часто применяемых на практике в различных системах обработки информации. Для упрощения математических выкладок предположим, что сигналы и фильтры являются вещественными. Однако результирующие формулы легко обобщаются на случай комплексных сигналов и фильтров.

2. Алгоритмы адаптивной фильтрации

.1 Оптимальный фильтр Винера

Прежде чем рассматривать собственно алгоритмы адаптации, необходимо определить те оптимальные параметры фильтра, к которым эти алгоритмы должны стремиться. Подход к задаче оптимальной фильтрации может быть как статистическим, так и детерминированным. Сначала рассмотрим статистический вариант.

Пусть входной дискретный случайный сигнал {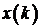} обрабатывается нерекурсивным дискретным фильтром порядка N, с коэффициентами {wn},=0,1,…,n. Выходной сигнал фильтра равен

. (1)

Кроме того, имеется образцовый (также случайный) сигнал d(k). Ошибка воспроизведения образцового сигнала равна

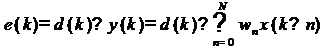 (2)

Необходимо найти такие коэффициенты фильтра {wn}, которые обеспечивают максимальную близость выходного сигнала фильтра к образцовому, то есть минимизируют ошибку 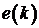. Поскольку  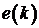также является случайным процессом, в качестве меры ее величины разумно принять средний квадрат. Таким образом, оптимизируемый функционал выглядит так

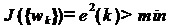
Для решения поставленной задачи перепишем (2) в матричном виде. Для этого обозначим вектор-столбец коэффициентов фильтра как w, а вектор-столбец содержимого линии задержки на k-м шаге как x(k):

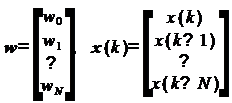
Тогда (2) примет вид:

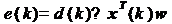. (3)

Квадрат ошибки равен

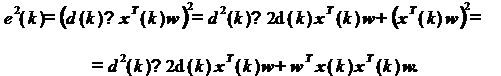
Статистически усредняя это выражение, получаем следующее:

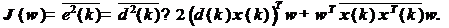    (4)

адаптивный сигнал фильтр алгоритм

Входящие в полученную формулу усредненные величины имеют следующий смысл:

ñ 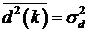 - средний квадрат образцового сигнала, не зависит от коэффициентов фильтра, потому может быть отброшено;

ñ 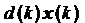 - вектор-столбец взаимных корреляций между k-м отсчетом образцового сигнала и содержимым линии задержки фильтра на k-м шаге. Будем считать случайные процессы x(k) и 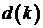 совместно стационарными, тогда вектор взаимных корреляций не зависит от номера шага k. Обозначим этот вектор как p:

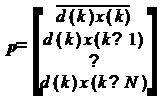
ñ 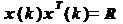 - корреляционная матрица сигнала, имеющая размер 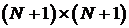. Для стационарного случайного процесса корреляционная матрица имеет вид матрицы Теплица, то есть вдоль ее диагоналей стоят значения корреляционной функции:

где 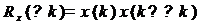 - корреляционная функция (КФ) входного сигнала.

С учетом введенных обозначений (4) принимает следующий вид:

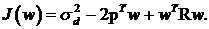 (5)

Данное выражение представляет собой квадратичную форму относительно w и потому при невырожденной матрице R имеет единственный минимум, для нахождения которого необходимо приравнять нулю вектор градиента:

 (6)

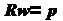 (7)

Умножив слева обе части на обратную корреляционную матрицу, получим искомое решение для оптимальных коэффициентов фильтра:

 (8)

Такой фильтр называется фильтром Винера. Подстановка (8) в (5) дает минимально достижимую дисперсию сигнала ошибки:

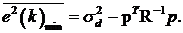 (9)

Несложно также показать, что  и 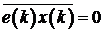 , то есть что сигнал ошибки для фильтра Винера не коррелирован со входным и выходным сигналами фильтра.

.2 Адаптивный алгоритм LMS

Один из наиболее распространенных адаптивных алгоритмов основан на поиске минимума целевой функции методом наискорейшего спуска. При использовании данного способа оптимизации вектор коэффициентов фильтра w зависит от номера итерации k: 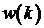, и должен на каждой итерации смещаться на величину, пропорциональную градиенту целевой функции в данной точке, следующим образом:

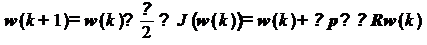,        (11)

где 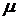- положительный коэффициент, называемый размером шага. Подробный анализ сходимости данного процесса приведен, например, в [фильтр Винера]. Показано, что алгоритм сходится, если

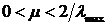,                                            (12)

где 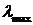- максимальное собственное число корреляционной матрицы R. Скорость сходимости при этом зависит от разброса собственных чисел корреляционной матрицы R- чем меньше отношение  тем быстрее сходится итерационный процесс.

Однако для реализации алгоритма требуется вычислять значения градиента, а для этого необходимо знать значения матрицы R и вектора р. На практике могут быть доступны лишь оценки этих значений, получаемые по входным данным. Простейшими такими оценками являются мгновенные значения корреляционной матрицы и вектора взаимных корреляций, получаемые без какого-либо усреднения:

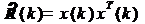
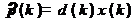
При использовании данных оценок формула принимает следующий вид:

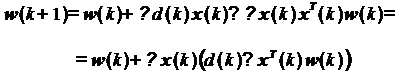                     (13)

Выражение, стоящее в скобках, согласно (3), представляет собой разность между образцовым сигналом и выходным сигналом фильтра на k-м шаге, то есть ошибку фильтрации е(k). С учетом этого, выражение для рекурсивного обновления коэффициентов фильтра оказывается очень простым:

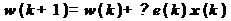                                      (14)

Алгоритм адаптивной фильтрации, основанный на данной формуле, получил название LMS (Least Mean Square, метод наименьших квадратов). Можно получить ту же формулу и несколько иным образом: использовав вместо градиента статистически усредненного квадрата ошибки 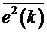 градиент его мгновенного значения .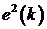

Анализ сходимости алгоритма LMS оказывается чрезвычайно сложной задачей, для которой не существует точного аналитического решения. Достаточно подробный анализ с использованием приближений приведен в книге С. Хайкина. Он показывает, что верхняя граница для размера шага 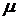 в данном случае является меньшей, чем при использовании истинных значений градиента. Эта граница примерно равна:

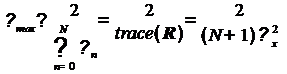         (15)

где 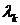 - собственные числа корреляционной матрицы R, а 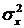 - средний квадрат входного сигнала фильтра.

На вышеприведенной формуле основан нормированный (normalized) LMS-алгоритм, в котором коэффициент на каждом шаге рассчитывается, исходя из энергии сигнала, содержащегося в линии задержки:

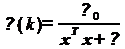                                         (16)

где µ0 - нормированное значение µ, лежащее в диапазоне от 0 до 2, а ε - малая положительная константа, назначение которой - ограничить рост µ при нулевом сигнале на входе фильтра.

Даже если LMS-алгоритм сходится, дисперсии коэффициентов фильтра при k→∞ не стремится к нулю - коэффициенты флуктуируют вокруг оптимальных значений. Из-за этого ошибка фильтрации в установившемся режиме оказывается больше, чем ошибка для винеровского фильтра :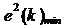

,

где Eex - средний квадрат избыточной ошибки (excess error) алгоритма LMS.

В той же книге С.Хайкина приводится следующая приближенная формула для так называемого коэффициента расстройства (misalignment), равного отношению средних квадратов избыточной и винеровской ошибок:

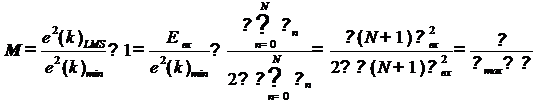 (17)

Значение коэффициента µ влияет на два главных параметра LMS-фильтра: скорость сходимости и коэффициент расстройки. Чем больше µ, тем быстрее сходится алгоритм, но тем больше становится коэффициент расстройки и наоборот.

Основным достоинством алгоритма LMS является предельная вычислительная простота - для подстройки коэффициентов фильтра на каждом шаге нужно выполнить N + 1 пар операций «умножение-сложение». Платой за простоту является медленная сходимость и повышенная (по сравнению с минимально достижимым значением) дисперсия ошибки в установившемся режиме.

.3 Детерминированная задача оптимальной фильтрации

При рассмотрении статистической задачи оптимизации входной сигнал считался случайным процессом и минимизировалась дисперсия ошибки воспроизведения образцового сигнала. Однако возможен и иной подход, не использующий статистические методы.

Пусть, как и раньше, обработке подвергается последовательность отсчетов {x(k)}, коэффициенты нерекурсивного фильтра порядка N образуют набор {wn}, а отсчеты образцового сигнала равны {d(k)}. Выходной сигнал фильтра определяется формулой (1), а ошибка воспроизведения образцового сигнала - формулой (2) или, в векторном виде, (3).

Теперь оптимизационная задача формулируется так: нужно отыскать такие коэффициенты фильтра {wn}, чтобы суммарная квадратичная ошибка воспроизведения образцового сигнала была минимальной:

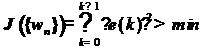       (18)

Для решения задачи необходимо перейти в формуле (3) к матричной записи вдоль координаты k, получив формулы для векторов-столбцов выходного сигнала у и для ошибки воспроизведения входного сигнала е :

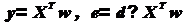 (19)

Здесь d - вектор-столбец отсчетов образцового сигнала, а X - матрица, столбцы которой представляют собой содержимое линии задержки фильтра на разных тактах:

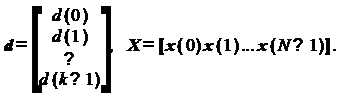
Выражение (18) для для суммарной квадратичной ошибки можно переписать в матричном виде следующим образом:

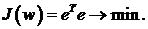 (20)

Подставив (19) в (20), имеем:

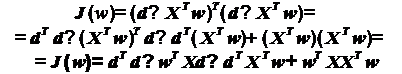
Для нахождения минимума необходимо вычислить градиент данного функционала и приравнять его нулю:

Отсюда легко получается искомое оптимальное решение:

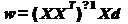 (21)

В формуле прослеживается близкое родство с формулой (8), описывающей оптимальный в статистическом смысле фильтр Винера. Действительно, если учесть, что 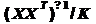 дает оценку корреляционной матрицы сигнала, полученную по одной реализации эргодического случайного процесса путем временного усреднения, а  является аналогичной оценкой взаимных корреляций между образцовым сигналом и содержимым линии задержки фильтра, то формулы (8) и (21) совпадут.

.4 Адаптивный алгоритм RLS

В принципе, в процессе приема сигнала можно на каждом очередном шаге пересчитывать коэффициенты фильтра непосредственно по формуле (21), однако это связано с неоправданно большими вычислительными затратами. Действительно, размер матрицы X постоянно увеличивается и, кроме того, необходимо каждый раз заново вычислять обратную матрицу .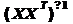

Сократить вычислительные затраты можно, если заметить, что на каждом шаге к матрице X добавляется лишь один новый столбец, а к вектору d - один новый элемент. Это дает возможность организовать вычисления рекурсивно. Соответствующий алгоритм называется рекурсивным методом наименьших квадратов (Recursive Least Square, RLS).

На k-м шаге оптимальный вектор коэффициентов фильтра, согласно (21), равен

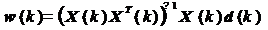 . (22)

К матрице X на каждом шаге добавляется новый столбец x(k+1), а к вектору d - новый элемент d(k+1) :

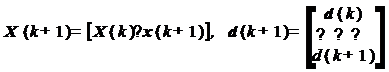 (23)

При использовании алгоритма RLS производится рекурсивное обновление оценки обратной корреляционной матрицы .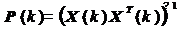

При переходе к следующему шагу имеем:

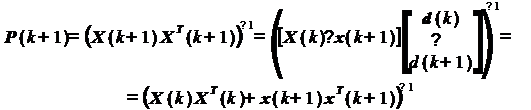 (24)

Теперь воспользуемся матричным тождеством

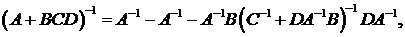 (25)

где А и С - произвольные квадратные невырожденные матрицы, а В и D - произвольные матрицы совместимых размеров.

Установим между (24) и (25) соответствие:

ñ 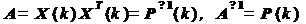 (квадратная матрица);

ñ 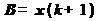 (вектор-столбец);

ñ  (скаляр);

ñ 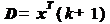 (вектор-строка).

В результате (24) можно записать следующим образом:

Заметим, что фрагмент выражения, возводимый в минус первую степень, представляет собой скаляр. Используем (23) и (26) в выражении (22) для коэффициентов фильтра:

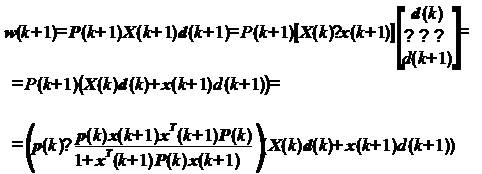
Раскроем скобки:

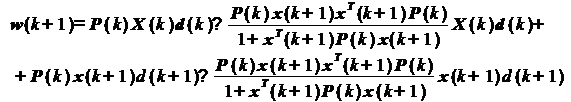
Первое слагаемое в полученной формуле, согласно (22), представляет собой коэффициенты оптимального фильтра для k-го шага - w(k). Этот же вектор можно выделить в качестве множителя во втором слагаемом. В третьем и четвертом слагаемых можно выделить общий множитель P(k)x(k+1)d(k+1):

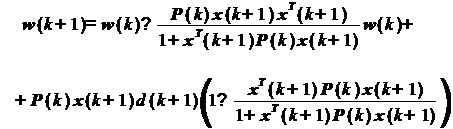
Выполнив вычисление в скобках и вынеся общий множитель, получаем:

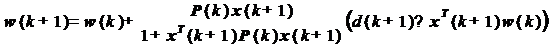
Заметим, что произведение 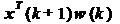есть результат обработки поступившего на k-м шаге входного сигнала фильтром со старыми коэффициентами w(k). То есть, это произведение представляет собой выходной сигнал адаптивного фильтра y(k+1). Соответственно, разность в скобках - это ошибка фильтрации e(k+1):

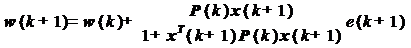
Теперь введем обозначение для вынесенного за скобки векторного множителя:

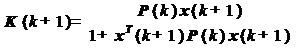
С учетом этого формула для коэффициентов фильтра примет вид:

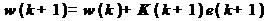 (27)

Вектор K(k+1) называют вектором коэффициентов усиления.

Итак, при использовании адаптивного алгоритма RLS необходимо на на каждом такте выполнять следующие шаги:

. При поступлении новых входных данных x(k) производится фильтрация сигнала с использованием текущих коэффициентов фильтра w(k-1) и вычисление величины ошибки воспроизведения образцового сигнала:

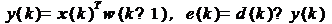
2. Рассчитывается вектор-столбец коэффициентов усиления (следует отметить, что вектор K всякий раз рассчитывается заново, т. е. Вычисления не рекурсивны, а также что знаменатель дроби является скаляром):

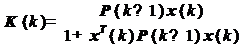 (28)

. Производится обновление оценки обратной корреляционной матрицы сигнала:

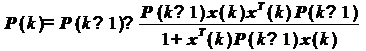 (29)

4. Наконец, производится обновление коэффициентов фильтра:

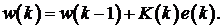
Что касается рекурсивно обновляемых матрицы P и вектора w, обычно вектор w принимается нулевым, а анализ матрицы Р показывает, что после заполнения линии задержки фильтра отсчетами сигнала результат не будет зависеть от начальных условий, если

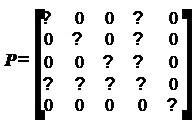
На практике диагональ заполняется большими положительными числами, например, 100/σ2x .

По сравнению с LMS-алгоритмом, алгоритм RLS требует значительно большего числа вычислительных операций (при оптимальной организации вычислений 2,5N2+4N пар операций «умножение-сложение»). Под оптимальной организацией здесь понимается учет симметрии матрицы P. Таким образом, число операций в алгоритме RLS квадратично возрастает с увеличением порядка фильтра.

Зато алгоритм RLS сходится значительно быстрее алгоритма LMS. Строго говоря, он даже не является алгоритмом последовательного приближения, поскольку на каждом шаге дает оптимальные коэффициенты фильтра, соответствующие формуле (21).

.5 Алгоритм RLS с экспоненциальным забыванием

В формулах (18) и (20) значениям ошибки на всех временных тактах придается одинаковый вес. В результате, если статистические свойства входного сигнала со временем изменяются, это приведет к ухудшению качества фильтрации. Чтобы дать фильтру возможность отслеживать нестационарный входной сигнал, можно применить в (18) экспоненциальное забывание (exponential forgetting), при котором вес прошлых значений сигнала ошибки экспоненциально уменьшается:

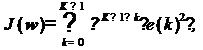
где λ - коэффициент забывания,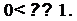

При использовании экспоненциального забывания формулы (28) и (29) принимают следующий вид:

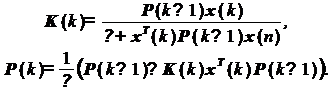
3. Адаптивные фильтры в идентификации систем

Адаптивные фильтры в настоящее время нашли применение во многих радиотехнических и телекоммуникационных системах обработки сигналов. Однако все способы использования адаптивных фильтров так или иначе сводятся к решению задачи идентификации, то есть определения характеристик некоторой системы.

Возможны два варианта идентификации - прямая и обратная. В первом случае адаптивный фильтр включается параллельно с исследуемой системой (рис. 2, а).

а б

Рис.2 Идентификация систем с помощью адаптивного фильтра :

а- прямая, б- обратная.

Входной сигнал является общим для исследуемой системы и адаптивного фильтра, а выходной сигнал системы служит для адаптивного фильтра образцовым сигналом. В процессе адаптации временные и частотные характеристики фильтра будут стремиться к соответствующим характеристикам исследуемой системы.

При обратной идентификации адаптивный фильтр включается последовательно с исследуемой системой (рис. 2, б). Выходной сигнал системы поступает на вход адаптивного фильтра, а входной сигнал системы является образцом для адаптивного фильтра. Таким образом, фильтр стремится компенсировать влияние системы и восстановить исходный сигнал, устранив внесенные системой искажения.

4. Реализация моделей адаптивных фильтров

В данной работе мы реализуем решение задачи прямой идентификации системы согласно рис.2.а с помощью трех алгоритмов - LMS, RLS и RLS с экспоненциальным забыванием.

Входным сигналом будет служить дискретный белый гауссов шум, а сама система будет представлять собой нерекурсивный фильтр 31-го порядка с импульсной характеристикой в виде экспоненциально затухающей синусоиды, на период колебаний которой приходится четыре отсчета. Кроме того, после обработки половины входного сигнала параметры системы скачкообразно изменятся - у ее импульсной характеристики поменяется знак. Это позволит нам посмотреть на то, как реагируют алгоритмы на резкое изменение статистических свойств обрабатываемого сигнала.

Текст программы, реализующей алгоритмы, см. в приложении 1.

Сравнение моделей

Итак, на рис.3 можно видеть, что на начальном этапе RLS-алгоритмы показывают гораздо более быстрый переход и меньшую ошибку по сравнению с LMS-алгоритмом. Теперь рассмотрим подробнее ошибку от времени на начальном этапе (Рис.4.).

На рис.4 видно, что LMS и RLS алгоритмы дают примерно одинаковую ошибку в установившемся режиме, тогда как алгоритм RLS с экспоненциальным забыванием ошибки практически не дает.

Вернемся к рис.3 и обратимся к скачкообразному изменению характеристик системы. Здесь мы видим, что LMS-алгоритм после некоторого переходного процесса свел ошибку фильтрации к тому же уровню, который она имела раньше, а вот RLS так и не смог приспособиться к изменившимся условиям.

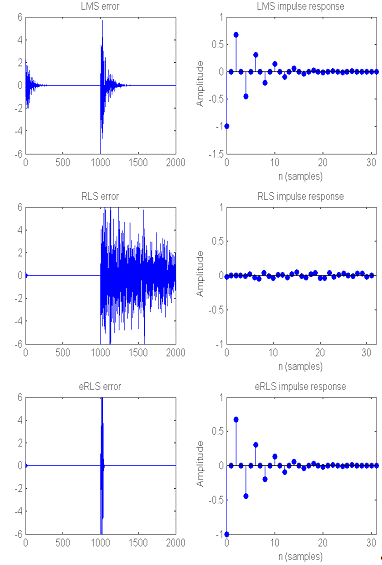
Рис.3. Результаты идентификации системы с помощью алгоритмов LMS (верхняя строка), RLS (средняя строка) и RLS с экспоненциальным забыванием (нижняя строка): слева - зависимость ошибки от времени, справа - итоговые импульсные характеристики фильтров.

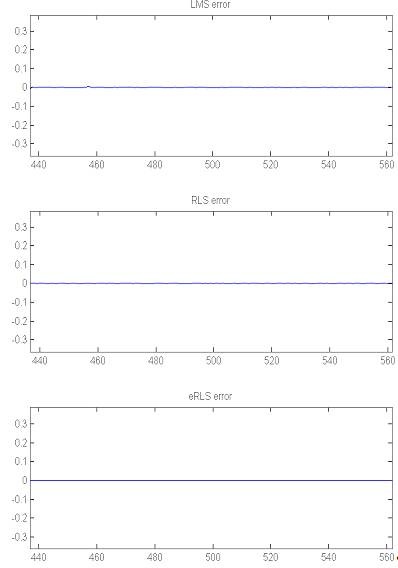
Рис.4. Увеличенный график ошибки от времени до изменения характеристик системы.

Однако RLS-алгоритм с экспоненциальным забыванием (который имеет возможность отслеживать изменения статистических свойств обрабатываемого сигнала) отлично справился с изменением характеристик системы, и даже с меньшим переходным процессом, чем LMS. Это подтверждают итоговые импульсные характеристики фильтров (рис.3, справа) - характеристики LMS-фильтра и RLS с экспоненциальным забыванием хорошо совпадают с экспоненциально затухающими колебаниями импульсной характеристики анализируемой системы (рис.6), а характеристика RLS-фильтра выглядит случайным набором значений.

Если увеличить графики ошибки фильтрации после изменения характеристик системы (рис.6), то можно видеть, что алгоритм RLS с экспоненциальным забыванием, как и прежде, дает меньшую ошибку, чем LMS-алгоритм. Алгоритм RLS на данном этапе мы не рассматриваем, поскольку его ошибку видно на рис.3, и она не сравнима с ошибками других алгоритмов.

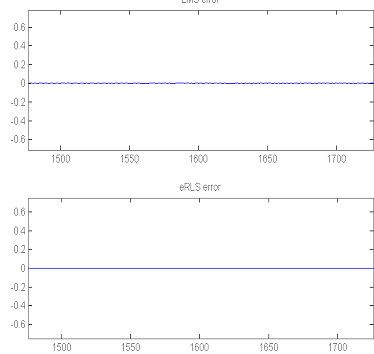
Рис.5. Увеличенный график ошибки фильтрации после скачкообразного изменения характеристик системы

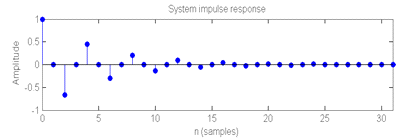
Рис.6. Импульсная характеристика системы

Выводы

Проделанная работа показала, что алгоритм LMS неплохо справляется как со стационарным сигналом, так и с сигналом с изменяющимися характеристиками. Алгоритм RLS в «чистом» виде дает отличные результаты по стационарному сигналу, однако с изменением характеристик системы справиться не способен. Алгоритм RLS с экспоненциальным забыванием отлично справляется с обоими вышеперечисленными сигналами и показывает гораздо меньший переходный процесс и меньшую ошибку по сравнению с остальными рассмотренными алгоритмами.

Однако не стоит забывать, что RLS алгоритмы требуют гораздо больше вычислительных мощностей, чем LMS (2,5N2+4N пар операций «умножение-сложение» по сравнению с N + 1 пар операций на каждом шаге для LMS).

Соответственно, можно сделать вывод, что для случаев, не требующих высокой точности, удобнее всего использовать алгоритм LMS. Если же требуется высокая точность и достаточно вычислительных мощностей, лучше подойдут RLS-алгоритмы. Кроме того, нужно помнить, что RLS-алгоритм в «чистом» виде можно применять только в системах со стационарным сигналом. Если же характер сигнала может меняться, необходимо использовать RLS-алгоритм с экспоненциальным забыванием.

Приложения

Приложение 1

Реализация адаптивных фильтров в MATLAB

Для начала формируем входной и выходной сигналы идентифицируемой системы:=randn(2000,1); %дискретный белый гауссов шум

% генерируем первую половину выходного сигнала

[y(1:1000), state] = filter(b, 1, x(1:1000));

% генерируем вторую половину выходного сигнала(1001:2000) = filter(-b, 1, x(1001:2000), state);

Далее создадим объекты адаптивных фильтров с помощью соответствующих конструкторов. Для LMS-алгоритма предварительно рассчитаем значение коэффициента μ, выбрав его в два раза меньшим предельного значения, определяемого формулой (15), а для RLS-алгоритма с экспоненциальным забыванием возьмем λ=0,6. Для всех остальных параметров используем значение по умолчанию:

%создаем объекты LMS- и RLS-адаптивных фильтров

N = 32; % длина фильтров= 1/N/var(y); %размер шага для LMS_lms = adaptfilt.lms(N,mu); % создание объекта для LMS_rls = adaptfilt.rls(N); % создание объекта для RLS_erls = adaptfilt.rls(N,0.6); % создание объекта для RLS с экспоненциальным забыванием

Теперь реализуем фильтрацию с помощью функции filter. В соответствии с рис.2, а входной сигнал адаптивного фильтра совпадает с входным сигналом исследуемой системы (x), а образцовый сигнал - это выходной сигнал системы (y):

%реализуем фильтрацию:

[y_lms, e_lms] = filter(ha_lms, x, y);

[y_rls, e_rls] = filter(ha_rls, x, y);

[y_erls, e_erls] = filter(ha_erls, x, y);

Теперь построим импульсную характеристику системы (рис.3) и графики зависимости сигнала ошибки от времени, а также выведем на экран импульсные характеристики фильтров, полученные на момент завершения обработки сигнала (рис.4):

% строим графики:

subplot(3,2,1)(e_lms)('LMS error')([0 2000 -6 6])(3,2,2)(ha_lms.coefficients)('LMS impulse response')(3,2,3)(e_rls)('RLS error')([0 2000 -6 6])(3,2,4)(ha_rls.coefficients)('RLS impulse response')([0 N -1 1])(3,2,5)(e_erls)('eRLS error')([0 2000 -6 6])(3,2,6)(ha_erls.coefficients)('eRLS impulse response') (4,2,8) (b)('System impulse response')

Библиографический список

1.           Сергиенко А.Б. Цифровая обработка сигналов.- 3-е изд. - СПб.: БХВ-Петербург, 2011. - 768 с.

2.      Хайкин С. Нейронные сети. Полный курс. - М.: Вильямс, 2006. - 1104 с.

.        Адаптивные фильтры: Пер. С англ./[Под ред. К.Ф.Н.Коуэнам и П.М.Гранта]. - М.: Мир, 1988. - 392 с.

.        Шахтарин Б.И. Случайные процессы в радиотехнике: Цикл лекций. - М.: Радио и связь, 2000. - 584 с.

.        Основы цифровой обработки сигналов: Курс лекций / А.И.Солонина, Д.А.Улахович, С.М.Арбузов, Е.Б.Соловьева . - 2-е изд., перераб. и испр. - Спб.: БХВ-Петербург, 2005. - 768 с.

.        Солонина А.И. Цифровая обработка сигналов. Моделирование в MATLAB / А.И.Солонина, С.М. Арбузов. - Спб.: БХВ-Петербург, 2008. - 816 с.

.        Джиган В. Адаптивные фильтры. Современные средства моделирования и примеры реализации. / В.Джиган // Электроника: наука технология бизнес. - 2012. - №7(00121). - С. 106-125.

.        Сеогиенко А.Б. Алгоритмы адаптивной фильтрации: особенности реализации в MATLAB. / А.Б.Сергиенко // Exponenta Pro. - 2003. - №1(1). - С. 18-28.