Акустика пузырьковой жидкости
МИНИСТЕРСТВО ОБРАЗОВАНИЯИ НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
БИРСКИЙ ФИЛИАЛ
ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Факультет физики и математики
Кафедра высшей и прикладной математики
Курсовая работа
Акустика пузырьковой жидкости
Выполнила:
студентка 3 курса,
группы
Гайнуллина Е.В.
Руководитель:
зав. каф. МА и ПМ, д.ф.-м.н.
профессор
Шагапов В.Ш.
Бирск - 2014
ВВЕДЕНИЕ
Актуальность темы. Проблема исследования нестационарных волновых
процессов в многофазных системах с учетом неравновесных эффектов межфазного
взаимодействия является одной из актуальных проблем механики сплошных сред. Из
многообразия неоднородных сред выделяются дисперсные смеси, представляющие
собой смесь нескольких фаз, одной из которых являются различные включения
(капли, пузырьки, твердые частицы) - аэрозоли, туманы, пузырьковые жидкости,
взвеси и т.д. При этом реальные многофазные системы являются существенно
полидисперсными и при описании движения таких систем следует учитывать реальное
распределение диспергированных включений по размерам, а также межфазный обмен
массой, импульсом и теплом.
В настоящее время интерес представляют исследования волновой динамики
дисперсных сред применительно к проблемам развития акустических методов
диагностики парогазокапельных сред и жидкостей с парогазовыми пузырьками, а
также методов подавления звуковых возмущений дисперсными смесями. Развитие
таких методов способствует как решению задач безопасности процессов на
промышленных объектах в машиностроении, энергетике и т.д., так и проблем
экологии атмосферы. Поэтому результаты таких исследований могут быть
использованы при решении фундаментальных проблем аэрогидромеханики.
Целью курсовой работы является теоретическое исследование распространения
акустических возмущений в смесях жидкости с газовыми пузырьками с учетом
нестационарных и неравновесных эффектов межфазного взаимодействия.
В соответствии с целью поставлены и решены задачи:
. Изучение литературы по исследуемой теме.
. Расчеты зависимости фазовой скорости и коэффициента затухания в
пузырьковой жидкости от частоты.
1. МОДЕЛИ
ГЕТЕРОГЕННЫХ СИСТЕМ
.1 ОСНОВНЫЕ
ПОНЯТИЯ И МЕТОДЫ ГИДРОДИНАМИКИ ДИСПЕРСНЫХ СИСТЕМ
В
окрестности точки, определяемой радиусом вектором 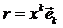 берем частицу с объемом
берем частицу с объемом 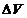 и с общей массой
и с общей массой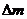 , при
этом полагаем, что
, при
этом полагаем, что
 >>
>>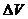 >>
>> >>
>>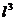
где
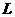 характерный линейный разрез задачи,
характерный линейный разрез задачи, 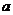 и
и 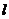 -линейные
размеры дисперсных частиц и среднее расстояние между соседними частицами.
-линейные
размеры дисперсных частиц и среднее расстояние между соседними частицами.
Для
дисперсной системы, состоящей из двух составляющих, можно записать
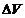 =
= +
+ и
и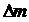 =
= +
+ (1.1)
(1.1)
где
 и
и  части
объема и массы в
части
объема и массы в  , приходящиеся к
, приходящиеся к
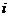 -ой фазе.
Введем следующие параметры [1]
-ой фазе.
Введем следующие параметры [1]
 ,
,  ,
, 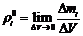 (1.2)
(1.2)
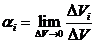 ,
, 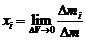 ,
, 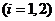
Здесь
 - средняя плотность смеси в целом и
- средняя плотность смеси в целом и 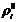 ,
,  - средние
и истинные плотности фаз,
- средние
и истинные плотности фаз,  и
и 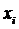 -
объемные и массовые содержания (или концентрации) фаз. Очевидно, что из
определения этих параметров следует зависимость между ними в виде, используя
[1]
-
объемные и массовые содержания (или концентрации) фаз. Очевидно, что из
определения этих параметров следует зависимость между ними в виде, используя
[1]
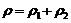 ,
, 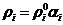 ,
,  (1.3)
(1.3)
 ,
, 
Кроме
того, на основе первого соотношения из (1.1) с учетом (1.2) нетрудно получить
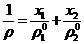 (1.4)
(1.4)
Пусть
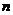 и
и 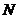 - число
дисперсных частиц в единице объема массы дисперсной системы, тогда между этими
параметрами имеется следующая связь
- число
дисперсных частиц в единице объема массы дисперсной системы, тогда между этими
параметрами имеется следующая связь
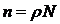 (1.5)
(1.5)
Для
дальнейшего примем, что дисперсная фаза представляет собой сферические частицы
одинакового радиуса 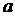 . Тогда имеет место кинематическая связь [1]
. Тогда имеет место кинематическая связь [1]
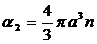 (1.6)
(1.6)
2. ОДНОСКОРОСТНАЯ
МОДЕЛЬ
Уравнения
неразрывности. Примем, что составляющие смеси движутся с одинаковыми скоростями
(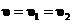 ). Это означает, что в изучаемой проблеме скольжение
фаз несущественно. Например, рассматриваются медленные процессы, когда
характерные времена задачи
). Это означает, что в изучаемой проблеме скольжение
фаз несущественно. Например, рассматриваются медленные процессы, когда
характерные времена задачи  значительно
превышают времена релаксации скоростей неравновесности
значительно
превышают времена релаксации скоростей неравновесности  для двухфазной смеси
для двухфазной смеси 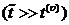 . По
аналогии с обычными однофазными системами в этом случае должно иметь место
следующее уравнение сохранения массы для всей смеси в целом [1]
. По
аналогии с обычными однофазными системами в этом случае должно иметь место
следующее уравнение сохранения массы для всей смеси в целом [1]
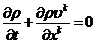 или
или  (2.1)
(2.1)
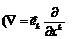 ,
, 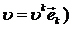
Эти
уравнения можно записать, используя
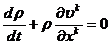 или
или 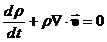 (2.2)
(2.2)
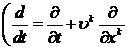 или
или

Пусть,
в общем случае, может происходить массообмен между составляющими двухфазной
системы. Такая ситуация может иметь место, например, в парокапельной смеси. Пар
может конденсироваться, или, наоборот, капельки могут испаряться. Введем
параметры 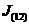 и
и  ,
описывающие интенсивность перехода массы из первой фазы во вторую и, наоборот,
из второй фазы в первую. Эти параметры отнесены к единице объема смеси. Тогда
для каждой составляющей двухфазной системы можем записать следующие уравнения,
выражающие закон сохранения масс [1]
,
описывающие интенсивность перехода массы из первой фазы во вторую и, наоборот,
из второй фазы в первую. Эти параметры отнесены к единице объема смеси. Тогда
для каждой составляющей двухфазной системы можем записать следующие уравнения,
выражающие закон сохранения масс [1]
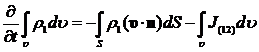 (2.3)
(2.3)
и

Используя
теорему Гаусса-Остроградского, из (2.3) можем получить уравнение неразрывности
в форме Эйлера [1]
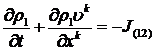 и
и 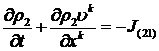 (2.4)
(2.4)
Складывая
эти уравнения, получаем уравнение неразрывности (2.1) для всей смеси в целом.
При этом необходимо отметить, что введенные параметры для описания межфазного
массообмена должны удовлетворять условию

Следовательно,
достаточно задавать один из этих параметров 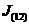 (или
(или  ). Для определенности в последующем примем обозначения
). Для определенности в последующем примем обозначения
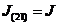 тогда
тогда
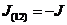 . В
случае отсутствия массообмена между фазами имеет место
. В
случае отсутствия массообмена между фазами имеет место 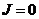 .
.
Запишем
уравнение импульсов для первой фазы 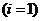 в
терминал истинная плотность - объемная концентрация при
в
терминал истинная плотность - объемная концентрация при 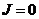 как
как
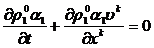 (2.5)
(2.5)
Если
это составляющее несжимаемое 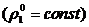 , отсюда
следует
, отсюда
следует
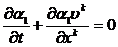 (2.6)
(2.6)
В
том случае, когда вторая фаза также несжимаема, то аналогично с (2.6) будем
иметь
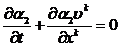 (2.7)
(2.7)
Складывая
уравнения (2.6) и (2.7) с учетом 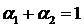 получим
получим
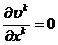 (2.8)
(2.8)
Таким
образом, в случае, когда обе фазы несжимаемые, уравнение неразрывности сводится
для поля скоростей к обычному виду для несжимаемой однофазной среды.
Подставляя
в уравнение неразрывности среднюю плотность в виде 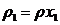 и учитывая уравнение неразрывности для всей смеси в
целом (2.1) можем получить:
и учитывая уравнение неразрывности для всей смеси в
целом (2.1) можем получить:
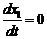 или
или  (2.9)
(2.9)
Если
предположить, что при течении дисперсной системы не происходит образование и
исчезновение дисперсных частиц (отсутствуют процессы дробления или слипания
частиц, например), то аналогично с уравнениям неразрывности фаз, можно записать
уравнение сохранения числа дисперсных частиц
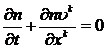 (2.10)
(2.10)
Подставляя
сюда выражение 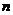 из (1.5) с учетом уравнения неразрывности всей смеси
(2.1) получим:
из (1.5) с учетом уравнения неразрывности всей смеси
(2.1) получим:
 или
или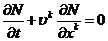 (2.10)
(2.10)
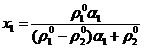 ,
,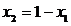 (2.11)
(2.11)
 ,
,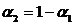 (2.12)
(2.12)
Уравнение
импульсов. Будем полагать, что двухфазную систему в целом можно рассмотреть как
идеальную среду с введением для нее еще одного параметра, а именно давления 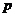 . Это допущение означает, что тензор напряжений
является чисто шаровым и его компоненты можно записать в виде
. Это допущение означает, что тензор напряжений
является чисто шаровым и его компоненты можно записать в виде
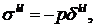
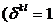 ,
, 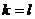 ;
; 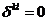 ,
, 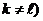 (2.13)
(2.13)
где
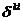 - символ Кронекера. Тогда уравнение импульсов для
всей смеси в целом запишется в виде
- символ Кронекера. Тогда уравнение импульсов для
всей смеси в целом запишется в виде
 (2.14)
(2.14)
 (k=1,2,3) (2.15)
(k=1,2,3) (2.15)
Здесь
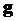 - удельномассовая сила.
- удельномассовая сила.
В
том случае, когда течение потенциальное, массовые силы потенциальные, а смесь в
целом можно считать баротропной средой  ,
уравнение импульсов (2.14) сводится к интегралу Коши-Лагранжа
,
уравнение импульсов (2.14) сводится к интегралу Коши-Лагранжа
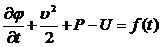 (2.16)
(2.16)
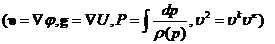
Уравнение
неразрывности (2.2) при этом можно привести к виду
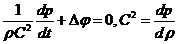 (2.17)
(2.17)
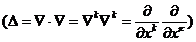
Введенный
здесь параметр 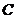 , как известно, выражает скорость звука в среде. Таким
образом, система уравнений для равновесной по скоростям двухфазной системы, в
рамках вышепринятых допущениях сводится к двум уравнениям из (2.16.) и (2.17).
При этом основная проблема сводится к построению уравнения состояния вида
, как известно, выражает скорость звука в среде. Таким
образом, система уравнений для равновесной по скоростям двухфазной системы, в
рамках вышепринятых допущениях сводится к двум уравнениям из (2.16.) и (2.17).
При этом основная проблема сводится к построению уравнения состояния вида 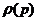 или
или 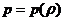 с учетом
специфики конкретных двухфазных систем.
с учетом
специфики конкретных двухфазных систем.
3. УРАВНЕНИЕ
СОСТОЯНИЯ ДЛЯ РАВНОВЕСНОЙ ПО СКОРОСТЯМ ГАЗОЖИДКОСТНОЙ СИСТЕМЫ
Вместо
индексов (1) и (2), соответствующих первой и второй фазам для газожидкостной
смеси будем использовать соответственно нижние индексы  и
и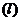 . Пусть
фазовые переходы отсутствуют
. Пусть
фазовые переходы отсутствуют 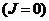 . Для
дальнейшего обозначим
. Для
дальнейшего обозначим 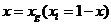 ,
, 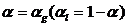 . Тогда
из уравнения неразрывности следует (2.9), которое запишется как
. Тогда
из уравнения неразрывности следует (2.9), которое запишется как
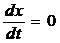 или
или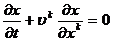 (3.1)
(3.1)
Выражения
(1.4) для средней плотности имеет вид
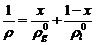 (3.2)
(3.2)
Будем
полагать, что в процессе движения жидкость ведет себя как акустически сжимаемая
среда, а поведение газа политропическое. Тогда можем записать
 и
и 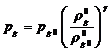 (3.3)
(3.3)
Здесь
 и
и 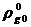 -
значения плотности, соответствующие значениям давления
-
значения плотности, соответствующие значениям давления 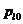 и
и 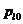 ;
; 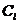 - величины скорости звука для жидкостной фазы, γ- показатель политропы. В частности, если поведение
газа изотермическое, то γ=1, а если адиабатическое, то величина γ равна показателю адиабаты для данного газа.
- величины скорости звука для жидкостной фазы, γ- показатель политропы. В частности, если поведение
газа изотермическое, то γ=1, а если адиабатическое, то величина γ равна показателю адиабаты для данного газа.
В
дальнейшем будем считать, что давление в фазах равны 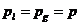 и, кроме того, вместо
и, кроме того, вместо 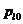 и
и  примем одно и тоже значение давления
примем одно и тоже значение давления 
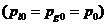 . Вместо
. Вместо 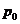 обычно будем использовать значение давления для
некоторого исходного равновесного состояния. Подставляя значение
обычно будем использовать значение давления для
некоторого исходного равновесного состояния. Подставляя значение 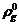 ,
,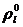 из (3.3) в (3.2) получим
из (3.3) в (3.2) получим
 (3.4)
(3.4)
Таким
образом, получим уравнение состояния вида

В
этом уравнении, величины 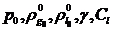 , определяющие исходное состояние системы и свойства
составляющих (газа и жидкости), входят как некоторые постоянные параметры. Что
касается величины массового содержания газа
, определяющие исходное состояние системы и свойства
составляющих (газа и жидкости), входят как некоторые постоянные параметры. Что
касается величины массового содержания газа 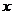 , то для
каждой лагранжевой частицы оно будет постоянным параметром. При эйлеровом
описании, в общем случае массовое газосодержание
, то для
каждой лагранжевой частицы оно будет постоянным параметром. При эйлеровом
описании, в общем случае массовое газосодержание 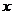 зависит
как от времени, так и от пространственных координат
зависит
как от времени, так и от пространственных координат 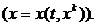 Однако, если для некоторого состояния оно (например,
при
Однако, если для некоторого состояния оно (например,
при  - однородно
- однородно 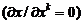 , то
массовое газосодержание будет постоянным и по времени и по координате. В
дальнейшем будем рассматривать именно такие ситуации. Тогда в (3.5) х также
будет постоянный параметр. В этом случае при течении такой смеси величина
плотности будет определяться значением давления и, следовательно,
газожидкостная смесь в целом будет баротропной средой.
, то
массовое газосодержание будет постоянным и по времени и по координате. В
дальнейшем будем рассматривать именно такие ситуации. Тогда в (3.5) х также
будет постоянный параметр. В этом случае при течении такой смеси величина
плотности будет определяться значением давления и, следовательно,
газожидкостная смесь в целом будет баротропной средой.
Определим
скорость звука для такой среды.
Для
этого продифференцируем левую и правую части уравнения (3.4) по давлению 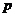 . Тогда будем иметь
. Тогда будем иметь
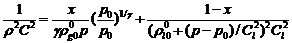 ,
, 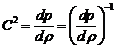 (3.5)
(3.5)
Это
уравнение можно записать как
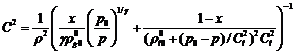 (3.6)
(3.6)
Формула
(3.6) совместно с (3.4) дает зависимость величины скорости звука от текущего
давления  .
.
Как
уже отмечено, если для исходного равновесного состояния газожидкостная смесь
однородна, то в (3.6) имеет место 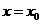 , где
, где 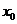 - значение массового содержания газа для исходного
состояния. В этом случае на основании (2.11) можем записать:
- значение массового содержания газа для исходного
состояния. В этом случае на основании (2.11) можем записать:
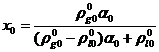 (3.7)
(3.7)
Подставляя
это выражение для 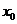 вместо
вместо 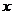 в (3.4)
и (3.6), получим уравнение состояния и формулу для скорости звука, в которых в
качестве параметра, ответственного за состав смеси, фигурирует начальное объемное
газосодержание
в (3.4)
и (3.6), получим уравнение состояния и формулу для скорости звука, в которых в
качестве параметра, ответственного за состав смеси, фигурирует начальное объемное
газосодержание 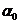 . Определим скорость звука для исходного состояния.
Подставляя в формулу (3.6)
. Определим скорость звука для исходного состояния.
Подставляя в формулу (3.6) 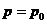 , получим
, получим
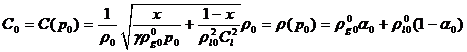 (3.8)
(3.8)
Отсюда
при  и
и  соответственно
получим выражение для скорости звука для «чистых» газа и жидкости
соответственно
получим выражение для скорости звука для «чистых» газа и жидкости
 и
и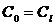 (3.9)
(3.9)
Проанализируем
формулу (3.8) для случая, когда массовое газосодержание мало 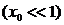 . Из формулы (3.7), учитывая при этом, что в
большинстве случаев имеет место
. Из формулы (3.7), учитывая при этом, что в
большинстве случаев имеет место  , получим
, получим
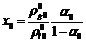 (3.10)
(3.10)
Отсюда
видно, что это условие 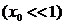 выполняется для объемных содержаний газовой фазы,
удовлетворяющих условию
выполняется для объемных содержаний газовой фазы,
удовлетворяющих условию
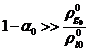 (3.11)
(3.11)
Для
водовоздушной смеси при нормальных условиях, например, имеет место , поэтому неравенство (3.11) выполняется и при
объемных содержаниях газа
, поэтому неравенство (3.11) выполняется и при
объемных содержаниях газа 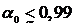 .
.
В
этом случае, с учетом 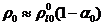 , из (3.8) получим следующую формулу для скорости
звука
, из (3.8) получим следующую формулу для скорости
звука
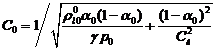 (3.12)
(3.12)
Из
этой формулы следует, что вклад сжимаемости жидкости, определяемый вторым
слагаемым в подкоренном выражении (3.12), растет с уменьшением объемного
содержания газа 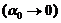 .
.
Проанализируем
эту формулу для пузырьковой жидкости (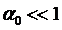 ).
Пренебрегая
).
Пренебрегая 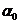 по сравнению с единицей из (3.12) получим
по сравнению с единицей из (3.12) получим
 (3.13)
(3.13)
Отсюда
получим, что сжимаемость жидкости в плане определения скорости звука скажется
при
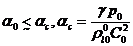 (3.14)
(3.14)
Для
водовоздушной смеси при нормальных условиях 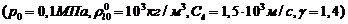 имеем
имеем 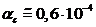 . Следовательно, сжимаемость жидкости проявляется лишь
при очень низких объемных содержаниях газа.
. Следовательно, сжимаемость жидкости проявляется лишь
при очень низких объемных содержаниях газа.
Пренебрегая
сжимаемостью жидкости (формально полагая в (3.12) 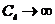 ), для скорости звука получим формулу Мэллока
), для скорости звука получим формулу Мэллока
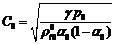 (3.15)
(3.15)
Из
этой формулы нетрудно видеть, что минимальная величина скорости звука
достигается при  . Для этой скорости из (3.15) следует
. Для этой скорости из (3.15) следует
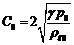 (3.16)
(3.16)
Для
водовоздушной смеси при нормальных условиях отсюда имеем  .
.
4. УРАВНЕНИЕ
СОСТОЯНИЯ ДЛЯ ОДНОТЕМПЕРАТУРНОЙ СМЕСИ
Адиабатическое
поведение газовой фазы предполагает, что межфазный теплообмен несущественен.
Можно рассмотреть другую ситуацию, когда за счет межфазного теплообмена
температура составляющих смеси равны 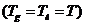 . Пусть
. Пусть 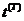 - некоторое характерное время релаксации
температурной неравновесности, зависящей от масштабов дисперсности
теплофизических характеристик составляющих двухфазной среды. Гипотеза
температурной равновесности означает, что рассматриваются достаточно медленные
процессы, для которых характерные времена
- некоторое характерное время релаксации
температурной неравновесности, зависящей от масштабов дисперсности
теплофизических характеристик составляющих двухфазной среды. Гипотеза
температурной равновесности означает, что рассматриваются достаточно медленные
процессы, для которых характерные времена  процесса
значительно выше времен температурной релаксации
процесса
значительно выше времен температурной релаксации 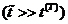 . Будем
также рассматривать газожидкостную смесь. Причем, газ будем считать калорически
совершенным, а жидкость несжимаемой. Поэтому, полагая, что удельномассовая
внутренняя энергия аддитивна по составляющим, можем записать
. Будем
также рассматривать газожидкостную смесь. Причем, газ будем считать калорически
совершенным, а жидкость несжимаемой. Поэтому, полагая, что удельномассовая
внутренняя энергия аддитивна по составляющим, можем записать
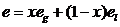 (4.1)
(4.1)
где
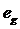 и
и 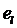 -
удельные внутренние энергии для газовой и жидкостной фаз, которые в свою
очередь могут быть представлены в виде
-
удельные внутренние энергии для газовой и жидкостной фаз, которые в свою
очередь могут быть представлены в виде
 и
и 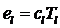 (4.2)
(4.2)
здесь
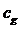 и
и 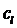 -
удельные теплоемкости газа при постоянном давлении и жидкости.
-
удельные теплоемкости газа при постоянном давлении и жидкости.
При
адиабатическом движении смеси в целом можем записать
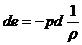 (4.3)
(4.3)
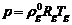 ,
, 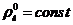 (4.4)
(4.4)
где
 - приведенная газовая постоянная.
- приведенная газовая постоянная.
Выражение
для средней плотности (3.2) с учетом (4.4) запишется как
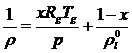 (4.5)
(4.5)
Поскольку
смесь полагается по температуре равновесной, уравнение (4.3) можно записать как
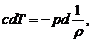
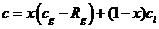 (4.6)
(4.6)
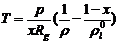 (4.7)
(4.7)
С
учетом отсутствия фазовых переходов 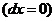 и
допущения о несжимаемости жидкости
и
допущения о несжимаемости жидкости 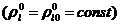 из (4.4)
и (4.5) следует
из (4.4)
и (4.5) следует
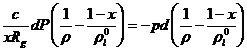 (4.8)
(4.8)
После
некоторых преобразований отсюда получим
межфазный
эффект газовый скорость
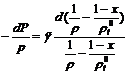 ,
, (4.9)
(4.9)
Пусть
для исходного равновесного состояния имеет место 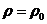 при
при 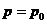 . Тогда, интегрируя уравнение (4.7), будем иметь
. Тогда, интегрируя уравнение (4.7), будем иметь
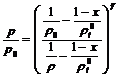 (4.10)
(4.10)
Здесь
безразмерный параметр 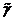 представляет собой приведенный показатель адиабаты
для смеси в целом. Поскольку
представляет собой приведенный показатель адиабаты
для смеси в целом. Поскольку 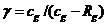 (
( 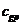 - теплоемкость газа,
- теплоемкость газа, 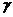 -
показатель адиабаты газа), выражение для показателя адиабаты смеси в целом из
(4.7) можно привести к виду
-
показатель адиабаты газа), выражение для показателя адиабаты смеси в целом из
(4.7) можно привести к виду
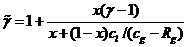 (4.11)
(4.11)
Для
большинства систем обычно  . Поэтому для смесей, с малым газосодержанием
. Поэтому для смесей, с малым газосодержанием 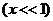 имеет место
имеет место 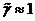 . Тогда
уравнение состояния (4.8) при
. Тогда
уравнение состояния (4.8) при  можно
записать как
можно
записать как
 (4.12)
(4.12)
Здесь
отметим, что данное уравнение состояния можно получить из (3.4), полагая
изотермическое поведение газа 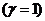 , а также
используя аналогичные допущение, использованные при выводе (4.10).
, а также
используя аналогичные допущение, использованные при выводе (4.10).
Для
скорости звука на основе (4.10) имеем
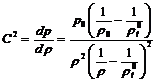 (4.13)
(4.13)
Отсюда,
для исходного состояния 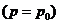 получим
получим
 (4.14)
(4.14)
Если
принять во внимание, что 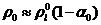 при
при  для
величины скорости звука из (4.12) следует
для
величины скорости звука из (4.12) следует
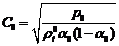 (4.15)
(4.15)
Из
сравнения этой формулы (3.15) видно, что при адиабатическом поведении газовой
фазы величина скорости звука в 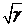 раза
выше, чем при изотермическом поведении.
раза
выше, чем при изотермическом поведении.
5. ОСНОВНЫЕ
УРАВНЕНИЯ ДЛЯ ПУЗЫРЬКОВОЙ ЖИДКОСТИ
Уравнение
неразрывности. Пусть в жидкости газовая фаза находится в виде распределенных по
объему пузырьков с радиусом 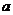 ,
являющимся функцией времени и координат. Параметры, относящиеся к жидкости и
газу, будут снабжаться индексами
,
являющимся функцией времени и координат. Параметры, относящиеся к жидкости и
газу, будут снабжаться индексами 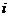 =
=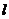 и
и 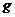 . При
отсутствии массообмена между фазами уравнения неразрывности жидкости запишется
как:
. При
отсутствии массообмена между фазами уравнения неразрывности жидкости запишется
как:
 (5.1)
(5.1)
Уравнение,
сохранения массы газовой фазы в случае отсутствия дробления и слипания
пузырьков примем в виде
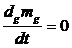 ,
, 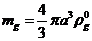 (5.2)
(5.2)
где
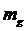 - масса одного пузырька. Из этого уравнения в
частности следует, что если для некоторого исходного состояния истинная
плотность газовой фазы
- масса одного пузырька. Из этого уравнения в
частности следует, что если для некоторого исходного состояния истинная
плотность газовой фазы 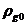 и радиуса пузырьков
и радиуса пузырьков 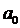 в
пространстве однородны, то
в
пространстве однородны, то
 или
или 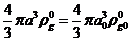 (5.3)
(5.3)
Кроме
того, в рамках принятых допущений, можно записать уравнение сохранения числа
пузырьков в виде:
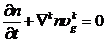 (5.4)
(5.4)
Помножив
это уравнение на  , после нескольких преобразований можем получить
уравнение неразрывности газовой фазы в виде
, после нескольких преобразований можем получить
уравнение неразрывности газовой фазы в виде
 (5.5)
(5.5)
Уравнение
импульсов. Рассматривая пузырьковую жидкость в целом идеальной средой, запишем
уравнение импульсов смеси в целом
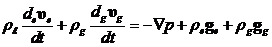 (5.6)
(5.6)
Для
пузырьковой жидкости всегда имеет место условие  .
Поэтому, в тех случаях, когда ускорения фаз сопоставимы
.
Поэтому, в тех случаях, когда ускорения фаз сопоставимы
 ,
,
уравнение
(5.6) можно упростить до вида:
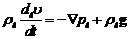
 ) (5.7)
) (5.7)
Поскольку
для пузырьковой жидкости  , здесь и в дальнейшем среднее давление в смеси будем
отожествлять со средним давлением в жидкостной фазе. Таким образом, уравнение
импульсов для смеси в целом фактически совпадает с уравнением импульсов для
несущей фазы.
, здесь и в дальнейшем среднее давление в смеси будем
отожествлять со средним давлением в жидкостной фазе. Таким образом, уравнение
импульсов для смеси в целом фактически совпадает с уравнением импульсов для
несущей фазы.
Запишем
для одного пузырька уравнение второго закона Ньютона
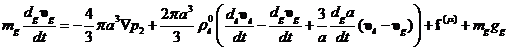 (5.8)
(5.8)

Поскольку
 , в этом уравнении можно пренебречь слагаемыми с
коэффициентом
, в этом уравнении можно пренебречь слагаемыми с
коэффициентом  . Тогда из (5.8) с учетом (5.7) и связи
. Тогда из (5.8) с учетом (5.7) и связи 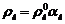 получим
получим
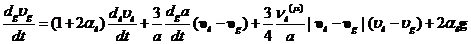 (5.9)
(5.9)
Если
массовые силы отсутствуют  , пренебрегая вторым и третьими слагаемыми в правой
части (5.3) с учетом того, что для пузырьковой жидкости
, пренебрегая вторым и третьими слагаемыми в правой
части (5.3) с учетом того, что для пузырьковой жидкости  , из уравнения (5.9) следует
, из уравнения (5.9) следует
 (5.10)
(5.10)
Если
в исходном состоянии пузырьковая жидкость находится в покое 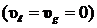 , то при инициировании течения в такой смеси скорости
фаз будут связаны как:
, то при инициировании течения в такой смеси скорости
фаз будут связаны как:
 (5.11)
(5.11)
Уравнение
для изменения давления в пузырьках. Будем учитывать, что давление 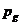 в пузырьках может отличаться от среднего давления в
смеси. Поэтому уравнение Клапейрона-Менделеева для газовой фазы запишем в виде:
в пузырьках может отличаться от среднего давления в
смеси. Поэтому уравнение Клапейрона-Менделеева для газовой фазы запишем в виде:
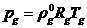 (5.12)
(5.12)
В
качестве исходного уравнения запишем уравнения первого начала термодинамики для
одного пузырька как
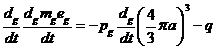 ,
,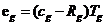 (5.13)
(5.13)
Здесь
 и
и 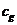 -
внутренняя энергия и теплоемкость газа при постоянном объеме,
-
внутренняя энергия и теплоемкость газа при постоянном объеме, 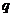 - интенсивность отвода тепла, отнесенная к одному
пузырьку. С учетом уравнения состояния (5.12) внутреннюю энергию для одного
пузырька можно представить как
- интенсивность отвода тепла, отнесенная к одному
пузырьку. С учетом уравнения состояния (5.12) внутреннюю энергию для одного
пузырька можно представить как
 (5.14)
(5.14)
где
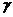 - показатель адиабаты. Подставляя (5.14) в (5.13)
получим следующее уравнение для давления
- показатель адиабаты. Подставляя (5.14) в (5.13)
получим следующее уравнение для давления
 (5.15)
(5.15)
При
отсутствии теплообмена  уравнение (5.15) можно привести к виду
уравнение (5.15) можно привести к виду
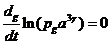 (5.16)
(5.16)
Если
для исходного равновесного состояния 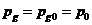 при
при  , и распределения
, и распределения  -
однородно, отсюда получим
-
однородно, отсюда получим
 (5.17)
(5.17)
Уравнение
радиального движения пузырьков. Самой главной особенностью пузырьковой жидкости
является проявление инерции жидкости при изменении объема пузырьков (при их
сжатии или расширении). Для учета этого эффекта примем, что среднее давление в
жидкости 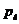 и давление газа
и давление газа 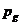 связаны
уравнением Релея-Ламба. С учетом относительного движения фаз, вязкости жидкости
и капиллярного давления на межфазной поверхности это уравнение имеет вид:
связаны
уравнением Релея-Ламба. С учетом относительного движения фаз, вязкости жидкости
и капиллярного давления на межфазной поверхности это уравнение имеет вид:

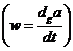
 (5.18)
(5.18)
где
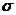 - коэффициент поверхностного натяжения.
- коэффициент поверхностного натяжения.
Для
замыкания представленной системы уравнений необходимо добавить уравнение
состояния несущей жидкости и кинетику межфазного теплообмена. В зависимости от
решаемой задачи несущую фазу можно считать несжимаемой или акустически
сжимаемой жидкостью.
Интенсивность
теплообмена задается аналогично случаю запыленного газа по формуле
 (5.19)
(5.19)
При
этом для рассматриваемой смеси жидкость можно принять термостатом 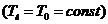 .
.
Наиболее
важной и сложной является корректное задание безразмерного числа Нуссельта  .
.
Оказывается,
в волновых процессах, эволюции возмущений сильно зависят от характера
теплопроводности в газовой фазе и следовательно, от его теплофизических
параметров. Поэтому в каждом конкретном случае проблема теплообмена должно быть
специально проанализирована. В некоторых волновых учет теплообмена может быть
осуществлен привлечением уравнений теплопроводности.
6. ЭЛЕМЕНТЫ
АКУСТИКИ ДИСПЕРСНЫХ СИСТЕМ
.1 ВОЛНОВОЕ
УРАВНЕНИЕ ДЛЯ РАВНОВЕСНЫХ СИСТЕМ
Распространение возмущений в дисперсных системах в общем случае вызывает
нарушение межфазного равновесия (например, скоростного, температурного) смеси и
поэтому представляет собой дисперсионное явление, при котором скорость и
затухание слабого возмущения зависят от его частотных характеристик. Эти
обстоятельства, в частности, приводят к размыванию и затуханию импульсных
сигналов. При этом неравновесные эффекты, связанные с вязкостью,
теплопроводностью в объеме несущей фазы (являющиеся главными механизмами в
процессе диссипации акустических волн в обычных однофазных системах) в случае
же дисперсных систем на фоне проявления этих явлений при двухфазной
неравновесности, как правило, несущественны. Наиболее общий подход, позволяющий
учитывать эти неравновесные процессы, основан на анализе решений
линеаризованных систем общей системы уравнений для двухфазных систем.
Если интересует чисто кинематическая задача, связанная со скоростью
распространения возмущений, то некоторые аспекты динамики волн могут быть
изучены на основе равновесных моделей. Но при таком подходе в каждой конкретной
ситуации необходимо проявить определенную осторожность. Это связано с тем, что
волновые свойства дисперсных систем определяются множеством характерных времен
(тем самым и характерных частот), разделяющих частотный диапазон на промежутки,
в каждом из которых акустические характеристики имеют схожие закономерности
(например, по скорости распространения или по затуханию). А возмущения же,
попадающие в различные частотные диапазоны, могут сильно различаться как по
скорости распространения, так и по закономерностям затухания.
Рассмотрим
малые возмущения в равновесной смеси, находящейся в покое  . Параметры, относящиеся к состоянию равновесия
(покоя), здесь и в дальнейшем будут снабжены нижним индексом (0). Давление,
плотность и скорость представим в виде:
. Параметры, относящиеся к состоянию равновесия
(покоя), здесь и в дальнейшем будут снабжены нижним индексом (0). Давление,
плотность и скорость представим в виде:
В
дальнейшем, как это принято в акустике, верхние индексы в виде штрихов для
возмущений параметров опустим. Полагая 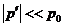 и
и 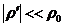 при отсутствии массовых сил
при отсутствии массовых сил  из уравнений (2.2) и (2.14) и условия баротропии
из уравнений (2.2) и (2.14) и условия баротропии  , произведя обычную процедуру линеаризации, получим:
, произведя обычную процедуру линеаризации, получим:
 ,
, 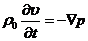 ,
, 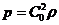 (6.2)
(6.2)
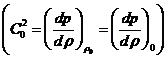
Из
уравнений (1.2), исключая скорости, нетрудно получить
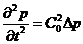
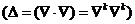 (6.3)
(6.3)
Кроме
того, вводя потенциал скоростей 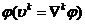 можно
также получить для него волновое уравнение
можно
также получить для него волновое уравнение
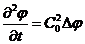 (6.4)
(6.4)
6.2 АКУСТИКА
ПУЗЫРЬКОВОЙ ЖИДКОСТИ
Из
уравнений неразрывности, сохранения числа пузырьков, состояния  и кинематической зависимости из в рамках
односкоростной схемы
и кинематической зависимости из в рамках
односкоростной схемы 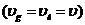 после их линеаризации, нетрудно получить
после их линеаризации, нетрудно получить
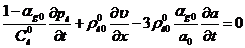
Линеаризируя
уравнение импульсов, имеем

Исключая
скорость после перекрестного дифференцировании, получим
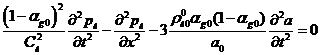
Из
уравнения Рэлея-Ламба после линеаризации в общем виде следует
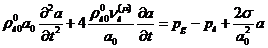

Пренебрегая
действием поверхностного натяжения на межфазной поверхности 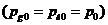 из этого уравнения получим
из этого уравнения получим
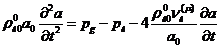
Дисперсия
звука из-за вязкости. Примем адиабатическое поведение газовых пузырьков [3] и
тогда
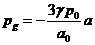
Решение
системы уравнений для возмущений 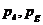 и
и 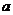 ищем в виде
ищем в виде  . Из
условия существования нетривиального решения получим следующее дисперсионное
уравнение
. Из
условия существования нетривиального решения получим следующее дисперсионное
уравнение
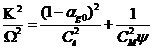 ,
, 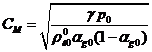
 ,
,  ,
, 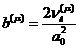 .
.
Будем
рассматривать  волны
волны 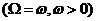 . Тогда
при
. Тогда
при  и
и 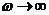 получим
соответственно равновесную и замороженную скорости звука.
получим
соответственно равновесную и замороженную скорости звука.
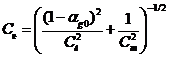 и
и 
Поскольку
для пузырьковой жидкости 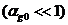 , то, как бы было ранее, при объемных содержаниях
газовой фазы, удовлетворяющих условию
, то, как бы было ранее, при объемных содержаниях
газовой фазы, удовлетворяющих условию 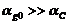 ,
, 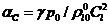 , сжимаемость жидкости несущественна и для величины
равновесной скорости звука можем записать
, сжимаемость жидкости несущественна и для величины
равновесной скорости звука можем записать
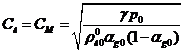
При
высоких частотах 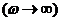 радиальное движение пузырьков «замораживается»
радиальное движение пузырьков «замораживается»  из-за инерции окружающей пузырек жидкости, и поэтому
сжимаемость смеси определяется сжимаемостью несущей фазы. Поэтому скорость
звука близка к скорости звука в чистой жидкости
из-за инерции окружающей пузырек жидкости, и поэтому
сжимаемость смеси определяется сжимаемостью несущей фазы. Поэтому скорость
звука близка к скорости звука в чистой жидкости 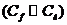 .
.
Для
низких частот  при
при 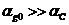 из
дисперсионного уравнения (2.6) следует
из
дисперсионного уравнения (2.6) следует

или
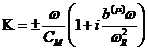
Отсюда
для фазовой скорости и коэффициента затухания можем получить
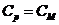 ,
, 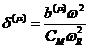 ,
, 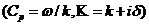
С
учетом выражений для 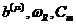 из (2.2) отсюда для коэффициента затухания
из (2.2) отсюда для коэффициента затухания  имеем
имеем
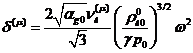
Интересно
отметить, что коэффициент затухания за счет вязкости несущей жидкости не
зависит от радиуса дисперсной фазы.
Дисперсия
из-за межфазного теплообмена.[3] Будем учитывать теплообмен газовых пузырьков с
окружающей жидкостью, но ее вязкостью пренебрегаем. Тогда на основе уравнений
(2.3), (2.4), а также уравнений для давления газа и теплопроводности из
предыдущего раздела вместо (2.5) получим дисперсионное уравнение вида (2.6).
При этом, для частотной функции 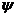 ,отвечающей
за дисперсию, будем иметь
,отвечающей
за дисперсию, будем иметь
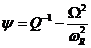 ,
, 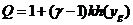
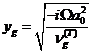 ,
, 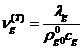 .
.
Рассмотрим
также  волны, для которых
волны, для которых  и
и 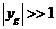
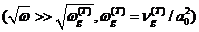 .
.
Для
такого частотного диапазона следует
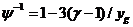
Подставляя
это выражение в дисперсионное уравнение из (2.6) получим

В
том случае, когда объемное содержание пузырьков мало 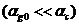 , из (2.15) для фазовой скорости
, из (2.15) для фазовой скорости  и коэффициента затухания
и коэффициента затухания 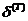
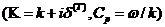 следует
следует
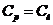 ,
, 
С
учетом выражения для  из (2.6) при
из (2.6) при  имеем
имеем
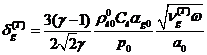
Когда
объемное содержание газовой фазы высоко 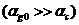 из
(2.15) получим
из
(2.15) получим
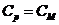 ,
, 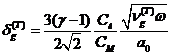
Выражение
для коэффициента затухания можно привести к виду
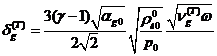
7. РЕЗУЛЬТАТЫ
ЧИСЛЕННЫХ РАСЧЕТОВ
В качестве примера пузырьковой жидкости [6] рассмотрим смесь воды с
воздушными включениями. В численных расчетах использовались следующие значения
теплофизических [5] параметров при p0=0.1 МПа, T0=300 К: для
воды- Cl=1500 м/с, l00=1000 кг/м3; для воздуха - g00=1.3 кг/м3, сg=1006
Дж/(кг·К), g=0.026 Вт/(м·К). Для значения радиуса
пузырьков приняли следующее значение a0=10-3 м. На рис.1 и рис.2 представлены зависимости фазовой скорости и коэффициента
затухания звука от частоты, иллюстрирующие влияние величины объемного
содержания воздуха. Сплошные и пунктирные линии здесь соответствуют значениям
объемного содержания газовой фазы αg0 =10-3 и 10-4.
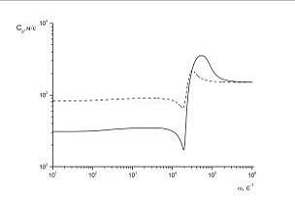
Рис. 1. Фазовая скорость
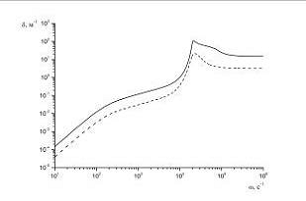
Рис. 2. Коэффициент затухания
Из
этих графиков видно три характерных диапазона частот, где существенно
различаются не только количественная, но и качественная картина дисперсионных
кривых. В области низких частот (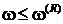 )
величина фазовой скорости в пузырьковой жидкости меньше скорости в чистой
жидкости, причем её величина с ростом частоты также растет от значения,
определяемого из выражения
)
величина фазовой скорости в пузырьковой жидкости меньше скорости в чистой
жидкости, причем её величина с ростом частоты также растет от значения,
определяемого из выражения
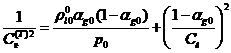
до
значения
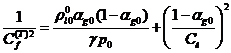
На
основе дисперсионного уравнения (2.6) нетрудно получить также следующие
асимптотические формулы для зависимости коэффициента затухания от частоты
возмущений
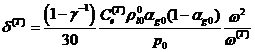 при
при  и
и
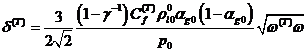 при
при  .
.
В
диапазоне частот 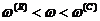
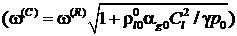 величины коэффициента затухания и фазовой скорости
принимают аномально высокие значения, поэтому эта зона частот соответствует
полосе непрозрачности. Вне этого диапазона
величины коэффициента затухания и фазовой скорости
принимают аномально высокие значения, поэтому эта зона частот соответствует
полосе непрозрачности. Вне этого диапазона 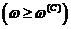 скорость
звука и коэффициент затухания стремятся к значениям
скорость
звука и коэффициент затухания стремятся к значениям
 и
и 
Поскольку
для пузырьковой жидкости  , то при объемных содержаниях газовой фазы,
удовлетворяющих условию
, то при объемных содержаниях газовой фазы,
удовлетворяющих условию 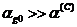 (
( ),
сжимаемость жидкости несущественна и для величины равновесной скорости звука из
формул следует, что
),
сжимаемость жидкости несущественна и для величины равновесной скорости звука из
формул следует, что  . При высоких частотах
. При высоких частотах 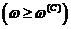 радиальное
движение пузырьков «замораживается» из-за инерции окружающей жидкости и,
поэтому, сжимаемость смеси определяется сжимаемостью несущей фазы. В связи с
этим скорость звука близка к скорости звука в чистой жидкости
радиальное
движение пузырьков «замораживается» из-за инерции окружающей жидкости и,
поэтому, сжимаемость смеси определяется сжимаемостью несущей фазы. В связи с
этим скорость звука близка к скорости звука в чистой жидкости  .
.
Далее проведем сравнительный анализ двух пузырьковых жидкостей, в
качестве второй возьмем этиловый спирт с воздушными включениями. В численных
расчетах использовались значения следующих теплофизических параметров при p0=0.1 МПа, T0=300 К: для воды - Cl=1500 м/с, l00=1000 кг/м3;
для воздуха - g00=1.3 кг/м3, сg=1006 Дж/(кг·К), g=0.026 Вт/(м·К), а для спирта : Cl=1150 м/с, l00=800 кг/м3. Для значения радиуса и объемного содержания
пузырьков приняли следующее значение a0=10-3 и αg0 =10-3 соответственно.

Рис. 3
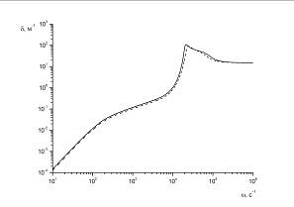
Рис. 4.
Из
рис.3 видно, что две дисперсные кривые малозначительно отличаются друг от
друга, хотя в диапазоне 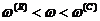 различие становится видимым. Но, несмотря на эти
различия, скорость звука при высоких частотах
различие становится видимым. Но, несмотря на эти
различия, скорость звука при высоких частотах 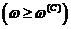 в
водовоздушной и спиртовоздушной смесях будет стремиться к скорости звука в
чистой жидкости. Что касается рис.4, то обе кривые практически совпадают на
всех диапазонах частот.
в
водовоздушной и спиртовоздушной смесях будет стремиться к скорости звука в
чистой жидкости. Что касается рис.4, то обе кривые практически совпадают на
всех диапазонах частот.
ЗАКЛЮЧЕНИЕ
В данной курсовой работе мы провели теоретическое исследование
зависимости фазовой скорости и коэффициента затухания от частоты в смеси воды с
воздушными включениями при значениях объемного содержания газовой фазы αg0 =10-3 и 10-4. Провели сравнительный
дисперсионный анализ двух пузырьковых жидкостей с различными несущими фазами.
Пришли к выводу, что скорость звука в водовоздушной и спиртовоздушной смесях
распространяется одинаково и стремится к скорости звука в чистой жидкости. Что
касается коэффициентов затухания, то они практически совпадают.
СПИСОК
ЛИТЕРАТУРЫ
1. Нигматулин
Р.И. Динамика многофазных сред. М.: Наука, 1987.
2. Накоряков
В.Е., Покусаев Б.Г., Шрейбер И.Р. Волновая динамика газо- и парожидкостных
сред. М.: Энергоатомиздат, 1990. 248 с.
3. Нигматуллин
Р. И., Шагапов В. Ш., Вахитова Н. К. Проявление сжимаемости несущей фазы при
распространении волн в пузырьковой среде ДАН СССР. 1989. Т. 304. № 35. С. 1077-1081.
4. Лепендин
Л.Ф. Акустика. М.: Высшая школа, 1978.
5. Варгафтик
Н.Б. Справочник по теплофизическим свойствам газов и жидкостей. М.: Наука,
1972.
6. Сарапулова
В.В. Особенности преломления и отражения звука на границе раздела между водой и
пузырьковой жидкостью // Вестник КемГУ. Вып. 2 (58). Т.2. 2014.