Моделирование системы управления
Содержание
Введение
. Постановка задачи управления
. Нахождение оптимального
управления по квадратичному функционалу качества
. Нахождение управления
оптимального по точности
. Нахождение управления
оптимального по критерию Кросовского
. Нахождение управления
оптимального по быстродействию
. Сравнение результатов
моделирования
Заключение
Библиографический список
Введение
Целью данной курсовой работы по дисциплине
«Основы автоматизированного вентильного электропривода» является нахождение и
моделирование оптимального управления объектом, заданным системой уравнений, по
квадратичному функционалу качества, по точности, по критерию Красовского и по
быстродействию.
Заключительным этапом работы является сравнение
полученных результатов моделирования, на основе которого сделаем вывод, какое
управление будет оптимально для заданного объекта.
управление моделирование краковский
математический
1.
Постановка
задачи управления
Задан нелинейный объект управления третьего
порядка, который описывается дифференциальными уравнениями:
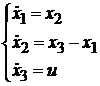
На управление накладывается
ограничение: 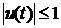 .
.
Необходимо выполнить следующее:
. составить структурную схему для
заданной системы;
. найти управление оптимальное по
точности, оптимальное по быстродействию, оптимальное по квадратичному
функционалу качества и по критерию Красовского.
. полученные результаты
промоделировать математическом пакете (в работе используется пакеты MathCAD и Matlab).
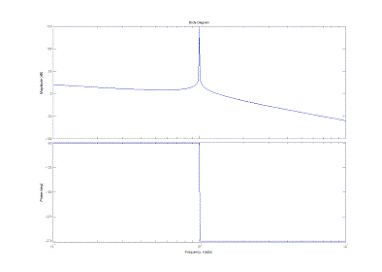
Рис. 1.1. ЛЧХ и ФЧХ системы
Учитывая критерий В.А. Бесекерского,
в нашем случае имеем неустойчивую систему.
Введем корректирующий устройство и
отрицательную обратную связь. Получим систему вида:
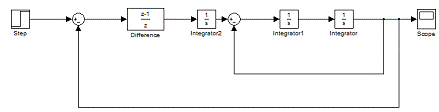
Рис. 1.2. Структурная схема
скорректированной системы.
Данная система устойчива, на чем
убеждаемся, посмотрев на график переходного процесса при подаче единичного
скачка на вход:
2. Нахождение оптимального управления по
квадратичному функционалу качества
Запишем уравнение Р. Беллмана
 (2.1)
(2.1)
Перепишем уравнение (2.1)
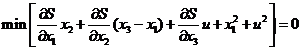 (2.2)
(2.2)
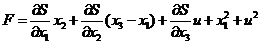 (2.3)
(2.3)
Для определения оптимального
управления дифференцируем выражение в фигурных скобках по u и получаем
уравнение (2.4).
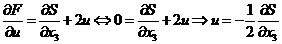 (2.4)
(2.4)
Уравнение (2.4) подставим в
уравнение (2.2) и получим уравнение (2.5) для рассматриваемой задачи
оптимального управления.
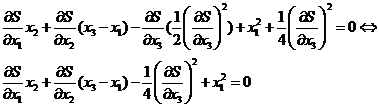 (2.5)
(2.5)
Функцию S(X) представим
в виде уравнения (2.6)

Продифференцируем уравнение (2.6) по
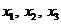 и получим
три уравнения
и получим
три уравнения

Подставляя производные (2.7), (2.8),
(2.9) в уравнение (2.5) и приравнивая коэффициенты при одинаковых произведениях
координат объекта, получим систему алгебраических уравнений для определения
коэффициентов 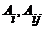 .
.
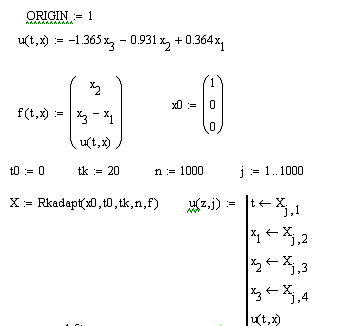

Рис. 2.1. График управления 

Рис. 2.2. Переходный процесс для 
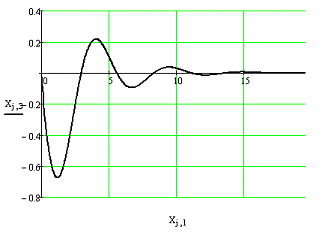
Рис. 2.3. Переходный процесс для 

Рис. 2.4. Переходный процесс для 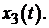
. Нахождение управления оптимального
по точности
Функциональное уравнение в общем
виде имеет вид:
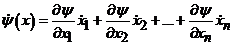 (3.1)
(3.1)
где n - порядок
системы.
Для нашей системы функциональное
уравнение примет вид:
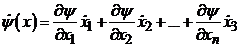 (3.2)
(3.2)
Поделим выражение на  и обозначим
и обозначим
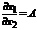 ,
,  , тогда
получим
, тогда
получим
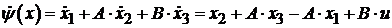 (3.3)
(3.3)
Пусть A=B= 1, тогда:
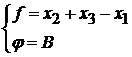 (3.4)
(3.4)
Для управляемости объекта по
точности, необходимо выполнить условие:
 (3.5)
(3.5)
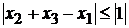 (3.6)
(3.6)
Управление примет вид
 (3.7)
(3.7)
Промоделируем систему в MathCAD при релейном
управлении:


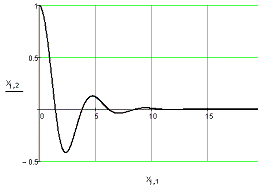
Рис. 3.2. Переходный процесс для 
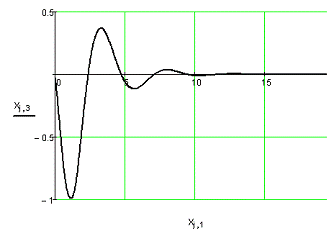
Рис. 3.3. Переходный процесс для 
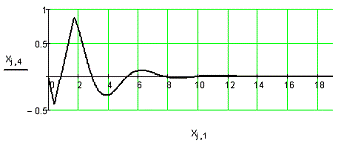
Рис. 3.4. Переходный процесс для 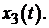
. Нахождение управления оптимального
по критерию Красовского
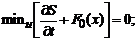 (4.1)
(4.1)
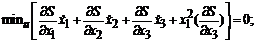 (4.2)
(4.2)
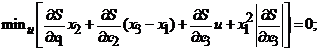 (4.3)
(4.3)
Согласно критерию Красовского:
 (4.4)
(4.4)
Подставим (4.4) в (4.3), получим:
 (4.5)
(4.5)
Функцию  будем
определять до третьей степени членов ряда в виде стандартного степенного ряда:
будем
определять до третьей степени членов ряда в виде стандартного степенного ряда:
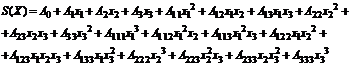 (4.6)
(4.6)
Частные производные от функции  по
координатам объекта
по
координатам объекта 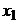 ,
, 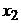 и
и 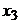 имеют вид:
имеют вид:
 (4.7)
(4.7)
Подставляя производные (4.7), в
уравнение (4.5) и приравнивая коэффициенты при одинаковых произведениях
координат объекта, получим систему алгебраических уравнений для определения
коэффициентов 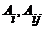 .
.
Так как мы ограничиваемся третьей степенью
членов ряда, решить систему уравнений (4.8) не представляется возможным,
поскольку каждая предыдущая система содержит неизвестные члены следующей
системы, и общее число неизвестных каждой системы, больше числа ее уравнений.
Следовательно, для данного объекта найти оптимальное управление по критерию
Красовского не представляется возможным.
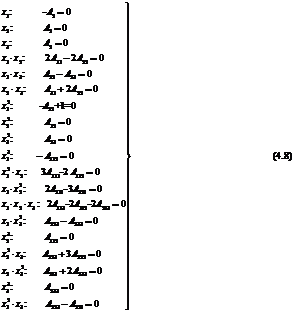
5. Нахождение управления оптимального по
быстродействию
Для поиска оптимального по быстродействию
управления используем способ, при котором функции переключения определяются,
начиная с последнего интервала до первого, поскольку в случае оптимальности
управления, рассмотрение его с конца по интервалам позволит получить общее
оптимальное управление, в противном случае полученное управление будет не
оптимальным. Найденные функции объединяются в одну общую функцию переключения и
записываются окончательное решение для оптимального управления.
На каждом интервале движения объект управления
теряет одну степень свободы, т.е. фазовое пространство объекта сжимается на
единицу, и на третьем интервале будет состоять всего из одной координаты, т.е.
функция переключения имеет вид:
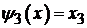 , (5.1)
, (5.1)
откуда следует, что эквивалентное
оптимальное управление на этом интервале запишется:
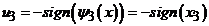 (5.2)
(5.2)
На 2-м интервале производная от
функции переключения имеет вид
 , (5.3)
, (5.3)
при  имеем:
имеем:
 , (5.4)
, (5.4)
с учетом (4.1) получим:
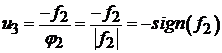 (5.5)
(5.5)
Согласно (4.3), (4.4) имеем
тождество:
 (5.6)
(5.6)
На основе (4.1) и (4.8) выражение
(4.5) имеет вид:
 (5.7)
(5.7)
Функция переключения на втором интервале:
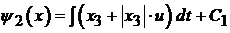 (5.8)
(5.8)
 (5.9)
(5.9)
Поделим выражение (5.7) на 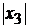 (поскольку
(поскольку
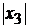 положительно
определенная функция, то это изменит только амплитуду и не повлияет на моменты
переключения):
положительно
определенная функция, то это изменит только амплитуду и не повлияет на моменты
переключения):
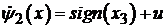 (5.10)
(5.10)
Введем замену: 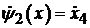 , при этом
константа С1 в (5.10) будет определять значение
, при этом
константа С1 в (5.10) будет определять значение 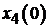 .
.
На 1-м интервале производная от
функции переключения имеет вид
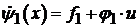 , (5.11)
, (5.11)
при 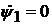 имеем:
имеем:
 , (5.12)
, (5.12)
с учетом (5.1) получим:
 (5.13)
(5.13)
Согласно (5.11) имеем тождество:
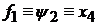 (5.14)
(5.14)
На основе (5.1) и (5.16) выражение
(5.13) имеет вид:
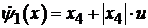 (5.15)
(5.15)
Функция переключения на первом
интервале:
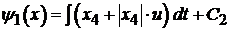 (5.16)
(5.16)
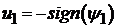 (5.17)
(5.17)
Поделим выражение (5.17) на  :
:
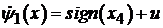 (5.18)
(5.18)
Введем замену: 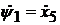 , при этом
константа С2 в (5.16) будет определять
, при этом
константа С2 в (5.16) будет определять 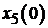 .
.
В итоге в системе MathCad необходимо
промоделировать следующую систему пятого порядка:
 , при
начальных условиях
, при
начальных условиях
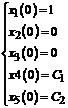 , (5.19)
, (5.19)
где 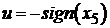 .
.

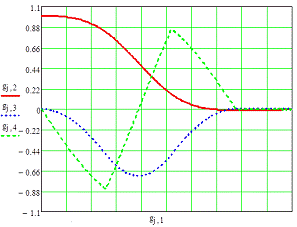
Рис. 5.1. Переходные процессы для 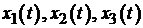
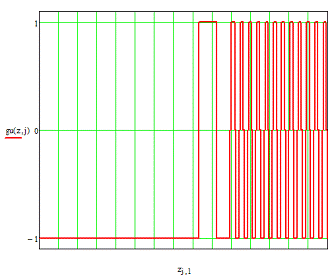
Рис. 5.2. График управления 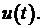
. Сравнение результатов
моделирования
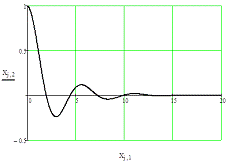
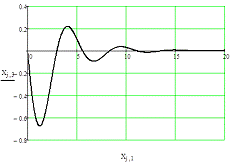
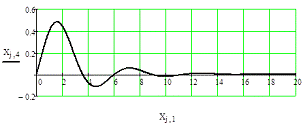
Рис. 6.1. Графики переходных процессов для x1,
x2,
x3
для управления, оптимального по квадратичному функционалу качества.
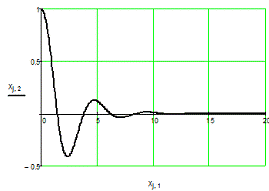
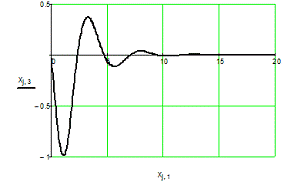
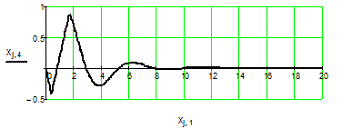
Рис. 6.2. Графики переходных процессов для x1,
x2,
x3
для управления, оптимального по точности.
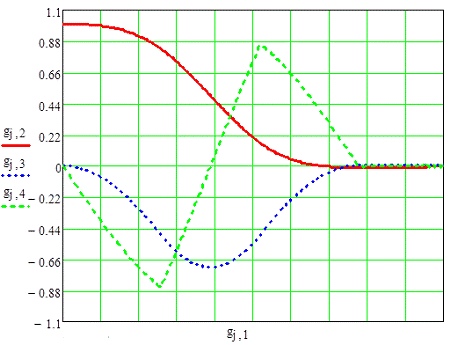
Рис. 6.3. Графики переходных процессов для x1,
x2,
x3
для управления, оптимального по быстродействию.
Заключение
В ходе выполнения данной курсовой работе на
первом этапе был получен закон оптимального управления по квадратичному
функционалу качества, для объекта, описываемого системой дифференциальных
уравнений, переходный процесс длится 13 секунд.
На втором этапе был получен закон оптимального
управления по точности - переходный процесс длится 11 секунд.
На третьем этапе был получен закон оптимального
управления по быстродействию. На этом этапе трудность решения задачи составляла
в подборе констант интегрирования С1 и С2.
После подбора и моделирования системы управления получили требуемый переходный
процесс, который длится 7.2 секунды.
После сравнения 3-х законов управления можно
сказать, что для исследуемой системы наиболее оптимальным управлением является
управление оптимальное по быстродействию, так как при этом управлении время
переходного процесса минимально.