Флуктуация и методы её вычисления

Содержание

флуктуация объём жидкость температура

Введение

Глава I.Понятие о флуктуации и методы её вычисления

.1 Общее понятие о флуктуации

.2 Расчет флуктуации с помощью канонического распределения Гиббса

1.3 Другой метод вычисления флуктуаций

1.4 Оценка вероятности флуктуации в малой подсистеме, находящейся в контакте с термостатом

1.5 Флуктуации объема и плотности

1.6 Флуктуации температуры, энтропии и давления

Глава 2. Флуктуации объёма и прогнозирование равновесных свойств жидкостей

.1 Флуктуации плотности и скорость звука

2.2 Методика расчета плотности под давлением по данным о флуктуации объема

Заключение

Список использованной литературы

Введение

Актуальность темы. Гипотеза о существовании атомов, из которых состоит вещество, родилась в древней Греции. Однако до середины 19 века она оставалась одним из возможных вариантов микроструктуры Вселенной.

В наше время развитие физики на мезоскопическом уровне и ее приложений (прежде всего в области нанотехнологий) связано с возрастанием интереса к изучению все более хаотических, в том числе низкоразмерных систем. Для подобных систем даже в тепловом равновесии или вблизи него весьма существенны флуктуации физических величин.

Разумно предположить, что место физики флуктуаций в будущем станет еще более значительным. Между тем с теоретической точки зрения ситуацию с описанием флуктуаций еще нельзя считать вполне удовлетворительной. Если даже отвлечься от нерешенной пока проблемы взаимосвязи квантоводинамических и термодинамических флуктуаций, следует признать, что последовательное описание собственно термодинамических флуктуаций физических величин, характеризующих макросистему в тепловом равновесии вблизи него, по существу отсутствует.

Основные положения теории флуктуаций были разработаны в начале прошлого столетия. Авторами этих публикаций были двое молодых ученых, работавших в одиночестве и вдалеке от ведущих научных центров: сотрудник патентного бюро в Цюрихе (Швейцария) Альберт Энштейн, родившейся в 1879 году, и профессор теоретической физики Львовского университета (Австро-Венгрия) Мариан Смолуховский, который родился на 7 лет раньше, в 1872 году. Кроме того, в соответствующих теоретических работах появилась непротиворечивая статистическая интерпретация второго закона термодинамики, причем, что очень важно, были поняты и сформулированы ограничения на его применение. Здесь имеются в виду совокупности работ по теории броуновского движения и теории флуктуаций.

Энштейн и Смолуховский работали над указанным кругом вопросов с начала 20 века и до первой мировой войны. Они решили ключевые проблемы, размышляя по большей части независимо, а иногда, - опираясь на результаты друг друга.

Задачи исследования. В связи с вышеизложенным в работе ставились следующие цели:

.        Рассмотреть понятие флуктуации, методы её вычисления и её связь с основными термодинамическими параметрами;

.        Исследовать возможность флуктуации объёма для прогнозирования равновесных свойств жидкостей.

Глава I.Понятие о флуктуации и методы её вычисления

.1 Общее понятие о флуктуации

Статистическая физика приводит к выводу, что в системе обязательно происходят самопроизвольные отклонения от равновесного состояния. При этом значения давления, плотности и других величин хаотически колеблются около некоторых средних или, как их еще называют, равновесных значений. Неупорядоченные спонтанные отклонения какого-либо параметра от его равновесного значения, возникающие вследствие хаотичности внутреннего движения в системе, называются флуктуациями этой физической величины

Обычно они малы и поэтому в макроскопическом плане не заметны. Однако есть явления, которые целиком объясняются флуктуациями тех или иных параметров. К ним относятся, например, молекулярное рассеяние света и броуновское движение. Очень важно, что флуктуации ставят естественный предел точности измерений физических величин.

Наличие флуктуации есть неизбежное следствие атомного строения вещества и хаотичности теплового движения, а эти представления лежат в основе статистической физики. Поэтому теоретическое исследование флуктуационных явлений в работах Эйнштейна, Смолуховского и других физиков и опытная проверка полученных результатов в начале нашего века были важным этапом в истории физики. Именно тогда впервые были получены прямые доказательства существования атомов и справедливости постулатов статистической теории, к которой некоторые ученые того времени относились с недоверием. До этого в физической науке признавали только строго детерминистские динамические закономерности. Вероятностные концепции физической статистики (а впоследствии и квантовой механики) потребовали радикального пересмотра самых фундаментальных представлений о строении и движении материи.

В качестве количественной меры флуктуаций любой физической величины берется среднеквадратичное oтклонение от среднего, т.е. равновесного значения. Флуктуацией параметра F будет величина

 (1)

Отношение

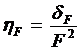 (2)

определяет относительную флуктуацию этого же параметра. Для нахождения hF и dF необходимо знать закон распределения вероятностей для микросостояний системы, поскольку каждому микросостоянию соответствует определенное значение величины F.

.2 Расчет флуктуации с помощью канонического распределения Гиббса

Системы, находящиеся в равновесии с термостатом, подчиняются каноническому распределению Гиббса. Температура, число частиц и внешние параметры таких систем считаются фиксированными, энергия и некоторые другие характеристики флуктуируют около равновесных значений. В качестве примера вычислим флуктуацию энергии Е. Согласно (1) расчет флуктуации потребует нахождения средних по распределению Гиббса.

Запишем классическое каноническое распределение. При e = E

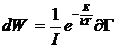 (3)

где I статистический интеграл и он равен

 (4)

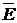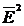Для вычисления dE необходимо знать  и . Эти величины определяются формулами

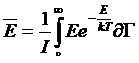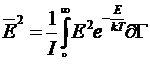;  (5)

Заметим, что

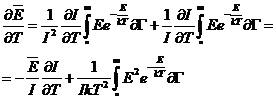 (6)

Воспользуемся ранее полученным выражением для энергии. Запишем его как

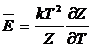 (7)

Учитывая, что в классической статистике роль статистической суммы Z играет интеграл I, получаем:

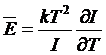 (8)

Используя это выражение, находим, что

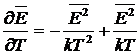 (9)

Таким образом, оказывается, что

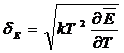 (10)

Величина 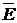 есть термодинамическая внутренняя энергия U. Используя известное соотношение

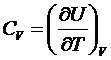 (11)

приходим к формуле

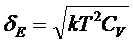 (12)

В частности, для одноатомного идеального газа

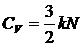 (13)

Откуда

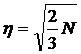; (14)

Поскольку обычно число частиц велико, флуктуации энергии пренебрежимо малы.

Нахождение флуктуации энергии оказалось относительно простым потому, что энергия в качестве переменной входит непосредственно в распределение Гиббса. Для вычисления флуктуации других величин удобнее использовать другие формы канонического распределения.

В частности, для нахождения флуктуации числа частиц применим каноническое распределение. Из формулы следует:

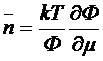 (15)

где Ф - статистическая сумма. Для среднего значения  имеем:

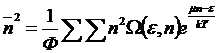 (16)

Дифференцируя (15) по μ, нетрудно показать, что

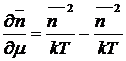 (17)

Таким образом,

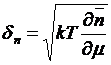 (18)

Применим эту формулу к идеальному газу, химический потенциал которого был найден. В результате простого расчета имеем:

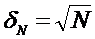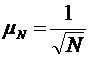
;  (19)

.3 Другой метод вычисления флуктуаций

Во многих задачах вычисление флуктуации через каноническое распределение оказывается слишком сложным. Другой подход, описанный ниже, позволяет выразить вероятность флуктуации любой физической величины через непосредственно измеряемые термодинамические характеристики системы.

Флуктуации соответствует переход системы от более вероятного состояния к менее вероятному, или, согласно термодинамике, переход из состояния с большей энтропией в состояние с меньшей энтропией. Эйнштейн предложил использовать формулу Больцмана , применив ее для вычисления вероятностей состояний системы через изменение энтропии. В соответствии с этим вероятность флуктуации, связанной с малым изменением параметра x определяется выражением

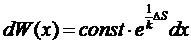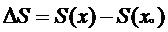 ;  (20)

где x0 - значение x в равновесном состоянии.

Чтобы понять, как это делается, рассмотрим рисунок (1). В равновесных системах при фиксированных внешних параметрах энтропия и внутренняя энергия являются функциями только температуры. Энергия - всегда однозначная функция состояния. Это позволяет построить зависимость энтропии от энергии рис. 1.

Рис. 1.

Предположим, что система находилась сначала в равновесном состоянии а, а потом и результате флуктуации перешла в состояние b, отличающееся от а значением некоторого параметра x . Переход ab неравновесный, на чертеже он изображен пунктиром. Флуктуации соответствует уменьшение энтропии на ∆S. Энергия системы осталась прежней, так как флуктуации происходят самопроизвольно, без внешнего воздействия.

Теперь мысленно проделаем следующее. Возьмем систему в равновесном состоянии c, близком к a. Это состояние выбирается из условия Sc = Sb. Далее, путем наложения на систему внешних полей приведем ее с помощью равновесного адиабатического процесса в состояние, в котором параметр x примет то же значение, что и в состоянии b. Этот переход изображен отрезком прямой cb. Если внезапно выключить внешнее поле, то система, до этого бывшая в состоянии равновесия, окажется вдруг в неравновесном состоянии b, том же самом, которое возникло в результате флуктуации.

При малых отклонениях от равновесия изменения всех величин будут незначительными. Поэтому с достаточной точностью можно полагать, что

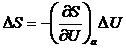 (21)

где ∆U - изменение энергии системы в результате воздействия внешних полей. Согласно термодинамике при адиабатическом процессе ∆U = - δA. Пусть δA элементарная работа системы при равновесном переходе cb. Замечая, что 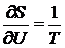, для оценки вероятности флуктуации получаем:

 (22)

Если в эту формулу ввести работу внешних сил над системой, то в показателе экспоненты изменится знак. Приложения найденного соотношения (22) для определения флуктуации термодинамических параметров системы рассматриваются в следующем параграфе.

.4 Оценка вероятности флуктуации в малой подсистеме, находящейся в контакте с термостатом

Найдем вероятность малого отклонения от равновесия, которое происходит в системе, находящейся в контакте с термостатом. Пусть это будет некоторая подсистема, погруженная в среду, с которой она находится во взаимодействии. Это может быть небольшая масса вещества, выделенная из полной массы. Формально допустимо полагать, что малая подсистема находится в цилиндре с идеально теплопроводными стенками. От остальной части вещества подсистему отделяет поршень, движущийся без инерции и трения. Предположим также, что выделенная подсистема может совершать работу над каким-нибудь внешним телом, не входящим и комплекс "подсистема-термостат". (В целом комплекс представляет собой сложную систему, заключенную в адиабатическую оболочку и имеющую постоянные внешние параметры.)

Допустим, что вся система сначала находилась в равновесии, а потом равновесие нарушилось. Отклонение от равновесия заключается в изменении состояния выделенной подсистемы, ее характеристики уже не совпадают с равновесными.

Изменится и состояние термостата вследствие взаимодействия с изучаемой подсистемой. Будем считать, что при этом равновесие в среде не нарушается, в ней сохраняются равновесные значения давления и температуры (Ро и То).

Такое же, как при флуктуации, изменение состояния подсистемы можно вызвать, предоставив ей возможность совершить работу над внешним телом. Именно эта работа входит в формулу (22). По предположению процесс, связанный с совершением работы, является равновесным. Поэтому работа может быть вычислена по формуле:

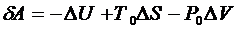 (23)

Простая система имеет только два независимых параметра. При малых ∆S и ∆V приращение ∆U c точностью до членов второго порядка малости включительно равно

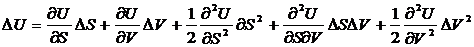 (24)

Производные берутся в точке начального равновесного состояния. Учитывая, что

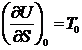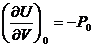;  (25)

получаем для работы выражение

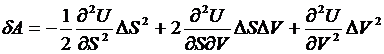 (26)

Выпадение членов первого порядка малости не является случайным. Состоянию равновесия соответствует максимум энтропии. Поэтому формула для вероятности флуктуации (20) с точностью до членов второго порядка малости имеет вид

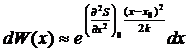 (27)

Мы получили важный результат: в указанном приближении распределение вероятностей для флуктуации имеет вид Гауссовского нормального распределения. Кроме того, поскольку (22) вытекает из (20), постольку работа (23) должна выражаться в итоге через квадратичные по (x-x0) члены. Этот вывод сохранит свое значение и для того случая, когда отклонение от равновесия сопряжено с изменением не одного, а нескольких параметров системы.

Используем теперь математические тождества

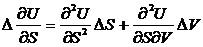 (28)

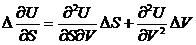 (29)

и запишем (26) в виде

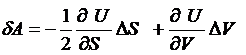 (30)

Учитывая, что

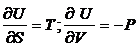 (31)

получаем:

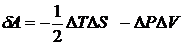 (32)

где ∆T ,∆S , ∆P и ∆V-изменения величин, возникшие в результате флуктуации.

Таким образом, вероятность произвольной флуктуации в выделенной подсистеме определяется формулой

 (33)

Чтобы система была устойчивой по отношению к флуктуациям, необходимо выполнение условия

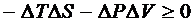 (34)

т.е. при любом отклонении от равновесия разность должна быть положительна. В противном случае оказывается, что вероятность флуктуации тем больше, чем дальше отходит от равновесия система. Тогда она не может существовать в прежнем состоянии, и равновесие будет неустойчивым.

.5 Флуктуации объема и плотности

Формула (33) удобна для нахождения флуктуации ряда величин. Рассмотрим флуктуации объема системы при постоянной температуре. В соответствии с условием задачи полагаем:

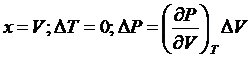 (35)

где ∆V = V - V0.

Tогда

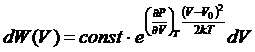 (36)

Причем из требования устойчивости равновесия следует неравенство

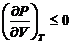 (37)

Запишем распределение (36) в стандартной форме Гауссовского распределения вероятностей:

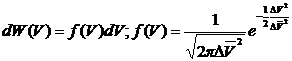 (38)

Сравнение формул (36) и (38) дает

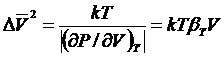 (39)

где βT - изотермический коэффициент сжимаемости. Для идеального газа

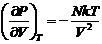 (40)

Следовательно,

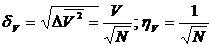 (41)

Флуктуации объема оказываются тем меньше, чем больше частиц в системе. Через флуктуацию объема легко выразить флуктуацию плотности:

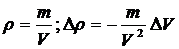 (42)

Из этого следует:

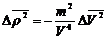 (43)

И

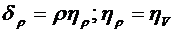 (44)

Отметим важную деталь. Найденное распределение (36) теряет смысл, если 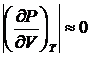. Когда эта производная равна нулю или просто мала, то становятся весьма вероятными большие отклонения от равновесия. Такая ситуация складывается, например, в критической точке и ее окрестности. Сжимаемость вещества в этой области настолько велика, что малые силы вызывают большие изменения объема. Из-за этого флуктуации плотности не только велики, но, что самое главное, они теряют свой местный, точечный характер, захватывая всю систему. Наш метод изучения флуктуации в этом случае не пригоден.

.6 Флуктуации температуры, энтропии и давления

Рассмотрим такие нарушения равновесия, когда изменяются сразу несколько термодинамических параметров. Пусть, например, одновременно отклоняются от равновесных значений объем и температура. В этом случае формула (33) принимает вид

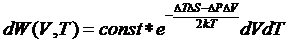 (45)

Изменения энтропии и давления определяются через приращение объема и температуры:

 (46)

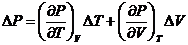 (47)

Если использовать термодинамические соотношения

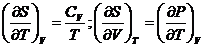 (48)

То

Отсюда

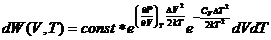 (50)

Данный результат показывает, что флуктуации температуры и объема статистически независимы и их можно рассматривать отдельно друг от друга. Сравнивая распределение вероятностей для значений температуры с Гауссовским нормальным распределением , находим флуктуацию температуры:

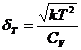 (51)

Заметим, что для устойчивости системы относительно флуктуации необходимо, чтобы CV > 0.

Выберем теперь в качестве независимых переменных энтропию и давление. Запишем формулу (36) в виде

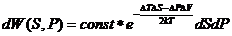 (52)

Раскроем значения приращений температуры и объема:

 (53)

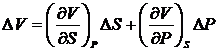 (54)

Если воспользоваться термодинамическими соотношениями

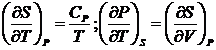 (55)

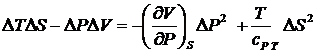 (56)

Получаем распределение

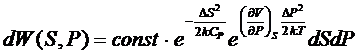 (57)

Отсюда следует, что флуктуации энтропии и давления независимы друг от друга. Если привести распределения для вероятностей флуктуации энтропии и давления к виду нормального Гауссовского распределения, то найдем значения флуктуации этих величин:

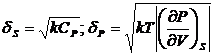 (58)

Очевидно, что изложенный метод пригоден для нахождения флуктуации любых термодинамических параметров.

Глава 2. Флуктуации объёма и прогнозирование равновесных свойств жидкостей

.1 Флуктуации плотности и скорость звука

Термодинамическая теория флуктуации указывает на тесную связь средней квадратичной флуктуации объема/плотности с упругими свойствами вещества, которая дается соотношением

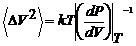 (66)

Сравнивая выражения для относительных флуктуаций объема идеального газа

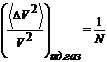 (67)

и произвольной среды при тех же условиях

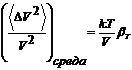 (68)

можно получить формулу для изотермической сжимаемости конденсированной системы

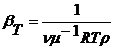 (69)

в которую входит безразмерный параметр n, равный отношению квадратов относительных флуктуациий объема идеального газа и данной среды.

Очевидно, что величина параметра n будет зависеть от характера и интенсивности межмолекулярных сил, т.е. в конечном счете, будет являться некоторой функцией плотности среды ρ, а в силу того, что флуктуации объема не зависят от температурных флуктуаций, можно ожидать, что n не будет явной функцией температуры T. Поэтому будем полагать, что

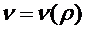 (70)

Из соотношения (69) можно получить и формулу для скорости звука

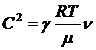 (71)

которая будет справедлива для различных сред.

Величина n изменяется в широких пределах: oт единицы в идеальном газе до нескольких десятков и сотен в конденсированной системе. При приближении к критической точке из-за неограниченного возрастания флуктуации плотности n→ 0.

Ранее на основе дифференциального уравнения состояния нами были получены формулы для изотермической сжимаемости βT и скорости звука С, с помощью которых легко установить, что n действительно определяется интенсивностью межмолекулярных сил и характером их зависимости от межмолекулярных расстояний.

В рамках классической статистической теории легко установить связь n с интегралом состояний:

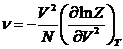 (72)

Здесь V- удельный объем, N - удельное число частиц в нем. Приведенное соотношение позволяет выделить в n часть, обусловленную взаимодействием частиц;

 (73)

Соотношение, аналогичное (69), впервые анализировалось в работах Филиппова. На основе большого эмпирического материала в указанных работах сделан вывод о том, что безразмерный параметр φ = n-1 зависит только от плотности и является исключительно удобным параметром теории соответственных состояний. В этих и других работах, однако не был вскрыт физический смысл величины φ, что не позволяло выделить φ из многочисленного семейства безразмерных параметров и объяснить его уникальные свойства. В силу указанных обстоятельств дополнительное внимание к изучению этого вопроса представляет вполне естественный интерес.

Используя имеющиеся экспериментальные данные по скорости звука, плотности, давлению насыщенных паров, теплоемкости, мы с помощью термодинамических соотношений произвели расчеты отношения теплоемкостей. Расчеты n выполнены далее по формуле (71). Полученные результаты были использованы для изучения зависимости n от ρ. С этой целью строились графики, в частности, в координатах ln (n-1) от ρ. Выбор логарифмической шкалы обусловлен экспоненциальным законом распределения флуктуаций, вычитание единицы из n связанное с тем, что в идеальном газе n=1.

Как следует из графиков, приведенных на рисунках 1-2, для жидкой фазы н-гексана и н-гептана, в весьма широкой области (от Тпл до Ткип) величина ln (n-1) практически линейно зависит от r. Это указывает на то, что зависимость n от r может быть представлена выражением

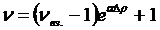 (74)

в котором a - эмпирическая константа, определяемая наклоном прямой, Dr - разность плотностей, соответствующих n и n0. Аналогичные зависимости n (r) в указанной области температур получены и для 1-хлоргексана и

-хлоргептана (рис. 4-5).

Если предположить, что характер зависимости n от r в однофазной области такой же, как и на линии насыщения, то с помощью соотношения (69) можно оценить величину изотермической сжимаемости вдоль произвольно выбранной изотермы.

В таблице I представлены значения изотермической сжимаемости н-гептана для нескольких изотерм в интервале давлений до 1000 бар и проведено сравнение с экспериментальными данными .

Как следует из табл.1, согласие представленных значений ßT вполне удовлетворительное.

Это свидетельствует о том, что линию насыщения можно рассматривать как совокупность базисных состояний жидкости, на основе которых формируются её свойства при других условиях.

Сходство молекулярной структуры и одинаковый характер меж-молекулярных сил н-алканов вполне оправдывает поиск корреляции их свойств с длиной цепи.

Таблица 1 ßT 10-11 Па-1

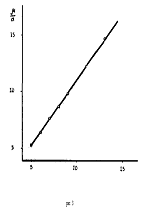
В связи с этим нами изучена зависимость константы a из (74) от числа метильных групп n. В результате установлено, что величина 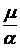 является практически линейной функцией n, которую можно представить соотношением

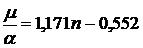 (75)

Об этом свидетельствуют график, представленный на рис. 3.

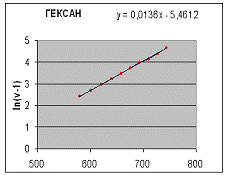
Рис. 1

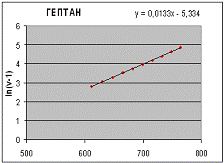
Рис. 2

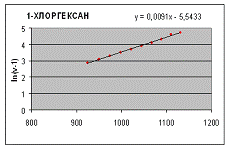
Рис. 4

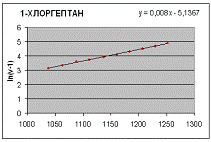
Рис. 5

2.2 Методика расчета плотности под давлением по данным о флуктуации объема

Общая теория флуктуаций, для вероятности произвольной флуктуации в выделенной термодинамической системе даёт формулу

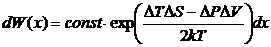 (76)

Эта формула удобна для нахождения флуктуации различных термодинамических величин. Рассмотрим флуктуацию объёма выделенной системы при постоянной температуре. В этом случае для вероятности флуктуации объёма получим следующее выражение

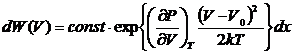 (77)

Так как вероятность флуктуации подчиняется каноническому распределению Гиббса, то значение const найдём из сравнения уравнения с уравнением, представляющим стандартную форму Гауссовского распределения вероятностей

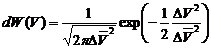 (78)

Сравнивая формулы (76) и (77) получим

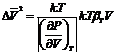 (79)

Для идеального газа эта формула будет иметь вид

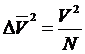 (80)

Как было показано в работе, сравнение выражений для относительных флуктуаций объема идеального газа и произвольной среды, взятой при тех же условиях, позволяет получить формулу

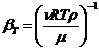 (81)

в которой n - безразмерный параметр, равный отношению квадратов относительных флуктуаций объемов идеального газа и данной среды.

Необходимо заметить, что ранее в работе для объяснения наблюдаемой величины времени релаксации в окрестности критической точки была получена аналогичное выражение:

в котором D - коэффициент переноса массы а D0 - его гипотетическое значение, которое было бы у системы с заданной плотностью, если бы она обладала свойствами идеального газа. Отсюда следует, что величина n, равная отношению квадратов относительных флуктуаций произвольной среды и идеального газа, эквивалентна отношению коэффициентов диффузии в среде и идеальном газе.

Из формулы (81) и выражения

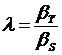 (83)

можно получить выражение для скорости звука

 (84)

Ранее в работе предпринималась попытка связать скорость звука с флуктуациями термодинамических величин. В результате была получена формула

 (85)

где 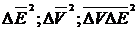 - средние квадратичные флуктуации внутренней энергии, объема и произведения объема и энергии соответственно. К сожалению, выражение (85) возможно применить только для идеального газа. Для реальных жидкостей и газов величины средних квадратичных флуктуации, входящих в формулу (85) неизвестны и, кроме того, их трудно выразить через термодинамические параметры среды. Применение (85) для идеального газа естественно приводит к известному выражению

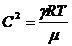 (86)

и не представляет интерес.

Из сравнения (84) и (86) следует, что для одинаковых состояний, квадрат скорости звука в реальных веществах в n раз больше чем в идеальном газе.

В рамках классической статистической теории легко установить связь n с интегралом состояний Z

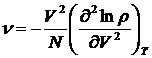 (87)

где V- удельный объем, N - удельное число частиц в нем.

Очевидно, что величина n-1 будет определяться интенсивностью и характером межмолекулярных сил и в силу этого будет некоторой функцией плотности.

В работе было показано, что в жидкой фазе н-гептана и других алканов в области температур от Тпл. до Ткип. величина ln(n-1) практически линейно зависит от r. В этом случае зависимость n от r будет экспоненциальной.

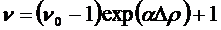 (88)

Здесь величина n0 соответствует некоторому начальному значению плотности, а a есть тангенс угла наклона прямой, на графике зависимости ln(n - 1) от r.

Экспериментальные данные, взятые для галогенозамещенных н-алканов, были использованы для расчета величины n. В результате появилась возможность проверить указанную выше зависимость ln(n-1) от r для нового класса веществ (1-хлоргексан, 1-хлоргептан,). Такой подбор веществ позволяет выявить степень универсальности наблюдаемого характера зависимости ln(n-1) от r.

Принимая во внимание независимость флуктуаций объема и температуры друг от друга, можно предположить, что величина n является только функцией плотности, характер зависимости которой в однофазной области такой же как и на линии насыщения. Указанная выше закономерность позволяет получить выражение для расчета плотности на изотерме в зависимости от давления.

Из уравнения (81) и определения изотермической сжимаемости

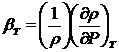 (89)

Получим

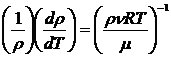 (90)

Разделяя переменные, будем иметь

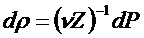 (91)

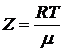где  а .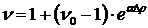

Далее, выполняя интегрирование приведенного выражения (91)

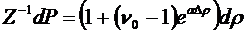 (92)

в промежутке от 0 до Dr, получим

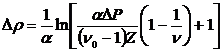 (93)

Приведенную формулу (93) можно использовать для подсчета величины Dr, характеризующей изменение плотности на изотерме, вызванное изменением давления на величину DR. При расчетах по формуле (93) следует принимать во внимание зависимость n от r.

Проверка уравнения (88) для различных жидкостей, включая инертные газы, циклические углеводороды и их галогенозамещенные позволяет сделать вывод, что соотношение (88) носит универсальный характер и может применяться для прогнозирования равновесных свойств жидкостей как на линии равновесия, так и в однофазной области.

Заключение

В заключение сделаем следующие выводы:

С помощью представления о флуктуациях объясняется ряд явлений, к которым относятся броуновское движение, опалесценция при критическом состоянии, рассеяние света в однородных жидкостях и газах, в частности голубой цвет неба. Теория флуктуаций позволяет выяснить механизм образования новой фазы в перенасыщенных парах и растворах при отсутствии зародышей.

Практическое значение флуктуаций возрастает с каждым годом, так как установлено, что флуктуации во многих случаях определяют свой предел чувствительности многих приборов, а также служат причиной случайных помех при радиоприеме и радиолокации ("флуктуационный фон").

Флуктуационные процессы широко распространены в природе. Приведем ряд примеров. Именно благодаря флуктуационным изменениям плотности воздуха обусловлен голубой цвет чистого неба. Благодаря флуктуациям осуществляется диффузия возникновение дефектов кристаллической решетки, так называемый "дробовой эффект" в электронных процессах, флуктуационными процессами обусловлена опалесценция в критической точке "жидкость-пар" и много-много других физических явлений, как в микромире так и в пределах космоса.

Проведенное в работе исследование позволяет сделать вывод о связи флуктуации плотности с скоростью звука. Рассмотрение характера этой связи приводит к выводу, что зависимость ln(n-1) от r является линейной для всех исследованных веществ. Можно высказать гипотезу об универсальности данной зависимости для широкого класса веществ. Это позволит использовать массив экспериментальных данных, полученных на линии насыщения, для прогнозирования равновесных свойств в однофазной области.

Список использованной литературы

1. Берклеевский. Курс физики, т. 5:Статистическая физика. М., Наука, 1973.

. Левич В.Г. Введение в статистическую физику. М., 1954

. Радушкевич Л.В. Курс статистической физики. М., Просвещение, 1966.

. Статистическая физика и квантовая теория поля / под ред. Боголюбова. М., Наука, 1973.

. Яворский Б.М. Справочник по физике. М., Наука, 1964.

. Мелентьев В.В. Комплексные исследования теплофизических свойств н-алканов и их галогенозамещенных. // Дисс. канд. физ.-мат. наук. - Курск: КГПУ, 1997. - 155 с.

. Скрипов В.П. Метастабильные жидкости. - М.: Наука, 1972. - 341 с.

. Неручев Ю.А., Зотов В.В., Шойтов Ю.С. Скорость звука и флуктуация плотности. // Ультразвук и термодинамические свойства вещества.- 1989.- С. 75.

. Пригожин И., Стенгерс И. Порядок из хаоса: Новый диалог человека с природой: Пер. с англ./ Общ. ред. В.И. Аршинова, Ю.Л. Климонтовича и Ю.В. Сачкова. - М.: Прогресс, 1986.-471 с.

. Эйнштейн А. Теоретическая атомистика // Эйнштейн А. Физика в реальность. М.: Наука, 1965. С. 20-33.

. Неручев В.А., Зотов В.В. Об уравнении состояния жидких н-алканов. - В сб.: Ультразвук и термодинамические свойства вещества. - Курск, 1986, с.84-89.

. Зотов В.В., Неручев Ю.А. Об упругих и калорических свойствах н-гексана на кривой равновесия жидкость-пар. В сб.: Ультразвук и термодинамические свойства вещества. - Курск, 1986, - с. 34-42