Аппроксимация функций методом наименьших квадратов

Министерство образования Российской Федерации

Санкт-Петербургский государственный горный институт им. Г.В. Плеханова (технический университет)

КУРСОВАЯ РАБОТА

По дисциплине ИНФОРМАТИКА

Тема: Аппроксимация функций методом наименьших квадратов

Автор: студент

Кузьмина В.Б.

Санкт-Петербург, 2012 год

Аннотация

Пояснительная записка представляет собой отчет о выполнении курсовой работы. В ней рассматриваются вопросы по получению эмпирических формул методом наименьших квадратов (МНК). Расчеты проведены средствами пакета Microsoft Excel.

The Summary

The explanatory note presents a report: in which we discuss questions of the construction of the empirical formulas using method of the least squares in Microsoft Excel.

аппроксимация корреляция график квадрат

Оглавление

Введение

.        Постановка задачи

.        Расчетные формулы

.1 Построение эмпирических формул методом наименьших квадратов

.2 Линеаризация экспоненциальной зависимости

.3 Элементы теории корреляции

.        Расчет коэффициентов аппроксимации в Microsoft Excel

3.1 Аппроксимация функции y = f(х) многочленом первой степени

.2 Аппроксимация многочленом второй степени

.3 Аппроксимация экспоненциальной зависимостью 

.4 Расчет коэффициентов детерминированности и корреляции

. Построение графиков функций и использование функции ЛИНЕЙН

.1 Построение графика зависимости

.2 Построение линии тренда

.3 Получение числовых характеристик зависимости

Заключение

Список литературы

Введение

Аппроксимация, или приближение - математический метод, состоящий в замене одних математических объектов другими, в том или ином смысле близкими к исходным, но более простыми. В нашем случае, аппроксимация заключается в том, что используя имеющуюся информацию по f(x) можно рассмотреть другую функцию φ(y) близкую в некотором смысле к f(x), позволяющую выполнить над ней соответствующие операции и получить оценку погрешность такой замены.

Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются, или свойства которых уже известны).

Как известно, между величинами может существовать точная (функциональная) связь, когда одному значению аргумента соответствует одно определенное значение, и менее точная (корреляционная) связь, когда одному конкретному значению аргумента соответствует приближенное значение или некоторое множество значений функции, в той или иной степени близких друг к другу.

При выборе аппроксимации следует исходить из конкретной задачи исследования. Обычно, чем более простое уравнение используется для аппроксимации, тем более приблизительно получаемое описание зависимости. Поэтому важно считывать, насколько существенны и чем обусловлены отклонения конкретных значений от получаемого тренда. Также очень важно уловить общую закономерность, которая в данном случае наиболее логично и с приемлемой точностью выражается именно двухпараметрическим уравнением степенной функции.

1. Постановка задачи

Во всех вариантах требуется:

1. Используя метод наименьших квадратов функцию , заданную таблично, аппроксимировать

а) многочленом первой степени ;

б) многочленом второй степени ;

в) экспоненциальной зависимостью .

. Для каждой зависимости вычислить коэффициент детерминированности.

. Вычислить коэффициент корреляции (только в случае а).

. Для каждой зависимости построить линию тренда.

. Используя функцию ЛИНЕЙН вычислить числовые характеристики зависимости y от x.

6. Сравнить свои вычисления с результатами, полученными при помощи функции ЛИНЕЙН.

7. Сделать вывод, какая из полученных формул наилучшим образом аппроксимирует функцию .

2. Расчетные формулы

.1 Построение эмпирических формул методом наименьших квадратов

Очень часто, особенно при анализе эмпирических данных возникает необходимость найти в явном виде функциональную зависимость между величинами x и y, которые получены в результате измерений.

При аналитическом исследовании взаимосвязи между двумя величинами x и y производят ряд наблюдений и в результате получается таблица значений:

Эта таблица обычно получается как итог каких-либо экспериментов, в которых  (независимая величина) задается экспериментатором, а  получается в результате опыта. Поэтому эти значения  будем называть эмпирическими или опытными значениями.

Между величинами x и y существует функциональная зависимость, но ее аналитический вид обычно неизвестен, поэтому возникает практически важная задача - найти эмпирическую формулу

 (2.1.1)

(где  - параметры), значения которой при  возможно мало отличались бы от опытных значений .

Обычно указывают класс функций (например, множество линейных, степенных, показательных и т.п.) из которого выбирается функция , и далее определяются наилучшие значения параметров.

Если в эмпирическую формулу (2.1.1) подставить исходные , то получим теоретические значения , где .

Разности  называются отклонениями и представляют собой расстояния по вертикали от точек  до графика эмпирической функции.

Согласно методу наименьших квадратов наилучшими коэффициентами  считаются те, для которых сумма квадратов отклонений найденной эмпирической функции от заданных значений функции

 (2.1.2)

будет минимальной.

Поясним геометрический смысл метода наименьших квадралтов.

Каждая пара чисел  из исходной таблицы определяет точку  на плоскости . Используя формулу (2.1.1) при различных значениях коэффициентов  можно построить ряд кривых, которые являются графиками функции (2.1.1). Задача состоит в определении коэффициентов  таким образом, чтобы сумма квадратов расстояний по вертикали от точек  до графика функции (2.1.1) была наименьшей.

Построение эмпирической формулы состоит из двух этапов: выяснение общего вида этой формулы и определение ее наилучших параметров.

Если неизвестен характер зависимости между данными величинами x и y, то вид эмпирической зависимости является произвольным. Предпочтение отдается простым формулам, обладающим хорошей точностью. Удачный выбор эмпирической формулы в значительной мере зависит от знаний исследователя в предметной области, используя которые он может указать класс функций из теоретических соображений. Большое значение имеет изображение полученных данных в декартовых или в специальных системах координат (полулогарифмической, логарифмической и т.д.). По положению точек можно примерно угадать общий вид зависимости путем установления сходства между построенным графиком и образцами известных кривых.

Для того, чтобы найти набор коэффициентов , которые доставляют минимум функции S, определяемой формулой (2.1.2), используем необходимое условие экстремума функции нескольких переменных - равенство нулю частных производных. В результате получим нормальную систему для определения коэффициентов :

 (2.1.3)

Таким образом, нахождение коэффициентов  сводится к решению системы (2.1.3).

Эта система упрощается, если эмпирическая формула (2.1.1) линейна относительно параметров , тогда система (2.1.3) - будет линейной.

Конкретный вид системы (2.1.3) зависит от того, из какого класса эмпирических формул мы ищем зависимость (2.1.1). В случае линейной зависимости  система (2.1.3) примет вид:

 (2.1.4)

Эта линейная система может быть решена любым известным методом (методом Гаусса, простых итераций, формулами Крамера).

В случае квадратичной зависимости  система (2.1.3) примет вид:

 (2.1.5)

2.2 Линеаризация экспоненциальной зависимости

В ряде случаев в качестве эмпирической формулы берут функцию в которую неопределенные коэффициенты входят нелинейно. При этом иногда задачу удается линеаризовать, т.е. свести к линейной. К числу таких зависимостей относится экспоненциальная зависимость

 (2.2.1)

где и  неопределенные коэффициенты.

Линеаризация достигается путем логарифмирования равенства (2.2.1), после чего получаем соотношение

 (2.2.2)

Обозначим  и  соответственно через  и , тогда зависимость (2.2.1) может быть записана в виде , что позволяет применить формулы (2.1.4) с заменой  на  и  на .

2.3 Элементы теории корреляции

График восстановленной функциональной зависимости  по результатам измерений  называется кривой регрессии. Для проверки согласия построенной кривой регрессии с результатами эксперимента обычно вводят следующие числовые характеристики: коэффициент корреляции (линейная зависимость), корреляционное отношение и коэффициент детерминированности. При этом результаты обычно группируют и представляют в форме корреляционной таблицы. В каждой клетке этой таблицы приводятся численности  тех пар , компоненты которых попадают в соответствующие интервалы группировки по каждой переменной. Предполагая длины интервалов группировки (по каждой переменной) равными между собой, выбирают центры  (соответственно ) этих интервалов и числа  в качестве основы для расчетов.

Коэффициент корреляции является мерой линейной связи между зависимыми случайными величинами: он показывает, насколько хорошо в среднем может быть представлена одна из величин в виде линейной функции от другой.

Коэффициент корреляции вычисляется по формуле:

, (2.3.1)

где , и  ¾ среднее арифметическое значение соответственно по x и y.

Коэффициент корреляции между случайными величинами по абсолютной величине не превосходит 1. Чем ближе  к 1, тем теснее линейная связь между x и y.

В случае нелинейной корреляционной связи условные средние значения располагаются около кривой линии. В этом случае в качестве характеристики силы связи рекомендуется использовать корреляционное отношение, интерпретация которого не зависит от вида исследуемой зависимости.

Корреляционное отношение вычисляется по формуле:

, (2.3.2)

где , а числитель характеризует рассеяние условных средних  около безусловного среднего .

Всегда . Равенство  соответствует некоррелированным случайным величинам;  тогда и только тогда, когда имеется точная функциональная связь между y и x. В случае линейной зависимости y от x корреляционное отношение совпадает с квадратом коэффициента корреляции. Величина  используется в качестве индикатора отклонения регрессии от линейной.

Корреляционное отношение является мерой корреляционной связи y с x в какой угодно форме, но не может дать представления о степени приближенности эмпирических данных к специальной форме. Чтобы выяснить насколько точно построенная кривая отражает эмпирические данные, вводится еще одна характеристика ¾ коэффициент детерминированности.

Для его описания рассмотрим следующие величины.  - полная сумма квадратов, где  среднее значение .

Можно доказать следующее равенство

.

Первое слагаемое равно  и называется остаточной суммой квадратов. Оно характеризует отклонение экспериментальных данных от теоретических.

Второе слагаемое равно и называется регрессионной суммой квадратов, и оно характеризует разброс данных.

Очевидно, что справедливо следующее равенство .

Коэффициент детерминированности определяется по формуле:

. (2.3.3)

Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента детерминированности , который показывает, насколько хорошо уравнение, полученное с помощью регрессионного анализа, объясняет взаимосвязи между переменными. Если он равен 1, то имеет место полная корреляция с моделью, т.е. нет различия между фактическим и оценочным значениями y. В противоположном случае, если коэффициент детерминированности равен 0, то уравнение регрессии неудачно для предсказания значений y.

Коэффициент детерминированности всегда не превосходит корреляционное отношение. В случае, когда выполняется равенство  то можно считать, что построенная эмпирическая формула наиболее точно отражает эмпирические данные.

3. Расчет коэффициентов аппроксимации в Microsoft Excel

Функция y = f(x) задана таблично

Исходные данные представлены в Таблице 1.1.

Вариант №5

Таблица 1. Исходные данные

аргумент функция

аргумент

функция

аргумент

функция

аргумент

функция

аргумент

функция

Требуется выяснить - какая из функций - линейная, квадратичная или экспоненциальная наилучшим образом аппроксимирует функцию заданную таблицей 1.

3.1 Аппроксимация функции y = f(х) многочленом первой степени

Поскольку в задании каждая пара значений (,) встречается один раз, то корреляционная таблица примет вид единичной матрицы. Значит условные средние  совпадают со значениями . Отсюда следует, что корреляционное отношение  равно 1 и, следовательно, между и  существует функциональная зависимость.

Для проведения расчетов используем средства табличного процессора Microsoft Excel.

Таблица 2

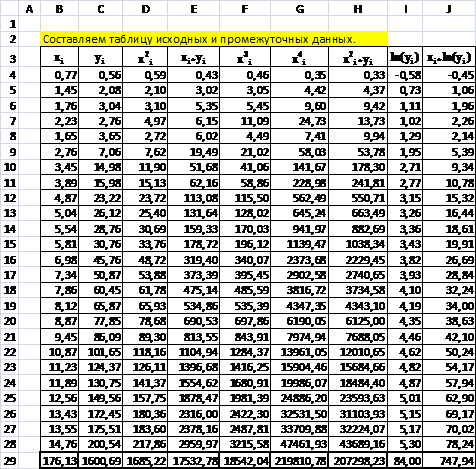
Поясним, как таблица 2 составляется.

Шаг 1. В ячейки B4:B28 заносим значения .

Шаг 2. В ячейки C1:C28 заносим значения .

Шаг 3. В ячейку D4 вводим формулу =B4^2.

Шаг 4. В ячейки D5:D28 эта формула копируется.

Шаг 5. В ячейку E4 вводим формулу =B4*C4.

Шаг 6. В ячейки E5:E28 эта формула копируется.

Шаг 7. В ячейку F4 вводим формулу =B4^3.

Шаг 8. В ячейки F5:F28 эта формула копируется.

Шаг 9. В ячейку G4 вводим формулу =B4^4.

Шаг 10. В ячейки G5:G28 эта формула копируется.

Шаг 11. В ячейку H4 вводим формулу =B4^2*C4.

Шаг 12. В ячейки H5:H28 эта формула копируется.

Шаг 13. В ячейку I4 вводим формулу =LN(C4).

Шаг 14. В ячейки I5:I28 эта формула копируется.

Шаг 15. В ячейку J4 вводим формулу =B4*LN(C4).

Шаг 16. В ячейки J5:K28 эта формула копируется.

Последующие шаги делаем с помощью автосуммирования .

Шаг 17. В ячейку B29 вводим формулу =СУММ(B4:B28).

Шаг 18. В ячейку C29 вводим формулу =СУММ(C4:C28).

Шаг 19. В ячейку D29 вводим формулу =СУММ(D4:D28).

Шаг 20. В ячейку E29 вводим формулу =СУММ(E4:E28).

Шаг 21. В ячейку F29 вводим формулу =СУММ(F4:F28).

Шаг 22. В ячейку G29 вводим формулу =СУММ(G4:G28).

Шаг 23. В ячейку H29 вводим формулу =СУММ(H4:H28).

Шаг 24. В ячейку J29 вводим формулу =СУММ(J4:J28).

Шаг 25. В ячейку K29 вводим формулу =СУММ(K4:K28).

Аппроксимируем функцию  линейной функцией . Для определения коэффициентов  и  воспользуемся системой

 (3.1.1)

Используя итоговые суммы таблицы 2.1,расположенные в ячейках B29, C29, D29 и E29, запишем систему 2.1 в виде

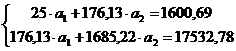 (3.1.2)

Результаты решения системы (3.1.2) представлены в таблице 3.       

Таблица 3

Таким образом, линейная аппроксимация имеет вид

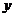= -35,1556+14,0781x (3.1.3)

В таблице 3 в ячейках B37:C38 введена формула {=МОБР(B33:C34)}.

В ячейках F37:F38 введена формула {=МУМНОЖ(B37:C38;D33:D34)}.

.2 Аппроксимация многочленом второй степени

Далее аппроксимируем функцию  квадратичной функцией . Для определения коэффициентов , и  воспользуемся системой

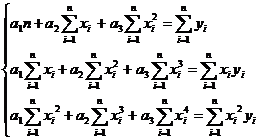 (3.2.1)

Используя итоговые суммы таблицы 3, расположенные в ячейках B29, C29, D29, E29, F29, G29 и H29, запишем систему (2.1.4) в виде

 (3.2.2)

решив которую, получим = -0,61511, = 0,55425и = -0,90104.

Результаты решения системы (3.2.2) представлены в таблице 4.

Таблица 4

Таким образом, квадратичная аппроксимация имеет вид

y=-0,61511+0,55425x-0,90104x² (3.2.3)

В таблице 2.3 в ячейках С47:E49 введена формула {=МОБР (C41:E44)}.

В ячейках G47:G49 введена формула {=МУМНОЖ (C47:E49,F41:F44)}.

.3 Аппроксимация экспоненциальной зависимостью

Теперь аппроксимируем функцию  экспоненциальной функцией . Для определения коэффициентов  и  прологарифмируем значения  и используя итоговые суммы таблицы 2, расположенные в ячейках B29, D29, I29 и J29, получим систему

 (3.3.1)

где =ln().

Результаты решения системы (2.3.3) представлены в таблице 5.

Таблица 5

Таким образом, система (2.3.3) имеет следующие решения: = 0,88433, =0,35140. После потенцирования получим = 2,42137.

Таким образом, экспоненциальная аппроксимация имеет вид

 (3.3.2)

В таблице 5 в ячейках B57:B58 введена формула {=МОБР (B53:C54)}.

В ячейках Е56:Е57 введена формула {=МУМНОЖ (B57:C58,D53:D54)}.

В ячейке Е58 введена формула =EXP(E56).

Вычислим среднее арифметическое  и по формулам

;

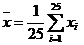Результаты расчета  и представлены в таблице 6.

Таблица 6

В ячейке В30 введена формула =B29/25.

В ячейке В31 введена формула =C29/25.

.4 Расчет коэффициентов детерминированности и корреляции

Для того чтобы рассчитать коэффициент корреляции и коэффициент детерминированности воспользуемся таблицей 7, которая является продолжением таблицы 2.

Таблица 7

В таблице 7 ячейки B4:B29 и C4:C29 уже заполнены (см. табл. 2).

В ячейку K4 введена формула =(B4-$B$30)*(C4-$B$31).

В ячейки K5:K28 эта формула копируется.

В ячейку L4 введена формула =(B4-$B$30)^2.

В ячейки L5:L28 эта формула копируется.

В ячейку M4 введена формула =(C4-$B$31)^2.

В ячейки M5:M28 эта формула копируется.

В ячейку N4 введена формула =($E$37+$E$38*B4-C4)^2.

В ячейки N5:N28 эта формула копируется.

В ячейку O4 введена формула =($ =($F$47+$F$48*B4+$F$49*B4^2-C4)^2.

В ячейки O5:O28 эта формула копируется.

В ячейку P4 введена формула =($E$58*EXP($E$57*B4)-C4)^2.

В ячейки P5:P28 эта формула копируется.

Последующие шаги выполнены с помощью автосуммирования Σ.

В ячейку K29 введена формула =СУММ(K4:K28).

В ячейку L29 введена формула =СУММ(L4:L28).

В ячейку M29 введена формула =СУММ(M4:M28).

В ячейку N29 введена формула =СУММ(N4:N28).

В ячейку O29 введена формула =СУММ(O4:O28).

В ячейку P29 введена формула =СУММ(P4:P28).

Для расчета коэффициента корреляции для линейной аппроксимации воспользуемся формулой:

 (2.3.1)

Для расчета коэффициента детерминированности воспользуемся формулой:

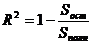 (2.3.3)

Результаты расчетов представлены в таблице 8.

Таблица 8

В таблице 8 в ячейке C71 введена формула =K29/(L29*M29)^0,5.

В ячейке F72 введена формула = =1-N29/M29.

В ячейке F73 введена формула =1-O29/M29.

В ячейке F74 введена формула = =1-P29/M29.

Анализ результатов расчетов показывает, что квадратичная аппроксимация наилучшим образом описывает экспериментальные данные.

4. Построение графиков функций и использование функции ЛИНЕЙН

Исследование характера зависимости проведём в три этапа:

1.      Построение графика зависимости.

2.      Построение линии тренда (в данном случае это прямая ).

.        Получение числовых характеристик коэффициентов этого уравнения.

.1 Построение графика зависимости

)        Выделим интервал B4:C28 (см. табл.2).

)        Нажимаем «Вставка», выбираем «Точечную диаграмму».

)        Среди точечных диаграмм выбираем диаграмму с маркерами.

)        Выбираем «Макет 1».

)        На появившейся диаграмме подписываем название «Линейная аппроксимация».

.2 Построение линии тренда

1)      Дважды щелкнем по диаграмме. Диаграмма активизируется.

2)      После нажатия правой кнопки мыши на график, выберем из открывшегося меню команду «Добавить линию тренда»

)        Появиться диалоговое окно «Линия тренда» - выберем на вкладке «Тип» - «линейный тип» и перейдем к вкладке «Параметры». На вкладке «Параметры» потребуем показывать уравнение тренда на диаграмме и показывать значение R². Нажмем кнопку «ОК».

)        На диаграмме появится линия тренда с соответствующим уравнением. При желании текстовое поле с уравнением можно перенести в более удобное место и отредактировать.

Рис.1

Для построения квадратичной аппроксимации на третьем шаге в диалоговом окне «Линия тренда» выберем на вкладке «Тип» полиномиальный тип степень 2. Результат представлен на рис.2.

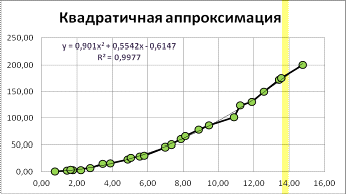
Рис. 2

Для построения экспоненциальной аппроксимации на третьем шаге в диалоговом окне «Линия тренда» выберем на вкладке «Тип» экспоненциальный тип. Результат представлен на рис.3.

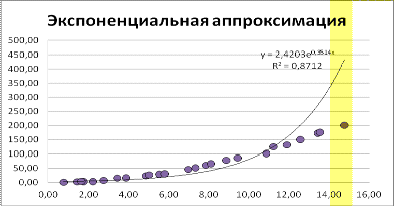
Рис. 3

Примечание: построения диаграмм велись в Microsoft Excel 2007.

.3 Получение числовых характеристик зависимости

1)      Создаем табличную формулу (5 строк и 2 столбца).

2)      Выделяем область C80:D84.

)        Вызываем «мастер функций».

)        Выбираем функцию ЛИНЕЙН.

)        Определяем аргументы функции - в графе «изв_знач_у» указываем В1:В25; в графе «изв_знач_х» указываем А1:А25; графу «константа» оставляем пустой; в графе «стат» набираем «истина».

)        Нажимаем кнопку «закончить» и устанавливаем курсор в строку формул.

)        Устанавливаем курсор в строку формул и нажимаем комбинацию клавиш Ctrl+Shift+Enter.

В результате получаем таблицу 9.

Таблица 9

Заключение

Сравнение результатов, полученных в среде Excel в матричной форме, с результатами работы функции ЛИНЕЙН показывает, что они полностью совпадают с вычислениями, проведенными выше. Отсюда следует, что вычисления проведены правильно.

Линейная аппроксимация имеет вид:=-35,1556+14,0781x

Квадратичная аппроксимация имеет вид:

y=-0,61511+0,55425x-0,90104x²

Экспоненциальная аппроксимация имеет вид:

y=2,42137 е^0,35140x

Анализ результатов расчетов показывает, что квадратичная аппроксимация наилучшим образом описывает экспериментальные данные, т.к. коэффициент корреляции равен 0,97186; Коэффициенты детерминированности линейной аппроксимации - 0,94452; квадратичной аппроксимации - 0,99772; экспоненциальной аппроксимация - 0,87120.

Список литературы

1. Б.П. Демидович, И.А. Марон. Основы вычислительной математики. М.: Государственное издательство физико-математической литературы, 1963.

2. Вычислительная техника и программирование. Под ред. А.В. Петрова. М.: Высшая школа, 1991.

3. Гончаров A., Excel 97 в примерах. - СПб: Питер, 1997.

4. Левин А., Самоучитель работы на компьютере. - М.: Международное агентство А.Д.Т., 1996.

5. Информатика: Методические указания к курсовой работе. Санкт-Петербургский горный институт. Сост. Д.Е. Гусев, Г.Н. Журов. СПб, 1999