Приёмы учебно-познавательной деятельности при решении стереометрических задач на построение

Приёмы учебно-познавательной деятельности при решении стереометрических задач на построение

Министерство просвещения ПМР

Приднестровский государственный университет имени Т.Г. Шевченко

Физико-математический факультет

Кафедра алгебры и геометрии

Квалификационная работа

Приёмы учебно-познавательной деятельности при решении стереометрических задач на построение

Выполнила: Войт Е.А.

группа №52

Научный руководитель: к.п.н.,

доцент Ермакова Г.Н.

Тирасполь - 2014

СОДЕРЖАНИЕ

Введение

Глава 1. Психолого-педагогические основы формирования приёмов в учебной деятельности

§1. Основные современные психолого-педагогические концепции учебной деятельности

§2. Теоретические трактовки некоторых психолого-педагогических понятий

§3. Психологическая трактовка основных общих умственных действий

§4. Приёмы учебно-познавательной деятельности по решению задач

Глава 2. Проблема формирования приёмов учебной деятельности в научно-методической литературе и практике обучения математики

§1. Проблема формирования приёмов учебной деятельности в научно-методической литературе

§2. Проблема формирования приёмов учебной деятельности в практике школьного обучения

Глава 3. Содержание и структура приёмов учебной деятельности в процессе решения задач на построение по теме «Прямая и плоскость»

§1. Стереометрическая задача на построение

§2. Методы решения геометрических задач на построение

§3. Основные соглашения и задачи

§4. Содержание и структура приёмов учебной деятельности учащихся в процессе решения стереометрических задач на построение по теме «Прямая и плоскость»

Заключение

Список литературы

ВВЕДЕНИЕ

Математика, как учебный предмет, является составной частью процесса обучения. Поэтому основные цели обучения математике в средней школе тесно связаны и являются составной частью целей обучения вообще.

В самом общем плане считается основной целью обучения - развитие учащегося. После такой общей формулировки возникает множество вопросов и проблем: какое место в формировании развивающейся личности занимают знания, умения и навыки по учебным предметам и по математике в частности: как понимать сам процесс развития, например развитие мышления, или общих и специальных способностей; каковы взаимосвязь процессов обучения, воспитания и развития учащихся и т.д.

В поисках ответов на эти вопросы педагоги определили многочисленные параметры общих целей обучения. К ним можно отнести:

. Знакомство с основами наук - получение прочного базового образования;

. Обеспечение всестороннего развития личности учащихся средствами всех учебных предметов;

. Обеспечение умственного развития учащегося;

. Развитие речи учащегося средствами каждого учебного предмета;

. Определение оптимального набора школьных предметов;

. Рассмотрение возможностей интеграции обучения за счёт создания интегрированных предметов;

. Необходимость широкого включения принципов политехнизма в учебно-воспитательный процесс;

. Обеспечение всех форм дифференцированного обучения каждому учебному предмету;

. Эстетическое «воздействие средствами всего комплекта учебных дисциплин [12, с. 3].

Перечисленные выше цели в разной степени проработаны по отношению к процессу обучения вообще и к обучению математике в частности.

Учёные дидакты, психологи, методисты и многие учителя хорошо осознают, что поставленные задачи невозможно решить на основе обучения по традиционной схеме “объяснение - закрепление”. Нужны новые подходы. Поэтому в течение последнего десятилетия осуществляется настойчивый поиск путей совершенствования принципов, форм, методов и приёмов обучения, воспитания и развития учащихся» [16, с.3], что приводит к изменению системы образования.

Изменения системы образования привели к созданию концепции демократизации образования, касающейся всех школьных предметов. Следовательно, основной проблемой становится дифференциация содержания обучения, которая ставит перед дидактами следующие вопросы:

. Какой математике учить?;

. На каком возрастном уровне изучать?;

. Как сочетать изучение различных разделов математики?;

. Чем должна быть «математика для всех»?;

. Как должно быть организовано обучение математике?;

. Какой должна быть роль учителя в процессе обучения математике?

Указанные проблемы рассматриваются в аспекте демократизации и дифференциации организационных форм работы учителя с учащимися, методов и стиля обучения, дифференциации дидактических материалов и средств, и т.д.

Существует такая гипотеза: математика остаётся одним из основных учебных предметов, но разные учащиеся будут изучать разную математику, либо одну и ту же математику, но в разном темпе, в зависимости от уровня их способностей или от заложенных в программы стандартов математической подготовки.

Направлениями решений дифференциации программ обучения являются:

. Дифференциация содержания обучения;

. Использование традиционных форм дифференциации (на уровне школ, классов, групп учащихся или индивидуальных занятий);

. Дифференциация с учётом потребностей будущей профессией;

. Модульная структура программ обучения в старых классах.

Возникает стремление к созданию методической системы обучения математике, ориентированной не только на общность тех или иных математических теорий, на логическую строгость их изложения, а так же на развитие наглядно-индивидуальной основы математике, её понятий, утверждений и задач во взаимосвязи с соответствующим восприятием окружающего мира, со способами мышления учащихся.

Новое направление в философии математики требует устранения безраздельного господства формализма, глобальной дедукции, логической строгости и повышения роли интуиции, и воображения. Это позволило поставить образ математики в центр внимания сферы образования. Что, в свою очередь, поставило проблему математического образования школьников в число вольнейших задач современной педагогической психологии, дидактики и методики преподавания математики.

Решаемые современной наукой проблемы проектирования и лучшей организации человеческой деятельности, открывают перед обществом новые возможности повышения эффективности и качества труда - важнейших социально-экономических задач, ориентированных на развитие этого общества.

Согласно взглядам отдельных учёных, общая теория деятельности опирается на следующие положения:

. Деятельность - есть жизненный процесс человека, отталкивающий его от животного;

. Именно в деятельности человек приобретает жизненный опыт человечества;

. Структурными единицами деятельности являются: потребность, мотив, цель и соотносимые с ними деятельность, действия, операции;

. Единицы деятельности взаимопереходят друг в друга: деятельность - действие - операции и мотив - потребность цель;

. Сущностными свойствами деятельности являются: целенаправленность, преобразующий характер, предметность и осознанность.

В соответствии с этим в последнее время педагоги и психологи обратились к деятельностному подходу. Идея деятельностного подхода в психологии основана на концепции развивающего обучения, которая в свою очередь отвечает на вопрос: «Можно ли посредствам обучения и воспитания сформировать у человека те или иные способности или качества, которых до этого у него не было?» [13, с. 240]

Рассматривая реальный учебный процесс, деятельностный подход даёт возможность выявить основные его компоненты, т.е. структуру учебного процесса. Это позволяет исследовать каждый элемент учебного процесса. Деятельностный подход к анализу процесса обучения помогает учителю установить влияние обучения на личность ученика.

Говоря о приоритете деятельностного подхода перед алгоритмическим подходом в обучении математики, А.А. Столяр отмечает: «деятельностный подход неалгоритмичен, неавторитарен. Технология деятельностного подхода не есть предписание алгоритмического типа, строго детерминирующее, что в каком порядке делать. Наоборот, она открывает широкие возможности для творческого поиска». [47, с.6]

В соответствии с деятельностным подходом, по мнению психологов, у учащихся должны формироваться не только знания, а определённые виды деятельности, в которую знания входят как определённый элемент. При этом обучение должно быть построено так, чтобы оно учитывало зону ближайшего развития личности, т.е. необходимо ориентироваться не на имеющийся сегодня уровень развития, а на более высокий, уровень которого ученик может достичь под руководством учителя.

Поэтому сущность деятельностного подхода к обучению состоит в том, что ведущим, организующим фактором является деятельность, её приёмы. Следовательно, приёмы деятельности должны составлять значительную часть содержания обучения и быть предметом целенаправленного формирования [49]. Но те или иные способы (приёмы) деятельности могут стать, а могут и не стать достоянием личности. В том случае, если они становятся её достоянием, способы деятельности превращаются в умение и навыки как личное достояние человека [17].

Общеучебные умения и навыки называют образовательно-педагогическими, к ним относятся: умения учения, самообразования, самовоспитания (планировать учебную работу, осуществлять самоконтроль, основные приёмы и действия учения, доводить учение до применения знаний, в том числе творческого, и включение их в систему научно-теоретического знания вплоть до системы мировоззрения личности); умения ориентироваться в целях образования в потоке информации и т.д.

В квалификационной работе необходимо было раскрыть сущность понятия и приёмы учебно-познавательной деятельности, определить её содержание, структуру, и на этой основе рассмотреть конкретные виды умений и навыков, способы формирования умений и навыков по решению стереометрических задач на построение.

Структура квалификационной работы. Работа состоит из введения, трёх глав, заключения, списка литературы.

Глава 1. Психолого-педагогические основы формирования приёмов в учебной деятельности

Математика, наряду с другими школьными предметами, решает задачи всестороннего гармонического развития и формирования личности. Полученные при обучении математике знания, умения и навыки, достигнутое умственное развитие должны помочь выпускникам школы в их адаптации к быстро меняющимся условиям производственной деятельности. Поэтому задача развития умственных способностей, мышления, общее развитие учащихся включается в основные задачи обучения математике.

Подходы к решению поставленной задачи, менялись на различных этапах развития образования в зависимости от требований, предъявляемых к школе обществом, от уровня разработанности психологических теорий научения и дидактических систем обучения. В последнее десятилетие в психологической и педагогической науке, в школьной практике активная познавательная деятельность рассматривается не только как средство овладения знаниями, умениями и навыками, но и как важнейший источник умственного развития школьников.

Реализация развивающего обучения состоит в том, что учитель не только применяет разнообразные методы и формы работы с учащимися на уроке, но и систематически обучает их способам выполнения тех или иных видов учебно-познавательной деятельности. Управление и самоуправление учебно-познавательной деятельностью возможно только при условии сформированности у учащихся приёмов умственной деятельности, а через них и рациональных приёмов учебной работы.

В связи с этим в разработке и становлении теоретических и методических основ обучения существенное значение имеют способы деятельности учащихся, то есть те умственные действия и приёмы учебной работы, с помощью которых школьники будут усваивать запланированный учебный материал. Выбор способов усвоения программного материала по математике зависит от конкретных дидактических и воспитательных целей, особенностей его содержания, подготовленности учащихся к восприятию нового и т.п. При этом важно учитывать, какими знаниями, действиями и приёмами учащихся уже владеют, а также должны быть сформированы на данном этапе обучения, а также принимать во внимание закономерности восприятия, памяти, мышления, возрастные и индивидуальные особенности учащихся на различных этапах обучения. Необходимо выбрать такой способ организации познавательной деятельности учащихся, при котором они в процессе усвоения знаний овладевают рациональными приёмами как практических, так и умственных действий. Общие и специфические приёмы умственных действий (а через них и рациональные приёмы учебной работы) должны стать объектом усвоения и сознательного их применения, контроля со стороны учителя и самоконтроля учащихся.

Наиболее общим показателем умственного развития школьника психологи считают его обучаемость. З.И. Калмыкова в статье «Обучаемость и принципы построения методов её диагностики» выделяет следующие составляющие обучаемости:

) Обобщённость мыслительной деятельности, направленность на абстрагирование и обобщение существенного в материале;

) Осознанность мышления, определяемая соотношением его практической и словесно-логической стороны;

) Гибкость мыслительной деятельности;

) Устойчивость мыслительной деятельности;

) Самостоятельность мышления, его восприимчивость к помощи.

Математика - это наука дедуктивная, и ведущим методом построения её современных теорий является аксиоматический метод. Овладение математическими знаниями развивает способности обобщать и абстрагироваться, формализовать знания, оперировать формальными структурами, числовой и знаковой символикой, переводить на язык символов словесно сформулированные закономерности; находить пути решения не подходящие под стандартное правило, поскольку в школьном курсе математики есть задачи, которые не алгоритмизируются; находить кротчайший, ведущий к данной цели логический путь; переключаться от одной умственной операции к другой, к пространственным представлениям.

В исследованиях психологов Н.А. Менчинской, Д.Н. Богоявленского, Е.Н. Кабановой-Миллер, Н.Ф. Талызиной, Г.С. Костюка, В.В. Давыдова, А.В. Занкова, Д.Б. Эльконина, В.И. Решетникова и др. показано, что уровень умственного развития школьников определяется не только содержанием знаний но и способами добывания их, которыми должны овладеть школьники. В настоящее время усилия психологов, дидактов, методистов на создание такой методической системы, в результате применения которой, учащиеся окончившие среднюю школу, овладели бы не только определённой системой знаний, но и рациональными приёмами учебной работы, были подготовлены к самостоятельному добыванию знаний.

Успешное решение поставленных задач невозможно без опоры на психологические теории учебной деятельности, определяющие сущность научения, его содержание, условия и основы.

§1. Основные современные психолого-педагогические концепции учебной деятельности

Современная дидактика под обучением понимает совместную деятельность учителя и учащихся при ведущей роли учителя. Процесс обучения выделяет две стороны:

) Преподавание - деятельность учителя, направленная на изложение программного материала, организацию учебно-познавательной деятельности учащихся, проверку усвоения или знаний, умений, навыков;

) Учение - сознательная деятельность учащихся под руководством учителя, направленная, на усвоение знаний, формирование умений и навыков, закрепление и применение знаний.

Для характеристики деятельности ученика пользуются понятиями «познавательная деятельность», «учебная деятельность», «учение». При этом в психолого-педагогической и методической литературе эти понятия имеют различное толкование. Так, например, Щукина Г.И. отождествляет познавательную деятельность и учение, Алексеев М.И. - учебную деятельность и учение. По мнению Рубинштейна С.Л. существует «два вида знания, точнее, два способа научения и два вида деятельности, в результате которых человек овладевает новыми знаниями и умениями. Один из них специально направлен на овладение этими знаниями и умениями как на свою прямую цель. Другой приводит к овладению этими знаниями и умениями, осуществляя иные цели. Учение в последнем случае - не самостоятельная деятельность, а процесс, осуществляющийся как компонент и результат деятельности, в которую он включён. На учение, доведённое до завершающих результатов, обычно осуществляется обоими способами, в этом или ином соотношении». Поэтому необходимо выделить два основных понятия: познавательная деятельность (учение) и учебная деятельность. Понятие «познавательная деятельность» более широкое, чем понятие «учебная деятельность», т.к. познавательная деятельность, направленная на овладение знаниями, умениями и навыками, является учебной деятельностью. Учебную деятельность можно рассматривать, таким образом, как вид познавательной деятельности, прямая цель которой - овладение учащимися знаниями, умениями и навыками, в результате которой происходит изменения в самом ученике, в его развитии.

Любой процесс получения знаний, как в результате организованный учебно-познавательной деятельности, так и стихийное приобретение знаний, умений и навыков, в психологии называют научением. Целенаправленное и организованное научение называют обучением. Обучение рассматривается как процесс стимуляции познавательной деятельности ученика и управления ею, в результате чего у ученика формируются знания, умения и навыки.

Современные психологические концепции научения - ассоциативная, условно рефлекторная, знаковая и операционная.

Ассоциативная концепция научения опирается на теорию познания Аристотеля. Основное понятие этой концепции научения - понятие «ассоциации». Под ассоциацией психологии понимают связь, которая образуется при определённых условиях между двумя и более психическими явлениями, действие этой связи - актуализация ассоциаций - состоит в том, что появление одного члена ассоциации регулярно приводит к появлению других. Психофизиологической основой ассоциации считается условный рефлекс.

Суть ассоциативной концепции научения: всякое познание начинается с ощущений и сводится к комбинации ощущений, восприятия образуются из соединения и слияния ощущений, тем же путём из восприятий образуются представления, а из последних - понятия. Сущность научения - усвоение человеком связей, существующих между объектами, их свойствами, действиями, психическими состояниями и т.д. Содержание научения - образование ассоциаций между элементами чувственного опыта человека. Условием научения является наличие между объединяемыми элементами сложности - физической (соседство в пространстве и времени), психологической (сходство и контраст), функциональный (отношения цели средства, качества и количества, причины и следствия, вещи и свойства и т.д.), логической (отношение частного к общему, вида к роду, посылок к заключению и т.д.). Основу научения составляют наблюдение и сравнение, различие и отождествление, разделение и объединение, соединение и расчленение. Отсюда прямо следуют принципы дидактики, сформулированные Яном Амосом Каменским: наглядность, доступность, прочность, систематичность, последовательность, пере-ход от части к целому, от знакомого к незнакомому, от близкого к далёкому.

Общая схема процесса обучения, основанная на ассоциативной концепции, была разработана немецким педагогом И. Гербартом. Модели процесса обучения, которые строились на основе ассоциативных концепций, недостаточно готовили школьников к жизни, к практической деятельности. В начале ХХ века, когда развитие производства выдвинуло новые социальные требования к школе, к уровню общего образования, ассоциативные теории научения оказались несостоятельными для построения моделей обучения, соответствующих новым требованиям.

Условно-рефлекторная концепция научения опирается на учение И.П. Павлова об условных и безусловных рефлексах. Сущность научения состоит индивидом существенных свойств предметов и явлений, полезных действий и форм поведения, опирающихся на эти свойства. Содержание научения заключается в образовании связей между безусловными (врождённы-ми) раздражителями и условными (усваиваемыми) реакциями организма или сигналами внешней среды. Условия образования связей для классических условных рефлексов являются подкрепление (один из сигналов должен отвечать определённым требованиям субъекта) и повторения (за достаточно короткое время совпадение условного и безусловного сигнала должно происходить на практике несколько раз).

Результатом научения являются анализ, синтез и оценка внешней информации, а также выбор и закрепление новых полезных видов поведения. Главное звено модели процесса обучения - обнаружение учащимися свойств и законов реальности на основе собственного опыта, исследований, попыток, проб и ошибок. Наиболее действенными методами научения являются методы, связанные с активной деятельностью ученика: наблюдение и эксперимент, различные виды труда, зарисовки и вычерчивания, моделирование, расчёты, оформление результатов и выводов, работа с литературой, подготовка рефератов, обсуждение и анализ результатов деятельности. Эта модель процесса обучения позволяет понять важность познавательной деятельности ребёнка, связь обучения с потребностями и нуждами учащихся, способствует активизации познавательной, исследовательской и практической деятельности учащихся. Однако, условно-рефлекторная концепция научения не в состоянии объяснить некоторые стороны процесса обучения, в частности системный подход к структуре учебно-познавательной деятельности. Кибернетика доказала, что для любых организационных систем целое определяют не связи отдельных элементов, а наоборот, целое определяет способы соединения элементов. В ассоциативной и условно-рефлекторной концепциях научения целое всегда строится из элементов, отношение - их отдельных связей этих элементов, а структура - из частных отношений.

Знаковая концепция научения опирается на учение Л.С. Выгодского о роли знаковых отношений в технической деятельности человека. В основу концепции положены смысловые связи, или знаковые, семиотические связи.

Суть знаковой концепции научения: появление у человека особой формы отражения реальности - понятий и специальной системы знаков (языка) для обозначения понятий и их отношений дало возможность осваивать накопленные человечеством знания об общих свойствах реальности.

Сущность научения состоит в формировании у учащихся понятий и их систем, отражающих существенные отношения реальности. Содержание научения - обнаружение и использование этих отношений, отображение их в понятиях и закрепление в словах. Условия научения - выявление и абстрагирование отношений, значимых для общественной практики, установление их характера и общности, закрепление их в словах. Основа научения - образование знаковых отношений между понятиями и соответствующими терминами, между понятиями и отображениями в них реальными отношениями.

Знаковая концепция научения вводит в процесс слово как орудие научения в дополнение к наблюдению и восприятию. При этом обучение рассматривается как формирование у учащихся системы понятий и принципов, а не только накопление суммы разнообразных знаний и сведений.

Опираясь на достижения Л.С. Выгодского С.Л. Рубинштейна основы знаковой концепции научения разрабатывали Н.А. Менчинская, Д.Н. Богоявленский, Г.С. Костюк, Е.Н. Кабанова-Миллер, В.В. Давыдов, Д.Б. Эльконин и др., в США Дж. Брунер.

В психологии принята трактовка механизма мышления, сформулированная С. Л. Рубинштейном: «Процесс мышления - это, прежде всего анализирование и синтезирование того, что выделяется анализом; это затем абстракция и обобщение, являющимися производными от них. Закономерности этих процессов в их взаимоотношениях друг с другом суть основные внутренние закономерности мышления».

Для ассоциативной, условно-рефлекторной и знаковой концепций научения общим является преимущественно отражательно-познавательный характер психической деятельности.

Операционная концепция научения опирается на учение об интериоризации. Процессом интериоризации называют процесс превращения внешних реальных действий с предметами во внутренние, идеальные. За основную структурную единицу процесса мышления в этой теории принимается действие. Операциональными структурами мышления являются практические действия над объектами, перенесённые в идеальный план и совершаемые как умственные действия над образами этих объектов.

Наиболее известными исследованиями в области операционной концепции научения являются работы Ж. Пиаже. Вариантом операционной концепции научения является «Теория поэтапного формирования умственных действий», разработанная П.Я. Гальпериным. Основное положение этой теории состоит в том, что психическая деятельность есть результат перенесения внешних материальных действий в план отражения - в план восприятия, представлений и понятий. Процесс такого переноса совершается через ряд этапов, на каждом из которых происходит новое отражение и восприятие и его систематическое преобразование.

Научение согласно теории Гальперина сводится к освоению ориентиров деятельности и умственных действий, нужных для её планирования и осуществления в данных условиях. Отсюда научение есть управление психической деятельностью ученика на основе обучения умственным действиям и познавательным структурам.

Для полноценного формирования любого знания и умения П.Я. Гальперин предлагает такую последовательность этапов:

. Создание мотивации. При этом внутренняя мотивация (интерес к самому процессу деятельности) оказывается надёжнее внешней (когда действие выполняется ради внешних по отношению к действию целей).

. Разъяснение или выделение схемы ориентировочной основы действия. На этом этапе учащиеся выясняют, как и в какой последовательности осуществляются ориентировочные, исполнительные и контрольные операции, входящие в состав действия.

. Формирование действия в материальной или материализованной форме. Эффективнее начинать обучение с формирования материализованной, а не материальной формы действий, направлению в основном на формирование теоретических знаний. Но после формирования материализованной формы действия необходимо переходить к этапу материального действия (к анализу реальных предметов). На третьем этапе вводится речь. Учащиеся комментируют совершаемое действие. Материальная форма действия - реальное преобразование, в котором структурные компоненты (все или некоторые) представлены в виде реальных предметов. Материализованная форма действия - реальное или графическое преобразование объектов, в котором структурные компоненты представлены в знаково-символической форме.

. Формирование действия в громкой речи без опоры на материально-материализованные средства. Все составляющие действия операции должны быть усвоены в речевой форме. Обычно соблюдается такая последовательность: вначале действие проговаривается «своими словами», затем постепенно переходит к научному языку, который выступает конечным результатом этого этапа.

. Формирование действия во внутренней речи (про себя), что является переходной ступенью для перевода действия в умственный план. На этом плане действие начинает сокращаться и автоматизироваться.

. Переход действия во внутреннюю речь, а внутренней речи - в чистую мысль. На этом этапе действие приобретает автоматическое течение и становится недоступным самонаблюдению. Сознанию открываются только продукты этого процесса.

По теории поэтапного формирования умственных действий этапы усвоения знаний рассматриваются совместно с этапами усвоения деятельности. Качество знаний при этом определяется их адекватностью деятельности, которая используется для их усвоения. По мнению Талызиной Н.Ф.: «Знания никогда нельзя дать в готовом виде. Они всегда усваиваются через включение их в ту или иную деятельность».

Теория поэтапного формирования умственных действий обосновывает требования к организации контроля в процессе усвоения знаний. На первых двух этапах усвоения знаний контроль должен быть пооперационным. На третьем и четвёртом этапах необходимо систематически контролировать каждое выполненное задание, на последующих этапах контроль может быть эпизодическим.

Теория поэтапного формирования умственных действий как и программированное обучение лучше других концепций научения решает проблему управления процессом обучения. Преимущество её перед программированным обучением в том, что она планирует не только содержание знаний, но и пути овладения ими, операции мышления, действия, строго адекватные усваиваемым знаниям, пути контроля усвоения знаний. Тем самым осуществляется программированное управление всем процессом обучения.

Основные принципы процесса обучения, вытекающие из операциональной теории научения, следующие:

. Введение понятий, идей и методов в ходе решения задач на их применение;

. Расчленение мыслительной деятельности на умственные действия, входящие в её состав;

. Формирование у учащихся системы умственных действий для решения различных типов учебных задач, видов учебно-познавательной деятельности;

. Сообщение учащимся ориентиров, определяющих тип учебных задач и основы их решения;

. Использование предметных и речевых действий, которые в процессе интериоризации переходят в умственные.

Из операционной теории научения и сформированных принципов следует модель обучения как управление психической деятельностью учащихся через организацию предметно-речевой деятельности.

Недостатком этой теории является обособление внутренней речи от первых этапов обучения, потому что речь важна на всех этапах познавательного процесса. Теория поэтапного формирования умственных действий ещё не достаточно полно разработана для всех уровней и сторон обучения, например, для уровня формирования и развития творческой деятельности учащихся.

Каждая из рассмотренных теорий научения и соответствующая модель процесса обучения направлены на повышение эффективности усвоения знаний, умений и навыков и объясняет стороны сложного и многогранного процесса обучения. Поэтому трудно принять за основу какую-либо одну из них, но выводы и принципы каждой из концепций научения и могут с успехом использоваться при обучении математике. Оптимальных результатов можно добиться при разумном сочетании различных подходов к организации учебно-воспитательного процесса. В последние годы исследования психологов и методистов, экспериментальное обучение и школьная практика подтверждают хорошие результаты в обучении математике при программировании содержании знаний и адекватных им умственных действий в сочетании с проблемным обучением.

Практика обучения показывает, что особенностью познавательной деятельности слабоуспевающих и среднеуспевающих по математике учащихся является несформированность общих умственных действий анализа, синтеза абстрагирования, обобщения и специфических действий присущих определённым видам деятельности. Это выражается в неумении выделять основное в учебном материале, устанавливать существенные связи между понятием и их свойствами, в медленном темпе продвижения, в быстром распаде усвоенных знаний, в трудности усвоения новых знаний и видов деятельности, что влечёт за собой умственную пассивность, неверие в свои силы, потребность в постоянной опеке. Поэтому главное в работе с неуспевающими и слабоуспевающими по математике учащимися - кропотливая, систематическая работа по формированию у них общих и специфических умственных действий.

§2. Теоретические трактовки некоторых психолого-педагогических понятий

Понятие деятельности - одно из основных в современной психологии. А.Н. Леонтьев определял деятельность как молярную единицу «жизни телесного материального объекта. В более узком смысле, - писал он, - т.е. на психологическом уровне, это единица жизни, опосредованный психологическим отражением, … это не реакция и не совокупность реакций, а система, имеющая строение, свои внутренние переходы и превращения, своё развитие». Таким образом, деятельность - процесс активности человека, характеризуемый предметом (на что направлен данный процесс), потребностью и мотивом, целями и условием их достижения, действиями и операциями. Предмет деятельности - то, на что направлен процесс (создание продукта деятельности, приобретение знаний саморазвитие). Потребность в деятельности - это основной источник активности человека, его нужда в предмете деятельности. Форма проявления потребности - мотив - это то, что побуждает человека к деятельности, связано с удовлетворением определённой потребности. Цель деятельности - её направленность на определённый результат.

Без умения оставить цели и достигать их потребности и мотивы остаются нереализованными. Цели деятельности определяют выбор действий, условия достижения цели - выбор операций (способов выполнения действий).

Деятельность субъекта определяют потребности, которые «способны выполнить эту функцию лишь при условии, что они являются предметными», т.е. наполнены конкретным содержанием, которое черпается из окружающего мира. Развитие потребностей происходит в форме развития их предметного содержания.

Действия, как было отмечено выше, соотносятся с целями, операции - с условиями их содержания. Цель действия есть представление человека о результате действия, отвечающее его потребностям. Условия достижения цели (выполнение действия) составляют не специфические особенности предмета, действия, непосредственно не связанные с достигаемой целью, а также особенности состояния человека в момент выполнения действия.

На начальном выполнении действия цель и условия выступают как задание, которое ставится перед человеком им самим или другими. Например, цель того или иного действия, входящее в другое действие, есть условие его выполнения.

В каждом выполняемом человеком действии различают результат этого действия и общих способов, с помощью которого выполняется данное действие. Если усилия человека направлено на овладение общими способами действий, то его деятельность становится целенаправленной.

Одно и то же действие осуществлять разные виды деятельности, переход из одного в другой. Различают виды деятельности в которых действия являются внутренними (мыслительная деятельность) и виды деятельности с внешними деятельностями (трудовая деятельность). Внутренние действия отделены от практических действий над самыми предметами, продукт внешних действий воплощается в некотором предмете. В любой деятельности человека участвуют теоретические действия, которые могут протекать как во внутренней, так и во внешней форме. Теоретические действия, проходят через внешнюю форму, постепенно становятся внутренними.

Таким образом, всякая деятельность, в том числе учебная и познавательная, деятельность учащихся в обучении содержит как внутренний, так и внешний компоненты. Внутренняя деятельность производна от внешней. Между ними имеет место двусторонняя связь, взаимопереходы, потому что внешняя и внутренняя деятельности имеют одну и ту же макроструктуру.

Управление процессом обучения через обработку макроструктуры деятельности учащихся составляет сущность деятельного подхода в дидактических и методических исследованиях.

Под учебной деятельностью Д.Б. Эльконин, В.В. Давыдов и др. понимают деятельность учащихся по приобретению теоретических знаний о предмете изучения на основе его преобразования, экспериментирования с ними. Усвоение знаний в этом случае носит творческий характер. Однако, в ряде психолого-педагогических исследований показано, что полноценное усвоение знаний возможно только в том случае, когда данный процесс строится на основе формирования операционных структур умственной деятельности, поэтому в процессе обучения объектами усвоения школьника должны являться не только знания, но и приёмы, способы учебной деятельности.

Таким образом, содержание учебной деятельности составляют как теоретические знания, так и приёмы. Способы деятельности, т.е. составляющие им умения и навыки. Следовательно, реализация учебной деятельности осуществляется посредством выполнения учащимися соответствующих действий.

Рассмотрим некоторые особенности, отличающие учебную деятельность от других видов деятельности.

Первая особенность учебной деятельности - направленность ученика на овладение определёнными знаниями и умениями, т.к. учебная деятельность не только объективно направленное на осуществление целей образования, как и все другие деятельности, но субъективно направленное на это. Она адекватно мотивирована, тогда как все другие деятельности в процессе обучения мотивированны неадекватно, хотя они и направлены на осуществление указанных целей, но мотивируются учеником (например, мотивами оценки, соревнования и т.д.). Выполняя учебную деятельность, ученик ставит перед собой вполне конкретные цели (освоить определённый учебный материал, овладеть каким-то действием, выработать привычку поведения и т.д.).

Вторая особенность учебной деятельности - направленность на освоение общих способов действий. Под способами действий в психологии понимаются особые системы, операции, благодаря которым человек открывает свойства предметов и явлений, в отношении которых и при опоре на которые осуществляются различные преобразования.

Третья особенность учебной деятельности - изучение учебного материала строится по принципу содержательного обобщения, когда освоение знаний общего и абстрактного характера предшествует знакомству с более частными и конкретными знаниями, - последние выводятся из первых как из своей единой основы. При таком усвоении ученик первоначально выделяет и фиксирует общую «клеточку» изучаемого материала, а затем, опираясь на неё, рассматривает различные частные её проявления. Другими словами, данная особенность учебной деятельности состоит в том, что её содержанием являются теоретические знания.

Четвёртая особенность - результатом учебной деятельности является изменение самого ученика, его развитие, т.к. все конкретные цели учащегося имеют общее направление на конечную цель - воспитание всесторонне развитой социально зрелой личности.

Условиями правильной организации учебной деятельности являются: потребности, самих учащихся осуществлять творческое преобразование учебного материала с целью овладения новыми знаниями; постановка учебной задачи, стимулирующей эту потребность; внимание учителя к полноценному выполнению учащимися учебных действий по решению учебной задачи. Таким образом, учитель обучает в соответствии с требованиями учебной деятельности (методом решения школьниками учебных задач), если, опираясь на потребностях и готовность школьников к овладению теоретическими знаниями, умеет построить перед ними на конкретном материале задачу и решить её с учащимися.

Теория учебной деятельности включает в себя три звена: мотивационно-ориентировочное (постановка учебной задачи), исполнительно-операционное (учебные действия для решения учебной задачи) и контрольно-оценочное. Основным содержанием учебной деятельности являются общие способы действий (алгоритмы, приёмы) по решению достаточно широких классов задач, когда деятельность учащихся направлена на овладение этими общими способами. Таким образом, целостную учебную деятельность определяет структура:

Схема 1

Основным компонентом учебной деятельности является учебная задача. Учебная задача - обобщённая цель учебной деятельности, поставленная перед учащимися в виде обобщённого учебного задания. Отличие учебной задачи от других задач в том, что её цель и результат состоят не в изменении предметов с которыми действует субъект, а в изменении самого действующего субъекта. Учебная задача связана с содержательным (теоретическим) обобщением, подводит учащегося к овладению обобщёнными отношениями в изучаемой области знаний, к овладению новыми способами действия (алгоритмами, приёмами). Принятие учащимися учебной задачи, её самостоятельная постановка связаны с мотивацией учения, с превращения её в объект деятельности.

Потребности в учебной деятельности побуждают учащихся к усвоению теоретических знаний, мотивы - к усвоению алгоритмов, приёмов (способов) их воспроизводства посредством учебных действий, направленных на решение учебной задачи.

Учебная задача требует от учащихся:

. Анализа фактического материала с целью обнаружения в нём общего (основного) отношения, отражающего закономерности усвоения этого материала, т.е. построение содержательной абстракции и содержательного обобщения (например, соответственно при определении понятия, при формировании приёма);

. Выявления структурной единицы (элемента, «клеточки»), целого в единстве его элементов и связей;

. Овладение в этом аналитико-синтетическом процессе способом построения изучаемого объекта.

Следовательно, при решении учебной задачи учащиеся первоначально овладевают общими решениями частных задач, т.е. как путь усвоения теоретических знаний осуществляют некоторый микроцикл восхождения от абстрактного к конкретному.

Результатом решения учебной задачи является овладение учащимися «общим способом построения изучаемого объекта, т.е. общим способом решения всех частных задач определённого типа (алгоритмом, приёмом, методом)».

В.В. Давыдов, отмечая, что теория учебной деятельности и теория проблемного обучения на ряду своих идей и понятий достаточно близки друг к другу (хотя и есть значительные расхождения при интерпретации содержания ряда понятий), утверждает, что общий смысл и общая роль учебной задачи в процессе усвоений и способов действий будут те же, что учебной проблемы. Учебная задача, как и учебная проблема, возникающая в мышлении учащегося при его взаимодействии с проблемной задачей, стимулирует мышление школьника к объяснению ещё неизвестного, к усвоению новых понятий и способов действия.

Наряду с понятием «учебная задача» в теории учебной деятельности применяется термин «конкретно-практическая задача». В ситуации практической задачи овладение способами действий не является главной целью учащегося, они выделяются лишь при решении серии этих задач. Конкретно-практические задачи в методических исследованиях называют предметными.

Учебную задачу можно представить в виде системы «учебная цель - предметные задачи». Особенностью учебной задачи является наличие учебной цели совпадающей с требованием предметной задачи на основе которых построена учебная.

Обобщённая учебной деятельности (учебная задача) может быть достигнута с помощью системой конкретных подцелей (или частных целей), которые позволяют выбрать конкретную (частную) задачу из данного множества предметных задач. Тогда учебная деятельность учащихся будет осуществляться на основе решения частных (конкретных) учебных задач. Таким образом, учебная задача, как обобщённая цель учебной деятельности, связана с задачами, которые являются условием и средством достижения обобщённой учебной задачи. Следовательно, частная учебная задача есть синтез предметной задачи с её условием и требованием и конкретной учебной цели, ради достижения которой она рассматривается.

Конкретная учебная цель, входящая в структуру частной учебной задачи, может быть предъявлена учащемуся в виде учебного задания (задачи).

Одна и та же предметная задача, входящая в структуру учебной задачи, может служить достижению нескольких конкретных целей. Значит, она может быть компонентом нескольких частных учебных задач. В то же время та или иная конкретная учебная цель может быть достигнута, особенно на первых этапах формирования соответствующих умений и навыков, в работе над несколькими предметными задачами.

Сказанное выше, можно изобразить следующей схемой:

Схема 2

Второй компонент учебной деятельности - учебные действия, при помощи которых решается учебная задача. В.В. Давыдов определил следующие учебные действия, которыми должны овладеть учащиеся в процессе решения учебных задач:

. Преобразование условий задачи с целью обнаружения всеобщего (основного) отношения изучаемого объекта;

. Моделирование выделенного отношения в предметной, графической или буквенной форме;

. Преобразование модели отношения для изучения его свойства в «чистом виде»;

. Построение системы частных задач, решаемым общим способом (алгоритмом, приёмом);

. Контроль за выполнением предыдущих действий;

. Оценка усвоения общего способа как результата решения данной учебной задачи.

Каждое из этих действий состоит из соответствующих операций, наборы которых меняются в зависимости от конкретных условий, определяющих ту или иную учебную задачу (действие соотносится с целью учебной задачи, а его операции - с её условиями).

Рассмотрим основные особенности учебных действий.

Первое учебное действие - преобразование условий учебной задачи выявляет основное отношение (существующее объективно) того объекта, который должен найти отражение в соответствующем теоретическом понятии. Это отношение, с одной стороны, является характеристическим свойством, определяющим элементы задачи, входящие в её структуру, с другой стороны - выступает как генетическая основа и источник всех частных его проявлений. Поэтому задачу можно рассматривать как систему отношений в которой на основе обобщения выделяется основное отношение с фиксированными на нём свойствами. Найденное отношение создаёт в задаче информационно-познавательное противоречие, помогающее учащемуся осознать условие и требование задачи. Основное отношение также управляет процессом поиска решения задачи.

Второе учебное действие - моделирование выделенного отношения является необходимым звеном процесса усвоения теоретических знаний и обобщённых способов действия. Содержание модели фиксирует внутренние характеристики изучаемого объекта, не наблюдаемые непосредственно (например, внутреннюю структуру объекта). Поэтому учебная модель, вступая, как модель мыслительного анализа, затем сама является особым средством мыслительной деятельности человека. Учебная модель, таким образом, фиксирует всеобщее (основное) отношение целостного объекта и обеспечивает его дальнейший анализ.

Третье учебное действие - преобразование модели основного отношения объекта В.В. Давыдов рассматривал в качестве средства изучения свойств, выделенного основного отношения. Работа с учебной моделью выступает как процесс изучения свойства содержательной абстракции основного отношения.

Ориентация учащихся на новое отношение изучаемого целостного объекта является основой формирования у них общего способа решения учебной задачи и тем самым формирование понятия об исходной «клеточке» этого объекта. Однако адекватность «клеточки» своему объекту обнаруживается тогда, когда из неё выводятся многообразные частные его проявления. Применительно к учебной задаче это означает выделение на её основе системы частных задач, при решении которых учащиеся конкретизируют найденный общий способ, а тем самым и соответствующее ему понятие, «клеточку». Поэтому следующее учебное действие - построение системы частных задач. Выполняя это действие, учащиеся конкретизируют исходную учебную задачу, превращая её в систему частных задач, на которых реализовано одно и тоже основное отношение и, следовательно, решаемое единым (общим), способом, который усвоили при выполнении предыдущих учебных действий.

Следовательно, частные учебные задачи при совпадении конкретной учебной цели могут отличаться содержанием предметных задач.

Приведём пример учебной задачи, как обобщённой цели учебной деятельности.

Учебная задача. Сформировать у учащихся умение, направленное на принятие задач с целью их последующего решения.

Учащийся принял задачу, если осознал её содержание (условие и требование), сопоставил её со своими возможностями и согласился её решать, сделав целью своей деятельности. Поэтому, конкретные учебные цели, выраженные в виде учебных задач, должны быть направлены на анализ текста задачи. Этот анализ включает:

. Анализ условия и требования задачи;

. Выявление функционального отношения в задаче, если оно не известно;

. Актуализацию теоретической и (или) практической основы решения задачи;

. Установление факта: известен или нет способ решения задачи. Если нет, то необходим поиск способа задачи.

Выше было установлено, что учебная задача может быть решена, при наличии предметной задачи и конкретной учебной цели, лишь с помощью системы частных учебных задач. Учебная цель при этом может и не совпадать с требованиями предметной задачи.

Приведём примеры частных учебных задач, направленных на решение данной выше учебной задачи, как обобщённой цели учебной деятельности.

Задача (предметная). Найти объём правильной пирамиды с боковым ребром L, если боковое ребро составляет с прилежащей стороной основания угол α.

Задание 1 (конкретная учебная цель). Проверить соответствует ли заранее выполненный чертёж условию и требованию задачи.

Задание 2. Написать формулу в обозначениях чертежа, отражающую зависимость объёма пирамиды от стороны основания и высоты пирамиды. Установить, какие величины входящие в формулу неизвестны.

Задание 3. Обосновать, почему вершина пирамиды проектируется в центр окружности, описанный около основания пирамиды. Является ли эта точка центром окружности, вписанной в основание пирамиды.

Задание 4. Указать вычисления площади треугольника, лежащего в основании пирамиды. Записать выбранную формулу в обозначениях чертежа.

Задание 5. Указать два возможных способа вычисления объёма пирамиды с учётом данных и неизвестных величин.

Принятие учащимися учебной задачи и осознание ими соответствующей цели деятельности связаны, как отмечалось выше, с мотивацией, превращение ученика в субъект деятельности.

Выполняя предложенные к данной задаче задания (конкретные цели), т.е. решая систему частных учебных задач, учащиеся непроизвольно становятся активными участниками этого процесса. Система учебных задач имплицитно управляет учебной деятельностью учащихся независимо от формы их деятельности в процессе обучения. Следовательно, частные учебные задачи в обучении математики являются необходимым средством активизации познавательной деятельности учащихся, т.к. учебная деятельность - это вид деятельности, направленной на овладение знаниями, умениями, навыками, на развитие учащихся.

Выделенная выше система частных учебных задач, направлена на достижение обобщённой цели учебной деятельности - формирование у учащихся способа принятия задачи.

Различают и другую форму частной учебной задачи, когда конкретная цель (задание) является либо вспомогательной задачей, либо подсказкой, которые обогащают решение предметной задачи, входящей в состав частной учебной задачи.

Предположим, что для достижения обобщённой цели учебной деятельности (т.е. учебной задачи) необходимо решить три частные учебные задачи.

Задача. Сторона основания правильной треугольной пирамиды равна а, боковая грань наклонена к плоскости основания под углом φ. Найти объём пирамиды.

Задание 1. Пользуясь условием данной задачи, найти радиусы окружностей вписанной и описанной около основания пирамиды и высоту пирамиды.

Задание 2. Исходя из условий данной задачи, найти боковое ребро пирамиды.

Задание 3. Решить данную задачу.

Здесь первое задание является вспомогательной задачей, т.к. она содержит несколько общих компонентов решения (два или более двух) в сопоставлении с данной предметной задачей. Второе задание является подсказкой необходимой для решения данной задачи, т.к. в структуре её решения содержится один компонент, имеющий место в структуре решения исходной задачи. Третье задание даёт указание: решить предметную задачу.

Первое и второе задания раскрывают учащемуся два различных способа нахождения высоты пирамиды, поэтому последовательность этих заданий может быть любой. В том случае, когда с помощью подсказок и вспомогательных задач раскрывается логическая структура фиксированного решения, необходимо, чтобы последовательность заданий была адекватной этой структуре.

Задания, входящие в состав частной учебной задачи рассматриваются не только как конкретные цели её решения, но и как ориентировочная основа деятельности учащихся при решении предметной задачи.

Специфика учебных действий контроля и оценки состоит в том, что они присутствуют на всех этапах решения учебной задачи.

Контроль состоит в установлении соответствия последовательно выполняемых учебных действий условиями и требованиями учебной задачи, контроль позволяет ученику, меняя операционный состав действий, выявить их связь с теми или иными особенностями условий задачи и свойствами полученного результата. Благодаря этому контроль обеспечивает нужную полноту операционного состава действий и правильность их выполнения. Таким образом, особенность контроля, как учебного действия состоит в том, что оно совершается как и поиск, сопоставление (сравнение и постепенное отбрасывание) разных способов действий при решении учебной задачи. Другая особенность контроля, как учебного действия, заключается в том, что оно тесно связано с другими учебными действиями, прежде всего с действием оценки. Поэтому контроль выступает как компонент целостной учебной деятельности.

Действие оценки позволяет определить, насколько выполнено требование учебной задачи, соответствует или нет (и в какой мере) результат учебных действий их конечной цели. Оценка - это формальная констатация, она предполагает содержательный, качественный анализ результата учебных действий и сопоставление их с целью.

Ещё одной особенностью действия оценки является то, что оно осуществляется и развёртывается ещё до принятия учащимся учебной задачи, тогда как учебные действия, связанные с преобразованием объекта, развёртываются постепенно и в определённой последовательности сменяют друг друга. Именно оценка позволяет ученику сделать вывод о том. Разрешима ли данная учебная задача, и можно ли переходить к выполнению практических действий или необходимо создавать новые варианты для достижения исходной цели.

Таким образом, действия контроля и оценки предполагают обращение внимания учащихся к содержанию своих действий, к рассмотрению их особенностей с точки зрения требуемого учебной задачей результата. На основе действий контроля и оценки формируется особая оценочная деятельность школьника - умение оценить свою деятельность с точки зрения общественно выработанных эталонов, преобразовать её и совершенствовать.

Рассмотренные выше особенности учебных действий, определяют структуру:

Схема 3.

Функции контроля и оценки усвоения знаний и способов действия наиболее эффективно могут быть реализованы на основе осуществления в обучении обратной связи и подкрепления.

Обратная связь и подкрепление выполняют разные функции и по содержанию могут не совпадать друг с другом.

Подкрепление - это такое воздействие на обучаемого, которое приводит к закреплению выполняемых им действий.

Обратная связь - это получение обучаемым информации о соответствии выполняемого действия заданному, т.е. контроль или самоконтроль за результатом действий.

Обратная связь может поступать как к обучаемому (учащемуся) - внутренняя обратная связь, так и к обучающему (учителю) - внешняя обратная связь. Подкрепление - это всегда действие только на обучаемого (учащегося) в случае получения им правильного ответа.

Информация, поступающая к учащемуся (внутренняя обратная связь) может служить одновременно и подкреплением. Но это возможно лишь в двух случаях:

. Когда у учащегося есть потребность в получении подкрепления, т.е. когда он не уверен в правильности своих действий;

. Когда мотивы (побуждение к деятельности, связанное с удовлетворением потребностей субъекта) и цели деятельности обучаемого совпадают, т.е. когда правильное выполнение задания само становится мотивом его учебной деятельности.

Подкрепление в процессе учебной деятельности может реализовываться в следующих основных формах:

. В форме объясняющего принципа правильного ответа;

. В форме мотивации, т.е. побуждения вызывающего активность учащегося в обучении;

. В форме укрупнения связей изучаемого (внутрипредметных и межпредметных связей);

. В форме ориентировочного - исследовательского принципа успешного ответа, т.е. построения ориентировочной основы действия;

. В форме образца действия;

. В форме поощрения;

. В форме оценки.

На начальных этапах формирования нового учебного действия учащийся самостоятельно не может оценить правильность его выполнения. Необходимым условием усвоения нового действия являются сведения о правильности его выполнения - внешняя обратная связь, определяющая степень точности выполняемого действия, его оценка.

Внутренняя обратная связь это механизм оценки сложившегося учебного действия. Это знания учащегося о выполняемом действии, выступающие в форме эталона (модели) правильного действия и условия его выполнения. На основе этого учащийся сам может оценить правильность выполненного им (или соучастника) действия. Такая ситуация в обучении наступает на одном из конечных этапов усвоения нового действия, когда учащийся сам может оценить правильность его выполнения, не ощущая при этом, необходимости в какой-либо дополнительной информации для осуществления такой оценки.

Учащийся вместе с системой знаний о содержании и условиях правильного выполнения действий постепенно усваивает и способы их оценки. На этой основе формируется механизм внутренней обратной связи, позволяющей учащемуся в дальнейшем самостоятельно оценивать правильность выполненных им действий.

Таким образом, процесс усвоения нового учебного действия есть процесс преобразование внешней обратной связи во внутреннюю. В результате чего учащийся усваивает учебный материал.

Следовательно, по мере становления усваиваемых учебных действий внешние обратные связи превращаются во внутренние и становятся способами самоконтроля за правильностью выполняемых действий.

Описанному процессу преобразования внешних обратных связей во внутренние, а, следовательно, и постепенному переходу учебных действий из внешнего плана действий, во внутренний план (интериоризация) наиболее адекватной является групповая форма деятельности с переходом к индивидуальной форме. В.В. Давыдов, опираясь на соответствующие экспериментальные исследования, показал, что в совместном выполнении группой учащиеся под руководством учителя распределённых между ними учебных действий постепенно происходит интериоризация коллективно распределённых действий, «превращение их в индивидуально осуществляемое решение учебных задач».

А.М. Матюшкиным показано, что преобразование внешних обратных связей во внутренние может быть описано с помощью трёх основных характеристик: частоты, глубины, гибкости (широты) обратной связи.

Частота обратной связи. На начальных этапах формирования учебных действий за правильностью его выполнения (каждой операции в составе действия) необходим пооперационный контроль, осуществляемых с помощью механизма внешней обратной связи. Пооперационный контроль позволяет контролировать как исполнительную, так и ориентировочную часть действия. Исполнительная - это практическая часть действия (собственно действия). Ориентировочная часть действия - это основные требования к выполняемому действию и его результату. Она обеспечивает не только правильное исполнение действия, но и рациональный выбор одного из множества возможных исполнений. Обучаемый, выполняя ориентировочную часть действия опирается но ориентировочную основу действия. Ориентировочной основой действия, её содержанием, может быть алгоритм действия; существенные признаки понятия, операции, входящие в состав учебного действия и др.

При пооперационном контроле осуществляется направленная коррекция в процессе выполнения самого действия, ещё до получения конечного результата. Этим обеспечивается получение правильного результата.

По мере усвоения действия происходит «укрепление» отдельных элементов действия, а внешние обратные связи замещаются внутренними. На конечных этапах формирования действия все необходимые промежуточные оценки его выполнения отпадают. В результате остаётся один лишь тип обратной связи - оценка конечного результата действия.

На начальных этапах формирования учебного действия имеют место два основных типа обратных связей - положительная и отрицательная. Наличие положительной обратной связи говорит о том, что процесс усвоения происходит успешно, т.е. ученик не допускает ошибок при выполнении предложенных ему учебных задач. Наличие отрицательной связи - о том, что ученик допускает при решении учебных задач, а значит необходимые знания или действия им ещё полностью не усвоены. Процесс усвоения можно считать успешным, если сумма положительных обратных связей для основных и положительных учебных заданий больше суммы отрицательных обратных связей. При этом имеются в виду, что учащийся, допускавший ошибки, выполнит правильно все основные и дополнительные учебные задания.

Глубина обратной связи говорит о степени преобразования внешней обратной связи во внутреннюю. Она задаёт уровни усвоения знаний и действий учащихся. Важным показателем глубины обратной связи является возможность обучаемого предвосхищения (экстраполяции) результата действия и оценки его правильности. Эта возможность обучаемого проявляется потому, что в процессе формирования внутренней обратной связи способы выполнения учебных действий становятся средствами самоконтроля. В свою очередь самоконтроль деятельности формируясь постепенно начинает осуществляться до того, как выполнено действие.

Гибкость обратной связи. Одним из показателей качества знаний и способов действия является возможность их переноса. Перенос выступает либо как возможность применения усвоения знаний и способов действия при решении новых задач, либо как возможность использования их в новых условиях. Возможность использования данного типа внутренней обратной связи (например, самоконтроля) для оценки правильности выполнения действия в различных условиях есть гибкость обратной связи.

Необходимым условием формирования гибкости обратной связи является возможность обучающей системы реагировать на любой ответ учащегося.

Действие контроля и оценки определяет структура:

Схема 4

Процесс становления учебной деятельности требует отработки каждого из её компонентов. Неусвоенность хотя бы одного из них приводит к деформации учебной деятельности.

Формирование учебной деятельности в процессе обучения школьников требует руководства со стороны учителя как их совместной, так и индивидуальной деятельностью.

В педагогической психологии установлено, что исходная форма учебных действий состоит в совместном выполнении группой учащихся под руководством учителя распределённых между ними действий. В процессе групповой деятельности учащихся постепенно происходит интериоризация (процесс преобразования внешних предметных действий во внутренние, умственные) этих коллективно распределённых учебных действий и превращением их и в индивидуально осуществляемое решение учебных задач. Следовательно, как только учащиеся усвоили учебные действия по решению учебных задач учителю необходимо от групповой формы перейти к индивидуальной форме деятельности учащихся. Такая организация обучения является необходимым условием успешного формирования учебной деятельности школьников.

Вопрос о том, как и в какой последовательности передавать отдельные компоненты учебной деятельности для самостоятельного выполнения ученику, в психических исследованиях ещё не до решён. Есть мнение о том, что рациональнее всего начать с самостоятельного контроля, причём от контроля за действиями другого к контролю за собственными действиями. Второе действие, которое должно быть передано учащимися для самостоятельного выполнения - это оценка, т.е. установление того, что усвоено, а над чем ещё надо работать.

Из сказанного следует, что целостную учебную деятельность определяет расширенная структура:

Схема 5.

1. преобразование условия учебной задачи;

. моделирование выделенного отношения;

. преобразование модели;

. построение системы частных задач.

Рассмотрим различные трактовки некоторых психологических понятий.

Умственные действия классифицируют по различным основаниям в зависимости от подхода к ним. С точки зрения основных психических процессов (восприятия, памяти, мышления) различают перцептивные, мнемические и мыслительные действия; с точки зрения ведущей функции, выполняемой действиями выделяют ориентировочные, исполнительные и контрольные; по степени стандартизации и формализации выделяют действия типа алгоритма, алгоритмического предписания, эвристики; по степени общности выделяют общие и конкретные действия.

Если рассматривать действия по степени использования их различных областях человеческой деятельности, то можно выделить общие действия, применяемые во всех областях знаний (например, анализ, синтез, абстрагирование, обобщение, сравнение и другие), и специфические действия, которые характерны для той или иной области знаний. При этом специфические действия могут различаться по степени общности. Например, действие поведения под понятие применяются во всех областях математической науки, действия рассмотрения элементов геометрических фигур с различных точек зрения характерны только для геометрии. В приведённой выше структуре учебные действия классифицированы с точки зрения функции:

1. Ориентировочные - оценка;

2. Исполнительные - преобразование условий учебной задачи, моделирование выделенного отношения, преобразования модели, построение системы частных задач;

3. Контрольные - контроль.

Под приёмом умственной деятельности Д.Н. Богоявленский понимает «систему процессов или операций анализа, синтеза, абстракции, обобщения и других специально организованных для решения задач - проблем определённого типа и разной степени обобщённости» [42].

Именно в связи с тем, что приёмы умственной деятельности и приёмы учебной деятельности неразрывно связаны, в последние годы дидакты употребляют в синтезе оба вида приёмов и говорят о приёмах учебно-познавательной деятельности (например, М.И. Махмутов).

Среди приёмов умственной деятельности в обучении математике можно выделить приёмы учебно-познавательной деятельности по решению задач. Н.Ф. Талызина даёт следующее определение: «В процессе решения задач человек, как правило, использует не отдельные действия, а целые их системы. Обычно такую совокупность действий, приводящих к решению задач определённого класса, называют приёмом, способом или методом решения» [49, с.196].

Приёмы умственной деятельности играют важную роль в обучении школьников и в частности в решении проблемы «учить учиться». Развитие умственных способностей, в том числе и развитие мышления, является компонентом общей задачи математического образования. В связи с этим в методической литературе часто говорят о развитии математического мышления. В современной психологии под мышлением понимается процесс опосредственного и обобщённого познания человеком предметов и явлений объективной действительности в их существенных свойствах, связях и отношениях. Мышление связанное с математической деятельностью вообще с усвоением математики школьниками в частности, полностью отвечает приведённой трактовке понятия мышления. Поэтому нет необходимости в введении понятия «математическое мышление», и в введении в нём своих особенностей и компонентов, а также в отождествлении математического мышления с логическим.

Большинство психологов, дидактов и учителей-практиков утверждают, что само обучение математике развивает мышление, т.е., что вооружение учащихся знаниями и их умственное развитие, включая развитие мышления, осуществляется совместно, т.к. формирование развитие мышления происходит только в процессе усвоения и применения знаний. Но С.Л. Рубинштейн указал, что неправомерно подчинять проблему развития мышления проблеме усвоения знаний. Каждая из этих проблем имеет самостоятельное значение и свой путь реализации.

Мышление в процессе обучения осуществляется на двух уровнях - эмпирическом и теоретическом. Основой эмпирического мышления является путь постепенного обобщения материала и варьированием многообразия частных случаев. В основе теоретического мышления лежит путь обобщения, связанный с анализом лишь одного явления в ряду сходных явлений и высшей формой анализа - анализа через синтез. Исследуя основы эмпирического и теоретического мышления и их роль в процессе обучения, В.В. Давыдов показал, что построение всех учебных предметов, в том числе и математики, причём математики в особенности, должно проектировать формирования у школьников современного научно-теоретического мышления, закономерности которого раскрываются математической диалектикой.

§3. Психологическая трактовка основных общих умственных действий

В работе «О мышлении и путях его исследования» С.Л. Рубинштейном наиболее полно дана психологическая характеристика механизма мышления и составляющих его действий. Автор показал ведущую роль анализа и синтеза в процессе мышления.

Рассмотрим, как трактуется в современной науке термины «анализ» и «синтез». Анализ - процедура мысленного, а часто также и реального расчленения предмета (явления, процесса), свойства предмета (предметов) или отношений между предметами на части (признаки, свойства, отношения), процедурой, обратной анализу, является синтез, с которым анализ часто сочетается в практической или познавательной деятельности.

Анализ (по-гречески analysis - разложение, расчленение, разбор) и синтез (synthesis - соединение, составление, объединение) изучают психология, теория познания и методология науки, логика. Но каждая из этих наук подходит к синтезу по-разному.

В психологии анализ и синтез - это составляющие психического процесса, который происходит на различных уровнях отражения действительности в мозгу человека.

Теория познания и методология науки интересуются проанализированностью, обобщённостью продуктов мышления как результатов человеческой мысли на пути движения к истине.

В логике анализ - это уточнение логической формы (строения, структуры), рассуждение, которое осуществляется средствами современной формальной логики.

В методике преподавания математики терминами «анализ» и «синтез» традиционно называют два противоположных по ходу действия мысли рассуждения, которые применяются при решении задач и доказательстве теории: анализ - это рассуждение, идущее от того, что надо найти или доказать, к тому, что дано или уже установлено ранее; синтез - рассуждение, идущее в обратном направлении.

Анализ служит для выявления идеи решения или доказательства. Даёт же доказательство синтез, который, опираясь на данные анализа, показывает, как из данных и ранее установленных утверждений находится искомое или вытекает доказываемое.

Большой интерес для методики и практики обучения математике представляют анализ и синтез как общие умственные действия (операции), лежащие в основе любого вида познавательной деятельности школьников.

На различных ступенях познания анализ принимает различные формы:

. Анализ чувственных образов предметов и явлений, или чувственный анализ;

. Мыслительный анализ словесных образов или абстрактно-логический анализ, который осуществляется с помощью понятий и суждений, выражаемый в языках (знаковых системах науки).

В реальной мыслительной деятельности анализ и синтез связаны неразрывно. Особенно ярко это наблюдается в математике при решении задач и доказательств теорем. Решение любой задачи и доказательство всякой теоремы начинается с анализа и формулировок, с вычленения того, что дано и что требуется найти (доказать), далее идёт соотношение условий и требований друг с другом, то есть синтез.

С.Л. Рубинштейн выделяет важную форму анализа - анализ, который осуществляется через синтез. Суть его заключается в том, что «объект в процессе мышления включается во всё новые и новые связи и в силу этого выступает во всё новых качествах, которые фиксируются в новых понятиях; из объекта, таким образом, как бы вычерпывается всё новое и новое содержание; он как бы поворачивается каждый раз другой своей стороной, в нём выявляются всё новые и новые свойства». Задачи, в решении которых применяется анализ через синтез, позволяют целенаправленно обучать учащихся приёму умственной деятельности, который в психологии называют приёмом переосмысливания элементов задачи, т.к. он позволяет один и тот же элемент задачи рассматривать с различных точек зрения.

Единство анализа и синтеза на уровне эмпирического мышления выступает в сравнении. Сравнение - это умственное действие, с помощью которого в предметах явлениях выделяются отдельные признаки, находятся общие и различные свойства. Сравнение начинается с соотношения или сопоставления предметов и явлений, то есть и синтеза. При помощи этого синтетического акта происходит анализ сравниваемых объектов, выделение в них общего и различного. Выделенное анализом общее, объединяет, т.е. синтезирует объекты. Тем самым осуществляется обобщение. К.Д. Ушинский указывал, что сравнение - основа всякого понимания и мышления, основное условие продуктивности мыслительных процессов, а значит и всей аналитико-синтетической деятельности.

Сравнение - обязательное условие всякой абстракции и любого обобщения. Есть две основные формы сравнения - сопоставление и противопоставление. Сопоставление - это умственное действие, направленное на выделение существенных признаков, общих для ряда объектов (позитивная абстракция). Противопостановление - умственное действие, направленное на выделение того, от чего следует отвлечься при определении существенных признаков (негативная абстракция).

Сравнение выполняется только в совокупности однородных объектов, образующих класс. При этом сравниваются признаки существенные для данного случая. Важный тип отношений, выявляемых путём сравнения, - это отношения тождества (равенства) и различия.

Абстракцию как общее умственное действие С.Л. Рубинштейн определил так: «…абстракция - это по существу тоже специфическая форма анализа, форма, которую анализ приобретает при переходе к абстрактному мышлению в понятиях. Аналитический характер научной абстракции заключается в том, что она выделяет существенное, отвлекаясь от несущественного. Она анализирует и членит то диффузное, ещё непроанализированное целое, в ко-тором существенное и несущественное ещё не расчленены».

По способам выполнения в психологии различают три вида абстракции:

1. Изолирующая абстракция, составляющая в вычленении определённого элемента (предметов, признаков, частей и т.д.) из других элементов;

2. Подчёркивающая абстракция, состоящая не только в выделении одного элемента, но и в указании на другие, выступающий как фон для выделенного элемента;

3. Противопоставляющая (расчленённая) абстракция, состоящая в сознательном расчленении существенного и несущественного и в их противопоставлении.

Термин «абстракция» (от латинского abstraction - отвлечение) употребляется такое обозначение метода научного исследования, основанного на том, что при изучении некоторого явления, процесса не учитывается его несущественные стороны и признаки, что позволяет упростить картину рассматриваемого явления и изучать его «в чистом виде».

Раскрывая природу мышления и его состав, С.Л. Рубинштейн указал, что мышление по своему составу выступает как анализ, синтез, абстракция и обобщение.

С.Л. Рубинштейн показал, нельзя рассматривать обобщение, как нахождение общего в предметах и явлениях, и определил, что «обобщение - практически значимое и научно оправданное - это не выделение вообще каких либо общих свойств, в которых предметы или явления схожи между собой независимо от того, что это за свойства; научное обобщение включает не вообще свойства, общие или сходные для ряда явлений, а свойства, существенные для них».

Под существенными понимают такие общие свойства, которые неотделимы от определённого класса предметов, однозначно отличают любой предмет данного класса предметов, однозначно отличают любой предмет данного класса предметов, однозначно отличают любой предмет данного класса от других предметов других классов.

В логике под существенными понимают такие независимые признаки объекта, каждый из которых является необходимым, а все вместе достаточными для того, чтобы объект принадлежал к данному понятию.

В зависимости от уровня познания обобщение выступает в двух основных формах:

. Генерализация - обобщение, которое совершается по признаку или свойству, являющемуся наиболее сильным раздражителем (первосигнальная генерализация);

. Понятийного обобщения (собственно обобщения), связанного со словом, как условием и формой своего существования.

В пределах понятийного обобщения также различают две разные формы: элементарное эмпирическое обобщение и обобщение на уровне теоретического мышления, когда обобщаются отношения, закономерно необходимые связи предметов и явлений.

Обобщение используется в разных видах учебно-познавательной деятельности при изучении математике: при формировании понятий, при доказательстве теорем, при решении задач. Поэтому учить приёмам правильного обобщения - одна из главных задач обучения математике.

Необходимым условием формирования правильных обобщений является варьирование несущественных признаков понятий, свойств, фактов при постоянных существенных.

В зависимости направления хода мысли в практике обучения математике используется два основных приёма обобщения:

. Учащиеся сопоставляют заданные объекты, вычленяют и формируют их общие существенные признаки, отвлекаясь (абстрагируясь) от несущественных и объединяют объекты по этим признакам обобщают. При этом приёме ученикам неизвестны общие существенные признаки, они их самостоятельно выявляют;

. Учащиеся знают, какие общие существенные признаки надо выявить, из данных объектов они выделяют те, которые входят в содержание формируемого понятия, сопоставляя, вычленяя в каждом объекте эти признаки и объединяя объекты по выделенным существенным признакам.

Из сказанного выше следует, что состав мышления может быть выражен структурой:

Приведённая структура показывает, что анализ и синтез входят в состав каждого из общих умственных действий.

Схема 6

. Изолирующая абстракция;

. Подчёркивающая абстракция;

. Противопоставляющая абстракция;

. Сопоставление;

. Противопоставление;

. Генерализация;

. Понятийное обобщение;

. Элементарное эмпирическое обобщение;

. Обобщение на уровне теоретического мышления.

§4. Приёмы учебно-познавательной деятельности по решению задач

Математика, наряду с другими школьными предметами решает задачу массовой подготовки учащихся к самообразованию. Задача учить учиться предусматривает развитие у школьников самостоятельного мышления, активизацию их подсознательной деятельности, творческой инициативы. Исследования психологов, дидактов, методистов установлено, что реальным инструментом самостоятельного познания для учащихся могут стать рациональные приёмы умственной деятельности, рациональные приёмы учебной работы. При этом учителем ставится цель прямо и косвенно формировать у учащихся приёмы общих и специфических умственных действий, входящих в состав различных видов учебно-познавательной деятельности.

Под приёмом умственной деятельности Д.Н. Богоявленский понимает «систему процессов или операций анализа, синтеза, абстракции, обобщения и других специально-организованных для решения задач - проблем определённого типа и разной степени обобщённости» [42].

В исследованиях В.И. Крупича выявлен и в обобщённом виде показан механизм реализации основных требований к методике формирования приёмов учебной деятельности в процессе обучения математике. Методическая схема формирования приёмов учебной деятельности в процессе обучения представляется таблицей 1 [18, с.50]. Центральным в таблице является второй столбец, отражающий психолого-дидактическое требование о поэтапном формировании приёмов учебной деятельности. Третий столбец и его связи со вторым конкретизируют первое требование к методике формирования приёмов в процессе обучения: формирование приёмов учебной деятельности должно быть основой обучения учащихся знаниям, умениям и навыкам. Первый столбец показывает, что анализ задач каждого типа может служить одним из критериев выбора методов обучения (третье требование к методике).

Наличие в таблице четвёртого столбца иллюстрирует один из аспектов реализации четвёртого требования к методике формирования приёмов учебной деятельности учащихся.

Следует отметить, что рассмотренная методическая схема только помогает определить необходимые компоненты методики обучения математике на основе формирования приёмов учебной деятельности учащихся. Она показывает, что закономерности процесса формирования обобщённых приёмов учебной деятельности, последовательность этапов и их специфика предъявляют определённые требования к методике обучения.

Методическая схема формирования приёмов учебной деятельности в процессе обучения

Однако, не следует понимать, что выделенные этапы обучения чётко определены друг от друга и взаимодействуют только в указанной последовательности. Как сами приёмы учебной деятельности учащихся, так и методы их формирования в процессе обучения не переплетаются в самых различных сочетаниях.

Приёмы учебной деятельности школьников, как основа любой деятельности, впервые были рассмотрены Д.Н. Кабановой-Мюллер и другими психологами. Исследования показали, что если у школьника формируется умение без предварительного формирования соответствующего рационального приёма, то нередко он овладевает неправильным умением [24]. Однако, приёмы учебной деятельности должны составлять систему, адекватную системе осуществляется с помощью классификации приёмов учебной деятельности.

Классифицируя приёмы по характеру учебной деятельности Е.Н. Кабанова-Мюллер различает: общие приёмы, направленные на организацию (управления) учебной деятельности и без индивидуальных различий (например, планирование, самоконтроль и т.п.); приёмы усвоения и применения знаний; приёмы самостоятельной работы; специальные приёмы, связанные с содержанием предмета.

Используя тоже основание В.И. Крупич выделяет в школьном курсе математики следующие четыре группы приёмов учебной деятельности:

1. Общеучебные приёмы, не зависящие от специфики предмета математики и используемые, поэтому в разных учебных предметах. Эти приёмы разделяются на две подгруппы:

− приёмы внешней (общей) организации учебной деятельности - организация внимания, планирования, самоконтроль, работа с учебником и справочной литературой, организация домашней работы и т.д.; их можно назвать приёмами управления учебной деятельностью;

− приёмы внутренней (мыслительной) деятельности - овладение и оперирование представлениями, понятиями, суждениями, умозаключениями, мыслительными операциями.

2. Общие приёмы учебной деятельности по математике (общематематические приёмы) используются во всех математических дисциплинах и так же подразделяются на две группы:

− приёмы внешней организации учебной деятельности - приёмы работы с учебником математики и математическими таблицами, приёмы организации домашней работы по математике и т.д. они незначительно отличаются от соответствующих общеучебных приёмов;

− приёмы мыслительной деятельности в сфере математических объектов; приёмы работы с математическими понятиями, суждениями (аксиомами и теоремами разных видов), умозаключениями (индуктивными и дедуктивными доказательствами теорем), приёмы характерных для математики мыслительных операций (анализ, абстрагирование, конкретизация и т.д.).

3. Специальные приёмы учебной деятельности по отдельным дисциплинам - это такие общематематические приёмы, которые принимают свою особую форму в соответствии со спецификой содержания курса и особенностями его задач. Они используются в любых разделах курса. В каждом из специальных приёмов можно выделить подгруппы частных приёмов, соответствующим данным задачам. Без усвоения специальных приёмов учебной деятельности содержание предмета усваивается формально.

4. Частные приёмы учебной деятельности - это такие специальные приёмы, которые конкретизированы для решения более узких задач и используются в определённых темах курса [18, с.15].

Структура приёмов учебной деятельности учащихся по обучению математике может быть наглядно представлена следующей схемой (схема 7):

Один и тот же приём деятельности в различных ситуациях может выступать как частный по отношению к более общему приёму и как обобщённый по отношению к ещё более узким приёмам. Таким образом, любой приём учебной деятельности, выступая как обобщённый, помогает учащимся овладеть обобщёнными способами действий, а также способствует выработке у него умений и навыков по самостоятельному добыванию знаний.

Но это и является основой деятельностного подхода, т.к. он предполагает такую организацию деятельности учащихся в процессе обучения, при которой создаются условия для эффективного усвоения учащимися знаний и способов деятельности, для их развития.

Следовательно, из двух путей усвоения приёмов деятельности (стихийного и управляемого), наиболее эффективным является второй путь, т.к. в этом случае приёмы служат предметом специального усвоения и резко сокращается процесс их формирования.

В педагогической психологии выделены основные этапы обучения приёмам:

) Введение или нахождение приёма;

) Обучение его применению;

) Обобщение приёма;

) Обучение нахождению новых приёмов.

Показателем сформированности приёмов учебной деятельности школьников является осознание ими этих приёмов, т.е. умение рассказать о составе приёма учебной деятельности, заключается в умении обосновать, аргументировать, правильность его выполнения [50].

В системе обучения школьников приёмам учебной деятельности немаловажную роль играет процесс обучения учащихся приёмам поиска решения задач, т.к. умение решать задачи является одним из основных показателей уровня математического развития ученика, глубины усвоения учебного материала.

В математике всегда уделялось много внимания обучению решения задач. Однако, до сих пор, во многих школах, единственным методом такого обучения остаётся показ способов решения определённых видов задач и практика по овладению ими.

Психологические исследования проблемы обучения решению задач показали, что основные причины несформированности у учащихся общих умений и способностей в решении задач состоят в том, что школьникам не даются необходимые знания о сущности задач и их решений, а потому они решают задачи не сознавая должным образом свою собственную деятельность и не воспринимая задачу как объект изучения, а её решение - как объект конструирования и изобретения. У учащихся не вырабатываются обобщённые приёмы учебной деятельности по решению задач, и поэтому им приходится осваивать эти приёмы в самом процессе решения задач, т.е. стихийно, что многим школьникам не под силу. Не стимулируется постоянный анализ учащимися своей деятельности по решению задач и выделению в них общих подходов и методов, их теоретического осмысления и обоснования. Всё это не способствует формированию учебной деятельности ученика можно судить по тому, насколько самостоятельно и сознательно он выполняет все указанные выше элементы структуры учебной деятельности, т.е. соотносит мотивы с целями учения и владения приёмами учебной деятельности.

Определённое влияние на методы обучения школьников решению задач оказывает тот факт, что в психологической и педагогической литературе нет единой трактовки понятия «задача». В зависимости от того, к каким системам применяется понятие «задача», можно выделить два направления:

) здесь задача трактуется как ситуация внешней деятельности, которая может быть проанализирована и описана в отрыве от субъекта, осуществляющего деятельность. Этот подход лишает понятия «задача» психологического содержания;

) здесь задача рассматривается как субъективное, психологическое отражение той внешней ситуации, в которой развёртывается целенаправленная деятельность субъекта. Поэтому без субъекта задачи - нет, а то, что является задачей для одного субъекта может не быть задачей для другого. В этом случае невозможно объективное изучение задач, независимое от рассмотрения деятельности субъекта. При таком подходе изучаются не сами задачи, а только процессы их решения.

В последние годы в психологии, кибернетики, логике делается попытка исследования задач как таковых, а не только процессов их решения. В исследованиях А.М. Матюшкина, А.В. Бургилинского, А.М. Фридмана, В.И. Крупича и др. задача рассматривается как сложный объект (система), не требующая для своей характеристики субъекта действия (первое направление). В этом случае создаётся возможность объективного изучения самих задач, не зависимо от деятельности субъекта [55].

Если мы попытаемся понять, как люди решают задачу какого-либо вида, необходимо иметь хорошие представления о структуре решаемой задачи [43, с.185].

Однако, при этом не отрицается, что задача может существовать в мышлении субъекта.

Таким образом, сущность рассмотренных подходов к понятию «задача» состоит в том, что задача - это сложный объект (система), несущая на себе две информации субъективную и объективную. При этом объективная информация, заключённая в задаче определяется её внутренней структурой, а субъективная - её информационной структурой (внешним строением задачи). Следовательно, школьную математическую задачу можно рассматривать, как диалектическую взаимосвязь субъективной информации, и выделить в ней две структуры: внешнюю и внутреннюю. Внешнее строение задачи (информационная структура) - определяет степень проблемной задачи, (этот вопрос будет рассмотрен в первом параграфе второй главы), внутреннее устройство задачи (внутренняя структура) - определяет стратегию решения задачи и её сложность [27, с.47]. Сказанное, можно изобразить следующей схемой:

Схема 8

Под приёмом деятельности понимается обобщённое знание о действиях или системе действий, необходимых при отыскании решения специфических для данной деятельности задач, причём это задание объективировано каким-либо образом, например, в виде словесного описания или схемы. Приём деятельности имеет свою структуру: предмет, цель или операционный состав [27, с.31]. Исходя из этого, можно предположить, что выявление системы приёмов решения математической задачи определяется внутренней структурой задачи. Однако это условие является необходимым, но не достаточным, для получения структуры выявления приёма деятельности по решению задачи. Приёмы решения задач помогают научить учащихся осознанному поиску способа решения конкретной математической задачи. Следовательно, прежде, чем приступить к решению задачи ученику предстоит определить тип задачи и её место в системе задач, а для этого необходима соответствующая классификация школьных математических задач.

С позиций деятельностного подхода к обучению школьные математические задачи можно разделить на алгоритмические, решение которых однозначно определяется некоторым алгоритмом; полу алгоритмические и полу эвристические, решение которых не однозначно определяется той или иной схемой, содержащей как алгоритмические, так и эвристические указания; эвристические, решение которых не гарантируется конечным числом шагов, а предполагает их выбор из многих вариантов. Однако, предложенная типология задач носит субъективный характер, т.к. одна и та же задача в зависимости от ряда условий (кто решает задачу, когда, на каком этапе обучения) может быть отнесена к разным типам. Для уточнения предложенной типологии, исходя из психологической структуры действия [30], можно выделить некоторые компоненты действия:

) Цель действия;

) Способ действия;

) Условия выполнения действий.

В процессе решения задач цель действия определяет конечный результат решения задачи (новые знания, закономерности, отношения, свойства, необходимые для обоснования решения задачи); способ действия определяет алгоритм (приём) или последовательность алгоритмов (приёмов) решения задачи; условия выполнения действий определяют теоретическая и практическая основа (базис) решения задачи, содержащей функциональное отношение.

Выделенные признаки (новые знания, закономерности, отношения, свойства, алгоритм (приём) решения задачи или их последовательность, теоретическая и практическая основа (базис) решения задачи составляют психологическую структуру алгоритмических, полуэвристических и эвристических задач, в зависимости от того, какие из них известны обучаемому в каждом из выделенных типов [27, с.26].

Принятые соглашения оформим в виде схемы (где знак «→» означает, что компонент действия известен или неизвестен; знак «→» - означает, что компонент действия известен; отсутствие стрелки (связи) показывает, что компонент действия неизвестен):

Схема 9

Рассматривая, выделенные в дидактике уровни познавательной деятельности учащихся [59] можно отметить, что репродуктивному уровню познавательной деятельности соответствуют алгоритмические задачи; частично поисковому - полуэвристические задачи; исследовательскому (творческому) уровню - эвристические задачи.

Выделенная типология задач будет в дальнейшем использована при построении системы стереометрических задач на построение по теме «Прямая и плоскость» и для определения степени проблемности рассмотренных групп задач.

В традиционной методике математики для облегчения поиска решения выделяют два вида задач: стандартные и нестандартные. Поэтому, учитывая, что в общем случае алгоритмические и полуэвристические задачи алгоритмически разрешимы, отнесём их к стандартным задачам. Эвристические задачи в процессе поиска решений позволяют выявить локальные алгоритмы; но для завершения процесса их решения необходим эвристический поиск, устанавливающий взаимосвязи между выявленными локальными алгоритмами. Следовательно, алгоритмические задачи алгоритмически неразрешимы и это позволяет отнести их к нестандартным задачам.

В состав мыслительной деятельности по решению любых задач входят общие умственные действия (анализ, синтез, сравнение, абстрагирование, обобщение, конкретизация, установление и использование аналогий), специфические умственные действия, характерные для решения задач (подведение под понятие, развёртывание условий, переосмысливание элементов задачи, установление существенных связей) и логико-математические, с помощью которых решающий логически преобразовывает математический материал. При этом учащиеся выполняют умозаключения индуктивного и дедуктивного характера, по аналогии, по интуиции с последующим обоснованием или опровержением их. Первоочередная задача развивающего обучения - прямо и косвенно формировать в процессе решения задач приёмы выполнения действий, составляющих механизм решения задачи.

В современной дидактике и психологии процесс решения задачи разделён на восемь этапов [55]:

. Анализ задачи;

. Схематическая задача;

. Поиск способа решения задачи;

.Осуществление решения задачи;

. Проверка решения задачи;

. Исследование задачи;

. Формирование ответа задачи;

. Анализ решения задачи.

Взаимосвязь между этапами выражает структуру процесса решения задачи [55]:

Схема 10

Необходимо отметить, что структура процесса решения задачи зависит прежде всего от характера задачи, и выполнение этапов выведенных за пределы линейной зависимости не всегда целесообразно, этапы связанные линейной зависимостью являются обязательными.

Предложенная структура разбивает познавательную деятельность учащихся на учебные действия, которые достигают своей цели тогда, когда они осуществляются с помощью приёмов, раскрывающих способы их осуществления.

Назовём общие приёмы учебной деятельности учащихся по решению задач с указанием адекватных им учебных действий:

1. Приём принятия учебной задачи соответствует первому этапу процесса решения - «анализ задачи» и выполняется с помощью первого учебного действия преобразование условий учебной задачи;

2. Приём поиска решения задач соответствует этапу - «поиск способа решения» и выполняется с помощью второго учебного действия преобразование модели;

3. Приём формирования общего способа решения учебной задачи соответствует этапу - «план решения» и выполняется с помощью третьего учебного действия преобразование модели;

. «Осуществление плана решения» и выполняется с помощью четвёртого учебного действия построение системы частных задач;

5. Приём осуществления контроля за процессом решения выполняется с помощью учебного действия контроль.

Выше было отмечено, что действие контроль присутствует на всех этапах решения учебной задачи. Поэтому, учитывая, что пооперационный контроль может быть рассмотрен только для задач определённого типа, выделим два приема, в которых контроль осуществляется по конечному результату:

• Приём проверки путём решения задачи различными способами соответствует этапу - «анализ решения»;

• Приём установления соответствия полученных результатов данным задачи соответствует этапу «проверка»;

6. Приём оценки результата соответствует этапу «исследование задачи» и выполнение с помощью учебного действия оценка.

Отметим, что приём поиска решения задачи раскрывает способы осуществления общих методов поиска решения определённого вида задач. Большинство задач школьного курса математики решается аналитико-синтетическим методом, поэтому приём, адекватный действию осуществления решения задачи в этом случае, назван приёмом аналитико-синтетического поиска решения задач [18, §3]. В более сложных задачах для поиска решения проводится анализ Евклида или совершённый анализ (рассуждений от требований к условиям). Пооперационный состав каждого приёма возможно выделить только для задач конкретного вида. В следующем параграфе будут рассмотрены содержание и структура приёмов учебной деятельности в процессе задач на построение по теме «Прямая и плоскость».

Выделение общие приёмы учебной деятельности учащихся по решению задач связаны с этапами решения задачи и адекватными или учебными действиями следующим образом (схема 11).

Схема 11

Взаимосвязи между приёмами учебной деятельности (УД) устанавливаются только для задач конкретного вида.

Выше было отмечено, что пооперационный состав каждого приёма учебной деятельности учащегося по решению задачи определяется для задач конкретного вида. Однако, анализ научно-методической литературы и диссертационных исследований показал, что для некоторых приёмов (например, приёма принятия учебной задачи) могут быть выделены общие операции не-зависящие от вида или от типа задач. Рассмотрим эти приёмы и выделим их пооперационный состав.

Предварительно напомним, что в традиционной методике математики выделяются такие виды задач: на вычисление, построение, доказательство и исследование, и, что в проведенной классификации нами выделены два типа задач: стандартные и не стандартные. К стандартным задачам были отнесены задачи алгоритмического и полуэвристического типов, к нестандартным - задачи эвристического типа. Учитывая, признаки задач алгоритмического, и эвристического типов, выделенные с помощью логико-дидактического анализа содержания структурных компонентов действия (цель, способ и условия выполнения действия), можно дать следующие определения стандартных и нестандартных задач.

Математические задачи, для решения которой в школьном курсе математики имеется теоретическая и практическая основа (базис решения, содержащий функциональное отношение), определяющие алгоритм (приём) или последовательность алгоритмов (приёмов) решения задачи, называется стандартной.

Из данного определения следует, что основным признаком стандартной задачи является наличие в курсе таких общих правил и положений, которые однозначно определяют программу решения задачи и выполнение каждого шага программы. Но тогда, нестандартная задача - это задача, для которой в курсе математики не имеется общих правил и положений, определяющих точную программу её решения.

Из процесса решения любой задачи можно выделить два составленных элемента: анализ задачи и поиск способа решения. Однако, наиболее важным элементом процесса решения задачи является поиск способа решения, который, исходя из данных выше определений, можно назвать основной отличительной особенностью решения стандартной задачи от решения нестандартной задачи. Следовательно, при определении операционного состава приёма поиска решения учебной задачи, необходимо учитывать вид задачи.

Первому из названных этапов решения задач (анализу задачи) соответствует приём принятия учебной задачи. Этот приём определяется мотивационно-ориентировочной компонентной учебной деятельности. Поэтому его содержание должно быть ориентировано на формирование у учащихся определённых мотивов учебной деятельности. С другой стороны реализация приёма осуществляется с помощью первого учебного действия - преобразование условий учебной задачи, которое выявляет основное отношение задачи. Найденное отношение, создавая в задаче информационно-познавательное противоречие, помогает учащемуся осознать условие и требование задачи. Сказанное, позволяет выделить общие операции приёма принятия учебной задачи при решении математической задачи учащимся:

. Внимательно прочитать текст задачи;

. Установить к какому виду принадлежит данная задача;

. Выявить условия (что дано?) и требования (что требуется?) задачи;

. Оформить чертёж, соответствующий условию и требованию задачи (если есть необходимость);

. Записать кратко условие и требование задачи.

Результатом этой деятельности, после выяснения характера задачи её вида, установления условий и требований (конечно, не всегда в полном объёме), является принятие задачи учащимся как цели своей деятельности.

Второй этап решения задачи (поиск способа решения) реализуется приёмом поиска решения учебной задачи с помощью второго учебного действия (моделирование выделенного отношения). На этом этапе, выделенное основное отношение фиксируется учебной моделью, содержащей внутренние характеристики задачи, не наблюдаемые непосредственно (внутреннюю структуру задачи).

Для стандартной задачи учебной моделью является программа - последовательность шагов решения задач данного вида, составленная (если, конечно, такая программа не рассматривалась в курсе математики) на основе общего правила (формулы, тождества) или общего положения (определения, теоремы). Тогда, следующий этап, само решение стандартной задачи состоит в применении полученной модели (общей программы) к условиям данной задачи. Если некоторые шаги программы решения требуют для своего выполнения использования каких-то программ, то в отношении их производятся рассмотренные выше операции (распознавание вида задачи, составление программ решения и осуществление решения на основе этой программы).

Анализ научно-методической литературы показал, что поиск решения любой нестандартной задачи школьного курса математики состоит в последовательном применении двух основных операций:

) Путём преобразования или переформирования свести нестандартную задачу к другой, ей эквивалентной, но уже к стандартной задаче;

) Разбить нестандартную задачу на несколько стандартных подзадач.

Таким образом, приём поиска решения учебной задачи реализуется при решении нестандартной задачи с помощью двух учебных действий: моделирование выделенного отношения и преобразования модели.

Сформируем общие операции приёма поиска решения учебной задачи при решении учащимся математической задачи:

. Провести анализ задачи и установить, к какому типу задач она принадлежит;

. Если предложенная задача является стандартной, то на основе общего правила (формулы, тождества) или общего положения (определения, теоремы) составить программу (если нет готовой) последовательности шагов решения задач данного вида;

. Если предложенная задача не является стандартной, то применить одну из операций:

.1 Разбить данную задачу на стандартные или более простые подзадачи с помощью разбиения на части:

а) условий задачи;

б) объекта задачи;

в) требований задачи;

.2 Ввести в условие вспомогательные элементы (вспомогательные параметры, вспомогательные построения) для:

а) сближения данных и искомых;

б) расчленения задачи на части;

в) придания задаче определённости;

.3 Переформулировать данную задачу, заменив её другой равносильной задачей, которая является стандартной или задачей способ решения кото-рой известен, с помощью:

а) преобразования условия;

б) замены переменных (неизвестных);

в) замены (кодирования) объектов другими;

. Построить учебную модель решения задач данного вида.

Таким образам, при решении математической задачи приём поиска решения учебной задачи определяется структурой (схема 12).

Из проведённых выше рассуждений, следует, что приёмы деятельности могут быть разной степени сложности и обобщённости. Более сложный приём состоит из большего числа действий, включает в себя в качестве составляющих другие приёмы. Приём деятельности назовём обобщённым, если он получен на основе анализа частных приёмов путём выделения общего, неизменного содержания деятельности по решению конкретных (частных) задач. Именно обобщённый приём создаёт ориентировочную основу необходимой деятельности по решению ряда учебных задач и обеспечивает переносимость приёма на широкий круг новых частных задач.

Схема 12

Таким образом, обобщённый приём решения школьных математических задач имеет структуру (схема 13).

Схема 13

психологический учебный познавательный математика

Глава 2. Проблема формирования приёмов учебной деятельности в научно-методической литературе и практике обучения математики

Проведённый в предыдущей главе анализ психолого-педагогических основ деятельностного подхода показал, что цели данного подхода в области обучения решению задач достигаются тогда, когда они реализуются через формирование приёмов учебной деятельности учащихся по решению задач. Следовательно, с точки зрения деятельностного подхода, процесс обучения решению задач происходит в процессе формирования у учащихся приёмов учебной деятельности по решению учебных задач.

Однако, прежде чем рассматривать формирование приёмов учебной деятельности учащихся по решению стереометрических задач на построение, выделенных в параграфе 4, необходимо рассмотреть следующие вопросы:

. Для каких видов задач выявлены приёмы учебной деятельности.

. Как формируются выделенные приёмы у учащихся в учебном процессе.

Ответ на первый вопрос может быть найден после проведения анализа научно-методической литературы, а на второй - практики школьного обучения.

§1. Проблема формирования приёмов учебной деятельности в научно-методической литературе

Рассматривая вопрос о формировании приёмов учебной деятельности в научно-методической литературе, выделим следующие направления:

. Разработка различных советов, рекомендаций, указаний, вопросов, правил и т.д. для решения математических задач.

. Выявление приёмов для решения и составления математических задач.

. Выявление приёмов учебной деятельности учащихся по решению математических задач.

Остановимся на каждом, из перечисленных выше, направлений.

Представители первого направления Д. Пойа, Ю.М. Калягин, Л.М. Фридман и другие предлагают различные рекомендации, советы в процессе решения задач.

При анализе условия и требования задачи Д. Пойа предлагает обращаться к учащимся со следующими вопросами: Что гласит задача? Что дано? Что нужно найти? Определено ли неизвестное данными задачи? Или недостаточны, или чрезмерны? Нельзя ли сформулировать задачу иначе? Нельзя ли найти связь между данной задачей и какой-нибудь задачей с известным решением? Или с задачей, решающейся проще? Решающейся сразу [39]?

Отвечая на вопрос: Как же научиться решать задачи? Л.М. Фридман предлагает следующее:

Во-первых, надо научиться анализировать сами задачи.

Это значит, что нужно уметь расчленять задачу на элементарные условия и требования. А в каждом элементарном условии видеть объект и его характеристику, если же объектов в условии несколько, то выявить их отношение (связь). Нужно также установить характер каждого требования (вопроса) и тем самым определить вид задачи;

Во-вторых, надо хорошо понять, что решение любой задачи есть последовательное применение каких-то знаний (главным образом математических) к условиям данной задачи, получение тем самым из этих условий следствий (промежуточных решений) до тех пор, пока не получим такие следствия, которые являются ответами на требования (вопросы) задачи.

А для того чтобы получать эти следствия, надо хорошо знать и помнить все знания (определения, правила, форму, теоремы и т.д.) из курса математики. Без этих знаний решать задачи невозможно;

В-третьих, надо уметь использовать основные методы решения задач. А их всего лишь три: разбиение задачи на подзадачи, преобразование (моделирование) задачи и метод вспомогательных элементов.

Получив задачу, проанализировав её, построив её схематическую запись (если надо), дальше надо действовать, как правило, в таком порядке:

. Если можно, разбить сложную задачу на более простые подзадачи.

При этом в ряде случаев это разбиение можно производить последовательно, вычисляя из данной задачи её подзадачи одну за другой.

. Если же разбить сложную задачу на подзадачи не удастся, то надо, если можно, преобразовать её в более простой, более знакомый вид.

Для этого можно использовать различные приёмы: тождественные преобразования данных выражений, замену переменных (неизвестных), различные замены объектов задачи другими более знакомыми или более удобными объектами и т.д.

Самый простой приём заключается в том, что сопоставляя между собой условия задачи, делают такие выводы, которые позволяют преобразовать задачу в более простой вид.

. Если же разбить задачу на подзадачи или преобразовать её в более простой вид непосредственно не удаётся, то надо попытаться ввести какие-либо вспомогательные элементы, с тем чтобы получить задачу, которую или можно разбить на подзадачи, или же преобразовать в более простой вид [54, с.179].

Различные приёмы и методы в поиске решения задач рассматривают Г. Д. Балк, М.Б. Балк, В.Г. Болтянский, Я.И. Груднев и другие. Разрабатывая различные методы и приёмы при решении задач они обращают внимание на то, что овладение различными эвристическими приёмами происходит не при изложении готового «отшлифованного» доказательства теоремы или решения задачи, а в процессе поиска доказательства или решения, в процессе самостоятельного открытия новых математических фактов. «Как искать решение? Как догадаться? Такие вопросы постоянно вставали перед учащимися» [3, с.55]. Основное внимание в поиске решения задач уделяется таким методам как анализ, синтез, обобщение, аналогия, интуиция, прогнозирование и перебор [4], в качестве эвристических приёмов рассматриваются такие приёмы как испытание на правдоподобность, обобщение плюс индукция, поиск решения путём предельных случаев, математическое экспериментирование и поиск неизвестных закономерностей, метод малых изменений, аналогия как средство поиска решения задач, введении вспомогательных неизвестных, переход к равносильной задаче, выделение подзадач и т.д. [3].

Говоря об эвристических приёмах при обучении геометрии А.К. Артемев выделяет такие приёмы: равносильного преобразования требования задачи, незавершённых задач, постановки и выполнения произвольного задания, сопоставительного вычисления [2, с.25-26].

Заметим, что перечисленные выше эвристические приёмы особенно эффективны при решении нестандартных задач. Однако вопрос о практическом вооружении учащихся эвристическими приёмами остаётся недостаточно разработанным.

Представители второго направления разрабатывают не только приёмы решения задач, но и приёмы их составления.

Рассматривая составление и решение задач, порождённых данной Е.С. Камин выделяет следующие приёмы составления таких задач: замена части данных исходной задачи другими данными без замены заключения задачи; обобщение данных и искомых; специализация задачи (обратное её обобщению); добавление новых заключений при сохранении данных; обращение задачи [25].

В учебно-методической литературе мало внимания уделяется вопросу воспитания у учащихся критического отношения к содержанию условия задачи. Поэтому особое значение при обучении учащихся анализировать условие и требование задачи имеют исследование И.Я. Кушнир, М.П. Буловацкого, Г.П. Недогарок, предлагающие различные приёмы определения доста-точности и недостаточности условий задач для её решения, а также различные вспомогательные задачи с недостающими и мнимыми данными, и пути их исследования [5, 28, 32].

Различные методы решения задач освещены в работах В.Н. Литвиненко, И.А. Терехова, И.В. Чичаевой [29, 51, 58].

Рассматривая роль метода вспомогательных задач в обучении учащихся решению задач, И.А. Терехов предлагает ученику, испытывающему затруднения при решении задачи, заранее подобранную задачу, в некоторых элементах решения аналогичную основной задаче. Автор выделяет два вида вспомогательных задач: эквивалентные и являющиеся частью основой. При этом, две задачи эквивалентны, если решение одной из них вытекает из решений другой.

На основании опыта преподавания геометрии в средней школе Г.Д. Зайцева предлагает один из возможных путей формирования умений учащихся решать стереометрические задачи. Идея заключается в составлении схемы «разложения» решений задачи на более простые - составляющие задачи. Применение такого разложения при решении ряда стереометрических за-дач даёт возможность учащимся осознать:

. Из решения каких частных задач состоит решение данных задачи.

. Какие составляющие задачи повторяются в «разложениях» разных задач.

. Где метод, результат решения составляющих задач можно использовать в дальнейшем.

Автор отмечает, что «разложение» задач на составляющие помогает учащимся осознанно выделить систему часто повторяющихся составляющих стереометрических задач, которую называет системой опытных задач. Приводится система правил для выбора необходимых опорных задач по решению данной задачи [21].

В исследованиях М.Е. Тимощук [53] по формированию навыков и умений учащихся решать стереометрические задачи основными моментами являются:

. Отбор задач.

. Использование обучающих воздействий, которые повышают познавательную активность учащихся, обеспечивают возможность переноса умений. При отборе задач необходим учёт их объективной и субъективной сложности, соответственные уровню развития учащихся.

В разграничении уровней объективной сложности задачи используются следующие понятия:

. Элементарные простые задачи - решаемые в один-два шага на основании известных теорем, аксиом, определений.

. Элементарные составные задачи - относительно простые по своей фабуле, они являются составляющими сложных задач.

. Сложные задачи первого уровня, которые в результате переформирования исходного требования сравнительно легко сводятся к цепочке элементарных задач.

. Сложные задачи второго уровня - сводятся к элементарным подзадачам (обычно этот процесс вызывает затруднения).

Автор уделяет особое внимание, выделению «ключевой подзадачи» в процессе сведения сложной задачи к элементам.

Для преодоления формализма в усвоении понятий двугранного угла и выработки навыков построения линейных узлов учащимся необходима определённая система задач [46]. Предлагаемые задачи разбиты на четыре группы:

. На доказательство того, что отмеченный на рисунке угол является линейным.

. На выделение линейного угла среди нескольких обозначенных на рисунке углов.

. На построение линейного угла данного двугранного угла.

. Вычислительные задачи.

В процессе решения этих задач учащихся вырабатывают навыки и умения построения линейных углов, двугранных углов, построения изображений пространственных фигур.

В своих исследованиях [44] Г.И. Саранцев отмечает, что в школьных учебниках решение геометрических задач основано на трансформации словесной формулировки задачи в чертёж, а обратная трансформация не используется, что ведет к перекосу в обучении умения решать геометрические задачи. В процессе составления задач на заданных чертежах формируется комплекс действий: преобразования требования задачи, выделение следствий из данных условий, представление фигуры в плане различных понятий и т.д. автор указывает, что в учебно-методической литературе выделяются опорные знания, задачи и конфигурации. Под последними понимаются такие геометрические конфигурации, которые несут основные теоретические положения темы или раздела, могут использоваться для ознакомления с понятиями и теоремами при решении задач. Опорные конфигурации должны являться источником составления задач. Составление задач по чертежу является хорошим средством интеллектуального развития учащихся.

В работе [10] С.Б. Верченко приходит к выводу о том, что планомерная и систематическая реализация разработанной системы упражнений помогает подвести учащихся младших классов к необходимому уровню развития пространственных представлений и подготовить их к изучению систематического курса геометрии, т.к. программа геометрии старших классов в значительной степени опирается на запас наглядных представлений конструктивных навыков, сформированных в IV-V классах. Автор предлагает конкретные методические рекомендации по формированию и развитию пространственных представлений при изучении геометрического материала в курсе математики IV-V классов.

Систематическое использование на уроках стереометрии устных упражнений и проведения устного опроса являются одним из средств повышения эффективности урока [7, 8, 14] и др. они служат для более глубокого и прочного понимания учащимися свойств параллельного проектирования, основных геометрических понятий, теорем аксиом плоскости и т.д. кроме того, устный опрос и устные упражнения способствуют развитию и формированию пространственного воображения учащегося. Однако, они носят логический характер и конструктивный характер, не касаясь решения стереометриических задач на построение.

Таким образом, представители второго направления приводят определённую работу по систематизации задач на основе выявления опорных задач при «разложении» задач на составляющие (Г.Д. Зайцева), элементарных задач, являющихся основой при решении других задач (Я.И. Груденов и др.), отбор задач с учётом их объективной и субъективной сложности (М.Е. Глинощук и др.), определение опорных конфигураций, являющихся источниками составления задач по данным чертежам (Г.Н. Саранцев), составление специальных упражнений для устного опроса (И.Б. Вейцман, В.П. Демидов и др.), направленных на формирование и развитие воображения учащихся на уроках математики.

Рассмотрим теперь исследования, выявляющие необходимые умения, приёмы решения отдельных типов задач.

В исследовании [6] Г.А. Буткин разработал умения, лежащие в основе геометрического доказательства. В качестве основных знаний и умений решения задач на доказательство он предлагает: действия подведения геометрических явлений под понятие; знание систем необходимых и достаточных признаков искомых геометрических понятий, умение развернуть условие, получить систему его следствий, обнаружить за содержащимися в нём понятиями признаки искомого понятия [6, с.190]. Однако не указываются условия и способы выработки у учащихся этих умений.

Рассматривая вопрос о решении геометрических задач на доказательство, А.Т. Кислицина в работе [26] предлагает системы указаний (обучающую и частичную) при решении геометрических задач на доказательство. Автором выделена следующая система общих указаний: «Чтобы решить геометрическую задачу на доказательство необходимо:

− Точно знать, в чём состоит условие, заключение теоремы;

− Заменить теоремы их определениями;

− Расчленить условие и заключение её на составные части;

− Использовать в рассуждениях условие теоремы и даже использовать его, вообще говоря, полностью;

− Преобразовать условие теоремы для того, чтобы легче было обнаружить справедливость её заключения;

− Преобразовать заключение теоремы;

− Из возможных способов решения выбрать такой, который допускает простое решение предложенной задачи»

При этом формирование выявленных общих умений осуществляется на основе обобщения частных умений.

В работе [45] С.Н. Садыхов и О.С. Садыхова рассматривают системы вопросов, предлагаемых учащимися на каждом этапе решения задачи на построение треугольников, направляющих мышление учащихся в процессе решения задач.

Например, на этапе анализа система вопросов имеет вид:

. Есть ли на данном рисунке фигуры (точка, отрезок, угол, окружность и т.д.), которые были частью искомого треугольника?

. Если есть, то, как их можно построить?

. Сколько при этом вершин искомого треугольника уже имеется?

Значение этих указаний при обучении учащихся решению задач велико. Однако эти указания пока остаются недостаточно обобщёнными.

В диссертационном исследовании Б.А. Абремского [1], на основе анализа использованного при решении задачи теоретического материала, выявляются частные приёмы решения планиметрических задач на вычисление. Исследуя полученные системы частных приёмов, автор выделяет общие приёмы решения геометрических задач на вычисление:

. Выявление (актуализация) такой зависимости между алгебраическими объектами задачной ситуации, которая содержит искомое.

. Непосредственное отыскание неизвестного из некоторой зависимости, не содержащей других неизвестных.

. Составление и решение уравнений или системы уравнений и последующее нахождение всех или некоторых неизвестных.

. Выделение вспомогательных задач на отыскание значения одной величины или значения комбинации каких-либо величин.

Однако, с точки зрения деятельностного подхода, в работе рассматривается только операционный состав каждого приёма.

В исследованиях Л.О. Демищевой, М.Б. Воловича, Н.С. Новичковой, И.Ф. Протасова [10, 15, 33, 41] рассматриваются приёмы работы с теоретическим материалом (приёмы работы с понятиями) и применения их при решении задач.

Например, в статье Л.О. Демищевой отмечается, что значительное число учащихся затрудняются составить план решения задачи, раскрыть его ход, даже в том случае, когда или получен правильный ответ, т.е. фактически задача решена. Это говорит о том, что учащиеся не осознают самого процесса получения результата, способа своей деятельности [15, с.15]. В этой же работе приведены приёмы учебной работы учащихся для определения критических точек и для нахождения первообразных функций, выявленные из теоретического материала данной темы.

О.Б. Епилиева, К.А. Загородных, О.К. Одинемадов в своих диссертационных исследованиях [19, 20, 35] рассматривают проблему формирования приёмов учебной деятельности учащихся при обучении решению задач.

О.Б. Епилиева рассматривает проблему формирования приёмов учебной деятельности учащихся на материале уравнений и неравенств. Основу исследования составляет методика формирования обобщённого приёма решения уравнений и неравенств с одной переменной, который получен путём обобщения частных приёмов решения конкретных задач по указанной теме.

В работе отмечено, что обобщение способов деятельности учащихся при решении уравнений и неравенств происходит постепенно. При этом вы-делены следующие этапы процесса обобщения приёмов решения уравнений:

− Решение простейших уравнений данного вида;

− Анализ действий необходимых для решения;

− Вывод алгоритма (формулы, правила) решения и запоминание его;

− Решение несложных уравнений данного вида, не являющихся простейшими; анализ действий, необходимых для их решения;

− Формулировка частного приёма решения;

− Применение полученного частного приёма по образцу, в сходных ситуациях, в легко создаваемых вариациях образца;

− Работа по описанным этапам для следующих видов уравнений согласно программе;

− Сравнение получаемых частных приёмов, выделение общих действий в их составе и формулировка обобщающего приёма решения;

− Применение обобщённого приёма в различных ситуациях, перенос и создание на его основе новых частных приёмов для других видов уравнений.

Проводя работу по этапам процесса обобщения, автор выделяет: обобщённый приём решения уравнения первой степени с одной переменной, обобщённый приём решения задач с помощью уравнений, обобщённый приём решения квадратного уравнения, обобщённый приём решения уравнений (неравенств) первой степени с одной переменной, обобщённый приём решения уравнений (неравенств) второй степени с одной переменной, обобщённый приём решения рациональных (тригонометрических, иррациональных, показательных, логарифмических) уравнений и неравенств. Разработана методика формирования обобщенных приёмов решения уравнений и неравенств.

Разработанная система общих приёмов учебной деятельности учащихся позволяет учителям спланировать свою деятельность в процессе обучения этим приёмам.

В исследовании К.А. Загородных [20] выявлены приёмы учебной деятельности учащихся по решению текстовых задач в IV-V классах. Здесь все адекватны действиям учащихся по решению учебной задачи, выделенным в концепции учебной деятельности.

О.К. Одинамадов на основе анализа задач на тождественные преобразования в курсе алгебры средней школы выявил приёмы деятельности учащихся по решению этих задач экспериментальное обучение показало эффективность этих приёмов при обучении учащихся решению задач на тождественные преобразования [35].

Анализ научно-методической литературы показал, что в отличие от первого и второго направления, третье направление ещё недостаточно разработано. Особенно это касается геометрического материала.

§2. Проблема формирования приёмов учебной деятельности в практике школьного обучения

Проведённый выше анализ научно-методической литературы показал, что поставленные перед школой задачи по овладению школьниками математических знаний, умений, необходимых в повседневной жизни и трудовой деятельности, могут быть решены лишь путём систематического обучения школьников эффективным рациональным приёмам умственной деятельности и рациональным приёмам учебной работы. При этом формирование соответствующих приёмов удобно осуществлять в процессе решения школьником предметной задачи. Таким образом, процесс формирования приёмов учебной деятельности предлагает организацию учебной деятельности учащихся по решению задач.

Существуют два пути усвоения приёмов деятельности: стихийный и управляемый. В первом случае приёмы учебной деятельности не являются предметом специального усвоения, их формирование идёт лишь по ходу усвоения знаний, в процессе решения задач и т.п.; при этом они не всегда осознаются и, следовательно, не всегда приводят к желаемому результату. В большинстве случаев в наше время процесс обучения протекает по этому пути.

Во втором случае приёмы служат предметом специального усвоения. Формирование приёмов может реализоваться при введении приёма «в готовом виде» учителем (с привлечением учащихся к активному решению задач), или при подведении учащихся к самостоятельному нахождению приёма (под общим руководством учителя) [23].

В случае управляемого усвоения приёмов учебной деятельности резко сокращается процесс их формирования, учащиеся учатся самостоятельно учиться, что и является главной целью деятельностного подхода.

Показателем сформированности приёмов учебной деятельности школьников является осознание ими этих приёмов, т.е. умение рассказать о составе приёма учебной деятельности, заключающейся в умении обосновать, аргументировать правильность его выполнения [50], а также самостоятельное применение учащимися этих приёмов при решении задач.

Говоря о сущности и значении сознания учащимися своих действий, психологи отмечают, что только тогда учащийся будет осознавать содержание того, что он усвоил, сознавать свой путь познания, т.е. формы своего мышления, ход его развития, когда в состоянии анализировать не только предмет своего изучения, лежащий вне его, но и свою мысль он рассматривает как объект изучения. Осознание своего сознания в процессе учения, т.е. появление учебного самосознания является показателем сдвига в умственном развитии.

О необходимости учёта психологических закономерностей мышления и формирования приёмов умственной деятельности школьников в процессе обучения математике говорят в последние годы не только психологи, дидакты, методисты, но и учителя-практики. Однако учителя математики в своей деятельности не всегда опираются на психологические и педагогические основы процесса обучения, не в полной мере используют достижения современной педагогической психологии и дидактики. Это объясняется тем, что при подготовке учителей математики по психологии и педагогике не всегда учитывается их будущая профессия, а учителя - практики недостаточно осведомлены о современных достижениях психологии и дидактики, т.к. в обще-доступной литературе по проблемам психологии и дидактики не рассматриваются вопросы применения результатов исследований психологов и дидактов в процессе обучения математике.

Таким образом, ставя перед учителем цель: прямо и косвенно формировать у учащихся приёмы общих и специфических умственных и учебных действий, входящих в состав различных видов учебно-познавательной деятельности; необходимо «вооружить» его способами управления учебной деятельностью учащихся при изучении программного материала, раскрыть психологические и дидактические предпосылки, обеспечивающие глубокое и прочное усвоение школьниками математических знаний и умений оперировать ими. При этом активная познавательная деятельность учащихся должна рассматриваться не только как средство овладения знаниями, умениями и навыками, но и как важнейший источник умственного развития школьников.

Опыт передовых учителей показывает, что реализация поставленной перед учителем задачи возможна лишь тогда, когда при подготовке к уроку учитель не только тщательно отбирает систему учебного материала, выделяет в нём «единицы усвоения», продумывает формы его представления, но и вычленяет, программирует способы деятельности учащихся, т.е. те умственные действия и приёмы учебной работы, с помощью которых школьники будут усваивать запланированный учебный материал. При этом важно учитывать, какими знаниями, действиями и приёмами учащиеся уже владеют, а какие должны быть сформированы на данном этапе обучения, а также принимать во внимание закономерности восприятия, памяти, мышления, возрастные и индивидуальные особенности учащихся на различных этапах обучения. Известно, что выбор способов усвоения программного материала по математике зависит от конкретных дидактических и воспитательных целей, особенностей его содержания, подготовленности учащихся к восприятию нового и т.п. Поэтому в одних случаях учебный материал объясняется учителем, а воспроизводится и закрепляется учащимися, в других случаях организуется поисковая деятельность: выявление существенных признаков понятий и конструирование определений, поиск доказательства теорем и алгоритма решения стандартных задач, эвристическая деятельность по нахождению способа решения нестандартных задач и т.д. Следовательно, задача учителя состоит в том, чтобы выбрать такой способ организации познавательной деятельности учащихся, при котором они в процессе усвоения знаний овладеют рациональными приёмами как практических, так и умственных действий. Общие и специфические приёмы умственных действий (а через них и рациональные приёмы учебной работы) становятся в этом случае объектом усвоения и сознательного их применения, контроля со стороны учителя и самоконтроля учащихся.

Но чтобы целенаправленно проводить эту работу, учитель сам должен хорошо знать содержание и структуру общих и специфических умственных действий, примеры их выполнения, видеть их роль в различных видах учебно-познавательной деятельности в процессе обучения математике.

В учебниках геометрии и соответствующих им учебных пособиях не рассматриваются проблемы выявления приёмов решения задач, а также вопросы о том каким образом найдено то или другое решение, как обобщить решение задачи или как выявить общий способ решения нескольких задач и т.п. В лучшем случае рассматривается только один из этапов процесса решения задачи - этап осуществления найденного способа решения задачи. Другими словами, приведённые в учебниках геометрии образы решения задач дают некоторые представления о способах решения, что соответствует первому типу ориентировочной основы действия, который характеризуется неполным составом ориентировочной основы, когда ориентиры представлены в частном виде.

Из сказанного следует, что в учебниках геометрии раскрытие процесса решения задач не направленно на достижение цели деятельностного подхода. Потому, что цели деятельностного подхода достигаются лишь в том случае, когда выявляется состав действий относящихся к третьему типу ориентировочной основы действия, которая имеет полный состав, ориентиры которого представлены для целого класса явлений.

В действующих учебниках отсутствуют первоначальные сведения о задачах (например, что собой представляет задача?; что значит решить задачу?; из каких этапов состоит процесс решения задач?). Поэтому у большинства учащихся весьма смутные, а порой и неверные представления о сущности решения задач, о самих задачах. Как могут учащиеся решить сложную задачу, если они не представляют, из чего складывается анализ задачи, как могут учащиеся решить сложную задачу, если они не знают в чём смысл доказательства [56, с.4].

Таким образом, в существующих программах и учебниках не уделяется должного внимания формированию приёмов деятельности, а что в процессе обучения этому также уделяется мало внимания.

О положении дел с формированием приёмов в учебном процессе Е.Н. Кабанова-Мюллер пишет: «В существующих условиях обучения школьники обычно не ставят перед собой цели овладеть приёмами. Они знакомы с терминами «понятие», «умение», но ничего не знают о приёмах учебной работы. И это не случайно, как уже говорилось, ни в программах, ни в методиках, ни в учебниках вопросу о приёмах не уделяется достаточного внимания» [24, с.50].

Поэтому многие учащиеся не знают, как взяться за решение задачи, как продолжить решение, как контролировать процесс решения и т.д. Об этом свидетельствуют и анализы письменных работ, предлагаемых на вступительных экзаменах в вузы: «Многие абитуриенты не решили геометрическую задачу, и это становится традицией» [11, с.34]. Из года в год во многих анализах письменных работ авторы отмечают низкий уровень знаний и умений учащихся, особенно по геометрии. Это известная в настоящее время проблема в математической подготовке школьников, и сдвигов в её решении пока не происходит [34, с.43].

Из сказанного, однако, не следует, что в практике работы не одной из школ не проводится специального обучения приёмам учебной деятельности. Об обратном говорят статьи и исследования, публикуемые в последнее время в журналах «Математика в школе», сборник статей «Из опыта преподавания математики в школе» и других источниках информации. Все статьи в этом случае представляют собой освещение опыта преподавания математики в средней школе. Часть статей, написанная в основном учителями, раскрывает конкретный опыт изучения соответствующих разделов программы. Встречаются также статьи которые отходят от буквального пересказа опыта и представляют собой обобщение опыта работы ряда учителей.

Проведём анализ некоторых статей, освещающих пути и методы формирования приёмов учебной деятельности учащихся по решению предметных задач.

В статье Т.С. Коржиковой «приёмы учебной работы при обучении решению задач» [22, с.113-118], на примере обучения решения текстовых задач методом уравнения, освещён опыт, ознакомление и обучение учащихся приёмам учебной работы, учителей Тимирязевского района города Москвы. Для облегчения пользования приёмами учебной работы ими был составлен плакат «Как решать задачу» (Таблица 2). Этот плакат вывешивается в классе на уроках, когда решаются текстовые задачи.

Приёмы учебной работы и примеры их применения к решению задач учащихся записывают в специальную тетрадь. Затраты времени на такую работу окупаются в дальнейшем. Эти записи помогают ученикам в затруднительных случаях быстро найти сходную задачу и ещё раз вспомнить подход к её решению, составить план решения очередной задачи.

Опыт обучения учащихся в соответствии с изложенными рекомендациями показал, что облегчается обучение учащихся решению задач, повышается интерес учащихся к решению задач, учащиеся легче осваивают оформление решений.

Описанию сравнительного общего подхода к обучению решению задач посвящена статья А.В. Рудник «Переформулирование текста задачи как путь отыскания её решения» [22]. Автор, опираясь на богатый опыт школы, удачно подметила, что затруднения при решении задач часто возникают потому, что учащиеся не поняли редакционного варианта изложения текста условия в целом, отдельных его частей или отдельных употребляемых в тексте терминов. Изменение редакции непонятных предложений, раскрытие содержания непонятных слов поможет усвоить условие задачи и найти её решение. При этом следует иметь в виду, что описанный в статье приём может помочь при изучении любого программного материала, как в курсе алгебры, так и в курсе геометрии.

Таблица 2

Как решать задачу

Методика введения понятия, освящается в статьях Е.Г. Глаголевой, Ю.В. Ревзина, Г.А. Ястребинецкого [22, с.129-167]. В каждой из этих работ приводится мысль о том, что формальное определение понятия не может служить оправданным пунктом изучения темы; оно должно быть логическим завершением работы по созданию индуктивно-наглядных образов.

В статье М.И. Бурда «Формирование умений осуществлять поиски геометрических доказательств» [37, с.99-105] показано, что нахождение пути доказательства геометрических утверждений во многом зависит от овладения учащимися ориентировочной деятельностью. Автором выделены компоненты, составляющие содержание ориентировочной деятельности, и кратко рассмотрена сущность каждого из них.

1. Распознавание понятий. Умение распознавать геометрические понятия, входящие в условия доказываемых утверждений, особенно важно тогда, когда признаки этих понятий содержатся в условиях в опосредованном виде, т.е. заданы через системы признаков других понятий.

2. Доказательства вспомогательных утверждений. Этот компонент ориентировочной деятельности часто облегчает отыскание пути доказательства основного утверждения. Важное значение при этом имеет выработка умения переносить принцип доказательства со вспомогательного утверждения не основное. Это умение, как показали исследования С.Л. Рубинштейна, Н.А. Менчинской, К.А. Славской и др., базируется на проведении анализа условия вспомогательного утверждения через его соотнесение с требованием основного.

3. Проведение анализа состава доказываемого утверждения. Успешному осуществлению такого ряда анализа способствует использование следующей системы указаний по его проведению:

) Выделить условие и требование доказываемого утверждения; сделать их сокращённую запись.

) Начать изучение условия утверждения по рисунку. При выполнении рисунка избегать частичных случаев; выделить на рисунке (цветом или толстой линией) данные и искомые элементы.

) Сформулировать определение тех понятий, которые содержатся в условии и заключении.

) Заменить понятия условия и заключения их определениями.

4. Поиск плана доказательства. При поиске плана доказательства геометрических утверждений полезно использовать следующие указания:

) Вспомнить и применить теорему (или другое истинное утверждение), которая непосредственно устанавливает зависимость между данными и искомыми величинами.

) Сделать попытку расчленить данные утверждения на ряд более простых утверждений, последовательное доказательство которых может привести к доказательству.

) Вспомнить утверждение, аналогичное данному. Воспользоваться его доказательства.

) Если возникает трудность при доказательстве равенства двух величин, то одну из них или обе заменить равносильными им величинами и доказывать равенство последних.

) При необходимости заменить утверждение, которое надо доказать, другим, равносильным данному.

5. Применение указаний по использованию конкретных методов доказательств.

. Применение обучающих алгоритмов доказательств (или предписаний) определённых типов утверждений. Следует отметить, что чем лучше учащиеся владеют различными алгоритмами доказательства тех или иных типов утверждений, тем выше уровень их умений осуществлять поиски доказательств.

Если обратиться к пособиям по геометрии, то нетрудно заметить, что систематически и целенаправленно такая работа не приводится и все же можно выделить ряд общих алгоритмов доказательства определённых типов теорем и задач на доказательство.

Усвоение всех выделенных компонентов осуществлять по методике, разработанной с учётом основных положений ассоциативной теории поэтапного формирования умственных действий. В соответствии с этой методикой можно выделить следующие пять основных этапов работы:

I. На приёмах специально подобранных доказательств в каждом из них выделяются компоненты, составляющие содержание ориентировочной деятельности.

II. Выделяются общие компоненты всех этих доказательств.

III. Проводится раздельное закрепление компоненты всех этих доказательств.

IV. На основе этих компонентов составляется план, алгоритм или эвристическая схема доказательства.

V. Осуществляется закрепление данных действий в целом.

На каждом этапе используются такие приёмы, как принцип вариаций, сравнение наблюдаемых частных фактов (сопоставление и противопоставление) и специальные проблемные ситуации, ставящие учащегося в положении исследователя.

Опыт показывает, что систематическое проведение такой работы обеспечивает повышение умений учащихся доказывать теоремы и решать задачи.

В статье «Геометрические задачи на построение как средство повышения интереса учащихся восьмилетней школы к изучению математики» [40, с.67-73] С.Н. Садыхов останавливается на следующих методических приёмах, хорошо себя зарекомендовавших на практике обучения в ряде школ Азербайджанской ССР:

. Решение задачи различными способами.

. Использование одной задачи для решения других типовых задач.

. Решение сложных задач комбинированием ранее решённых простых задач.

Южусов Ф.М. в статье «Некоторые аспекты совершенствования обучения геометрии в восьмилетней школе» [40, с.74-77] рассматривает роль системы задач в качестве средства обучения для эффективного изучения математики учащимися. Автор подчёркивает, что задачи являются тем средством обучения, без применения которого нельзя добиться прочного и сознательного усвоения учащимися программного материала, всестороннего развития и воспитания, приобщения учащихся к труду. В некоторых случаях упорядоченные комплексы математических задач выступают в качестве ведущего средства обучения при изучении того или иного раздела математики (например, в форме проблемного обучения, в ходе применения исследовательского и частично-поискового методов обучения).

Решая математические задачи, представленные в продуманной системе, учащиеся не только активно овладевают содержанием курса математики, но и приобретают умения мыслить творчески. Это проявляется, например, в умении изменить условие задачи с целью применить тот или иной метод. Приём; в умении изобретать новые приёмы для решения задач; в умении выделять и накапливать потенциально полезную информацию; в умении конструировать на базе данной задачи новые; в умении осуществлять самоконтроль, исследовать результат решения и т.п.

В статье Саранцева Г.И. «О методике обучения школьников поиску решения математических задач» [40, с.123-131], исходя из концепции обучения деятельности, рассматривается обучение школьников решению геометрических задач. Наряду с вопросами теории обучения решению задач (Закономерности поиска решения геометрических задач. Умение анализировать условие задачи.), рассматриваются эвристические приёмы поиска решения геометрических задач.

Эвристическая схема, способствующая поиску решения наиболее распространённых задач с определённым требованием, может быть таков.

. Прочитайте задачу.

. Выделите условие и требование задачи, запишите их, сделайте рисунок.

. Замените термины, содержащиеся в требовании задачи, определением понятий, которые они обозначают, либо их признаками.

. Если необходимо, преобразуйте требование задачи в равносильное ему. Попробуйте выразить требование задачи на векторном, координатном языке.

. Установите те положения, из которых следует требование задачи.

. Прочитайте ещё раз условие и, сообразуясь с соотношениями, из которых следует требование задачи, выберите одно из них.

. Выявите информацию, непосредственно содержащуюся в условии.

. Старайтесь из полученной информации получить новую информацию и так до тех пор, пока не осуществите «стыковку» полученной информации с положением, принятым в п.6.

. Если выбранный путь не привёл к успеху, то рассмотрите другой путь, «идя» по нему до «стыковки» с новым положением п.5.

. Продолжайте рассматривать возможные пути до тех пор, пока не придёте к одному из положений п.5.

Эта схема не только направляет процесс поиска решения задачи, но и является источником самостоятельных обобщений заданных в схеме принципов.

Если же рассматриваемая задача содержит неопределённое требование, то, после того как высказана гипотеза, осуществляется поиск согласно приведённой схемы.

Целесообразность выбора метода решения задачи осуществляется после п.5. Сообразуясь с условием данной задачи, выбирается один из известных учащимся методов решения. С этого момента «включаются» в работу и специфические умения, характеризующие деятельность по овладению тем или иным методом.

Статья Канина Е.С. и Нагибина Ф.Ф. [40, с.131-138] «Заключительный этап решения учебных задач» ограничивается рассмотрением заключительного этапа решения задач, методика которого по существу не разработана.

Выдающийся советский математик-педагог А.Я. Хинчин в известной статье о формализме в школьном преподавании математики делился своим опытом работы с математической статьёй: «…я начинаю размышлять над тем, какие новые задачи встают в связи с результатами усвоенной мной статьи. Все возникшие в моём воображении задачи я тщательно записываю в виде вопросов и пытаюсь их разрешить, продолжая эти попытки до тех пор, пока мне не удаётся изучить степень сложности каждой из поставленных задач [57]. Американский математик Норбет Винер писал: «В науке часто недостаточно решить какую-нибудь задачу или группу задач. После этого нужно присмотреться к этим задачам и заново осмыслить, какие же задачи вы решили. Нередко, решая одну задачу, мы автоматически находим ответ и на другой вопрос, о котором раньше вовсе не думали» [9]. Д. Пойа, успешно разрабатывающий проблемы методики математических задач, писал о решении математических задач: «Резервируйте при этом немного времени для ретроспективного разбора законченного решения - это может помочь при решении последующих задач» [38].

Приведенные высказывания дают основания сделать следующий вывод:

) заключительный этап является необходимой и существенной частью решения задачи;

) основным содержанием его должно быть осмысление выполненного решения, формулирование и решение (если оно окажется возможным) других задач, явно связанных с решённой, и извлечение из всей проделанной работы выводов о том, как находятся и выполняются решения.

Эти общие положения подтверждающиеся и повседневной практикой обучения математике, в особенности опытом учителей математики, добивающихся высокого уровня математической подготовки своих учеников.

Авторы рассматривают составные части заключительного этапа решения задачи:

I. Обсуждение задачи и её решения. Эта часть включает в себя:

а) Более полное использование входной информации задачи (того, что дано) с целью сделать более полной выходную информацию (то, что находится);

b) Математические выводы, к которым приводят задача и полученная выходная информация;

c) Обсуждение работы по поиску решения;

d) Выявление связи задачи с ранее решёнными задачами.

II. Поиски и осуществление новых способов решения задачи их сравнение и выбор лучшего варианта решения. Решение задачи несколькими способами являются одним из путей проверки правильности полученного результата.

III. Формулирование и решение некоторых других задач, «порождённых» разобранной. Эту часть заключительного этапа можно назвать развитием темы задачи. В методическом отношении развитие темы задачи особенно ценно тем, что приучает учащихся к переконструированию задач, а это, как известно приём поиска решений.

IV. Полезные выводы из проделанной работы. Имеются в виду фиксации из проделанной работы о том, как в подобных случаях находится и осуществляется решение. А также, какие особенности задач подсказывают приём решения.

Основные методические приёмы проведения заключительного этапа по работе с задачей - это классная беседа, изложение учителя, самостоятельная работа учащихся и фронтальное или индивидуальное чтение учебника. Особенно часто пользуются первым из этих приёмов. На заключительном этапе работы с задачей учащимся могут быть предложены следующие вопросы:

) Что общего в этих задачах?

) Чем они отличаются?

) С какими задачами они сходны?

) чем отличаются от них?

) Какие выводы должны быть сделаны из решения данных задач?

) Что лежит в основе решения данных задач?

) В чём состоит идея решения данной задачи?

) Какое решение более удачное, рациональное, изящное?

) Что вы узнали нового из решения данных задач?

) Какие задачи вы научились решать?

В пособии «параллельные проекции и решение задач по стереометрии» наряду с другими вопросами А. Б. Василевский рассматривает «Обобщённые приёмы решения задач по геометрии в десятом классе» [7].

При изучении тем «Координатный метод в пространстве», «Многогранники», «Фигуры вращения» применяются все основные свойства фигур, рассмотренных в девятом классе. Поэтому успешное изучение материала десятого класса невозможно без систематического повторения важнейших понятий стереометрии и взаимного положения прямых и плоскости. Такое повторение целесообразно вести через решение задач. Анализ действующих учебных пособий по геометрии для IX-X класса показывает, что в них есть задачи, работа над которыми позволяет обучить учащихся обобщённым приёмам, которые дают возможность им успешно определять элементы многогранников и фигур вращения.

Перечислим обобщённые приёмы решения задач по геометрии в десятом классе:

. Систематическая работа по построению чертежей, их обоснование и составление плана решения задачи по готовым чертежам.

. Систематическая работа по составлению устных планов решения задач по готовым чертежам.

. Решение задач на определение радиуса шара, вписанного в многоугольник, и шара, описанного вокруг многоугольника.

. Обучение учащихся векторному решению геометрических задач, применяя общий план векторного решения задач.

. Осуществление единого подхода при выводе формул объёмов многогранников и фигур вращения.

. Осуществление единого подхода к определению и выводу формул площадей всех фигур вращения.

Таким образом, в опыте работы передовых учителей новизна в методах обучения математике проявляется в том, что основной акцент ставится не на запоминание школьником учебной информации, а её глубокое понимание, сознательное и активное усвоение, на формирование у школьников умения самостоятельно и творчески применять эту информацию в рамках учебной практики.

Именно эту мысль имел в виду один из известных специалистов по технической кибернетике А.А. Фельдбаум, говоря о том, что накопление знаний играет в процессе обучения немалую, но отнюдь не решающую роль. Человек может добыть многие конкретные факты, на базе которых совершенствовались его качества. Но если они достигли высокого уровня, то человек справится со сложнейшими задачами, а это означает, что он достиг высокого уровня культуры (мышления) [52].

Глава 3. Содержание и структура приёмов учебной деятельности в процессе решения задач на построение по теме «Прямая и плоскость»

Изучение темы «Прямая и плоскость» является начальным этапом обучения учащихся Х классов основам стереометрии.

При изучении предыдущего раздела геометрии (Планиметрия) у учащихся выработался определённый порядок привычных действий, называемых в физиологии динамическим стереотипом.

Приступая к изучению нового раздела геометрии, ученики встречаются с новым видом учебного материала - задачами на построение в пространстве. Для решения такой задачи, необходимо представить себе очертания и форму геометрической фигуры, данной в условии, уяснить взаимосвязь отдельных элементов фигуры между собой и общий вид предполагаемого решения. Это заставляет учеников приспосабливаться к новой форме изучения материала, т.е. вырабатывать новый динамический стереотип. Его динамичность заключается в постоянном изучении и совершенствовании. Если эти изменения происходят постепенно, то переход от одного динамического стереотипа к другому не вызывает никаких трудностей. В описываемом процессе происходит довольно резкая смена динамических стереотипов, что и составляет физиологическую суть трудностей, возникающих у учеников, особенно в начальной стадии изучения темы.

Используемые в настоящее время учебные пособия и учебники не в полной мере отвечают требованиям обучения учащихся решению задач на построение в пространстве. Они больше пригодны для контроля знаний и содержат недостаточное количество задач по указанной теме.

С целью облегчения процесса обучения на кафедре методики преподавания математики и математического анализа Приднестровского Государственного Университета разработаны методики основы формирования приёмов учебной деятельности учащихся в процессе решения задач на построение на взаимное расположение прямых и плоскостей в пространстве, а так же построена система задач, обладающая свойством структурной полноты.

В этой главе рассмотрим приёмы учебно-познавательной деятельности учащихся при решении стереометрических задач на построение, выявленные среди приёмов умственной деятельности обучении математике, на основе современных психологических и дидактических теорий. Кроме этого использовались результаты, полученные в предыдущей главе: структура обобщённого приёма решения математических задач; общие приёмы учебной деятельности учащихся по решению задач с указанием адекватных им учебных действий; взаимосвязь этапов решения задачи с приёмами учебной деятельности; общие операционные составы приёмов принятия учебной задачи и поиска решения учебной задачи при решении учащимися математической задачи, структура приёма поиска решения учебной задачи.

Предварительно рассмотрим некоторые особенности геометрических задач на построение и приём соглашения, позволяющие рассматривать примеры решения указанных задач.

§1. Стереометрическая задача на построение

Задачи на построение являются традиционными задачами в курсе геометрии. Разработкой методов решения этих задач математики занимаются ещё с времён Древней Греции. Уже математики школы Пифагора (VI в. до н.э.) решили довольно сложную задачу построения правильного пятиугольника. Интерес к задачам на построение объясняется не только их красотой и оригинальностью методов решения, но и большой практической ценностью. Проектирование строительства, архитектура, конструирование различной техники основаны на геометрических построениях.

Обычно задача на построение ставится как требование из заданных элементов в соответствии с какими-то условиями, с помощью определённых инструментов построить названную геометрическую фигуру или же совокупность удовлетворяющих указанным свойствам [54, с.106].

Таким образом, в каждой задаче на построение требуется построить фигуру F-искомую - по другой фигуре f-данной, к которой она должна находиться в определённом отношении.

При решении конструктивных задач на плоскости мы при помощи чертёжных инструментов проводим простейшие построения, которые постепенно расширяют данную фигуру f, добавляя к ней прямые и окружности, пока не получится фигура, содержащая фигуру F.

Геометрические построения в пространстве более трудны, чем геометрические построения на плоскости. Стереометрические задачи на построение решаются двумя различными методами: в воображении и при помощи выполняемых чертёжными инструментами построений на проекционном чертеже, развёртке геометрического тела или на каком либо его сечении.

В первом случае мы ограничиваемся воображаемым построением прямых, плоскостей, сфер, мысленно определяем их взаимное расположение и находим точки и линии их пересечения, т.к. в действительности не существует реальных инструментов, при помощи которых можно было бы строить сферы, плоскости и прямые в пространстве.

Геометрические построения на проекционном чертеже обладают «эффективностью», т.е. задачи с различными пространственными фигурами решаются на таком чертеже почти так же, как это должно было бы осуществляться в самом пространстве с выполнением необходимых операций и фактическим построением искомых элементов. Во многих случаях при этом чертёж должен быть полным и метрическим.

Любая задача на плоскости в стереометрии может быть решена на проекционном чертеже, но в начале она должна быть решена мысленно, т.е. решающему задачу должно быть ясно, что и как надо сделать, какие геометриические образы использовать, какие операции необходимо проделать, каким преобразованиям следует подвергнуть фигуру, чтобы решить задачу, а затем уже это решение перенести на чертёж.

При решении планиметрических задач на построение пользуются схемой решения состоящих из четырех этапов:

) анализа;

) построения;

) доказательства;

) исследования.

Рассмотрим цели каждого этапа выше указанной системы.

1. Анализ. Это самая важная часть решения, т.к. целью её является разыскивание цели построений, способных привести от данной фигуры к искомой.

Сначала строим искомую фигуру произвольно, а данную - в том отношении к искомой, которое указано в задаче. После этого ищем цепь построений, приводящих от данной фигуры к искомой. Для этого, прежде всего смотрим, нельзя ли, пользуясь уже известными нам решениями более простых задач построить по данной фигуре хотя бы часть искомой им, вообще, такую фигуру, от которой легче перейти к искомой. Указанным способом мы пытаемся свести решения данной задачи к решению более простых. Если этого сделать не удаётся или же решение задач, к которым мы свели данную задачу, нам неизвестно, то можно обратиться к свойствам различных геометрических преобразований - стереометрии, гомотетии и т.д., применение этих свойств называется, методом симметрии, методом гомотетии и т.д. (методы решения геометрических задач на построение рассмотрим ниже).

Таким образом, анализ на построение включает следующие этапы процесса решения математических задач: «анализ задачи» и «поиск способа решения».

Заметим так же, что для анализа выбирается фигура F возможно более общего вида. Вследствие этого найденное построение может оказаться непригодным при более частном виде фигуры F, но этот вопрос удобнее рассматривать при исследовании задачи. Однако, сказанное означает, что в ряде случаев анализ (поиск решения) содержит и этап - «исследование задачи» или «анализ решения».

2. Построение. В этой части результаты анализа приводятся в порядок, т.е. указывают последовательность гласных операций, которые необходимо выполнить для построения искомой фигуры. Этого будет достаточно, если задача решается в воображении. Если она решается на проекционном чертеже, то решение должно быть оформлено графически при помощи чертёжных инструментов.

Итак, этап «построение» при решении геометрической задачи на построение включает этапы: «план решения» и «осуществление решения» (если задача решается на проекционном чертеже) процесса решения математических задач.

3. Доказательство. Из рассуждений, приводимых при анализе, следует, что искомая фигура, если она имеет достаточно общий вид, может быть получена из данной, связанной с нею условием задачи, с помощью найденного построения. Но, в некоторых случаях, одно и тоже построение может привести к нескольким фигурам F. В большинстве случаев все эти фигуры удовлетворяют условию задачи. Но возможны и исключения вследствие того, что при анализе условие задачи принимается во внимание не полностью. Таким образом, доказать - это значит проверить, что найденное построение приводит только к фигурам, удовлетворяющим условию задачи. В том случае, когда построение приводит только к одной фигуре F, необходимость в доказательстве отпадает.

Этапу доказательство соответствует этап «проверка» процесса решения математических задач.

4. Исследование. До сих пор только искомая фигура F предполагалась заданной произвольно, а данная фигура f должна была находиться к искомой в отношении, указанном в задаче. Но если задать произвольную фигуру f, то может случиться, что не существует фигуры F, связанной с ней условием задачи. Далее, может случиться, что в зависимости от выбора данной фигуры f меняется число решений задачи. Сюда можно включить и случай невозможности решения, когда число решений равно нулю. Выяснение числа решений в зависимости от выбора данных составляет основную цель исследования задачи. На этот вопрос даёт ответ изучение найденного построения. Например, решение не возможно тогда и только тогда, когда найденное построение не выполнимо. В самом деле, из анализа видно, что в том случае, когда искомая фигура F существует, она всегда может быть получена из данной фигуры f с помощью найденного построения.

Таким образом, производя исследование, необходимо их конфигурации рассматривать в их логической последовательности. Результаты исследования целесообразно оформлять в виде таблицы.

Этапу «исследование» - соответствует этап «исследование задачи» процесса решения математических задач.

Из рассуждений, проведённых выше, следует, что взаимосвязь этапов решения задачи на построение с этапами решения произвольной математической задачи можно изобразить следующей схемой:

§2. Методы решения геометрических задач на построение

Для решения геометрических задач на построение существуют следующие методы: метод геометрических мест, метод параллельного перенесения, метод симметрии, метод обратности и алгебраический метод. Все перечисленные методы основываются:

) на геометрических местах точек;

) на геометрических соответствиях

) на применении алгебры.

Схема 14

Таблица 2

Изложим краткую суть каждого из перечисленных методов.

Метод геометрических мест основан на понятии о геометрическом месте точек.

Геометрическим местом точек называется такой геометрический образ, все точки которого обладают определённым свойством, каким не обладают точки, не принадлежащие этому геометрическому образу.

В курсе геометрии средней школы основными геометрическими местами являются следующие:

В планиметрии:

) прямая (одна прямая, пересекающиеся прямые, параллельные прямые, определённый отрезок прямой);

) окружность (одна окружность, две концентрические окружности; дуга сегмента, вмещающего данный угол).

В стереометрии:

) прямая в пространстве (параллельные прямые);

) плоскость (параллельные плоскости);

) боковая поверхность круглого цилиндра;

) боковая поверхность круглого конуса;

) шаровая поверхность.

Метод геометрических мест состоит в следующем: предложенную геометрическую задачу на построение, прежде всего, сводят к отысканию одной или нескольких точек, каждая из которых должна удовлетворять определённым условиям.

Если требуется найти точку, которая удовлетворяла бы двум определённым требованиям или условиям I и II, то эту задачу разбивают на две подзадачи: 1) найти точку, удовлетворяющую условию I и 2) найти точку, удовлетворяющую условию II. Бесконечное число точек, являющихся решением 1-й подзадачи, представит собою некоторое вполне определённое геометрическое место точек (прямую или окружность, или отрезок прямой, или другую окружность и т.д.). Обозначим это геометрическое место точек буквой G₁. Равным образом, бесконечное число точек, являющихся решением 2-й подзадачи, также образует геометрическое место точек, которое обозначим буквой G₂. Затем выясним, пересекаются ли найденные геометрические месс-та G₁ и G₂. Если G₁ и G₂ не пересекаются и не касаются друг друга, то искомая тачка не существует, и, значит, задача не имеет ни одного решения. Если геометрические места G₁ и G₂ касаются одно другого в одной или нескольких точках, то каждая из них является искомой. Равным образом, если G₁ и G₂ пересекаются в одной или в нескольких точках, то каждая из них является искомой.

Вопрос о числе общих точек двух геометрических образов можно решить с помощью таблицы 3, которая может быть дополнена различными сочетаниями пространственных геометрических мест.

Метод параллельного перенесения состоит в том, что в наброске предполагаемого решения геометрической задачи на построение производят параллельное перенесение фигуры или отрезков, входящих в искомую фигу-ру, чтобы обнаружить зависимости, позволяющие выполнить требуемое по-строение.

Смотря по тому, что именно подвергалось параллельному перенесению, в результате можем получить либо новое расположение линий, которое делает очевидным, как надо выполнить требуемое построение либо новое

Таблица 3

расположение фигур, позволяющее установить путь к решению, либо новую фигуру, которая является частью искомой фигуры, конструктивно с нею связана, легко может быть построена.

Метод симметрии состоит в том, что для точек, линий и фигур, имеющиеся в чертеже предполагаемого решения геометрической задачи на пост-роение, вводят их симметричные геометрические образы и, рассматривая их связи с начальным чертежом, определяют зависимости позволяющие выполнить требуемое построение.

В геометрии различают два вида симметрии: относительно точки и относительно прямой. При решении геометрических задач на построение, определяемых программой средней школы, большей частью приходится иметь дело с симметрией относительно оси.

Применяя метод симметрии, следует за ось симметрии принимать такую прямую, которая либо дана, либо легко может быть построена. В несложных задачах, решаемых методом симметрии, лишь только перегнём чертёж по целесообразно выбранной оси симметрии, как становится очевидным тот приём, каким может быть получено требуемое построение. В более сложных задачах, решаемых методом симметрии, требуемое построение находится следующим образом:

) во вспомогательном чертеже, сделанном в предположении, что задача решена, строят симметричную фигуру (линию, точку);

) временно изменяют условие предложенной задачи, а именно: тем требованиям, какие относятся к данной фигуре (линии, точке), подчиняют симметричную ей фигуру (линию, точку) и решают эту вспомогательную задачу;

) когда выполнено построение, представляющее собою решение вспомогательной задачи, посредством каких операций можно получить решение предложенной задачи.

В пространстве рассматривают третий вид симметрии относительно плоскости.

Метод спрямления состоит в том, что, с целью открыть зависимости для решения данной геометрической задачи на построение, в чертеже предполагаемого решения некоторые отрезки перекладывают так, чтобы вместо ломанной линии получится отрезок, равный сумме или разности её звеньев, и вместе с тем образовалась фигура, которая конструктивно связана с данной и легко может быть построена.

Применение этого метода состоит из следующих операций:

) если в условии задачи дана сумма (S) определённых отрезков, то на схематическом чертеже, представляющем собою предполагаемое решение, продолжают определённые отрезки, на полученной прямой откладывают примыкающие к этому отрезку другие отрезки и получают отрезок, равный S. Если же в условии задачи дана разность (d) двух определённых отрезков, то на схематическом чертеже, на большем из этих отрезков, откладывают меньший так, чтобы получить отрезок, равный d;

) найденный таким образом отрезок, равный сумме или разности определённых отрезков, приводят посредством вспомогательных линий в связи со схематическим чертежом и получают новый, более сложный, схематический чертёж;

) выясняют, посредством каких операций можно построить этот новый схематический чертёж, но строят его так, чтобы входящие в него линии имели длину, указанную в условии задачи;

) когда новый вспомогательный чертёж построен, то остаётся выяснить, что надо сделать, чтобы получить требуемое в задаче построения.

Метод подобия состоит в следующем: если данные геометрической за-дачи на построение таковы, что, отбросив одно из них, можно построить множество фигур, подобных искомой, то сначала строят какую-нибудь из этих фигур, а затем, принимая во внимание отброшенное данное, строят искомую фигуру.

Метод подобия основан на такой конструктивной связи между искомой фигурой и той, которая дана или которую легко построить, которая состоит в том, что искомая фигура подобна вспомогательной, причём известные величины двух сходных отрезков этих фигур.

Метод обратности заключается в том, что в некоторых случаях сначала так изменяют условие предложенной геометрической задачи на построение, чтобы искомые стали данными, а данные исходными, а затем решив эту обратную задачу, определяют те зависимости, посредством которых можно решить предложенную задачу.

Алгебраический метод решения геометрических задач на построение состоит в следующем:

) неизвестные величины, фигурирующие в условии задачи, обозначают буквами x, y, z и т. д.;

) составляют уравнения, связывающие эти неизвестные с данными в задаче величинами a, b, c, …;

) решают составные уравнения;

) исследуют полученные ответы;

) выполняют требуемое построение.

Для выполнения построений необходимо уметь строить отрезки, которые определяются следующими формулами:

1. , где n целое число;

2. ;

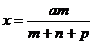3. ;

4. ;

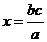5. ;

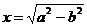6. ;

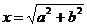7. ;

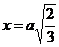8. .

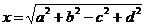§3. Основные соглашения и задачи

Во всякой геометрической задаче на построение требуется по каким-либо данным найти некоторые геометрические элементы, удовлетворяющие тем или иным условиям. Однако содержание планиметрической задачи на построение не исчерпывается указанием данных и формулировкой того, что требуется найти. Столь же важное значение имеет и указание на те средства, с помощью которых задача должна быть решена, на те инструменты, при помощи которых построение должно быть выполнено. В зависимости от того, какие инструменты имеются ввиду, смысл одной и той же задачи коренным образом меняется. Например, задача «разделить на три равные части угол 1200» решается непосредственно с помощью транспортира, но не разрешима с помощью циркуля и линейки.

В пространстве вопрос о допустимых средствах решения представляется менее определённым и поэтому более сложным. Это объясняется тем, что фактически не существует таких инструментов, которые в пространстве играли бы ту же роль, какую на плоскости играют линейка и циркуль. В пространстве приходится в процессе решения задачи строить по тем или иным данным плоскости, линии пересечения плоскостей и производить различные планиметрические построения в построенных плоскостях. Очевидно, что такие построения нельзя выполнить с циркулем и линейкой. Начертательная геометрия даёт способы построения указанных фигур, но это выходит за рамки элементарной геометрии. Поэтому, мы, чтобы иметь определённое указание на допустимые средства решения, примем следующие определения.

Под пространственным решением стереометрической задачи на построение мы будем понимать сведение её к конечному числу некоторых простых задач, которые считаются непосредственно разрешимыми.

За непосредственно разрешимые задачи примем следующие:

Задача I. Провести плоскость через три известные точки, не лежащие на одной прямой.

Задача II. Определить линию пересечения двух известных плоскостей.

Задача III. В известной плоскости решить любую задачу, разрешимую «с помощью циркуля и линейки». Решить задачу на построение в плоскости с помощью циркуля и линейки - значит, свести её к выполнению точно определённого числа следующих построений:

а) провести прямые линии через две известные точки;

b) определение точки пересечения двух известных прямых;

с) провести окружность с известным центром и известным радиусом;

d) определение точки пересечения известной окружности (частный случай - откладывание отрезка равного данному);

е) определение точек пересечения двух известных окружностей.

Задача IV. Выбрать произвольную точку, лежащую или не лежащую на известной прямой (в соответствии с аксиомой стереометрии), лежащую или не лежащую в известной плоскости (в соответствии с аксиомой стереометрии); выбрать произвольную прямую проходящую или не проходящую через известную точку, лежащую или не лежащую в известной плоскости; выбрать произвольную плоскость, проходящую или не проходящую через известную точку, проходящую или не проходящую через известную прямую.

В приведённых формулировках под «известными» понимаются те точки, прямые, окружности и плоскости, которые либо даны в самом условии задачи, либо уже определены на предыдущих этапах решения задачи, либо выбраны произвольно (в соответствии с аксиомами) в задачах II, III(b), III(d), III(e) предлагается оговорка «если эти прямые (точки) существуют».

Перечислим несколько самых простых задач на построение, которые легко сводятся к задачам I-IV, т.е. главным в решении задач является то, что отыскание искомой прямой или искомой плоскости сводятся к конечному числу задач I-IV.

Задача 1. Провести плоскость через прямую и не лежащую на ней точку, через две пересекающиеся прямые, через две параллельные прямые.

Задача 2. Построить точку пересечения данной прямой и данной плоскости.

Задача 3. Через данную точку, не лежащую на данной прямой провести прямую параллельную данной прямой.

Задача 4. Даны скрещивающиеся прямые, провести через одну из них плоскость параллельную другой.

Задача 5. Даны две скрещивающиеся прямые, провести через каждую из них по плоскости так, чтобы они были параллельны между собой.

Задача 6. Построить плоскость, проходящую через данную точку и параллельную двум данным прямым.

Из сказанного выше следует, что выполнение геометрического построения в пространстве основывается на возможности производить следующие семь элементарных операций.

Для оформления решения задач примем следующие соглашения:

) для обозначения точек будем употреблять большие латинские буквы: A, B, C, D … и т.д.; для обозначения прямых - малые латинские буквы: a, b, c, d, … и т. д.; для обозначения плоскостей - греческие буквы: α, β, γ, …;

) точку A пересечением прямых a и b будем обозначать так: A = a∩b; прямую a - пересечением плоскостей α и β будем обозначать так: a=α∩β;

) если точка A принадлежит плоскости α или прямой a, то вместо слова «принадлежит» будем писать значок : Aα, Aa;

) если прямая a лежит в плоскости α, то будем писать: aα;

5) кроме указанных сокращений будем использовать традиционные: a||b (прямая a параллельна прямой b), aα (прямая a перпендикулярна к плоскости α) и т.д.