|
Виды
деятельности
|
Кол-во
заданий
|
%
от максимального балла за всю работу
|
|
1
|
Знать
и понимать
|
3
|
20
|
|
2
|
Применять
знания и умения в знакомой ситуации
|
6
|
30
|
|
3
|
Применять
знания и умения в измененной ситуации
|
4
|
25
|
|
4
|
Применять
знания и умения в новой ситуации
|
2
|
25
|
Для учащихся, собирающихся продолжить обучение в
старшей школе важно сформировать представление о геометрии как об
аксиоматической науке. Это позволит им получить целостное представление о
математике и иметь предпосылки для успешного обучения в будущем.
Для учителей математики будет полезна следующая
система работы в 9-х классах во время подготовки к ГИА в новой форме. [10]
Введение государственной итоговой аттестации по
математике в новой форме (ГИА) в 9 классе вызывает необходимость изменения в
методах и формах работы учителя.
Данная необходимость обусловлена тем, что
изменились требования к знаниям, умениям и навыкам учащихся в материалах
экзамена по математике. Само содержание образования существенно не изменилось,
но существенно сместился акцент к требованиям умений и навыкам. Изменилась
формулировка вопросов: вопросы стали нестандартными, задаются в косвенной
форме, ответ на вопрос требует детального анализа задачи. И это всё в первой
части экзамена, которая предусматривает обязательный уровень знаний. Содержание
задач изобилует математическими тонкостями, на отработку которых в
общеобразовательной программе не отводится достаточное количество часов. В
обязательную часть включаются задачи, которые либо изучались давно, либо на их
изучение отводилось малое количество времени (проценты, стандартный вид числа,
свойства числовых неравенств, задачи по статистике, чтение графиков функций), а
также задачи, требующие знаний по другим предметам, например, по физике.
К сожалению, научно-методические службы не
обеспечивают школы новыми, соответствующими современным требованиям,
учебно-методическими комплексами, поэтому учителям приходится самим находить
пути решения данной проблемы. И здесь уже однозначного решения нет:
подготовленность детей разная, уровень классов разный. В этой ситуации в
наиболее выгодном положении находятся классы с углубленным изучением
математики.
Изменение тематического планирования. Составить
планирование таким образом, чтобы осталось достаточное число часов на
повторение всего учебного материала. Количество часов можно сэкономить на тех
темах, которые не требуют выработки навыков, а проходят в плане ознакомления, а
также сократить число часов на отработку навыков невостребованных тем. Это надо
делать очень осторожно, тщательно проанализировав содержание экзаменационных
работ.
Включать в изучение текущего учебного материала
задания, соответствующие экзаменационным заданиям.
В содержание текущего контроля включать
экзаменационные задачи.
Изменить систему контроля над уровнем знаний
учащихся по математике
Итоговое повторение построить исключительно на
отработке умений и навыков, требующихся для получения положительной отметки на
экзамене.
Уроки повторения строятся следующим образом. На
уроке разбираются типовые задачи по 2-3 темам. На дом задаются аналогичные
задачи. На следующем уроке выясняются затруднения, которые возникли у учеников,
прорабатывают эти задачи. Затем даётся проверочная работа. Ученики, не сдавшие
зачёт, обязаны дома проработать дополнительный вариант и сдать зачёт на
дополнительном занятии. Через определённое число уроков проводится
тренировочная работа по целому блоку тем, анализируется, корректируется и
проводится зачетная работа по данному блоку тем. Затем цикл повторяется по
другим темам. После обобщающего повторения проводятся (две) предэкзаменационные
работы в условиях, приближенных экзаменационным.
Важно, чтобы все ученики сдали обязательную
часть зачетной работы. В зачётную работу можно (нужно) включать не только
обязательные задания, но и более сложные (для подготовленных учеников).
Подготовка ко второй части работы осуществляется
как на уроках, так и во внеурочное время на элективных курсах. Используются
сборники для подготовки к экзаменам, рекомендованные ФИПИ и МИИО.
Важным условием успешной подготовки к экзаменам
является тщательность в отслеживании результатов учеников по всем темам и в
своевременной коррекции уровня усвоения учебного материала.
Конечно же, данная система требует большего
количества времени учителя на подготовку к урокам, на проверку работ, на
проведение дополнительных занятий. Но, если учитель заинтересован в результатах
своего труда, то ему в любом случае необходимо совершенствовать систему
контроля над уровнем знаний и умений учащихся.
Основными целями математического образования
являются:
интеллектуальное развитие учащихся, формирование
качеств мышления, характерных для математической деятельности и необходимых
человеку для полноценной жизни в обществе;
- овладение конкретными математическими
знаниями, умениями и навыками, необходимыми для применения в практической
деятельности, для изучения смежных дисциплин, для продолжения образования;
- воспитание личности в процессе освоения
математики и математической деятельности;
- формирование представлений об идеях и методах
математики, о математике как форме описания и методе познания действительности.
В основу отбора содержания общего
математического образования положен принцип реализации поставленных целей на
небольшом по объему информационно емком и практически значимом материале,
доступном для учащихся школьного возраста. При этом представляется необходимым
руководствоваться принципом преемственности, или разумного консерватизма, что
обусловлено в первую очередь тем объективным фактом, что традиционное
содержание обучения математике, сложившееся в течение многих десятилетий,
отражает тот объем математических знаний, которые, с одной стороны, являются
фундаментом математической науки, а с другой - доступны учащимся. Принцип
преемственности должен сочетаться с современными тенденциями развития
отечественной и зарубежной школы.
Геометрические фигуры, измерение геометрических
величин, изучение геометрии подвергается весьма существенному пересмотру,
предлагается отказаться от строго дедуктивного построения курса, усилив
внимание к его наглядно - эмпирическому аспекту.
Проблемой обучения учащихся решению
планиметрических задач занимались математики: Семенов А.В., Трепалин А.С.,
Ященко И.В., Лысенко Ф.Ф., Кулабухова С.Ю. и др. Много было выпущено литературы
для подготовки к ГИА этими математиками. Так же и для этого года выпущена
специальная литература: «ГИА 2013. Математика. Семенов А.В., Трепалин А.С.,
Ященко И.В. и др. (2013, 88с.)», «Математика. 9 класс. Тренажер по новому плану
ГИА. Алгебра, геометрия, реальная математика. Под ред. Лысенко Ф.Ф., Кулабухова
С.Ю. (2013, 160с.)», «ГИА. Математика. 9 класс. Практикум по выполнению типовых
тестовых заданий. Реальные тесты. Лаппо Л.Д., Попов М.А. (2013, 80с.)» и др.
Спецификация контрольных измерительных
материалов для проведения в 2013 году государственной (итоговой) аттестации (в
новой форме) по МАТЕМАТИКЕ обучающихся, освоивших основные общеобразовательные
программы основного общего образования:
Модуль «Геометрия».
Часть 1. В этой части экзаменационной работы
содержатся задания по всем ключевым разделам курса геометрии основной школы,
отраженным в кодификаторе элементов содержания. Распределение заданий по
разделам содержания приведено в таблице 3.
Табл. 3. Распределение заданий части 1 по
разделам содержания
|
Код
по КЭС
|
Название
раздела содержания
|
Число
заданий
|
|
1
|
Числа
и вычисления
|
2
|
|
2
|
Алгебраические
выражения
|
2
|
|
3
|
Уравнения
и неравенства
|
2
|
|
4
|
Числовые
последовательности
|
1
|
|
5
|
Функции
и графики
|
1
|
Табл. 4. Распределение заданий части 1 по КЭС
|
Код
по КЭС
|
Название
раздела содержания
|
Число
заданий
|
|
7.1
|
Геометрические
фигуры и их свойства
|
1
|
|
7.2
|
Треугольник
|
1
|
|
7.3
|
Многоугольники
|
1
|
|
7.4
|
Окружность
и круг
|
1
|
|
7.5
|
Измерение
геометрических величин
|
1
|
Требования к уровню подготовки выпускников,
соответствующие Федеральному компоненту государственного образовательного
стандарта, зафиксированы в кодификаторе требований (КТ).
Табл. 5. Распределение заданий части 1 по
требованиям
|
Код
по КТ
|
Название
|
Число
заданий
|
|
5
|
Уметь
выполнять действия с геометрическими фигурами, координатами и векторами
|
4
|
|
7.8
|
Проводить
доказательные рассуждения при решении задач, оценивать логическую
правильность рассуждений, распознавать ошибочные заключения
|
1
|
Требования к уровню подготовки выпускников
распределяются по следующим категориям познавательной деятельности:
знание/понимание (владение терминами;
распознавание); применение знаний для решения математической задачи (умение
решить геометрическую задачу, предполагающую применение системы знаний,
включение известных понятий, приемов и способов решения в новые связи и
отношения, распознавание стандартной задачи в измененной формулировке);
рассуждение (умение оценивать логическую
правильность рассуждений, распознавать ошибочные заключения).
Табл. 6. Распределение заданий части 1 по
категориям познавательной деятельности
|
Категория
познавательной деятельности
|
Число
заданий
|
|
Знание
/понимание
|
1
|
|
Применение
знаний для решения математической задачи
|
3
|
|
Рассуждение
|
1
|
Часть 2. Задания второй части экзаменационной
работы направлены на проверку таких качеств геометрической подготовки
выпускников, как:
умение решить планиметрическую задачу, применяя
различные теоретические знания курса геометрии;
умение математически грамотно и ясно записать
решение, приводя при этом необходимые пояснения и обоснования;
владение широким спектром приемов и способов
рассуждений.
Все задания Части 2 базируются на содержании,
регламентируемом Федеральным компонентом государственного стандарта общего
образования по математике. Распределение заданий по разделам кодификаторов
элементов содержания и требований к уровню подготовки выпускников представлено
в таблицах 7 и 8.
Табл. 7. Распределение заданий части 2 по
разделам содержания
|
Код
по КЭС
|
Название
раздела содержания
|
Число
заданий
|
|
7
|
Геометрия
|
3
|
Табл. 8. Распределение заданий части 2 по
требованиям
|
Код
по КТ
|
Название
|
Число
заданий
|
|
7.8
|
Проводить
доказательные рассуждения при решении задач, оценивать логическую
правильность рассуждений, распознавать ошибочные заключения
|
1
|
|
5
|
Уметь
выполнять действия с геометрическими фигурами, координатами и векторами
|
2
|
[#"788875.files/image017.gif">
Решение: Проведём радиусы ОА, ОВ, ОС, ОD.
Треугольники АОВ и СОD равны по трём сторонам. ОК и ОL - их высоты, проведённые
к равным сторонам, следовательно, они равны как соответственные элементы равных
треугольников.
Часто решающий задачу интуитивно использует
дополнительное построение, но, не выделяя его как метод, может не увидеть
целесообразности его применения в других, более сложных или даже аналогичных
задачах.
Как узнать, какое дополнительное построение
следует выполнять в том или ином случае? Ответ на этот вопрос дает своего рода
классификация дополнительных построений, связанная с характерными признаками
фигуры, данной в задаче. Тщательный анализ решений достаточно большого
количества задач, в которых дополнительное построение используется прямо или
косвенно, показал, что целесообразность применения того или иного
дополнительного построения зависит от этих признаков.

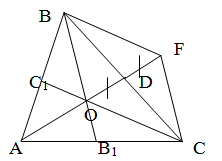
Дополнительное построение 1. Если в треугольнике
задана медиана, то треугольник достраивается до параллелограмма с центром в
основании этой медианы (рис. 1).
В зависимости от содержания задачи такое
достраивание можно выполнять для одной, двух или даже трех медиан. При этом
возможно использование не всего параллелограмма, а лишь его части (например,
треугольника ABA2).
Задача №1. Две стороны треугольника равны 27 и
29, а медиана, проведенная к третьей стороне равна 26. Найти высоту,
проведенную к стороне 27.

Дано:
∆ABC, AB=27,BC=29,BO=26 − высота −
медиана
Найти CD.
Решение:
. Дополнительное построение: строим OE=BO, ABCE-
параллелограмм (по признаку) BC=AE=29. AB=EC=27
. S∆ABC= S∆ABE
.S∆ABE= (по
формуле Герона)
(по
формуле Герона)
S∆ABE=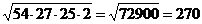 ∆ABC=
∆ABC=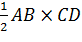 ,
,
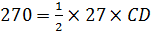 ,
CD=20
,
CD=20
Ответ: 20
Дополнительное построение 2. Если дана трапеция,
то ее диагональ или боковая сторона параллельно переносятся (рис. 2).
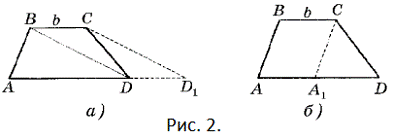
Задача №2. Найти высоту равнобедренной трапеции,
если её диагонали взаимно перпендикулярны, а площадь трапеции равна S.

Дано:− равнобедренная трапецияи BD −
диагонали
AC BD− площадь трапеции
BD− площадь трапеции
Найти h − высоту трапеции
Решение:
. Дополнительное построение: строим
CE||BD
.  равнобедренный (т.к AC=BD, BD=CE,
равнобедренный (т.к AC=BD, BD=CE, AC=CE)
AC=CE)
.  прямоугольный (т.к CO
прямоугольный (т.к CO BD, BD||CE
BD, BD||CE CE
CE CO)
CO)
. Проводим высоту CF - она является
медианой и биссектрисой 

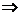
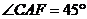

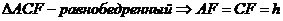
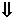
AE=2AF=2h
Sтр.=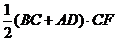 +AD=AE (т.к BCED- параллелограмм)
+AD=AE (т.к BCED- параллелограмм) 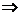 BC=DEтр.=
BC=DEтр.=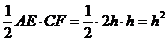 h=
h=
Ответ: 
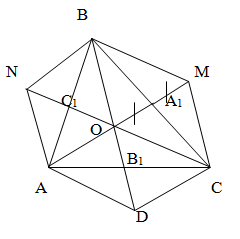
Дополнительное построение 3.
продолжить на 1/3 длины всей медианы и достроить до параллелограмма
B
E
A1
O
B1 C
Задача №3. Длина
треугольника выражается формулой a=2/3√2(mb2+mc2)-ma2 ; где ma, mb, mc,
длины медиан треугольника. Докажите.
Доказательство:
Отметим на медиане AD точку O
пересечения медиан треугольника; согласно свойству (три медианы треугольника
пересекаются в одной точке, которая делит каждую медиану в отношении 2:1,
считая от вершины треугольника), она делит AD в отношении AO:OD=2:1
Продолжим OD на расстояние
DF=OD=1/3ma и соединим точку F с B и C
Теперь составим уравнение,
связывающее длины сторон BO=2/3mb, CO=2/3mc и диагоналей OF=2/3ma, BC=a
параллелограмма OBFC
(2/3ma)2+a2=2((2/3mb)2+(2/3mc)2)=2/3√2(mb2+mc2)-ma2
что и требовалось доказать.
Дополнительное построение №4. Если в
задаче дана длина всех трёх медиан, то как правильно, для того чтоб найти
площадь треугольника, продолжают все медианы на1/3 её длины и достраивают до
параллелограмма.
Задача №4. Медианы треугольника ABC,
AA1=3см, BB1=4см, CC1=5 см Найти площадь треугольника ABC
Решение:
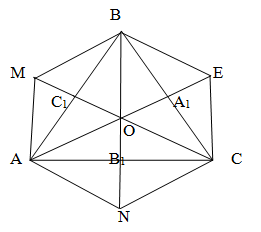
Продолжим медианы AA1 BB1 и CC1 на
длину отрезков A1E, B1N, C1M равные по длине OA1, OB1, OC1 соответственно
получим шесть равновеликих треугольников MBO, MOA, AON, NOC, COE, OEB стороны
которых равны 2/3 длины медиан
SOBE=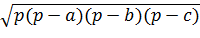 =
=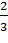 mb; OE=
mb; OE=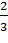 AA1; BE=
AA1; BE=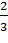 mc=
mc=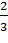 ·4=
·4=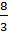 OE=
OE=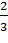 ·3=2 =
·3=2 =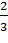 ·5=
·5=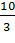 S=
S=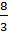 =SBOA1+SCOA1=SBOA1+SBA1E=SBOE=3SBOE=8cм
=SBOA1+SCOA1=SBOA1+SBA1E=SBOE=3SBOE=8cм
Ответ 8 cм
Дополнительное построение 5. Если
дан четырехугольник, у которого суммы противоположных сторон равны, то в него
вписывается окружность.
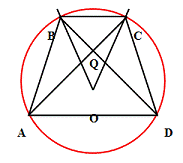
Задача №5. В трапеции ABCD (AB и CD
основания) меньшее основание равно a, углы, прилежащие к этому основанию, равны
 , а
диагонали взаимно перпендикулярны. Найти площадь трапеции.
, а
диагонали взаимно перпендикулярны. Найти площадь трапеции.
Дано:- трапецияи CD - основания
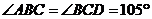
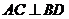
Найти S трапеции
Решение:
.Дополнительное построение: строю
описанную окружность (т.к трапеция равнобедренная, то можно описать окружность)
.Sтр.=
. Пусть QB=x, AB=2x (т.к  ), AQ=y
), AQ=y
По теореме Пифагора: 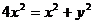
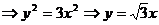
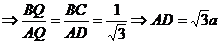
. BQ=QC=x
По теореме Пифагора из  BQC:
BQC: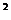 +x
+x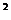 =a
=a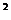
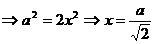
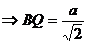
. AQ=QD=y
По теореме Пифагора из 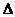 AQD:
AQD:
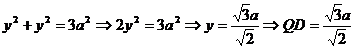
7. BD=BQ+QD=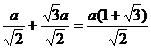
. S=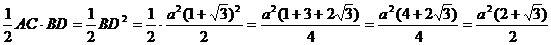
Ответ: 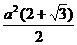 [8]
[8]
Аналитические методы
Один из основных аналитических
методов решения планиметрических задач является векторный метод. Примерная
схема решения геометрических задач векторным методом:
Прочитать задачу, выделить условие и
требование задачи, выполнить чертёж.
Ввести в рассмотрение векторы
(выбрать базис - два неколлинеарных вектора на плоскости, три некомпланарных
вектора в пространстве).
«Перевести» геометрическое условие
задачи на язык векторов. Векторы, необходимые для решения, выразить через
базисные.
«Перевести» геометрическое
требование задачи на язык векторов (можно устно).
С помощью векторной алгебры
(преобразований векторных выражений) перейти от векторного условия задачи к
требованию.
Полученному векторному выражению
дать геометрическое истолкование. [ лекции по ТиМОМ НГПУ 2012 год]
С помощью данного метода можно
решать геометрические задачи представленные во второй части модуля «Геометрия».
Приведу пример одного из решений основанного на данном методе:
Задача№ 6. На катетах прямоугольного
треугольника АВС с прямым углом С построены квадраты АСQP и BCRS. Точка М
середина гипотенузы АВ. Доказать, что отрезки СМ и QR перпендикулярны.
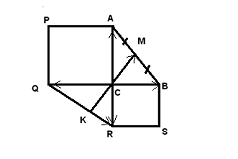
Решение:
) Так как М середина АВ, то  =
=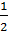 ∙(
∙( +
+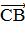 )
)
) 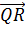 =
=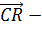
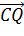
) 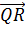 ∙
∙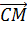 =
= 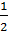 (
(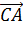 +
+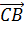 ) ∙ (
) ∙ (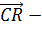
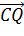 ) =
) = 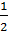 (
(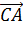 ∙
∙ 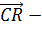
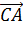 ∙
∙ 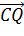 +
+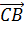 ∙
∙ 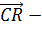
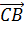 ∙
∙ 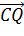 )
)
Так как CA и CQ перпендикулярны, то 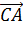 ∙
∙ 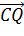 =0;
аналогично
=0;
аналогично 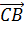 ∙
∙ 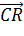 =0.
=0.
Учитывая это, получим: 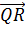 ∙
∙ 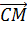 =
= 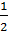 (
(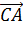 ∙
∙ 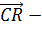
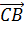 ∙
∙ 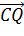 ) =
) =
= 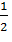 (CA∙ CR ∙cos180° - CB∙
CQ ∙cos180°) =
(CA∙ CR ∙cos180° - CB∙
CQ ∙cos180°) = 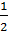 (
(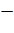 CA∙
CR+CB∙ CQ)
CA∙
CR+CB∙ CQ)
) Итак, 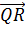 ∙
∙ 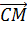 = 0, поэтому
отрезки QR и CM перпендикулярны.
= 0, поэтому
отрезки QR и CM перпендикулярны.
Что и требовалось доказать.
Также к аналитическому методу
относиться метод координат с помощью которого можно решать планиметрические
задачи в ГИА;
Примерная схема решения геометрических
задач методом координат:
Прочитать задачу, выделить условие и
требование задачи, выполнить чертёж.
Выбрать систему координат (наиболее
рациональным способом).
Записать координаты точек,
необходимых для решения. «Перевести» геометрическое условие задачи на язык
координат.
«Перевести» геометрическое
требование задачи на язык координат (можно устно).
С помощью алгебраических
преобразований перейти от условия задачи к требованию.
Полученному алгебраическому
выражению дать геометрическое истолкование. [ лекции по ТиМОМ НГПУ 2012 год]
Приведу пример одного из решений
основанного на данном методе:
Задача №7. В прямоугольном
равнобедренном треугольнике проведены медианы острых углов. Вычислите косинус
угла между ними.
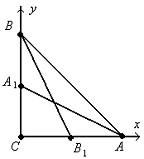
Решение: 1. Введем систему координат
так, в этом случае вершины треугольника будут иметь координаты: С(0,0), А(а,0),
В(0,а), а середины катетов:  . (Здесь а - длина катета.)
. (Здесь а - длина катета.)
. Вычислим координаты векторов 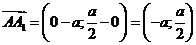 и
и 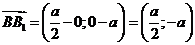 .
.
. Теперь используем формулу для
вычисления косинуса угла между векторами. (Этот угол совпадает с углом между
медианами.)
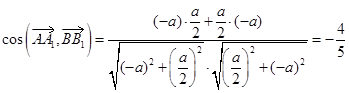
Ответ: 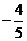 .
.
Данные методы решения
планиметрических задач помогут учащимся наиболее продуктивно подготовится к
решению модуля «Геометрия». Ученик должен ознакомиться с определенным набором
достаточно трудных геометрических задач, научиться решать задачи, следуя известным
образцам. В геометрии в отличие от алгебры алгоритмов очень мало, почти нет.
Поэтому при обучении возрастает значение опорных задач, обобщающих полезный
факт, либо иллюстрирующий метод или прием.
§ 3. Специальные приёмы решения
планиметрических задач школьного курса геометрии
повторение математика
планиметрический урок
Метод площадей
Метод площадей (формулы площадей
треугольников, многоугольников, свойства площадей используются при решении
задач и доказательстве теорем, в условиях и требованиях которых ничего не
говорится о площадях.)
Основные приемы:
Линейные (угловые) элементы и
соответствия между ними можно найти, применяя различные формулы для вычисления
площади треугольника (многоугольника).
Если треугольник (многоугольник)
разбит на несколько треугольников, то можно использовать свойство о том, что
сумма площадей частей равна площади исходного многоугольника.
Отношение отрезков можно заменить
отношением площадей треугольников.
Если угол одного треугольника равен
углу другого треугольника, то можно использовать тот факт, что отношение
произведений сторон, заключающих равные углы, равно отношению площадей
соответствующих треугольников.
При доказательстве геометрических
неравенств можно использовать неравенство для треугольника: 2s<аb. [9]
Также можно использовать теоремы
позволяющие решать планиметрические задачи:

Теорема 1. Если треугольники имеют
общую вершину и их основания лежат на одной прямой, то площади треугольников
пропорциональны длинам их оснований :
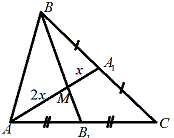
Задача №8. В треугольнике АВС
проведены медианы, М - точка их пересечения. Найти площадь треугольника АВМ,
если площадь исходного треугольника равна 9.
Решение:
Теорема 2. Если треугольники имеют
общую сторону, то их площади пропорциональны длинам отрезков, высекаемых
продолжением их общей стороны на прямой, соединяющей их вершины:
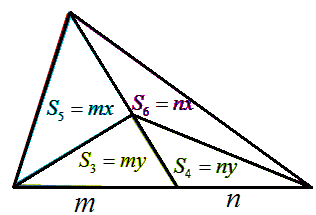
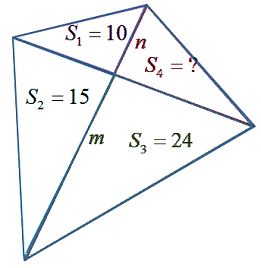
Задача №9. Диагонали разделили
четырехугольник на треугольники, площади трех из которых равны 10, 15 и 24.
Найти площадь четвертого треугольника.
Решение:
В современных учебниках, пособиях и
различного рода задачниках, к сожалению, уделяется мало внимания
психологическим факторам, влияющим на успешность обучения математике. А именно,
воспитание у учащихся уверенности в своих силах, развитие умения пользоваться
прошлым опытом.
Берутся два общеизвестных
утверждения, которые являются базовыми. На основе этих утверждений
выстраиваются две «цепочки» задач по нарастающему уровню сложности. Решения
задач в этих «цепочках» основаны на базовых утверждениях и на решении
предыдущих задач.
Утверждение 1. Два треугольника
являются равновеликими, если равны их высоты и основания.
Задача 10. Докажите, что диагональ
параллелограмма делит его на два равновеликих треугольника.
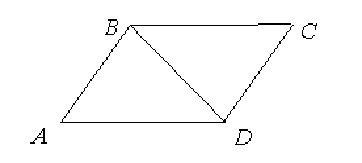
Решение: Высоты треугольников ABD и
BCD равны. AD = BC (по свойству параллелограмма). Тогда в силу утверждения 1 S▲ABD
= S▲BCD
Задача 11. На стороне CD
параллелограмма ABCD взята произвольная точка Е. Зная, что S▲ABE = S,
найдите площадь параллелограмма ABCD.
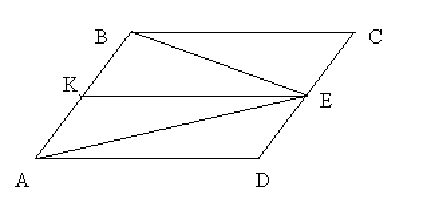
Решение: Проведем дополнительное
построение: КЕ║AD. Тогда из задачи 1 следует, что S▲KBE = S▲CBE,
а S▲AKE = S▲ADE . Отсюда SABCD = 2S.
Задача 12. В параллелограмме ABCD на
сторонах AB и CD взяты произвольные точки M и N. Докажите, что площадь
четырехугольника KMEN равна площади четырех образовавшихся треугольников.
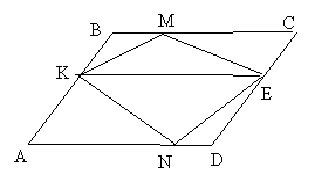
Решение: Проведем отрезок КЕ. Тогда
в силу задачи 2 S▲KME = S▲KMB + S▲MEC, а S▲KNE = S▲AKN
+ S▲EDN
Отсюда S▲KMEN = S▲KMB +
S▲MEC + S▲KNE + S▲EDN
Задача 13. Внутри параллелограмма
ABCD взята произвольная точка О. Зная площадь трех треугольников с вершиной в
точке О, найдите площадь четвертого треугольника.
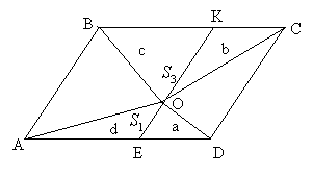
Решение: Пусть S▲ADO = S1, S▲ABO
= S2, ▲BOC = S3. Произведем дополнительное построение: КЕ║АВ.
Введем следующие обозначения: ▲EOD
= a, S▲KCO = b, S▲BKO = c, S▲AEO = d.
Тогда S2 = с
+d , S▲DOC = a + b, S1 + S3 = a + b + c + d .
Отсюда S▲DCO
= S1 + S3 - S2
Задача 14. Каждая диагональ
четырехугольника делит его на треугольники одинаковой площади. Докажите, что
это параллелограмм.
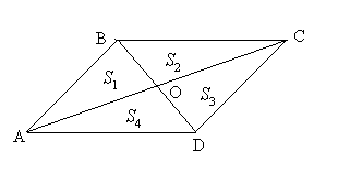
Решение: Из условия следует, что
верны равенства: S1 + S2 = S3 + S4 и S1 + S4 = S3 + S2 . Откуда получим, что S1
= S3, а S2 = S4. Отметим, что S2:S1= AO:ОС, S4:S3=AO:OC. Кроме этого,
соответствующие высоты треугольников BOC, COD и AOB, AOD равны, соответственно,
площади относятся как длины оснований. Из того, что S1 = S3 и S2 = S4. следует,
что AO:OC =AO:OC. Следовательно, AO = OC. Аналогично можно доказать, что BO =
OD . Можно сделать вывод, что диагонали четырехугольника точкой пересечения
делятся пополам, а это значит, что ABCD - параллелограмм.
Нестандартные решения стандартных
задач помогают воспитать заинтересованный подход к изучению материала. Основной
специальный метод решения планиметрических задач это метод площадей, который
позволяет решать задачи в которых присутствует понятие площади. Данный метод
решения используется при решении планиметрических задач первой части в ГИА,
также его знание может пригодится на экзамене и в других задания нахождения
элементов через площадь фигуры, так как каждый год в содержании заданий
происходит изменение.
Вывод к первой главе
Подготовка к государственной
итоговой аттестации (ГИА) - неотъемлемая часть современного курса математики.
Задачи по геометрии занимают примерно третью часть всех заданий КИМов.
Геометрия является очень мощным средством развития личности в самом широком
диапазоне.
Большинство учеников к 9 классу
забывают основные понятия курса планиметрии, не говоря уже о формулах, поэтому
при итоговом повторении курса планиметрии ученики вспоминают основные понятия и
формулы, что позволит им применить их на при сдаче ГИА. Итоговое повторение позволяет
ученикам в полной мере подготовиться к экзамену.
Основные методы решения
планиметрических задач помогут учащимся наиболее продуктивно подготовится к
решению модуля «Геометрия». Ученик должен ознакомиться с определенным набором
достаточно трудных геометрических задач, научиться решать задачи, следуя
известным образцам. В геометрии в отличие от алгебры алгоритмов очень мало,
почти нет. Поэтому при обучении возрастает значение опорных задач, обобщающих
полезный факт, либо иллюстрирующий метод или прием.
Нестандартные решения стандартных
задач помогают воспитать заинтересованный подход к изучению материала,
используя специальный метод решения планиметрических задач это метод площадей,
который позволяет решать задачи в которых присутствует понятие площади. Данный
метод решения используется при решении планиметрических задач первой части в
ГИА.
Глава II.
§1. Тематическое планирование уроков
Проводить итоговое повторение по
планиметрии очень важно. Однако, в виду загруженности программы и нехватки часов
итоговое повторение осуществляется не в полном объеме, или не осуществляется
вовсе. Поэтому нужно ознакомиться с тематическим планированием и постараться
выделить в нем время для проведения повторения планиметрии. Лишь малый процент
учеников решает задачи из второй части модуля «Геометрия», на это стоит
обратить внимание и непросто «натаскать» учеников на решение задач, а научить
осознано решать типологические задачи используя основные методы решения
планиметрических задач.
Основной тип литературы по подготовке
к ГИА направлен на «натаскивание» учеников решения задач, нет в литературе
теоритических пояснений к решению задач, не выделены методы с помощью которых
решаются задачи, а также можно решить данные задачи. В связи с этим нужно
обратить внимание на построение плана повторения.
Построение итогового повторения
курса математики, подготовка к государственной итоговой аттестации:
Итоговое повторение учебного
материала необходимо проводить, используя блочно - модульное структурирование
учебного материала, укрупнение учебных единиц.
Выстраивать повторение, соблюдая
«правило спирали» - от простых заданий до заданий более сложных.
Использовать на уроках раздаточный
материал с проверкой основных приемов и специальных методов решения простейших
заданий.
Контроль за успеваемостью учащихся,
проверка усвоения повторяемого материала.
В свете всего выше сказанного можно
судить о том, что итоговое повторение в 9 классе не только обязательно, но и
необходимо, особенно при подготовке к ГИА. Касаемо планиметрических задач в
итоговом повторении следует уделить внимание не только отработке
непосредственно приемов решения задач, но и умению правильно проводить
дополнительные построения, уметь выделять необходимые компоненты фигуры. Важно
организовать повторение так, чтобы оно естественным образом вписывалось в урок,
проходило на более высоком уровне, устанавливая новые связи между старыми
известными звеньями.
Тематическое планирование итогового
повторения
|
Тип
урока
|
Задача
|
Цель
|
Планируемый
результат
|
|
Решение
планиметрических задач по теме треугольник
|
Совместно
с учащимися рассмотреть решение основных планиметрических задач: нахождение
внешнего угла треугольника, нахождение площади треугольника, нахождение
элементов прямоугольного треугольника.
|
В
результате ученик: Умеет решать основные планиметрические задачи; Умеет
находить внешний угол треугольника, площадь треугольника, элементы
прямоугольного треугольника; Знает, как применять полученные знания при
решении планиметрических задач.
|
Усвоение
основных приемов решения планиметрических задач на понятие треугольника
|
|
Решение
планиметрических задач по теме треугольник
|
Совместно
с учащимися рассмотреть решение основных планиметрических задач: на
доказательство, на нахождение площади треугольника.
|
В
результате ученик: Умеет решать основные планиметрические задачи; Умеет
находить внешний угол треугольника, элементы треугольника; Знает, как
применять полученные знания при решении планиметрических задач.
|
Усвоение
основных приемов решения планиметрических задач на понятие треугольника
|
|
Решение
планиметрических задач по теме четырехугольник
|
Совместно
с учащимися рассмотреть решение основных планиметрических задач: нахождение
площади четырехугольника, нахождение элементов четырехугольника
|
В
результате ученик: Умеет решать основные планиметрические задачи; Умеет
находить элементы четырехугольника; Знает, как применять полученные знания
при решении планиметрических задач.
|
Усвоение
основных приемов решения планиметрических задач на понятие четырехугольника
|
|
Решение
планиметрических задач по теме четырехугольник
|
Совместно
с учащимися рассмотреть решение основных планиметрических задач: нахождение
площади четырехугольника, нахождение элементов четырехугольника.
|
В
результате ученик: Умеет решать основные планиметрические задачи; Умеет находить
элементы четырехугольника; Знает, как применять полученные знания при решении
планиметрических задач.
|
Усвоение
основных приемов решения планиметрических задач на понятие четырехугольника
|
|
Решение
планиметрических задач по теме окружность
|
Совместно
с учащимися рассмотреть решение основных планиметрических задач: на
нахождение острого угла окружности, нахождение радиуса окружности, на
доказательство.
|
В
результате ученик: Умеет решать основные планиметрические задачи; Умеет
находить элементы окружности; Знает, как применять полученные знания при
решении планиметрических задач.
|
Усвоение
основных приемов решения планиметрических задач на понятие окружности
|
§2. Практическое исследование
Урок 1 по теме: «Решение планиметрических задач
по теме треугольник».
Тема урока: Решение планиметрических задач на
понятие треугольника.
Класс: 9
Учебная задача: совместно с учащимися
рассмотреть решение основных планиметрических задач: нахождение внешнего угла
треугольника, нахождение площади треугольника, нахождение элементов
прямоугольного треугольника.
Диагностируемые цели урока:
В результате ученик:
Умеет решать основные планиметрические задачи;
Умеет находить внешний угол треугольника,
площадь треугольника, элементы прямоугольного треугольника;
Знает, как применять полученные знания при
решении планиметрических задач.
Инструменты: доска, маркеры, линейка,
треугольник.
Ход урока:
Мотивационно-ориентировочный этап.
Актуализация.
Мотивация.
Постановка учебной задачи.
Операционно-познавательный этап.
Нахождение внешнего угла треугольника.
Нахождение площади треугольника.
Нахождение высоты треугольника.
Нахождение тангенса острого угла в прямоугольном
треугольнике.
Нахождение гипотенузы в прямоугольном
треугольнике.
Рефлексивно-оценочный этап.
Домашнее задание
Подведение итогов.. Мотивационно-ориентировочный
этап.
Учитель: Здравствуйте, ребята, садитесь. Как вы
знаете, ГИА по математике охватывает все разделы как по алгебре, так и по
геометрии. Были ли среди заданий проверочной контрольной работы по ГИА задачи
по планиметрии?
Ученики: Да, это задания модуля «Геометрия».
Учитель: Сколько заданий в данном модуле?
Ученики: 6 заданий в первой части и 2 во второй.
Учитель: Какие фигуры встречались задания в
пробном ГИА?
Ученики: Треугольник, четырех угольники,
окружности.
Учитель: К какому разделу геометрии можно
отнести эти фигуры?
Ученики: К разделу планиметрии.
Учитель: Все ли вы решили задачи из данного
раздела?
Ученики: Нет, не все.
Учитель: Планиметрия изучается с 7 класса,
основные понятия и основные приемы решения планиметрических задач вы изучали,
но как показал результат контрольной позабыли, значит, что нужно сделать?
Ученики: Необходимо повторить основные понятия
планиметрии и приемы решения планиметрических задач.
Учитель: Целью нашего сегодняшнего и последующих
занятий будет рассмотреть основные типы планиметрических задач, рассмотреть
основные приемы решения этих задач. Тема нашего урока: «Решение
планиметрических задач по теме треугольник».
II. Операционно-познавательный этап.
Учитель: Какая фигура называется треугольником?
Ученики: Треугольник - это геометрическая
фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной
прямой точки.
Учитель: Начертите треугольник и покажите его
стороны, вершины и углы. Что такое периметр треугольника?
Ученики: Периметр треугольника равен сумме всех
трех сторон треугольника.
Учитель: Какой угол называется внешним углом
треугольника?
Ученики: Внешним углом треугольника при данной
вершине называется угол, смежный с углом треугольника при этой вершине.
Учитель: Какой отрезок называется биссектрисой
треугольника?
Ученики: Биссектрисой треугольника, проведённой
из данной вершины, называют отрезок, соединяющий эту вершину с точкой на
противоположной стороне и делящий угол при данной вершине пополам.
Учитель: Какой отрезок называется медианой
треугольника? Сколько медиан имеет треугольник?
Ученики: Медианой треугольника, проведённой из
данной вершины, называется отрезок, соединяющий эту вершину с серединой
противолежащей стороны. Треугольник имеет три медианы, так как имеет три
вершины.
Учитель: Какой отрезок называется высотой
треугольника? Сколько высот имеет треугольник?
Ученики: Высотой треугольника, проведённой из
данной вершины, называется перпендикуляр, опущенный из этой вершины на
противоположную сторону или её продолжение.
Учитель: Какой треугольник называется
остроугольный? Какой треугольник называется тупоугольным?
Ученики: Если все углы треугольника острые, то
треугольник называется остроугольным; Если один из углов треугольника тупой
(больше 90°), то треугольник называется тупоугольным.
Учитель: Какой треугольник называется
прямоугольным? Как называются стороны прямоугольного треугольника?
Ученики: Если один из углов треугольника прямой
(равен 90°), то треугольник называется прямоугольным. Две стороны, образующие
прямой угол, называются катетами, а сторона, противолежащая прямому углу,
называется гипотенузой.
Учитель: Какой треугольник называется
равнобедренным? Как называются его стороны?
Ученики: Равнобедренный треугольник - это
треугольник, в котором две стороны равны между собой по длине. Равные стороны
называются боковыми, а последняя - основанием.
Учитель: Вы повторили основные определения,
связанные с понятием треугольник. Теперь решим некоторые задачи на понятие
треугольник представленные в пробных вариантах ГИА.
Задача 1: Внешний угол при основании
равнобедренного треугольника равен 1400. Найдите угол между боковыми сторонами
этого треугольника.
Учитель: (Просит ученика решить задачу устно,
ученик решает, идет обсуждении решения).
Задача 2: Найдите площадь треугольника,
изображенного на рисунке.
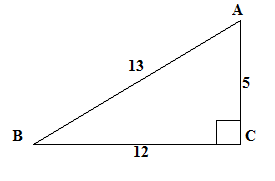
Учитель: (Вызывает ученика к доске, ученик
решает на доске,) остальные записывают решение в тетрадях.
Ученик: 
Задача 3: Используя данные на рисунке, найдите
высоту СН.
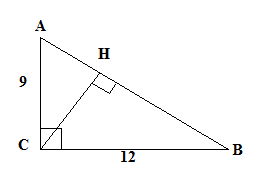
Учитель: (Вызывает ученика к доске, ученик
решает задачу) остальные записывают решение в тетради.
Ученик: 1)Треугольник ABC прямоугольный, АВ
гипотенуза, 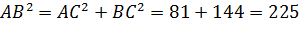 , АВ=15.
, АВ=15.
) Найдем площадь ABC, она равна половине
произведения катетов, то есть  .
.
) Так же площадь треугольника равна половине
произведения АВ на СН, площадь известна, тогда 54=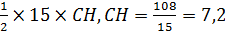 .
.
Учитель: (Хвалит ученика), есть ли еще варианты
решения задачи? Вы решили данную задачу с помощью метода площадей. (Предлагает
свой более быстрый способ решения). Данную задачу можно решить в два действия,
традиционным методом решения, то есть с помощью формул, сначала находим
гипотенузу, а потом сразу находим высоту CH. Высота опущенная к гипотенузе
равна произведению катетов деленных на гипотенузу: CH= .
(Ученики обсуждают предложенный вариант и записывают в тетради).
.
(Ученики обсуждают предложенный вариант и записывают в тетради).
Задача 4: Используя данные, указанные на
рисунке, найдите тангенс угла Р.

Учитель: Чему равен тангенс острого угла в
прямоугольном треугольнике?
Ученик: Отношению противолежащего катета к
прилежащему.
Учитель: Значит чему равен тангенс угла Р?
Ученик: Тангенс угла Р равен 
Учитель: Правильно, (вызывает к доске ученика и
решить 5 задачу).
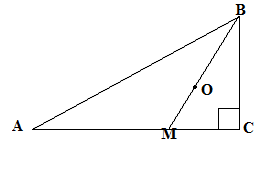
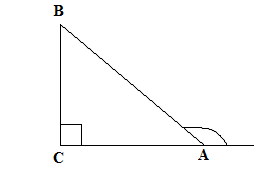
Задача 5: Дан прямоугольный треугольник АВС с
прямым углом С. Через центр О вписанной в треугольник окружности проведен луч
ВО, пересекающий катет АС в точке М. Известно, что АМ=8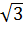 ,
а
,
а  Найдите
гипотенузу треугольника АВС.
Найдите
гипотенузу треугольника АВС.
Решение:
Учитель: Как будем решать данную задачу? Что
известно?
Ученик: Известно, что АМ=8 ,
а
,
а 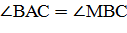 ,
ВО - биссектриса угла В, так как О центр вписанной окружности, а следовательно,
,
ВО - биссектриса угла В, так как О центр вписанной окружности, а следовательно,
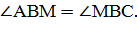
 Обозначим
Обозначим 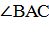 за
х. Имеем 3х=900, откуда х=300.
за
х. Имеем 3х=900, откуда х=300.
Учитель: Обрати внимание на треугольник АМВ, что
в нем известно?
Ученик: В треугольнике АМВ: 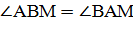 ,
а значит он равнобедренный, следует что МВ=АМ=8
,
а значит он равнобедренный, следует что МВ=АМ=8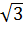 .
.
Рассмотрим прямоугольный треугольник МВС:
ВС=МВ*cos300=12
В прямоугольном треугольнике АВС: АВ=2*ВС=24
Ответ: 24.
Учитель: (хвалит ученика) Мы рассмотрели более
простые задачи из первой части модуля «Геометрии» встречающиеся в ГИА..
Рефлексивно-оценочный этап.
Учитель: Запишите домашнее задание
Д/З: В треугольнике АВС угол С равен 900, sinA=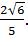 Найти косинус внешнего угла при вершине А.
Найти косинус внешнего угла при вершине А.
Учитель: Следующее занятие начнем с проверки
домашнего задания, ребята что сегодня повторили на уроке?
Ученики: Понятие треугольника, виды
треугольников, элементы треугольника.
Учитель: На следующем занятии рассмотрим более
сложные задачи из второй части модуля «Геометрия». Спасибо за внимание, урок
окончен.
Урок 2 по теме: «Решение планиметрических задач
по теме треугольник».
Тема урока: Решение планиметрических задач на
понятие треугольника.
Класс: 9
Учебная задача: совместно с учащимися
рассмотреть решение основных планиметрических задач: на доказательство, на
нахождение площади треугольника.
Диагностируемые цели урока:
В результате ученик:
Умеет решать основные планиметрические задачи;
Умеет находить внешний угол треугольника,
элементы треугольника;
Знает, как применять полученные знания при
решении планиметрических задач.
Инструменты: доска, мел, маркеры, линейка,
треугольник.
Ход урока:. Мотивационно-ориентировочный этап..
Операционно-познавательный этап.. Рефлексивно-оценочный этап..
Мотивационно-ориентировочный этап.
Учитель: Здравствуйте ребята, садитесь. Сегодня
начнем наш урок с проверки домашнего задания. Какой у кого получился ответ?
Ученики: (у всех получился разный ответ)
Учитель: Общего ответа нет, значит нужно
разобраться какой будет ответ. И так продолжим тему предыдущего урока «Решение
планиметрических задач по теме треугольник». Выясним какой же на самом деле
ответ получился в домашней задаче.. Операционно-познавательный этап.
Задание 1: В треугольнике АВС угол С равен 900,
sinA=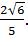 Найти косинус внешнего угла при вершине А.
Найти косинус внешнего угла при вершине А.
Решение: (учитель вызывает ученика к доске,
остальные записывают в тетради)
Ученик: sinA=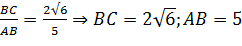 =AB2-BC2=25-24=1,
AC=1
=AB2-BC2=25-24=1,
AC=1
Учитель: Незабываем, что находим косинус
внешнего угла, а значит:
cos(1800- =
=
Учитель: (спрашивает ученика) понял в чем была
ошибка? (ученик говорит что понял, учитель спрашивает некоторых учеников из
класса) понял где была ошибка в решении, почему получилось - 0,2 а не
0,2?(ученик говорит что понял) присаживайся(говорит ученику у доски) и так
решим следующую задачу(вызывает следующего ученика)
Задание 2. В параллелограмме ABCD точка Е -
середина стороны АВ. Известно, что ЕС = ED. Докажите, что данный параллелограмм
- прямоугольник.
Учитель: Обрати внимание на треугольники ВЕС и
АЕD.
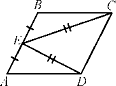
Ученик:
Доказательство.
Треугольники ВЕС и AED равны по трём сторонам.
Значит, углы СBE и DAE равны. Так как их сумма
равна 180° , то углы равны 90° . Такой параллелограмм - прямоугольник.
Учитель: За данную задачу на экзамене можно
получить 2 балла, задача доказывается в два действия, все ли было понятно?
(говорит ученику чтоб тот садился на место)
Ученики: Все ясно.
Учитель: Чем мы пользовались при доказательстве
данной задачи?
Ученики: Равенством треугольников, свойством
треугольников. Решим следующую задачу (вызывает ученика к доске)
Задача 3: Площадь треугольника АВС равна 40.
Биссектриса AD пересекает медиану ВК в точке Е, при этом BD:CD=3:2. Найдите
площадь четырехугольника EDCK. (данная задача способствует повторению метода
площадей)
Решение:
Учитель: Как будешь решать данную задачу?
(ученик начинает размышлять в слух, учитель предлагает ученику обозначить
сторону треугольника за x и подводим ученика к методу площадей)
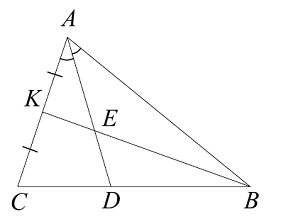
Ученик: Пусть AK=KC=x. По свойству биссектрисы 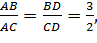 откуда
АВ=3х.
откуда
АВ=3х.
Учитель: Обрати внимание на треугольник ABK.
Ученик: Из треугольника АВК, где АЕ -
биссектриса, находим, что 
Учитель: Для простоты дальнейших рассуждений
обозначь площадь треугольника АВС какой ни будь буквой и воспользуйся свойством
площадей.
Ученик: Пусть S - площадь треугольника АВС,
тогда 
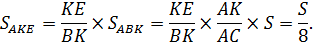
Таким образом, 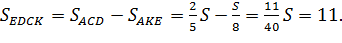
Учитель: Какое свойство использовали при решении
данной задачи?
Ученики: Свойство биссектрис, а так же свойство
площадей.. Рефлексивно - оценочный этап
Учитель: Запишите домашнее задание, повторить
все понятия связанные с четырехугольниками, а так же решить задачу: Основания
трапеции равны 4 см и 9 см, а диагонали равны 5 см и 12 см. Найти площадь
трапеции и угол между её диагоналями. (ответ: 30 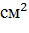 ,
90°).
,
90°).
Что вы сегодня повторили на уроке?
Ученики: Решение планиметрических задач
связанных с понятием треугольника.
Учитель: Какие методы использовали при решении
задач?
Ученики: Метод дополнительного построения, метод
площадей.
Учитель: Спасибо за внимание, урок окончен.
Урок 3 по теме: «Решение планиметрических задач
по теме четырехугольник».
Тема урока: Решение планиметрических задач на
понятие четырехугольника.
Класс: 9
Учебная задача: совместно с учащимися
рассмотреть решение основных планиметрических задач: нахождение площади
четырехугольника, нахождение элементов четырехугольника.
Диагностируемые цели урока:
В результате ученик:
Умеет решать основные планиметрические задачи;
Умеет находить элементы четырехугольника,
площадь четырехугольника;
Знает, как применять полученные знания при
решении планиметрических задач.
Инструменты: доска, маркеры, линейка,
треугольник.
Ход урока:
I. Мотивационно-ориентировочный этап.
Актуализация.
Мотивация.
Постановка учебной задачи.
Операционно-познавательный этап.
Решение задач
Рефлексивно-оценочный этап.
Домашнее задание
Подведение итогов.. Мотивационно-ориентировочный
этап.
Учитель: Здравствуйте, ребята, садитесь. На
предыдущих занятиях вы повторили основные понятия и методы решения
планиметрических задач на понятие треугольника. Вам на дом была предложена
задача, все ли ее решили?
Ученики: Да, она несложная, похожие задачи
встречаются в ГИА в первой части.
Учитель: Чем вы пользовались при решении данной
задачи?
Ученики: Теоремой Пифагора, площадью трапеции.
Учитель: Все ли задания в ГИА связанные с
понятием четырехугольника так просто решаются?
Ученики: Нет, встречаются задачи которые
непонятно как решать.
Учитель: Что нужно сделать что бы было понятно
как решать задачи данного типа?
Ученики: Необходимо повторить основные приемы
решения планиметрических задач на понятие четырехугольника.
Учитель: Целью нашего сегодняшнего занятий будет
рассмотреть основные типы планиметрических задач, на понятие четырехугольника.
Тема нашего урока: «Решение планиметрических задач по теме четырехугольник».
II. Операционно-познавательный этап.
Учитель: Какая фигура называется
четырехугольником?
Ученики: Четырёхугольник - это геометрическая
фигура, состоящая из четырёх точек, никакие три из которых не лежат на одной
прямой, и четырёх отрезков, попарно соединяющих эти точки.
Учитель: Что такое параллелограмм?
Ученики: Параллелограмм - это четырёхугольник, у
которого противоположные стороны попарно параллельны, то есть лежат на
параллельных прямых.
Учитель: Сформулируйте свойства параллелограмма.
Ученики: Противоположные стороны параллелограмма
равны, противоположные углы параллелограмма равны, диагонали параллелограмма
пересекаются и точкой пересечения делятся пополам, сумма всех углов равна 360°.
Учитель: Какой параллелограмм называется
прямоугольником?
Ученик: Прямоугольник - параллелограмм, у
которого все углы прямые (равны 90 градусам).
Учитель: Какой параллелограмм называется ромбом?
Ученики: Ромб - это параллелограмм, у которого
все стороны равны.
Учитель: Какой прямоугольник называется
квадратом?
Ученики: Квадрат - правильный четырёхугольник, у
которого все углы и стороны равны.
Учитель: Какой четырёхугольник называется
трапецией?
Учитель: Трапеция - четырёхугольник, у которого
только одна пара сторон параллельна (а другая пара сторон не параллельна).
Учитель: Какая трапеция называется
равнобедренной?
Ученики: Трапеция, у которой боковые стороны
равны, называется равнобокой или равнобедренной.
Учитель: Вы повторили основные определения связанные
с понятием четырехугольника, теперь порешаем задачи из демонстрационных
вариантов ГИА наиболее простые.
Задача 1: Найдите площадь трапеции, изображенной
на рисунке.
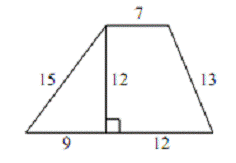
Учитель: (спрашивает ученика устно) Как будешь
находить площадь трапеции?
Ученик: По формуле  и
получаем 168.
и
получаем 168.
Учитель: А есть ли еще варианты решения?
Ученик: Вроде бы как и нет.
Учитель: На самом деле есть, запишите у себя в
тетрадях формулу с помощью которой можно найти площадь данной трапеции:  ,
где a и b - основания трапеции, а c и d - боковые стороны трапеции. Данная
формула может пригодиться при решении задач когда известны основания и стороны
трапеции, а высота неизвестна. Решим следующую задачу.
,
где a и b - основания трапеции, а c и d - боковые стороны трапеции. Данная
формула может пригодиться при решении задач когда известны основания и стороны
трапеции, а высота неизвестна. Решим следующую задачу.
Задача 2: Две стороны параллелограмма равны 10 и
9. Из одной вершины на две стороны опустили высоты, как показано на рисунке.
Длина большей из высот равна 6. Найдите длину другой высоты.

Учитель: (спрашивает ученика устно) Как будешь
решать данную задачу? Обрати внимание что дано.
Ученик: Даны стороны параллелограмма, так же
дана высота, нужно найти высоту.
Учитель: При нахождении чего используется высота
параллелограмма?
Ученик: При нахождении площади.
Учитель: Чему равна площадь данного
параллелограмма?
Ученик: Произведению основания равного девяти и
высоты равной шести и будет равно 54. Можем найти другую высоту, она будет
равна 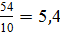 .
.
Учитель: Правильно, решим следующую задачу
(вызывает ученика к доске)
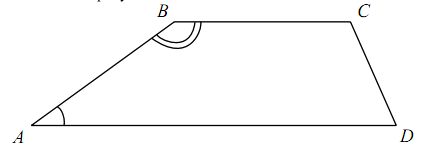
Задача 3: Угол В трапеции ABCD в четыре раза
больше угла А. Найдите угол В. Ответ дайте в градусах.
Учитель: Какие будут предложения по решению
данной задачи?
Ученик: Может обозначим угол А через х и найдем
угол В. Пусть х - угол А, В=4х, тогда  ,
то есть х+4х=1800, 5х=1800, х=360.
,
то есть х+4х=1800, 5х=1800, х=360. 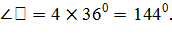
Учитель: Правильно, решим следующую задачу
(вызывает следующего ученика).
Задача 4: Основания трапеции равны 4 см и 9 см,
а диагонали равны 5 см и 12 см. Найти площадь трапеции и угол между её
диагоналями.
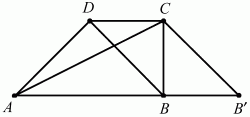
Учитель: Данную задачу можно решить с помощью
дополнительного построения, проведем из вершины С прямую параллельную DB до
пересечения с лучом АВ.
Ученик: Пусть ABCD - данная трапеция, CD = 4 см,
АВ = 9 см, BD = 5 см и АС = 12 см. Чтобы известные элементы включить в один
треугольник, перенесём диагональ BD на вектор DC в положение СВ'. Рассмотрим
треугольник АСВ'. Так как ВВ'CD - параллелограмм, то В'С = 5 см, АВ' = АВ + ВВ'
= АВ + CD = 13 см.
Учитель: Теперь известны все три стороны
треугольника АВ'С.
Ученик: Так как АС2+ В'С2= (АВ')2= 52+ 122= 132,
то треугольник АВ'С - прямоугольный, причем 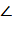 АСВ'
= 90°. Отсюда непосредственно следует, что угол между диагоналями трапеции,
равный углу АСВ', составляет 90°.
АСВ'
= 90°. Отсюда непосредственно следует, что угол между диагоналями трапеции,
равный углу АСВ', составляет 90°.
Учитель: Чему равна площадь трапеции?
Ученик: Площадь трапеции, как и всякого
четырёхугольника, равна половине произведения диагоналей на синус угла между
ними. Отсюда площадь равна 1/2AC * BD * sin 90° = 1/2 * 12 * 5 * 1 = 30  .
.
Ответ: 30  ,
90°.
,
90°.
Учитель: Данную задачу решили с помощью
дополнительного построения, что помогло наиболее легко ее решить. . Рефлексивно
- оценочный этап
Учитель: Запишите домашнее задание: Д/з. В
квадрате со стороной 6 найдите: 1) диагональ; 2) радиус описанной окружности;
3) площадь описанного круга; На следующем занятии будем решать более сложные
задачи представленные во второй части модуля «Геометрия». И так что вы сегодня
на уроке повторили?
Ученики: Основные определения связанные с
понятием четырехугольника,
Нахождение площади трапеции, высоту
параллелограмма, углы в трапеции.
Учитель: Спасибо за внимание, урок окончен.
Урок 4 по теме: «Решение планиметрических задач
по теме четырехугольник».
Тема урока: Решение планиметрических задач на
понятие четырехугольника.
Класс: 9
Учебная задача: совместно с учащимися
рассмотреть решение основных планиметрических задач: нахождение площади
четырехугольника, нахождение элементов четырехугольника.
Диагностируемые цели урока:
В результате ученик:
Умеет решать основные планиметрические задачи;
Умеет находить элементы четырехугольника,
площадь четырехугольника;
Знает, как применять полученные знания при
решении планиметрических задач.
Инструменты: доска, маркеры, линейка,
треугольник.
Ход урока:
I. Мотивационно-ориентировочный этап.
Актуализация.
Мотивация.
Постановка учебной задачи..
Операционно-познавательный этап.
Решение задач
III. Рефлексивно-оценочный этап.
Домашнее задание
Подведение итогов.. Мотивационно-ориентировочный
этап.
Ученики: Да, она простая.
Учитель: (проверяет в тетрадях наличие Д/з) Чем
вы пользовались при решении данной задачи?
Ученики: Теоремой Пифагора, радиусом описанной
окружности, площадью описанного круга.
Учитель: На прошлом уроке повторили задачи
наиболее простые, сегодня повторим решение более сложных, запишите тему урока:
«Решение планиметрических задач по теме четырехугольник»..
Операционно-познавательный этап.
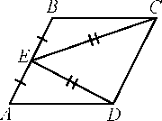
Задача 1: В параллелограмме ABCD точка E -
середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм -
прямоугольник.
Учитель: Какая фигура называется
параллелограммом? (спрашивает ученика)
Ученик: Параллелограмм - это четырёхугольник, у
которого противоположные стороны попарно параллельны, то есть лежат на
параллельных прямых.
Учитель: Какой параллелограмм называется
прямоугольником?
Ученик: Прямоугольник - параллелограмм, у
которого все углы прямые (равны 90 градусам).
Учитель: Выйди к доске и докажи.
Ученик: Треугольники BEC и AED равны по трём
сторонам.
Значит, углы CBE и DAE равны. Так как их сумма
равна 180°, то углы равны 90°. Такой параллелограмм - прямоугольник.
Учитель: Правильно, за такое решение на экзамене
можно получить за данную задачу 3 балла. Решим следующую задачу.
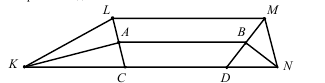
Задача: Основания трапеции равны 6 и 10, а
боковые стороны равны 2 и 4. Биссектрисы углов при одной боковой стороне
пересекаются в точке А, а при другой - в точке В. Найдите АВ.
Учитель: В первую очередь нужно правильно
начертить чертеж и обозначить что нам дано (вызывает ученика к доске).
Ученик: Пусть LC - биссектриса угла KLM трапеции
KLMN с основаниями KN и LN, KN = 10, LM = 6, KL = 4, MN = 2.
Учитель: Что из рисунка видно?
Ученик: Треугольник KLC равнобедренный с
основанием LC. В нем КА - высота, биссектриса и медиана. Аналогично, пусть MD -
биссектриса угла LMN. Тогда NB - высота, биссектриса и медиана треугольника
MND.
Учитель: Что получаем в итоге?
Ученик: Получаем: КС = LК = 4; МN = ND = 2,
поэтому CD = KN - (KC + ND) = 10 - 6 = 4.
Учитель: Чем является отрезок АВ?
Ученик: В трапеции СLМD отрезок АВ - средняя
линия. СD = 4, LМ = 6, поэтому АВ = 5.
Учитель: Правильно, всем ли были понятны
рассуждения (обращается к ученикам) решим еще одну интересную задачу.
Задача №3. Диагонали АС и BD трапеции АВСD
пересекаются в точке О. Площади треугольников AOD и ВОС равны соответственно 16
см2 и 9 см2. Найдите площадь трапеции.
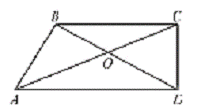
Учитель: (вызывает ученика к доске) Данная
задача решается методом площадей, в первую очередь нужно обратить внимание на
треугольники AOD и ВОС, что про них известно и какой вывод можно сделать?
Ученик: Так как SAOD ≠ SBOC, поэтому АD и
ВС являются не боковыми сторонами, а основаниями трапеции.
Учитель: Какими являются данные треугольники?
Ученик: Треугольники АОD и ВОС подобны по двум
углам.
Учитель: Чему будет равно отношение площадей
данных треугольников?
Ученик: Отношение их площадей равно квадрату
коэффициента подобия k. Поэтому k =  .
.
Учитель: Что видно из треугольников АВО и СВО?
Учитель: Аналогичные задания встречаются в ГИА
которые нужно уметь решать.. Рефлексивно - оценочный этап
Учитель: Запишите домашнее задание: Повторить
все основные определения связанные с понятием окружность, так же решите задачу:
К окружности с центром в точке О проведены касательная АВ и секущая АО. Найдите
радиус окружности, если АВ = 12 см. АО = 13 см. И так что вы сегодня на уроке
повторили?
Ученики: Приемы решения более сложных задач.
Учитель: Все ли было понятно из сегодняшнего
урока?
Ученики: Да.
Учитель: Спасибо за внимание, урок окончен.
Урок 5 по теме: «Решение планиметрических задач
по теме окружность».
Тема урока: Решение планиметрических задач на
понятие окружности.
Класс: 9
Учебная задача: совместно с учащимися
рассмотреть решение основных планиметрических задач: на нахождение острого угла
окружности, нахождение радиуса окружности, на доказательство.
Диагностируемые цели урока:
В результате ученик:
Умеет решать основные планиметрические задачи;
Умеет находить элементы окружности;
Знает, как применять полученные знания при
решении планиметрических задач.
Инструменты: доска, маркеры, линейка,
треугольник.
Ход урока:
I. Мотивационно-ориентировочный этап.
. Актуализация.
2. Мотивация.
Постановка учебной задачи.
Операционно-познавательный этап.
Повторение теории
Решение задач.
Рефлексивно-оценочный этап.
Подведение итогов.. Мотивационно-ориентировочный
этап.
Учитель: Здравствуйте, ребята, садитесь. На
предыдущих занятиях вы повторили основные понятия и методы решения
планиметрических задач на понятие четырехугольника. Вам на дом была предложена
задача, все ли ее решили?
Ученики: Да, она несложная, похожие задачи
встречаются в ГИА в первой части.
Учитель: Чем вы пользовались при решении данной
задачи?
Ученики: Теоремой Пифагора, определение радиуса
окружности.
Учитель: Все ли задания в ГИА связанные с
понятием окружности так просто решаются?
Ученики: Нет, встречаются задачи которые
непонятно как решать.
Учитель: Что нужно сделать что бы было понятно
как решать задачи данного типа?
Ученики: Необходимо повторить основные приемы
решения планиметрических задач на понятие окружности.
Учитель: Целью нашего сегодняшнего занятий будет
рассмотреть основные типы планиметрических задач, на понятие окружность. Тема
нашего урока: «Решение планиметрических задач по теме окружность».
II. Операционно-познавательный этап.
Учитель: Что такое окружность?
Ученик: Окружность - геометрическое место точек
плоскости, удалённых от некоторой точки - центра окружности - на заданное
расстояние, называемое радиусом окружности.
Учитель: Какая прямая называется касательной к
окружности?
Ученики: Прямая, имеющая с окружностью ровно
одну общую точку, называется касательной к окружности, а их общая точка
называется точкой касания прямой и окружности.
Учитель: Какой угол называется центральным?
Ученики: Центральный угол - угол с вершиной в
центре окружности. Центральный угол равен градусной мере дуги, на которую
опирается.
Учитель: Какой угол называется вписанным в
окружность?
Ученики: Вписанный угол - угол, вершина которого
лежит на окружности, а стороны пересекают эту окружность. Вписанный угол равен
половине градусной меры дуги, на которую опирается.
Учитель: Какая окружность называется вписанной в
треугольник?
Ученики: Окружность называется вписанной в
треугольник, если она касается через все его сторон.
Учитель: Какая окружность называется описанной
около треугольника?
Ученики: Окружность называется описанной около
треугольника, если она проходит через три его вершины.
Учитель: Решим некоторые задачи на понятие
окружности.
Задача 1: Чему равен острый вписанный угол,
опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.
Учитель: (вызывает ученика к доске) Начни
решение с чертежа.
Ученик: (чертит чертеж, в водит обозначения)
Рассмотрим треугольник AOB. Он равносторонний,
так как AO = OB = AB = R.
Учитель: Правильно, решим следующую задачу.
Задача 2. Центральный угол на 360 больше острого
вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол.
Ответ дайте в градусах.
Учитель: (вызывает ученика к доске) На первый
взгляд задача кажется сложнее предыдущей, но на самом деле решается в одно
действие.
Учитель: Теперь решим задачу более сложную.
Задача 3. Основание АС равнобедренного
треугольника АВС равно 12. Окружность радиуса 8 с центром вне этого треугольника
касается продолжений боковых сторон треугольника и касается основания АС.
Найдите радиус окружности, вписанной в треугольник АВС.
Учитель: В данной задаче главное правильно
начертить чертеж.
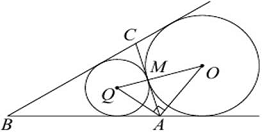
Ученик: Пусть О - центр данной
окружности, а Q - центр окружности, вписанной в треугольник АВС.
Точка касания М окружностей делит АС
пополам.
Учитель: Чертеж наглядно показывает
что еще дано в задаче.
Ученик: АО и АQ - биссектрисы
смежных углов, значит, угол QАО прямой.
Учитель: Что можно найти из данного
прямоугольного треугольника?
Ученик: Из прямоугольного
треугольника QАО получаем AM2 = QM OM Следовательно, QM =
OM Следовательно, QM = 
Учитель: Данная задача относится ко
второй части ГИА, в ней главное правильно начертить чертеж и увидеть, что дано
и что можно найти.
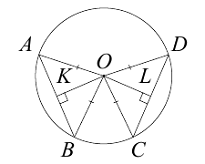
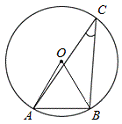
Задача 4. В окружности с центром О
проведены две равные хорды АВ и СО. На эти хорды опущены перпендикуляры ОК и OL
соответственно. Докажите, что ОК и OL равны.


Учитель: Данная задача легко
доказывается с помощью дополнительного построения.
Ученик: Проведём радиусы ОА, ОВ, ОС,
ОD.
Треугольники АОВ и СОD равны по трём
сторонам. ОК и ОL - их высоты, проведённые к равным сторонам, следовательно,
они равны как соответственные элементы равных треугольников.
Учитель: Такие задачи на понятие
окружности наиболее часто встречаются в ГИА, поэтому умение их решать
способствует наиболее удачной сдаче экзамена.. Рефлексивно - оценочный этап
Учитель: Запишите домашнее задание:
Посмотрите еще раз все записи в ваших тетрадях с предыдущих занятии связанных с
повторением планиметрии и с сегодняшнего, то что мы с вами повторили поможет
вам наиболее успешно написать модуль «Геометрия» по математике. И так что вы
сегодня на уроке повторили?
Ученики: Основные определения
связанные с понятием окружность, нахождение элементов окружности.
Учитель: На протяжении 5 уроков в
целом задачи на какие понятия рассмотрели?
Ученики: На понятие треугольника, на
понятие четырехугольника, на понятие окружности.
Учитель: Все ли было понятно?
Ученики: Да.
Учитель: Спасибо за внимание, урок
окончен.
Вывод ко второй главе
Практика помогает наиболее
углубленно изучить проблему итогового повторения планиметрии. По уровню
учеников можно выявить кто что помнит, так же можно выявить каких учеников как
готовить к ГИА, более слабых готовить на уровне понятия, а более сильных на
уровне системы понятий.
Так же практика показывает, что
ученики наиболее запоминают материал при блочно - модульном повторении, при
рассмотрении понятия треугольника они акцентируют внимание только на понятия
связанные с ним, при четырехугольнике и окружности аналогично. Решение задач от
более простых к более сложным также способствует наилучшей сдаче экзамена, так
как более слабые ученики повторив задания более легкие, могут решить их на
экзамене, ученики более сильные повторив более легкие обязаны их решить на
экзамене и повторив более сложные могут с большей вероятностью сдать экзамен на
положительную отметку.
Заключение
Данное исследование проводилось с
целью изучить возможности организации повторения в курсе планиметрии в 9 классе
для подготовки к ГИА. Основные задачи, которые ставились перед началом
исследования, были выполнены в процессе написания работы.
Определены основные требования к
организации повторения. В работе рассмотрены основные методы решения
планиметрических задач, также специальные методы.
Выявлены основные формы и методы
повторения, которые способствуют повышению интереса и активности учащихся при
повторении.
Разработанное планирование к
подготовке уроков повторения позволяет устранить существующие недостатки в
организации и методике проведения повторения.
Гипотеза, выдвинутая в начале работы
подтвердилась в ходе проведения исследования.
Список литературы
Баврин
И. И. Геометрия. 9 класс. - М.: Дрофа, 2011.
Геометрия.
7 - 9 классы. Учеб. для общеобразоват. учреждении / [Атанасян Л.С. и др.] 20-е
изд. - М.: Просвещение, 2010. - 384 с.
Геометрия.
7 - 9 классы: учеб. для общеобразоват. учреждении / А.В. Погорелов. - 10 - е
изд. - М.: Просвещение, 2009 - 224 с.
Гордин
Р.К. Геометрия. Планиметрия. 7 - 9 классы. - 3 - е изд., испр. - М.: МЦНМО,
2006. - 416 с.: ил.
ГИА
2013. Математика. Семенов А.В., Трепалин А.С., Ященко И.В. и др. М.: 2013 - 88
с.
ГИА.
Математика. 9 класс. Практикум по выполнению типовых тестовых заданий. Реальные
тесты. Лаппо Л.Д., Попов М.А. М.: 2013 - 80 с.
Далингер
В. А. Методические рекомендации к проведению обобщающего повторения //
Математика в школе. - 1986. - №2
Капленко
Э.Ф. Новый метод решения планиметрических задач: Пособие для учителей и
учащихся. - Воронеж: ВГПУ, 1998.
Кузнецова
Л.И., Кириллова С.В., Огурцова О.К. Элементарная математика: геометрические
фигуры и их свойства в задачах на доказательство и вычисление: Учебно -
методическое пособие для студентов факультета математики, информатики и физики.
Н. Новгород: НГПУ, 2011. 71с.
Кузнецова
В.К. Подготовка к ГИА по математике в 9-м классе //Справочник заместителя
директора школы, 2011, №4.- с. 52-57.
Математика:
ГИА: Учебно-справочные материалы для 9 класс / Л. В. Кузнецова, С. Б. Суворова,
В. А. Булычёв, Е. А. Бунимович, Л. О. Рослова, Н. X. Агаханов. - М.; СПб.:
Просвещение, 2012.
Мищенко
Т. М. Заключительное повторение курса планиметрии. // Математика в школе. -
2001. - №2.