Программная реализация решения обратной задачи методом наименьших квадратов

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Институт недропользования

Кафедра технологий геологической разведки

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовой работе по дисциплине

Решение обратных задач в геофизике

Программная реализация решения обратной задачи методом наименьших квадратов

Выполнил студент группы ГИС -10

Н.Б. Намдаков

Нормоконтроль

Е.В. Агеенков

Иркутск 2014 г.

Введение

В связи с ростом населения Земли, всё острее стоит вопрос нехватки ресурсов. Поэтому методология их поиска очень актуальна. Для осуществления геофизической разведки, особенную важность имеет решение обратных задач.

Обратная задача - тип задач, часто возникающий во многих разделах науки когда значения параметров модели должны быть получены из наблюдаемых данных.

Для того, чтобы получить представления о свойствах объекта, необходимо создать его модель.

Модель будет включать в себя следующие параметры: глубины границ раздела слоев и свойства пород в каждом слое. Используя математические зависимости между элементами модели и полем, мы можем вычислить теоретические значения поля для заданных условий его наблюдения.

Процесс перехода от модели к полю называют решением прямой задачи. Переход от значения поля к параметрам модели среды - решением обратной задачи. Одним из простейших вариантов решения обратной задачи является подбор такой модели, которая дала бы теоретическое поле, совпадающее или близкое к наблюдаемому.

Прямая задача, как правило, имеет единственное решение. Заданной модели при заданных условиях наблюдения соответствует единственное поле. В обратной задаче - одному и тому же полю может соответствовать множество моделей. Поэтому при решении задач возникает вопрос: какой ответ мы получили единственный или один их множества и какой из множества ответов наиболее близок к реальному. Прямые задачи являются, как правило, устойчивыми. Обратные задачи очень часто оказываются неустойчивыми, т.е. небольшие искажения в данных наблюдений могут приводить к значительным погрешностям в параметрах модели.

1. Теоретическая часть

.1 Программные средства

Наиболее удобной, в смысле программной реализации, средой программирования является Delphi. Среда визуального программирования Delphi, разработанный компанией Borland. Среда Delphi включает в себя полный набор визуальных инструментов для скоростной разработки приложений, поддерживающий разработку пользовательского интерфейса и подключение к корпоративным базам данных. VCL - библиотека визуальных компонент, включает в себя стандартные объекты построения пользовательского интерфейса, объекты управления данными, графические объекты, объекты мультимедиа, диалоги и объекты управления файлами, управление DDE и OLE.

Среда Delphi является очень удобной при решении различного рода задач, так как позволяет находить коэффициенты аппроксимирующих полиномов (многочленов) для табулированной функции, и создать удобный для пользователя интерфейс. Поэтому эта среда разработки широко используется как на производстве, так и в учебных заведениях и научных учреждениях.

.2 Физическая модель

Апроксимация функций методом наименьших квадратов

При решении многих практических задач часто приходится вычислять значения каких-то функциональных зависимостей y = f(x).

При этом, как правило, имеют преобладающее место две ситуации.

1. Явная зависимость между х и y на [a, b] отсутствует, а имеется только таблица экспериментальных данных {x_i, y_i}, 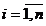 и возникает необходимость определения y = f(x) на интервале [x_i, x_i/2] Î [a, b]. К этой задаче относится также уточнение таблиц экспериментальных данных.

. Зависимость y = f(x) известна и непрерывна, но настолько сложна, что не пригодна для практических расчетов. Стоит задача упрощения вычисления значений y = f(x) и ее характеристик (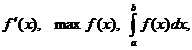и т.д.). Поэтому, с точки зрения экономии времени и материальных ресурсов, приходят к необходимости построения какой-то другой функциональной зависимости y = F(x), которая была бы близка к f(x) по основным ее параметрам, но более проста и удобна в реализации при последующих расчетах, т.е. ставится задача о приближении (аппроксимации) в области определения y = f(x). Функцию y = F(x) называют аппроксимирующей.

Аппроксимация является частным случаем интерполирования и применяется для определения аналитического вида функции, заданной таблично. Задача аппроксимации сводится к определению свободного параметра (параметров) функции заданного вида, который обеспечит наилучшее приближение функции, заданной таблично модельной аналитической функцией.

Метод наименьших квадратов

Пусть таблично задана функция 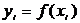. Определить аппроксимационный многочлен вида:

(1)

Для определения коэффициентов  (где i=1,2…m) используют аппроксимацию методом наименьших квадратов [3]. Функционал находится по формуле

,

где n - количество пар значений аргумента x_i и функции y_i. Т.к. S должен быть минимален, то первые частные производные от S по всем коэффициентам полинома должны равняться нулю.

Вычислим их и приравняем к нулю:

 (1)

После преобразования система слегка упростится:

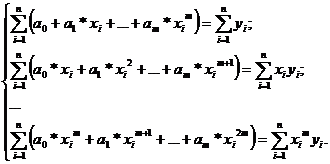 (2)

Если полином первой степени, то 2 уравнения, если шестой степени, то 7 уравнений. Введём следующие обозначения:

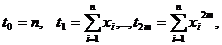
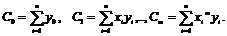
С учётом этих обозначений система (2) перепишется следующим образом:

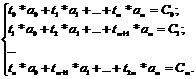(3)

Решив эту систему одним из известных методов определится ряд значений 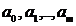, с помощью которого и строится многочлен (1).

Среднеквадратичное отклонение вычисляется по формуле:

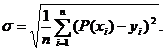
1.3 Алгоритм решения

аппроксимация квадрат программирование полином

1. Вводим исходные данные Xi и Yi из файла.

.Вычисляем коэффициенты Т [ссылка на теорию по методу], где

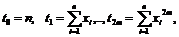
. Вычисляем коэффициенты С, где

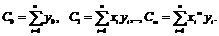
4. Формируем расширенную матрицу системы уравнений, т.е. из системы:

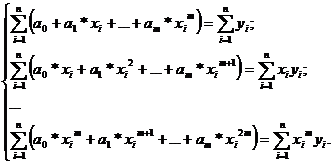
с учетом введённых обозначений получаем систему:

..Приводим расширенную матрицу системы уравнений к треугольному виду (прямой ход метода Гаусса).

.Вычисляем коэффициенты полинома (обратный ход метода Гаусса).

.Выводим коэффициенты полинома (в зависимости от степени полинома используем массивы соответствующей размерности и присваиваем элементам значения, полученные после решения системы методом Гаусса).

. Вычисляем среднеквадратичное отклонение, для этого вычисляем значение функции с помощью полученного полинома, затем вычисляем сумму квадратов разностей экспериментального значения функции и рассчитанного с помощью полинома и окончательное вычисляем среднеквадратичное отклонение. Выводим среднеквадратичное отклонение.

1.4 Блок-схема

2. Практическая часть

.1 Решение задачи в Delphi

В программе будут два интерфейса (окна). Первый, или главная форма, предназначен для ввода данных, расчета коэффициентов. Вторая форма или подчиненная, будет служить для отображения графиков, вычисляемой нами обратной задачи.

На форме у нас 3 компоненты: TMemo, и 4 компоненты TButton (рис. 1).

Рис.1. Главная форма

Заходим в инспектор объектов компонента TButton1, на свойстве Caption пишем: "Загрузить данные". Таким же образом меняем свойство Caption на "Выполнить", "График" и "Выход" соответственно.

Создаем вторую форму. Кидаем на форму компоненты: TPanel, TChart и TButton. Главная рабочая компонента это TChart, в основном работаем с ней. Щелкните два раза, откроется следующее диалоговое окно (рис. 2).

Рис. 2. Компонента TChart

Далее нажимаем на кнопку "Add..." создаем новые линии. В данной задаче у нас 4 линии: полиномы 3-ей, 5-ой и 7-ой степени, а также исходные данные. Исходные данные необходимы для сравнения, сильно ли исказился наш график.

Дальше пишем процедуру программы [Приложения].

2.2 Графическое представление результатов

Нахождение коэффициентов аппроксимирующих полиномов 3-ей, 5-ой и 7-ой степени (рис. 3).

Рис. 3. Выполнение программы

Графическое представление нахождения коэффициентов аппроксимирующих полиномов (рис. 4).

Рис. 4. График функции полиномов и исходных данных

Заключение

В результате курсовой работы был разработан алгоритм аппроксимации данных методом наименьших квадратов. Для полинома каждой степени было рассчитано среднеквадратичное отклонение. Установлено, что чем больше степень полинома, тем ближе значения аппроксимирующей функции к значениям заданным таблично.

С помощью данного алгоритма можно вычислить коэффициенты аппроксимирующего полинома и другой степени (не меньшей 1 и не большей 8) при другом количестве экспериментальных точек.

Использованная литература

1. Delphi для «чайников». Нейл Дж. Рубенкинг. Киев - Москва: Диалектика, 1997.

2. <http://www.delphi-manual.ru/>

. Метод наименьших квадратов (МНК) 2010г. - (<http://www.cleverstudents.ru/articles/mnk.html>)

. Аппроксимация функции полиномом методом наименьших квадратов - (<http://alexeypetrov.narod.ru/C/sqr_less_about.html>)

Приложение

Unit1;, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,,StdCtrls,Series, TeEngine, TeeProcs, Chart, ExtCtrls,buttons, Math, Unit2;= class(TForm): TMemo;: TMemo;: TButton;: TMemo;: TButton;: TButton;: TButton;: TLabel;: TLabel;Button1Click(Sender: TObject);Button2Click(Sender: TObject);Button3Click(Sender: TObject);FormCreate(Sender: TObject);Button4Click(Sender: TObject);

{ Private declarations }

{ Public declarations };: TForm1;: array [0.. 8] of extended;: array [0.. 8] of extended;: array [0.. 8] of extended;: array [0.. 39] of extended;: array [0.. 39] of extended;

{$R *.dfm}Polynom(n, m: integer);: array [0.. 16] of extended;, A: array [0.. 8] of extended;: array [0.. 8, 0.. 9] of extended;, DataY: text;, StrYi: string;, ii, j, jj, k, s, Code: integer;, Yi, Y, Bik, Delta: extended;:= 0;i := 0 to 16 do[i] := 0;i := 0 to 8 do[i] := 0;[i] := 0;i := 0 to 8 doj := 0 to 9 do[i, j] := 0;(DataX, 'Xi.txt');(DataY, 'Yi.txt');(DataX);(DataY);i := 1 to m do(DataX, StrXi);(DataY, StrYi);(StrXi, Xi, Code);(StrYi, Yi, Code);[ii] := Xi;[ii]:= Yi;:= ii + 1;j := 1 to 2 * n do[j] := T[j] + exp(j * ln(Xi));j := 0 to n do[j] := C[j] + Yi * exp(j * ln(Xi));;[0] := m;(DataX);(DataY);i := 0 to n doj := 0 to n do[i, j] := T[j + i];i := 0 to n do[i, n + 1] := C[i];k := 0 to n - 1 doi := k to n do:= B[i, k];j := k to n + 1 doi = k then[i, j] := B[i, j] / Bik[i, j] := B[i, j] / Bik - B[k, j];;.Memo3.Lines.Add('Коэффициенты полинома степени: ' + IntToStr(n));i := n downto 0 do[i] := (B[i, n + 1] - B[i, 1] * A[1] - B[i, 2] * A[2] - B[i, 3] * A[3] - B

[i, 4] * A[4] - B[i, 5] * A[5] - B[i, 6] * A[6] - B[i, 7] * A[7] - B

[i, 8] * A[8]) / B[i, i];i := 0 to n do(n = 3) then[i] := A[i]if (n = 5) then[i] := A[i][i] := A[i];.Memo3.Lines.Add('A[' + IntToStr(i) + ']=' + FloatToStr(A[i]));

end;.Memo3.Lines.Add('Среднеквадратичное отклонение:');

reset(DataX);(DataY);:= 0;i := 1 to m do(DataX, StrXi);(DataY, StrYi);(StrXi, Xi, Code);(StrYi, Yi, Code);:= 0;j := 0 to n do:= Y + A[j] * exp(j * ln(Xi));:= Delta + sqr(Y - Yi);;:= sqrt(Delta / m);.Memo3.Lines.Add('Дельта = ' + FloatToStr(Delta));(DataX);(DataY);;TForm1.Button1Click(Sender: TObject);.Enabled := true;.Lines.LoadFromFile('Xi.txt');.Lines.LoadFromFile('Yi.txt');;TForm1.Button2Click(Sender: TObject);(3, 40);(5, 40);(7, 40);.Enabled := true;;TForm1.Button3Click(Sender: TObject);i:integer;.Show;i := 0 to 39 do.Series1.AddXY(x[i], (p3[0] + p3[1] * x[i] + p3[2] * sqr(x[i])

+ p3[3] * power(x[i], 3)));.Series2.AddXY(x[i], (p5[0] + p5[1] * x[i] + p5[2] * sqr(x[i])

+ p5[3] * power(x[i], 3) + p5[4] * power(x[i], 4)

+ p5[5] * power(x[i], 5)));.Series3.AddXY(x[i], (p7[0] + p7[1] * x[i] + p7[2] * sqr(x[i])

+ p7[3] * power(x[i], 3) + p7[4] * power(x[i], 4)

+ p7[5] * power(x[i], 5) + p7[6] * power(x[i], 6)

+ p7[7] * power(x[i], 7)));.Series4.AddXY(x[i],f[i]);;;TForm1.FormCreate(Sender: TObject);.Clear;.Clear;.Clear;.Enabled := false;.Enabled := false;;TForm1.Button4Click(Sender: TObject);;;.Unit2;, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,,StdCtrls,Series, TeEngine, TeeProcs, Chart, ExtCtrls,buttons, Math;= class(TForm): TPanel;: TChart;: TLineSeries;: TLineSeries;: TPointSeries;: TLineSeries;: TButton;Button1Click(Sender: TObject);

{ Private declarations }

{ Public declarations };: TForm2;

{$R *.dfm}TForm2.Button1Click(Sender: TObject);.Close;;.