Программирование игр и головоломок

МИНОБРНАУКИ РОССИИ

Орский гуманитарно-технологический институт (филиал) федерального государственного бюджетного образовательного учреждения высшего профессионального образования

«Оренбургский государственный университет»

Экономический факультет

Кафедра прикладной информатики в экономике

КУРСОВАЯ РАБОТА

по дисциплине: «Интеллектуальные информационные системы»

Программирование игр и головоломок

Руководитель М.А. Жук

Исполнитель А.И. Петров

Орск 2014

Аннотация

Курсовая работа по дисциплине «Интеллектуальные информационные системы» на тему «Программирование игр и головоломок» состоит из двух частей.

В первой главе рассмотрены основы математической теории игр, показаны возможные представления игр и их классификация.

Во второй главе показана практическая реализация логической игры с выигрышной стратегией средствами языка программирования С++.

Содержание

Введение

. Основы математической теории игр

.1 Теория игр как раздел теории принятия решений

.2 Бесконечные и конечные игры

.3 Антагонистические игры

.4 Позиционные игры

.5 Кооперативные и некооперативные игры

. Реализация логической игры

.1 Обоснование программных средств реализации

.2 Описание выигрышной стратегии логической игры

.3 Описание интерфейса программы и результатов тестирования

Заключение

Список использованных источников

Приложение

Введение

Издавна люди сталкивались с проблемой принятия решений в тех или иных ситуациях. При этом естественно стремление к таким решениям, которые приводят к наилучшим результатам. Такой выбор принято называть оптимальным.

Говоря о факторах, обуславливающих правильность принятия того или иного решения, следует выделить две основные группы - объективные и субъективные факторы.

К объективным факторам, в первую очередь, относятся:

˗        исходные данные, использующиеся при принятии решения;

˗        модели, методы и алгоритмы принятия решений;

˗        условия, при которых происходит принятие решений, и требования, предъявляемые к принимаемым решениям;

˗        имеющиеся базы данных, знаний для данной области принятия решений;

˗        применяемые средства автоматизации принятия решения.

К субъективным факторам следует отнести:

˗        возраст, пол, общее физическое состояние человека;

˗        тип характера человека-оператора;

˗        психоэмоциональное состояние человека в данной ситуации при принятии решения;

˗        условия работы;

По мере развития общественно-экономических отношений усложнялись поставленные задачи, которые для своего решения требовали разработки новых методов вычислений. На смену простейшим арифметическим и геометрическим вычислениям пришли алгебраические и тригонометрические вычисления. Организация современного производства требует не только наличия современных станков и оборудования, но и разработки новых технологических процессов и современных методов управления производством. Для решения каждой из поставленных задач разрабатываются математические модели, анализируя которые удается найти наилучшее решение поставленной задачи. Создание математической модели - сложная кропотливая работа, которая в современных условиях под силу коллективам разработчиков. Для создания математической модели одного и того же объекта различные коллективы могут использовать различный математический аппарат. После создания математической модели специалистами-аналитиками за дело принимаются специалисты-программисты, которые реализуют созданную модель в виде программных кодов. Далее с математической моделью работают специалисты-практики. Целенаправленно воздействуя на модель, они изучают ее поведение и подбирают оптимальный режим работы для реального объекта. Одной из таких моделей является игровая модель и поиск стратегий поведений в условиях полной или частичной неопределенности. В очень редких (исключительных) случаях для игровых моделей можно определить количественную оценку или указать оптимальное решение. В игровых моделях не ставится задача найти какое-то числовое решение, а требуется лишь или очертить область возможных решений, или предоставить некоторые дополнительные сведения о возможном развитии событий и рекомендовать правила поведения.

1. Основы математической теории игр

1.1     Теория игр как раздел теории принятия решений

Теория игр как раздел математики возникла сравнительно недавно. Она связана с такими концептуальными понятиями как принятие решений, исследование операций, конфликт, принцип оптимальности и т. д. Принятие решений - это достаточно широкое понятие. С точки зрения математического описания под принятием решения понимается выбор из некоторого множества U элемента u. При этом определяется правило выбора u ∈ U и целесообразность выбора.

Математическая теория принятия оптимальных (рациональных, целенаправленных) решений называется теорией исследования операций. Таким образом, задачей теории исследования операций является построение количественных методов анализа процессов принятия решений во всех областях человеческой деятельности. Эта деятельность должна быть, во-первых, целенаправленна, т. е. направлена на достижение определенной цели или целей, и, во-вторых, при предварительном анализе целесообразности должны быть использованы количественные методы, т. е. формализованные (математические) модели.

Совокупность целенаправленных действий, т. е. действий, направленных на достижение некоторых целей, называется операцией. Термины "операция", "исследование операций" впервые были введены при формализованном анализе военных операций. В настоящее время круг задач, входящих в теорию исследования операций, значительно расширен. Однако введенная ранее терминология устоялась и сохранилась.

При анализе операции следует ввести понятия оперирующей стороны и исследователя операций. Оперирующей стороной называется лицо или совокупность лиц, которые стремятся в данной операции к поставленной цели. Общепринятым аналогом оперирующей стороны является лицо, принимающее решение (ЛПР). Исследователь операций проводит исследование в интересах оперирующей стороны. Он преследует ту же цель, но сам, как правило, не принимает окончательного решения, а дает научно-обоснованные рекомендации, т. е. проводит качественный и количественный анализ и обосновывает целесообразность принятия тех или иных решений. Ответственность за принятие решений и окончательный выбор лежит на оперирующей стороне.

Исследователь операций и оперирующая сторона могут иметь различную информацию, так как во время анализа предстоящей операции и ее проведения информация может меняться, поступать в динамике. Кроме того, время для исследований может быть также различно.

Совпадение интересов оперирующей стороны и исследователя операций должно быть основано на хорошо построенном организационно-экономическом механизме, заинтересовывающем исследователя операций поддерживать именно те цели, которые преследует оперирующая сторона.

Рассмотрим простейшую модель исследования операций. Она включает: U - множество значений контролируемых факторов, которые выбираются оперирующей стороной; А - множество значений неконтролируемых факторов α , которые выбираются партнерами по операции или определяются внешней средой ("природой"); функцию g(u,α ), отражающую целенаправленность действий оперирующей стороны (например, стремление к максимизации этой функции водностью описывает интересы оперирующей стороны и, соответственно, исследователя операций).

Примером неконтролируемых факторов, выбираемых целенаправленно партнерами по операции, являются военные действия противника, экономические планы взаимодействующих экономических субъектов и т. п. Если неконтролируемые факторы определяются "природными" условиями, то в этом случае модель исследования операций можно свести к модели взаимодействия с разумным партнером. Действительно, если исследователь операции и оперирующая сторона осторожны, то они считают, что природные факторы "выбираются" природой из условия минимизации целевой функции g.

Конфликтом (конфликтной ситуацией) называется процесс столкновения интересов нескольких участвующих сторон.

Он может быть задан следующими компонентами:

) перечнем субъектов, участвующих в конфликте;

) определением множеств их выборов;

) интересами (мотивами), определяющими выбор.

Кроме того, при моделировании конфликта очень важно описать информационную обстановку, т. е. всю информацию, которая уже имеется у субъектов конфликта и может поступать со временем. Также необходимо учитывать возможность обмена информацией, добывания ее и добровольной передачи информации одним субъектом другому. Математическая модель конфликтной ситуации называется игрой. Таким образом, теория игр - это математическая теория принятия решений в условиях конфликта. Из этого определения следует, что теория игр есть важная часть теории исследования операций, изучающая вопросы принятия решений в конфликтных ситуациях.

Основной задачей игр является не описание, а разрешение конфликтов, т.е. построение компромиссных взаимовыгодных решений, которые полностью или хотя бы частично согласовывают интересы всех взаимодействующих сторон.

Если удается формализовать (смоделировать) конфликт и определить принцип оптимальности, т.е. принцип выбора оптимального решения в игре, то получается математическая задача, которую можно решать математическими методами, без учёта её содержательной постановки.

В теории игр используется разнообразный и хорошо разработанный математический аппарат (теория множеств, теория вероятностей, топология, теория функций, теория дифференциальных уравнений, методы оптимизации, вариационное исчисление, динамическое программирование, оптимальное управление и др.). Однако следует подчеркнуть, что математические модели теории игр (теоретико-игровые модели) имеют свою специфику. Они описывают процесс принятия решений, которые трудно формализовать. Поэтому в рамках теории игр развивается специфический математический аппарат, направленный на моделирование процессов принятия решений в сложных социально-экономических, политических и прочих конфликтах. При этом возникают новые ранее не изученные математические задачи.

Как в любой математической дисциплине, в теории игр прослеживается несвязанное развитие двух направлений:

) "чисто" математическое, определяемое внутренней логикой развития теории игр;

) прикладное, ориентированное на широкий круг практически интересных задач.

Возникновение теории игр и термина "игра" связано с попыткой использовать математику в задачах анализа ситуаций, возникающих в азартных играх, анализа конфликтных ситуаций в военном деле, при принятии решений в условиях неопределенности, поиска компромисса в неантагонистических конфликтах и т.д.

При анализе возможностей приложений теории игр следует обратить внимание на то, что при моделировании конфликтных ситуаций, например процессов принятия решений в сложных социально-экономических системах, трудность вызывает формализация мотивации поведения этой системы.

Сложность практических задач анализа конфликтных ситуаций приводит к необходимости использования современных методов анализа и вычислительной техники. Для решения задач принятия решений оказывается недостаточным ограничиться какой-то одной "универсальной" моделью или даже системой моделей. Необходимо иметь "инструмент" - системный проблемно-ориентированный комплекс, представляющий собой систему (сеть) ЭВМ и математическое обеспечение (система моделей, методов, алгоритмов и программ), ориентированную на решение конкретных классов проблем. Для создания и использования такого мощного инструмента необходимо привлечение коллектива людей различных (далеко не родственных) специальностей: системных аналитиков, специалистов в прикладной области, математиков, программистов и т. д. Фактически построение такого инструмента эквивалентно построению языка общения всех участвующих в работе специалистов и ЛПР.

1.2     Основные понятия и классификация игр

Теория игр занимается исследованием математических моделей принятия оптимальных решений в конфликтных ситуациях. Формальное описание принятия решений удобно разбить на две части:

) математическая модель конфликтной ситуации или игра - описание конфликтной ситуации, включающее в себя описание субъектов, принимающих решения, их возможностей и интересов;

Оптимальность и не оптимальность того или иного исхода конфликта зависит от интересов и возможностей его участников. В этом смысле принцип оптимальности является функцией игры. Можно рассматривать различные принципы оптимальности, но если один из них выбран, то для каждой игры можно однозначно указать множество ее рациональных исходов. Математическая модель конфликта и принцип оптимальности дают полное описание принятия решений в условиях конфликта. Именно в этом смысл они весьма тесно взаимосвязаны. Однако на начальной стадии обучения проще их рассматривать отдельно.

Задать игру можно различными способами. Здесь нам удобно воспользоваться нормальной формой описания игр. Другие способы задания игр будут рассмотрены в последующих главах.

В описании игры можно выделить следующие элементы:

) коалиции действий - совокупность действующих совместно в данной конфликтной ситуации субъектов;

) коалиции интересов - множество одинаково заинтересованных в исходе конфликта сторон;

) множества возможных выборов каждой из коалиций действия;

) описание предпочтений каждой из коалиций интересов;

) множество возможных исходов конфликта.

Появление слова "коалиция" указывает на тот факт, что участниками конфликта могут быть не только отдельные лица, но и большие, сложно организованные группы лиц. Коалиции действия и интересов могут не совпадать. Например, пассажиры самолета бывают заинтересованы в его скорейшем прибытии к месту назначения и, таким образом, образуют коалицию интересов, однако они не могут предпринять никаких действий, направленных на достижение этой цели, т. е. не являются коалицией действия. Если коалиция действия совпадает с коалицией интересов, то такую монолитную коалицию можно считать одним лицом, поэтому ее называют игроком. Если все коалиции действия совпадают с соответствующими коалициями интересов, то игру называют бескоалиционной, а ее участников - игроками.

Множество возможных исходов конфликта определяет совместные ограничения на действия участников конфликта. Если такие ограничения задаются формально (в виде прямого произведения множеств), то соответствующую называют игрой без запрещенных ситуаций, если эти ограничения существенны, то - игрой с запрещенными ситуациями.

Для принятия решений необходимо обладать определенной информацией. При этом как сам выбор из множества стратегий, так и ожидаемый результат зависят в значительной степени от информации, которой обладает игрок к моменту принятия решения: о множествах выбора, мотивах поведения или принципе оптимальности игроков, о природных неопределенных факторах, той информации, которую сейчас игрок не имеет, но которая будет поступать к нему, в том числе та, которой он будет обладать в результате добровольного обмена или ее добывания. Поэтому целесообразно дать общее определена стратегии. 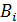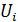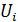Если множество Bi описывает информацию, которую коалиция (игрок) i использует при принятии решений, то под стратегией будем понимать отображение :  → , где  - множество выборов или управлений коалиции действия i. В результате выбора каждой коалиции действия элемента и множества управлений определяется исход конфликта. Соответственно выбор коалициями действия стратегии определяет ситуацию в множестве стратегий

.

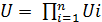Таким образом, можно трактовать множество управлений U как "физические", а множество стратегий U как "физические" и информационные возможности. Заинтересованность j-го субъекта формализуется, как правило, функцией выигрыша, которая определяется отображением : U → R, где U - множество исходов. Выбор стратегии или управления определяется принципом оптимальности.

Таким образом, для описания конфликтной ситуации необходимо задал систему:

логический игра программный интерфейс

Г={N,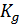,,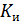{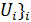∈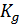,{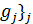∈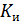, S},

Где N - множество игроков,

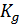 - множество коалиций действия,

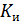 - множество коалиций интересов,

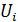 - множество выборов коалиции i∈Kg ,

 - функция выигрыша коалиции j∈Kи ,- множество возможных исходов игры.

Игры, как и все задачи исследования операций бывают статическими и динамическими.

Фиксация параметров, а также различная их суперпозиция позволяют классифицировать игры. Рассмотрим основные классы теоретико-игровых моделей.

В качестве первого классификационного признака возьмем множество игроков. Различают игры 2-х лиц и игры n лиц (n>2). Игры 2-х лиц называются антагонистическими, если игроки преследуют противоположные цели. Если в антагонистической игре игрок 1 стремится максимизировать свой выигрыш g1, то целью игрока 2 является минимизация выигрыша игрока 1, так что g1 = -g2. Поэтому антагонистическую игру можно задать следующим образом:

Г=(U1,U2,g),

где g - выигрыш игрока 1.

Антагонистические игры получаются не только при описании конфликтов типа военных, но и при описании игры с природой, когда исследователь операции или оперирующая сторона проявляет осторожность при принятии решений в условиях неопределенности.

Можно говорить так же о неантагонистических играх 2-х лиц (g1 ≠ -g2).

Другой важный принцип классификации связан с вопросом о допустимости образования тех или иных коалиций. Если в игре образование коалиций недопустимо, то такая игра называется бескоалиционной. Она определяется заданием множества игроков, пространств их стратегий и набором их функций выигрыша.

К бескоалиционным играм могут быть сведены также игры, в которых . В истинно же коалиционных играх разрешены такие коалиции, что . Среди подобных игр наиболее распространены кооперативные игры, в которых образуется одна коалиция. Целью этой коалиции является максимизация суммарного выигрыша, с тем, чтобы впоследствии разделить его между членами коалиции по соглашению.

Отдельный класс составляют игры с бесконечным числом игроков.

Следующим признаком классификации являются стратегии. Если множество стратегий всех игроков конечно, то игра называется конечной. Когда хотя бы одно из множеств 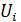, i = 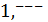n, бесконечно, игра называется бесконечной. Для теоретического анализа более удобны конечные игры, однако они имеют меньшую практическую ценность, чем бесконечные.

Игры можно квалифицировать и в соответствии с формой их задания. При этом различают позиционные игры и игры в нормальной форме. Если процесс принятия решений описывается в виде динамического процесса, где игроки выбирают свои стратегии последовательно по шагам, обладая при этом определенной информацией при каждой шаге выбора стратегии, то такие игры называются позиционными. Классическим примером такой игры являются шахматы. Если в динамических играх конфликт моделируется дифференциальными уравнениями, то такие игры называют дифференциальными. Если же в игре стратегия представлена как одноактный выбор, то такая игра считается заданной в нормальной форме.

Интерес представляют игры с непрерывными функциями выигрышей: классы выпуклых, вогнутых, выпукло-вогнутых игр. Кроме упомянутых классов существует множество их модификаций. С достаточно полной классификацией игр, равно как и с другими важными вопросами теории.

При проведении предварительного анализа конфликта использование исходных множеств управлений 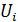 может привести к нежелательному для оперирующей стороны результату: либо решения не существует, либо (если это решение существует) количественная оценка этого решения неудовлетворительна. Тогда целесообразно расширить класс используемых управлений. Расширения класса стратегий можно добиться путем расширения либо области определения функции (информированности игроков), либо за счет расширения множества значений, т. е. физических возможностей. Достаточно традиционным способом расширения множества значений является использование выпуклой оболочки множества управлений путем перехода в пространство вероятностных мер. Исходные элементы множества 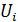 называются чистыми стратегиями, а их произвольная выпуклая комбинация (мера) - смешанной стратегией.

Существует два способа реализации смешанных стратегий:

) введение искусственной рандомизации, т. е. использование функции распределения на исходном множестве управлений;

) введение повторения, т.е. проведения конфликта многократно.

При этом с определенной частотой выбирают некоторые элементы исходного множества. В обоих способах соответствующим образом определяются функции выигрыша.

При расширении класса стратегий прежде всего преследуется задача не построения более сложной модели конфликтной ситуации, адекватно отражающей реальность, а осмысленного и целенаправленного изменения реальности и построения соответственно этой усложненной реальности более сложной модели конфликтной ситуации. При этом следует учитывать и затраты на расширение множества стратегий: проведение повторных операций, увеличение информированности и т. д. Далее эти затраты должны быть соотнесены с тем выигрышем, который можно получить дополнительно за счет расширения класса стратегий.

Наиболее интересная постановка проблемы расширения класса стратегий связана с увеличением информированности игроков. Действительно, чем больше неопределенность, тем больше разброс в ожидаемом результате при реализации выбранной стратегии. Таким образом, оказывается очень выгодно делать ситуацию более определенной. Для этого необходимо четко фиксировать ожидаемую информацию, уметь ее структурировать с целью возможности ее математической записи, оценивать результаты реализации стратегий, построенных в заданной информации, и, наконец, видеть пути увеличения объема информации и оценивать, с одной стороны, ее результат и, с другой стороны, затраты на получение дополнительной информации.

.3 Бесконечные и конечные игры

Существует, по меньшей мере, два типа игр. Один можно назвать конечными играми, а другой - бесконечными.

В конечные игры играют с целью добиться выигрыша, а в бесконечные - для того чтобы продолжать играть.

Конечная игра может быть выиграна кем-либо только тогда, когда она придет к очевидному концу. Заканчивается же она когда кто-либо выиграл.

А узнаем мы о том, что игра кем-то выиграна тогда, когда все игроки согласились кто из них победитель. Никакой другой критерий, кроме как согласие среди игроков о победителе, абсолютно не важен в определении победителя.

Может казаться, что одобрение зрителей или судей также важно для выбора победителя. Однако если сами игроки не определились в своем выборе, это просто означает, что игра еще не закончилась - и игроки еще не достигли изначальной цели игры. Даже если внешние обстоятельства вынудили их покинуть игровое поле и препятствуют продолжению игры, игроки не будут считать игру законченной..

Если игроки, не по своей воле, вынуждены участвовать в игре - это не конечная игра. Никто не может играть по принуждению.

Это неизменный принцип любых игр, конечных или бесконечных, - тот кто играет, играет по своей воле. Тот кто вынужден играть, не в состоянии играть.

Так же как это важно чтобы конечная игра имела выраженное окончание, она должна иметь четко определенное начало. Поэтому о конечных играх можно говорить как о имеющих временные границы - с определением которых, конечно, все игроки должны быть согласны.

Бесконечные игры - идентичны конечным, в одном, и только одном свойстве. Об игроках бесконечных игр мы также можем сказать, что если они играют, то делают это без принуждения; если они вынуждены играть, они не могут играть.

Во всех остальных отношениях, бесконечные и конечные игры представляют собой диаметральные противоположности.

Игроки в бесконечные игры не только не могут сказать, когда началась их игра, но и им это безразлично. А безразлично им это потому, что их игра не ограничена временем. Более того, единственная цель их игры - это предотвратить ее окончание, сделать так чтобы каждый продолжал играть.

В бесконечных играх нет ни пространственных, ни количественных ограничений. Ни один мир не расчерчен границами игрового поля бесконечных игр, и не существует вообще вопроса доступа к игре, так как каждый, кто хочет, может присоединиться к бесконечной игре.

1.4 Антагонистические игры

Антагонистической игрой называется некооперативная игра, в которой участвуют два игрока, выигрыши которых противоположны.

Формально антагонистическая игра может быть представлена тройкой <X, Y, F>, где X и Y - множества стратегий первого и второго игроков, соответственно; F - функция выигрыша первого игрока, ставящая в соответствие каждой паре стратегий (ситуации) (x и y), x X, y Y действительное число, соответствующее полезности первого игрока при реализации данной ситуации. Так как интересы игроков противоположны, функция F одновременно представляет и проигрыш второго игрока.

Исторически антагонистические игры являются первым классом математических моделей теории игр, при помощи которых описывались азартные игры. Считается, что благодаря этому предмету исследования теория игр и получила свое название. В настоящее время антагонистические игры рассматриваются как часть более широкого класса

Игра с нулевой суммой (zero-sum game) - состязание, в котором проигрыш одного игрока равнозначен выигрышу другого. Игры можно разделить на две категории: с нулевой и с ненулевой суммой. Если сумма выигрышей всех игроков остается постоянной при любых вариантах исхода игры, ее относят к категории игр с постоянной суммой. Но поскольку математически выплаты могут быть смещены по шкале, удобнее и нормальнее называть их играми с нулевой суммой. В игре с нулевой суммой при любом варианте ее исхода выигрыш победителя (победителей) всегда равен убытку проигравшего (проигравших). Большинство игр в обычном смысле слова, без избирательного вмешательства извне, являются именно такими играми. К ним принадлежат, в частности, шахматы и футбол (даже если какая-то посторонняя организация присуждает за победу установленную награду). Однако футбольная игра, в которой игрокам платят за то, чтобы они сыграли вничью, или игра в слова (в которой игроки получают очки, составляя слова из случайных разрозненных букв), где награда дается за наибольшую сумму набранных очков, представляют собой примеры игр с нулевой суммой. Такое определение предпочтительнее чем "с положительным результатом" или "с отрицательным результатом". Несмотря на широкое употребление двух последних определений, они обычно создают путаницу, а иногда и оказываются неверными, т.к. не дают точного определения тому, с чем сравнивать положительный результат. В 1944 г. Дж. фон Нейман и О. Моргенштерн выдвинули теорию, согласно которой во всех играх с нулевой суммой и двумя участниками существует особое равновесие, когда каждый участник выбирает стратегию, которая сводит до минимума его потери при любой возможной стратегии противника (см. также: "Минимакс"; "максимин"). Это элегантное математическое построение имеет ограниченное практическое значение, хотя и свидетельствует о существовании оптимальной стратегии игры в шахматы. К счастью, эта стратегия до сих пор не найдена. Игры с нулевой суммой имеют в политике менее формальное значение. Если в игре участвуют два партнера, объединение между ними не возможно; при большем количестве игроков возникают широкие, часто безграничные возможности создания временных коалиций одной части игроков против другой. Поэтому игры с образованием коалиций имеют нулевую сумму. Некоторые авторы причисляют к этой категории и другие политологические игры, например, гонку вооружений или промышленный конфликт. Это неизменно приводит к мрачным прогнозам, поскольку в данных случаях исключается длительное взаимодействие. Игры с ненулевой суммой дают игрокам возможность взаимодействия для получения оптимального результата. Это остается в силе независимо от того, подразумевает игра взаимодействие или нет. Даже в игре без взаимодействия, например в "дилемме заключенных" (prisoners dilemma), игроки имеют возможность размышлять о ходе мыслей противника. В повторяющихся играх без взаимодействия игроки могут координировать свои действия на основе равновесия взаимодействия (более высокого по уровню). Большинство политологических игр, кроме игр с образованием коалиций, наверное, лучше всего рассматривать как игры с ненулевой суммой".

1.5 Позиционные игры

Одним из классов игр, описывающих конфликты, динамика которых оказывает влияние на поведение участников, являются так называемые позиционные игры.

Позиционная игра - это бескоалиционная игра, моделирующая процессы последовательного принятия решений игроками в условиях меняющейся во времени и, вообще говоря, неполной информации. Процесс самой игры состоит в последовательном переходе от одного состояния игры к другому состоянию, который осуществляется либо путем выбора игроками одного из возможных действий в соответствии с правилами игры, либо случайным образом (случайный ход).

В качестве примеров позиционных игр можно привести крестики-нолики, шашки, шахматы, карточные игры, домино и др. Интересно, что право выбора первого хода в этих играх часто определяется случайным образом.

Состояния игры принято называть узлами или позициями (от сюда и название - позиционные игры), а возможные выборы в каждой позиции - альтернативами. Окончательные позиции называются вершинами.

Характерной особенностью позиционной игры является возможность предоставления множества позиций в виде древовидного упорядоченного множества, которое называется деревом игры.

Замечание. Символы О, А или В в кружке указывают, кто из игроков (О, А или В) делает очередной ход и данной позиции. При этом символом О обычно обозначается ход в игре, осуществляемый не игроком, а каким-нибудь случайным механизмом (иногда его называют природой).

Описание конечной игры двух лиц с помощью дерева, узлы (точки ветвления) которого соответствуют ситуациям, в которых стороны осуществляют свои выборы (ходы), а вершины - ситуациям завершения операции (с указанием достигаемых сторонами значений полезностей), является моделью игры в позиционной или развернутой форме.

Термин «развернутая форма» отражает то обстоятельство, что рассматриваемая модель характеризует процесс выбора решений как развертывающийся во времени.

Для определенности мы будем рассматривать позиционные игры, в каждой позиции которых, за исключением окончательных, ровно две альтернативы - первая и вторая. По графическому описанию игры в виде дерева можно заметить, что процесс игры состоит в переходе от начальной позиции к вершине через непосредственно следующие одна за другой промежуточные позиции. Каждая вершина определяет единственную цепь (последовательность идущих друг за другом звеньев), связывающую начальную позицию с данной вершиной (рисунок 1). Такая цепь называется партией. На рисунке 1 одна из партий выделена жирными линиями. Число различных партий ровно числу вершин. В каждой вершине 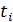 задан числовой выигрыш игрока А.

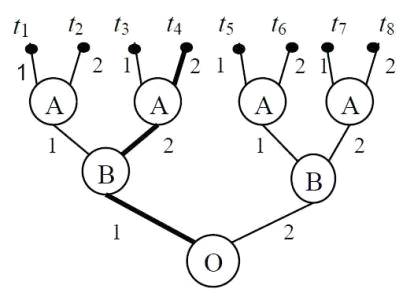
Рисунок 1. - Модель позиционной игры

Различают позиционные игры с неполной и полной информацией.

В позиционных играх с неполной информацией (например - домино) игрок, делающий ход, не знает точно, в какой именно позиции дерева игры он фактически находится. Этому игроку известно лишь некоторое множество позиций, включающее в себя его фактическую позицию. Такое множество позиций называется информационным множеством. Позиции, принадлежащие одному и тому же информационному множеству, объединяются пунктирными линиями. Предполагается, что понятие дерева игры включает и группирование узлов этого дерева в информационные множества, отражающие осведомленность игроков обо всех выборах, предшествующих текущему ходу.

.6 Кооперативные и некооперативные игры

Игра называется кооперативной, если в ней игрокам разрешается обсуждать перед игрой свои стратегии и договариваться о совместных действиях (добровольный обмен между игроками информацией, совместный выбор стратегий, передача игроками части выигрыша друг другу и т.п.);

Иначе говоря, игроки могут образовывать коалиции. Теория кооперативных игр исследует типы коалиций, образующихся в процессе игры и условия, необходимые для их устойчивого существования.

Кооперативной называется игра, в которой группы игроков - коалиции - могут объединять свои усилия. Этим она отличается от игр, в которых коалиции неприемлемы и каждый обязан играть за себя.

Теория игр занимается изучением конфликтов, то есть ситуаций, в которых группе людей необходимо выработать какое-либо решение, касающееся их всех. Некооперативная теория игр изучает то, как должны действовать игроки, чтобы прийти к тому или иному результату, кооперативная же теория игр изучает вопрос о том, какие исходы достижимы и условия достижения этих исходов. Некооперативной игрой называется математическая модель взаимодействия нескольких сторон (игроков), в процессе которого они не могут формировать коалиции и координировать свои действия. Некооперативная игра в нормальной форме предполагает следующий порядок разыгрывания.

1. Игроки одновременно и независимо друг от друга выбирают из множеств 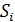 свои стратегии. Вектор стратегий 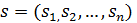всех игроков представляет собой ситуацию в игре.

. Каждый игрок получает выигрыш, определяемый значением функции 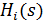, на этом взаимодействие между ними прекращается.

Нормальная форма игры описывает статическое взаимодействие игроков, не предусматривая возможности последовательных ходов, накопления информации о действиях соперника и повторяющегося взаимодействия. Для моделирования этих аспектов используется развернутая форма игры. Некооперативная игра в развернутой форме с множеством игроков 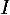 представляется с использованием ориентированного <#"787330.files/image021.gif">, соответствующей нетерминальной позиции, определен игрок 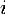, совершающий в ней ход и множество ходов этого игрока 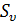. Каждому ходу s  соответствует ребро, выходящее из вершины 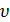. Для учета несовершенства информации, имеющейся у игроков, нетерминальные вершины могут объединяться в информационные множества <#"787330.files/image021.gif">, соответствующей терминальной позиции, определены функции выигрыша всех игроков .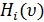

Игра предполагает следующий порядок разыгрывания:

. Игра начинается из начальной позиции.

. В любой нетерминальной позиции 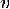 игрок, имеющий в ней право хода, выбирает ход s , в результате чего игра попадает в следующую позицию, в которую входит ребро, соответствующее ходу S. Если эта позиция является нетерминальной, то повторяется п. 2.

. Если игра попадает в терминальную позицию υ, то все игроки получают выигрыши 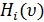, и игра завершается.

Принципы оптимальности Основным принципом оптимальности стратегий для некооперативных игр в нормальной форме является равновесие Нэша <#"787330.files/image027.jpg">

Рисунок 2. - Игровой процесс

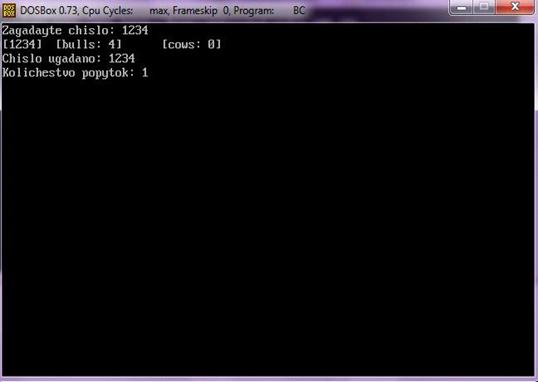
Рисунок 3. - Игровой процесс

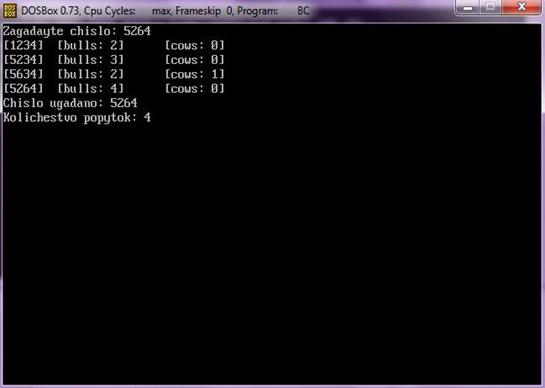
Рисунок 4. - Игровой процесс

Заключение

В результате выполнения курсовой работы по дисциплине «Интеллектуальные информационные системы» на тему «Программирование игр и головоломок» были рассмотрены основы математической теории игр, показаны возможные представления игр и их классификация.

Разработан и реализован вариант игры «Быки и коровы». Игры бывают разные, и стратегии у них разные, у каждой игры она индивидуальная. Для игры «Быки и коровы» главной задачей компьютера является - отгадать число, которое загадал пользователь за минимально возможное количество ходов.

Созданная игра является одной из самых примитивных, но в процессе ее разработки, я смог больше узнать о базовых концепциях программирования интеллектуальных информационных систем под операционную систему Windows.

Программирование игр - довольно сложный процесс, и самая большая сложность заключается в том, чтобы запрограммировать компьютер на различные ответные реакции на действия со стороны пользователя. Тем не менее, это довольно увлекательный процесс. Для начала надо на бумаге попытаться написать некий алгоритм действий, который будет выполняться в игре, а затем уже пробовать этот алгоритм изобразить в виде кода.

Список использованных источников

1. Колобашкина Л.В., Алюшин М.В. - Информационные технологии принятия решений в условиях конфликта, 2010 г. - 164 с.

. Н. Н. Писарук - Введение в теорию игр, 2013 г. - 239 с.

. Н. Н. Воробьева - Бесконечные антагонистические игры, 1963 г. - 195 с.

. Джеймс Карс - Книга “Конечных и Бесконечных Игр” - 113 с.

. Н. С. Садовин, Т. Н. Садовина - Основы теории игр, 2011 г. - 120 с.

. Васин А. А., Морозов В. В. - Теория игр и модели математической экономики. - М., 2005г. - 127 с.

. Петросян Л. А., Зенкевич Н.А., Семина Е.А. - Теория игр: Учеб. пособие для ун-тов, 1998 г. - 304 с.

. Д. Андерхилл, С. Барретт, П. Бернелл, П. Бернем, и др. Общая редакция: д.э.н. Осадчая И.М. Политика. Толковый словарь. - М., 2001 г. - 235 с.

Приложение. Текст программы

#include <conio.h>

#include <stdio.h>

#include <stdlib.h>GetCows(int n[4], int m[4])

{c = 0;(int i = 0; i < 4; i++)(int j = 0; j < 4; j++)(n[i] == m[j] && i != j) c++;c;

}GetBulls(int n[4], int m[4])

{b = 0;(int i = 0; i < 4; i++)(n[i] == m[i]) b++;b;

}main()

{m[4] = { 1, 2, 3, 4 };temp[4], n[4], number, bulls, cows, w, t, s, c, attempts = 1;();("Zagadayte chislo: ");("%d", &number);[0] = number / 1000;[1] = number % 1000 / 100;[2] = number % 100 / 10;[3] = number % 10;= GetBulls(n, m);= GetCows(n, m);("[%d%d%d%d]\t[bulls: %d]\t[cows: %d]\n", m[0], m[1], m[2], m[3], bulls, cows);= 0;= 5;= bulls + cows;(bulls + cows != 4)

{++;(w == 4)

{= 0;++;

}[0] = m[0]; temp[1] = m[1]; temp[2] = m[2]; temp[3] = m[3];[w] = c;++;= GetBulls(n, temp);= GetCows(n, temp);("[%d%d%d%d]\t[bulls: %d]\t[cows: %d]\n", temp[0], temp[1], temp[2], temp[3], bulls, cows);(bulls + cows > s)

{[w - 1] = c;++;= bulls + cows;

}

}= 0;= 0;= bulls;(bulls != 4)++;(t == 4)++;= 0;(w == t) t++;[0] = m[0]; temp[1] = m[1]; temp[2] = m[2]; temp[3] = m[3];= temp[w];[w] = temp[t];

temp[t] = c;++;

bulls = GetBulls(n, temp);("[%d%d%d%d]\t[bulls: %d]\n", temp[0], temp[1], temp[2], temp[3], bulls, cows);(bulls > s)= m[w];[w] = m[t - 1];[t - 1] = c;++;= 0;= bulls;("Chislo ugadano: %d%d%d%d\n", m[0], m[1], m[2], m[3]);("Kolichestvo popytok: %d", attempts);

getch();

}