Программирование алгоритмов на примере численных методов

Программирование алгоритмов на примере численных методов

СОДЕРЖАНИЕ

Введение

. Постановка задачи

. Математическое описание метода

.1 Метод половинного деления

.2 Метод Крамера

.3 Метод прямоугольников

. Блок-схема программы

.1 Блок-схема модуля1 (процедура polovin )

.2 Блок-схема модуля 2 (процедура kramer)

.2.1 Блок-схема модуля 2 (функция det, op)

.3 Блок-схема модуля 3 (процедура pr)

. Описание стандартных функций

. Описание не стандартных функций

.1 Модуль 1 (процедура polovin)

.2 Модуль 2 (процедура kramer)

.2.1 Модуль 2 (функция op)

.3 Модуль 3 (процедура pr)

. Описание интерфейса

. Численный пример

Заключение

Список используемых источников

Приложение

ВВЕДЕНИЕ

В настоящее время резко возрос интерес к языкам высокого уровня благодаря возможности использования в научных исследованиях, в технике и экономике вычислительных машин, выполняющих построение некоторых величин в точном соответствии с указанным алгоритмом. Эта возможность привлекательна по той причине, что явления процессы, которые изучают в рамках упомянутых исследований, часто удается описать с помощью понятий математики - функций, систем уравнений, неравенств и для получения конкретных сведений об изучаемых явлениях и процессах надо провести некоторые действия над математическими объектами. Человеку достаточно описать алгоритм необходимых преобразований и вычислений, а сами действия выполнит вычислительная машина.

1. ПОСТАНОВКА ЗАДАЧИ

Целью данной курсовой работы является изучение методов структурного программирования на примере численных методов, в частности написание нескольких модулей и связь их в одну общую программу.

Составить программу приближенного вычисления методом половинного деления следующего уравнения с заданной точностью ε =10-4 x2+2x+ln(x)=0. Описать вышеуказанный метод, составить блок-схему программы, описать стандартные и не стандартные функции, применяемые в задаче, описать интерфейс и привести пример.

Составить программу для вычисления системы уравнений методом Крамера:

 .

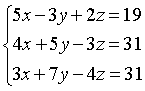Описать вышеуказанный метод, составить блок-схему, описать стандартные и не стандартные функции, а так же интерфейс задачи.

Составить программу вычисления определенного интеграла с пределами интегрирования от (а;в) по формуле прямоугольников для функции: 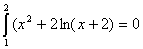 и заданным количеством шагов n=20 и точностью ε =10-4 . Описать вышеуказанный метод, составить блок-схему программы, описать стандартные и не стандартные функции, применяемые в задаче, описать интерфейс и привести пример.

2. Математическое описание методОВ

.1 Метод половинного деления

Его ещё называют методом дихотомии. Этот метод решения уравнений отличается от других методов тем, что для него не требуется выполнения условия, что первая и вторая производная сохраняют знак на интервале [a, b]. Метод половинного деления сходится для любых непрерывных функций f(x) в том числе недифференцируемых.

Разделим отрезок [a, b] пополам точкой 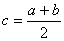. Если 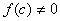(что практически наиболее вероятно), то возможны два случая: либо f(x) меняет знак на отрезке [a, c] (Рисунок 1), либо на отрезке [c, b] (Рисунок 2).

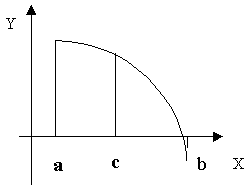
Рисунок 1.

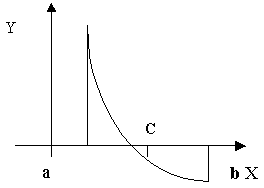
Рисунок 2.

Выбирая в каждом случае тот отрезок, на котором функция меняет знак и, продолжая процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения.

2.2 Метод Крамера

Пусть нам требуется решить систему линейных алгебраических уравнений

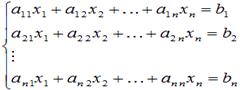
в которой число уравнений равно числу неизвестных переменных и определитель основной матрицы системы отличен от нуля, то есть, .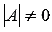
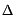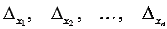Пусть  - определитель основной матрицы системы, а  - определители матриц, которые получаются из А заменой 1-ого, 2-ого, …, n-ого столбца соответственно на столбец свободных членов:

Основной определитель считается следующим образом:

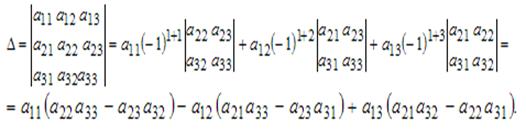
Аналогично считаются определители матриц, которые получаются из А заменой 1-ого, 2-ого, …, n-ого столбца соответственно на столбец свободных членов. После этого решение системы линейных алгебраических уравнений методом Крамера осуществляется по следующим формулам .

.

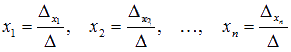.3 Метод прямоугольников

Численное интегрирование состоит в нахождении интеграла 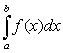 от непрерывной функции f(x) по формуле

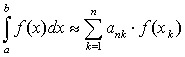, (2)

где коэффициенты ank - действительные числа, а точки хk принадлежат отрезку [a, b], k изменяется от 1 до n.

Вид суммы 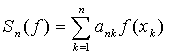 определяет метод численного интегрирования, а разность 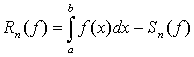- погрешность метода.

Для метода прямоугольников формула примет вид

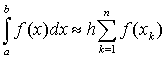, (3)

где 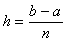, х0=а, xk=xk-1+(i+0,5)h, i=0,1...n-1.

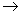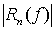Правая часть формулы прямоугольников является интегральной суммой и при h0 стремится к данному интегралу. Однако при фиксированном h отличается от соответствующего интеграла на величину Rn(f). По заданной абсолютной погрешности ε подбирается параметр n, при котором выполняется равенство < ε.

3. БЛОК-СХЕМА ПРОГРАММЫ.

3.1 Блок-схема modul 1(процедура polovin)

3.2 Блок-схема модуля 2(процедура kramer)

3.2.1Блок-схема модуля 2(функция op)

3.3 Блок-схема модуля 3(процедура pr)

4. ОПИСАНИЕ СТАНДАРТНЫХ ФУНКЦИЙ

При выполнении оператора ввода Read() переменным присваиваются значения исходных данных.

Процедура Readln() выполняет процедуру Read(), после чего переходит на следующую строку. Readln() без параметров осуществляет переход на начало следующей строки без предварительного считывания.

С помощью процедур вывода Write() строится последовательность значений, которая является результатом выполнения программы. Параметр, заключенный в круглые скобки может содержать указания ширины поля и количества десятичных знаков. Выражения вывода могут быть следующих типов: char, integer, real, string, packet string или boolean. Процедура вывода, таким образом, позволяет выделить из всего набора вычисленных значений те, которые служат ответом к решавшейся при выполнении программой задаче.

Процедура Writeln() выполняет процедуру Write(), а затем осуществляет переход в начало следующей строки. Процедуры ввода и вывода часто применяют вместе. Например, для ввода трех чисел и вывода их суммы

Read (a,b,c);

х:= a+b+c;(x);

Последней общей для всех модулей функцией является функция ReadKey, которая считывает символ с клавиатуры . Она описана в стандартном модуле Crt. Возвращаемый тип данных - тип char. Функция ReadKey принимает значение считываемого символа, при этом символ не выводится на экран.

Если до обращения к ReadKey значение KeyPressed было равно True, то считывание происходит незамедлительно. В противном случае программа ожидает ввода с клавиатуры. Для считывания кода, соответствующего специальным клавишам, к функции ReadKey необходимо обратиться два раза.

(Под специальными, подразумеваются функциональные клавиши, клавиши управления курсором, клавиши, нажатые одновременно с Alt и т.д.). Первый раз функция ReadKey принимает значения х0, а во второй раз - значение расширенного кода, соответствующего данной специальной клавише. Значение х0 не может быть присвоено ReadKey никаким другим способом. Поэтому если ReadKey =х0 , то следующее значение ReadKey обязательно должно трактоваться как расширенный код. Не смотря на то, что применение функции очень широко, однако чаще всего она используется для задержки программы при отладке. Пример применения функции

Ch: = ReadKey - возвращает считанный символ.

5. ОПИСАНИЕ НЕСТАНДАРТНЫХ ФУНКЦИЙ

Программа GLAV сама по себе использует нестандартные модули 1, 2, 3, которые также содержат процедуры и функции, выполнение которых приводит к выполнению основной программы. Поэтому описание не стандартных процедур и функций, по сути, сводится к описанию процедур и функций, содержащихся в выше перечисленных модулях.

5.1 Модуль1 (процедура polovin)

Процедура polovin содержит пять внутренних переменных типа real, три из них получают первоначальное значение, используя стандартные процедуры ввода-вывода write-read. В ходе выполнения цикла while происходит проверка модуля разности интервала а и b и данного значения сумма, а также вычисление значений корня уравнения согласно формуле метода половинного деления. Действие цикла прекращается сразу же, как только модуль разности текущего значения х станет меньше допустимой погрешности. Процедура выводит найденное значение на экран монитора. Делает проверку правильности полученного ответа путем подстановки в само уравнение и ожидает нажатия любой клавиши для завершения. Выводимое на экран значение имеет тип real. Выше указанная процедура использует стандартные процедуры и функции (clrscr, write, read, writeln, readkey), стандартные операторы (присвоение) и цикл while.

5.2 Модуль 2 (процедура kramer)

Эта процедура использует значительно большее количество внутренних переменных(a,b,vv,pop-массивы real, gop-real, i,j-integer). Кроме того, она использует внутреннюю функцию ор для расчета определения матрицы. Используя стандартные процедуры ввода-вывода, получаем значения коэффициентов при неизвестных и значение равенства.

Вычисляется главный определитель. Затем, используя цикл for, производится поочередная замена столбца на значение уравнения, вычисление определителя матрицы и возврат замененных столбцов. В результате получаем массив дополнительных определителей и главный определитель. Применяя метод Крамера, получаем значения неизвестных системы уравнений, как частное от деления дополнительного определителя матрицы данного столбца на главный определитель. Выводимые на экран монитора решения системы уравнений имеют тип real. Процедура делает проверку правильности найденных значений путем подстановки их поочередно во все три равенства. Выше указанная процедура использует стандартные процедуры и функции (clrscr, write, read, writeln, readkey) стандартные операторы присвоения и цикл for.

Указанная процедура является универсальной для всех систем уравнений удовлетворяющих правилу Крамера (коэффициенты по главной оси матрицы имеют наибольшие значение модуля по сравнению с остальным коэффициентами уравнения), с числом строк равных 3 и числом столбцов h=3, при изменении константы n на любое другое число делает указанную процедуру универсальной.

Как уже говорилось, выше названная процедура использует свою внутреннюю функцию det() являющуюся так же не стандартной.

5.2.1 Модуль 2 (функция op)

Данная функция предназначена для нахождения определителя матрицы способом последовательного обнуления коэффициентов стоящих ниже главной оси матрицы. Для этого используется главное свойство матрицы: если одну строку или столбец матрицы умножить на одно число, а затем сложить с другой строкой или столбцом матрицы, то определитель матрицы не изменится. Следовательно, новый коэффициент матрицы будет

равен старому коэффициенту матрицы плюс значение вышестоящего коэффициента данной строки умноженного на к, где к равно минус частное от деления первого не нулевого коэффициента данной строки на выше стоящий коэффициент. Функция, используя цикл for, строит квадратную матрицу, имеющую нули ниже главной оси. Таким образом, значение определителя матрицы будет равно произведению коэффициентов главной оси. Функция det() имеет внутренние переменные i,j,h-типа integer и k,op- типа real. Она использует стандартные операторы присвоения цикл for.

Данная функция является универсальной для подсчета определителя матрицы любого размера при выполнении условия метода Крамера, что первый левый член матрицы не равен 0.

5.3 Модуль 3 (процедура pr)

Процедура pr является внешне самой простой из приведенных выше нестандартных процедур. Так как просто производит вычисление суммы всех значений в контрольных точках, и полученный результат умножается на h равной половине разности конечного значения и начального. Процедура имеет свои внутренние переменные (i,n-integer и x,s,a,b,h-real), три из которых получают свои значения, используя стандартные функции ввода-вывода. После чего начальному значению суммы присваивается значение 0, и вычисляется шаг вычисления h. Далее в цикле for производится вычисление значений аргумента и сумма значений функций в этих значениях.

Вычисленное значение суммы, умноженное на шаг вычислений, и будет значение интеграла по формуле прямоугольников. Выводимое значение процедуры на экран монитора имеет тип real. Далее процедура осуществляет проверку путем вычисления определенного интеграла методом Ньютона-Лейбница и сравнением его с полученным результатом. Процедура использует стандартные процедуры и функции (clrscr, write, read, writeln, readkey), стандартные операторы присвоения и цикл for.

6. ОПИСАНИЕ ИНТЕРФЕЙСА

Основная программа GLAV (использующая методы структурного программирования) работает следующим образом. Используя способ запроса, определяет дальнейший ход развития. При получении любого результата отличного от 1,2,3 вновь возвращается на начало программы. Тем самым, исключая возможность ошибочного ввода. При получении ответа соответствующего цифрам 1,2,3 передает управление одной из процедур описанных в не стандартных модулях пользователя. При этом выполнение главной программы практически заканчивается за исключением оператора выхода. Управление передается соответственно одному из модулей (модуль 1, модуль 2, модуль 3) или другими словами процедурам пользователя (polovin, kramer, pr)

Каждый из перечисленных модулей по сути своей представляет отдельную программу, являющуюся составной частью другой. Это позволяет в зависимости от выбора пользователя выполнить тот или иной самостоятельный модуль, входящий в главную программу.

При выборе 1 управление передается модулю 1 (процедура polovin ) выполнение которого приводит к выходу из программы.

Аналогично построены и два других модуля входящих в программу GLAV, за исключением того, что процедура kramer в ходe своего выполнения не однократно передает управление функции det, op являющейся неотъемлемой частью выше названной процедуры.

7. Численный пример

Все вышеперечисленное в данном курсовом проекте проиллюстрировано на конкретных примерах.

Задано алгебраическое уравнение x2-2ln(x+2)=0 с заданной точностью вычисления ε=10-4 , которые необходимо решить методом половинного деления.

Для этого первоначально берем произвольные значения х и рассчитываем для них значения функции у, которые сводим в таблицу 1.

Таблица 1. Данные для построения графика функции у=x2-2ln(x+2)=0

Из таблицы 1, что корень уравнения лежит на отрезке от 1 до 2 , т. к. функция меняет знак на противоположный (в соответствие с методом половинного деления). График функции у= x2-2ln(x+2) представлен на рисунке 1.

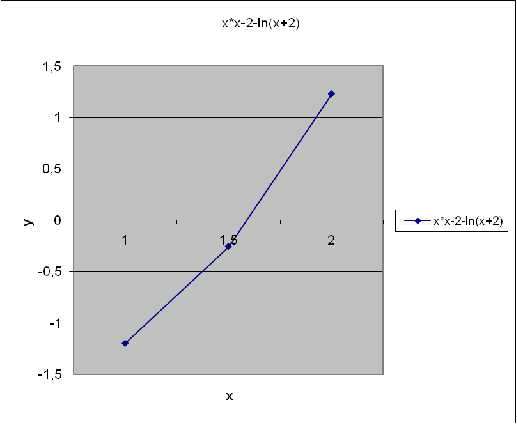
Рис. 1. График функции у= x2-2ln(x+2)

Результаты решения по методу половинного деления были полученные с помощью программы Exсel и сведены в таблицу 2.

Решением функции у= x2-2ln(x+2) по методу половинного деления являются значения х=1,6007 а данным значением ε=0,0001 и значением функции f(x)= - 0,000015 отрезке [1;2].

Результаты программного решения дают следующие значения.

Таблица 2. Результаты расчета функции у= x2-2ln(x+2)по методу половинного деления.

Таким образом, результаты расчета функции у= x2-2ln(x+2) по методу половинного деления полученные с помощью программы Exсel дают более точный результат.

Необходимо решить систему уравнений методом Крамера.

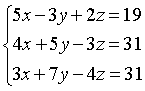
Для этого считает основной определитель матрицы:

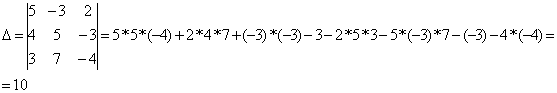
Аналогично считаются определители матриц, которые получаются из А заменой 1-ого, 2-ого, …, n-ого столбца соответственно на столбец свободных членов. После этого решение системы линейных алгебраических уравнений методом Крамера осуществляется по следующим формулам .

..

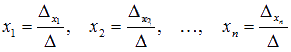Определитель матрицы, полученный заменой столбца х на столбец свободных членов, считается по формуле:

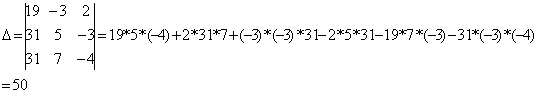
Определитель матрицы, полученный заменой столбца у на столбец свободных членов, считается по формуле:

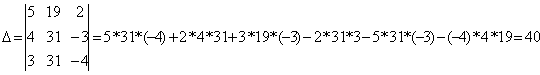
Определитель матрицы, полученный заменой столбца z на столбец свободных членов, считается по формуле:

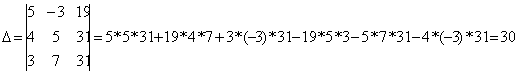
Находим значения х, у и z по формулам:

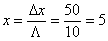
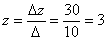
Проверка результатов расчета осуществляются подстановкой данных в систему уравнений:

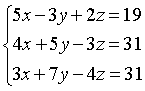
Что дает абсолютно точный результат.

Результаты программного решения показывают также абсолютно точный результат.

Необходимо вычислить определенный интеграл 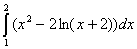 на отрезке [1,2] методом прямоугольников c заданным количеством шагов n=20 и точностью ε =10-4.

Для этого находим шаг изменения аргумента .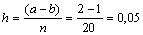

Отсюда x=n+(i+0,5)*h и считается для всех шагов n=20

X1=1+(1+0,5)*0,05=1,075

X2=1+(2+0,5)*0,05=1,125

X3=1+(3+0,5)*0,05=1,175

X4=1+(4+0,5)*0,05=1,225

X5=1+(5+0,5)*0,05=1,275

X6=1+(6+0,5)*0,05=1,325

X7=1+(7+0,5)*0,05=1,375

X8=1+(8+0,5)*0,05=1,425

X9=1+(9+0,5)*0,05=1,475

X11=1+(11+0,5)*0,05=1,575

X12=1+(12+0,5)*0,05=1,625

X13=1+(13+0,5)*0,05=1,675

X14=1+(14+0,5)*0,05=1,725

X15=1+(15+0,5)*0,05=1,775

X16=1+(16+0,5)*0,05=1,825

X17=1+(17+0,5)*0,05=1,875

X18=1+(18+0,5)*0,05=1,925

X19=1+(19+0,5)*0,05=1,975

X20=1+(20+0,5)*0,05=2,025

Результаты расчетов представлены в таблице 3 полученной с помощью программы Excel

Таблица 3. Результаты расчетов по методу прямоугольников

Значения функции f(x) определяются по формуле f(x)= x*x-2ln(x+2) отсюда:

(x1)= 1,075*1,075-2ln(1,075+2)= -1,17281(x2)= 1,125*1,125-2ln(1,125+2)= -1,1399(x3)= 1,175*1,175-2ln(1,175+2)= -1,09274(x4)= 1,225*1,225-2ln(1,225+2)= -1,03052(x5)= 1,275*1,275-2ln(1,275+2)= -0,95244(x6)= 1,325*1,325-2ln(1,325+2)= -0,85769(x7)= 1,375*1,375-2ln(1,375+2)= -0,74548(x8)= 1,425*1,425-2ln(1,425+2)= -0,615(x9)= 1,475*1,475-2ln(1,475+2)= -0,46546(x10)= 1,525*1,525-2ln(1,525+2)= -0,29606(x11)= 1,575*1,575-2ln(1,575+2)= -0,10601(x12)= 1,625*1,625-2ln(1,625+2)= 0,105489(x13)= 1,675*1,675-2ln(1,675+2)= 0,339219(x14)= 1,725*1,725-2ln(1,725+2)= 0,595972(x15)= 1,775*1,775-2ln(1,775+2)= 0,876538(x16)= 1,825*1,825-2ln(1,825+2)= 1,181702(x17)= 1,875*1,875-2ln(1,875+2)= 1,512251(x18)= 1,925*1,925-2ln(1,925+2)= 1,868968(x19)= 1,975*1,975-2ln(1,975+2)= 2,252637

f(x20)= 2,025*2,025-2ln(2,025+2)= 2,66404

Находим суммарное значение полученных функций:

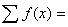-1,09098-1,01324-0,92999-0,84124-0,74701-0,64731-0,54217-0,43158-0,31556-0,19414-0,06731+0,064916+0,202519+0,345491+0,493824+0,647508+

,806534+0,970892+1,315575+1,140576=-1,38629

Нахождение определенного интеграла по формуле прямоугольников сводится к нахождению произведения суммы значений функции в изменение значений аргумента с шагом равным частному от деления разности конечного и начального значений аргумента на заданное количество шагов

А также по формуле S=h*f(x) определяем значение интегралов на каждом из отрезков:

S1=0,05*(-1,09098)= -0,0461=0,05*(-1,01324)= -0,04333=0,05*(-0,92999)= -0,04041=0,05*(-0,84124)= -0,03732=0,05*(-0,74701)= -0,03407=0,05*(-0,64731)= -0,03065=0,05*(-0,54217)= -0,02705=0,05*(-0,43158)= -0,02326=0,05*(-0,31556)= -0,01929=0,05*(-0,19414)= -0,01512=0,05*(-0,06731)=-0,01076=0,05*(0,064916)= -0,00619=0,05*(0,202519)= -0,00143=0,05*(0,345491)= 0,003543=0,05*(0,493824)= 0,008721=0,05*(0,647508)= 0,01411=0,05*(0,806534)= 0,019712=0,05*(0,970892)= 0,025528=0,05*(1,315575)= 0,03156=0,05*(1,140576)= 0,03781

Суммарное значение интегралов равно:  -1,17281-1,1399-1,09274-1,03052-0,95244-0,85769-0,74548-0,615-0,46546-0,29606-0,106010,1054890,3392190,5959720,8765381,1817021,5122511,868968

,2526372,66404=0

Погрешность метода находим по формуле .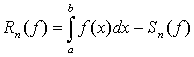

Для метода прямоугольников формула примет вид

.

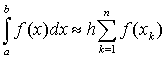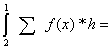0,05*(-3,87969)=-0,1938

=

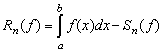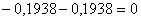
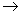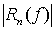Правая часть формулы прямоугольников является интегральной суммой и при h0 стремится к данному интегралу. Однако при фиксированном h отличается от соответствующего интеграла на величину Rn(f). По заданной абсолютной погрешности ε подбирается параметр n, при котором выполняется равенство < ε.

0<0,0001, что соответствует условию задачи.

Рис. 2. График функции построенной по методу прямоугольников

функции вида. дает следующий результат: определенный интеграл равен 0,99959.Rn(f)<E, где Rn(f)=  Sn(f)= 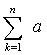n x*f(xk)

ЗАКЛЮЧЕНИЕ

структурный программирование функция уравнение

В заключение хотелось бы отметить, что применение языка программирования Turbo Pascal 7.0 значительно упрощает работу по вычислению значений функций, нахождения корней уравнений и вычисления программы. Достаточно усовершенствовать отдельный модуль откомпилировать его и появляется возможность решать различные варианты задач с использованием данных методов. Более того, текст главной программы более читаем, и занимает меньше места. Имеющиеся наработки в отдельных модулях можно использовать в других программах. Четко выраженная структура программы позволяет более ясно представить цели и задачи стоящие перед программистом.

Список используемЫХ ИСТОЧНИКОВ

1.       Информатика: учебник для вузов / А.Н. Гуда [и др.]; под ред. В.И. Колесникова. - М.: Дашков и К, 2008. - 400 с.

2.       Чекмарев, Ю.В. Вычислительные системы, сети и телекоммуникации [Электронный ресурс]/ Ю.В. Чекмарев.- «ДМК Пресс», 2010. - Загл. с экрана.- Режим доступа: http://e.lanbook.com/books/element.php?pl1_cid=258&pl1_id=1108.

.        Шаньгин, В.Ф. Защита компьютерной информации [Электронный ресурс]/ В.Ф. Шаньгин.- «ДМК Пресс», 2010. - Загл. с экрана.- Режим доступа: http://e.lanbook.com/books/element.php?pl1_cid=258&pl1_id=1146 .

4.       Артемова, С.В. Информатика. Методические указания по выполнению лабораторных работ/ С.В. Артемова, Т.И. Чернышова, Н.Г. Чернышов. - Тамбов, Тамб. гос. техн. ун-т, 2006. - 54 с.

5.       Галявов, И.Р. Borland C++ для себя [Электронный ресурс]/ И.Р.. Галявов. - «ДМК Пресс», 2009. - Загл. с экрана.- Режим доступа: http://e.lanbook.com/books/element.php?pl1_cid=258&pl1_id=1230.

6.       Алексеев, Е.Р FreePascal и Lazarus: Учебник по программированию [Электронный ресурс]/ О.В. Чеснокова, Т.В.Кучер.- «ДМК Пресс», 2010. - Загл. с экрана.- Режим доступа: http: //e.lanbook.com/books/element.php?pl1_cid =258&pl1_id =1267.

7.       Буч, Г. Язык UML руководство пользователя [Электронный ресурс]/ Г.Буч, Д. Рамбо, И. Якобсон. - «ДМК Пресс», 2008. - Загл. с экрана.- Режим доступа: http: //e.lanbook.com/books/element.php?pl1_cid =258&pl1_id =1246.

8.       OpenOffice.org для профессионала [Электронный ресурс].- «ДМК Пресс», 2009. - Загл. с экрана.- Режим доступа: http: //e.lanbook.com/books/ element.php?pl1_cid =258&pl1_id =1223.

.        Дьяконов, В.П. MATHLAB 9.5 /10/11 в математике, физике и образовании [Электронный ресурс]/ В.П.Дьяконов. -«ДМК Пресс»,- 2010. - Загл. с экрана.- Режим доступа: http: //e.lanbook.com/books/ element.php?pl1_cid =258&pl1_id =1181.

10.     http//crems.jesby.tstu.ru.88

11.     www.kib.ru/info/course

12.     http://study.utmn.ru/~izaharova

ПРИЛОЖЕНИЕ

program glav; {присвоение имени программы}

uses crt, modul1, modul2, modul3; {объявление модулей} {объявление переменных}

w:integer; { объявление переменной: w тип целые}

begin {начало тела программ

repeat {начало цикла «repeat - until»}('1-polovin del, 2-kramer, 3 - integral'); {вывод сообщения в ‘ ‘ на экран}(w); {ввод значения переменной w}

if w=1 then polovin; {расчет методом половинного деления}

if w=2 then kramer; {расчет методом Крамера}

if w=3 then pr; {расчет по формуле прямоугольников}

until (w=1) or (w=2) or (w=3);; {задержка экрана}

end. {окончание программы}

unit modul1; {объявление модуля 1}crt;polovin; {определение процедуры polovin }{раздел реализации процедуры} { объявление переменных типа действительные числа}

a,b,e,x,c:real;f(x:real): real; { объявление функции f } { начало тела функции}

f:= x*x-2ln(x+2) {вычисление значения функции}

end;

procedure polovin; { конец тела функции} {начало тела процедуры}

clrscr;

write('a= '); {ввод начального значения}

readln(a);

write('b= '); {ввод конечного значения}

readln(b);

write('e= '); {ввод погрешности вычисления}

readln(e);

c:=(a+b)/2; {расчет начального значения аргумента}

while abs(b-a)>e do { начало цикла «while», проверка условия}

begin

if f(a)*f(c)<0 then b:=c { проверка условия «f(a)*f(c)<0» и присвоение}

else a:=c; {значения a или b }

c:=(a+b)/2; { конец цикла «while»}:=(a+b)/2;

writeln('x= ',x:4:2); {Вывод значения x}

writeln('f(x)= ',f(x):4:4); {Вывод значения f(x)}

readln;

end; {окончание процедуры polovin}

end.modul2; {объявление модуля} crt;n=3; {определение постоянной n=3 }

type matr=array[1..3,1..5] of real; {определение типа matr}kramer; {определение процедуры kramer }kramer; {раздел реализации процедуры}

var { объявление переменных типа действительные числа}

a:matr;,j,m,k:integer;,s2,d,opred,det: real;,x,v,popr:array[1..n] of real;op(a:matr):real; {определение функции op }

var { объявление переменных функции op },j,m: integer;{начало тела функции op}

for i:=1 to 3 doj:=1 to 2 do begin[i,j+n]:=a[i,j];('a[',i,',',j+n,']= ',a[i,j+n]:4:2); {добавление к матрице 2 и 3 столбца };:=0;m:=0 to 2 do begin

d:=1;i:=1 to n do:=d*a[i,i+m]; {нахождение произведения элементов главных диагоналей}:=s1+d; {сумма произведений элементов главных диагоналей}

end;:=0;m:=6 downto 4 do:=1;i:=1 to n do

d:=d*a[i,m-i]; {нахождение произведения элементов побочных диагоналей}:=s2+d; {сумма произведений элементов побочных диагоналей};:=s1-s2; {расчёт определителя матрицы}; { конец тела функции}{начало тела процедуры}

for i:=1 to n doj:=1 to n do

write('vvedite a[',i:2,',',j:2,']= '); {ввод значений элементов матрицы А}

readln(a[i,j]);;

write('vvedite b[',i:2,']= '); {ввод значений элементов матрицы В}(b[i]);;:=op(a); {вызов функции op для расчёта главного определителя матрицы}

writeln('det= ', det:4:2);i:=1 to n do beginj:=1 to n do begin

v[j]:=a[j,i]; {присвоение временной переменной значений столбца}[j,i]:=b[j]; {присвоение значению столбца значений матрицы- столбца В};[i]:=op(a); {вызов функции op для расчёта побочных определителей }

writeln('popr',i:1,'=',popr[i]:4:2);j:=1 to n do[j,i]:=v[j]; {возврат значений i-го столбца};;i:=1 to n do

begin[i]:=popr[i]/det; {расчёт неизвестных переменных}('x',i:1,'=',x[i]:4:2); {вывод неизвестных переменных}

end;;.modul3; {объявление модуля 3}crt;pr;{раздел реализации процедуры}pr; {определение процедуры pr }

var { объявление переменных типа действительные числа},b,n,i:integer; {и действительные числа}

s,p,h,x:real;{начало тела функции};

writeln('vvedite a'); {ввод начального значения отрезка}(a);('vvedite b'); {ввод конечного значения отрезка}(b);('vvedite n'); {ввод количества отрезков}(n);:=(b-a)/n; {вычисление шага}:=0;i:=1 to n-1 do {суммируем значения функции на x1...xn}x:=a+(i+0.5)*h; {вычисляем значение х на данном шаге}:= s+(x*x-2ln(x+2)) {значение функции от данного х};:=s*h; {находим значение функции методом прямоугольник}

writeln(s:4:4);;;.