Применение теории матриц в компьютерной графике
БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ЧУВАШСКОЙ РЕСПУБЛИКИ
СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО
ОБРАЗОВАНИЯ
«ЧЕБОКСАРСКИЙ ТЕХНИКУМ СВЯЗИ И
ИНФОРМАТИКИ»
МИНИСТЕРСТВА ОБРАЗОВАНИЯ И МОЛОДЁЖНОЙ
ПОЛИТИКИ ЧУВАШСКОЙ РЕСПУБЛИКИ
НАУЧНО-ПРАКТИЧЕСКАЯ КОНФЕРЕНЦИЯ
СТУДЕНТОВ
Секция «Математические науки»
Тема: Применение теории матриц в
компьютерной графике
Автор -
Лисицын Виктор Валерьевич, 2 курс, гр.ПКС-1-14
Научный
руководитель -Захарова Тамара Ивановна
Чебоксары - 2015 г.
Оглавление
Что такое матрица
Матричное представление преобразований
Составные преобразования
Аффинное преобразование и его матричное представление
Для чего же нужна трехмерная графика?
Список источников
Что такое
матрица
Матрица - довольно многозначное слово, которое пришло в нашу речь из
немецкого языка. Это слово можно встретить в сфере математики, техники и
электроники и даже в сфере киноиндустрии. Но сейчас не об этом. Итак, что же
такое матрица?
В математике термин "матрица" обозначает математический объект,
который представляет собой прямоугольную таблицу, состоящую из целых или
дробных чисел. По сути дела, это совокупность строк и столбцов, на пересечении
которых располагаются элементы матрицы. Размер матрицы определяется как раз
количеством строк и столбцов. Для чего нужны матрицы в математике? В основном
они применяются для удобного и компактного расположения систем линейных
уравнений. При такой записи количество строк матрицы будет равно количеству
уравнений в системе, а столбцы будут соответствовать неизвестным. Таким образом
упрощается поиск неизвестных. С матрицами можно производить алгебраические
операции: умножение, сложение, умножение на матрицу вектора и на скаляр.
Ма́трица - математический объект,
записываемый в виде прямоугольной таблицы чисел и допускающий алгебраические
операции (сложение, вычитание, умножение и др.) между ним и другими подобными
объектами.
Обычно матрицу обозначают заглавной буквой латинского алфавита и выделяют
круглыми скобками «(…)» (встречается также выделение квадратными скобками
«[…]», двойными прямыми линиями "||…||").
Числа, составляющие матрицу (элементы матрицы), обозначают той же буквой,
что и саму матрицу, но маленькой.
У каждого элемента матрицы есть 2 нижних индекса (
) - первый «i» обозначает номер
строки, в которой находится элемент, а второй «j» - номер столбца. Говорят
матрица размерности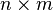 
подразумевая, что в матрице n строк и m столбцов.
Матричное
представление преобразований
Матрица m×n - это набор чисел, распределенных по m строкам и по n
столбцам. На приведенном ниже рисунке изображены различные матрицы.
Две матрицы одинакового размера можно складывать путем складывания
соответствующих элементов матриц. На приведенном ниже рисунке показано два
примера сложения матриц.
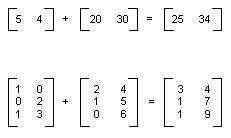
Матрицу размера m×n можно умножить на матрицу размера n×p,
в результате чего
получится матрица размера m×p. Число столбцов в первой из
перемножаемых матриц должно совпадать с числом строк во второй из перемножаемых
матриц. Например, матрицу размером 4×2 можно умножить на матрицу размером 2×3,
в результате чего получится
матрица размером 4×3.
Точки на плоскости, а также строки и столбцы матрицы можно рассматривать
как векторы. Например, (2, 5) - это вектор из двух компонентов, а (3, 7, 1) -
это вектор из трех компонентов. Скалярным произведением двух векторов называется
число, получаемое по следующим правилам:
(a, b) • (c, d) = ac + bd
(a, b, c) • (d, e, f) = ad + be + cf
Например, скалярное произведение векторов (2, 3) и (5, 4) равно (2)(5) +
(3)(4) = 22. Скалярное произведение векторов (2, 5, 1) и (4, 3, 1) равно (2)(4)
+ (5)(3) + (1)(1) = 24. Обратите внимание, что скалярное произведение векторов
- это число, а не вектор. Также обратите внимание, что скалярное произведение
двух векторов можно вычислить, только если у этих векторов одинаковое
количество компонентов.
Обозначение A(i, j) соответствует элементу матрицы A, расположенному на
пересечении i-ой строки и j-го столбца. Например, запись A(3, 2) обозначает
элемент матрицы A, расположенный на пересечении 3-ей строки и 2-го столбца.
Предположим, что A, B и C - это матрицы, причем AB = C. Элементы матрицы C
вычисляются следующим образом:
(i, j) = (i-я строка A) • (j-й столбец B)
На приведенном ниже рисунке показано несколько примеров перемножения
матриц.
Если рассматривать точки на плоскости в качестве матриц размером 1×2,
эти точки можно
подвергать преобразованиям, умножая их матрицы на матрицу размером 2×2. На приведенном ниже рисунке
изображены результаты применения различных преобразований к точке с
координатами (2, 1).
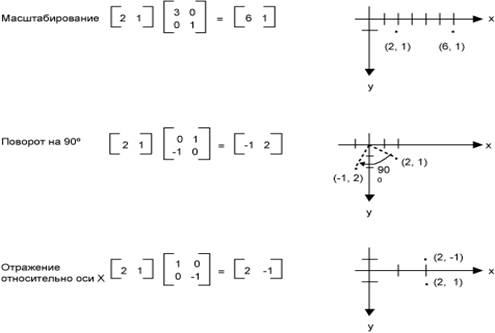
Все преобразования, показанные на приведенном ранее рисунке, являются
линейными преобразованиями. Некоторые другие преобразования, такие как сдвиг,
не являются линейными и не могут быть осуществлены путем умножения на матрицу
размером 2×2. Предположим, что нужно взять точку с координатами (2, 1),
повернуть ее на 90 градусов относительно начала координат, сдвинуть на 3
единицы вдоль оси X и на 4 единицы вдоль оси Y. Такое преобразование можно
выполнить путем выполнения умножения и сложения матриц.
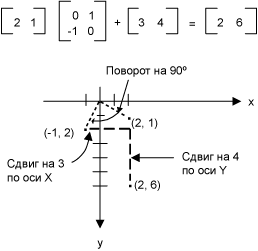
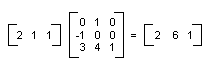
В предыдущем примере точка (2, 1) преобразуется в точку (2, 6). Обратите
внимание, что третий столбец матрицы размером 3×3 содержит числа 0, 0, 1.Такие значения
обязательны для всех матриц размером 3×3, задающих аффинные преобразования.
Смысловую нагрузку несут только шесть чисел в первом и втором столбцах матрицы
преобразования. Верхняя левая часть матрицы размером 2×2
задает линейную часть
преобразования, а первые два числа в третьей строке матрицы задают сдвиг.
Интерфейс
GDI+ позволяет хранить аффинные преобразования в объекте Matrix
<#"787258.files/image010.gif">
Тот
факт, что матрица составного преобразования может быть создана путем
перемножения отдельных матриц преобразования, означает, что любая
последовательность аффинных преобразований может быть задана одним объектом
Matrix
<#"787258.files/image011.gif">
Аффинное
преобразование и его матричное представление
Матрица перемещения
Мы можем переместить вектор (x, y, z, 1) на px единиц по оси Х, py единиц
по оси Y и pz единиц по оси Z умножив его на следующую матрицу:
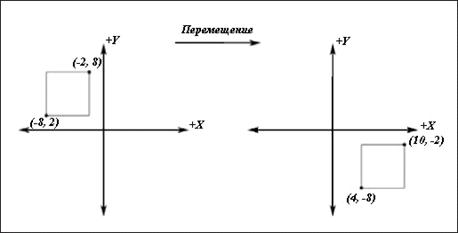
Перемещение на 12 единиц по оси X и на -10 единиц по оси Y
Для создания матрицы перемещения в библиотеке D3DX используется следующая
функция:DXMATRIX *D3DXMatrixTranslation(DXMATRIX* pOut, // Результатx, //
Количество единиц для перемещения по оси Xy, // Количество единиц для
перемещения по оси Yz // Количество единиц для перемещения по оси Z
);
Матрицы вращения
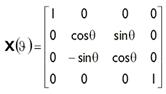
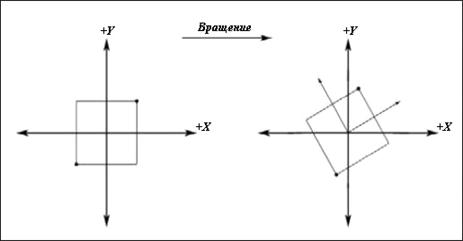
Поворот на 30 градусов против часовой стрелки вокруг оси Z
Используя приведенные ниже матрицы мы можем повернуть вектор на φ
радиан вокруг осей X, Y
или Z. Обратите внимание, что если смотреть вдоль оси вращения по направлению к
началу координат, то углы измеряются по часовой стрелке.
Для создания матрицы вращения вокруг оси X в библиотеке D3DX используется
следующая функция:DXMATRIX *D3DXMatrixRotationX(DXMATRIX* pOut, // РезультатAngle
// Угол поворота в радианах
);
);
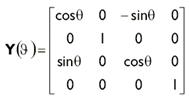
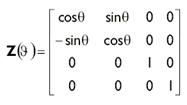
Для создания матрицы вращения вокруг оси Z в библиотеке D3DX используется
следующая функция:DXMATRIX *D3DXMatrixRotationZ(DXMATRIX* pOut, //
РезультатAngle // Угол поворота в радианах
);
Инверсией матрицы вращения R является результат транспонирования этой
матрицы: RT = R-1. Такие матрицы называются ортогональными.
Матрица масштабирования
Мы можем масштабировать вектор с коэффициентом qx по оси Х, коэффициентом
qy по оси Y и коэффициентом qz по оси Z, умножив его на следующую матрицу:
Масштабирование с коэффициентом 1/2 по оси X и коэффициентом 2 по оси Y
Для создания матрицы масштабирования в библиотеке D3DX используется
следующая функция:DXMATRIX *D3DXMatrixScaling(DXMATRIX* pOut, // Результатsx, //
Коэффициент масштабирования по оси Xsy, // Коэффициент масштабирования по оси
Ysz // Коэффициент масштабирования по оси Z
);
матрица операция трехмерный графика
DirectX (от английского direct - прямой, непосредственный) - это набор
библиотек, разработанных компанией Microsoft для создания наиболее эффективных
мультимедиа-приложений под операционную систему Windows. Этот набор библиотек
активно используется при программировании компьютерных игр, симуляторов,
некоторых научных пакетов и некоторых программ создания 3д-графики.
Библиотеки DirectX обычно устанавливаются вместе с операционной системой
Windows, в момент её инсталляции на компьютер. Но лучше, всё же, самостоятельно
обновлять их, скачивая с сайта, поскольку DirectX обновляется значительно чаще,
чем выходят новые дистрибутивы операционной системы и потому желательно всегда
иметь обновлённую версию - часто она не только работает быстрее, но и устраняет
некоторые, ране наблюдавшиеся проблемы (баги, несовместимости с оборудованием и
так далее).
Для чего же
нужна трехмерная графика?
Трёхмерная (или 3D-) графика применяется далеко не только для увеличения
кассовых сборов в кино, но и в бизнесе. Её можно встретить в любых
презентационных материалах - будь то сайт или каталог, где необходимо
продемонстрировать покупателям будущие интерьеры, либо внешний вид
разрабатываемых продуктов, показать инвесторам как то или иное строение будет
смотреться в городском ландшафте. И список далеко не полный.
Процесс создания трёхмерной графики соединяет в себе как создание
художественных образов, так и математическое моделирование. Так, первым этапом
в этом процессе разработки изображения является создание модели объектов и их
размещения. Затем к объектам применяется компьютерная визуализация (или
рендеринг) , подразумевающая появление на изображении самих объектов в
соответствии с выбранными физическими моделями. После этого дизайнер
дорабатывает детали и проводит нюансировку чтобы добиться максимальной
фотографичности изображения - и в лучших работах им это удаётся.
Учитывая сложность технологических процессов создания трёхмерной графики
сроки и стоимость проектов могут отличаться в разы. Как правило, сложность
работы определяется по следующим характеристикам: ясность образа, размер
изображения, количество объектов, а также сложность и детализация частей.
Перефразируя народную мудрость, скажем: лучше один раз показать, чем сто
раз описать.
Список
источников
<http://compgraphics.info/2D/affine_transform.php>://
<http://compgraphics.info/2D/affine_transform.php>compgraphics
<http://compgraphics.info/2D/affine_transform.php><http://compgraphics.info/2D/affine_transform.php>info
<http://compgraphics.info/2D/affine_transform.php>/2
<http://compgraphics.info/2D/affine_transform.php><http://compgraphics.info/2D/affine_transform.php><http://compgraphics.info/2D/affine_transform.php>affine
<http://compgraphics.info/2D/affine_transform.php><http://compgraphics.info/2D/affine_transform.php>transform
<http://compgraphics.info/2D/affine_transform.php><http://compgraphics.info/2D/affine_transform.php>php
<http://compgraphics.info/2D/affine_transform.php>://msdn.microsoft.com/ru-ru/library/8667dchf(v=vs.110).aspx?cs-save-lang=1&cs-lang=vb#code-snippet-1
<http://msdn.microsoft.com/ru-ru/library/8667dchf(v=vs.110).aspx?cs-save-lang=1&cs-lang=vb>
<http://ru.vlab.wikia.com/wiki/%D0%9C%D0%B0%D1%82%D1%80%D0%B8%D1%86%D0%B0_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0)>
<http://netlib.narod.ru/library/book0032/part1_03.htm>
<http://netlib.narod.ru/library/book0051/ch02_01.htm>
<http://sea.2bb.ru/viewtopic.php?id=162>
<http://dev.mindillusion.ru/><http://dev.mindillusion.ru/>
<https://ru.wikipedia.org/wiki/%D0%97%D0%B0%D0%B3%D0%BB%D0%B0%D0%B2%D0%BD%D0%B0%D1%8F_%D1%81%D1%82%D1%80%D0%B0%D0%BD%D0%B8%D1%86%D0%B0>D1%81%D1%82%D1%80%D0%B0%D0%BD%D0%B8%D1%86%D0%B0
<https://ru.wikipedia.org/wiki/%D0%97%D0%B0%D0%B3%D0%BB%D0%B0%D0%B2%D0%BD%D0%B0%D1%8F_%D1%81%D1%82%D1%80%D0%B0%D0%BD%D0%B8%D1%86%D0%B0>