Эквивалентность и минимизация конечных автоматов

Федеральное агентство по образованию

Сибирская государственная автомобильно-дорожная академия (СибАДИ)

Факультет: Информационные системы в управлении

Специальность: 090103 Информационная безопасность АС

Кафедра: Информационная безопасность

Курсовая работа

по дисциплине Конечные автоматы

Тема работы: «Эквивалентность и минимизация конечных автоматов»

Выполнил: студент гр. БИ-11И1

Галкин Кирилл Андреевич

Омск - 2014

Содержание

Введение

1. Теоретическая часть

1.1 Определение автоматов Мили и Мура

1.2 Эквивалентность конечных автоматов

1.3 Минимизация конечного автомата

2. Практическая часть

Заключение

Список литературы

Введение

В данной курсовой работе будут рассмотрены основные понятия конечных автоматов, а также их эквивалентности и минимизации. Будет выполнено подробное решение нескольких типовых задач для подробного изучения алгоритмов минимизации конечных автоматов Мили и Мура.

Цель работы:

.        Ознакомиться с теоретическими основами конечных автоматов-распознавателей;

.        Представить несколько примеров построения конечных автоматов, распознающих некоторые языки.

1.     
Теоретическая часть

Конечные автоматы [1] являются математической моделью устройств, перерабатывающих дискретную входную информацию в режиме "реального времени", т.е. в темпе ее поступления (рис.1).

Рисунок 1 - Автомат

На такие устройства в последовательные дискретные моменты времени 1,2, ..., t, t+1,... поступают входные сигналы x(1),x(2), ..., x(t),x(t+1),... и в ответ на них автомат A вырабатывает выходные сигналы y(1) y(2), ..., y(t), y(t+1),.... Конечные автоматы характеризуются двумя особенностями:

1.   Отсутствие предвосхищения: выходной сигнал y(t), выдаваемый автоматом в момент t, зависит лишь от полученных к этому времени входов x(1), x(2), ..., x(t), т.е. автомат не может предвосхитить будущие входы и заранее на них отреагировать. Таким образом, имеется некоторая функция выходов λ(x(1), x(2), …, x(t)) = y(t), определяющая очередной выход по предшествующему входу.

.     Конечная память: в каждый момент t информация в автомате о полученном к этому моменту входе x(1), x(2), ..., x(t) конечна. Это свойство удобно интерпретировать следующим образом: автомат имеет конечное множество состояний S и в каждый момент находится в одном из этих состояний. При получении очередного входа состояние может измениться. Таким образом, состояние q ϵ S, в котором находится автомат после получения входной последовательности x(1), x(2), ..., x(t), и представляет информацию об этой последовательности, используемую в дальнейшей работе автомата при определении следующего состояния и выхода.

1.1 Определение автоматов Мили и Мура

Определение 1. Конечным автоматом Мили (рис.2)[2] называется шестерка объектов: А = <S, X, Y, s₀, δ, λ>, где

·        S - конечное непустое множество (состояний);

·        X - конечное непустое множество входных сигналов (входной алфавит);

·        Y - конечное непустое множество выходных сигналов (выходной алфавит);

·        s₀ - начальное состояние;

·        δ : S×X ® S - функция переходов;

·        λ : S×X ® Y - функция выходов.

Для построения графа автомата Мили (рис.2) нам необходимо обозначить его состояния в виде вершин графа, а переходы и выходы - рёбрами.

Рисунок 2 - Графическое представление автомата Мили

Кроме графического способа (рис.2) отображения для автомата можно использовать и табличное (табл.1), задавая функции переходов и выходов в виде таблиц.

Таблица 1 - Табличное представление автомата Мили (таблицы переходов и выходов)

δ	0	1	2
s0	s1	s2	s3
s1	s1	s0	s0
s2	s2	s1	s3
s3	s3	s3	s2
λ	0	1	2
s0	y1	y2	y3
s1	y1	y0	y3
s2	y1	y2	y3
s3	y1	y2	y3

Определение 2. Конечным автоматом Мура (рис.3) называется шестерка объектов А = <S, X, Y, s₀, δ, λ>, где:

·        S - множество состояний;

·        X - входной алфавит;

·        Y - выходной алфавит;

·        s0 - начальное состояние;

·        δ : S ´ X ® S - функция переходов;

·        λ: S ® Y - функция выходов.

Для построения графа автомата Мура (рис.3) нам необходимо обозначить его состояния и выходы с помощью вершин графа, а переходы - с помощью рёбер.

Рисунок 3 - Графическое представление автомат Мура

Как и в случае с автоматом Мили для автомата Мура возможно и табличное представление (табл.2).

Таблица 2 - Табличное представление автомата Мура

s	λ	δ
		0	1
s0	y1	s1	s2
s1	y2	s1	s0
s2	y2	s2	s1

1.2 Эквивалентность конечных автоматов

Пусть S - алфавит (конечное множество символов) и S* - множество всех слов в алфавите S. Будем обозначать буквой e пустое слово, т.е. вовсе не содержащее букв (символов из S), а знаком × - операцию приписывания (конкатенации) слов.

Так, аав × ва = аавва. Знак × операции приписывания часто опускают.

Слова в алфавите S будем обозначать малыми греческими буквами a, b, g, .... Очевидно, e является единицей для операции приписывания:

ae = ea = a.

Очевидно также, что операция приписывания ассоциативна, т.е. (ab)g = a(bg).

Таким образом, множество S* всех слов в алфавите S относительно операции приписывания является полугруппой с единицей, т.е. моноидом;

S* называют свободным моноидом над алфавитом S.

Определение 3. Пусть А = (S, X, Y, s₀, d, l) - конечный автомат.

Расширенными функциями перехода и выхода автомата А называются функции

d *: S ´ X* ® S и l* : S ´ X* ® Y*,

определенные так:

d *(s, e) = s; d *(s, аa) = d *(d(s, а), a);

l*(s, e) = e; l*(s, аa)=l(s, а)×l*(d(s, а), a),

где а - любая буква входного алфавита X, а a - любое слово в алфавите X , т.е. a Î X*.

Расширенные функции переходов и выходов определены на множестве входных слов, в отличие от обычных функций переходов и выходов, которые определены на множестве входных сигналов - букв алфавита.

Пусть в некоторое состояние автомата не существует пути из начального состояния. Иными словами, в эти состояния автомат не может попасть.

Такие состояния автомата называются недостижимыми, остальные - достижимыми.

Очевидно, что недостижимые состояния и переходы из них можно отбросить: они не влияют на поведение конечного автомата. Дадим формальное определение.

Определение 4. Пусть А = (S, X, Y, s₀, d, l) - конечный автомат. Состояние sÎS называется достижимым тогда и только тогда, когда

($a Î X*) d*(s₀, a) = s

(т.е. под воздействием какого-либо входного слова автомат попадает в это состояние).

Таким образом, состояние s ÎS конечного автомата является недостижимым тогда и только тогда, когда

("aÎ X*) d*(s₀, a) ¹ s

(т.е. под воздействием любого слова автомат не переходит в это состояние).

Множество D достижимых состояний КА автомата

А = (S, X, Y, s₀, d, l) строится с помощью алгоритма, основанного на индукции.

. Положим Q₀ = {s₀}.

. На i-м шаге будем строить множество Qi состояний, достижимых из начального состояния автомата некоторого слова длины не более чем i.

Очевидно, что для любого i

Q_i+1 = Q_i È {d(s, x) | sÎQ_i, xÎX}.

. Ясно также, что не более чем за n = |S| шагов Q_k+1 = Q_k.

Положим D = Q_k.

Определение 5. Конечные автоматы А = (S_A, X_A, Y_A, s_0A, d_A, l_A) и В = (S_B, X_B, Y_B, s_0B, d_B, l_B) называются эквивалентными, если выполнены два условия:

а) их входные алфавиты совпадают:

Х_A = Х_B = X;

б) реализуемые ими отображения выходов совпадают:

("aÎ X*) l*_A (s_0A,a) = l*_B (s_0B,a) .

Определение 6. Прямым произведением конечных автоматов А =(S_A, X_A, Y_A, s_0A, d_A, l_A) и В = (S_B, X_B, Y_B, s_0B, d_B, l_B).

с одинаковый входным алфавитом X называется автомат

А´В = (S_A´S_B, X, Y_A ´Y_B, (s_0A, s_0B), d_A´B, l_A´B),

где:

a)      ("s_A Î S_A) ("s_B Î S_B) ("xÎ X) d_A´B((s_A, s_B),x) = (d_A (s_A, x), d_B(s_B, x));

б) ("s_A Î S_A) ("s_B Î S_B) ("xÎ X) l_A´B((s_A, s_B), x) = (l_A (s_A, x), l_B(s_B, x)).

Теорема Мура

Два конечных автомата с одинаковым входным алфавитом X являются эквивалентными тогда и только тогда, когда для любого достижимого состояния (s_A, s_B) в их прямом произведении (рис.4) А ´ В справедливо [2]:

("xÎX) l_A (s_A, x) = l_B (s_B, x).

Прямое произведение конечных автоматов А и В, изображенных на рис. 4, представлено на рис. 4А. На рис. 4В показан этот же автомат с выброшенными недостижимыми состояниями.

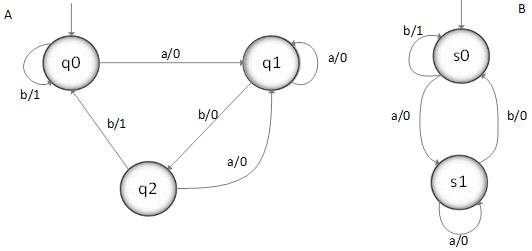
Рисунок 4 - Конечные автоматы

Рисунок 5 - Прямое произведение конечных автоматов

По графу переходов (рис.5) видно, что из всех достижимых состояний под воздействием входных сигналов автомат А ´ В выдает пары одинаковых выходных сигналов.

Следовательно, автоматы А и В эквивалентны.

1.3    Минимизация конечного автомата

Разные конечные автоматы могут функционировать одинаково, даже если у них разное число состояний. Важной задачей является нахождение минимального конечного автомата, который реализует заданное автоматное отображение [3].

Эквивалентными естественно назвать два состояния автомата, которые нельзя различить никакими входными словами.

Определение 1: Два состояния р и q конечного автомата

А = (S,X,Y,s₀,d,l) называются эквивалентными (обозначается p~q), если ("aÎ X*)l*(p,a) =l*(q, a).

Эквивалентные состояния можно объединить в один класс и построить новый автомат, состояниями которого являются классы эквивалентных состояний. Если мы можем определить на множестве состояний КА «максимально возможное» разбиение на классы эквивалентности, то, выбирая его классы эквивалентности как новые состояния, получим минимальный автомат, эквивалентный исходному.

Алгоритм минимизации КА

Алгоритм минимизации конечного автомата [3] [4] состоит в последовательном построении на множестве состояний автомата А разбиений p₀, p₁, …, p_¥, таких, что в один класс разбиения p_k попадают k-эквивалентные состояния, т.е. те, которые неразличимы входными словами длиной £ k. Такие состояния будем считать находящимися в отношении эквивалентности ~k. Если p и q не являются k-эквивалентными, то р и q назовем k-различимыми. Из определения 1 вытекает, что

р ~kq Û ("aÎ X*, |a| £ k) l*(p,a) =l*(q,a).

Очевидно, что в любом автомате все состояния 0-эквивалентны, поскольку при подаче пустого слова e на вход автомата выходом является также пустое слово e независимо от состояния, в котором автомат находится.

Следующее разбиение p1 также легко построить. Действительно, по определению в один блок p1 попадают все состояния, в которых автомат одинаково реагирует на входные сигналы: р ~1 q Û ("xÎ X) l(p, x) =l(q, x). Разбиения p₀, содержащее один единственный блок, в который входят все состояния автомата, и p₁, в каждом блоке которого собраны состояния, не различимые входными сигналами, являются исходными при построении цепочки разбиений p₀, p₁, …, p_¥.

Если мы сможем определить, как строить следующее разбиение из предыдущего, то начиная с p₁ мы сможем последовательно построить и всю цепочку.

Теорема 2. Пусть р ~k q, k > 1. Для того чтобы p ~k+1 q, необходимо и достаточно, чтобы ("xÎ X) d(p, x) ~k d(q, x).

Действительно, для того чтобы входное слово длины k+1, например, слово x₀x₁x₂…x_k, не различала пару состояний р и q, нужно всего лишь, чтобы автомат из этих состояний переходил под воздействием х0 в такие состояния, которые не различимы словом x₁x₂…x_k, т. е. чтобы d(p,x₀) и d(q,x₀) были бы k-неразличимы (см. рисунок).

Очевидно, что если р и q (k+1)-эквивалентны, то они k-эквивалентны. Иными словами, блоки разбиения p_k+1 являются подблоками разбиения p_k.

Поскольку число состояний конечно, может быть только конечное число последовательно уменьшающихся разбиений p_k, начиная с «самого крупного» разбиения p₀, содержащего один единственный блок.

Более того, очевидно, что их не больше, чем число состояний конечного автомата.

Однако последовательное построение уменьшающихся разбиений, можно не продолжать дальше, как только два последовательных разбиения совпадают, поскольку справедлива теорема:

Теорема 3. Пусть p_k+1 = p_k. Тогда i > k Þ p_i = p_k. В частности, p_k = p_¥.

Из этой теоремы следует, что как только мы получим совпадение p_k+1=p_k, то алгоритм прекращает свою работу и разбиение p_¥ = p_k будет максимальным разбиением множества состояний конечного автомата на классы эквивалентных состояний, по которому и определяется минимальный конечный автомат, эквивалентный данному.

эквивалентность автомат распознаватель минимизация

2. Практическая часть

Пример 1

Минимизация конечного автомата Мили, заданного таблицей переходов (табл. 3) проводится последовательным построением разбиений π0, π1, …

Таблица 3 - таблица переходов для примера 1

S	δ		λ
	x1	x2	x1	x2
0	1	2	y1	y2
1	3	4	y3	y2
2	4	5	y3	y2
3	6	4	y1	y2
4	6	5	y1	y2
5	6	3	y1	y2
6	6	0	y1	y2

0)      Начальное разбиение представляет собой один блок, включающий в себя все состояния, поскольку входные слова длиной 0 (пустое слово ε) не различают состояний: независимо от того, в каком состоянии автомат находился при подаче входа ε, выходом тоже будет ε.

         Поэтому π₀ = {A₀ = {0,1,2,3,4,5,6}}.

1)      Разбиение π₁ в один блок объединяет те состояния, которые нельзя различить при подаче слов длиной 1.

Функция выходов λ при подаче слов x₁ и x₂ не может различить 0,3,4,5,6 поскольку для каждого из этих состояний при подаче на вход автомата x₁ он выдаёт y₁, а при подаче на вход x₂ он выдаёт y₂.

Состояния 1 и 2 попадают в другой блок, но между собой входным словом длины 1 их различить нельзя.

Поэтому π₁ = {А₁ = {0,3,4,5,6,}, B₁ = {1,2}}

2)      Следующее разбиение π₂ объединяет в один блок те состояния, которые нельзя различить при подаче слов длиной 2.

Построим таблицу переходов (табл.2), но вместо значения состояния δ(S,x) будем писать блок разбиения π₁, в которое попадает δ(S,x).

Таким образом, например, δ(0,x₁) = 1, а это состояние находится в блоке B₁; δ(0,x₂) = 2, а это состояние находится в блоке B₁.

Таблица 4 - таблица переходов для разбиения π₂.

S	δ		λ		π1
	x1	x2	x1	x2	B1	B1
0	1	2	y1	y2	A1	A1
1	3	4	y3	y2	A1	A1
2	4	5	y3	y2	A1	A1
3	6	4	y1	y2	A1	A1
4	6	5	y1	y2	A1	A1
5	6	3	y1	y2	A1	A1
6	6	0	y1	y2	A1	A1

После такого построения видно, что состояния 0,3,4,5,6, нужно разбить на 2 блока {0} и {3,4,5,6}. Состояния 1 и 2 попадают в одни и те же блоки предыдущего разбиения π₁, поэтому они попадут в один и тот же блок разбиения π₂. Таким образом, π₂ = {A₂ = {0}, B₂ = {3,4,5,6}, C₂ = {1,2}}.

)        Аналогично строится разбиение π₃.

Таблица 5 - Таблица переходов для разбиения π₃

S	δ		λ		π1		π2
	x1	x2	x1	x2	B1	B1	C2	C2
0	1	2	y1	y2	A1	A1	B2	B2
1	3	4	y3	y2	A1	A1	B2	B2
2	4	5	y3	y2	A1	A1	B2	B2
3	6	4	y1	y2	A1	A1	B2
4	6	5	y1	y2	A1	A1	B2	B2
5	6	3	y1	y2	A1	A1	B2	B2
6	6	0	y1	y2	A1	A1	B2	A2

На данном шаге блок {3,4,5,6} нужно разбить на два блока {3,4,5} и {6}.

Таким образом, π₃ = {A₃ = {0}, B₃ = {3,4,5}, C₃ = {6}, D₃ = {1,2}}.

)        Построим π₄.

Таблица 6 - Таблица переходов для разбиения π₄

S	δ		λ		π1		π2		π3
	x1	x2	x1	x2	B1	B1	C2	C2	D3	D3
0	1	2	y1	y2	A1	A1	B2	B2	B3	B3
1	3	4	y3	y2	A1	A1	B2	B2	B3	B3
2	4	5	y3	y2	A1	A1	B2	B2	C3	B3
3	6	4	y1	y2	A1	A1	B2	B2	C3	B3
4	6	5	y1	y2	A1	A1	B2	B2	C3	B3
5	6	3	y1	y2	A1	A1	B2	B2	C3	B3
6	6	0	y1	y2	A1	A1	B2	A2	C3	A3

π₄ = {A₄ = {0}, B₄ = {3,4,5}, C₄ = {6}, D₄ = {1,2}}.

Разбиение π₄ совпадает с разбиением π₃. На основании теоремы 3 искомое разбиение π_∞ совпадает с π₃.

Итак, минимальный автомат с эквивалентным поведением имеет 4 состояния, представляющих собой блоки разбиения π₃, а его функции переходов и выходов представлены в таблице 7, а граф переходов на рис. 6.

Таблица 7 - Таблица переходов и выходов для минимизированного автомата из примера 1

S	δ		λ
	X1	X2	X1	X2
A	D	D	y1	y2
B	B	C	y1	y2
C	C	A	y1	y2
D	B	B	y3	y2

Рисунок 6 - Минимизированный автомат (пример 1)

Пример 2

Минимизация конечного автомата Мили, заданного таблицей переходов (табл. 8)

Таблица 8 - Таблица переходов для примера 2

S	δ			λ
	α	β	γ	α	β	γ
1	2	2	5	1	1	1
2	1	4	4	0	1	1
3	2	2	5	1	1	1
4	3	2	2	0	1	1
5	6	4	3	1	1	1
6	8	9	6	0	1	1
7	6	2	8	1	1	1
8	4	4	7	1	1	1
9	7	9	7	0	1	1

)        Начальное разбиение представляет собой один блок, включающий в себя все состояния, поскольку входные слова длиной 0 (пустое слово ε) не различают состояний: независимо от того, в каком состоянии автомат находился при подаче входа ε, выходом тоже будет ε.

Поэтому π₀ = {A₀ = {1,2,3,4,5,6,7,8,9}}.

)        Разбиение π₁ в один блок объединяет те состояния, которые нельзя различить при подаче слов длиной 1.

Функция выходов λ при подаче слов α, β и γ не может различить 1,3,5,7 и 8, поскольку для каждого из этих состояний при подаче на вход автомата α он выдаёт 1, при подаче на вход β - 1 и при подаче на вход γ он выдаёт 1.

Состояния 2,4,6 и 9 попадают в другой блок, но между собой входным словом длины 1 их различить нельзя.

         Поэтому π₁ = {A₁ = {1,3,5,7,8}, B₁ = {2,4,6,9}}.

)        Следующее разбиение π₂ объединяет в один блок те состояния, которые нельзя различить при подаче слов длиной 2.

Построим таблицу переходов (табл.9), но вместо значения состояния δ(S,x) будем писать блок разбиения π₁, в которое попадает δ(S,x).

Таблица 9 - Таблица переходов для разбиения π₂

S	δ			λ			π1
	α	Β	γ	α	β	γ	α	β	γ
1	2	2	5	1	1	1	B1	B1	A1
2	1	4	4	0	1	1	A1	B1	B1
3	2	2	5	1	1	1	B1	B1	A1
4	3	2	2	0	1	1	A1	B1	B1
5	6	4	3	1	1	1	B1	B1	A1
6	8	9	6	0	1	1	A1	B1	B1
7	6	2	8	1	1	1	B1	B1	A1
8	4	4	7	1	1	1	B1	B1	A1
9	7	9	7	0	1	1	A1	B1	A1

После такого построения видно, что состояния 2,4,6,9 нужно разбить на 2 блока {2,4,6} и {9}.

Таким образом, π₂ = {A₂ = {1,3,5,7,8}, B₂ = {2,4,6}, C₂ = {9}}.

3)      Аналогично π₃ (табл.10)

Таблица 10 - Таблица переходов для разбиения π₃

S	λ			π1			π2
	α	β	γ	α	β	γ	α	β	γ	α	β	γ
1	2	2	5	1	1	1	B1	B1	A1	B2	B2	A2
2	1	4	4	0	1	1	A1	B1	B1	A2	B2	B2
3	2	2	5	1	1	1	B1	B1	A1	B2	B2	A2
4	3	2	2	0	1	1	A1	B1	B1	A2	B2	B2
5	6	4	3	1	1	1	B1	B1	A1	B2	B2	A2
6	8	9	6	0	1	1	A1	B1	B1	A2	C2	B2
7	6	2	8	1	1	1	B1	B1	A1	B2	B2	A2
8	4	4	7	1	1	1	B1	B1	A1	B2	B2	A2
9	7	9	7	0	1	1	A1	B1	A1	A2	C2	A2

На данном шаге блок {2,4,6} нужно разбить на два блока {2,4} и {6}. Таким образом, π₃ = {A₃ = {1,3,5,7,8}, B₃ = {2,4} C₃ = {6}, D₃ = {9}}.

)        Построим π₄ (табл.11)

Таблица 11 - Таблица переходов для разбиения π₄

S

δ

λ

π1

π2

π3

α

β

γ

α

β

γ

α

β

γ

α

β

γ

α

β

γ

1

2

2

5

1

1

1

B1

B1

A1

B2

B2

A2

B3

B3

A3

2

1

4

4

0

1

1

A1

B1

B1

A2

B2

B2

A3

B3

B3

3

2

2

5

1

1

1

B1

B1

A1

B2

B2

A2

B3

B3

B3

4

3

2

2

0

1

1

A1

B1

B1

A2

B2

B2

A3

B3

B3

5

6

4

3

1

1

1

B1

B1

A1

B2

B2

A2

C3

B3

A3

6

8

9

6

0

1

1

A1

B1

B1

A2

C2

B2

A3

D3

C3

7

6

2

8

1

1

1

B1

B1

A1

B2

B2

A2

C3

B3

A3

8

4

4

7

1

1

1

B1

B1

A1

B2

B2

A2

B3

B3

A3

9

7

9

7

0

1

1

A1

B1

A1

A2

C2

A2

A3

D3

A3

На данном шаге блок {1,3,5,7,8} нужно разбить на два блока {1,3,8} и {5,7}.

π₄ = {A₄ = {1,3,8}, B₄ = {5,7} C₄ = {2,4}, D₄ = {6}, E₄ = {9}}.

)        Построим π₅ (табл.12)

Таблица 12 - Таблица переходов для разбиения π₅

S

δ

λ

π1

π2

π3

π4

α

β

γ

α

β

Γ

α

β

γ

α

β

γ

α

β

γ

α

β

γ

1

2

2

5

1

1

1

B1

B1

A1

B2

B2

A2

B3

B3

A3

C4

C4

B4

2

1

4

0

1

1

A1

B1

B1

A2

B2

B2

A3

B3

B3

A4

C4

C4

3

2

2

5

1

1

1

B1

B1

A1

B2

B2

A2

B3

B3

B3

C4

C4

B4

4

3

2

2

0

1

1

A1

B1

B1

A2

B2

B2

A3

B3

B3

A4

C4

C4

5

6

4

3

1

1

1

B1

B1

A1

B2

B2

A2

C3

B3

A3

D4

C4

A4

6

8

9

6

0

1

1

A1

B1

B1

A2

C2

B2

A3

D3

C3

A4

E4

D4

7

6

2

8

1

1

1

B1

B1

A1

B2

B2

A2

C3

B3

A3

D4

C4

A4

8

4

4

7

1

1

1

B1

B1

A1

B2

B2

A2

B3

B3

A3

C4

C4

B4

9

7

9

7

0

1

1

A1

B1

A1

A2

C2

A2

A3

D3

A3

B4

E4

B4

π₅ = {A₅ = {1,3,8}, B₅ = {5,7} C₅ = {2,4}, D₅ = {6}, E₅ = {9}}.

Разбиение π₅ совпадает с разбиением π₄. На основании теоремы 3 искомое разбиение π_∞ совпадает с π₄.

Итак, минимальный автомат с эквивалентным поведением имеет 4 состояния, представляющих собой блоки разбиения π₄, а его функции переходов и выходов представлены в таблице 13, а граф переходов на рисунке 7.

Таблица 13 - Таблица переходов и выходов для минимизированного автомата из примера 2.

S	δ			λ
	α	β	γ	α	β	γ
A	C	C	B	1	1	1
B	D	C	A	1	1	1
C	A	C	C	0	1	1
D	A	E	D	0	1	1
E	B	E	B	0	1	1

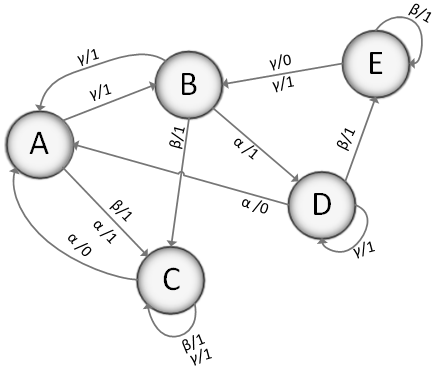
Рисунок 7 - Минимизированный автомат (пример 2)

Пример 3

Минимизация конечного автомата Мура, заданного таблицей переходов (табл. 14)

Таблица 14 - Таблица переходов для примера 3

S	λ	δ
		x1	x2
1	y1	1	5
2	y2	2	5
3	y1	3	5
4	y1	4	2
5	y1	1	7
6	y1	2	2
7	y2	1	2

)        Начальное разбиение представляет собой один блок, включающий в себя все состояния, поскольку входные слова длиной 0 (пустое слово ε) не различают состояний: независимо от того, в каком состоянии автомат находился при подаче входа ε, выходом тоже будет ε.

Поэтому π₀ = {A₀ = {1,2,3,4,5,6,7}}.

)        Разбиение π₁ в один блок объединяет те состояния, которые нельзя различить при подаче слов длиной 1.

Состояния 2 и 7 попадают в другой блок, но между собой входным словом длины 1 их различить нельзя.

Поэтому π₁ = {А₁ = {1,3,4,5,6}, B₁ = {2,7}}

)        Следующее разбиение π₂ объединяет в один блок те состояния, которые нельзя различить при подаче слов длиной 2.

Построим таблицу переходов (табл.15), но вместо значения состояния δ(S,x) будем писать блок разбиения π₁, в которое попадает δ(S,x).

Таблица 15 - таблица переходов для разбиения π₂.

S	λ	δ		π1
		x1	x2	x1	x2
1	y1	1	5	A1	A1
2	y2	2	5	B1	A1
3	y1	3	5	A1	A1
4	y1	4	2	A1	B1
5	y1	1	7	A1	B1
6	y1	2	2	B1	B1
7	y2	1	2	A1	B1

После такого построения видно, что состояния 1,3,4,5,6 нужно разбить на 3 блока {1,3}, {4,5}, {6}, а состояния 2,7 - на два блока {2}, {7}.

Таким образом, π₂ = {A₂ = {1,3}, B₂ = {4,5}, C₂ = {6}, D₂ ={2}, E₂={7}}.

3)      Переходы состояний 2,6,7 теперь можно не рассматривать, поскольку классы распались до первого элемента и меньше уже не станут. Обозначим это символами «-» в таблице.

Таблица 16 - Таблица переходов для разбиения π₃

S	λ	δ		π1		π2
		x1	x2	x1	x2	x1	x2
1	y1	1	5	A1	A1	A2	B2
2	y2	2	5	B1	A1	-	-
3	y1	3	5	A1	A1	A2	B2
4	y1	4	2	A1	B1	B2	D2
5	y1	1	7	A1	B1	A2	E2
6	y1	2	B1	B1	-	-
7	y2	1	2	A1	B1	-	-

π₃ = {A₃ = {1,3}, B₃ = {4}, C₃ = {5}, D₃ = {6}, E₃={2}, F₃={7}}.

4)      Построим π₄. Переходы состояний 4,5 также можно не рассматривать далее, поскольку классы не станут меньше в дальнейших итерациях.

Таблица 17 - Таблица переходов для разбиения π₄

S	λ	δ		π1		π2		π3
		x1	x2	x1	x2	x1	x2	x1	x2
1	y1	1	5	A1	A1	A2	B2	A3	C3
2	y2	2	5	B1	A1	-	-	-	-
3	y1	3	5	A1	A1	A2	B2	A3	C3
4	y1	4	2	A1	B1	B2	D2	-	-
5	y1	1	7	A1	B1	A2	E2	-	-
6	y1	2	2	B1	B1	-	-	-	-
7	y2	1	2	A1	B1	-	-	-	-

π₄ = {A₄ = {1,3}, B₄ = {4}, C₄ = {5}, D₄ = {6}, E₄={2}, F₄={7}}.

Разбиение π₄ совпадает с разбиением π₃. На основании теоремы 3 искомое разбиение π_∞ совпадает с π₃.

Итак, минимальный автомат с эквивалентным поведением имеет 4 состояния, представляющих собой блоки разбиения π₃, а его функции переходов и выходов представлены в таблице 18, а граф переходов на рисунке 8.

Таблица 18 - Таблица переходов и выходов для минимизированного автомата из примера 3.

S	δ		λ
	X1	X2
A	A	C	y1
B	B	E	y1
C	A	F	y1
D	E	E	y1
E	E	C	y2
F	A	E	y2

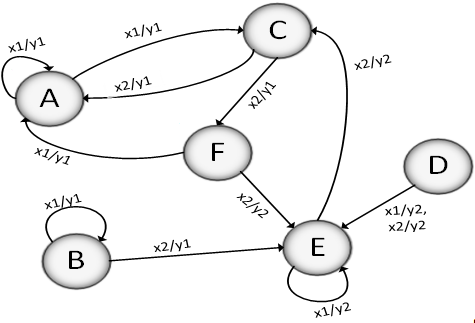
Рисунок 8 - Минимизированный автомат (пример 3)

Пример 4

Минимизация конечного автомата Мура, заданного таблицей переходов (табл. 19)

Таблица 19 - Таблица переходов для примера 4

S	λ	δ
		x1	x2	x3
a	y1	d	a	e
b	y1	g	b	b
c	y2	g	b	b
d	y2	d	b	g
e	y1	d	b	g
f	y1	c	a	d
g	y2	g	b	d

0)      В данном примере начальное разбиение будет представлять собой два блока, включающих в себя все состояния.

Поэтому π₀ = {A₀ = {a,b,e,f}, B₀ = {c,d,g}}.

1)      Разбиение π₁ в один блок объединяет те состояния, которые нельзя различить при подаче слов длиной 1.

Таблица 20 - Таблица переходов для разбиения π₁

S	λ	δ			π0
		x1	x2	x3	x1	x2	x3
a	y1	d	a	e	B0	A0	A0
b	y1	g	b	b	B0	A0	A0
c	y2	g	b	b	B0	A0	A0
d	y2	d	b	g	B0	A0	B0
e	y1	d	b	g	B0	A0	B0
f	y1	c	a	d	B0	A0	B0
g	y2	g	b	d	B0	A0	B0

π₁ = {А₁ = {a,b}, B₁ = {e,f}, C₁ = {c}, D₁ = {d,g}}.

2)      Следующее разбиение π₂ объединяет в один блок те состояния, которые нельзя различить при подаче слов длиной 2.

Построим таблицу переходов (табл.21), но вместо значения состояния δ(S,x) будем писать блок разбиения π₁, в которое попадает δ(S,x).

Переходы состояния «с» теперь можно не рассматривать, поскольку классы распались до первого элемента и меньше уже не станут. Обозначим это символами «-» в таблице.

Таблица 21 - таблица переходов для разбиения π₂.

S	λ	δ			π0			π1
		x1	x2	x3	x1	x2	x3	x1	x2	x3
a	y1	d	a	e	B0	A0	A0	D1	A1	B1
b	y1	g	b	b	B0	A0	A0	D1	A1	A1
c	y2	g	b	b	B0	A0	A0	-	-	-
d	y2	d	b	g	B0	A0	B0	D1	D1	D1
e	y1	d	b	g	B0	A0	B0	D1	D1	D1
f	y1	c	a	d	B0	A0	B0	C1	D1	D1
g	y2	g	b	d	B0	A0	B0	C1	D1	D1

После построения видно, что состояния a,b и e,f нужно разбить на 2 блока {a}, {b} и {e}, {f}.

Таким образом, π₂ = {A₂ = {a}, B₂ = {b}, C₂ = {e}, D₂ ={f}, E₂={c}, F₂ = {d,g}}.

)        Построим разбиение π₃. Построим разбиение π₃. Переходы состояний «a», «b», «e», «f» можно не рассматривать далее, поскольку классы распались до первого элемента. Обозначим это символами «-» в таблице.

Таблица 22 - Таблица переходов для разбиения π₃

S

δ

π0

π1

π2

x1

x2

x3

x1

x2

x3

x1

x2

x3

x1

x2

x3

a

y1

d

a

e

B0

A0

A0

D1

A1

B1

-

-

-

b

y1

g

b

b

B0

A0

A0

D1

A1

A1

-

-

-

c

y2

g

b

b

B0

A0

A0

-

-

-

-

-

-

d

y2

d

b

g

B0

A0

B0

D1

D1

D1

F2

B2

F2

e

y1

d

b

g

B0

A0

B0

D1

D1

D1

-

-

-

f

y1

c

a

d

B0

A0

B0

C1

D1

D1

-

-

-

g

y2

g

b

d

B0

A0

B0

C1

D1

D1

F2

B2

F2

π₃ = {A₃ = {a}, B₃ = {b}, C₃ = {e}, D₃ ={f}, E₃={c}, F₃ = {d,g}}.

Разбиение π₃ совпадает с разбиением π₂. На основании теоремы 3 искомое разбиение π_∞ совпадает с π₂.

Итак, минимальный автомат с эквивалентным поведением имеет 4 состояния, представляющих собой блоки разбиения π₃, а его функции переходов и выходов представлены в таблице 23, а граф переходов на рис. 9.

Таблица 23 - Таблица переходов и выходов для минимизированного автомата из примера 1

S	δ			λ
	X1	X2	X3
A	F	A	C	y1
B	F	B	B	y1
C	F	B	F	y1
D	E	A	F	y1
E	F	B	B	y2
F	F	B	F	y2

Рисунок 9 - Минимизированный автомат (пример 4)

Заключение

В процессе написания данной курсовой работы были изучены конечные автоматы Мили и Мура, эквивалентность и их минимизация. Подробно разобраны примеры решения типовых задач.

Список литературы

1)  НОУ Интуит, лекция «Конечные автоматы»

2)      Карпов Ю.Г. Теория автоматов [Учебное издание для вузов]. Издательство: «Питер», 2003г., 206 стр.

)        НОУ Институт, лекция «Минимизация и эквивалентность конечных автоматов»

)        Минимизация конечных автоматов