Создание фракталов
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Кафедра информатики и вычислительной
математики
Курсовая работа
Создание фракталов
Научный руководитель:
2010 г.
Введение
Фракталы вокруг нас повсюду, и в очертаниях гор, и в извилистой линии морского
берега. Некоторые из фракталов непрерывно меняются, подобно движущимся облакам
или мерцающему пламени, в то время как другие, подобно деревьям или нашим
сосудистым системам, сохраняют структуру, приобретенную в процессе эволюции.
Х. О. Пайген и П. Х. Рихтер
Существует большое число математических объектов называемых фракталами:
треугольник Серпинского, снежинка Коха, кривая Пеано, множество Мандельброта,
лоренцевы аттракторы. Фракталы с большой точностью описывают многие физические
явления и природные образования: горы, облака, турбулентные течения, корни,
ветви и листья деревьев, кровеносные сосуды, что далеко не соответствует
простым геометрическим фигурам.
Термин «фрактал» был введен Б.Мандельбротом в 1975 г.. Согласно
Мандельброту, фракталом (от лат. «fractus» - дробный, ломанный, разбитый)
называется структура, состоящая из частей, подобных целому. В более широком
смысле под фракталами понимают множества точек в евклидовом пространстве,
имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа),
либо метрическую размерность, строго большую топологической.
Определение 1: Фракталами называют бесконечно самоподобные фигуры, каждый
фрагмент которых повторяется при уменьшении масштаба.
Определение 2: Фрактал - это геометрическая фигура, состоящая из частей и
которая может быть поделена на части, каждая из которых будет представлять
уменьшенную копию целого (по крайней мере, приблизительно).
Фрактал - это такой объект, для которого не важно, с каким усилением его
рассматривать в увеличительное стекло, но при всех его увеличениях структура
остается одной и той же. Большие по масштабу структуры полностью повторяют
структуры, меньшие по масштабу.
Следует отметить, что слово «фрактал» не является математическим термином
и не имеет общепринятого строгого математического определения. Оно может
употребляться, когда рассматриваемая фигура обладает какими-либо из
перечисленных ниже свойств:
· Обладает
нетривиальной структурой на всех шкалах. В этом отличие от регулярных фигур
(таких, как окружность, эллипс <#"786118.files/image001.gif">
Рис.1. Кривая Пеано
На первом шаге он брал прямую линию и заменял ее на 9 отрезков длинной в
3 раза меньшей, чем длинна исходной линии (Часть 1 и 2 рис.1). Далее он делал
то же самое с каждым отрезком получившейся линии. И так до бесконечности. Ее
уникальность в том, что она заполняет всю плоскость. Доказано, что для каждой
точки на плоскости можно найти точку, принадлежащую линии Пеано. Кривая Пеано и
пыль Кантора выходили за рамки обычных геометрических объектов. Они не имели
четкой размерности. Пыль Кантора строилась вроде бы на основании одномерной
прямой, но состояла из точек (размерность 0). А кривая Пеано строилась на
основании одномерной линии, а в результате получалась плоскость. Во многих
других областях науки появлялись задачи, решение которых приводило к странным
результатам, на подобие описанных выше (Броуновское движение, цены на акции).
Эти удивительные фигуры стали широко известны в 70-х годах прошлого века
благодаря Бенуа Мандельброту, работавшему тогда математическим аналитиком в
фирме IBM. Сопоставляя факты, он пришел к
открытию нового направления в математике - фрактальной геометрии. Он придумал и
само слово «фрактал», которое образовано от латинского fractus - дробный».
Рождение фрактальной геометрии принято связывать с выходом в 1977 году
книги Мандельброта «Фрактальная геометрия природы». Фрактальная геометрия - это
один из разделов теории хаоса. Фракталами называют бесконечно самоподобные
фигуры, каждый фрагмент которых повторяется при уменьшении масштаба. Масштабная
инвариантность, наблюдаемая во фракталах, может быть либо точной, либо
приближенной. Самоподобное множество - множество, представимое в виде
объединения одинаковых непересекающихся подмножеств подобных исходному
множеству.
Классификации фракталов
фрактал кох серпинский
Существует множество классификаций фракталов. В основном фракталы делят
на геометрические, алгебраические и стохастические. Однако существуют и другие
классификации:
· Рукотворные и природные. К рукотворным относятся те фракталы,
которые были придуманы учёными, они при любом масштабе обладают фрактальными
свойствами. На природные фракталы накладывается ограничение на область
существования - то есть максимальный и минимальный размер, при которых у
объекта наблюдаются фрактальные свойства.
· Детерминированные (алгебраические и геометрические) и
недетерминированные (стохастические).
Геометрические фракталы применяются для получения изображений деревьев,
кустов, береговых линий и т. д. Алгебраические и стохастические - при
построении ландшафтов, поверхности морей, карт раскраски, моделей биологических
объектов и др.
Основные свойства фракталов:
· Они имеют тонкую структуру, т.е. содержат произвольно малые
масштабы.
· Они слишком нерегулярны, чтобы быть описанными на
традиционном геометрическом языке.
· Они имеют некоторую форму самоподобия, допуская приближенную.
· Они имеют дробную «фрактальную» размерность, называемую также
размерностью Минковского. (для самоподобных множеств, типа канторового
множества)
Геометрические фракталы.
История фракталов началась с геометрических фракталов, которые
исследовались математиками в XIX веке.
Фракталы этого класса самые наглядные. В двухмерном случае их получают с
помощью некоторой ломаной (или поверхности в трехмерном случае), называемой
генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную,
заменяется на ломаную - генератор, в соответствующем масштабе. В результате
бесконечного повторения этой процедуры (а точнее, при переходе к пределу)
получается фрактальная кривая. При видимой сложности полученной кривой, её
общий вид задается только формой генератора.
Примерами таких кривых служат:
· кривая дракона;
· кривая Коха - несамопересекающаяся непрерывная кривая
бесконечной длины, не имеющая касательной ни в одной точке;
· кривая Леви;
· кривая Минковского;
· кривая Пеано - непрерывная кривая, проходящая через все точки
квадрата.
К геометрическим фракталам также относят фракталы, получаемые похожими
процедурами, например:
· множество Кантора - нигде не плотное несчётное совершенное
множество. Модифицировав процедуру, можно также получить нигде не плотное множество
положительной длины.
· треугольник Серпинского - аналог множества Кантора на
плоскости.
· коврик Серпинского - аналог множества Кантора на плоскости.
· губка Менгера - аналог множества Кантора в трёхмерном
пространстве.
· дерево Пифагора.
В машинной графике использование геометрических фракталов необходимо при
получении изображений деревьев, кустов, береговой линии. Двухмерные
геометрические фракталы используются для создания объемных текстур (рисунка на
поверхности объекта).
Снежинка
Коха.
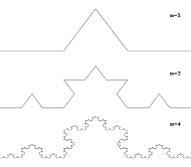
Рис
2. Построение триадной кривой Коха
Из
этих геометрических фракталов очень интересным и довольно знаменитым является
кривая Коха (снежинка Коха). Строится она на основе равностороннего
треугольника, каждая сторона которого единичной длины. На рис.2 показана одна
сторона треугольника (одно звено) - это 0-е поколение кривой Коха. Далее каждое
звено (в нулевом поколении один отрезок) заменяется на образующий элемент,
обозначенный на рис.2 через n=1. В результате такой замены получается следующее
поколение кривой Коха. В 1-ом поколении - это кривая из четырех прямолинейных
звеньев, каждое длиной по 1/3 исходной. Для получения 3-го поколения
проделываются те же действия - каждое звено заменяется на уменьшенный
образующий элемент. Итак, для получения каждого последующего поколения, все
звенья предыдущего поколения необходимо заменить уменьшенным образующим
элементом. Таким образом, с каждой итерацией длина кривой увеличивается на
треть. Кривая n-го поколения при любом конечном n называется предфракталом. На
рис.1 представлены пять поколений кривой. При n стремящемся к бесконечности
кривая Коха становится фрактальным объектом, который покрывает ограниченную
площадь (рис. 3).

Рис.
3. Треугольник Серпинского
Для
построения треугольника Серпинского (рис.4) из центра треугольника мысленно
вырежем кусок треугольной формы, который своими вершинами будет упираться в
середины сторон исходного треугольника. Повторим эту же процедуру для трех
образовавшихся треугольников (за исключением центрального) и так до
бесконечности. Если мы теперь возьмем любой из образовавшихся треугольников и
увеличим его - получим точную копию целого. В данном случае мы имеем дело с
полным самоподобием.
Рис. 4.
Драконова ломаная
Драконова ломаная относится к классу самоподобных рекурсивно порождаемых
геометрических структур. Пусть образующим элементом будут два равных отрезка,
соединенных под прямым углом. В нулевом поколении заменим единичный отрезок на
этот образующий элемент так, чтобы угол был сверху. Можно сказать, что при
такой замене происходит смещение середины звена.
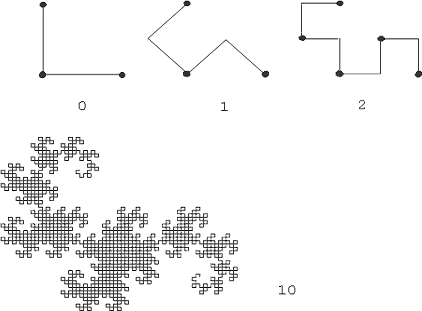
Рис
5. Построение "дракона" Хартера-Хейтуэя
При построении следующих поколений выполняется правило: самое первое
слева звено заменяется на образующий элемент так, чтобы середина звена
смещалась влево от направления движения, а при замене следующих звеньев,
направления смещения середин отрезков должны чередоваться (каждый первый угол
оказывается "вывернутым" наружу, а каждый второй - вовнутрь). На
рисунке проиллюстрирован алгоритм построения драконовой ломаной и изображен
вполне взрослый "дракон" десятого порядка. Предельная фрактальная
кривая (при n стремящемся к бесконечности) называется драконом Хартера-Хейтуэя.
Алгебраические фракталы.
Для построения алгебраических фракталов используются итерации нелинейных
отображений, задаваемых простыми алгебраическими формулами. Интерпретируя
нелинейный итерационный процесс, как дискретную динамическую систему, можно
пользоваться терминологией теории этих систем: фазовый портрет, установившийся
процесс, аттрактор и т.д.
Наиболее изучен случай, когда динамическая система задаётся итерациями
многочлена или голоморфной функции комплексной переменной на плоскости. Первые
исследования в этой области относятся к началу XX века и связаны с именами Фату
и Жюлиа.
Известно, что нелинейные динамические системы обладают несколькими
устойчивыми состояниями. То состояние, в котором оказалась динамическая система
после некоторого числа итераций, зависит от ее начального состояния. Поэтому
каждое устойчивое состояние (или как говорят - аттрактор) обладает некоторой
областью начальных состояний, из которых система обязательно попадет в
рассматриваемые конечные состояния. Таким образом, фазовое пространство системы
разбивается на области притяжения аттракторов. Если фазовым является двухмерное
пространство, то, окрашивая области притяжения различными цветами, можно
получить цветовой фазовый портрет этой системы (итерационного процесса). Меняя
алгоритм выбора цвета, можно получить сложные фрактальные картины с
причудливыми многоцветными узорами. Неожиданностью для математиков стала
возможность с помощью примитивных алгоритмов порождать очень сложные
нетривиальные структуры.
Примеры алгебраических фракталов:
· множество Мандельброта;
· множество Жюлиа;
· бассейны Ньютона;
· биоморфы
<#"786118.files/image006.gif">. Для
всех точек прямоугольной или квадратной области на комплексной плоскости
вычисляем достаточно большое количество раз zi + 1 = F(zi), каждый раз находя
абсолютное значение z. При этом значения функции для разных точек комплексной
плоскости могут иметь разное поведение:
· С течением времени | z | стремится к бесконечности;
· | z | стремится к 0;
· | z | принимает несколько фиксированных значений и не выходит
за их пределы;
· Поведение | z | хаотично, без каких-либо тенденций.
Множества значений z0, для которых последовательность демонстрирует один
конкретный тип поведения, а также множества точек бифуркации между различными
типами, часто обладают фрактальными свойствами.

Рис.6.
Множество Жюлиа
Другой
вариант получения фрактальных множеств - введение параметра в многочлен F(z) и
рассмотрение множества тех значений параметра, при которых последовательность
zn демонстрирует определённое поведение при фиксированном z0. Так, множество
Мандельброта - это множество всех 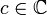 , при
которых zn для F(z) = z2 + c и z0 = 0 не стремится к бесконечности.
, при
которых zn для F(z) = z2 + c и z0 = 0 не стремится к бесконечности.
Ещё
один известный пример такого рода - бассейны Ньютона.
Одним
из самых распространённых способов раскрашивания точек будет сравнение | z | с
заранее выбранным числом, которое считается «бесконечным», т. е. цвет точки
равен номеру итерации, на которой | z | достиг «бесконечности», или чёрному в
противном случае.
Также
можно изменить вид фрактала, если контроль значения z вести другим образом,
например:
· Действительная часть z меньше определённого числа;
· Мнимая часть z меньше определённого числа;
· И мнимая и действительная части z меньше какого-либо числа;
· Другие способы.

Рис.
7. Фрактальная форма подвида цветной капусты (Brassica сauliflora)
И,
наконец, ещё один интересный эффект - изменение палитры. После того, как изображение
построено, можно циклически изменять цвета закрашенных областей, и тогда и без
того удивительное изображение «оживёт» на экране.
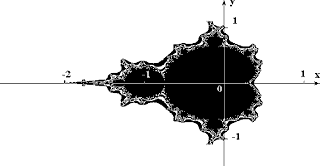
Рис 8. Множество Мандельброта
В качестве примера рассмотрим множество Мандельброта (см. pис.8 и рис.9).
Алгоритм его построения основан на простом итеративном выражении:
[i+1] = Z[i] * Z[i] + C,
где Z[i] и C - комплексные переменные. Итерации выполняются для каждой
стартовой точки C прямоугольной или квадратной области - подмножестве
комплексной плоскости. Итерационный процесс продолжается до тех пор, пока Z[i]
не выйдет за пределы окружности радиуса 2, центр которой лежит в точке (0,0),
(это означает, что аттрактор динамической системы находится в бесконечности),
или после достаточно большого числа итераций (например, 200-500) Z[i] сойдется
к какой-нибудь точке окружности. В зависимости от количества итераций, в
течение которых Z[i] оставалась внутри окружности, можно установить цвет точки
C (если Z[i] остается внутри окружности в течение достаточно большого
количества итераций, итерационный процесс прекращается, и эта точка растра
окрашивается в черный цвет).

Рис 9. Участок границы множества Мандельброта, увеличенный в 200 pаз
Вышеописанный алгоритм дает приближение к так называемому множеству
Мандельброта. Множеству Мандельброта принадлежат точки, которые в течение
бесконечного числа итераций не уходят в бесконечность (точки, имеющие черный
цвет). Точки, принадлежащие границе множества (именно там возникает сложные
структуры), уходят в бесконечность за конечное число итераций, а точки, лежащие
за пределами множества, уходят в бесконечность через несколько итераций (белый
фон).
Стохастические
фракталы.
Кривая
Коха, как бы ни была похожа на границу берега, не может выступать в качестве её
модели из-за того, что она всюду одинакова, самоподобна, слишком «правильна».
Все природные объекты создаются по капризу природы, в этом процессе всегда есть
случайность. Фракталы, при построении которых в итеративной системе случайным
образом изменяются какие-либо параметры, называются стохастическими. К этому
классу фракталов относится и фрактальная монотипия, или стохатипия
<#"786118.files/image012.gif">
Рис.10.
Рандомизированный фрактал на основе множества Жюлиа
Рандомизованный (стохастический) фрактал строится по обычному алгоритму,
за исключением того, что при вычислении на каждой итерации добавляются
случайные величины.
Плазма
Типичный представитель данного класса фракталов "Плазма". Для
её построения возьмём прямоугольник и для каждого его угла определим цвет.
Далее находим центральные точки прямоугольника и его сторон, и раскрашиваем их
в цвет, равный среднему арифметическому цветов по углам прямоугольника плюс
некоторое случайное число, пропорциональное размеру разбиваемого
прямоугольника. Прямоугольник разбиваем на 4 равных прямоугольника, к каждому
из которых применяется та же процедура. Далее процесс повторяется. Чем больше
случайное число - тем более «рваным» будет рисунок.

Рис.11.
Плазма
Если
мы теперь скажем, что цвет точки это высота над уровнем моря - получим вместо
плазмы - горный массив. Именно на этом принципе моделируются горы в большинстве
программ. С помощью алгоритма, похожего на плазму, строится карта высот, к ней
применяются различные фильтры, накладывается текстура и т. д.
Системы
итерируемых функций
Метод
"Систем Итерируемых Функций" (Iterated Functions System - IFS)
появился в середине 80-х годов как простое средство получения фрактальных
структур.
В программе IFS Builder 3d собраны последние достижения в области
трёхмерного фракталостроительства. С помощью IFS Builder 3d, можно строить
трехмерные фракталы, стереоизображения (т. е. 2 изображения, посмотрев сквозь
которые, можно увидеть одно трёхмерное) и анимации фракталов - их движение,
полёт в глубь и морфинг (изменения формы и превращения одного фрактала в
другой).представляет собой систему функций из некоторого фиксированного класса
функций, отображающих одно многомерное множество на другое. Наиболее простая
IFS состоит из аффинных преобразований плоскости:
X' = A*X + B*Y + C
Y' = D*X + E*Y + F
В 1988 году известные американские специалисты в теории динамических
систем и эргодической теории Барнсли и Слоан предложили некоторые идеи,
основанные на соображениях теории динамических систем, для сжатия и хранения
графической информации. Они назвали свой метод методом фрактального сжатия
информации. Происхождение названия связано с тем, что геометрические образы,
возникающие в этом методе, обычно имеют фрактальную природу в смысле
Мандельброта.
На основании этих идей Барнсли и Слоан создали алгоритм, который, по их
утверждению, позволит сжимать информацию в 500-1000 раз. Вкратце метод можно
описать следующим образом. Изображение кодируется несколькими простыми
преобразованиями (в нашем случае аффинными), т.е. коэффициентами этих
преобразований (в нашем случае A,B,C,D,E,F).
Например, закодировав какое-то изображение двумя аффинными
преобразованиями, мы однозначно определяем его с помощью 12-ти коэффициентов.
Если теперь задаться какой-либо начальной точкой (например, X=0 Y=0) и
запустить итерационный процесс, то мы после первой итерации получим две точки,
после второй - четыре, после третьей - восемь и т.д. Через несколько десятков
итераций совокупность полученных точек будет описывать закодированное
изображение. Но проблема состоит в том, что очень трудно найти коэффициенты
IFS, которая кодировала бы произвольное изображение.
Для построения IFS применяют кроме аффинных и другие классы простых
геометрических преобразований, которые задаются небольшим числом параметров.
Например, проективные:
X' = (A1*X + B1*Y + C1) / (D1*X + E1*Y + F1)
Y' = (A2*X + B2*Y + C2) / (D2*X + E2*Y + F2)
или квадратичные:
X' = A1*X*X + B1*X*Y + C1*Y*Y + D1*X + E1*Y + F1
Y' = A2*X*X + B2*X*Y + C2*Y*Y + D2*X + E2*Y + F2
преобразования на плоскости.
В качестве примера использования IFS для построения фрактальных структур,
рассмотрим кривую Коха (Рис.2{пункт «геометрические фракталы»}) и
"дракона" Хартера-Хейтуэя (Рис.5{пункт «геометрические фракталы»}).
Выделим в этих структурах подобные части и, для каждой из них вычислим
коэффициенты аффинного преобразования. В аффинный коллаж будет включено столько
аффинных преобразований, сколько существует частей подобных целому изображению.
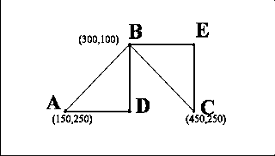
Рис
12. Заготовка для построения IFS "дракона" Хартера-Хейтуэя
Построим IFS для "дракона" Хартера-Хейтуэя. Для этого
расположим первое поколение этого фрактала на сетке координат дисплея 640 x 350
(Рис.12). Обозначим точки получившейся ломаной A, B, C. По правилам построения
({пункт «геометрические фракталы»}) у этого фрактала две части, подобные целому
- на рис.12 это ломаные ADB и BEC. Зная координаты концов этих отрезков, можно
вычислить коэффициенты двух аффинных преобразований, переводящих ломаную ABC в
ADB и BEC:
X' =
-0.5*X -0.5*Y + 490
Y' =
0.5*X -0.5*Y + 120
X' =
0.5*X -0.5*Y + 340
Y' =
0.5*X +0.5*Y - 110
Задавшись начальной стартовой точкой (например, X=0 Y=0) и итерационно
действуя на нее этой IFS, после десятой итерации на экране получим фрактальную
структуру, изображенную на рис.13, которая представляет собой
"дракон" Хартера-Хейтуэя. Его кодом (сжатым описанием) является набор
коэффициентов двух аффинных преобразований.

Рис
13. "Дракон" Хартера-Хейтуэя, построенный с помощью IFS в
прямоугольнике 640x350
Аналогично можно построить IFS для кривой Кох. Нетрудно видеть, что эта
кривая имеет четыре части, подобные целой кривой ({пункт «геометрические
фракталы»} рис.2). Для нахождения IFS опять расположим первое поколение этого
фрактала на сетке координат дисплея 640 x 350 (Рис.14).
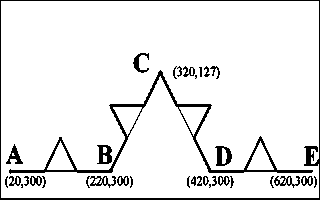
Рис
14. Заготовка для построения IFS кривой Кох
Для
ее построения требуется набор аффинных преобразований, состоящий из четырех
преобразований:
X' = 0.333*X + 13.333' = 0.333*Y + 200' = 0.333*X +
413.333' = 0.333*Y + 200' = 0.167*X + 0.289*Y + 130' = -0.289*X + 0.167*Y +
256' = 0.167*X - 0.289*Y + 403' = 0.289*X +
0.167*Y + 71
Результат
применения этого аффинного коллажа после десятой итерации можно увидеть на
рис.15.

Рис
15. Кривая Кох, построенная с помощью IFS в прямоугольнике 640x350
Использование
IFS для сжатия обычных изображений (например, фотографий) основано на выявлении
локального самоподобия, в отличие от фракталов, где наблюдается глобальное
самоподобие и нахождение IFS не слишком сложно (мы сами в этом убедились). По
алгоритму Барнсли происходит выделение в изображении пар областей, меньшая из
которых подобна большей, и сохранение нескольких коэффициентов, кодирующих преобразование,
переводящее большую область в меньшую. Требуется, чтобы множество
"меньших" областей покрывало все изображение. При этом в файл,
кодирующий изображения будут записаны не только коэффициенты, характеризующие
найденные преобразования, но и местоположение и линейные размеры
"больших" областей, которые вместе с коэффициентами будут описывать
локальное самоподобие кодируемого изображения. Восстанавливающий алгоритм, в
этом случае, должен применять каждое преобразование не ко всему множеству
точек, получившихся на предыдущем шаге алгоритма, а к некоторому их
подмножеству, принадлежащему области, соответствующей применяемому
преобразованию.
системы
Любителям фракталов и математических картинок известны фантастические
изображения растений, полученные с помощью программ. Это так называемые
L-системы. В основе их построения лежат два принципа. Первый - это так
называемая «черепашья графика» (оператор draw) патриарха GWBASIC и его детей
Turbo Basic и QBasic, когда движение рисуется пошагово в приращениях относительно
текущей точки. Либо моделируется данное поведение, задавая движение в
приращениях координат. Второй принцип - изюминка метода: каждое единичное
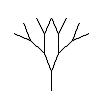
движение заменяется на весь рисунок. Например, нарисуем вилку-рогатульку. На
следующем шаге работы программы каждая из трех палочек вилки заменяется такой
же вилкой, превращая вилку в ветку с сучками, после следующего шага получим
лохматый куст, потом пушистое дерево, красивое, фрактальное. Меняя вид
начальной картинки можно получать самые разные изображения от зонтиков укропа
до колючего перекати-поле или пучка водорослей.
Суть L-кодирования сводится к следующему. Представим себе некое
виртуальное программируемое устройство, состоящее из пера, управляющего им
механизма и листа бумаги. Управляющий пером механизм способен исполнять
несколько команд. А именно: он может опустить перо на бумагу и вычертить прямой
отрезок заданной длины в направлении текущей ориентации пера (команда F). Он
может изменить ориентацию пера по отношению к текущей на какой-то заданный
относительный угол по часовой или против часовой стрелки (команды + и -). Он
может также запоминать (заносить в стек) свое текущее состояние (команда [) и
вспоминать (извлекать из стека) ранее запомненное состояние (команда ]). Под
состоянием в данном случае понимается тройка чисел (x, y, a), где x и y - это
координаты пера и а - это угол, определяющий направление ориентации пера. Таким
образом, задав некое начальное направление а0, определив относительный угол
поворота в 900 и задав длину отрезка, при помощи последовательности команд F+F+
F+F мы можем нарисовать квадрат. Определив относительный угол поворота в 600,
при помощи последовательности команд F++F++F можно нарисовать равносторонний
треугольник.
Предположим
также, что в программы для нашего виртуального устройства, кроме пяти
перечисленных команд, можно включать любые другие символы, которые управляющий
механизм будет просто игнорировать. То есть если мы введем программу
F+BF+CCF+CF, то устройство все равно нарисует квадрат. Теперь мысленно оснастим
наше устройство приставкой, которая перед тем, как передать введенную программу
на управляющий механизм, может заданное число раз просматривать ее, и при
каждом очередном просмотре заменять любые символы последовательности по
предварительно указанным правилам. Исходную программную последовательность
символов теперь будем называть аксиомой. Например, введем аксиому FB+, и
определим правило B < F+FB. Зададим также количество просмотров, равное,
например, двум. Тогда на входе механизма после обработки введенной аксиомы
приставкой получим последовательность FF+FF+FB+. Вот, собственно, и все. При
помощи описанного несложного виртуального устройства можно строить множество
самых разнообразных фрактальных форм - от традиционных математических
фракталов, таких, как, например, снежинка Коха или кривая Гильберта, до
структур, очень напоминающих растительную или подводную жизнь. Можете
посмотреть на исходный код программы, объясняющий вышесказанное
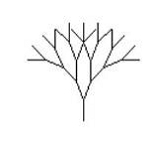
На
рисунке приведено несколько примеров фрактальных структур, построенных при
помощи этой программы.
Рассмотрим,
как кодируются L-системы в общепринятых обозначениях.
Движение
вперед обозначается буквой F (Forward - вперед), поворот по часовой стрелке
обозначим «+», а против - «-», причем само значение поворота задается в
программе и постоянно для всех движений. Буквой В (Back- назад) обозначается
возврат без прорисовки, нам это не пригодится.
Для
нас важнее механизм возврата. Точка, в которую надо возвращаться, обозначим
«[», а место, откуда происходит возврат, обозначим «]». Тогда вилка будет иметь
вид: F - движение вперед [ - запомнить позицию + - поворот вправо на 22.5
(например) градусов F - движение вперед после поворота ] - возврат в
запомненную позицию [ - запомнить позицию - - поворот влево относительно
направления в запомненной точке F - движение вперед после поворота] - возврат в
запомненную позицию. Это движение можно закодировать. Можно и более сложное.
Можно закодировать и следующий шаг - замену каждого прямого отрезка на такую же
вилку. Два шага нарисуют три шага, три шага - четыре шага. Прорисовывать каждый
шаг заменой текста программы довольно утомительно, и мы вспоминаем о рекурсии.
Выполнив необходимые объявления переменных и передаче значений координат точек
возврата, мы добиваемся, что любое дерево рисуется по заранее заданной формуле
одной маленькой процедурой, которая сама себя и вызывает. Программа позволит вам
с восхищением (ибо порядок прорисовки фрактально непредсказуем) отслеживать на
экране рост дерева.
Запустив
программу, вы увидите, как она нарисует ветку, клонимую ветром. Меняя
переменную Kmax можно уменьшать или увеличивать глубину рекурсии, или, что тоже
самое, «пушистость» ветки. А меняя закон движения можно получать самые
удивительные и фантастические изображения.


Таким
образом, суть L - системы состоит в том, что имеется определенных набор
символов системы, каждый из которых обозначает определенное действие и набор
правил преобразования символов.
Применение фракталов
Фракталы находят все большее и большее применение в науке и технике.
Основная причина этого заключается в том, что они описывают реальный мир иногда
даже лучше, чем традиционная физика или математика. Можно до бесконечности
приводить примеры фрактальных объектов в природе, - это и облака, и хлопья
снега, и горы, и вспышка молнии, и наконец, цветная капуста. Фрактал как
природный объект - это вечное непрерывное движение, новое становление и
развитие. Фракталы приходят на помощь, например, когда требуется, с помощью
нескольких коэффициентов, задать линии и поверхности очень сложной формы.
Фактически найден способ легкого представления сложных неевклидовых объектов,
образы которых весьма похожи на природные.
Кроме
того, фракталы находят применение в децентрализованных компьютерных сетях и
«фрактальных антеннах». Весьма интересны и перспективны для моделирования
различных стохастических (не детерминированных) «случайных» процессов, так
называемые «броуновские фракталы». В случае нанотехнологии фракталы тоже играют
важную роль, поскольку из-за своей иерархической самоорганизации многие
наносистемы обладают нецелочисленной размерностью, то есть являются по своей
геометрической, физико-химической или функциональной природе фракталами.
Например, ярким примером химических фрактальных систем являются молекулы
«дендримеров <#"786118.files/image025.gif">

ПРИЛОЖЕНИЕ 2
Дракон
Хартера - Хейтуэя. Он представляет собой своеобразную гирлянду в форме
двухсторонней правой спирали, состоящую из подобных друг другу спиралевидных
звеньев, непрерывно уменьшающихся в размерах от центра к периферии. Эта линия
показалась похожей ее первооткрывателю Дж.Хейтуэю на китайских драконов,
поэтому она и получила такое название. Эта ломанная не пересекает саму себя, и
она регулярно заполняет часть плоскости.
Пример рекурсивной программы «Кривая Дракона»:
program
dragon;graph;k,d,m:integer;ris(x1,y1,x2,y2,k:integer);xn,yn:integer;k>0
then:=(x1+x2) div 2 +(y2-y1) div 2;:=(y1+y2) div 2 -(x2-x1) div
2;(x1,y1,xn,yn,k-1);(x2,y2,xn,yn,k-1);begin line(x1,y1,x2,y2); end;;( k );{задаем порядок кривой}:=detect;(d,m,'e:\bp\bgi');(200,300,500,300,k);
readln;
end.
Для
того, чтобы понять как строится Дракон с помощью L - систем,
рассмотрим более подробно сам метод построения. Сначала берется отрезок
единичной длины. Затем он заменяется на два отрезка, образующих боковые стороны
равнобедренного прямоугольного треугольника, для которых исходный отрезок
является гипотенузой. В результате отрезок как бы прогибается под прямым углом.
Направление прогиба чередуется. Первый отрезок прогибается вправо (по ходу движения
слева направо), второй - влево, третий - опять вправо и т.д. Таким образом,
после каждого шага число имеющихся отрезков удваивается, а длина каждого
соответственно уменьшается в 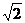 раз.
раз.


ПРИЛОЖЕНИЕ 3.
Фрактал Ресслера.
Построить фрактал Ресслера.
Для отображения необходимо построить решения следующей системы
дифференциальных уравнений:
dx/dt = -y - z/dt = x + ay/dt = b + z(x-c)
#include <graphics.h>
#include <stdio.h>
#include <conio.h>
#include <math.h>x, y, z, dt, a, b, c, x1, y1, z1;x2,
y2;main(void) {gdriver = DETECT, gmode, errorcode;(&gdriver, &gmode,
"");= 3.051522;= 1.582542;= 15.62388;= 0.0001;= 0.2;= 0.2;=
5.7;(getmaxcolor());(!kbhit()) {= x + (-y-z)*dt;= y + (x+a*y)*dt;= z +
(b+z*(x-c))*dt;= x1;= y1;= z1;(ceil(19.3*(y - x*0.292893) + 320), ceil(-11*(z +
x*0.292893) + 392), WHITE);
}();();0;
}
ПРИЛОЖЕНИЕ 4
Плазма.
Рассмотрим способ
построения плазмы с помощью рекурсивного задания портрета самой плазмы и
дальнейшего изменения ее цветов по соответствующим уравнениям гармонических
колебаний (таким образом, обеспечив плавность переходов цвета):
for (i=0;i<=170;i++){[3*i]=(63* sin( ( (double)i/170.0)
*M_PI) );[3*i+256]=(63*sin((double)i/170.0*M_PI));[(3*i+512)%768]=floor(63*sin((double)i/170*M_PI));
Здесь pal-массив, хранящий палитру (с помощью него мы будем ее задавать)
сам портрет плазмы строится таким образом: на краях экрана берутся 4 точки и
окрашиваются произвольно. Далее берутся точки на середине расстояний между
соседними точками, а также точка в середине области, и заполняются как среднее
арифметическое соответственно 2 лежащих на одном соответствующем с ней отрезке
или 4 для серединной.
Полученный результат отклоняется функцией ncol и присваивается
соответствующему пикселю. Далее - функция вызовется рекурсивно для полученных 4
подобластей на экране.
Исходный код на Turbo Pascal:
{$A+,B-,D+,E+,F-,G+,I-,L+,N-,O-,P-,Q-,R-,S-,T-,V+,X+,Y+}crt;:
integer;: byte;: array[0..768]of byte;: array[0..63999]of byte absolute
$A000:0;col(a,b,dvd : integer): integer;: integer;:=(a+b-random(b)) div
dvd;:=loc;loc>255 then col:=255;loc<0 then col:=0;plasma(x1,y1,x2,y2 :
integer);,yn,dxy,p1,p2,p3,p4 : integer;(x2-x1<2) and (y2-y1<2) then
EXIT;:=screen[320*y1+x1];:=screen[320*y2+x1];:=screen[320*y1+x2];:=screen[320*y2+x2];:=(x2+x1)
div 2;:=(y2+y1) div 2;:=(x2-x1+y2-y1);screen[320*y1+xn]=0 then
screen[320*y1+xn]:=col(p1+p3,dxy,2);screen[320*yn+x1]=0 then
screen[320*yn+x1]:=col(p1+p2,dxy,2);screen[320*yn+x2]=0 then
screen[320*yn+x2]:=col(p3+p4,dxy,2);screen[320*y2+xn]=0 then
screen[320*y2+xn]:=col(p2+p4,dxy,2);[320*yn+xn]:=col(p1+p2+p3+p4,dxy,4);(x1,y1,xn,yn);(xn,y1,x2,yn);(x1,yn,xn,y2);(xn,yn,x2,y2);ax,13h10h;i:=1
to 170 do pal[3*i]:=round(63*sin(i/170*pi));i:=1 to 170 do
pal[3*i+256]:=round(63*sin(i/170*pi));i:=1 to 170 do pal[(3*i+512) mod
768]:=round(63*sin(i/170*pi));(1,1,319,199);:=0;(2000);[$3C8]:=counter;si,offset
palcx,768dx,$3C9outsb;(counter);keypressed;ax,3h 10h
end;
end.

ПРИЛОЖЕНИЕ 5
Фрактальная графика. Используя фрактал, построить лист папоротника.
Лист папоротника - достаточно простой и наглядный пример построения
фрактала с помощью вероятностных распределений. С их помощью можно строить
достаточно красивые и сложные фигуры.
Суть метода заключается в фиксировании на начальном этапе какой-либо
точки, и в дальнейшем циклическом аффинном преобразовании системы координат, в
которой точка строится.
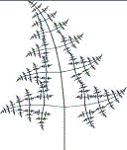
program Paporotnik;
Uses
crt, graph;= 1;, gm: integer;linetol(x, y,: integer; l, u: real);(x, y, round(x
+ l*cos(u)), round(y - l*sin(u)));;Draw(x, y: integer; l, u: real);KeyPressed
then exit;l>min then begin(x, y, l, u);:= round(x + l*cos(u));:= round(y -
l*sin(u));(x, y, l*0.4, u - 14*pi/30);(x, y, l*0.4, u + 14*pi/30);(x, y, l*0.7,
u+pi/30);;;:= detect;(gd,gm,’c:\borlalnp\bgi’);(320, 460, 140, pi/2);;;
End.
ПРИЛОЖЕНИЕ 6.
Дерево Пифагора. Пифагор, доказывая свою знаменитую теорему, построил
фигуру, где на сторонах прямоугольного треугольника расположены квадраты. В наш
век эта фигура Пифагора выросла в целое дерево. Впервые дерево Пифагора
построил А.Е.Босман во время Второй Мировой Войны, используя обычную чертежную
линейку.
Program Pif;crt, graph;Draw(x, y, l, a: real);Rect(x1, y1, l:
integer, al: real);(x1, y1);(x1 + round(l*cos(al)), y1 - round(l*sin(al)));(x1
+ round(l*sqrt(2)*cos(al + pi/4)), y1 - round(l*sqrt(2)*sin(al + pi/4)));(x1 +
round(l*cos(al + pi/2)), y1 - round(l*sin(al + pi/2)));(x1, y1);;l>4 then
begin(round(x), round(y), round(l), a);(x - l*sin(a), y - l*cos(a),l/sqrt(2),
a+pi/4);(x - l*sin(a) + l/sqrt(2)*cos(a+pi/4), y - l*cos(a)* l/sqrt(2)*
sin(a+pi/4),l/sqrt(2), a-pi/4);;;
Var,
gm: integer;:= detect;(gd,gm,’c:\borlalnp\bgi’);(280, 460, 100, 0);;;
End.
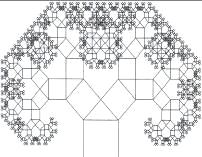

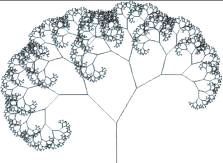
Одним из свойств дерева Пифагора является то, что, если площадь первого
квадрата равна единице, то на каждом уровне площадь квадратов тоже будет равна
единице.
Заметим, что дерево Пифагора является разновидностью двомчного дерева.
Если в классическом дереве Пифагора угол равен 45 градусам, то, как
обобщение классического дерева Пифагора, можно строить обобщенное дерево
Пифагора или как его по-другому называют обдуваемое ветром дерево Пифагора.
Можно также упростить дерево Пифагора и рисовать не квадраты, а только
отрезки соединяющие «центры» треугольников. При этом сами треугольники не
рисуются. Будем называть такой фрактал Обнаженным Деревом Пифагора.
Program DPif;crt, graph;= 3;
Var,
gm: integer;
Procedure linetol(x, y: integer; l, u: real);(x, y, round(x +
l*cos(u)), round(y - l*sin(u)));;Draw(x, y: integer, l, u: real);(x1, y1);(x1 +
round(l*cos(al)), y1 - round(l*sin(al)));(x1 + round(l*sqrt(2)*cos(al + pi/4)),
y1 - round(l*sqrt(2)*sin(al + pi/4)));(x1 + round(l*cos(al + pi/2)), y1 -
round(l*sin(al + pi/2)));(x1, y1);;KeyPressed then exit;l>max then
begin:=l*0.7;(x, y, l, u);:=round(x + l*cos(u));:=round(y - l*sin(u));(x , y,
l, u+pi/4);{угол поворота}(x , y, l, u-pi/6);{угол поворота};;
Begin:=
detect;(gd,gm,’c:\borlalnp\bgi’);(320, 460, 200, pi/2);;;
End.
ПРИЛОЖЕНИЕ 6
Одномерное множество Кантора. Георг Кантор (1845-1918) явился одним из
основателей теории множеств. Он придумал один из старейших фракталов -
множество Кантора(описано им в 1883 г.). На Западе подобные множества называют
иногда пылью. Существование этого фрактала отмечалось до этого Генри Смитом в
1875 году. Фрактальные свойства пыли Кантора имеют огромное значение, особенно
учитывая тот факт, что многие известные фракталы являются близкими
родственниками этого фрактала.
Способ построения этого множества следующий. Берется отрезок прямой
единичной длины. Затем он делится на три равные части, и вынимается средний
отрезок. Это первый шаг итерационной процедуры. На втором шаге подобной
процедуре деления на три равные части и последующего удаления середины
подвергается каждый из двух оставшихся отрезков. Так продолжая до
бесконечности, получим множество Кантора. Нетрудно заметить, что суммарная
длина получившихся в пределе отрезков равна нулю, так как мы исключили в
результате длину, равную 1:
/3+2/9+4/27+…=1/3*(1+2/3+4/9+…)=1/3*1/(1-2/3)=1.
Также нулю равна и топологическая размерность.
Program Cantor;
Uses crt, graph;
Const= 1;
Var,
gm: integer;
Procedure Draw(x, y: real; size: real);: real;size> min
then begin:= size/3;(x, y + 20, S );(x +S*2, y +20,S);;(round(x), round(y),
round(x+ size), round(y + 5));;
Begin:=
detect;(gd,gm,’c:\borlalnp\bgi’);(10, 30, 500);;;
End.

Множество Кантора
Множество Кантора не очень удобно строить на экране компьютера,
вследствие сильной разреженности конечных точек, поэтому удобнее строить
разновидность, называемую Гребнем Кантора. Для его построения нужно в программе
множества Кантора заменить строчку
Bar(round(x), round(y), round(x+ size), round(y + 5));
На
rectangle(round(x), round(y), round(x+ size), round(y + 20));,
Гребень Кантора.
ПРИЛОЖЕНИЕ 7.
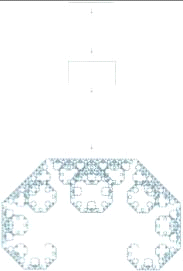
Кривая Леви
Кривая Леви - фрактал, предложенный французским математиком П. Леви,
получается, если взять половину квадрата вида /\, а затем каждую сторону
заменить таким же фрагментом, и, повторяя эту операцию, в пределе мы получим
кривую Леви.
Свойства
· Кривая Леви нигде не дифференцируема и не спрямляема.
· На любом интервале кривой Леви есть точка самопересечения.
· Хаусдорфова размерность кривой Леви приблизительно равына
1.9340.
ПРИЛОЖЕНИЕ 8
Кривая Минковского. Кривая Минковского или колбасы Минковского -
классический геометрический фрактал, предложенный Минковским. Инициатором
является отрезок, а генератором является довольно сложная ломаная из восьми
звеньев (два равных звена продолжают друг друга).

Свойства
· Кривая Минковского нигде не дифференцируема и не спрямляема.
· Кривая Минковского не имеет самопересечений.
· Кривая Минковского имеет Хаусдорфову размерность = 3/2.
ПРИЛОЖЕНИЕ 9
Примеры кривых, построенных в программе IFS Builder 3d:
Кривая Леви:
position (0.7,-0.5,-2.5) direction(0,0,1) vertical(0,1,0)
fov(50);color(1,1,0,3) position(1, 1,-3);color(1,1,0,1)
position(3,-1,-1);(1,1,1,0.05);:=scale(sqrt(.5))translate(1,-1,0)rotate(45);:=scale(sqrt(.5))rotate(-45);F=(f1+f2)F;//Dimension
of boundary = 1.9340071829f1*F;(2,1,0);f2*F;(0,1,0);
Дерево Пифагора:
position (0.5,0.3,-1.8) direction(0,0,1) vertical(0,1,0)
fov(50);color(1,1,0,3) position(1, 1,-3);
light color(1,1,0,1) position(3,-1,-1);
ambient(1,1,1,0.05);:= translate(1,0) scale(sqrt(.5))
rotate(-45) translate(-1,0);:= scale(sqrt(.5))
rotate(45);Segment=scale(.5)(id()+translate(1/3,0))
Segment;Square=(translate(1/3,0)+translate(1/3,-1/3)+
(translate(1/3,0)+translate(2/3,0))*rotate(-90))
Segment;F=(f1+f2)F;
//Dimension of the PythagoreanTree = 2
//Dimension of boundary =
1.9340071829PythagoreanTree=(f1+f2)PythagoreanTree+Square;PythagoreanTree;
Кривая Минковского:
position (0.5,0,-0.85) direction(0,0,1) vertical(0,1,0)
fov(50);color (0,2,0) position (1, 1,-3) shadows(0);color (2,2,0) position
(3,-1,-1) shadows(0);(1,1,1, .05);(0,1,1,0.5);
// Hutchinson operator for Minkowski Curve:=
(id()+translate(1/4,0)*rotate(90)+translate(1/4,1/4)+(1/2,1/4)*rotate(-90)+translate(1/2,0)*rotate(-90)+(1/2,-1/4)+translate(3/4,-1/4)*rotate(90)+(3/4,0))*scale(1/4);
//build F F(Segment =
scale(1/2)*(id()+translate(1,0,0))Segment);camera position (0.42,-0.17,-1.3)
direction(0,0,1) vertical(0,1,0) fov(50);color(1,1,0,3) position(1,
1,-3);color(1,1,0,1)
position(3,-1,-1);(1,1,1,0.05);:=scale(sqrt(1/2));:=translate(1,0,0)rotate(-135)f0;:=rotate(-45)f0;F=(f1+f2)F;//Dimension
of boundary = 1.5236270862f1*F;(2,1,0);f2*F;(0,1,0);MinkowskiCurve =
F(MinkowskiCurve);
Кривая дракона Хартера-Хейтуэя:
position (0.42,-0.17,-1.3) direction(0,0,1) vertical(0,1,0)
fov(50);color(1,1,0,3) position(1, 1,-3);color(1,1,0,1)
position(3,-1,-1);(1,1,1,0.05);:=scale(sqrt(1/2));:=translate(1,0,0)rotate(-135)f0;:=rotate(-45)f0;F=(f1+f2)F;//Dimension
of boundary = 1.5236270862f1*F;(2,1,0);f2*F;(0,1,0);
Снежинка Коха:
position (0,0,-2.3745022657807842) direction(0,0,1)
vertical(0,1,0) fov(50);color (1,1,1,2) position (1, 1,-3) shadows(0);color
(1,1,1,4) position (3,-1,-1) shadows(0);(1,1,1,.05);(0,1,1,0);=1/sqrt(3);:=
translate(1/2,s/2,0)*rotate(-150);:= translate(1,0,0)*rotate(150);:=
translate(-1/2, 1/s/2,0)*rotate(-30);:= translate(-1/2,-1/s/2,0)*rotate( 90);:=
translate(1,0,0)*rotate(-150);Curve = (f1+f2)scale(s)Curve;Snowflake =
(f3+f4+f5)scale(1/s)Curve; color (0,1,1);
//build
(1+s*rotate(30))*Snowflake;S=s*rotate(30)*(Snowflake+S); color (0,1,0);
Треунольник Серпинского:
// Sierpinsky's triangleposition (0,0.24,-1.6)
direction(0,0,1) vertical(0,1,0) fov(50);color(2,2,0)
position(1,1,-3);color(4,4,0)
position(3,-1,-1);(1,1,1,0.05);(0,1,1,0.3);=sqrt(2)/3;=sqrt(6)/3;:=
translate(0,2*a,0) scale(0.5) translate(0,-2*a,0);:= translate( b,-a,0)
scale(0.5) translate(-b,a,0);:= translate(-b,-a,0) scale(0.5) translate( b,a,0);F=(f1+f2+f3)
F;
Губка Менгера:
position (-1.6,-1.6,-1.6) direction(1,1,1) vertical(0,1,0)
fov(50);color (0,1,1,.35) direction (1,
1,1);(1,1,1,.05);(0,1,1,0.0);(1,1,1,0);:=translate;Sponge=scale(1/3)*((-2,-2,-2)+T(0,-2,-2)+T(2,-2,-2)+(-2,
0,-2)+ T(2, 0,-2)+(-2, 2,-2)+T(0, 2,-2)+T(2, 2,-2)+(-2,-2, 0)+ T(2,-2, 0)+(-2,
2, 0)+ T(2, 2, 0)+(-2,-2, 2)+T(0,-2, 2)+T(2,-2, 2)+(-2, 0, 2)+ T(2, 0, 2)+(-2,
2, 2)+T(0, 2, 2)+T(2, 2, 2)
)*Sponge;
ПРИЛОЖЕНИЕ 10
Построение L-фрактала возможно по алгоритму построения множества Жюлиа,
это множество порождает свой фрактал исходя из известных начальных значений.
Для описания множества нужно задать значения C, комплексного числа (в форме a +
(b * i)). Начальное значение Z также соответствует комплексному числу.
Действительная часть данного числа соответствует координате x, а мнимая
координате y. Чтобы нарисовать фрактал, нужно последовательно применить
уравнение z' = λz(1-z) для каждого из значений Z из ряда
(0,…,n).
Для данной задачи λ возьмём равное 0.85+0.6i, чтобы отображение фрактала
было более плотным.
#include <conio.h>
#include <graphics.h>
#include <math.h>
#include <complex.h>main() {gd = DETECT, gm;mx, my;l,
z;it=35, max=100;k;(&gd, &gm, ""); // подключение графики= getmaxx() / 2; // масштаб
my = getmaxy() / 2;(int x = -mx; x <= mx; x++) { // определение
комплексных λ и z
for (int y = -my; y <= my; y++) {= complex(x*0.01,
y*0.01);= complex(0.85, 0.6);;= 0;((k < it)&&(abs(z) < max)) { //
реализация формулы= l*z*(1-z);++;
}(k<it) putpixel(mx+x, my+y, k % 16); // прорисовка
}
}();();;
}