Методы многомерной безусловной минимизации. Сравнение правой РП и центральной РП на примере минимизации функции нескольких аргументов методом сопряженных градиентов
Министерству
образования и науки Российской Федерации
Федеральное
государственное автономное образовательное учреждение
высшего
профессионального образования
«Волгоградский
государственный университет»
(ВолГУ)
Институт
математики и информационных технологий
Лабораторная
работа №3
по
курсу «Численные методы оптимизации»
Методы
многомерной безусловной минимизации. Сравнение правой РП и центральной РП на
примере минимизации функции нескольких аргументов методом сопряженных
градиентов
Выполнили:
Студенты 3-го курса
группы ПМ-101
Самородов Е. А.
Гусынин О. С.
Болотин А. В.
Принял:
Яновский Т.А.
Волгоград
2013
Задание:
Сравнить правую и центральную разностную
производную на примере минимизации функции нескольких аргументов методом
сопряженных градиентов. В качестве функции взята функция Пауэлла.
Метод:
Метод сопряженных градиентов (метод
Флетчера-Ривса)
В основе метода лежит построение направлений
поиска минимума 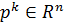 , являющихся
линейными комбинациями градиента
, являющихся
линейными комбинациями градиента 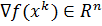 предыдущих
направлений поиска
предыдущих
направлений поиска 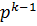 . При этом весовые
коэффициенты
. При этом весовые
коэффициенты  выбираются так,
чтобы сделать направления сопряженными относительно матрицы Гессе
выбираются так,
чтобы сделать направления сопряженными относительно матрицы Гессе 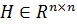 .
Для повышения скорости сходимости метода, в случае не квадратичной
.
Для повышения скорости сходимости метода, в случае не квадратичной  используется
рестарт: через каждые n циклов направление поиска
используется
рестарт: через каждые n циклов направление поиска 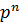 заменяется
на
заменяется
на 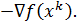 Наряду
с начальной точкой
Наряду
с начальной точкой 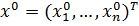 и вектором
положительных приращений координат
и вектором
положительных приращений координат  ,
алгоритм метода требует априорного задания параметра точности поиска ε
> 0 .
,
алгоритм метода требует априорного задания параметра точности поиска ε
> 0 .
Алгоритм:

Функция:
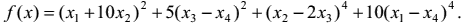
Результаты работы программы:
Был проведен ряд расчетов с целью определения
отличий центральной РП и правой РП. Для этой цели в качестве переменных
параметров были взяты eps1 и h. Где eps1 - максимальная величина нормы
градиента при которой продолжается расчет, h - шаг который используется в РП
для нахождения производной функции.
В качестве метода одномерной минимизации взят
метод золотого сечения.
При минимизации отрезка использован постоянный
шаг 0.01. Для цели работы он не важен, как и точность с которой будет найден
alfa методом золотого сечения.
Пример работы программы:
Используем для расчета Центральную РП.

Здесь под МСГ понимается количество итераций
пройденных методом сопряженных градиентов, под ОМ - количество итераций при
нахождении отрезка минимизации, под ЗС - количество итерации в методе золотого
сечения.
Теперь используем Правую РП.

На первый взгляд видно, что разница между ЦРП и
ПРП только в количестве итераций. С помощью ЦРП требуемый результат найден чуть
быстрее. Теперь изменим eps1 и h. Возьмем eps1 = 0.1, h =0.001 . С центральной
РП:

С правой РП:
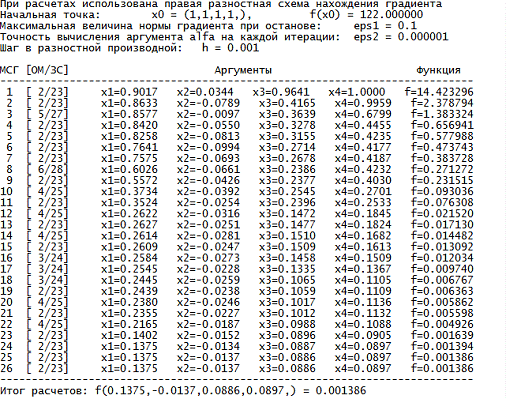
Очевидно, что использование ЦРП, при более
грубом шаге h и низкой точности eps1, способствует быстрейшему и более
точнейшему нахождению минимума функции в отличие от ПРП.
Выводы
Экспериментально для данной задачи удалось
установить наиболее эффективное количество итераций n, после которых нужно
производить рестарт. При использовании n = 6 достигается требуемая точность
нахождения минимума при наименьшем количестве итераций.
Ниже приведена таблица количеств итерации при
различных n и h ,и одинаковых точностях ( ,
,
 ),
при центральной РП и правой РП (ЦРП/ПРП).
),
при центральной РП и правой РП (ЦРП/ПРП).
многомерный минимизация
производная функция
|
n
|
h
|
|

|
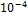
|
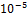
|
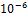
|
|
4
|
49
/ 49*
|
48
/ 55*
|
48
/ 172
|
48
/ 51
|
|
5
|
31
/ 71*
|
31
/ 49*
|
31
/ 34
|
31
/ 26
|
|
6
|
24
/ 37*
|
24
/ 31*
|
24
/ 28
|
24
/ 26
|
|
7
|
37
/ 71*
|
35
/ 42*
|
35
/ 49
|
|
8
|
40
/ 49*
|
43
/ 64*
|
43
/ 59
|
43
/ 55
|
|
9
|
30
/ 46*
|
30
/ 36*
|
30
/ 48
|
30
/ 37
|
|
10
|
42
/ 31*
|
42
/ 50*
|
42
/ 45
|
42
/ 42
|
|
11
|
36
/ 34*
|
36
/ 34*
|
36
/ 37
|
36
/ 41
|
|
12
|
38
/ 49*
|
39
/ 48*
|
39
/ 39
|
39
/ 37
|
|
13
|
37
/ 53*
|
38
/ 52*
|
38
/ 43
|
38
/ 40
|
|
14
|
37
/ 43*
|
37
/ 57*
|
37
/ 43
|
37
/ 51
|
|
15
|
41
/ 46*
|
42
/ 75*
|
42
/ 48
|
42
/ 43
|
|
16
|
35
/ 49*
|
35
/ 66*
|
35
/ 37
|
35
/ 35
|
|
17
|
41
/ 52*
|
40
/ 51*
|
40
/ 55
|
40
/ 41
|
|
18
|
41
/ 37*
|
44
/ 90*
|
42
/ 45
|
43
/ 44
|
Как видно из таблицы правая РП более
чувствительна к изменению шага h чем центральная. Из этого следует, что ЦРП
имеет меньшею погрешность нахождения производной, чем ПРЦ.
К тому же, при больших значения h применение
ПРП, в данном примере, привило к очень малому изменению аргументов, т.е. к
зацикливанию.
В таблице (*) помечено то количество итераций,
где применение ПРП привело к зацикливанию, что не позволило достичь заданной
точности (из-за этого значения некоторых чисел у ПРП меньше чем у ЦРП).
Можно увидеть, что при h равном 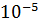 и
и
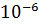 использование
ЦРП эффективнее чем ПРП.
использование
ЦРП эффективнее чем ПРП.
Для сравнения ПРП и ЦРП при большом шаге h
точность для останова сделаем более грубой 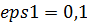 .
Тогда увидим, что:
.
Тогда увидим, что:
|
n
|
h
|
|
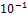
|

|

|
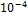
|
|
5
|
22
/ 21*
|
20
/ 36*
|
20
/ 21
|
|
6
|
13
/ 25*
|
15
/ 19*
|
15
/ 26
|
15
/ 18
|
|
7
|
20
/ 29*
|
19
/ 29*
|
19
/ 23
|
19
/ 19
|
Видно, что при h равном 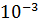 и
и
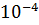 использование
ЦРП по-прежнему эффективнее, чем ПРП. А при h равном
использование
ЦРП по-прежнему эффективнее, чем ПРП. А при h равном 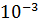 и
и
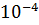 ,
даже при не достижении требуемой точности у ПРП, количество итераций при использовании
ЦРП меньше чем при использовании ПРП.
,
даже при не достижении требуемой точности у ПРП, количество итераций при использовании
ЦРП меньше чем при использовании ПРП.
Можно сделать вывод, что применение центральной
РП предпочтительней, как с точки зрения эффективной работы программы, так и с
точки зрения быстроты получения результата.
Код программы на Си:
#include <stdio.h>
#include <math.h>
#include <windows.h>
#define EPS 0.000000002
#define f function
#define nv the_number_of_variables
#define CENTRAL 0
#define RIGHT 1
#define LEFT 2int
the_number_of_variables = 4;function(double * x){pow(x[0]+10*x[1],2)+5*pow(x[2]-x[3],2)+pow(x[1]-2*x[2],4)+10*pow(x[0]-x[3],4);
}* ToRus(const char text []);*
gradient(double * x, double h, int ds);CentralDS(double * x, double h, int
i);RightDS(double * x, double h, int i);LeftDS(double * x, double h, int
i);(*DS[3])( double * x, double h, int i ) = {CentralDS, RightDS,
LeftDS};NormaV(double * x, int n);* minimi(double * x, double * p, double
dx);zoloto(double * x, double * p, double a, double b, double
eps);argminf(double * x, double * g, double eps);main(){i, k, n, ds;*g, *g_old,
*x, *p, yI,yII;eps1, eps2, h, Sc, Sz, betta, alfa;= (double
*)malloc(nv*sizeof(double));= (double *)malloc(nv*sizeof(double));
k = 1;= 6;//цикличность(через сколько итерации
произойдет рестарт)= 0.001;= 1e-6;=1e-6;//шаг при вычисления градиента в РС
ds = CENTRAL;//RIGHT("%s
",ToRus("При расчетах
использована"));(ds+1){1:
printf("%s",ToRus("центральная"));break;2:
printf("%s",ToRus("правая"));break;3:
printf("%s",ToRus("левая"));break;
}(" %s\n",ToRus("разностная схема
нахождения градиента"));("%s:\tx0 = (",ToRus("Начальная
точка"));
for( i = 0; i < nv; i ++ ){[i] =
1;printf("%.0lf,",x[i]);
}("),\t f(x0) =
%.6lf\n",function(x));
printf("%s:\teps1 =
%.3lf\n",ToRus("Максимальная величина нормы градиента при
останове"),eps1);("%s:\teps2 = %lf\n",ToRus("Точность
вычисления аргумента alfa на каждой итерации"),eps2);("%s:\th =
%lf\n",ToRus("Шаг в разностной производной"),h);
g_old = gradient(x,h,ds);( i = 0; i
< nv; i ++ )p[i] = - g_old[i];("\n%s\t\t\t %s\t\t\t
%s\n",ToRus("МСГ
[ОМ/ЗС]"),ToRus("Аргументы"),ToRus("Функция"));("---------------------------------------------------------------------------");("%2d
",k);= f(x);= argminf(x,p,eps2);( i = 0; i < nv; i ++ ){x[i] +=
alfa*p[i];}( i = 0; i < nv; i ++ ){printf("x%d=%.4lf ",i+1,x[i]);}("f=%.6lf\n",f(x));++;yII
= f(x);{= gradient(x,h,ds);= 0;= 0;( i = 0; i < nv; i ++ ){+= g[i]*g[i];+=
g_old[i]*g_old[i];
}= Sc/Sz;(k%n==1){=
0;(fabs(yI-yII)<EPS){
eps1 =
NormaV(g,nv)+1.;("\t%s\n",ToRus("Остановка по причине
черезвычайно малого изменения y(x)"));
}
}( i = 0; i < nv; i ++ ){_old[i]
= g[i];[i] = betta*p[i] - g[i];
}("%2d ",k);=
argminf(x,p,eps2);( i = 0; i < nv; i ++ ){x[i] += alfa*p[i];}( i = 0; i <
nv; i ++ ){printf("x%d=%.4lf ",i+1,x[i]);}= yI;=
f(x);("f=%.6lf\n",yI);++;
}while(NormaV(g,nv) > eps1);("---------------------------------------------------------------------------");("%s:
f(",ToRus("Итог расчетов"));(
i = 0; i < nv; i ++ ){printf("%.4lf,",x[i]);}(") =
%.6lf\n",f(x));(x);(g);(g_old);(p);0;
}CentralDS(double * x, double h, int
i){j;* y;df;= (double *)malloc(nv*sizeof(double));(j=0;j<nv;j++){[j] = x[j];
}[i] += 0.5*h;= f(y);[i] -= h;-=
f(y);/= h;(y);df;
}RightDS(double * x, double h, int
i){j;* y;df;= (double *)malloc(nv*sizeof(double));(j=0;j<nv;j++){[j] = x[j];
}[i] += h;= ( f(y) - f(x)
)/h;(y);df;
}LeftDS(double * x, double h, int
i){j;* y;df;= (double *)malloc(nv*sizeof(double));(j=0;j<nv;j++){[j] = x[j];
}[i] -= h;= ( f(x) - f(y)
)/h;(y);df;
}* gradient(double * x, double h,
int ds){i;(ds > 2 || ds < 0)ds = 0;* g;= (double *)malloc(nv*sizeof(double));(i=0;i<nv;i++){[i]
= DS[ds](x,h,i);
}g;
}NormaV(double * x, int n){i;Sk =
0;( i = 0; i < n; i++ ){+= x[i]*x[i];
}sqrt(Sk);
}argminf(double * x, double * p,
double eps){
double alfa;* ab = minimi(x,p,0.01);//0.01 -
оптимальный шаг (подобран экспериментально)
alfa =
zoloto(x,p,ab[0],ab[1],eps);(ab);alfa;
}* minimi(double * x, double * p,
double dx){i;m=0, a, b, k=1, alfa = 0;* xda =
(double*)malloc(nv*sizeof(double));* xdb =
(double*)malloc(nv*sizeof(double));(i=0;i<nv;i++){[i] = x[i] + alfa*p[i];[i]
= x[i] + (alfa+dx)*p[i];
}(f(xda) < f(xdb))m =- 1;m = 1;*=
m;= alfa+dx;= alfa+3*dx;j=1;{(i=0;i<nv;i++){[i] = x[i] + b*p[i];[i] = x[i] +
a*p[i];
}*=2;+= k*dx;= b-2*k*dx;++;
}while(f(xda) > f(xdb));("
[%2d/",j);(xda);(xdb);-= k*dx;= b-2*k*dx;*s;= (double*)malloc(2*sizeof(double));(m==1){
s[0] = a; s[1] = b;}{s[0] = b; s[1] = a;}s;
}zoloto(double * x, double * p,
double a, double b, double eps){i;x1, x2, tau, A, B;* xd1 =
(double*)malloc(nv*sizeof(double));* xd2 = (double*)malloc(nv*sizeof(double));=
(sqrt(5.)+1.)/2.;= a+(b-a)/(tau*tau);= a+(b-a)/tau;(i=0;i<nv;i++){[i] = x[i]
+ x1*p[i];[i] = x[i] + x2*p[i];
}= f(xd2);= f(xd1);j=0;{( A <= B
){= x2;= x1;= a + b - x2;= A;(i=0;i<nv;i++){[i] = x[i] + x1*p[i];
}= f(xd1);
}{= x1;= x2;= a + b - x1;=
B;(i=0;i<nv;i++){[i] = x[i] + x2*p[i];
}= f(xd2);
}++;
}while(fabs(b-a) >
eps);("%2d]\t",j);(xd1);(xd2);(b+a)/2.;
}* ToRus(const char text []){* buf =
(char*)malloc(strlen(text)+1);(text, buf);buf;
}