|
Значение параметров для системы линейных
уравнений
|
|
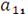
|
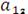
|

|

|
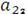
|
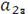
|

|
|

|
|
|
|
1
|
-2
|
1
|
-2
|
-2
|
-2
|
3
|
2
|
1
|
5
|
-4
|
3
|
Дана система алгебраических линейных уравнений:
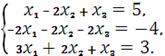
I. Решение
методом Крамера
Основная матрица имеет вид 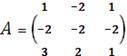
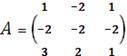 ,
,
вектор свободных членов 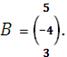
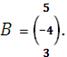
Вычислим определитель основной матрицы
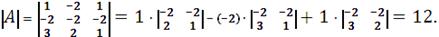
Найдем определители матриц, полученных из исходной заменой
соответственных столбцов вектором-столбцом В:
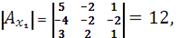
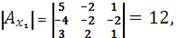
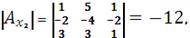
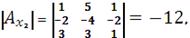
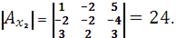
Неизвестные находим по формуле 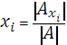
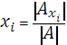 :
:
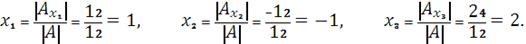
Выполним решение с помощью MathCAD:
· На новом рабочем листе вводим исходную
матрицу, используя панель "Matrix", ниже считаем ее определить;

Рисунок 5. Окно определения переменной - матрицы
· Повторяем для матриц с измененными
столбцами;

Рисунок 6. Скриншот экрана промежуточных расчетов
· Вводим переменные для посчитанных
определителей и корней;
· Выводим значение корней.
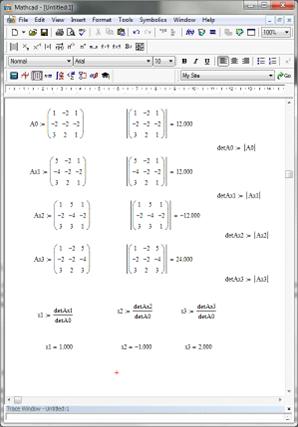
Рисунок 7. Окончательный вид рабочей области MathCAD решения системы уравнений методом Крамера
Выполним решение с помощью MS Excel:
· откроем созданную в задание 1 Книгу 1,
перейдем на новый лист, переименуем его "Задание 2 - Крамер";
· введем данную матрицу и столбец свободных
членов;
· на строке ниже посчитаем определитель
данной матрицы;
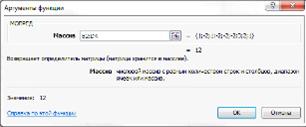
Рисунок 8. Вычисление определителя матрицы А
· создадим измененную матрицу А1, скопировав
исходную и изменив в ней первый столбец (вставив на его место скопированный
столбец свободных членов) и на строке ниже повторим расчет определителя;
повторим данные операции для еще двух матриц;
· в ячейках напротив полученных
определителей рассчитаем корни системы уравнений введением формул;

Рисунок 9. Скриншот экрана расчета корней методом Крамера
· оформим лист имеющимися средствами.
Окончательный вид приведен на рисунке 6.
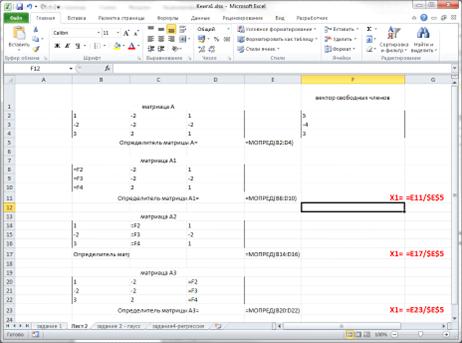
Рисунок 10. Лист расчета корней в режиме отображения формул
II.
Решение
 методом Гаусса
методом Гаусса
Составим расширенную матрицу и приведем ее к треугольному виду:


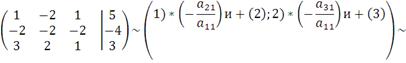 .
.
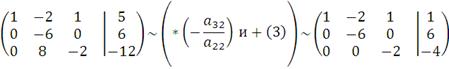
Теперь рассчитаем корни:
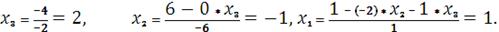
Проведем решение с помощью MS Excel:
· на новом листе введем значение матрицы и
вектора свободных членов;
· сформируем новую матрицу, используя
формулы пересчета коэффициентов;
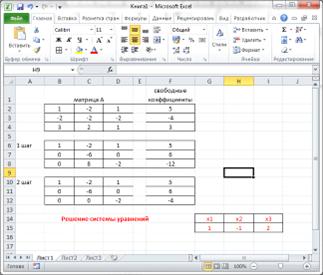
Рисунок 11. Решение системы уравнений методом Гаусса
· повторим пересчет матрицы;
· теперь рассчитаем корни системы уравнений
в новых ячейках.
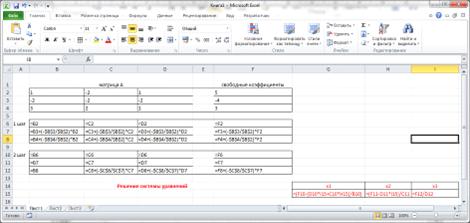
Рисунок 12. Лист расчета корней методом Гаусса в режиме
отображения формул
Решение системы уравнений равны при всех использованных методах.
Задание 3
Интерполяция экспериментальных данных с применением средств MathCad.
Пусть имеется полученная экспериментальным путем кривая
намагничивания стали 3. Необходимо провести кубическую сплайн-интерполяцию
кривой намагничивания и получить интерполяционную функцию.
массив данных
|
х
|
0,95
|
1
|
1,05
|
1,14
|
1,2
|
1,23
|
1,26
|
1,35
|
1,48
|
1,53
|
|
у
|
2,1
|
2,15
|
2,2
|
2,28
|
2,34
|
2,37
|
2,4
|
2,48
|
2,61
|
2,65
|
Выполним решение с помощью MathCAD:
· на рабочем листе вводим вектор-столбцы В и
Н (рисунок 13);

Рисунок 13. Начальный ввод данных для интерполяции
программа интерполяция транзистор автоматизация
· в новой переменной ВН1 - векторе вычисляем
вторые производные в опорных точках наблюдений;
· вводим вектор В1 - значений изменения
магнитной индукции от 0 до 2 с равным шагом;
· проводим кубическую интерполяцию -
формируем новый вектор Н0 (В1) (рисунок 14);
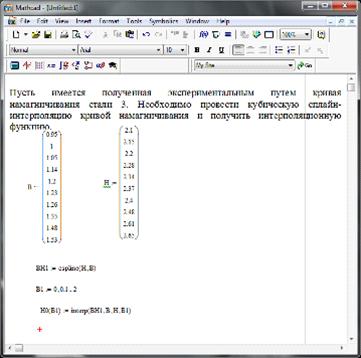
Рисунок 14. Расчет вторых производных и интерполяция
· для построения графика используем окно
графиков - выбираем 2D-plot - двумерный график;
· в новой области построения графика вводим
значения для вывода - по осям, с помощью свойств редактируем внешний вид
графика (строим сетку, вводим новый вид маркеров для исходных данных) - рисунок
15.
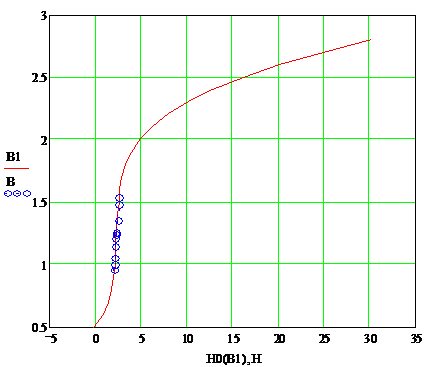
Рисунок 15. Интерполяционная кривая намагничивания
|
№ опыта
|
Х1
|
Х2
|
У
|
|
1
|
4,2
|
7,4
|
414,25
|
|
2
|
8
|
10,5
|
874,25
|
|
3
|
3,5
|
6,7
|
339,03
|
|
4
|
10,6
|
13,1
|
1310,1
|
|
5
|
4
|
7,2
|
392,17
|
|
6
|
8,9
|
11,4
|
1016,1
|
|
7
|
3,9
|
7,1
|
381,31
|
7,2
|
9,7
|
756, 19
|
|
9
|
5
|
8,2
|
507,3
|
|
10
|
8,6
|
11,1
|
967,75
|
Рисунок 16. Интерполяционная кривая намагничивания
Задание 4
Регрессионный анализ экспериментальных данных с применением
средств MathCad и MS Excel.
Решение:
исследуемая величина y зависит от двух факторов, результаты
опытов
Уравнение регрессии берем в виде полинома второй степени:
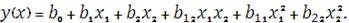
Необходимо рассчитать 6 коэффициентов, введем новые
переменные:
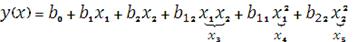
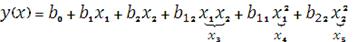 ,
,
И искомая функция становится линейной, зависящей от 6 переменных:
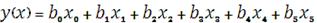
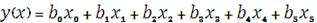 .
.
Рассчитаем значения новых переменных и получим новую таблицу
опытов:
|
№
|
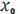
|
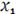
|

|

|
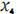
|
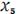
|
y
|
|
1
|
1
|
4,2
|
7,4
|
31,08
|
17,64
|
54,76
|
414,25
|
|
2
|
1
|
8
|
10,5
|
84
|
64
|
110,25
|
874,25
|
|
3
|
1
|
3,5
|
6,7
|
23,45
|
12,25
|
44,89
|
339,03
|
|
4
|
1
|
10,6
|
13,1
|
138,86
|
112,36
|
171,61
|
1310,1
|
|
5
|
1
|
4
|
7,2
|
28,8
|
16
|
51,84
|
392,17
|
1
|
8,9
|
11,4
|
101,46
|
79,21
|
129,96
|
1016,1
|
|
7
|
1
|
3,9
|
7,1
|
27,69
|
15,21
|
50,41
|
381,31
|
|
8
|
1
|
7,2
|
9,7
|
69,84
|
51,84
|
94,09
|
756, 19
|
|
9
|
1
|
5
|
8,2
|
41
|
25
|
67,24
|
507,3
|
|
10
|
1
|
8,6
|
11,1
|
95,46
|
73,96
|
123,21
|
967,75
|
Рисунок 17. Таблица результатов опытов для новых переменных
Т.е. по 10 опытам имеем систему 10 линейных уравнений с 6
неизвестными. Для нахождения коэффициентов используем матричный метод решения
систем линейных уравнений.
Выполним решение с помощью MathCad.
· вводим матрицу планирования (после
пересчета в новых переменных) Х размером 10х6 и вектор результатов опытов У;
· транспонируем матрицу Х, пользуясь блоком
"Matrix";
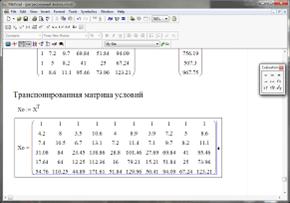
Рисунок 18. Скриншот экрана промежуточных расчетов:
транспонирование
· в новых переменных получаем результат умножения матриц 
 ;
;

Рисунок 19. Умножение матриц
· рассчитываем обратную матрицу 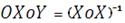
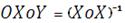 ;
;
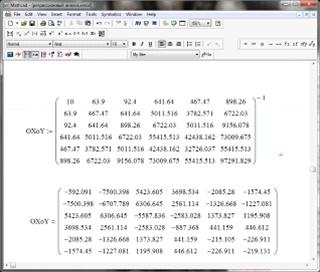
Рисунок 20. Нахождение обратной матрицы
· определяем коэффициенты регрессии 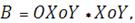
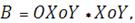 т.е.
т.е. 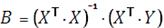
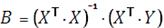
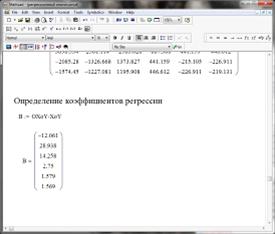
Рисунок 21. Нахождение коэффициентов регрессии
И полученное уравнение регрессии имеет вид:

Вернемся к исходным переменным:
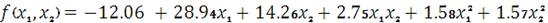
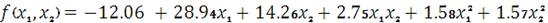 .
.
Построим график данной функции двух переменных:
· определяем функцию 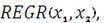
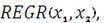 тождественную полученной регрессии;
тождественную полученной регрессии;
· используем "3D-plot" - в открывшемся окне трехмерного
графика вводим имя переменной 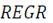
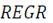 без указания аргументов;
без указания аргументов;
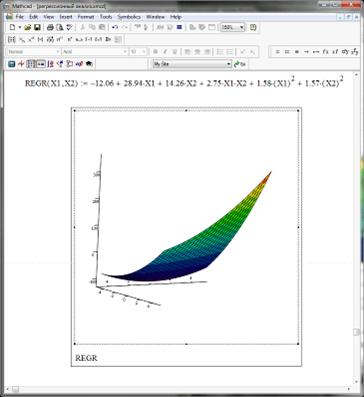
Рисунок 22. Скриншот экрана MathCAD - построение 3D графика
функции регрессии
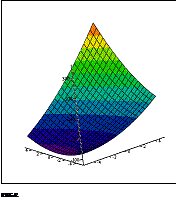
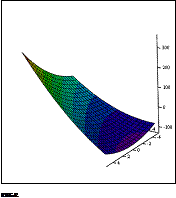
Рисунок 23. Функция регрессии - изменение положения осей координат
в пространстве
Используем возможности редактирования графика - используем цвет,
трассировку поверхности линиями, для просмотра меняем положение осей координат
в пространстве.
Проведем решение с помощью MS Excel:
· на новом листе вставим скопированные из
данного документа данные по опытам;
· рассчитаем числовые значения новых
переменных;
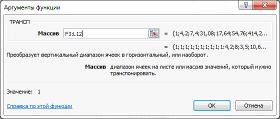
Рисунок 24. Использование функции транспонирования матриц в Excel
· выполним умножение матриц Х0 и Х, выделив
диапазон ячеек 10х10;
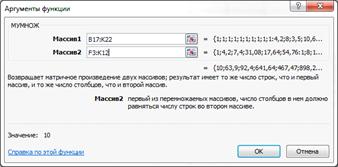
Рисунок 25. Функция умножения матриц Excel
· выполним умножение матрицы Х0 и вектор
столбца У, выделив 6 ячеек по столбцу;
· рассчитаем обратную матрицу;
· определим коэффициенты регрессии.
Коэффициенты, полученные с помощью Excel, такие же, как
полученные ранее.
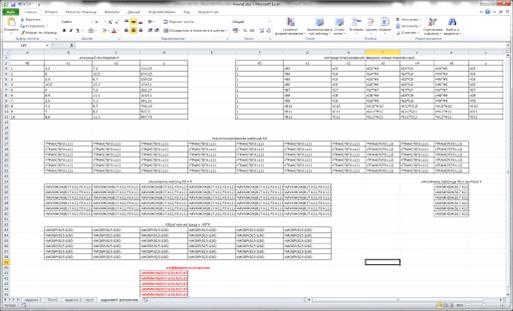
Рисунок 26. Скриншот экрана листа Excel с расчетами по регрессионному анализу.