Роль и место наглядности в обучении математике в средней школе

Роль и место наглядности в обучении математике в средней школе

ДИПЛОМНАЯ РАБОТА

По теме: «Роль и место наглядности в обучении математике в средней школе»

Содержание

Введение

Глава I Психолого-педагогические аспекты реализации средств наглядности при изучении математики в средней школе

§1. Познавательные процессы и их формирование

§2. История становления средств наглядности

§3. Сочетание слова учителя и средств наглядности

§4. Функции средств наглядности

§5. Классификация средств наглядности

§6. Организация восприятия средств наглядности и требования, предъявляемые к ним при обучении математике

Глава II Методические рекомендации по применению наглядности в обучении математике в средней школе

§1. Наглядность и моделирование

§2. Применение компьютерных технологий в обучении математике

§3. Возможности программы “Живая Математика” в обучении геометрии в 7 классе

§4. Фрагменты конспектов уроков - примеры применения компьютерных технологий при изучении геометрии в 7 классе c учетом принципа наглядности

Заключение

Список использованной литературы

Введение

«Лучше один раз увидеть, чем сто раз услышать»

Наглядность - принцип, восходящий к определенным фундаментальным отношениям, гносеологически связывающим человека и тот мир, в котором он живет, человека и людей, с которыми он общается. Как принцип, она нуждается в специальной инструментовке, позволяющей «обнаружиться» объективным законам, в соответствии с которыми процесс познания становится эффективным.

Принцип - это регулятив деятельности, который является незыблемым и отличается от правила тем, что его нельзя нарушить ни при каких условиях, ибо он отражает фундаментальные основания мироздания, указывая на сущность определенных процессов.

Человечество, как совокупный субъект педагогической деятельности, в поисках наилучших средств наглядности прошло длительный путь от «мира чувственных вещей в картинках» Я.А. Коменского до мира бесчувственных виртуальных вещей компьютера. Первоначально человек учился у жизни, глядя на мир, слушая мир, осязая мир и через это делая его для себя очевидным. При этом перед ним возникало своеобразное смысловое несоответствие: «наглядность мира» при его неоглядности, бесконечности, возможности узнавать, помещая в разные отношения к себе как к человеку познающему.

В истории педагогической культуры постоянно идет развитие принципа наглядности. От работы с формой, педагогика движется к наглядному представлению сущности. При этом обогащается круг средств, носителей наглядности.

Наглядность является исходным моментом обучения главным образом в младших классах. По мере движения учащихся к старшим классам педагог постепенно должен находить в обучении историко-индуктивный путь пополнения знаний: постановка проблемы, история ее решения и современное состояние, затем практические или лабораторные работы. Здесь наглядность получает свою реализацию дважды: как иллюстрация истории открытия и как способ раскрытия современного решения проблемы.

Первоначальное зрительное освоение математической действительности, сопровождаемое, по возможности, соответствующими рисунками, простейшими чертежами, упражнениями с листом бумаги (перегибами и разрезаниями), изготовлением и склеиванием моделей геометрических тел, прямыми измерениями, взвешиванием и другой подобной практической деятельностью с вещами и приборами, - обогащает исходный набор представлений и сеть ассоциаций, лежащих в основе овладения любыми знаниями, в том числе и математическими.

На пороге XXI века встала серьезная проблема, связанная с переоценкой ценностей в области образования. Во главу угла ставятся личность ученика и свобода его выбора. На смену консервативным методам приходят технологии, позволяющие максимально активизировать деятельность учащихся. С появлением компьютеров развивается совершенно новый вид наглядности. Пока трудно оценить, лучше или хуже эта наглядность, но то, что она строится на иных основах, уже очевидно.

Применение компьютеров в учебном процессе увеличивает объем информации, сообщаемой ученику на уроке, активизирует, по сравнению с обычными уроками, организацию познавательной деятельности учащихся.

Вообще, наличие компьютера предоставляет множество дидактических возможностей, таких как:

подача дозированной текстовой и графической информации;

постановка различных задач учащимся;

организация индивидуальной и коллективной мыслительной деятельности;

демонстрация схем, чертежей и другой видеоинформации;

контроль знаний;

работа с электронными учебниками и т.д.

Надо отметить, что наряду с компьютерными средствами наглядности, другие средства наглядности отнюдь не отходят на второй план. Перед учителем стоит непростая задача: не ограничиться каким-либо одним средством наглядности, а по мере возможностей использовать их разумное сочетание, итогом которого будет являться желаемый результат. Очень важен тот факт, что, несмотря на многообразие и доступность наглядных пособий и средств только каждый конкретный учитель, основываясь на личном опыте донесения материала до учащихся, учитывая свои возможности и техническое оснащение школы, должен выбирать те, которые позволят ему быстро и качественно достигнуть поставленной цели.

Принцип наглядности и компьютерные технологии тесно взаимосвязаны и их грамотное сочетание может привести к хорошим результатам в обучении учащихся. Несмотря на то, что разработано довольно много компьютерных программ для использования в школе при обучении математике, далеко не все из них удовлетворяют принципу наглядности.

Актуальность исследования определяется возрастанием роли информационных технологий в математических исследованиях и их влиянием на образование.

В связи с вышеизложенным целью дипломной работы является показать, что рациональное использование компьютерных технологий с другими наглядными средствами обучения приводит к улучшению качества знаний учащихся и повышению их интереса к изучаемому предмету (на примере уроков геометрии в 7 классе).

Поставленная цель потребовала решения ряда конкретных задач, а именно:

Изучить психолого-педагогическую и методическую литературу по теме дипломной работы.

Выявить особенности конструирования урока по математике с применением среды «Живая Математика».

Разработать систему уроков по геометрии в 7 классе с применением программы «Живая Математика».

Практическая значимость дипломной работы состоит в том, что ее результаты могут быть использованы другими учителями математики при прохождении соответствующих тем школьного курса геометрии 7 класса c использованием компьютерной среды «Живая Математика».

В соответствии с поставленными задачами определена структура дипломной работы.

В первой главе рассматриваются вопросы психолого-педагогического аспекта реализации принципа наглядности: познавательные процессы и их формирование, история становления средств наглядности, сравнительный анализ слова учителя и средств наглядности, вопрос классификации средств наглядности, их функции, организация восприятия и условия оптимального применения наглядных средств обучения.

Во второй главе рассмотрен принцип моделирования, как высшая ступень принципа наглядности, а также рассматриваются вопросы взаимосвязи применения компьютерных технологий и средств наглядности. Показаны примеры использования компьютерных технологий при создании уроков геометрии в 7 класса с учетом принципа наглядности.

Глава I. Психолого-педагогические аспекты реализации принципа наглядности при изучении математики в средней школе

§1. Познавательные процессы и их формирование

Организация и систематизация чувственных данных, в число которых входит предмет нашего рассмотрения - наглядность, в процессе усвоения учебного материала осуществляется на основе общих закономерностей процесса познания со всей их сложностью и противоречивостью.

На каждой стадии познания зарождаются своего рода соотношения образного и логического, конкретного и абстрактного, что требует особых способов, методов организации чувственного познания при изучении учебного материала. С.П.Баранов считает, что общие основы управления чувственным познанием учащихся определяются тремя факторами ([6]):

качеством отражения действительности в чувственном образе; т.е. тем, как ученик представляет изучаемое явление на основе оригинала или по модели, насколько выражена тенденция к представлению объекта в реальных условиях бытия;

количеством чувственных образов, т.е. тем, насколько адекватно ученик представляет в осваиваемой закономерности окружающую действительность или её отдельные стороны, охватывает ли совокупность чувственных образов те группы предметов и явлений, которые отражены в понятии;

мерой чувственного при отражении закономерности, т.е. такой совокупностью чувственных образов, которая позволяет представить в обобщенном виде те группы предметов и явлений, которые отражены в изучаемой закономерности и обеспечивают тенденции к представлению постигаемых явлений в оригинале.

Эти факторы в большей или меньшей степени, стихийно или преднамеренно всегда проявляются в учебном процессе, определяя степень его эффективности. Поэтому управление чувственным познанием обучающихся является педагогической закономерностью, которая проявляется в принципах и методах обучения.

В зависимости от учебной задачи чувственное познание употребляется как средство формирования абстракций и как средство сосредоточения внимания, активизации познания, организации наблюдений. Чувственный образ частично характеризуется в связи с принципом наглядности и наглядным обучением, его функции неразрывно связаны с наглядными средствами обучения.

Функции чувственного образа (как прообраза наглядного) в обучении должны соответствовать тем функциям, которые выполняет чувственное познание в процессе отражения человеком окружающего мира. Бесспорно, они изменяются в структуре познавательной деятельности на каждой ступени процесса познания и в особенности при переходе мысли от одного этапа к другому. С.П.Баранов выделяет две основные функции чувственного познания в процессе обучения ([6]):

Первая заключается в том, что чувственный образ имеет самостоятельное значение в ходе овладения учебным материалом, т.е. учебная задача считается выполненной, если сформирован чувственный образ в сознании ученика.

Вторая состоит в том, что чувственный образ играет вспомогательную роль, по большей части как средство вырабатывания абстракций, т.е. чувственный образ содействует выполнению учебной задачи, но не приводит к её решению.

Любая из этих функций в процессе реализации приобретает несколько значений. Рассмотрим первую из них. Самостоятельное значение чувственного образа может выражаться в следующем:

в формировании или воспроизведении у школьников представления реального объекта с помощью наглядных пособий, экскурсий, наблюдений;

в формировании обобщенного образа совокупности предметов, явлений окружающего мира;

в систематизации чувственных образов на основе доступных школьникам научных идей, преимущественно философских. Например, представление мира с точки зрения категории пространства и времени;

в формировании компонента чувственного в структуре абстрактной мысли. Всякие научные понятия или абстракции вообще не могут не только быть постигнутыми школьниками, но и существовать, если в них отсутствует компонент чувственного познания. Преимущественно, этот компонент выражается в знаковом отображении абстракции. Например, в буквах и словах, цифрах, схемах, формулах и вообще графической записи. Восприятие и изображение учеником этих знаков является необходимой составляющей процесса усвоения понятий. Отметим, что основная идея здесь заключается не только в том, чтобы изобразить знак, но и в том, чтобы соотнести его с представлением адекватной ему реальности. Например, изображение геометрической фигуры с представлением соответствующих пространственных соотношений;

в расширении рубежей чувственного познания учащегося. В процессе обучения формируются представления объектов, явлений, которые не могут быть представлены в жизненном опыте ребенка, например, бесконечности вселенной. Подобные чувственные образы обогащают развитие ученика, приближают его к результатам общественно-исторического познания, создают тенденции к формированию мировоззрения, повышают общеобразовательную культуру.

Каждое из этих утверждений приводит к определенным учебным задачам. Их постановка и решение зависят от той ступени познания, на которой находится школьник. Иначе говоря, их возможности зависят от того, какое место занимает чувственный образ в процессе формирования конкретного или абстрактного этапов познания, а также движения мысли от конкретного к абстрактному и наоборот.

Вторая функция чувственного образа сводится, большей частью, к вспомогательному средству усвоения понятий, также приобретает различные значения и приводит к постановке соответствующих этим значениям учебных задач. Итак, чувственный образ рассматривается:

как база для первоначальных научных абстракций. Например, применение счетных палочек для постижения математических абстракций младшими школьниками. В данном случае, палочки - вспомогательное средство для овладения счетом. Как только сформирована соответствующая абстракция, т.е. ребенок научился считать, наглядные пособия становятся излишними. Чувственный образ не только лишается роли вспомогательного средства, но и оказывает тормозящее влияние на овладение абстракциями, если, допустим, при счете первоклассник постоянно представляет палочки или другой счетный материал;

в процессе овладения учебным материалом приобретает иллюстративное значение. Он помогает эффективному усвоению учебного материала;

в виде средства ускоряющего процесс познания. Например, задачи на смекалку, сообразительность, логику, в которых восприятие конкретной ситуации рождает проблему, или решение примеров, упражнений, задач с интересным смысловым содержанием.

Во все времена разрабатывались всевозможные методы, способствующие достижению успешности и прочности в усвоении знаний. В этом ракурсе данная работа рассматривает принцип наглядности как один из ведущих и эффективных принципов обучения.

В литературе по психологии под наглядностью понимают следующее:

Наглядность - свойство, особенность психических образов этих объектов.

Наглядность - показатель простоты и понятности для данного человека того психического образа, который он создает в процессе восприятия, памяти, мышления и воображения.

Познавательные процессы: восприятие, внимание, память, воображение, мышление - являются составной частью любой человеческой деятельности. Они тесно взаимосвязаны между собой и в чистом виде не существуют. Говоря об общих способностях личности, имеют в виду и уровень развития и характерные особенности его познавательных процессов. Чем лучше развиты эти процессы, тем более способен и большими возможностями обладает человек.

Познавательные процессы развиваются в деятельности и сами представляют собой особые виды деятельности. Так в результате практического манипулирования с предметами ребёнок обучается воспринимать и оценивать формы; в результате осуществления соответствующих действий и операций (структурирование, осмысление, ассоциирование материала и т.п.) запоминает материал.

Согласно теории поэтапного формирования умственных действий, психические процессы можно формировать через организованную по особым правилам внешнюю деятельность. Интериоризированными психическими процессами являются познавательные процессы: восприятие, внимание, воображение, память и мышление.

НАГЛЯДНОСТЬ - свойство, выражающее степень доступности и понятности психических образов объектов познания для познающего субъекта; один из принципов обучения. В процессе создания образа восприятия объекта наряду с ощущением участвуют память и мышление. Образ воспринимаемого объекта является наглядным только тогда, когда человек анализирует и осмысливает объект, соотносит его с уже имеющимися у него знаниями. Наглядный образ возникает не сам по себе, а в результате активной познавательной деятельности человека. Образы представления существенно отличаются от образов восприятия. По содержанию они богаче образов восприятия, но у разных людей они различны по отчётливости, яркости, устойчивости, полноте. Степень наглядных образов представления может быть различной в зависимости от индивидуальных особенностей человека, от уровня развития его познавательных способностей, от его знаний, а также от степени наглядных исходных образов восприятия. Существуют также образы воображения - образы таких объектов, которые человек никогда непосредственно не воспринимал. Однако они составлены, сконструированы из знакомых и понятных ему элементов образов восприятия и представления. Благодаря образам воображения человек способен вначале представить себе продукт своего труда и лишь затем приступить к его созданию, представить различные варианты своих действий. Чувственное познание даёт человеку первичную информацию об объектах в виде их наглядных представлений. Мышление перерабатывает эти представления, выделяет существенные свойства и отношения между разными объектами и тем самым помогает создавать более обобщенные, более глубокие по содержанию психические образы познавательных объектов.

Так как в процессе познания окружающей действительности (то же и в процессе учения) участвуют все органы чувств человека, то принцип наглядности выражает необходимость формирования у учащихся представлений и понятий на основе всех чувственных восприятий предметов и явлений. Однако пропускная способность у органов чувств или «каналов связи» человека с окружающим миром различна. По мнению некоторых специалистов, если, например, орган слуха пропускает 1 000 условных единиц информации за единицу времени, то орган осязания за ту же единицу времени пропускает 10 000 условных единиц информации, а орган зрения - 100 000, то есть около 80% сведений об окружающем мире человек получает с помощью зрения.

Таким образом, отмечая наибольшую пропускную способность информации у органов зрения, ставим принцип наглядности на первое место. Однако он предусматривает не только опору на зрение, но и на все другие органы чувств. На это положение обращал внимание и великий русский педагог К.Д.Ушинский. Он отмечал, что чем большее количество органов чувств принимает участие в восприятии какого-нибудь впечатления, тем прочнее оно закрепляется в нашей памяти. Физиологи и психологи объясняют это положение тем, что все органы чувств человека взаимосвязаны. Экспериментально доказано, что если человек получает информацию одновременно с помощью зрения и слуха, то она воспринимается более обострённо по сравнению с той информацией, которая поступает только через посредство зрения, или только через посредство слуха.

Обратившись к семантике слова «наглядность», приходим к тому, что в самом слове для учителя очень многое лежит на поверхности, но и многое скрыто. Наглядность - глядеть, разглядывать. Этот явно подсказанный самим словом смысл указывает на модальность восприятия. Глядят глазами! Но если углубиться в размышления о целях использования наглядности в педагогической практике, обнаруживается: в первую очередь, для того, чтобы сделать знание очевидным. В прямом значении - доступным очам, в переносном - явным, явившимся. Но являться в конечном итоге не обязательно визуально. Значит, и наглядность может быть разного рода.

Усвоения математических понятий, умения доказывать математические утверждения можно достичь лишь при правильном применении средств наглядности и компьютерных технологий, хорошо зная функции, роль и место наглядности в обучении математике в средней школе.

§2. История становления средств наглядности

Использование наглядности в обучении имеет длительную историю. К ней прибегали и тогда, когда не существовало письменности и даже самой школы.

В школах древних стран - Китая, Египта, Греции, Рима и других стран - она была достаточно широко распространена. В практике обучения использовались чувственные образы в процессе изучения книжного материала. Книги снабжались нередко рисунками, но это было лишь эмпирическое применение наглядности без теоретического обоснования её. Так как по началу словесно-схоластический путь обучения исключал применение наглядных пособий и слово являлось, по сути дела, единственным средством обучения. И лишь позже появились наглядные средства в учебном процессе.

Вопрос, касающийся соотношения слова и средств наглядности в обучении, получает своё подлинное значение тогда, когда требование наглядности обучения становится одним из краеугольных камней дидактики.

Первым, кто возвёл наглядность до уровня стержневого вопроса дидактики, разработал и дал нам определенную теорию о ней как об обще дидактическом принципе обучения, был Ян Амос Коменский. Он писал: «…Пусть будет для учащихся золотым правилом: все, что только можно, предоставлять для восприятия чувствами, а именно: видимое - для восприятия зрением, слышимое - слухом, запахи - обонянием, что можно вкусить - вкусом, доступное осязанию - путем осязания. Если какие-либо предметы сразу можно воспринять несколькими чувствами, пусть они сразу схватываются несколькими чувствами» ([24]). Ученики должны непосредственно знакомиться с предметами в натуре; если это не представляется возможным, следует использовать в обучении специально изготовленные копии или изображения вещей.

Осуждая широко распространенное в то время в школах схоластическое, догматическое обучение, Я.А.Коменский подчеркивал, что знания следует черпать прежде всего из собственных наблюдений, а не из чужих слов, которые принимаются на веру в силу авторитета наставника. Обучение надо ставить так, чтобы изучение слов и изучение вещей шли в полном соответствии друг с другом.

Дальнейшая разработка теоретических положений принципа наглядности и их проверка в практике обучения тесно связаны с именем Иоганна Генриха Песталоцци. «Моей самой существенной исходной точкой зрения, - писал Песталоцци, - является следующая: созерцание (чувствительное восприятие) человеком самой природы является единственным истинным фундаментом обучения, так как оно (созерцание) является единственной основой человеческого познания. Всё, что следует затем, является просто результатом, или абстракцией, от этого чувственного восприятия» ([35]). И.Г. Песталоцци значительно обогатил принцип наглядности, но в отличие от Коменского, он считал наблюдение лишь стадией в процессе обучения, для него это лишь средство для развития логического мышления детей.

Стараясь отыскать законы, которым подчиняется развитие человеческого ума, и «найти в них надежную нить, из которой можно выплесть общий психологический метод обучения», И.Г. Песталоцци пришёл к выводу, что «всё наше знание вытекает из трёх основных способностей: a) из способности производить звуки, из чего происходит способность речи; b) из неопределённой, исключительно чувственной способности представления, из которой происходит знание всех форм; с) из определенной, не исключительно чувственной способности представления, из которой следует выводить понимание количества» ([35]). На этом основании И.Г. Песталоцци считал, что слово, форма и число должны быть приняты за начальные пункты всякого обучения. Если человек хочет растолковать и уяснить то, что находится перед ним в беспорядочном виде, он непременно обратит внимание на то: а) сколько различных предметов перед ним, б) каковы их форма и контур, в) как они называются.

Под средствами наглядности И.Г. Песталоцци понимал только натуральные предметы или их вещественные модели. Знак, цифра, число для него лишены наглядности. Он не учитывал того, что с развитием изменяется уровень мышления учащихся, а вместе с этим должны изменяться средства наглядности и методика их использования.

Отвечая на возражения тем, кто считал, что «много кричат» о наглядности, А. Дистервег утверждал, что не пришло еще время остановиться, так как тысячи учителей еще следуют абстрактному методу обучения.

К.Д. Ушинский также придавал огромное значение наглядному методу обучения; он призывал сочетать применение наглядности с развитием речи, мышления, а образную речь относил к своеобразной наглядности.

Обосновывая свои дидактические положения, К.Д. Ушинский опирался на обширные и разносторонние данные современной ему психологической и физиологической науки. Он подчеркивал, что применение наглядности соответствует природе ребёнка, который «мыслит формами, красками, звуками, ощущениями вообще…». Соответственно особенностям ребёнка учение надо строить не на отвлечённых представлениях и словах, а на конкретных образах, являющихся результатом непосредственного восприятия. Учение должно идти в направлении от конкретного к отвлечённому, от представления к мысли - такая последовательность соответствует законам психики.

Борьба за использование наглядных средств в обучении была прогрессивной, так как она выступала против научного догматизма и догматических методов обучения, против идеализма. В требовании наглядности обучения у таких дидактов, как Дистервег и Ушинский, отражена материалистическая позиция (изучение действительности и познание реального мира на основе непосредственных восприятий).

Значение наглядности в обучении вытекает из материалистической концепции высшей нервной деятельности, которая предполагает, что наглядные средства могут эффективно способствовать развитию первой сигнальной системы, делая ребёнка очень восприимчивым ко всему конкретному, наглядному, что можно непосредственно увидеть, услышать, потрогать руками, а на её основе и второй сигнальной системы, благодаря которой ребёнок способен самостоятельно делать некоторые обобщения, выводы, находить причины явлений.

О весьма существенной роли наглядности в учебном процессе свидетельствуют повседневные наблюдения, обыденный опыт людей (лучше один раз увидеть, чем сто раз услышать), а также специальные эксперименты.

Наглядность должна способствовать активизации умственной деятельности учащихся через концентрацию внимания на том материале, который является главным в излагаемом материале. «...Если обучение должно основываться на естественном ходе развития человека, то оно должно начинать с того же, с чего начинает природа - пробуждать чувственный разум человека и постепенно переводить его к отвлечениям. Наглядное обучение есть единственно правильный и естественный метод обучения, вполне отвечающий ходу развития отдельных личностей...» (П.Ф. Каптерев, [21]). В большинстве проведенных исследованиях изучается только та сторона понятия наглядности, которая рассматривает её как средство обучения, учебную модель, изоморфно отражающую существенные черты некоторого явления. Однако С.П. Баранов отмечает: «...Не само наглядное пособие, а тот чувственный образ, который возникает у школьников в результате его использования, является главным в структуре познания...» ([5]). Учебная модель упрощает рассматриваемое явление, потому что изоморфно может быть отражена одна или небольшое число его характеристик. «...Наглядное пособие моделирует определенные стороны изучаемого объекта и дает возможность через эту модель представить оригинал...» (С.П. Баранов, [5]).

Однако достижение полного изоморфизма объекта и модели не является дидактической целью введения средств наглядности в учебный процесс. Взамен утраченных характеристик объекта модель приобретает простоту восприятия. В.Г. Болтянский называет формулу наглядности: изоморфизм плюс простота ([9]). Он также выделяет важное свойство наглядных пособий - «быстродействие», которое характеризуется быстротой приведения средства обучения в рабочее состояние, экономией времени доставляемой его применением. Под изоморфизмом понимается полное соответствие учебно-наглядного пособия изучаемому понятию. Требование и понятное, и не совсем понятное. Если изучается правильная треугольная пирамида, то ее модель, изготовленная из картона, проволоки т.д., конечно, не должна являть собой неправильную пирамиду. Но для иллюстрации общего понятия правильной пирамиды нужны две-три модели правильных пирамид с разным числом сторон в основании. Но и в этом случае можно согласиться с термином «изоморфизм», хотя понятие одно, а количество наглядных пособий - больше. В случае с другими более сложными понятиями необходимо привлекать большее число наглядных пособий, варьируя несущественные свойства объектов. Например, в объем понятия «функция» входят разнообразные функции (непрерывные, разрывные, ограниченные и неограниченные, периодические и непериодические и т.д.). Для того чтобы проиллюстрировать моделью квадрат никому в голову не придет показать ученикам прямоугольник или параллелограмм общего вида. Более важным требованием к наглядным пособиям, направленным на формирование понятия, является достаточно полное раскрытие сторон понятия с вариацией несущественных свойств, с выпуклым показом основных, существенных свойств.

Существует и другая сторона понятия наглядности. Она рассматривается в качестве метода обучения. Как показал П.Ф. Каптерев: «...Существенный признак наглядного метода заключается не в иллюстрации общих положений и суждений, а в его элементарности, выражающейся в том, что содержание науки разлагается на составляющие её элементы, которые изучаются строго последовательно от элементов к их сочетаниям и затем сложным образованиям...» ([21]). В понимании П.Ф. Каптерева, «элементарное обучение» наглядно по своей природе, наглядно психологически, отвечает естественному развитию мышления учащегося. По его мнению, только при таком наглядном методе приобретают дидактическую ценность и другие наглядные средства обучения.

Понимание наглядности как существенного свойства педагогического изложения и естественного метода обучения прослеживается и в некоторых работах современных дидактов, например, М.Б. Волович утверждает, что «...наглядность.., как правило, ничего общего не имеет с представлением учащимся натуральных объектов, и психологические функции наглядности здесь совсем иные...» ([12]). С.Л. Баранов пишет: «...Наглядность в современной теории и практике обучения можно понимать двояко. Либо подразумевать под наглядностью процесс чувственного отражения в обучении, либо говорить об изучении учебного материала на основе наглядных пособий...» ([5]).

Таким образом, представление наглядности только как средства обучения является упрощенным и односторонним толкованием сущности наглядного обучения. Но если наглядность понимать и как метод, и как постоянную опору учащихся на чувственные образы в процессе усвоения содержания учебного предмета, то наглядность является дидактическим принципом, проявляющимся на всех ступенях учебного процесса.

А.Н. Леонтьев выделял две функции наглядности: «...первая направлена на расширение чувственного опыта; вторая - на раскрытие сущности изучаемых процессов, явлений...» ([25]). Наглядность призвана не просто расширить чувственный опыт, но усилить опыт вообще. Н.Г. Салмина вводит различение средств наглядности и материализации, понимая под материализацией средство обеспечения выделения существенного в плане восприятия, а под наглядностью - средство выделения существенного в действии...» ([43]).

Под наглядностью будем понимать следующее: наглядность в обучении математике - это совокупность материальных, материализованных, идеальных действий, совершаемых как обучающим, так и обучаемым в ходе реализации дидактической цели обучения.

педагогический наглядность математика школа

§3. Сочетание слова учителя и средств наглядности

Сочетание слова учителя с применяемыми им наглядными средствами - одно из наиболее распространенных явлений в практике обучения. Применяя средства наглядности педагог использует при этом и слово: сообщает учащимся знания, руководит процессом наблюдения учащимися объектов и т.д. Поэтому возникают вопросы, касающиеся соотношения слова и наглядности в обучении. Наглядные восприятия обладают высокой «пропускной» способностью. Сами наглядные средства и их сочетание с речью и практической деятельностью, обладают наиболее высокой эффективностью для запоминания.

Прежде всего, основное отличие состоит в том, что источник получения информации учащимися - разный. В первом случае используются такие приемы, как рассказ, беседа, устное или печатное слово. Когда учитель предлагает наблюдение тех или иных наглядных объектов, источником знания служат предметы и их изображения. Разнообразность источников, из которых учащиеся получают знания, а также их чередование имеют очень важное значение.

Однако аспект соотношения слова и наглядности не является единственным. Несомненно, существенным является вопрос о роли слова для того, чтобы сделать восприятие учащимися наглядных объектов более плодотворным, содержательным, организованным. Необходимо уметь правильно называть предметы, чтобы достигнуть большей точности и легкости их различения и иметь истинное представление об их отличительных признаках.

Существенное значение имеет выявление различных сторон вопроса о роли слова и наглядных средств в высказываниях выдающихся прогрессивных педагогов прошлого.

Проблема соотношения слова и средств наглядности становится во главу угла в тех педагогических концепциях, в которых слово занимает первое место. В связи с этим обратимся к концепции Н.И. Пирогова ([37]). Он раскрыл иной аспект применения слова в обучении. Пирогов считал, что из каждого учащегося надо сформировать истинного человека и видел в этом основную цель воспитания. Для ее достижения большую роль приобретают упражнения на внимание учащихся. Существует два направления внимательности - внешняя и внутренняя. В этом случае педагогу важно не допускать односторонности. Наглядность имеет главное воздействие на внешние чувства, заставляет обращать взор внутрь себя, вглубь своих внутренних ощущений. Слово действует своими звуками на существенную деятельность человека - мыслить.

Нам кажется важным подчеркнуть тот факт, что слово нельзя ставить выше наглядности, как это делал Н.И. Пирогов, считая, что: «...Наглядный объект может глубоко врезаться в память ребенка, однако сам по себе, без помощи слова, всегда останется чем-то отрывочным и несвязным, тогда как впечатление, произведенное словом, будет более цельное и связное. В известных случаях слово может заменить наглядность: с помощью слова педагог создает образное представления у учащихся...» ([37]).

Необходимо отметить, что когда учитель в процессе урока подкрепляет словесные обращения наглядными средствами, умственная деятельность учеников повышается, мышление соединяется с непосредственным восприятием, появляется возможность познавать что-либо через конкретные ощущения, то есть путем непосредственного воздействия предметов реальной действительности на рецепторы. Ощущения, которые отображают внешнюю сторону предметов, не способны отобразить внутренние связи явлений, их закономерный характер. Мышление характеризуется тем, что происходит отвлечение от того своеобразия, которое свойственно единичным явлениям, и выделение черт, присущих тому или иному кругу явлений. Таким образом, ощущения - отображение явления, мышление - отображение сущности. Отвлеченное мышление, которое характерно для человека, нераздельно связано с языком, а одновременно - основой мышления, сознания. Реальность мысли обнаруживается в языке, отвлечение и обобщение, характерные для мыслительной деятельности человека, осуществляются при помощи языка. Слова и предложения выражают отвлечение и обобщение свойств вещей, связей отношений между ними.

Внедрение наглядных средств в сочетании со словом, вызывает у учащихся непосредственное восприятие, и процессы абстрактного мышления представляют различные формы отражения объективного мира. Этим формам свойственна относительная противоположность - противоположность отдельного, случайного и общего, необходимого.

В связи с тем, что отдельное и общее переходят друг в друга, можно, отталкиваясь от наблюдений, явлений в непосредственной данности, вскрыть сущность. В виду того, что общее и отдельное представляют собой связь противоположностей, переход от явления к сущности в процессе познания сложен.

Объективность понятий, точно так же, как и объективность ощущений, проверяется практикой. Контроль знаний о действительности есть высшая ступень процесса познания, отражение законов объективного мира в голове человека.

Под сочетанием, прежде всего, имеется в виду внутреннее отношение между применением слова учителя и использованием наглядных средств. Это отношение определяется тем, какую роль выполняет внедрение наглядности для осуществления определенной учебной задачи. От отношения между применением слова и использованием наглядных средств зависят соотношения наглядных образов и понятий в сознании учащихся.

Истинное понимание употребления средств наглядности в сочетании со словом содержат необходимый компонент: представление взаимосвязи слова как обобщающего начала и ощущения, являющегося непосредственным отражением предметов материального мира. В советской дидактике вопросы использования слова и наглядности в обучающем процессе представляются, главным образом, двумя пунктами:

в виде рассмотрения источников восприятия учащимися учебного материала;

в виде рассмотрения путей познания в усвоении знаний учащимися. Б.П. Есипов отмечает следующие источники: слово учителя (объяснение, рассказ);

наблюдение изучаемых предметов, явлений; рассматривание наглядных пособий, изображающих изучаемые явления; использование учебников, книг и других печатных материалов ([18]).

М.А. Данилов различает два пути познания в усвоении учениками знаний ([15]):

путь непосредственного восприятия изучаемых объектов;

опосредованный путь познания, в котором первое место занимает объяснение учителя.

Таким образом, источниками восприятия нового учебного материала, помимо слова и использования текстов книг, являются средства наглядности.

Есть также мнения о том, что представления о предмете образуются у школьников путем наблюдения и путем описания. Очень важно, что во всех положениях, упомянутых выше, слово и наглядность рассматриваются с точки зрения путей познания в учебном процессе. Основополагающим является соотношение слова и наглядности во времени. Существуют огромные различия в протекании психической деятельности учащегося в том случае, когда те или иные знания сообщены ему исключительно словесным путем, а только потом в учебный процесс вводятся средства наглядности, или наоборот, учащийся проводит наблюдение объекта, после чего учитель, опираясь на проведенные школьником наблюдения, сообщает новые знания.

Большое значение этому различию придавал П.Ф.Лесгафт. По его мнению, путем словесного описания, даваемого преподавателем, ученик составляет весьма приблизительное представление, которое переводится в более ясное только тогда, когда учащийся сам производит то действие, описание которого воспринял слухом, или когда ему показывают то, о чем раньше ему было сказано ([26]).

Вслед за П.Ф. Лесгафтом эту идею развивает С. Познер ([40]), считая, что наглядные средства должны быть использованы лишь после того, как учащиеся получат словесное описание сделанное учителем, или прочтенное в книге. Он также считает, что предварительное словесное описание способствует обострению внимания и сознательному характеру проводимых наблюдений.

Временное соотношение слова и наглядности имеет спорные пункты, одним из которых является тот, что учащиеся должны одинаково уметь облечь свои предметные представления в форму слова и наоборот. Именно об этом говорит В.В. Половцев, всячески подчеркивая немаловажный факт, указывающий на то, что при неумелом использовании вышеупомянутого пути может случиться так, что по слову ученики будут создавать себе совершенно неверные представления, которые затем придется переделывать путем наглядного знакомства с соответствующими объектами ([41]).

Существуют методики, согласно которым следует обеспечить одновременность словесного сообщения знаний об объекте и демонстрации соответствующих моделей и процессов или их изображений, демонстрация должна быть вплетена в ткань словесного изложения. Также методики говорят о том, что надо применять наглядные средства не до рассказа о нем и не после, а одновременно. А.И. Великороднова ([10]) делает вывод о преимуществе методики, использующей наглядное пособие «таблица - свиток», постепенно разворачивающийся перед учащимися.

Таким образом, ставится проблема о наиболее целесообразном сочетании слова и наглядного показа. Возникают следующие важные вопросы:

Должен ли наглядный показ повторять то, что уже было разъяснено словами?

Когда именно целесообразно использовать сочетание слова и наглядного показа?

Как изменяется соотношение слова и показа в зависимости от того, какая учебная задача стоит перед учителем?

Наглядный материал служит как бы внешней опорой внутренних действий, совершаемых ребенком под руководством учителя в процессе овладения знаниями.

Не секрет, что в большинстве случаев ещё до поступления в мозг информация начинает перерабатываться. Как известно, селекция зрительной информации осуществляется уже в сетчатке глаза, причем на сетчатке «встречаются» как воспринимаемые извне образы, так и образы из долговременной памяти мозга. Рассмотрим концепцию Н.А. Амосова о процессе мышления, согласно которой мозг человека перерабатывает информацию этажной системой кодов. По отношению друг к другу они не только находятся в субординации, но и обладают известной функциональной самостоятельностью (код знаков и звуков ® код слов ® код фраз ® код смысла) ([53]). Другими словами, в процессе мышления значительный объем информации перерабатывается и усваивается именно на нижних этажах кодовой системы, независимо от словесных уровней. П.М. Эрдниев замечает, что нередко понимание дела наступает с восприятием удачной формы записи или иллюстрации, т.е. сразу на низшем уровне, до перекодировки на словесном уровне ([53]). Приведем его слова, которые в полной мере отражают главную идею принципа наглядности: «...Очевидно то, что очам видно!». В качестве примера он приводит две записи таблицы умножения:

Как видим, крупная цифра 2, использованная во второй записи, только своими размерами неотразимо выполняет «свою информирующую роль», т.е. она показывает в явном, наглядном виде, что число 2 есть общий множитель для всех трех параметров. Практика показывает, что опытный учитель, встретившись со случаем непонимания учениками изучаемого материала, всячески упрощает объяснение, спускаясь на нижние уровни информационной лестницы и подбирая все более понятные упрощенные толкования усваиваемой темы. Указанный выше пример отчетливо показывает, что от удачного, продуманного информационного оформления мысли на «нижних уровнях» зависит и скорость «подъема мысли» по лестнице кодов, а значит и успешность обучения в целом, прочность запоминания материала и сознательность усвоения.

В математике достаточно сложно назвать такой раздел, чтобы при его изучении было бы невозможно улучшить информационные «детали» нижних этажей, далеко не маловажные, а иногда и решающие для усвоения содержания. Так, в частности, при введении взаимно обратных операций, бесспорно, направляют элементы бессознательного симметричного изменения положений отдельных символов в двух строках записи, расположенных друг под другом. В идеале математические иллюстрации или записи на доске, к которым относят рисунки, схемы, символы, графики и т.д., должны быть осмысливаемой цветной картиной. В подтверждение нашим словам приведем пример, описанный П.М. Эрдниевым ([53]), о совместности записи двух формул:

Такая запись с двумя знаками четко сообщает о соответствии членов пары противоположных понятий: суммы и разности кубов. Также можно рассмотреть совмещенную запись переместительного закона для сложения и умножения:

Как видим, обобщенность букв в этих двух формулах сама по себе, и до словесных объяснений, обеспечивает понимание того, что сложение и умножение аналогичны относительно свойства перестановочности компонентов, т.е. коммутативности. При подобных соединениях носителей информации во времени и пространстве достигается органическое воздействие нижних и верхних кодовых систем (до словесных и словесных средств переработки информации). Вот почему в учебной литературе используются сдвоенные правила и формулы, однако, по возможности, их надо больше выделять такими эффективными наглядными средствами, как цвет, шрифт и т.д.

Значение символики или даже разумной компоновки математического текста подчеркивалось и подчеркивается самими математиками. Например, успешная символика, введенная Лейбницем для математического анализа, активизировала в свое время во многом получение существенных результатов в новой тогда отрасли математики. Когда пишут n ® ¥, e ® 0, ассоциации обретают силу безусловного рефлекса. К записи e ® ¥ при n ® 0 никаких формально-логических прицепок предъявлено не может быть, однако же такой произвол с использованием символов означает для мышления математика поистине кошмар.

П.М. Эрдниев отмечает, что неверные связи в мышлении иногда появляются на уровне «кода символов», чему виной бывают неудачные в психологическом отношении обозначения в некоторых учебных пособиях ([53]). В качестве примера он приводит почти все учебники аналитической геометрии, где коэффициенты уравнения прямой обозначают строчными буквами (ах + by + с = 0), тогда как коэффициенты уравнения плоскости принято обозначать почему-то… заглавными (Ах + By + Cz +D = 0), отметив также неблагозвучность чтения этих букв (a «малое», A «большое» и т.п.). Описанный пример показывает исключительную важность тщательно продуманной наглядности и единства символики и терминологии в учебниках.

В символическом оснащении учебников, которыми пользуются миллионы учащихся, важно добиться предельной наглядности, а именно слитности слова-термина и соответствующего знака-символа. Последнее возможно только тогда, когда символ вначале выступает как аббревиатура соответствующих терминов в алфавите родного языка.

Несомненно, опытный учитель искусно учитывает все технологические, в том числе и наглядные детали, тонкости своего мастерства для более эффективного, быстрого и легкого усвоения учащимися изучаемого материала. Такой учитель тщательно и сознательно оформляет записи и иллюстрации, рисунки, содействуя, тем самым, четкости и соответствующих словесных пояснений. Он знает и хорошо понимает, что большим подспорьем для развития мышления служит своевременное внедрение тщательно продуманных математических символов. Именно этот педагог всегда помнит, что укрупнению единиц усвоения также благоприятствует расположение записей структурно связанных упражнений в двух параллельных столбцах, друг против друга. Ведь то, что зрительно воспринимается рядом, легче противопоставить и связать логически, словесно. Собственно такой учитель действительно понимает, что математика начинается с грамотной символики и соответствующей терминологии. Только такой педагог виртуозно использует взаимопереходы между образным, символическим и словесным, прекрасно осознавая, что сочетание именно этих видов мышления - важнейший секрет обучения!

§4. Функции средств наглядности

Наглядные пособия призваны облегчить усвоение учебного материала. Эмоциональность их восприятия способствует прочности запоминания.

Рассмотрим функции средств наглядности.

Наблюдения показали, что большинство учителей считают, что наглядность выполняет только лишь функцию иллюстрации. Но эта функция не единственная. Наглядность может выполнять объяснительную, операторную и т.д. функции.

Как подчеркивает А.Н. Леонтьев: «Одно дело, когда в процессе обучения возникает задача дать учащимся живой, красочный образ недостаточно известного им кусочка действительности, расширить в этом направлении их чувственный опыт, обогатить их впечатления - словом, сделать для них возможно более конкретно, более реально и точно представленным тот или иной круг явлений… Совсем другое дело в случае, когда наглядность непосредственно включается в процесс обучения в связи со специальной педагогической задачей… Здесь роль наглядного материала, конечно не в том, чтобы например, изображения карандашей на таблице обогащали чувственный опыт ребёнка, они служат не для этого, а для обучения счету» ([25]).

Отвечая на вопрос о психологической функции наглядного материала включенного в процесс обучения, А.Н. Леонтьев указывает, что она состоит в том, что «он служит как бы внешней опорой внутренних действий, совершаемых ребенком под руководством учителя в процессе овладения значениями» ([25]).

Говоря о функциях средств наглядности в процессе преподавания математики в средней школе, необходимо подчеркнуть и общепедагогические функции средств наглядности:

образовательная функция;

развивающая функция;

воспитательная функция.

Все эти функции существуют одновременно, составляют одно целое со своими внутренними диалектическими противоречиями, только в зависимости от локальных учебных целей, учебного материала и учебной ситуации одна из этих функций в педагогическом процессе выдвигается на первый план.

Кратко остановимся на каждой из них.

Образовательная функция. Средства наглядности являются носителями большой информации. Наиболее важным (с точки зрения объема охватываемой информации) применением средств наглядности является использование схем, таблиц, формул на уровне отвлеченного мышления, то есть без соответствующей конкретизации общих положений частными случаями.

В процессе использования средств наглядности учащиеся получают определённые сведения из семиотики (наука о знаках). В связи с этим они изучают и запоминают многие правила синтактики (наука, изучающая синтаксис, то есть отношение знака к знаку), семантики (наука, изучающая отношение знака к обозначаемому объекту) и прагматики (наука, изучающая отношение знака к научно-практическим потребностям человека).

Развивающая функция. Наглядность - это не только основа чувственного восприятия, необходимая для сознательного усвоения новых знаний, но и путь, ведущий к развитию мышления.

В процессе обучения математике в средней школе перед средствами наглядности ставится одна из важнейших задач - способствовать развитию у учащихся интеллектуальных способностей, самостоятельности умственных действий, логического мышления.

Воспитательная функция. Огромна воспитательная роль средств наглядности. Учащиеся относят математику к числу важнейших школьных предметов не только потому, что в настоящее время математические методы исследования проникают во все области человеческих знаний, но также и потому, что, изучая математику, они находят богатую пищу для всестороннего развития своих способностей.

Особенно возрастает интерес к математике, когда методы обучения разнообразны и учитель задумывается над ролью данной темы в развитии способностей ученика. В этом большую помощь могут оказать средства наглядности в процессе обучения математике.

Рассмотрим некоторые воспитательные функции средств наглядности:

эстетическое воспитание

Эстетика, как известно, - это наука о закономерностях эстетического освоения человеком мира, о сущности и формах творчества по законам красоты. Некоторые предполагают, что между математикой и эстетикой нет ничего общего. Это весьма ошибочное мнение. Многие известные ученые деятели всегда подчеркивали это. Например: «Математика - один из видов искусства» (Норберт Винер), «В математике тоже есть красота, как в живописи и поэзии» (Н.Е. Жуковский), «В математике красота играет громадную роль» (Н.Г. Чеботарев), «Великая книга природы написана математическими символами» (Г. Галилей).

В формировании эстетического отношения к фактам и явлениям в процессе обучения математике важную роль играет правильное применение наглядности, ибо наглядность хорошо может показать определённые элементы красоты математических фактов, изящество доказательств теорем или решения задач.

нравственное воспитание

Изготовление и применение средств наглядности повышают интерес к предмету, вырабатывают у учащихся чувство собственного достоинства, и вследствие этого у них формируются определённые нравственные качества.

умственное воспитание

Поиски новых способов повышения эффективности обучения и умственного развития учащихся осуществляется в разных направлениях. Огромные возможности умственного воспитания содержит обучение математике с применением средств наглядности. Формирование абстрактных математических понятий с применением средств наглядности способствуют активному отношению учащихся к окружающему миру явлений. А с этим неразрывно связана наблюдательность, способность выделять в явлениях и фактах их наиболее существенные стороны и взаимосвязи.

Вследствие правильного применения средств наглядности в процессе обучения у учащихся повышается организованность в своей деятельности, они тщательно анализируют исходные положения и проверяют их, определяют наиболее рациональные пути решения математических задач.

§5. Классификация средств наглядности

Всё многообразие видов наглядности (по характеру отражения окружающей действительности), используемых в школе, можно свести к нескольким типам, различным по своему содержанию и функциям:

натуральные вещественные модели (муляжи, геометрические тела и фигуры, макеты различных предметов, технические образцы и их перспективные изображения, модели, панорамы, …);

условные графические изображения, отличающиеся разнообразием форм и содержания (чертежи, разрезы, сечения, эскизы, наглядные изображения в системе аксонометрических, изометрических проекций,.. );

знаковые модели (графики, диаграммы, формулы, уравнения, отдельные математические выражения и символы, математические знаки);

инструменты (линейка, циркуль, транспортир, угольник, …);

таблицы (плакаты);

экранные средства;

дискретные, точечные средства.

Все эти виды наглядности по-разному связаны с объектом изображения и имеют неодинаковую значимость в раскрытии его отдельных свойств.

Натуральные модели и их наглядные изображения являются простыми заменителями реальных объектов, с которыми они сохраняют полное сходство. Являются наглядной опорой для формирования у учащихся конкретных образов изучаемых объектов, они передают, как правило, конкретные чувственно воспринимаемые свойства отдельных объектов во всей их полноте, многообразии и выполняют роль иллюстраций при усвоении знаний. Эффективность применения моделей становится особенно ясной, если вспомнить такие образцы, как шарнирные параллелограмм и ромб, равносоставленные фигуры, треугольник, основание которого сохраняется постоянным, а вершина перемещается параллельно основанию (стороны его образуются резиновой нитью или шнуром) - в планиметрии, динамические модели тел вращения, модели многогранников, различные стереометрические наборы, прозрачные и полупрозрачные модели сечений, вписанных и описанных тел и т. д. - в стереометрии, модель термометра - для демонстрации свойств целых чисел и т. д.

Например, c помощью модели пирамиды можно пояснить понятие ребра, вершины, высоты, линейного угла двугранного угла и пр. Каркасная (проволочная) модель позволяет показать сечение многогранника плоскостью, взаимное расположение многогранников. С помощью моделей можно облегчить понимание школьниками доказательства теорем.

Важное значение модели приобретают при изучении стереометрии. Исследователи, занимающиеся изучением практики работы учителей на уроках геометрии в 10 - 11 классах, делают выводы, что большинство из учителей находятся под влиянием учебников, в которых вынужденно не используются наглядные пособия. Доказательства теорем проводятся только с использованием чертежей, тогда как в некоторых случаях их с большим эффектом и пользой можно провести на соответствующей модели. Для подтверждения слов приведем пример доказательства следующей теоремы: «Объем наклонной призмы равен произведению площади её перпендикулярного сечения на боковое ребро».

Для доказательства нужно изготовить из бумаги (картона, дерева) два многогранника, дополняющие друг друга до прямой призмы (рис. 1). Поменяв положение многогранников так, чтобы совпали грани ABC и KLM, получим нужную наклонную призму с перпендикулярным сечением. Для неё легко провести рассуждения, доказывающие сформулированную теорему.

Рис. 1

Однако необходимо проследить за тем, чтобы использование моделей не привело к ухудшению навыков изображения учащимися пространственных фигур. Для этого нужно организовывать соответствующую деятельность в необходимом объеме.

Условные графические изображения, в отличие от натуральных моделей, способствуют передаче скрытых от непосредственного восприятия свойств изучаемого объекта. Они передают, главным образом, конструкцию (строение) объекта, его геометрическую форму, пропорции, пространственное расположение отдельных составных частей.

Условные графические изображения являются более абстрактными (удаленными от объекта изображения), чем натуральная модель. Однако они дают возможность выявить более существенные связи и отношения. Поэтому условные графические изображения выполняют в процессе обучения объясняющую функцию, углубляя представления об изучаемом объекте, позволяя проникать в его более существенные связи и отношения, скрытые от непосредственного наблюдения.

Условные графические изображения позволяют представить не один, а сразу несколько различных предметов, обладающих общими конструктивными особенностями. На их основе создаются схематизирующие обобщения.

Условно графические изображения могут передавать различные состояния объектов - статическое и динамическое: процесс создания, изменения, изготовления.

Основная трудность у учащихся состоит в том, что за статическим изображением схемы они «не видят» динамических изменений объектов. Они без труда воспроизводят схему, но не могут представить по ней объект - движущийся, видоизменяющийся, преобразующийся, что ведет к «рассогласованию» образа схемы и объекта.

Знаковые модели существенно отличаются как от предметных, так и от условных изображений, рассмотренных выше. Это наглядность, но наглядность особая. В ней уже не просматривается связь с реальным объектом. С её помощью моделируются не отдельные свойства, и даже не их конструктивные особенности, а всеобщие абстрактные зависимости, общие объектам, разнородным по своему внешнему виду и конкретным особенностям.

Знаковые модели очень специфичны и поэтому не могут использоваться с другими видами наглядности без специального обучения способам их восприятия, содержания и назначения. Они несут в себе семантическую функцию, являются наглядными «носителями» теоретических знаний. Например, при изучении свойств функций (возрастание, убывание, максимум, минимум, нули функции и др.) целесообразно их аналитическую запись переводить на язык графиков и на этой основе тренировать учащихся «читать» графики функций.

Одной из разновидностей учебно-наглядных средств являются инструменты. Они представляют собой устройства, позволяющие производить некоторые математические действия. Дидактическая ценность их значительно выше, чем-то внимание, которое уделяется им в школьной практике. Вот некоторые виды инструментов: линейка, циркуль, транспортир, угольник, пропорциональный циркуль, центроискатель, поперечный масштаб, пантограф, эккер, малка, астролябия, биссектор и т.д. Все они описаны в соответствующей литературе, однако на практике широко применяются только первые четыре.

Требование активной деятельности учащихся является важнейшим при использовании наглядных пособий. Его забвение может также привести к формализму в знаниях учащихся. Участие последних в конструировании пособий способствует более осмысленному овладению учебным материалом, формированию необходимых образов осуществления способов действий. Особенно это относится к сложным учебно-наглядным пособиям, в том числе и к инструментам. Формальное заучивание способа их применения без вскрытия существа дела будет препятствовать осознанию учениками сути, и приводить к ошибкам. Глубокое понимание содержательной стороны, основанное на образных представлениях, возможно только тогда, когда ученик прослеживает генезис применяемого учебно-наглядного пособия.

Следующим указанным видом учебно-наглядных средств являются таблицы. Таблицы (плакаты) делятся на справочные, иллюстративные, рабочие и комбинированные. Справочные таблицы содержат справочный материал по той или иной теме школьного курса математики. Это могут быть тригонометрические формулы, формулы площадей, объемов, таблицы квадратов чисел и т.д. Хорошо структурированные, они помогают ученикам быстрее запомнить нужную информацию, лучше понять связи между формулами. Если же не ставить такой цели, то применение таблиц может оказать негативное влияние, выражающееся в том, что школьники не будут стремиться запомнить соответствующий материал. Предназначение иллюстративных таблиц - разъяснять возникновение математических понятий, применение на практике, раскрывать их содержание, иллюстрировать применение алгоритмов, формул, методов решения задач и т.д.

Обычно стены классов школ заполнены различными таблицами. Предполагается, что учащиеся будут применять их в своей самостоятельной работе. Тем не менее, картина такова: в поисках ответа ученики предпочитают заглядывать в учебники, тетради или пользоваться заранее приготовленными шпаргалками. Особую трудность в быстром и оперативном использовании представляют таблицы, предлагающие набор формул или графиков. Такие таблицы составляются как справочный материал и содержат большой запас сведений теоретического характера. Распознавание объектов, закономерностей связей между ними затруднено из-за обилия информации, сосредоточенной в столбцах и строках, не всегда удобной для восприятия структурой и т.д. Одно из важнейших требований к таблицам - материал, помещенный в них, должен способствовать активной деятельности учеников, а не сводить их роль к пассивному созерцанию информации. При этих условиях многократное использование таблиц обеспечит более глубокое запоминание содержащегося в них материала, с одной стороны, и даст возможность быстро навести необходимую справку - с другой. Но если некоторый объект должен рождаться пред глазами учащихся, преобразовываться, то помещение его в готовом виде на таблице не принесет для учащихся пользы, а будет скорее во вред.

В отдельный вид можно отнести экранные средства. К ним относятся: кодоскоп (графопроектор), эпидиаскоп, диапроектор, кинопроектор. Главная задача технических средств обучения - повышение эффективности учебно-воспитательного процесса. Обеспечивая образную сторону знаний учащихся, технические средства обучения отвечают принципам научной достоверности, доступности обучения, принципу систематичности, связи теории с практикой, сознательности и активности мышления. Технические средства обучения воздействуют на учащихся, определяют возникновение непроизвольного внимания, что содействует непроизвольному запоминанию материала. А такой характер усвоения, как известно, наиболее надежен.

С появлением компьютеров и сетевого пространства развивается совершенно новый вид наглядности. Её можно назвать дискретной, точечной. С помощью «клика» (по-английски «click» - нажатие клавиши или компьютерной мышки) можно последовательно обращаться в любую точку информационного пространства. При этом сознание по закону соответствия структур начинает работать в совершенно новом режиме мышления. «Точечная наглядность» формирует в сознании современного поколения новую для педагогики картину мира. Пока трудно оценить, лучше или хуже эта новая наглядность, но то, что она строится на иных основах, уже очевидно. Об этом виде наглядности речь пойдет в следующей главе.

Необходимо подчеркнуть, что результативное использование средств наглядности в учебном процессе не ограничивается подбором соответствующих пособий и техникой их демонстрирования. Наиболее существенной стороной здесь является решение вопроса о том, как целесообразней сочетать разные средства. Ведь цель любого педагога - достижение активной учебно-познавательной деятельности школьников.

Таким образом, наглядные и технические средства обучения способствуют не только эффективному усвоению соответствующей информации, но и активизируют познавательную деятельность обучающихся;

развивают способность увязывать теорию с практикой, с жизнью;

формируют навыки технической культуры;

воспитывают внимание и аккуратность;

повышают интерес к учению;

делают процесс обучения более доступным.

Следует отметить, что все названные основные виды наглядности очень часто дополняются ещё одним своеобразным видом, это так называемая внутренняя наглядность, когда в процессе обучения как бы осуществляется опора на прежний опыт обучающихся, когда им предлагается просто представить какую-либо ситуацию, какое-то явление. Например, при решении задач на движение по и против течения реки учащимся совсем не надо совершать «путешествие» по воде. Здесь можно предложить ситуацию собственного «перемещения» в ветреную погоду: при каком условии легче идти, когда ветер дует навстречу вашему движению или наоборот. Таким образом, логически рассуждая, приходим к выводу скорости движения объекта по и против течения реки.

§6. Организация восприятия средств наглядности и требования, предъявляемые к ним при обучении математике

Для эффективного использования наглядности в процессе усвоения знаний большую роль играет не только тщательный отбор наглядных средств, в соответствии с содержанием знаний, но и организация их восприятия. Важное значение имеет постановка перед учащимися сенсорных задач в момент предъявления наглядного материала (указание на то, что в заданном материале необходимо найти, определить, сравнить, мысленно преобразовать и т.п.). Именно указание на способ работы с наглядным материалом формирует активность, динамичность и осознанность восприятия, без чего не может быть полноценного усвоения знаний.

Наглядный материал служит как бы внешней опорой внутренних действий, совершаемых ребёнком под руководством учителя в процессе овладения знаниями. Введение в обучение наглядного материала должно учитывать по крайней мере два следующих психологических момента: какую конкретную роль наглядный материал должен выполнять в усвоении и в каком отношении находится предметное содержание данного наглядного материала к предмету, подлежащему осознанию и усвоению.

Место и роль наглядного материала в процессе обучения определяются отношением деятельности учащихся с наглядным материалом к той деятельности, которая составляет суть процесса обучения.

Это отношение может быть трояким. Во-первых, та и другая деятельность могут совпадать между собой, что обеспечивает прямую действенность наглядности. Далее, первая деятельность может подготовлять собой вторую, и тогда требуется лишь правильно и чётко выделить соответствующие этапы педагогического процесса. И наконец, та и другая деятельность могут не быть связаны между собой, в таком случае наглядный материал бесполезен, а иногда может играть даже роль отвлекающего фактора. Пример этого: в учебнике по алгебре авторов Ш.А.Алимова и др. для учащихся 7 класса (М., «Просвещение», 2006) есть задача на странице 115: «Из пункта А в пункт В катер движется со скоростью 20 км/ч, а из В в А - со скоростью 30 км/ч. Какова средняя скорость катера?» Она иллюстрируется следующим рисунком 2.

Рис. 2

Этот рисунок в данном случае выступает в роли наглядного материала. Какова будет деятельность школьников с этим материалом? Очевидно, что они будут просто рассматривать изображённые катера, дома, замечать некоторые их особенности. Но эта деятельность совершенно не связана с той, которая достигает цели обучения: в данном случае - выявление общего способа решения задач «на нахождение средней скорости».

Поэтому приведённый рисунок не только не помогает осуществлению цели обучения, а мешает этому. В данном случае целесообразней использовать, например, схему-модель на рисунке 3.

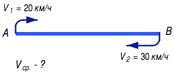
Рис. 3

Важно не только уметь воспринимать предъявленную наглядность, переосмысливать её с учетом учебной задачи, но и перекодировать её содержание. Последнее требование связано с тем, что учащиеся постоянно имеют дело с разнотипной наглядной информацией, переходят от использования одних видов наглядности к другим. На уроках математики учащиеся постоянно обращаются к геометрическим моделям, двух- и трехмерным изображениям, работают в системе и тех и других, постоянно переходят от одних к другим. Овладевая понятиями, они воспроизводят их словесно, условно - символически, наглядно - графически. Например, при усвоении понятия «числовые промежутки» учащиеся должны уметь называть их словесно, фиксировать с помощью символической записи и изображать графически (рис. 4).

Рис. 4

Нередко требование выразить одно и тоже знание в различных системах, то есть перекодировать их, вызывает серьезные трудности у школьников. Ведь создаваемые при этом образцы имеют не одинаковое содержание. Различны условия их создания и оперирования ими.

Целостность восприятия, за которую отвечает правое полушарие головного мозга человека, возможна только при установлении логических связей между составляющими элементами, свойствами понятия. Поэтому наглядное пособие должно помогать их установлению. Если свойство объекта не является решающим в отнесении его к некоторому понятию, то оно должно быть представлено в наглядном пособии вариативно, чтобы не послужить причиной неверного обобщения учащимися. Надо отметить, что сплав наглядно-образного и понятийно-логического является важным в формировании содержательных знаний.

Известные в психологии примеры двойственных изображений подсказывают включить требование отсутствия двойственности восприятия учебно-наглядного пособия, если таковое не является специальной целью.

Возможность двойственной трактовки наглядного пособия иногда помогает выполнению поставленных задач или формулированию новых.

Например, наглядное пособие в виде треугольной призмы (или её изображения) с построенным в ней сечением плоскостью, проходящей через три точки, принадлежащие граням (рис. 5), можно воспринять как объекты (или их изображения), находящиеся в одной плоскости. Тогда это двойственное толкование поможет сформулировать интересную задачу: «Даны три параллельные прямые и три точки, лежащие внутри полос, определяемых этими прямыми (рис. 6). Построить треугольник с вершинами на данных прямых так, чтобы его стороны проходили через данные точки».

Рис. 5     Рис. 6

Характеристикой учебно-наглядных пособий является их статичность или динамичность. К статичным относят такие, у которых нельзя изменить взаимное расположение их элементов; к динамичным - те пособия, которые позволяют сделать это. Опыт показывает, что, динамичные пособия более функциональны. Однако важно, чтобы динамичность достигалась не в ущерб основным требованиям к пособиям.

Некоторые учителя смотрят на наглядность как на средство, специально придуманное для работы с учащимися. Такой узко дидактический взгляд на наглядность принижает её роль в познании и не может привести к правильному формированию математических понятий ни на каком этапе познания действительности.

При использовании средств наглядности следует придерживаться следующих правил обучения:

Нельзя игнорировать даже самые простые, технически несовершенные, устаревшие наглядные средства, если они дают положительный результат. Это могут быть, к примеру, самодельные пособия, изготовленные учителем или учащимися. Такие старые пособия порой не дают должного эффекта не потому, что они плохи сами по себе, а потому что неправильно используются.

Наглядные пособия необходимо использовать не для того, чтобы «осовременить» процесс обучения, а как важнейшее средство успешного обучения.

При использовании наглядных средств обучения должно соблюдаться определённое чувство меры. Если учитель даже располагает большим количеством хороших пособий по конкретному учебному материалу, это не значит, что они все обязательно должны быть использованы на уроке. Это ведёт к рассеиванию внимания, и усвоение материала будет затруднено.

Демонстрировать наглядные пособия нужно лишь тогда, когда они необходимы по ходу изложения учебного материала. До определённого момента желательно, чтобы все приготовленные наглядные пособия (модели, схемы и пр.) были каким-то образом закрыты от взора учащихся. Их необходимо демонстрировать в определённой последовательности и в необходимый момент. Исключение составляют наглядные пособия типа плакатов каких-либо сложных математических формул, таблиц умножения, математических постоянных величин, которые необходимо запомнить и т.п. Такие наглядные пособия должны постоянно находиться перед глазами учащихся.

С целью концентрации внимания учащихся необходимо руководить их наблюдениями. Прежде чем демонстрировать наглядное пособие, нужно разъяснить цель и последовательность наблюдения, предупредить о каких-то побочных, несущественных явлениях.

Ориентировать учащихся на всестороннее восприятие предмета с помощью разных органов чувств.

А.Н. Колмогоров отмечает эвристическую роль наглядности: «В основе большинства математических открытий лежит какая-либо простая идея: совсем наглядное геометрическое построение, какое-либо новое геометрическое неравенство и т.д.»

Под эвристическим методом понимается такая организованная учителем учебная деятельность, при которой вместо изложения учебного материала в готовом виде учитель подводит учащихся к «переоткрытию» теорем, их доказательств, к самостоятельному формулированию определений, к составлению задач. Далее, везде, где это, возможно, математики стремятся сделать изучаемые ими проблемы геометрически наглядными. В средней школе достаточно ясно показывается, на сколько полезны графики для изучения свойств функций. Поэтому … «геометрическое изображение, или, как говорят, «геометрическая интуиция», играет большую роль при исследовательской работе во всех разделах математики, даже самых отвлеченных». (Колмогоров А.Н. [23]). Наглядным примером, раскрывающим суть эвристического метода, может служить следующий фрагмент. В классе предстоит решить задачу: «Доказать, что в прямоугольном треугольнике медиана, проведённая к гипотенузе, равна её половине». Вместо неё предлагается задание: «Попытайтесь установить зависимость между длиной медианы, проведённой из вершины тупого угла треугольника, и длиной стороны, к которой она проведена». Обычно никто из учащихся эту зависимость не обнаруживает, так как они стараются выразить её формулой. Тогда предлагается то же задание, но для медианы, проведенной из вершины острого угла треугольника. Как только кто-либо из учащихся догадывается, что в первом случае длина медианы меньше половины длины стороны, а во втором - больше, наступает оживление. В классе возникает проблемная ситуация. Ставится вопрос: «А как будет в случае прямоугольного треугольника?» Учащиеся формулируют соответствующие задачи и решают их. Работа ускоряется, если учащимся предлагается проследить за указанной зависимостью при изменении угла на таком чертеже, как на рисунке 7.

Рис. 7

Глава II. Методические рекомендации по применению наглядности в обучении математике в средней школе

§1. Наглядность и моделирование

Исследуя проблему наглядности, В.В. Давыдов приходит к следующему весьма важному выводу: «…там, где содержанием обучения выступают внешние свойства вещей, принцип наглядности себя оправдывает. Но там, где содержанием обучения становятся связи и отношения предметов, - там наглядность далеко не достаточна. Здесь… вступает в силу принцип моделирования». ([14]). А так как в курсе математики основным содержанием являются разного рода отношения, то, следовательно, основным для этого курса является не принцип наглядности, а принцип моделирования.

Принцип моделирования не противопоставляется принципу наглядности - он лишь является его высшей ступенью, его развитием и обобщением, связанным с принципиальными изменениями в целях обучения и типах учебного процесса.

Рассмотрим понятие модели. Под моделью понимается такая мысленно представляемая или материально реализованная система, которая, отображая или воспроизводя объект исследования, способна замещать его так, что её изучение даёт новую информацию об этом объекте.

Все модели можно разделить на два типа: Материальные модели (геометрически подобные оригиналам) и Идеальные модели. Идеальные в свою очередь делятся на образные (рисунки, чертежи, схемы), знаковые (математические уравнения), мысленные (наши представления о каком-либо явлении).

Создание материальных и идеальных (образных и знаковых) моделей производится на основе предварительного создания мысленных моделей - наглядных образов моделируемых объектов. Те и другие связаны друг с другом. Идеальная (мысленная) модель может быть прототипом материальной модели, как её план, предваряющий создание некоторого образца. В свою очередь материальная модель может послужить основанием для переформирования идеального содержания и создания идеальной модели.

Модель не просто даёт нам возможность создать наглядный образ моделируемого объекта, а создаёт образ его наиболее существенных свойств, отражённых в модели. Все остальные свойства, не существенные в данном случае, отбрасываются.

Использование моделирования в обучении имеет два аспекта. Во-первых, моделирование служит тем содержанием, которое должно быть усвоено учащимися в результате обучения, тем методом познания, которым они должны овладеть, и, во-вторых, моделирование является тем учебным действием и средством, без которого невозможно полноценное обучение.

Рассмотрим оба этих аспекта использования моделирования в обучении.

Метод моделирования в содержании обучения.

В недавнем прошлом в нашей школе господствовал объяснительно-созерцательный тип обучения, когда в основе учебного процесса «лежит воспроизводящая познавательная деятельность учащихся», которая и развивает «главным образом воспроизводящее мышление» (М.Н.Скаткин [44]).

В современных условиях, когда объём необходимых для человека знаний резко и быстро возрастает, важно прививать умение самостоятельно пополнять свои знания, ориентироваться в стремительном потоке научной и политической информации.

Поэтому необходимо, чтобы учащиеся в процессе обучения овладели общими методами познания, общими способами учебной познавательной деятельности. А для этого нужно выделить, отделить эти методы и способы от тех понятий и явлений, для изучения которых они используются, и сделать их самостоятельным предметом изучения.

Как это можно сделать? Выход в том, чтобы дать учащимся модели этих методов и способов в виде наглядных и легко обозримых схем, графиков или в каком-то другом виде. Тогда непосредственным предметом изучения станут эти чувственно воспринимаемые модели, а через них - опосредствованно - и сами методы и способы.

Итак, моделирование в обучении необходимо для того, чтобы сделать возможным полноценное и прочное овладение учащимися методами познания и способами учебной познавательной деятельности.

В качестве примера такого использования моделирования может служить эвристическая схема умственного действия распознавания принадлежности объекта к указанному понятию (множеству).

Задача состоит в том, чтобы установить принадлежит ли заданный объект к указанному понятию (множеству) или нет. Например, надо узнать, является ли данный четырёхугольник параллелограммом или нет.

Для решения подобных задач можно вместе с учащимися составить эвристическую схему распознавания:

Выбрать удобное определение понятия или какое-нибудь общее необходимое и достаточное условие.

Проанализировать выбранное определение (условие) и выделить в нём все признаки понятия.

Установить, какими логическими цепочками связаны между собой эти признаки.

Если все цепочки типа «и», то надо проверить последовательно выполнение для данного объекта всех признаков, и если хотя бы один признак не выполняется, то объект не принадлежит к указанному понятию; если же все признаки выполняются, то он принадлежит к этому понятию.

Если же некоторые признаки связаны цепочками типа «или», то для принадлежности объекта к понятию достаточно выполнения хотя бы одного (или только одного - в случае строго разделительного смысла цепочки «или») из этих признаков. Эту схему удобно изобразить в виде блок-схемы (рис. 8).

Рис. 8

Пример граф-схемы распознавания параллелограмма на основе его определения: «Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом» (рис. 9).

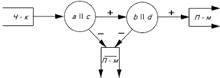
Рис. 9

Обозначения:

Ч-к - четырёхугольник со сторонами a, b, c и d

П-м - параллелограмм

П-м - не параллелограмм

Знак «+» означает, что соответствующий признак выполняется, а знак «-», что этот признак не выполняется.

Опыт и эксперименты показывают, что такие схемы и графы легко усваиваются даже учащимися 6-го класса, и они с интересом занимаются их построением и использованием в своей работе.

Но моделирование в обучении необходимо не только для этого. Важнейшей задачей общего образования является формирование у учащихся научного, диалектико-материалистического мировоззрения. Научное мировоззрение предполагает, что у учащихся сформированы ясное понимание соотношения объективного мира и научных знаний, чёткое осмысление и оценка явлений окружающего мира в свете научных теорий. У школьников должно быть сформировано понимание значимости научных абстрактных понятий (т.е. научных моделей) в познании реальной действительности, ибо «абстрактно отражают природу глубже, вернее, полнее» (В.И. Ленин, полн. собр. соч., Т29, с 152). Поэтому совсем небезразлично, как воспринимают учащиеся изучаемые научные понятия. Значит, явное знакомство учащихся с модельным характером науки, с понятиями моделирования и модели необходимо также в целях формирования у них диалектико-материалистического мировоззрения.

Рассмотрим модельный характер математики. Все математические понятия (например, геометрическая фигура) представляют собой особые модели количественных отношений и пространственных форм окружающей действительности. Эти модели математика сконструировала в процессе своего многовекового исторического развития. Но и в настоящее время любое творчество в области математики связано с созданием новых моделей. Для изучения построенных математических моделей в математике разработаны многочисленные методы (измерение длин, площадей и объёмов геометрических фигур и тел). Все эти методы и составляют в совокупности аппарат математики. Наконец, в математике разработаны и особые методики для использования в практике результатов исследования математических моделей. Примером такой методики являются приёмы решения практических задач с помощью уравнений. Эти методики использования математики в практике образуют особую область математической науки, которую обычно называют прикладной математикой.

Отсюда понятно, что основы науки, которые составляют содержание соответствующего учебного предмета, содержат и систему научных моделей, и аппарат для исследования этих моделей, и методики использования в практике результатов исследования моделей.

Возникает вопрос: а нужно ли, чтобы учащиеся знали модельный характер изучаемых понятий, разве недостаточно того, что они их изучают и учатся в какой-то мере ими оперировать? Что изменится от того, что учащиеся узнают, например, что уравнение, полученное в ходе решения текстовой задачи, есть математическая модель этой задачи?

Нужно, чтобы учащиеся не просто узнали, что слово «модель» может быть отнесено к полученному уравнению. Они должны узнать, что текстовая задача - это описание на естественном языке определённой ситуации. И для решения этой задачи математическими средствами надо построить её математическую модель. Уравнение и есть один из видов математических моделей. При этом учащиеся должны узнать, что это общий метод математического исследования реальных явлений, математического решения реальных задач, возникающих в ходе исследования этих явлений. Тем самым, если раньше математический смысл решения подобных задач был учащимся непонятен или понимался искажённо (так, на вопрос: «Что значит решить задачу?» большинство учащихся отвечает: «Получить ответ»), то при модельном подходе к решению задач этот смысл будет правильно осознан и составление уравнений займёт совсем иное структурное место в деятельности учащихся.

Таким образом, явное введение в содержание образования понятий модели и моделирования, выяснение сущности и роли моделирования в научном познании существенно меняет отношение учащихся к учебному предмету, к учению, делает их учебную деятельность более осмысленной и продуктивной.

Результаты педагогических исследований показывают, что целенаправленное формирование модельного подхода к изучению математики создаёт благоприятные условия для развития у учащихся основ теоретического мышления, внутренней мотивации учения.

Назрела необходимость явного включения моделирования в содержание учебных предметов, необходимость ознакомления учащихся с современной научной трактовкой понятий моделирования и модели, овладения моделированием как методом научного познания и решения практических задач.

Моделирование как учебное действие.

Необходимость овладения методом моделирования диктуется так же и психолого-педагогическими соображениями.

Задача привить учащимся умения ориентироваться в потоке научной информации требует отказа от объяснительно-созерцательного типа учебного процесса и перехода к новому, активно-творческому типу.

Для этого необходима серьёзная перестройка процесса обучения. Необходимо организовать у учащихся формирование:

и полноценных понятий;

и общих способов умственных действий с этими понятиями (решение задач).

Это означает, что учащиеся должны видеть в изучаемых понятиях наиболее существенные свойства и особенности и понимать их значение для решения соответствующих задач. Для осуществления такого формирования полноценных понятий психология указывает два пути.

Первый путь - это путь варьирования объектов, описываемых изучаемым понятием. Этот путь основан на положении о том, что существенные признаки понятия только тогда осознаются правильно, когда одновременно с ними осознаются вариативные несущественные признаки.

На этом пути достаточна обычная наглядность, но при её применении нужно учитывать необходимость варьирования несущественных признаков. Это значит, что, знакомя учащихся, например, с какой-либо геометрической фигурой, нужно её чертить не в одном каком-то стандартном виде со стандартными обозначениями, а в разнообразных видах, варьируя её положения на плоскости, размеры, обозначения и расположение отдельных элементов. Например, варьировать изображения ромба (стоит на вершине, лежит на стороне). Точно так же при знакомстве учащихся с каким-либо видом алгебраических выражений надо варьировать несущественные его признаки (обозначения переменных, коэффициенты и др.).

Второй путь - это вооружение учащихся при изучении какого-либо понятия ориентировочной основой действий с этим понятием для решения соответствующих задач.

Понятие ориентировочной основы умственных действий введено П.Я. Гальпериным, который считает, что в каждом разумном действии есть ориентировочная, исполнительная и контрольная части. Роль ориентировочной части действия при формировании понятий связана с тем, что «обобщение всегда идёт лишь по тем предметам, которые вошли в состав ориентировочной основы действий, направленных на анализ этих предметов» (Н.Ф. Талызина [45]).

Таким образом можно выделить три различных типа ориентировки в процессе обучения. Первый тип отличается существенной неполнотой ориентиров, даваемых учащимся (обычно в виде образца действия), по сравнению с теми условиями, на которые необходимо ориентироваться для правильного выполнения действия. Такой тип ориентировки по сей день является весьма распространённым в школе. Учитель показывает образец решения задачи нового вида, а затем учащиеся, ориентируясь на этот образец, фронтально и самостоятельно решают огромное число однотипных задач. Опыт показывает, что несмотря на большие затраты времени и сил, лишь некоторые учащиеся овладевают умениями в самостоятельном решении подобных задач, большинство же учащихся так и не научаются безошибочно и самостоятельно решать задачи, если они отличаются от данного образца хотя бы несущественными особенностями.

Метод вариации здесь не может помочь, так как для задач определённого вида имеется всегда огромное число варьируемых признаков и исчерпать их в учебной работе просто невозможно.

Второй тип ориентировки характерен тем, что даётся полная система указаний для безошибочного выполнения действий, но эти указания даются учащимся, во-первых, в готовом виде, а во-вторых, в конкретной форме, пригодной лишь для ориентировки в одном частном случае.

Примером может служить даваемое учащимся в готовом виде правило умножения одночленов («нужно перемножить все числовые множители, а произведения одинаковых букв заменить степенью этой буквы»). Ученик, пользуясь этим правилом, сумеет безошибочно найти произведение одночленов, но для выполнения других действий над одночленами и многочленами уже нужны другие правила. Поэтому школьникам приходится запоминать большое число частных правил действий над одночленами и многочленами.

При третьем типе учащимся даётся метод анализа объектов для самостоятельного составления полной ориентировочной основы действий.

Этот тип ориентировки для случая действий над буквенными выражениями может быть дан учащимся в виде общей схемы:

чтобы произвести какое-либо действие над буквенными выражениями, нужно каждое из них заключить в скобки и затем соединить соответствующим знаком действия в одно сложное буквенное выражение;

чтобы сложное буквенное выражение преобразовать к стандартному виду, можно использовать все известные правила действий над числами и законы этих действий (переместительный, сочетательный и распределительный) как в прямом, так и в обратном порядке. На основе этой общей схемы частные правила действий над одночленами и многочленами учащиеся могут получить самостоятельно, и все их запомнить тогда уже нет необходимости.

Для того, чтобы учащиеся могли усвоить этот общий метод анализа объектов и составления ориентировочной основы действий по решению частных задач при третьем типе ориентировки, нужно этот метод выделить и отделить от самих конкретных действий по решению частных задач и представить его в легко обозримом и наглядном виде. Cделать это можно путём моделирования, построив обобщённую модель действий по решению любых задач данного вида, например в виде схемы.

В практике обучения математике второй путь является основным, а первый лишь вспомогательным, нужный для первоначального знакомства учащихся с изучаемым понятием. Таким образом, моделирование в современных условиях работы учителя математики нужно использовать для формирования у учащихся полноценных умственных действий по третьему типу ориентировки, являющемуся наиболее эффективным и развивающим типом учения. Кроме того, моделирование в обучении математике необходимо и для формирования научно-теоретического стиля мышления. Моделирование следует использовать в обучении математике и для развития рефлексирующей деятельности учащихся. Ведь очень важно, чтобы учащиеся не только умели произвести те или иные умственные действия, но и могли проанализировать эти действия, а главное - имели потребность в таком анализе, имели привычку к нему. К такому анализу надо постепенно приучать учащихся. Этому будут способствовать задания на составление различных схем-моделей изученного материала, составление схем действий по решению задач определённого вида и прочее.

Таким образом, принцип моделирования в обучении математике означает, во-первых, изучение самого содержания школьного курса математики с модельной точки зрения, во-вторых, формирование у учащихся умений и навыков математического моделирования различных явлений и ситуаций, в-третьих, широкое использование моделей как внешних опор для внутренней мыслительной деятельности, для развития научно-теоретического стиля мышления.

§2. Применение компьютерных технологий в обучении математике

Внедрение новых технических средств в учебный процесс расширяет возможности наглядных средств обучения. В современных условиях особое внимание уделяется применению такого средства наглядности, каким является компьютер. Применение компьютеров в учебном процессе увеличивает объем информации, сообщаемой ученику на уроке, активизирует, по сравнению с обычными уроками, организацию познавательной деятельности учащихся.

Появление компьютеров вызвало небывалый интерес к их применению во всех сферах деятельности человека. Возможности компьютеров растут столь стремительно, что прогнозы специалистов об их ближайшем будущем напоминают научную фантастику. Так как компьютер стал средством повышения производительности труда во всех сферах деятельности человека, практически все развитые страны начали широко разрабатывать компьютерные технологии обучения.

Умелое использование различных компьютерных технологий приобретает в наши дни общегосударственное значение, и одна из важнейших задач школы - вооружать учащихся знаниями и навыками использования современных компьютерных технологий.

С компьютеризацией обучения во всем мире связаны надежды повысить эффективность учебного процесса, уменьшить разрыв между требованиями, которые общество предъявляет подрастающему поколению, и тем, что действительно дает школа.

Благодаря компьютеру учитель получает возможность более совершенного контроля над процессом обучения, в котором уменьшается степень инструктивного введения в учебные ситуации и необходимость замены пассивных иллюстраций примерами.

Применение компьютерных программных средств на уроке могут позволить учителю:

сделать мыслительное - наглядным, а именно повысить уровень наглядности при обучении математике;

повысить индивидуализацию обучения;

облегчить проверку и анализ различных проверочных работ;

повысить интерес и познавательную активность учащихся.

К сожалению, существует также и ряд проблем при реализации обучения, с использованием компьютерных технологий, а именно:

проблемы технические, поскольку во многих школах отсутствует современная техника (переносные компьютерные классы);

методические проблемы, поскольку существует недостаточное количество подходящих обучающих программ;

ресурсные проблемы, поскольку большинство программ являются лишь техническим инструментом;

временные программы, поскольку пока не разработана методика, требуется значительно больше времени при подготовке к уроку.

Из всего вышесказанного следует, чтобы применять компьютерные технологии на уроках необходимо преодолеть различные трудности, а так же прежде чем вводить какие-либо обучающие программы следует оценить все плюсы и минусы их использования.

При компьютеризации обучения компьютер начинает оказывать решающее влияние на формирование позитивного отношения к учению только при работе школьников с эффективными обучающими программами. Такие программы предполагают ненавязчивый способ оказания помощи, возможность для учащегося самому выбрать темп учения, наличие игровых моментов, неограниченные способы предъявления иллюстративного материала, наличие задач исследовательского характера и т.д. Кроме того, компьютер, вовремя оказывая учащемуся необходимую помощь, избавляет его от чувства неудачи. А, как говорил Г.Селье: «...ничто не обескураживает больше, чем неудача, ничто не ободряет сильнее, чем успех...».

Применение возможностей компьютера в учебном процессе позволяет реализовать принцип индивидуализации обучения, активность обучаемых, интенсифицировать учебный процесс.

Использование компьютера и обучающих программ в учебном процессе предоставляет ряд новых потенциалов и преимуществ, как учителю, так и обучаемому по сравнению с традиционным способом обучения. Учитель, использующий на своих уроках компьютерные средства обучения, имеет возможность:

Легко распространять свой опыт, свою модель обучения той или иной учебной дисциплины, так как единожды созданная методика преподавания той или иной темы с помощью обучающей программы легко тиражируется.

Можно реализовать различные методы обучения одновременно для разных категорий учащихся, индивидуализировать тем самым процесс обучения.

Уменьшить количество излагаемого материала за счет использования демонстрационного моделирования.

Проводить отработку различных навыков и умений обучаемых, используя компьютер как тренажер.

Осуществлять постоянный и непрерывный контроль над процессом усвоения знаний.

Поддерживать историю обучения каждого ученика, вести и отрабатывать статистические данные, тем самым более точно и достоверно осуществлять управление учебной деятельностью.

Уменьшить количество рутиной работы, тем самым освободить время для творческой работы и индивидуальной работы с учащимися.

Сделать более эффективной самостоятельную работу учащихся, которая становится контролируемой и управляемой.

Для ученика предусмотрены следующие возможности:

Получает возможность вести работу в оптимальном для него темпе.

Обучается тем методом и на том уровне изложения, который наиболее соответствует уровню его подготовленности и психофизическим характеристикам.

Имеет возможность вернуться к изученному ранее материалу, получить необходимую помощь, прервать процесс обучения в произвольном месте, а затем к нему возвратиться.

Может наблюдать динамику различных процессов, взаимодействие различных механизмов и т.п.

Легче преодолевать барьеры психологического характера (несмелость, нерешительность, боязнь насмешек и т.п.) из-за определенной анонимности контакта с компьютером.

Отрабатывать необходимые умения и навыки до той степени подготовленности, какая требуется вследствие исключительной "терпеливости" компьютера.

Возможности компьютера как средства учебной деятельности ещё до конца не раскрыты. Тем не менее, уже сегодня можно утверждать, что по своим функциям он является средством не только исполнения алгоритма, но и поиска способа оптимального решения. Компьютер является средством, позволяющим учащимся лучше познать самих себя, индивидуальные особенности своего учения, и в будущем он, несомненно, сможет взять на себя функции «наставника». В последнем случае ситуация учения перейдет в ситуацию обучения.

В процессе обучения, с использованием компьютерных технологий формируется продуктивное (творческое) мышление. Основными показателями такого мышления являются:

оригинальность мысли, возможность получения ответов, далеко отклоняющихся от привычных;

быстрота и плавность возникновения необычных ассоциативных связей;

«восприимчивость» к проблеме, ее непривычное решение;

беглость мысли как количество ассоциаций, идей, возникающих в единицу времени в соответствии с некоторым требованием;

способность найти новые непривычные функции объекта или его части.

Использование компьютера при обучении позволяет создать необходимую информационную обстановку, стимулирующую интерес и пытливость ребенка в изучении математики.

Прежние попытки вести регулярное обучение с помощью компьютерных программ терпели неудачу в первую очередь потому, что не удавалось получить явное преимущество компьютерных технологий перед традиционными формами обучения, из-за несовершенства программных средств. Другая важная причина - компьютер не являлся общедоступным средством обучения.

В настоящее время ситуация меняется. Компьютер становится совершенно естественным средством познания окружающего мира. Эффективность обучения с помощью компьютера зависит от программных средств, которые используются при обучении. Для оценки качества педагогических программных средств (ППС) с целью определения возможности их использования в процессе обучения проводят классификацию по методическому назначению, согласно которой принято выделять следующие программы

обучающие, которые предназначены для изучения школьниками нового материала;

тренировочные (тренажеры), позволяющие отработать умения и навыки при повторении и закреплении изученного материала;

контролирующие, предназначенные для контроля уровня усвоения учебного материала;

информационно-справочные, которые предназначены для получения учащимися необходимой информации;

моделирующие, позволяющие создать модели объекта, процесса, явления с целью изучения и исследования;

демонстрационные, предназначенные для наглядного представления учебного материала, визуализации изучаемых закономерностей, взаимосвязи между объектами;

игровые, которые дают возможность «проигрывать» учебную ситуацию с целью принятия оптимального решения или выработки оптимальной стратегии действий;

досуговые, предназначенные для внеклассной работы (например, с целью развития внимания, реакции и т.п.).

В качестве наглядного средства обучения компьютер способен реализовать все преимущества технических средств обучения. Современные компьютерные программы позволяют создавать тексты, различные виды графики, мультипликацию со звуковым сопровождением, кино и видеоизображения. При этом важно понимать, каковы границы применения компьютерных программных средств. Компьютер может обеспечить:

индивидуализацию и дифференциацию процесса обучения, а также оптимизацию темпа работы ученика;

осуществление контроля за работой всех учащихся за короткий промежуток времени;

осуществление самоконтроля и самокоррекции;

сокращение времени выработки необходимых навыков учащихся за счет возможности увеличения количества тренировочных заданий;

высвобождение учебного времени за счет выполнения на ЭВМ трудоемких вычислительных работ;

визуализация учебной информации;

моделирование и имитацию изучаемых или исследуемых объектов, процессов или явлений;

повышение мотивации к обучению;

создание на уроке игровых познавательных ситуаций;

проведение лабораторных работ в условиях имитации в компьютерной программе реального опыта или эксперимента;

развитие определенного вида мышления и формирование умения принимать решение в сложной ситуации;

вооружение обучаемого стратегией усвоения учебного материала;

формирование культуры учебной деятельности, информационной культуры обучаемого и обучающего.

Применение компьютерных технологий позволяет повысить уровень самообразования, дает совершенно новые возможности для творчества, обретения и закрепления различных, профессиональных навыков.

Говоря о преимуществах, нельзя не указать явные недостатки применения компьютера в учебном процессе:

диалог с программой лишен эмоциональности и, как правило, однообразен, то есть нарушается живой диалог «учитель-ученик»;

не обеспечивается развитие речевой, графической и письменной культуры учащихся;

контроль знаний ограничен несколькими формами - тестами или программированными опросами;

увеличивается риск появления большего числа детей компьютерных фанатов;

допускается возможность сбоя работы компьютерной программы, что может привести к досадным ошибкам и недоразумениям;

неполная реализация потенциальных возможностей компьютера.

Наконец, среди имеющегося программного обеспечения много некачественного, не учитывающего специфику работы со школьниками, имеющего много фактических или методических ошибок (программисты часто просто не учитывают содержания школьных программ, не владеют методиками обучения предмету, не учитывают психолого-педагогический аспект учения) и др.

§3. Возможности программы “Живая Математика” в обучении геометрии в 7 классе

Чтобы определить возможность использования программных продуктов в процессе обучения каждый учитель должен знать комплекс требований к ним.

Педагогические требования - требования целесообразности использования того или иного программного средства (с точки зрения повышения эффективности обучения);

Дидактические требования заключаются в обеспечении научности, доступности, адекватности ранее приобретенным знаниям, самостоятельности и активизации деятельности учащихся, прочности результатов обучения и др.

Методические требования к демонстрации наглядных пособий:

наглядное пособие нужно демонстрировать тогда, когда в этом возникла необходимость во времени и по содержанию изучаемого материала;

нельзя перегружать занятие демонстрацией наглядных пособий;

в процессе восприятия демонстрируемого наглядного пособия следует вовлекать возможно большее количество органов чувств (зрение, слух, осязание и т.д.);

рационально сочетать слово и демонстрацию. Слово предваряет, сопровождает и заключает демонстрацию наглядного пособия;

побуждать учащихся при изучении наглядных пособий проявлять инициативу, мыслительную деятельность и самостоятельность;

умело использовать “эффект новизны” - не показывать наглядное пособие учащимся до момента его демонстрации;

действующие и динамические наглядные пособия обязательно показывать в динамике, в действии;

обеспечивать условия хорошей видимости демонстрируемого наглядного пособия (место расположения, освещенность, четкость изображения).

Эргономические требования:

Психологические требования к содержанию и оформлению программных средств обусловлены необходимостью создавать условия, обеспечивающие повышение уровня мотивации обучения и поддержание высокой работоспособности обучаемого за счет грамотной организации диалога, дружественного интерфейса.

Гигиенические требования к изображению информации: к цветовой гамме, к разборчивости, четкости и контрастности изображения, к пространственному размещению информации на экране в соответствии с гигиеническими требованиями и санитарными нормами работы с вычислительной техникой.

Технические требования определяют необходимость обеспечения устойчивости к ошибочным и некорректным действиям пользователя, защиты от несанкционированных действий и др.

Грамотное и рациональное использование качественных компьютерных программных средств повышает эффективность процесса обучения, предоставляя учащимся возможность активного, деятельностного подхода в обучении.

Появляется возможность использовать программы, в которых ученику предоставляется среда, в которой можно выполнять любые аналоги построений с помощью циркуля и линейки. Это прекрасные технические инструменты, приходящие на смену карандашу, линейке, циркулю и резинке. Быстро, аккуратно, точно и красочно можно выполнить практически любые геометрические построения и операции: ввести привычные обозначения, автоматически измерить длины и т.д.

Особенностями этих программ являются:

возможность строить аккуратные чертежи;

возможность трансформировать уже готовый чертеж, двигая одну из исходных точек или прямых (построение при этом сохранится);

возможность анимации (в ряде программ).

Возможность трансформации чертежа интересна тем, что

не надо задумываться о положении базовых точек (при построении на бумаге может оказаться, что в одном месте чертежа точек много, а в другом мало, - приходится перерисовывать);

появляется возможность легко проверить построение;

возможность организовать самостоятельную деятельность.

Программы этого типа позволяют ученику самостоятельно заметить закономерность, выдвинуть собственную гипотезу на основе полученных с помощью компьютера фактов.

Например, построив треугольник и проведя медианы, можно осуществить различные изменения формы треугольника и констатировать, что каждый раз медианы пересекаются в одной точке. Или, проводя соответствующие измерения, выяснить, в каком отношении делятся медианы их точкой пересечения.

Одной из таких программ является программа «Живая Математика». Более подробно остановлюсь на использовании данного компьютерного продукта, так как при прохождении педагогической практики именно он был главным и основным инструментом наглядности для детей, с которыми я работал в условиях дистанционного обучения.

Программа «Живая Математика» представляет собой электронный аналог готовальни, позволяющей выполнять красочные, варьируемые и легко редактируемые чертежи, которые можно компоновать в своеобразные геометрические мультфильмы, вызывая тем самым интерес у учащихся и способствуя развитию наблюдательности и восприятия. Например, учащимся даётся следующее задание: выяснить каким свойством обладают точки биссектрисы угла. При этом предлагается передвигать курсором мыши точку на биссектрисе угла и наблюдать за значениями двух величин, являющихся расстояниями от точки до сторон угла. Провести аналогичный эксперимент для точки, не лежащей на биссектрисе и сделать соответствующий вывод. При этом учащиеся самостоятельно могут управлять движением точек и включать кнопку анимации (рис. 10).

Рис. 10

«Живая Математика» будет полезна учащимся при изучении как геометрии, так и алгебры, тригонометрии, математического анализа.

У преподавателя появляются дополнительные возможности представления математических концепций, формулирования вопросов и побуждения учащихся к построению и экспериментальной проверке гипотез. Занятия могут проходить в компьютерном классе или в аудитории, оснащенной демонстрационным экраном.

Компьютерная среда помогает поставить мысленный эксперимент типа "что если?", почувствовать свойства изучаемой математической конструкции, получить новые результаты, а, кроме того, создать иллюстрации высокого качества.

Вообще говоря, «Живая Математика» создает документы, содержащие математические чертежи, т.е. графики и геометрические фигуры. Каждый чертеж конструируется из отдельных объектов, которые определяются в зависимости от математических связей (отношений) между ними. Интерактивное управление документами и объектами в документах осуществляется с помощью сочетания инструментов и команд меню.

Следует отметить, что сама среда не является обучающей и «сама ничего не делает», - все чертежи в ней создаются пользователем, а программа лишь предоставляет для этого необходимые средства, так же как и возможности для усовершенствования чертежей и их исследования.

С некоторой точки зрения, математика - это своего рода искусство накопления знаний при помощи отыскания новых интересных отношений (связей) между объектами. Программа «Живая Математика» предоставляет возможность создания богатого набора математических объектов и способов их связи. Можно исследовать поведение объектов и отношений между ними, находить новые связи и зависимости, а также изображать полученные результаты.

Объекты программы «Живая Математика» подразделяются на несколько основных категорий.

Геометрические объекты: точка, прямая, луч, сегмент, круг, дуга, внутренняя область, геометрическое место точек и некоторые итерационные процессы.

Числовые или алгебраические величины: измерение, параметр, координатная система, вычисление, функция.

Дополнительные объекты: надпись и исполнительная кнопка, преимущественно используемые для описания, объяснения и представления результатов.

Со времен Евклида основными инструментами геометрии являются циркуль и линейка. Готовальня «Живой Математики» содержит эти инструменты для построения окружности и прямой, а также несколько других, позволяющих выделять и перетаскивать объекты, создавать точки, формировать и изменять текст и имена. Кроме того, есть возможность определить новый инструмент - инструмент пользователя - и управлять им.

Документ программы «Живая Математика» содержит одну или несколько страниц чертежей, т.е. одну или несколько коллекций связанных между собой математических объектов. Для создания объектов используется набор инструментов и меню команд.

Документ отображается на экране компьютера в виде окна и может быть сохранен на жестком диске. Сохраненный документ в дальнейшем можно заново открыть и вновь отредактировать.

Если документ содержит более одного чертежа, то каждый чертеж называется страницей. Документ может содержать сколько угодно инструментов: как основных, например, Точка, Циркуль и Линейка в Готовальне, так и созданных пользователем.

В окне документа в каждый данный момент отображается одна страница. Для управления страницами и инструментами, содержащимися в документе, служит команда Настройки документа. Настройки документа в меню Файл.

Программа «Живая Математика» содержит следующие команды меню: меню Файл используется при создании, сохранении и печати документов, меню Правка и Вид содержат команды, которые видоизменяют чертеж, форматируют его и определяют наличие или отсутствие объектов, меню Построения, Преобразования, Измерения и Графики определяют математическое содержание чертежа в виде отношений объектов друг к другу, меню Окно позволяет работать с открытыми документами, а меню Справка консультирует в трудных случаях. Наконец, Контекстное меню, вызываемое щелчком правой клавиши мыши, предоставляет те или иные возможности в зависимости от объекта щелчка.

Для создания чертежей используются стандартные геометрические операции такие как - проведение прямой (луча, отрезка) через две точки, построение окружности по заданному центру и точке на окружности (или по заданным центру и радиусу), биссектрисы угла, середины отрезка, проведение перпендикулярных и параллельных прямых, фиксация пересечения прямых, окружностей, прямой и окружности. Имеется хорошо развитая система измерений длин, углов, площадей, периметров, отношений с достаточно большой точностью, которая легко регулируется. Имеющаяся система преобразований позволяет производить над объектами такие операции как отражение, растяжение, сдвиги, повороты. А главное, во время работы с «Живой Математикой» вы берете мышкой точку на созданном вами чертеже и перемещаете ее по предписанной траектории. При этом изменяется длина, форма линий, то есть первоначальное изображение принимает совсем иные формы. И согласитесь, что ощущение от этого совсем иные, чем при разглядывании статистического чертежа! Таким образом, одно из главных достоинств «Живой Математики» - возможность непрерывно менять объекты, что создает предпосылки для развития компьютерного эксперимента. При этом прослеживается четкая вовлеченность учащихся в сознательную деятельность. Настолько это ярко, привлекательно и доступно на понятийном уровне!

Использование компьютерного продукта влечет за собой повышение качества преподавания, так как программа позволяет усваивать метрические соотношения не догматически, а экспериментально - в том числе и учащимся с затрудненным восприятием геометрии. Поясню на примере: около произвольного треугольника описана окружность и, соответственно, вписана. Ставится задача, как изменится треугольник, если совместить центры двух окружностей? Мы то знаем ответ на вопрос, но для детей это является своего рода открытием, достижением. И, понятно, что традиционными способами такого эксперимента провести нельзя. А вот еще один пример: просим учащихся на сторонах произвольного треугольника во внешнюю часть построить квадраты и понаблюдать за треугольником в случае, когда сумма площадей двух меньших квадратов окажется равной площади большего квадрата, сделать выводы. Какой же восторг испытывают учащиеся, когда приходят к желаемому результату. Значит, один из важнейших критериев заключается в эмоциональной сфере. Можно утверждать, что применение программы уже что-то дало учащемуся, если он издает довольные звуки (вопреки правилам поведения на уроке), гордо показывает свои творения одноклассникам. К тому же факты, открытые учащимися самостоятельно, усваиваются ими лучше, чем преподнесенные учителем в готовом виде.

Меняется отношение учащихся и к геометрическому объекту, созданному своими трудами, по отношению к тому, как если бы его просто дали в готовом виде или определили. Ведь ученик помнит весь процесс творения - с чего начинался объект, какие трудности пришлось преодолеть, прежде чем прийти к желаемому результату. Он сам размещает чертеж на экране, определяет, какие элементы конструкции должны быть видимыми, а какие - нет, каким объектам дать имена, а какие будут безымянными. В соответствии со своим вкусом выбирает цвет, толщину линий, насыщенность, может сопровождать свои чертежи пояснениями, надписями и т. п. Затратив значительные усилия на создание чертежа, добившись своей цели, учащийся начинает ценить свою работу - а, следовательно, и созданные им объекты.

Важно, что ученик практически никогда не работает с каким-то единственным, скажем треугольником или четырехугольником, а всегда - с целым семейством. Геометрическая интуиция ребенка, который с помощью одного движения мышки может проследить за целой кривой треугольников или четырехугольников, развивается гораздо лучше, чем у ребенка, лишенного такой возможности.

Таким образом, компьютерная среда позволяет учащимся при индуктивном подходе обнаруживать закономерности в наблюдаемых геометрических явлениях, а при дедуктивном - помогает, как формулировать теоремы для последующего доказательства, так и подтверждать уже доказанные факты и развивать их понимание, то есть работа ведется по таким направлениям, как анализ, исследование, построение, доказательство. Даже возникает возможность открытия новых фактов в классической геометрии.

Итак, применение программы «Живая Математика» в процессе обучения:

развивает навыки самостоятельного мышления;

формирует положительное и ответственное отношение к учебе, прослеживается рост успеваемости;

повышается самооценка учащегося, самокритичность;

появляется заинтересованность и потребность в получении дополнительных знаний;

раскрывается интерес к научной деятельности;

высокий эстетический уровень оформления работ, делает изучение математики привлекательным.

Наглядность должна использоваться в той мере, в какой она способствует формированию знаний и умений, развитию мышления. Демонстрация и работа с предметами должны вести к очередной ступени развития, стимулировать переход от конкретно-образного и наглядно-действенного мышления к абстрактному, словесно-логическому.

При подготовке к занятию необходимо:

определить дидактические задачи, решаемые с помощью наглядности;

детальное знание наглядного пособия, намеченного к применению на занятии;

определение места наглядности на занятии;

определение способов применения наглядных пособий на занятии.

Во время занятия:

подготовка учащихся к восприятию демонстрации пособия.

создание проблемной ситуации;

руководство восприятием учащимися пособия (попутные пояснения, выделение главного, комментирование и т.п.);

анализ совместно с учениками учебного материала, получаемого с помощью наглядного пособия;

руководство самостоятельной работой учащихся по осмыслению материалов, получаемых с помощью наглядных пособий;

рациональное сочетание различных форм и методов сообщения учебного материала и учебного труда учащихся с учетом содержания и специфики наглядных пособий.

Дидактические задачи, решаемые с помощью применения наглядных пособий:

сообщение учащимся более полной и точной учебной информации, повышение в результате этого качества обучения;

повышение доступности обучения;

повышение темпа изложения учебного материала;

повышение интереса учащихся, удовлетворение их запросов и любознательности;

снижение утомляемости учащихся на занятиях;

переключение сэкономленного времени на творческую деятельность;

увеличение доли времени на самостоятельную работу учащихся;

облегчение труда преподавателя и учащихся.

Пример урока с использованием компьютерной среды «Живая Математика» в классе по теме «Теорема о сумме углов треугольника» (по учебнику «Геометрия, 7-9» авторов Л.С.Атанасян и др.)

Пособие составлено для урока изучения и первичного закрепления новых знаний по соответствующей теме урока.

Структура подачи материала

Подготовка учащихся к усвоению новых знаний

В начале урока проводится устный счет: учащимся предлагается найти сумму углов треугольника (остроугольного, прямоугольного, тупоугольного).

Постановка задачи

Учитель ставит перед учащимися задачу: сделать предположение о сумме углов треугольника. После того, как сделаны соответствующие выводы, проводится строгое их обоснование.

Вариант постановки задачи

Можно подвести учащихся к способу дополнительного построения при доказательстве и с помощью наводящих вопросов дать четкое обоснование того, что сумма углов любого треугольника равна 180 градусам.

Первичное закрепление и усвоение новых знаний

Проводится посредством устной работы по готовым чертежам, разбора и записи задачи на нахождение углов треугольника с использованием аппарата алгебры (составление уравнения).

Контроль знаний

Проводится самостоятельная работа обучающего характера с дальнейшей взаимопроверкой или самопроверкой.

Подведение итогов урока

Проводится с помощью наводящих вопросов с использованием чертежей, с помощью которых проводились доказательство теоремы и решались задачи. Делаются выводы.

Информация о домашнем задании

Проводится запись домашнего задания и инструктаж к нему.

Как работать с пособием

Название

После объявления учителем темы урока, нажимается соответствующая кнопка "название", которая влечет за собой появление надписи «Теорема о сумме углов треугольника» (рис.11):

Рис. 11

Вывод на экран основного чертежа

Как только перед учащимися поставлена задача о нахождении суммы углов треугольника, происходит щелчок по второй кнопке "треугольник" (на стр.1), который влечет за собой появления треугольника ABC и измерения его углов (рис. 12).

Рис. 12

Демонстрация изменяющегося треугольника и эксперимент

Двигая одну из вершин треугольника, добиваемся того, чтобы треугольник принял вид остроугольного, тупоугольного или прямоугольного.

Основное предположение

Затем, учащимися сравниваются результаты получившихся сумм углов треугольников, и делается предположение, что она всегда неизменна и равна 180 градусам.

Проверка формулировки предположения

Нажатие кнопки "вывод" влечет за собой появление надписи "Сумма углов любого треугольника равна 180°".

Доказательство предположения

Учитель предлагает учащимся научно обосновать данный факт, с этой целью осуществляется переход на страницу 2 данного пособия, нажатием на клавишу "2" в нижнем левом углу страницы (это панель переключения на соответствующие страницы пособия).

Вторая страница пособия раскрывается с формулировкой теоремы и готовым рисунком треугольника ABC (рис. 13).

Рис. 13

Дополнительное построение

Обсуждается с учащимися вопрос о дополнительном построении - проведение прямой DF, параллельной стороне AC треугольника, проходящей через вершину B. Прямая DF появляется нажатием на кнопку «прямая».

Задача о парах равных углов

Перед учащимися ставится задача о нахождении равных углов при выполненном дополнительном построении.

Демонстрация основного момента доказательства

Как только найдены пары накрест лежащих углов, то «включаются» поочерёдно две кнопки «вперёд» и на экране происходит демонстрация, наглядно показывающая наложение одного угла (сектора) на другой (рис. 14).

Рис. 14

Показ полной записи доказательства по шагам

После того как завершается доказательство теоремы, нажимается кнопка «док-во» и перед учащимися появляются все шаги проведённых рассуждений (рис. 15).

Рис. 15

Особенности мультимедийной демонстрации

На основании этой записи можно ещё раз закрепить доказательство теоремы о сумме углов треугольника. С помощью кнопки «назад» происходит перемещение углов (секторов) в их первоначальное положение, что делает демонстрацию многократной.

Закрепление формулировки и доказательства

После проведенных доказательных рассуждений, осуществляется процесс первичного закрепления полученных знаний. С этой целью на страницах 3 - 10 данного пособия расположены задачи по готовым чертежам по одной на каждой странице (для удобства).

Структура набора задач

Каждая страница разворачивается с номером задачи, вопросом о том, что нужно найти и готовым чертежом со всеми данными. Задачи предполагается решать устно, комментируя каждый шаг в решении. При необходимости и желании может быть использована кнопка «решение», которая скрывает подробное решение и ответ задачи (рис. 16).

Рис. 16

Особенности работы с задачей на составление уравнения

На странице 11 пособия находится задача, решение которой сначала предлагается разобрать, а затем подробно записать. Для появления текста задачи необходимо нажать кнопку «задача», для появления треугольника - кнопку «рисунок». Треугольник не имеет названия, так как для данной задачи это не принципиально. Учитель, на своё усмотрение может открыть решение задачи, нажав соответствующую кнопку, вначале, в ходе решения, в конце или по окончанию решения задачи (рис. 17).

Рис. 17

Самостоятельная работа обучающего характера

На странице 12 пособия расположен текст самостоятельной работы. В каждом варианте имеется 5 задач по готовым чертежам, в каждой из них требуется найти неизвестные углы треугольника (рис. 18).

Рис. 18

Учащиеся записывают в тетрадях только ответы, производя вычисления в уме. Затем происходит взаимопроверка (или самопроверка) выполнения заданий, с этой целью учитель переходит на страницу 13 пособия, где расположены ответы самостоятельной работы. По мере оглашения ответов учениками, с помощью нажатия кнопок «№1», «№2», «№3», «№4», «№5» появляются соответствующие ответы на экране.

Оценивание работы

Проверив работы друг друга (или свою), учащиеся выставляют оценки, которые на усмотрение учителя могут быть поставлены в журнал.

Подведение итогов

Учащимся предлагается сделать вывод о том, что нового было изучено на уроке, в чём состоит особенность доказательства теоремы о сумме углов треугольника, как найти углы равнобедренного и прямоугольного треугольников, если задан один угол (не считая прямого угла). С этой целью можно вернуться на страницы 2,6,7,8 данного пособия.

Домашнее задание и заключение

Страница 14 содержит информацию о домашнем задании, страница 15 - благодарит учащихся за работу на уроке (рис. 19).

Рис. 19

Варианты использования данного материала

Пособие является лишь примерным в плане построения урока и отбора содержания учебного материала, а так же форм организации познавательной деятельности учащихся. Например, часть задач можно оставить для бумажного варианта решения, готовые бланки для самостоятельной работы (стр. 12) можно раздать всем учащимся.

Форма работы с задачей на стр. 11 может зависеть от конкретных поставленных учителем целей работы с данным классом. Например, можно сначала провести коллективное обсуждение, затем индивидуальное решение; можно разбиться на группы, в которых обсуждать ход решения; можно сначала провести этап индивидуального решения, а затем сверить и обсудить результаты и т.д.

Открытость пособия (добавление и изменение)

Учитель легко может изменить, исключить или добавить новую страничку в пособие или скорректировать уже имеющиеся. Для этого достаточно иметь полную версию программы (для знакомства с работой пособия достаточно демо-версии).

Вариант компьютерного класса или ноутбуков

При этом появляется ряд новых методических возможностей.

Учащиеся индивидуально могут двигать вершину треугольника на стр. 1, меняя его вид, и делать свои предположения, а также могут сами провести работу над доказательством теоремы (стр. 2) и над решением задач в удобном для них темпе.

Итак, использование компьютера позволяет разнообразить традиционные формы обучения.

Но следует отметить, что компьютер не может заменить учителя во многих областях педагогической деятельности. Это учитель, используя в собственных интересах специфические возможности программ, определяет, какую пользу приносит компьютер. Нет никакого сомнения, что эффективное применение компьютеров улучшает качество обучения и позволяет учителю обеспечить лучший уровень преподавания. Компьютерное обучение должно составлять часть общей педагогической тактики и объединяться вместе с другими процессами в единый педагогический цикл. Чтобы учителя и ученики не рассматривали компьютер как своеобразную игрушку, необходимо проводить оценку эффективности этого технического средства обучения. С помощь компьютера ученики могут приобретать опыт, получение которого в другой ситуации сопровождалось бы неизбежными трудностями. Однако не всякий опыт является желательным, и учитель должен тщательно следить за целесообразностью и эффективностью его содержания. Применение компьютерных технологий позволяет ставить вопрос о построении учебных курсов, которые бы органически объединяли знания в области науки, техники и производства, что является одной из предпосылок преодоления разрыва между школьным обучением и практикой. Несомненным плюсом автоматизации учебного процесса является то, что компьютер:

существенно увеличил возможности подачи учебного материала;

позволяет усилить мотивацию учения;

активно вовлекает учащихся в учебный процесс;

расширяет наборы применяемых учебных задач;

позволяет качественно изменить контроль над деятельностью учащегося и обеспечить гибкость управления учебным процессом;

способствует формированию у школьников рефлексии своей деятельности.

Однако, компьютерные методы обучения, впрочем, как и любое другое явление, имеет как положительные, так и отрицательные стороны.

При создании чертежей в «Живой Математике», легко учитываются особенности восприятия визуальной информации учащимися: экран дисплея не перегружается большими текстами, а учебный материал располагается так, чтобы улучшить его читаемость и понятность; цветовая гамма тщательно продумывается, чтобы не вызывать утомления у учащихся. Основные акценты ставятся на индивидуализацию и дифференциацию обучения, в тоже время, учитываются возможности коллективной работы в классе; диалог с компьютером с помощью учителя и без; уровень подготовки учеников и самих учителей к работе с компьютером.

При прохождении педагогической практики на 5 курсе, я работал с учащимися 7 класса. С этой параллели начинается систематическое изучение курса геометрии и поэтому на первый план выдвигается значимость геометрического чертежа (как основного средства наглядности), умение его изобразить и умело использовать для работы над теоремой или задачей.

Запись условия математического утверждения с помощью чертежа предельно компактна и геометрически выразительна, что позволяет учащимся охватить все условие целиком, то есть помогает лучше усвоить его и понять. Поняв условие, учащиеся начинают рассуждать по чертежу, выполняя разные дополнительные построения, а также анализировать данные математического утверждения. Так что представить доказательство теоремы или решение геометрической задачи без чертежа невозможно.

Но вместе с тем в пользовании чертежом имеется своя специфика. Переход от абстрактного (мышление) к конкретному (чертеж) воспринимается учащимися легко. А вот обратный переход, от конкретного к абстрактному, представляет для их понимания немалые трудности. Объясняется это тем, что учащиеся привыкли «доверять» чертежу полностью, а значит, относиться к нему критически не умеют. Для них чертеж - та же объективная реальность, которая неразрывно связана с процессом мышления. Поэтому, чтобы научить учащихся относиться к чертежу критически, надо оторвать их мышление от него, чему и способствует учебное правило: «Не разрешается использовать в рассуждениях свойства фигуры, видные на чертеже, если мы не можем обосновать их, опираясь на аксиомы и теоремы, доказанные ранее». Смысл этого правила простой - доверяй да проверяй. В этом смысле применение компьютерной среды «Живая Математика» помогает учащимся не строить свои рассуждения, основываясь на разглядывании статистического чертежа, а позволяет варьировать чертежом, что избавляет учащегося от стереотипности чертежа (если б он был предъявлен статистически) и позволяет избегать ошибок в ходе проведения доказательных рассуждений.

Данная специфика пользования чертежом относится и к определениям. Так в одном из учебников по геометрии имеется следующая иллюстрация чертежа к понятиям углов, образованных при пересечении двух прямых секущей (рис. 20). Если же изобразить прямые таким образом, чтобы они попарно пересекались (как на рис. 21), то у учащихся уже возникают трудности с определением видов углов на данном чертеже.

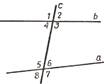
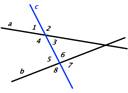
Рис. 20                Рис. 21

Компьютерная среда «Живая Математика» помогает учащимся избежать подобного рода «стандартизации» расположения прямых a и b и служит прекрасным средством для более глубокого и вдумчивого понимания данных понятий. При этом ещё и возникает возможность проведения эксперимента, позволяющего увидеть, что если внутренние накрест лежащие углы одной пары равны, то внутренние накрест лежащие углы другой пары тоже равны (если внутренние накрест лежащие углы равны, то сумма внутренних односторонних углов равна 1800. И наоборот: если сумма внутренних односторонних углов равна 1800, то внутренние накрест лежащие углы равны).

На чертеже отмечаются соответственно равные стороны и углы, другие данные теоремы или задачи, используемые в решении. То есть он не столько является простой иллюстрацией, сколько геометрической записью того, что выражается словами. Что это означает? А то, что чертеж должен быть удобным для пользования. Пользуясь таким чертежом сначала при письменном оформлении доказательства или решения, а затем при его проверке, учащиеся могут выполнить задание быстрее и, главное, качественнее. Благодаря этому чертеж превращается в эффективное средство контроля и самоконтроля, что особенно важно для развития у учащихся самостоятельности и сознательности в обучении.

Итак, чертеж является органической частью записи того, что дано и что требуется доказать или найти. Все, что можно записать геометрически, должно быть отражено на чертеже. Кроме равенства сторон и углов, на нем отмечаются данные численные или буквенные значения, неизвестные величины обозначаются через x, y, … . Подготовка чертежа к работе заканчивается тогда, когда условие теоремы или задачи полностью разобрано, нанесены на чертеж все данные и сделаны необходимые обозначения. Затем составляется краткая запись того, что дано и что требуется доказать. При этом учитывается специфика чертежа с таким расчетом, чтобы избежать лишнего дублирования. Если чертеж дает достаточно полное представление о содержании доказываемой теоремы или решаемой задачи (или когда оно простое), то можно обойтись и без подобной записи. Но загромождать чертеж маловыразительными деталями ради этого тоже не стоит. Лучше всего, когда и чертеж является просторным, и запись условия короткая. Для сокращения записи следует использовать традиционную общепринятую символику. Некоторые фигуры, видные на чертеже, в записи условия могут отсутствовать. Словом, к записи условия и заключения подходить надо творчески, исходя при этом из интересов учащихся.

Примеры использования чертежей для решения задач и доказательства теорем с учетом выше изложенного выполненных в программе «Живая Математика».

Признак параллельности прямых

Теорема о соотношении между сторонами и углами треугольника

Задача 1 (на применение теоремы о соотношении между сторонами и углами треугольника)

Задача 2 (на применение теоремы о соотношении между сторонами и углами треугольника)

§4. Фрагменты конспектов уроков - примеры применения компьютерных технологий при изучении геометрии в 7 классе c учетом принципа наглядности

Урок - главная составная часть учебного процесса. Учебная деятельность учителя и учащихся в значительной мере сосредотачивается на уроке. Вот почему качество подготовки учащихся по той или иной учебной дисциплине во многом определяется уровнем проведения урока, его содержательной и методической наполненностью, его атмосферой, наглядностью. Как сделать так, чтобы урок не только вооружал учащихся знаниями и умениями, значимость которых невозможно оспорить, но чтобы все, что происходит на уроке, вызывало у детей искренний интерес, подлинную увлеченность, формировало их творческое сознание?

В этом нам помогут компьютерные технологии, а именно программа «Живая Математика». Компьютерные презентации можно использовать не только на уроках, но и при индивидуальной работе с сильными, отстающими или пропустившими материал учениками.

В программе «Живая Математика» можно создавать различные типы уроков:

урок усвоения новых знаний;

урок усвоения навыков и умений;

урок обобщения и систематизации знаний;

урок проверки, оценки и коррекции знаний, навыков и умений;

комбинированный урок.

В работе представлены фрагменты комбинированных уроков.

Данный тип урока имеет наиболее сложную структуру, включающую в себя следующие элементы: организационную часть; проверку знаний ранее изученного материала и выполнения домашнего задания; изложение нового материала; первичное закрепление новых знаний; применение их на практике и инструктаж по домашнему заданию.

Изложение нового материала начинается с объяснения содержания новой темы, увязки ее с ранее пройденным. При изложении нового материала на комбинированном уроке применяются такие методы, как рассказ, беседа, объяснение и значительно реже - лекция. Обычно один метод является ведущим, а другие привлекаются для активизации процесса обучения. Возможно использование различных дидактических приемов: информирование о плане сообщения нового материала; интересное, нестандартное его изложение; создание проблемных ситуаций; обращение к жизненному опыту учащихся; демонстрация фрагментов диафильмов; запись материала на доске или использование наглядных пособий, применение компьютерных технологий.

Первичное закрепление знаний является, как правило, обязательной частью большинства комбинированных уроков. Формы и методы закрепления материала могут быть разнообразными, но они должны стимулировать мыслительную деятельность учащихся.

Комбинированный урок имеет несколько равных по своему значению образовательных целей. Известны уроки с различными сочетаниями целей, например: контроль и оценка знаний и умений школьников и усвоение новых знаний; контроль и оценка знаний и умений и формирование умений и навыков; контроль и оценка знаний и умений, а также обобщение и систематизация учебного материала и т.д.

Проведение комбинированного урока предполагает реализацию основных структурных элементов тех уроков, которые соответствуют целям комбинированного урока. При этом одни из этапов могут выпадать из структуры комбинированного урока, другие - объединяться.

Подбор материала к урокам данной дипломной работы проводился тщательным образом. Из доступного материала был отобран только тот, который служит решению поставленных задач наиболее простым способом.

В уроках подобраны задачи, в процессе выполнения которых учащиеся знакомятся с условием теорем, методом и идеей доказательства теорем, с существенными свойствами и признаками понятий. А также задачи, которые позволяют не только готовиться к изучению нового материала, но и самостоятельно «открывать» и формулировать новые теоремы. При подборе заданий к этапу творческого переноса знаний и навыков, были использованы различные сочетания индивидуальной и коллективной работы, например, работа над условием, обсуждение идеи решения осуществляются коллективно, а оформление решения - самостоятельно.

Контроль за усвоением знаний на комбинированном уроке с применением компьютерных технологий, а именно программы «Живая Математика», проводился на каждом из этапов урока с помощью вопросов, требующих мыслительной и практической активности учащихся и постоянных обращений к учащимся. В случае возникновения затруднений, учитель в любое время может вернуться на нужный слайд презентации и при необходимости еще раз разъяснить пройденный материал.

Хотелось бы отметить, чтобы сделать учение привлекательным, нужно проводить уроки в интересной форме. А это достигается применением интересных средств обучения, в частности компьютерных технологий, а именно программы «Живая Математика», которая отвечает требованиям наглядности.

Мною были разработаны 7 уроков по курсу геометрии 7 класса по темам «Основные понятия и элементы геометрии», «Треугольники» с учетом принципа наглядности в компьютерной среде «Живая Математика».

Это первые уроки при изучении систематического курса геометрии и именно они должны быть выстроены, преподнесены и оформлены таким образом, чтобы дети «влюбились» в предмет, увлеклись им, и, конечно же, полностью разобрались в изучаемом материале.

Урок по теме «Основные элементы геометрии»

В данном уроке учащиеся знакомятся с основными неопределяемыми понятиями - точкой, прямой и плоскостью, их изображениями и обозначениями. Вводятся знаки принадлежности и непринадлежности точки прямой, рассматривается вопрос об изображении части прямой линии большей длины, чем сама линейка.

Предлагаются задачи для самостоятельного решения, часть из которых может быть использована при закреплении материала, а другая - предложена в качестве домашнего задания.

Урок по теме «Отрезок»

Данный урок построен таким образом, что он подытоживает все знания, накопленные до этого учащимися по теме «Отрезок» - это понятие отрезка, его длины, единиц измерения, середины отрезка. Рассматривается свойство отрезка - если отрезок разделен на два отрезка, то длина всего отрезка равна сумме длин этих двух отрезков. Наглядно в уроке представлено сравнение отрезков. Разбираются задачи, связанные с понятием отрезка.

Урок по теме «Луч и угол»

Данный урок (так же как и предыдущий) с одной стороны подытоживает знания, полученные учащимися в курсе математики 5-6 классов, по теме «Луч и угол», а с другой стороны систематизирует и расширяет их. В уроке в наглядном виде представлены все виды углов, понятие биссектрисы угла. А также особое внимание уделяется свойству угла, когда луч проходит между его сторонами. Представлен ряд задач с готовыми решениями и задачи для самостоятельно выполнения.

Урок по теме «Взаимное расположение прямых на плоскости. Смежные и вертикальные углы»

В данном уроке рассматриваются способы взаимного расположения прямых на плоскости - пересекающиеся и непересекающиеся прямые. Говорится о том, что понятие для непересекающихся прямых будет введено позже, так как им уделяется особое внимание, а останавливаются в уроке на случае пересекающихся прямых, которые в своем пересечении образуют четыре угла. Их то и рассматривают, вводя понятия смежных и вертикальных углов. Есть ряд анимационных эффектов, позволяющих практическим путем прийти к свойствам смежных и вертикальных углов. Затем проводится доказательное рассуждение этих свойств, не произнося слова «доказательство». Убедившись в справедливости соответствующих утверждений, учащиеся переходят к решению задач, в которых можно воспользоваться подсказкой в случае затруднения или для проверки. А так же показывается способ построения перпендикулярных прямых с помощью чертежного угольника и линейки.

Урок по теме «Перпендикуляр к прямой. Треугольник и его элементы»

В данном уроке вводится понятие перпендикуляра к прямой и рассматриваются два способа его построения - с помощью чертежных инструментов и способ перегибания листа бумаги.

Впервые вводится понятие теоремы и ее доказательства на примере единственности существования перпендикуляра к прямой. Дается определение треугольника, его элементов - вершин, углов и сторон. Вводятся понятия медианы, биссектрисы, высоты и серединного перпендикуляра для треугольника.

Заключение

В процессе проведения работы было выявлено, что дидактический принцип наглядности, являющийся ведущим в обучении, следует понимать несколько шире, нежели возможность зрительного восприятия. Воздействуя на органы чувств, средства наглядности обеспечивают более полное представление образа или понятия, что способствует более прочному усвоению материала. Они повышают интерес к знаниям, позволяют облегчить процесс их усвоения, поддерживают внимание учащихся.

Итак, проведенное исследование дало следующие результаты:

Отмечено, что принцип наглядности вытекает из сущности процесса восприятия, осмысления и обобщения учащимися изучаемого материала.

Установлено, что наибольшей эффективности в учебном процессе можно добиться при правильном сочетании слова и средств наглядности.

Произведена классификация учебно-наглядных пособий, выделены их существенные признаки, освещены требования к их выбору и правила их применения.

Установлено, что результативное использование средств наглядности в учебном процессе не ограничивается подбором соответствующих пособий и техникой их демонстрирования.

Использовать наглядные средства нужно целенаправленно, не загромождать уроки большим количеством наглядных пособий, ибо это мешает учащимся сосредоточиться и обдумать наиболее существенные вопросы. То есть соблюдать чувство меры, в противном случае это вредит процессу обучения.

Основным для курса математики является принцип моделирования, являющийся более высокой ступенью по отношению к принципу наглядности, так как в ней основным содержанием выступают разного рода отношения,

Выявлены условия для наиболее эффективного использования компьютера в современном учебном процессе.

Обозначены возможности, которые предоставляет компьютер для операционной стороны учебной деятельности, рассмотрены отрицательные и положительные стороны автоматизации учебного процесса.

Показано, что компьютер не может заменить учителя в педагогической деятельности, а компьютерное обучение должно составлять лишь часть общей педагогической тактики.

Разработано ряд уроков по геометрии с использованием компьютерной среды «Живая Математика» с целью показа преимущественного применения компьютерного чертежа по сравнению с традиционным. Опытная проверка разработанных материалов проводилась в 7-х классах ЦО «Технологии обучения». При этом учащиеся показали хорошие результаты при обучении геометрии.

Список использованной литературы

Алимов, Ш.А., Колягин, Ю.М. и др. Алгебра: 7 кл, Алгебра: 8 кл, Алгебра: 9 кл. - М.: Просвещение, 2006.

Атанасян, Л.С. и др. Геометрия: 10-11 кл. - М.: Просвещение, 2007.

Атанасян, Л.С. и др. Геометрия: 7-9 кл. - М.: Просвещение, 1995.

Бабанский, Ю.К. Методы обучения в современной общеобразовательной школе. - М.: Просвещение, 1985.

Баранов, С.П. Сущность процесса обучения. - М.: Просвещение, 1981.

Баранов, С.П. Чувственный образ в познавательной деятельности школьника //Чувственный образ в развитии интеллекта школьника: Межвузовский сборник научных трудов. - М.: MПГУ, ЕГПИ. - 1999.

Блох, А.Я., Гусев, В.А., Дорофеев, Г.В. и др.; Сост. Мишин, В.И. Методика преподавания математики в средней школе. Частная методика. - М.: Просвещение, 1987.

Болтянский, В.Г. и др. Оборудование кабинета математики. Пособие для учителя. - М., 1981.

Болтянский, В.Г. Формула наглядности. Изоморфизм плюс простота: Советская педагогика №5. - 1970.

Великороднова, А.И. Роль слова учителя и наглядных пособий в формировании у учащихся представлений и первоначального понятия о развитии животного мира: Дисс. канд. пед. наук. - Л., 1952.

Волович, М.Б. Наука обучать. Технология преподавания математики. - М., Linka-Press, 1995.

Волович, М.Б. Средства наглядности как материальная основа управления процессом усвоения знаний //Советская педагогика. - 1979. - № 9.

Гальперин, П.Я., Талызина, Н.Ф. Зависимость обучения от типа ориентировочной деятельности. - М., 1968.

Давыдов, В.В. Виды обобщения в обучении. - М., 1972.

Данилов, М.А. Активное восприятие и осознание учащимися нового учебного материала: Известия АПН РСФСР: выпуск 20. - 1949.

Евдокимов, В.И. К вопросу об использовании наглядности в школе: Сов. Педагогика №3. - 1982.

Епишева, О.Б., Крупич, В.И. Учить школьников учиться математике. - М.: Просвещение, 1990.

Есипов, Б.П. Активизация мышления учащихся в процессе обучения: Известия АПН РСФСР, выпуск 20. - 1949.

Зильберберг, Н.И. Урок математики. Подготовка и проведение: Книга для учителя. - М.: Просвещение, АО Учебная литература, 1996.

Ильина, Т.А. Педагогика. - М.: Просвещение, 1984.

Каптерев, П.Ф. Дидактические очерки: теория образования. - Пч., 1915.

Карпов, Г.В., Романин В.А. Технические средства обучения. - М.: Просвещение, 1979.

Колмогоров, А.Н. О профессии математика. - М.: Советская наука, 1964.

Коменский, Я.А. Великая дидактика: Изб. пед. соч., т.1. - М., 1982.

Леонтьев, А.М. Деятельность. Сознание. Личность. - М.: 1975.

Лесгафт, П.Ф. Руководство по физическому образованию детей школьного возраста: Избранные педагогические сочинения, т.2. - М.: Издательство АПН РСФСР, 1952.

Макарычев, Ю.Н., Миндюк, Н.Г., Нешков, К.И. Алгебра: 7 кл, Алгебра: 8 кл, Алгебра: 9 кл. - М.: Мнемозина, 2005.

Математика. Арифметика. Алгебра. Анализ данных. 7 кл.: Учеб. для общеобразоват. заведений. / Под ред. Дорофеева Г.В. - 2-е изд. - М.: Изд. дом. Дрофа,1998.

Медяник, Л.И. Учителю о школьном курсе геометрии. - М.: 1984.

Мордкович, А.Г. Алгебра: 7 кл: Учеб. для общеобразоват. учреждений. - 2-е изд. - М.: Мнемозина, 1999.

Мордкович, А.Г. Алгебра: Метод. пособие для учителей. - М.: Мнемозина, 1997.

Мордкович, А.Г., Тульчинская, Е.Е., Мишустина, Т.Н. Алгебра: 7 кл: Задачник для общеобразоват. учреждений. - 2-е изд. - М.: Мнемозина, 1998.

Окунев, А.А. Спасибо за урок, дети!. - М.: Просвещениe, 1988.

Осмоловская, И.М. Словесные методы обучения. - М.: Издательский центр Академия, 2008.

Песталоцци, И.Г. Как Гертруда учит своих детей: изб. пед. соч., т. 3. - М.: 1909.

Песталоцци, И.Г. Метод: изб. пед. соч. в 2-х т. - М.: 1981.

Пирогов, Н.И. Дневник старого врача: Избранные пед. соч. - Изд-во АПН РСФСР, 1953.

Писарев, Д.И. Промахи незрелой мысли. Старое барство. - М.: Гос. изд-во, 1923.

Погорелов, А.В. Геометрия: 7-9 кл. - М.: Просвещение, 2007.

Познер, С. Урок чтения с природоведческим материалом: Начальная школа №4. - 1945.

Половцов, В.В. Основы общей методики естествознания. - Петроград: Госиздат, 1922.

Программы по математике для общеобразовательных школ, гимназий, лицеев: Математика: 5-11 кл. / Сост. Кузнецова, Г.М. , Миндюк, Н.Г. - 2-е изд. - стереотип. - М.: Дрофа, 2001.

Салмина, Н.Г. Виды и функции материализации в обучении. - М.: МГУ, 1981.

Скаткин, М.Н. Совершенствование процесса обучения. - М.: 1971.

Талызина, Н.Ф. Управление процессом усвоения знаний. - М.: 1975.

Фридман, Л.М. Логико-психологический анализ школьных учебных задач. - М.: 1977.

Фридман, Л.М. Наглядность и моделирование в обучении, Педагогика и психология №6. - 1984.

Фридман, Л.М. Психолого-педагогические основы обучения математике в школе. - М.: Просвещение, 1983.

Фридман, Л.М. Учитесь учиться математике: Книга для учащихся. - М.: Просвещение, 1985.

Шаповаленко, С.Г. Методы научного исследования в области методики химии: выпуск 4. - Известия АПН РСФСР, 1946.

Шарыгин, И.Ф. Геометрия: 7-9 кл. - М.: Дрофа, 2002.

Шарыгин, И.Ф., Ерганжиева Л.Н. Наглядная геометрия: Учебное пособие для учащихся V-VI классов. - М.: МИРОС, 1995.

Эрдниев, П.М., Эрдниев, Б.П. Укрупнение дидактических единиц в обучении математике. - М.: Просвещение, 1986.

Якиманская, И.С. Развивающее обучение. - М.: Педагогика, 1979.

Яковлев, Н.М., Сохор, А.М. Методика и техника урока в школе. - М.: Просвещение, 1985.