Теорема Чеви та її застосування
МІНІСТЕРСТВО ОСВІТИ І НАУКИ
УКРАЇНИ
Чернівецький національний
університет імені Юрія Федьковича
Факультет прикладної математики
Кафедра алгебри та інформатики
Курсова робота
з математики
на тему:
«Теорема Чеви та її застосування»
студентки
3 курсу 306 групи
напряму
підготовки «Математика»
Стус
Ірина Ігорівна
Керівник:
асистент
кафедри алгебри та інформатики Довгей Ж.І.
Чернівці - 2013
АНОТАЦІЯ
У даній курсовій роботі розглядається теорема Чеви, наслідки
з неї та пов’язані з нею інші теореми, які суттєво спрощують розв’язання деяких
задач з планіметрії. Також на прикладах проілюстровано застосування теореми
Чеви та деяких похідних теорем.
ЗМІСТ
ВСТУП
§1. Поняття чевіани. Теорема Чеви
.1 Основні поняття. Узагальнена теорема синусів
.2 Знаки відрізків. Відношення трьох точок
.3 Теореми Чеви
.4 Наслідки з теореми Чеви
.5 Теорема Чеви: випадок зовнішньої точки
§2. Теорема Карно
§3. Деякі чудові перетворення, пов'язані з теоремою
Чеви
§4. Зовнівписані кола
.1 Вираження площі трикутника через радіуси вписаного
круга і півпериметр
.2 Залежність між радіусом вписаного кола і радіусами
зовнівписаних кіл
.3 Означення довжини відрізка від вершини трикутника
до точок дотику зовнівписаного кола
§5 Центр мас периметра трикутника
§6. Теорема Ван-Обеля та наслідки з неї
§7. Приклади застосування теореми Чеви
ВИСНОВОК
СПИСОК ВИКОРСТАНИХ ДЖЕРЕЛ
ВСТУП
Теорема Чеви вказує на деякі співвідношення між сторонами
трикутника. Чева винайшов загальний метод, що дозволяє визначати, чи
перетинається відповідна трійка прямих в одній точці, чи ні. Дана теорема була
доведена у кінці XVII ст., але є актуальною і на сьогоднішній день.
Джованні Чева народився в 1647 році в Італії. Він закінчив
єзуїтський коледж в Мілані, після чого став студентом Університету в місті
Піза, де пізніше і став працювати професором математики. З 1686 року Чева
працював в Університеті в Мантуї, залишаючись на цій посаді до самого кінця
свого життя. До речі, брат Джованні, Томасо Чева, також був досить талановитим
та відомим математиком, а також поетом.
Більшу частину життя Чева вивчав геометрію, намагаючись
відродити грецьку геометрію; крім того, сьогодні його пам'ятають і за
дослідженнями в області механіки.
У 1678-му Чева опублікував свою теорему «Про прямі, що
взаємно перетинаються», яка стала знаменитою; теорема ця згодом отримала його
ім'я - теорема Чеви. Вона сьогодні є класичною теоремою геометрії трикутника.
Говорячи простою мовою, Чева винайшов якийсь загальний метод, що дозволяє за
положенням точок на сторонах трикутника визначати, чи перетинається відповідна
трійка прямих в одній точці чи ні. Вона афінна, тобто теорему цю можна
сформулювати використовуючи тільки характеристики, що зберігаються при афінних
перетвореннях. До речі, відрізок, що з'єднує вершину трикутника з деякою точкою
на протилежній стороні, називається чевіаною - також на ім'я Джованні Чеви.
Можна сказати, що ця теорема служить фундаментом всієї геометрії трикутника.
Відомо, що опублікував вчений не тільки свої теореми, але і
допрацював і популяризував теореми Менелая. У роботі «Геометрія руху» він
розглянув природу руху.
Відомо, що Джованні був і інженером-гідравліки, а також
економістом, і кілька разів йому довелось попрацювати на уряд Мантуї, був він
урядовим комісаром Мантуанського герцогства. У 1728 році він опублікував «Opus
hydrostaticum», в якому обговорював проблеми в гідравліці.
Джованні Чева помер 15 червня 1734 року, у віці 85 років;
смерть його настала під час облоги Мантуї франко-сардінської армією.
Розглянемо проблему, яку поставив перед собою математик. Більшість
чудових точок трикутника можуть бути отримані за допомогою наступної процедури.
Нехай у нас є деяке правило, згідно з яким ми можемо вибрати певну точку 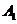 на стороні
на стороні 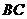 (або
її продовженні) трикутника
(або
її продовженні) трикутника 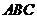 (наприклад,
виберемо середину цієї сторони). Потім побудуємо аналогічні точки
(наприклад,
виберемо середину цієї сторони). Потім побудуємо аналогічні точки 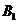 ,
, 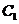 на
двох інших сторонах трикутника (у нашому прикладі - ще дві середини сторін).
Якщо правило вибору вдале, то прямі
на
двох інших сторонах трикутника (у нашому прикладі - ще дві середини сторін).
Якщо правило вибору вдале, то прямі 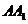 ,
,
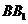 ,
,  перетнуться
в деякій точці
перетнуться
в деякій точці 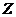 (вибір середин сторін у цьому сенсі, звичайно,
вдалий). Наприклад, всі чудові точки виходять саме так.
(вибір середин сторін у цьому сенсі, звичайно,
вдалий). Наприклад, всі чудові точки виходять саме так.
Тому хотілося б мати який-небудь загальний метод, що дозволяє за
положенням точок на сторонах трикутника визначати, чи перетинається відповідна
трійка прямих в одній точці, чи ні.
Універсальну умову, що «закрила» цю проблему, знайшов в 1678 р.
італійський інженер Джованні Чева. Можна сказати, що ця теорема служить
фундаментом всієї геометрії трикутника.
§1. Поняття чевіани. Теорема Чеви
.1 Основні поняття. Узагальнена теорема
синусів
Означення 1.1. Відрізок, що з’єднує вершину трикутника з деякою точкою
на протилежній стороні називається чевіаною [1].
Зауваження. В [2] означення чевіани дається наступним чином:
Означення 1.1΄. Прямі, що виходять з вершин трикутника і перетинають протилежну його
сторону в деякій точці, називаються прямими Чеви або чевіанами.
Цей термін походить від імені італійського математика Джованні Чеви,
який в 1678 році опублікував дуже важливу теорему.
Означення 1.2. Якщо три чевіани 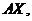

 (по
одній з кожної вершини) трикутника
(по
одній з кожної вершини) трикутника 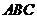 проходять
через одну точку, то вони називаються конкурентними.
проходять
через одну точку, то вони називаються конкурентними.
Теорема синусів - це тригонометрична теорема, якою ми часто
користуємося. В підручниках вона, зазвичай, подається у неповній формі, та
втрачається деяка інформація, яку несе узагальнена теорема, тому ми дозволимо
собі довести теорему синусів у потрібній нам формі.
Теорема 1 (узагальнена теорема синусів). Для трикутника 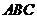 з радіусом описаного кола
з радіусом описаного кола  виконуються співвідношення
виконуються співвідношення
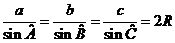 .
.
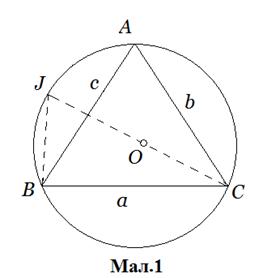
Доведення. Розглянемо трикутник 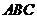 (позначений
довільним способом) і опишемо навколо нього коло з центром в точці
(позначений
довільним способом) і опишемо навколо нього коло з центром в точці 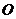 і радіусом
і радіусом  ,
як показано на малюнках 1 і 2. Проведемо діаметр
,
як показано на малюнках 1 і 2. Проведемо діаметр 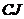 і
хорду
і
хорду 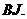 В обох випадках
В обох випадках 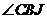 -
прямий, оскільки він вписаний в півколо. Звідси випливає, що на обох малюнках
-
прямий, оскільки він вписаний в півколо. Звідси випливає, що на обох малюнках  . На малюнку 1
. На малюнку 1 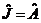 , оскільки ці кути опираються на спільну дугу кола.
, оскільки ці кути опираються на спільну дугу кола.
На
малюнку 2 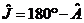 , оскільки протилежні кути вписаного чотирикутника є
доповняльними. Згадуючи, що
, оскільки протилежні кути вписаного чотирикутника є
доповняльними. Згадуючи, що  ,
отримаємо, що в обох випадках
,
отримаємо, що в обох випадках  ,
а отже
,
а отже  , тобто
, тобто 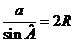 .
.

Якщо цю ж саму операцію ми застосуємо до інших кутів трикутника  то отримаємо
то отримаємо
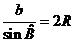 ,
,
 . ▲
. ▲
Отже, теорему доведено.▲
1.2 Знаки відрізків. Відношення трьох точок
Відрізки, що лежать на одній прямій, порівнюються не лише за величиною,
але й за напрямком. Для можливості такого порівняння виберемо на прямій певний
напрямок, який будемо вважати додатнім. Протилежний напрям назвемо від’ємним.
За такою умовою кожному відрізку буде відповідати число, що дорівнює довжині
цього відрізка і має знак плюс при додатному напрямку відрізка і знак мінус,
при від’ємному напрямку.
Наприклад, якщо відрізку 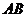 буде
відповідати додатне число, то відрізку
буде
відповідати додатне число, то відрізку  -
від’ємне.
-
від’ємне.
Називаючи відрізок двома буквами, ми першою буквою позначаємо початкову
точку, а другою - кінцеву точку відрізка. При введеній нами умові відрізки 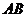 і
і  є
однаковими за величиною і протилежні за знаком:
є
однаковими за величиною і протилежні за знаком:  або
або
 .
.
Теорема 2. При довільному розміщенні трьох точок 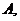
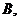
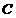 на
напрямленій прямій, справедливе наступне співвідношення:
на
напрямленій прямій, справедливе наступне співвідношення:  .
.
Доведення. Нехай жодна з пар точок 
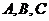 не
співпадає, тобто жоден відрізок не дорівнює нулю.
не
співпадає, тобто жоден відрізок не дорівнює нулю.
Існує шість можливих розміщень трьох точок на прямій, два з яких
вказані на малюнку 3.

-й випадок: з малюнка 3а бачимо, що
 .
.
-й випадок: з малюнка 3б бачимо, що
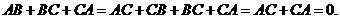
Аналогічно доводиться теорема в решті випадків.
Теорема залишається справедливою, якщо один з відрізків перетворюється
в нуль, наприклад, замість 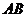 маємо
маємо
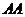 . ▲
. ▲
1.3 Теорема Чеви

Теорема 3 (Менелая) [4]. Нехай дано трикутник 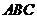 і точки
і точки 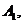
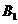 і
і 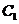 -
такі, що лежать на сторонах
-
такі, що лежать на сторонах 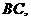

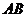 -
відповідно (мал. 4б). Точки
-
відповідно (мал. 4б). Точки 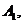
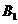 і
і 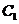 лежать
на одній прямій тоді і тільки тоді, коли виконується рівність
лежать
на одній прямій тоді і тільки тоді, коли виконується рівність

Теорема 4 (Чеви - пряма) [1]. Нехай дано трикутник 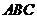 і точки
і точки 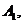
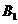 і
і 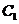 -
такі, що лежать на сторонах
-
такі, що лежать на сторонах 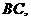

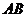 -
відповідно (мал. 4а). Якщо в трикутнику
-
відповідно (мал. 4а). Якщо в трикутнику 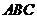 відрізки
(або прямі)
відрізки
(або прямі) 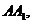

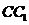 є
конкурентними, тоді виконується співвідношення:
є
конкурентними, тоді виконується співвідношення:
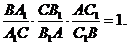
Доведення. Для доведення теореми Чеви згадаємо, що площі трикутників з
рівними висотами пропорційні основам трикутників. Посилаючись на малюнок 4а, ми
маємо:
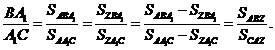
Аналогічно,
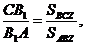
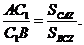
Тепер, якщо ми їх перемножимо, то отримаємо
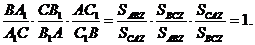
Теорему доведено.  ▲
▲
Теорема, обернена до даної також вірна:
Теорема 5. (Чеви - обернена) Нехай дано трикутник 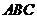 і точки
і точки 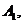
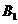 і
і 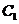 -
такі, що лежать на сторонах
-
такі, що лежать на сторонах 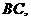

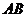 -
відповідно (мал. 4а). Якщо три чевіани
-
відповідно (мал. 4а). Якщо три чевіани 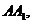

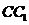 задовольняють
співвідношення
задовольняють
співвідношення
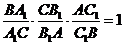 ,
,
то вони конкурентні.
Доведення. Припустимо, що дві перші чевіани перетинаються у точці 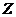 , як і раніше, а третя, що проходить через точку
, як і раніше, а третя, що проходить через точку 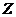 , буде
, буде  .
Тоді, за теоремою 4,
.
Тоді, за теоремою 4,  . Але за припущенням
. Але за припущенням 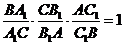 . Звідси випливає, що
. Звідси випливає, що  ,
точка
,
точка 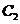 співпадає з точкою
співпадає з точкою  і
ми довели, що відрізки
і
ми довели, що відрізки 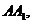

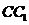 є
конкурентними. ▲
є
конкурентними. ▲
Теорема 6. [1] Теорема Чеви може бути записана так:

або
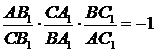 ,
,
або
 ,
,
або

Теорема Чеви залишається вірною і у випадку, якщо точка перетину
прямих, що виходять з вершин трикутника, знаходиться поза трикутником.
Теорема 7 (Чеви в формі синусів) [3]. Умову Чеви можна
записати також у вигляді:
 .
.
Доведення. Застосувавши теорему синусів до трикутників 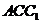 і
і  (мал. 4),
маємо:
(мал. 4),
маємо:
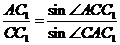 і
і
 .
.
Розділивши одну рівність на іншу, одержуємо:
 .
.
Аналогічно:
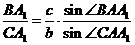 ,
,
 .
.
Остаточно маємо:
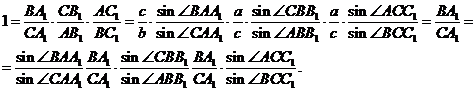 ▲
▲
1.4 Наслідки з теореми Чеви
1. Медіани
трикутника перетинаються в одній точці.
Доведення.
Нехай задано трикутник 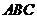 (Мал. 4),
(Мал. 4), 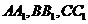 - медіани
трикутника. Тоді
- медіани
трикутника. Тоді  ,
, 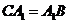 ,
, 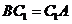 , звідси отримаємо наступні рівності:
, звідси отримаємо наступні рівності:
 ,
,
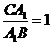 ,
, 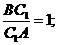
Перемноживши їх, матимемо:
 ▲
▲
2. Бісектриси
внутрішніх кутів трикутника перетинаються в одній точці.
Доведення. Нехай 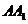 ,
, 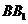 ,
,
 - бісектриси внутрішніх кутів трикутника (Мал. 4):
- бісектриси внутрішніх кутів трикутника (Мал. 4):
 ,
,
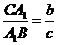 ,
, 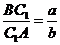 .
.
Звідси:
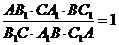 .▲
.▲
3. Висоти
трикутника перетинаються в одній точці, яка називається ортоцентром трикутника.
Доведення. Маємо (з мал. 5):
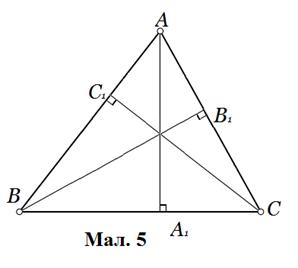
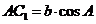 ,
,
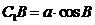 ,
,
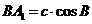 ,
,
 ,
,
 ,
,
 .
.
Звідси випливає:
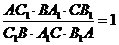 .▲
.▲
Приклад 1. Центр описаного кола. Очевидно, що два серединних
перпендикуляра, проведені до сторін трикутника, перетинаються в точці,
рівновіддаленій від усіх трьох вершин трикутника, і значить, ця точка лежить і
на третьому серединному перпендикулярі.
Але як довести цей факт, користуючись теоремою Чеви? Це хотілося б
зробити і в даному випадку. Проте тут виникають труднощі, оскільки за природою
своєю теорема Чеви створена для виявлення конкурентності чевіан, а не
перпендикулярів до сторін трикутника. Проблему, що виникла можна подолати,
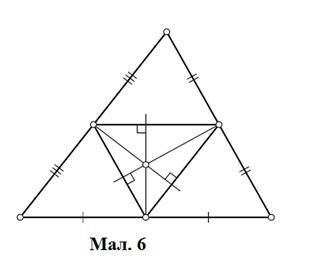
розглянувши серединний трикутник (Мал. 6). Оскільки середні лінії паралельні
сторонам вихідного трикутника, серединні перпендикуляри є висотами серединного
трикутника. І ми звели задачу до випадку доведення третього наслідку!
Є і більш змістовний підхід до цієї проблеми.
Приклад 2. Точка Нагеля  .
Прямі, що проходять через вершини трикутника і ділять периметр навпіл -
конкурентні і точка їх перетину є точкою Нагеля.
.
Прямі, що проходять через вершини трикутника і ділять периметр навпіл -
конкурентні і точка їх перетину є точкою Нагеля.
Доведення. Нехай 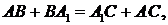 тобто точка
тобто точка 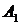 ділить
периметр навпіл. Аналогічно
ділить
периметр навпіл. Аналогічно 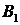 та
та
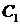 . Звідси ми можемо записати добуток:
. Звідси ми можемо записати добуток:

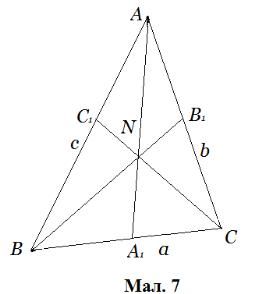
А звідси, за теоремою Чеви, прямі - конкурентні.▲
4. Прямі,
які з’єднують вершини трикутника з точками дотику вписаного круга,
перетинаються в одній точці, ця точка називається точкою Жергона.
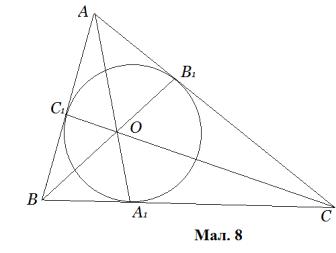
Доведення. Нехай 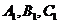 - точки дотику вписаного кола. Тоді
- точки дотику вписаного кола. Тоді
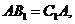
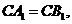
 .
.
Отже,
1.5 Теорема Чеви: випадок зовнішньої точки
Теорема Чеви залишається справедливою для випадку зовнішньої точки 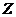 (точка перетину прямих, що проходять через вершини
трикутника) і точок
(точка перетину прямих, що проходять через вершини
трикутника) і точок 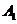 ,
, 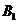 ,
,
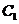 , одна з яких належить стороні трикутника (в нашому
випадку
, одна з яких належить стороні трикутника (в нашому
випадку 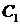 ), а дві інші є продовженням сторін. (Звичайно, і
«правило обходу» залишається в силі. Варто тільки пам'ятати, що при складанні
відношення, виходячи з вершини, ми спочатку виходимо з точки поділу - вона може
тепер бути розташована поза стороною, а потім - до наступної вершини.) Однак,
розглядаючи зовнішню точку
), а дві інші є продовженням сторін. (Звичайно, і
«правило обходу» залишається в силі. Варто тільки пам'ятати, що при складанні
відношення, виходячи з вершини, ми спочатку виходимо з точки поділу - вона може
тепер бути розташована поза стороною, а потім - до наступної вершини.) Однак,
розглядаючи зовнішню точку 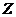 ,
ми натрапляємо на деякі складності.
,
ми натрапляємо на деякі складності.
Наприклад, якщо 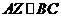 , чому дорівнює
, чому дорівнює  (Мал.
9)? Де взагалі в такому випадку розташовується точка
(Мал.
9)? Де взагалі в такому випадку розташовується точка 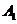 ?
?
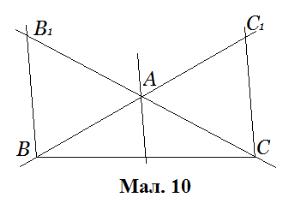

Як нескладно перевірити, користуючись теоремою Фалеса, умові Чеви
задовольняють і точки 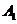 ,
, 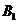 ,
,
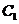 , для яких прямі
, для яких прямі 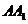 ,
,
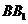 ,
,  паралельні
(Мал. 10).
паралельні
(Мал. 10).
Щоб не виділяти ці ситуації в окремі випадки, зручно вважати, що
площина містить нескінченно віддалену пряму, складену з нескінченно віддалених
точок, в кожній з яких перетинається якась сім’я паралельних прямих. Можна тому
вважати, що нескінченно віддалена точка вказує напрямок прямої. Таку модель в
математиці називають проективною площиною. На проективній площині будь-які
паралельні прямі перетинаються в деякій точці! - звичайно, нескінченно
віддаленій.
§2. Теорема Карно
Подивимося, як «працює» теорема Чеви.
Теорема 8 (Карно) [3]. Нехай точки 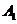 ,
,
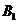 ,
, 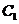 лежать
на прямих
лежать
на прямих 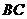 ,
,  ,
,
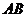 відповідно. Нехай також,
відповідно. Нехай також, 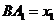 ,
, 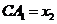 ,
,  ,
, 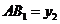 ,
,  ,
, 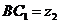 . Тоді наступні умови рівносильні:
. Тоді наступні умови рівносильні:
) перпендикуляри до відповідних сторін трикутника, проведені в точках 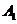 ,
, 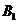 ,
,
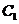 , перетинаються в одній точці;
, перетинаються в одній точці;
)  (умова Карно).
(умова Карно).
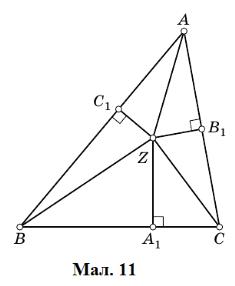
Доведення. Доведення базується лише на теоремі Піфагора. Нехай
перпендикуляри перетинаються в точці 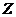 .
Не важко отримати наступні рівності (Мал. 11):
.
Не важко отримати наступні рівності (Мал. 11):
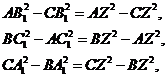
склавши які, і отримуємо умову Карно. ▲
Доведення зворотної теореми Карно (як і зворотної теореми Чеви)
використовує пряму теорему.
Із теореми Карно конкурентність серединних перпендикулярів випливає так
само природно, як і конкурентність медіан з теореми Чеви.
Можна показати, що рівні відрізки дотичних виражаються через
півпериметр і сторони трикутника наступним чином:
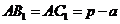 ,
,
 ,
, 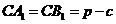 .
.
теорема сінус чеви трикутник
§3. Деякі чудові перетворення,
пов'язані з теоремою Чеви
Ізотомічне спряження. Зафіксуємо на площині трикутник 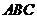 . Виберемо деяку точку площини
. Виберемо деяку точку площини 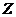 і проведемо через неї і вершини трикутника прямі, що
перетинають сторони трикутника (або їх продовження) в точках
і проведемо через неї і вершини трикутника прямі, що
перетинають сторони трикутника (або їх продовження) в точках 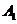 ,
, 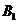 ,
,
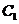 відповідно. Кожну таку точку відобразимо симетрично
щодо середини тієї сторони, на якій вона лежить.
відповідно. Кожну таку точку відобразимо симетрично
щодо середини тієї сторони, на якій вона лежить.
Отримані три точки позначимо через  ,
,
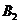 ,
, 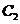 (Мал.
12). Тоді прямі
(Мал.
12). Тоді прямі  ,
,  ,
,
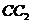 також перетинаються в деякій точці
також перетинаються в деякій точці  . Ця точка називається ізотомічно спряженою до точки
. Ця точка називається ізотомічно спряженою до точки 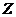 відносно трикутника
відносно трикутника 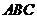 .
.
Коректність визначення ізотомічного спряження випливає із теореми Чеви:
в умові Чеви чисельники міняються місцями зі знаменниками, і якщо вихідний
добуток дорівнював одиниці, то «перевернутий» добуток теж дорівнює одиниці.
Ізогональне спряження. Зафіксуємо на площині трикутник 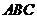 . Знову виберемо деяку точку площини
. Знову виберемо деяку точку площини 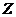 і проведемо через неї і вершини трикутника прямі, що
перетинають сторони трикутника (або їх продовження) в точках
і проведемо через неї і вершини трикутника прямі, що
перетинають сторони трикутника (або їх продовження) в точках 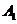 ,
, 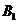 ,
,
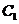 відповідно.
відповідно.
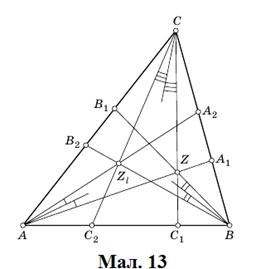
Тоді прямі  ,
,  ,
,
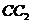 , симетричні до прямих
, симетричні до прямих 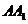 ,
,
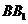 ,
,  щодо
бісектрис відповідних кутів трикутника, перетинаються в одній точці
щодо
бісектрис відповідних кутів трикутника, перетинаються в одній точці  (Мал. 13). Ця точка називається ізогональною до
сполученої точки
(Мал. 13). Ця точка називається ізогональною до
сполученої точки 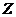 відносно трикутника
відносно трикутника 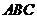 .
.
Для доведення коректності тут зручно скористатися теоремою Чеви в формі
синусів: записана таким чином умова Чеви «перевертається», і якщо добуток
відношень дорівнював одиниці, після «перевороту» він теж буде дорівнювати
одиниці.
Ізотомічне та ізогональне спряження як перетворення площини. В
геометрії спряженням називають перетворення 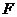 площини,
що повертає кожну точку назад після дворазового застосування. Формально це
можна записати так:
площини,
що повертає кожну точку назад після дворазового застосування. Формально це
можна записати так: 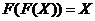 для будь-якої точки
для будь-якої точки  ,
або
,
або 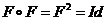 (перетворення
(перетворення 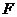 в
квадраті дає тотожне). Такою властивістю володіють симетрії відносно точки,
прямої або кола (Інверсія). Очевидно, що і щойно розглянуті нами перетворення
володіють цією ж властивістю. Однак вони влаштовані більш складним чином,
наприклад, не зберігають прямі і кола (тобто образ прямої або кола може бути
чимось іншим. Крім того, безпосередньо із означення випливає, що і ізотомічне,
і ізогональне спряження «погано» діють на точки, розташовані на сторонах (або
їх продовженнях) трикутника, що породжує ці перетворення. Будь-яка така точка
під дією цих перетворень переходить в протилежну вершину, а вершини - в
будь-яку точку на протилежній стороні. Порушується однозначність! Але якщо
виключити з області визначення прямі, що містять сторони трикутника,
однозначність відновлюється.
в
квадраті дає тотожне). Такою властивістю володіють симетрії відносно точки,
прямої або кола (Інверсія). Очевидно, що і щойно розглянуті нами перетворення
володіють цією ж властивістю. Однак вони влаштовані більш складним чином,
наприклад, не зберігають прямі і кола (тобто образ прямої або кола може бути
чимось іншим. Крім того, безпосередньо із означення випливає, що і ізотомічне,
і ізогональне спряження «погано» діють на точки, розташовані на сторонах (або
їх продовженнях) трикутника, що породжує ці перетворення. Будь-яка така точка
під дією цих перетворень переходить в протилежну вершину, а вершини - в
будь-яку точку на протилежній стороні. Порушується однозначність! Але якщо
виключити з області визначення прямі, що містять сторони трикутника,
однозначність відновлюється.
Однією з важливих характеристик перетворення є наявність (або
відсутність) нерухомих точок, тобто точок, що залишаються під дією перетворення
на місці. Легко зрозуміти, що нерухомими точками ізотомічного спряження є точка
перетину медіан і точки, симетричні до вершин трикутника відносно середин
відповідних сторін; нерухомими точками ізогонального спряження є центри
вписаної й трьох описаних кіл.
За допомогою ізотомічного і ізогонального спряжень можна отримувати
нові чудові точки, наприклад, анти ортоцентр - Hm (точку, ізотомічно спряжену
до ортоцентра) або точку перетину антибісектрис - Im (точку, ізотомічно
спряжену до центру вписаного кола).
Точкою Лемуана 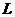 називають точку, ізогонально спряжену до точки
перетину медіан трикутника. Вона володіє багатьма цікавими властивостями.
називають точку, ізогонально спряжену до точки
перетину медіан трикутника. Вона володіє багатьма цікавими властивостями.
§4. Зовнівписані кола
Бісектриси зовнішніх кутів при двох вешинах трикутника перетинаються на
бісектрисі внутрішнього кута при третій його вершині. Точка перетину двох
бісектрис зовнішніх кутів і бісекриси внутрішнього кута при третій вершині
трикутника є центром кола, що дотикається до одніє сторони трикутника і
продовжень до двох інших сторін (мал. 14).
Таке коло називається зовнівписаним колом.
Щоб обчислити радіус зовнівписаного кола, розглянемо площі трикутників 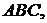


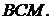 Позначимо радіус зовнівписаного кола, що дотикається
до сторони
Позначимо радіус зовнівписаного кола, що дотикається
до сторони 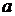 символом
символом 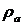 .
.

Тоді
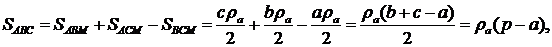
де 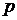 - півпериметр трикутника
- півпериметр трикутника 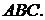 Отже
Отже 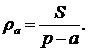
Аналогічно:
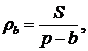
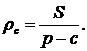
4.1 Вираження площі трикутника через
радіуси вписаного круга і півпериметр

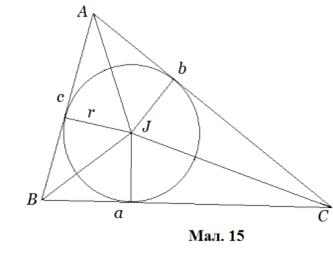
Вираження площі трикутника через радіуси зовнівписаних і вписаного
кругів:
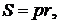

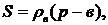

перемножимо ці рівності і отримаємо:
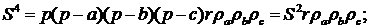

4.2 Залежність між радіусом
вписаного кола і радіусами зовнівписаних кіл
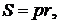

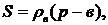

звідси маємо:
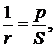

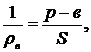

з цих рівностей отримуємо:
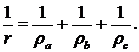
4.3 Означення довжини відрізка від
вершини трикутника до точок дотику зовнівписаного кола (мал. 14)

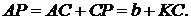
Оскільки  то
то 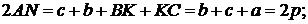

Відрізок від вершини трикутника до точок дотику зовнівписаного кола
дорівнює півпериметру.
§.5 Центр мас периметра трикутника
Теорема 9. Центр мас периметра трикутника розміщений в центрі круга,
вписаного в трикутник, вершини якого співпадають з серединами сторін даного
трикутника.

Доведення. Центр мас сторони трикутника співпадає з її серединою.
Розмістивши, на середині кожної сторони масу, пропорційну довжині сторони, ми
зведемо дану задачу до побудови центра мас системи трьох матеріальних точок з
масами 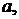
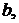
 зосередженими відповідно у вершинах
зосередженими відповідно у вершинах 

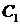 (мал. 16) трикутника
(мал. 16) трикутника 
Центр мас системи двох точок - 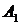 з
масою
з
масою 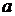 і точки
і точки 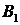 з
масою
з
масою 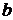 - точка
- точка 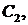 що
розміщена на відрізку
що
розміщена на відрізку 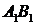 так, що
так, що
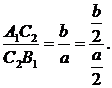
З отриманих рівностей випливає, що 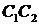 -
бісектриса внутрішнього кута при вершині
-
бісектриса внутрішнього кута при вершині 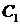 трикутника
трикутника

§6. Теорема Ван-Обеля та наслідки з неї
Теорема 10. Для кожної з прямих Чеви, що перетинаються всередині в
трикутнику, вірним є наступне співвідношення (мал.17):

Доведення. З вершини 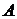 проведемо
пряму
проведемо
пряму 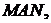 паралельну до
паралельну до 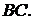
З подібності трикутників 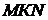 та
та
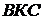 маємо:
маємо:
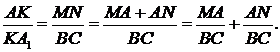

З подібності трикутників  та
та

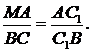
Із подібності трикутників  та
та
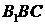 :
:
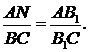
А звідси маємо:
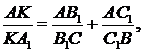
що і доводить теорему. ▲
Цікаві частинні випадки цієї теореми:
а) якщо 

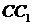 - медіани, тоді маємо:
- медіани, тоді маємо:

Тобто, медіана ділиться точкою перетину медіан у відношенні 2:1,
рахуючи від вершини трикутника.
б) 

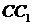 - бісектриси внутрішніх кутів.
- бісектриси внутрішніх кутів. 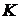 - центр вписаного круга:
- центр вписаного круга:
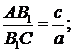
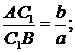
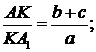
в) 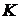 - точка Жергона:
- точка Жергона:
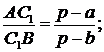

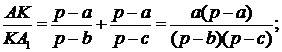
г) 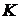 - точка Негеля:
- точка Негеля:
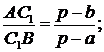

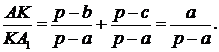
Покажемо, що теорема Ван-Обеля може бути поширена на прямі Чеви, що
перетинаються поза трикутником, якщо відрізки, що розглядаються в теоремі,
вважати напрямленими.
Нехай в трикутнику  проведено
прямі
проведено
прямі 

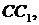 що перетинаються в точці
що перетинаються в точці 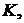 яка лежить за межами трикутника (мал.18).
яка лежить за межами трикутника (мал.18).
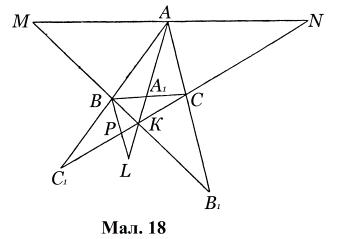
З подібності трикутників  і
і
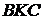 маємо:
маємо:

з подібності трикутників 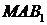 і
і
 та подібності трикутників
та подібності трикутників 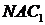 і
і  маємо:
маємо:
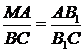 та
та
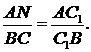
А отже:

Варто відмітити, що для напрямлених відрізків всі три дроби - від’ємні.
Визначимо 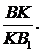 Проведемо з вершини
Проведемо з вершини 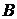 пряму
пряму
 З подібності трикутників
З подібності трикутників  та
та 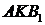 маємо:
маємо:
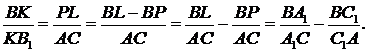
Якщо звернути увагу на те, що для напрямлених відрізків  - від’ємне, то
- від’ємне, то

Якщо вважати в теоремі Ван-Обеля відрізки напрямленими, то теорема
дійсна і для прямих Чеви, які перетинаються у внутрішній точці трикутника.
Назвемо відношення трьох точок, що лежать на прямих Чеви, відношенням
Чеви (наприклад, відношення 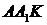 -
мал. 17).
-
мал. 17).
Теорема 11. Різниця між сумою трьох відношень Чеви та їх добутком є
величиною сталою і дорівнює 2.
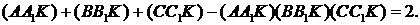
Доведення. Доводиться ця теорема на основі теореми Ван-Обеля. Доведення теореми
є в [1].
Перепозначимо:

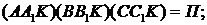
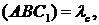
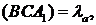
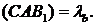
Обчислимо значення  для
частинних випадків:
для
частинних випадків:
) Нехай прямі Чеви - медіани. Тоді 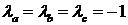 і
і
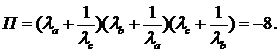
2) Нехай прямі Чеви - бісектриси внутрішніх кутів. Тоді
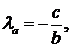
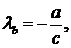


3) Нехай прямі Чеви - прямі Жергона:
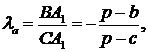
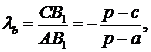
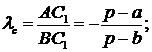

Французьким математиком у 1818 році Жергоном була доведена наступна
теорема:
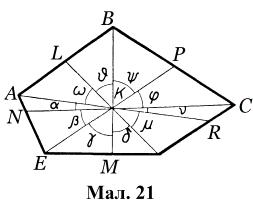
Теорема 12. Якщо прямі 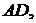
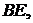
 що виходять з вершини трикутника
що виходять з вершини трикутника 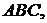 перетинаються в точці
перетинаються в точці 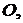 що
є внутрішньою для трикутника (мал. 21), то
що
є внутрішньою для трикутника (мал. 21), то
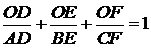 і
і
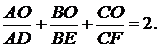
Доведення. Теорема доведена в [1].
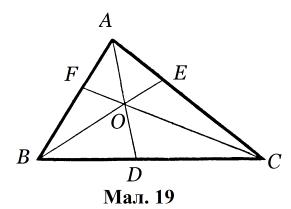
В теоремі Жергона розглядаються властивості прямих Чеви, що
перетинаються всередині трикутника, або на його стороні. Розглянемо, чи не
можна поширити теорему на випадок, коли точка перетину знаходиться за межами
трикутника.
За теоремою Жергона (мал. 19)
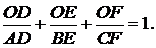
Запишемо цю рівність наступним чином:

Якщо точка 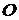 лежатиме на одній зі сторін трикутника, наприклад на
лежатиме на одній зі сторін трикутника, наприклад на 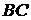 , тобто співпаде з точкою
, тобто співпаде з точкою 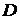 , то
, то  і
отримаємо:
і
отримаємо:
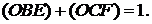
Нехай точка 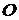 знаходиться за межами трикутника
знаходиться за межами трикутника  (мал. 20). Тоді
(мал. 20). Тоді
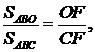
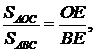
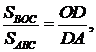

Отже, відповідно,

або
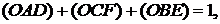
тобто теорема Жергона справедлива і в цьому випадку.
Теорема 13 (Понселе). Прямі, що з’єднують Будь-яку точку з вершинами
многокутника, який має непарне число сторін, утворює на протилежних його
сторонах такі відрізки, що добуток відрізків, що не мають спільних точок
дорівнює добутку решти відрізків.
Доведення. Нехай всередині п’ятикутника  (мал.
21) взята точка
(мал.
21) взята точка 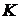 і з’єднана з усіма вершинами. Потрібно довести, що
і з’єднана з усіма вершинами. Потрібно довести, що
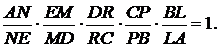
Розглянемо відношення площ трикутників  та
та
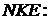
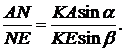
Аналогічно отримуємо
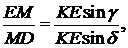
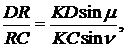
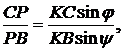

Оскільки кути 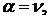
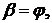


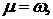 то
то
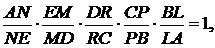
що і потрібно було довести.
Те ж саме можемо записати наступним чином:
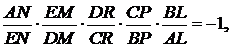
або
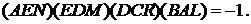
§7. Приклади застосування теореми
Чеви
Задача 1. Знайти всередині трикутника таку точку 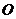 , щоб добуток
, щоб добуток 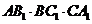 мав
найбільшу величину (
мав
найбільшу величину (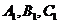 - точки перетину прямих
- точки перетину прямих  зі
сторонами
зі
сторонами 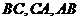 ).
).
Розв’язання. Проведемо медіани  трикутника
трикутника
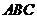 , що перетинаються в точці
, що перетинаються в точці 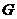 . Оскільки середнє геометричне двох величин не
перевищує їх середнього арифметичного, то
. Оскільки середнє геометричне двох величин не
перевищує їх середнього арифметичного, то

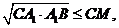
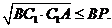
Підносячи до квадрату кожну з отриманих нерівностей і перемножуючи їх,
отримаємо:

На основі теореми Чеви маємо:
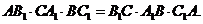
Очевидно, що має місце нерівність:

Нерівність перетворюється у рівність у випадку, якщо основи прямих Чеви
дорівнюють серединам відповідних сторін. Отже, в цьому випадку добуток 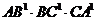 має найбільшу величину, що дорівнює
має найбільшу величину, що дорівнює  , де
, де  -
сторони трикутника.
-
сторони трикутника.
Отже, шуканою точкою є точка перетину медіан трикутника.
Задача 2. Опустити за допомогою однієї лінійки, з точки, що знаходиться
ззовні або всередині круга, перпендикуляр на діаметр.
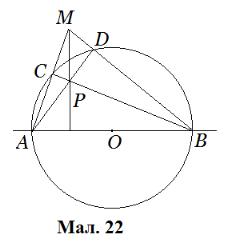
Розв’язання. Нехай з точки  (Мал.
22) на діаметр
(Мал.
22) на діаметр 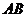 потрібно опустити перпендикуляр. З’єднаємо точку
потрібно опустити перпендикуляр. З’єднаємо точку  з кінцями діаметра. Точку
з кінцями діаметра. Точку 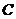 - точку перетину
- точку перетину  з
колом - з’єднуємо з кінцем діаметра
з
колом - з’єднуємо з кінцем діаметра 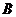 ,
а точку
,
а точку  - точку перетину
- точку перетину 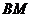 з
колом - з’єднуємо з кінцем діаметра
з
колом - з’єднуємо з кінцем діаметра 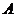 .
Прямі
.
Прямі 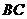 та
та  перетинаються
в точці
перетинаються
в точці 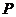 . Пряма
. Пряма  проходить
через точку перетину двох висот і через вершину трикутника
проходить
через точку перетину двох висот і через вершину трикутника 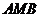 і тому перпендикулярна до
і тому перпендикулярна до  .
.
Теорема 14. Прямі, що виходять з вершин трикутника і ділять протилежні
сторони пропорційно до протилежних кутів, перетинаються в одній точці .(Мал.
23).
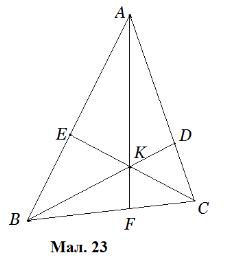
Доведення. Маємо:
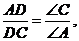
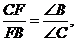
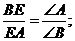
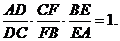
Теорема доведена. ▲
Ця теорема може бути узагальнена наступним чином:
Зауваження. Прямі, що виходять з вершин трикутника і ділять протилежні
сторони пропорційно до одних і тих же функцій прилеглих кутів, перетинаються в
одній точці:
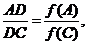
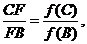
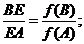
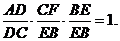
ВИСНОВОК
Отже, в даній курсовій роботі розглядається теорема Чеви, наслідки з
неї та приклади застосування даної теореми. Також наведено декілька теорем, які
є наслідками з теореми Чеви. Зокрема, це такі теореми, як Карно, Ван-Обеля
тощо. У моїй роботі вказано декілька прикладів застосування теореми Чеви. Ця
теорема була і залишається актуальною. Вона є своєрідним фундаментом для
встановлення нових важливих висновків.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
1. Коксетер
Г.С.М. , Грейтцер С.Л. Новые всречи с геометрией. - М.: Наука, 1978.- 224с.
2. Зетель
С.И. Новая геометрия треугольника. - М.: УЧПЕДГИЗ, 1962. - вип.2 -152с.
3. Мякишев
А.Г. Елементы геометрии треугольника. - М.: МЦНО, 2002. - 32с.
4. Ефремов
Д. Новая геометрия треугольника, - Одеса: «Вестника опытной физики и
элементарной математики», 1903.
. В.В.
Ткачук, Математика абитуриенту. - М.: МЦНМО, 2004. - 971с.
. ЖИДКОВ
С. І. Теореми Чеви i Менелая: від теорії - до практики. -Х. : Вид. група
«Основа», 2010. - 159с.