Краевая задача для одного вырождающегося уравнения гиперболического типа
Краевая задача для одного
вырождающегося уравнения гиперболического типа
Выполнил
Каримов Динар
Данилович
Введение
Актуальность работы состоит в том, что изучение краевых задач для
уравнений гиперболического типа находится в центре внимания специалистов по
дифференциальным уравнениям с частными производными благодаря глубокому
математическому содержанию этих задач и наличию многочисленных приложений при
исследовании проблем математической физики. Эта теория включает рассмотрение
ряда трудных и интересных задач. К их числу относятся краевые задачи для
уравнений гиперболического типа с двумя линиями вырождения.
Исследования данной работы примыкают с одной стороны к направлениям,
связанным с краевыми задачами для уравнений гиперболического типа, а с другой -
к направлению, связанному с теорией дробного интегро-дифференцирования. Теория
краевых задач для уравнений гиперболического типа является одним из важных
разделов современной теории дифференциальных уравнений с частными производными,
который интенсивно развивается. Такой интерес объясняется как теоретической
значимостью получаемых результатов, так и их важными практическими
приложениями. Возникшая в начале 20-ых годов прошлого столетия теория
вырождающихся гиперболических уравнений получила значительное развитие
благодаря многочисленным приложениям в газовой динамике, в магнитной
гидродинамике, в теории бесконечно малых изгибаний поверхностей, в теории
оболочек, в прогнозировании уровня грунтовых вод и других областях науки и
техники (см. Берс JI. [2], Векуа И.Н. [4], Франкль Ф.И. [10]).
Изучение краевых задач для вырождающихся уравнений гиперболического типа
проводилось в работах М.А. Лаврентьева, Ф.И. Франкля, И.Н. Векуа, А.В. Бицадзе,
К.И. Бабенко, Т.Д. Джураева, В.Ф. Волкодавова, С.П. Пулькина, М.М. Смирнова,
М.С. Салахитдинова, В.И. Жегалова, A.M. Нахушева, Е.И. Моисеева, А.П.
Солдатова, А.Н. Зарубина, К.Б. Сабитова, Л.С. Пулькиной, В.З. Вагапова и других
математиков.
Профессором В.Ф. Волкодавовым рассмотрены краевые задачи для уравнения смешанного
эллептико-гиперболического типа, линия изменения типа которых является их
характеристикой. В постановках таких задач условие сопряжения на линии
изменения типа состоит в склеивании производной по нормали из области
эллиптичности с дробной производной из области гиперболичности.
Целью настоящей работы является доказательство существования и
единственности решения краевой задачи для одного уравнения гиперболического
типа со специальными условиями сопряжения на линии изменения типа.
Методы исследования. Основные результаты работы получены с использованием
классических методов решения дифференциальных уравнений и аппарата специальных
функций гипергеометрического типа.
Структура и объем дипломной работы. Дипломная работа состоит из введения,
двух параграфов, заключения и библиографического списка и составляет страниц.
§1. Постановка задачи
краевой задача гиперболический уравнение
Уравнение
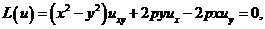 (1)
(1)
где
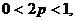 рассмотрим на множестве
рассмотрим на множестве 
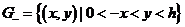 ,
, 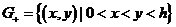 .
.
Задача.
Найти непрерывное в  и
и 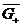 решение
уравнения (1), удовлетворяющее на множестве
решение
уравнения (1), удовлетворяющее на множестве 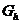 краевым
условиям:
краевым
условиям:
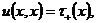
 (2)
(2)
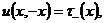
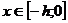 (3)
(3)
на
линии  : условиям сопряжения по функции
: условиям сопряжения по функции
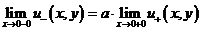 , (4)
, (4)
и
интегродифференциального вида
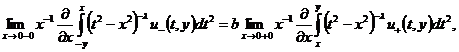 (5)
(5)
где
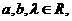
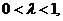
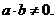
§2. Класс решения
Обоснование
единственности и существования решения поставленной задачи мы произведем в
специальных классах решений по областям 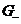 и
и 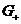 .
.
По
аналогии с [8,9] с помощью интеграла дробного порядка введем класс обобщенных
решений.
Определение
1. Будем считать, что  , если она определяется формулой
, если она определяется формулой
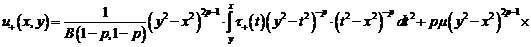
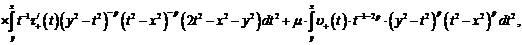
дающей
решение задачи Коши в 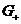 , в которой
, в которой
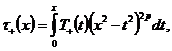 (6)
(6)
где
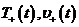 - достаточно гладкие функции,
- достаточно гладкие функции,  .
.
Это
решение имеет вид:
 (7)
(7)
где
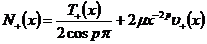 . (8)
. (8)
Определение
2. Будем считать, что функция 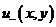 принадлежит
классу решений
принадлежит
классу решений  , если она определяется формулой:
, если она определяется формулой:

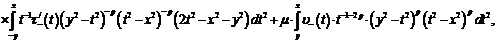
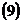
где
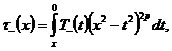
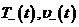 - достаточно гладкие функции,
- достаточно гладкие функции, 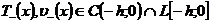 .
.
Решение
этого класса имеет вид:


где
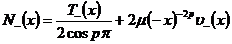 .
. 
§3. Доказательство существования и единственности решения
задачи
Рассмотрим
функции, определенные формулами  и
и  . Требуется выяснить условия на
. Требуется выяснить условия на 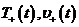 и
и 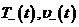 , чтобы
данные формулы определяли решение поставленной задачи (1) - (5) в
рассматриваемых классах решений
, чтобы
данные формулы определяли решение поставленной задачи (1) - (5) в
рассматриваемых классах решений  и
и  .
.
Рассмотрим
условие сопряжения по функции . В
формулах (7) и (10) перейдем к пределу при
. В
формулах (7) и (10) перейдем к пределу при  слева и
справа соответственно. Подставляя полеченные выражения в (4), придем к
интегральному уравнению:
слева и
справа соответственно. Подставляя полеченные выражения в (4), придем к
интегральному уравнению:

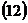
Прежде,
чем удовлетворить решения классов  и
и 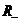 интегродифференциальному условию сопряжения
интегродифференциальному условию сопряжения 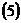 , вычислим следующие интегралы, подставив в левую и
правую части условия (5) формулы (7) и (10) соответственно и поменяв порядки
интегрирования:
, вычислим следующие интегралы, подставив в левую и
правую части условия (5) формулы (7) и (10) соответственно и поменяв порядки
интегрирования:
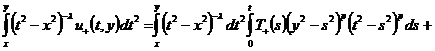
+
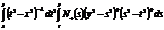 =
=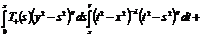
+
Вычислим
внутренние интегралы, обозначив их соответственно 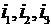 .
.
В
первом интеграле произведем замену переменных:
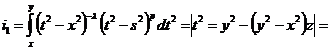
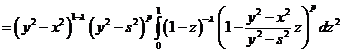 .
.
Согласно
интегральному представлению гипергеометрической функции Гаусса 2.12.(1) [1]
получим:
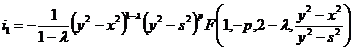 .
.
Второй
интеграл вычислим аналогично:
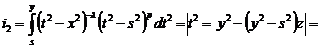
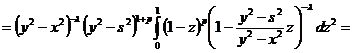
=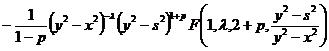 .
.
В
третьем интеграле после замены получается бета-функция [8, 9]:
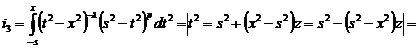
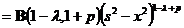 .
.
Таким
образом, получим
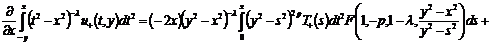
+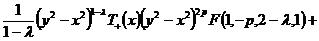

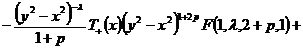
 .
.
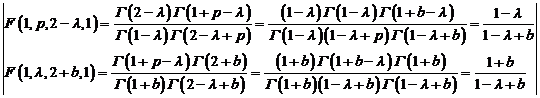 .
.
Тогда

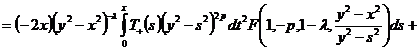
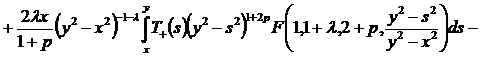
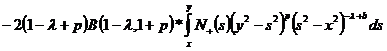 , где
, где  .
.
Переходя
к пределу, при стремлении аргумента к линии  справа,
получим выражение для правой части условия (5):
справа,
получим выражение для правой части условия (5):
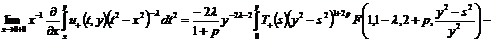
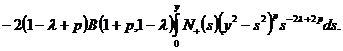 (13)
(13)
Рассмотрим теперь интеграл, стоящий в левой части условия (5):
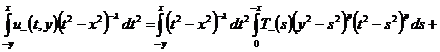
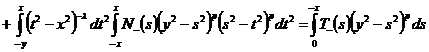 ,
,
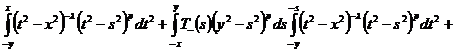
 .
.
Вычислим
внутренние интегралы каждого из них в отдельности:

 ,
,
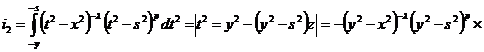
 ,
,
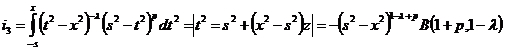 .
.
Собирая
полученные результаты и упрощая, получим выражение:


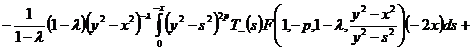
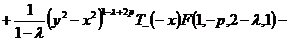
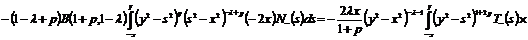
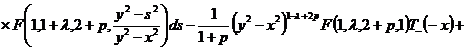
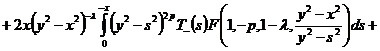
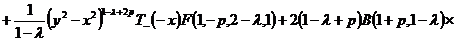
 .
.
В
данном результате перейдем к пределу, при стремлении аргумента x к
нулю слева:
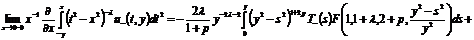
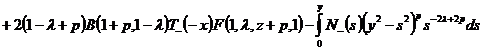 .(14)
.(14)
Чтобы «связать» между собой соотношения (12), (13) и (14)
продифференцируем обе части равенства (12) по переменной y (при этом применяется формула
дифференцирования интеграла с переменным верхним пределом):
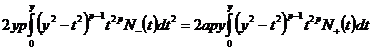 ,
,
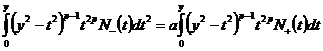 .
.
К
обеим частям полученного тождества применим интегральный оператор
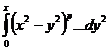 .
.
Тогда
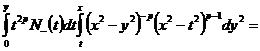
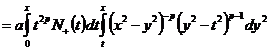 .
.
Вычисляя
внутренние интегралы, имеем:
 .
.
Дифференцируя
обе части по переменной x, получим соотношение
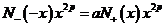 ,
,
или
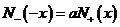 .(15)
.(15)
С учетом последних соотношений, формула (14) принимает вид:
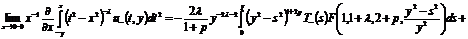
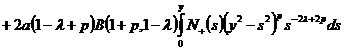 .(16)
.(16)
Удовлетворим (13) и (16) условию (5). Тогда
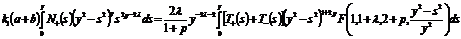 (16*)
(16*)
Для дальнейшего дифференцирования (16), найдем отдельно, используем
формулу сокращенного дифференцирования 28(23) [1]
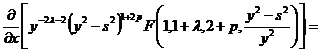

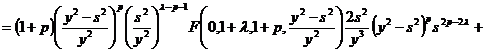
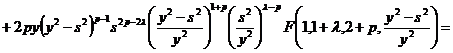
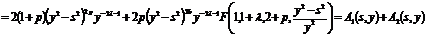 . (17)
. (17)
С
учетом последнего тождества (17) продифференцируем обе части тождества (16).
Будем иметь:
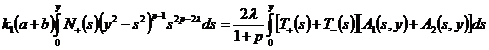 .
.
К
обеим частям полученного тождества применим оператор
 .
.
Получим
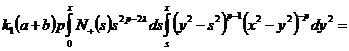
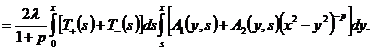 (18)
(18)
Внутренний интеграл представим в виде суммы

Вычислим
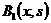 :
:
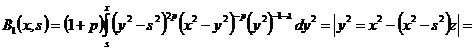
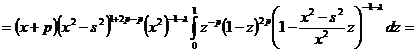
 .
.
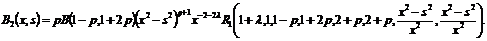
Здесь
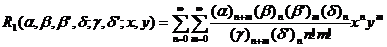 -
-
гипергеометрическая
функция, введенная профессором Волкодавовым В.Ф. [5].
Продифференцируем
обе части тождества (18). Имеем
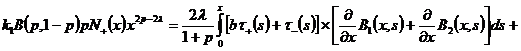
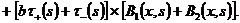 (19)
(19)
Для
производных получим выражения
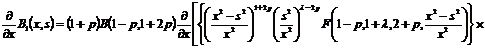
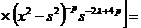


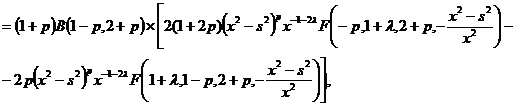
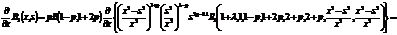
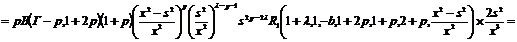
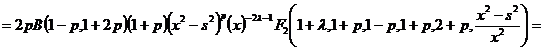

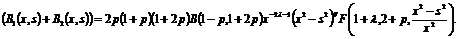 (20)
(20)
С учетом (20) и(11) равенство (19) примет вид:
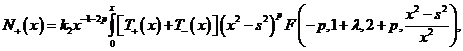
где
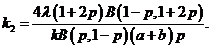
Для
граничных функций будем иметь:
 ,
,
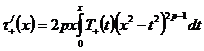 .
.
Вновь
применяя интегральное преобразование (*), получим
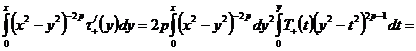
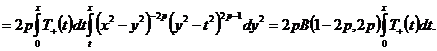
Полностью
аналогично поступим со второй граничной функцией
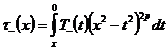 ,
,
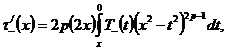
Применим
оператор 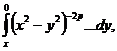 имеем:
имеем:
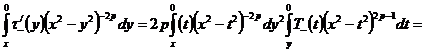
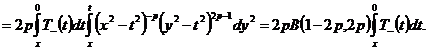
Откуда
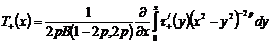 ,(21)
,(21)
 .(22)
.(22)
Тогда
 (23)
(23)
Преобразуем выражение
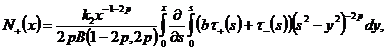

Интегрируя
по частям,положив:
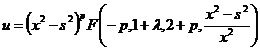 ,
,
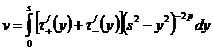 ,
,
получим:
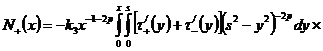
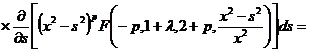
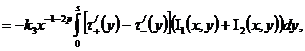
где
 ,
,
 .
.
Каждый
из интегралов рассмотрим отдельно. Произведем замену переменной 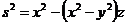 . Тогда для первого интеграла:
. Тогда для первого интеграла:

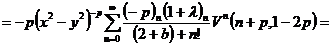
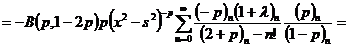
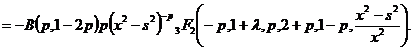
Для второго:
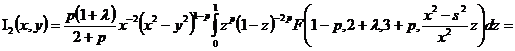
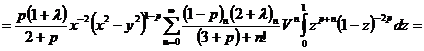

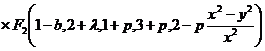 .
.
С учетом известного соотношения для бета-функции [1]:
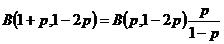
получим:
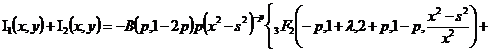

Учитывая,
что

где
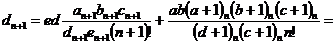
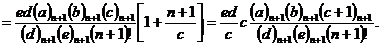
получим

С учетом полученных соотношений (21) и (24) решение (7) примет вид:
 (25)
(25)
Где
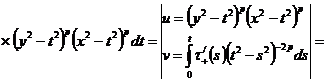
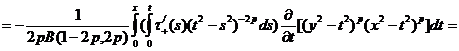
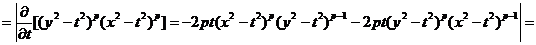
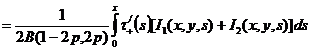 .
.
Внутренние интегралы определяются следующим образом:
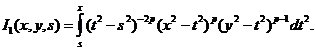
производя
замену 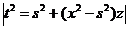 и вычисляя, получим:
и вычисляя, получим:

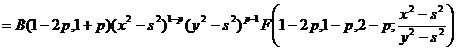 ,
,
Для
второго интеграла поступим аналогично:
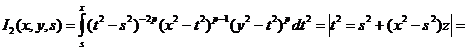
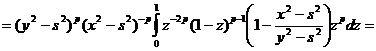
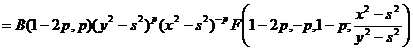 .
.
Тогда
для суммы будем иметь:

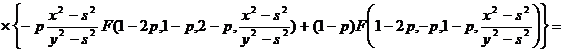
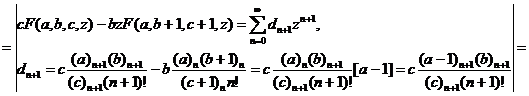
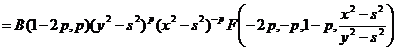 .
.
С
учетом всех сделанных преобразований решение примет вид:
 (26)
(26)
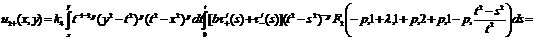
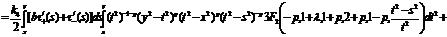
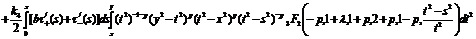 (27)
(27)


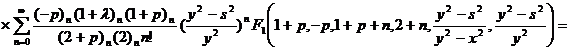
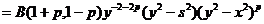 , (28)
, (28)
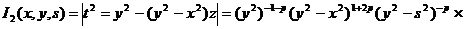

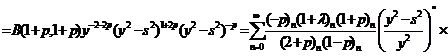
 (29)
(29)
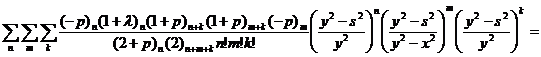
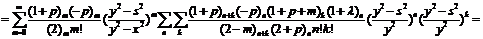
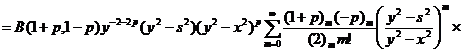
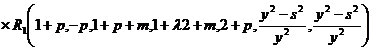 .
.
Теорема.
Если 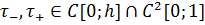 , то существует единственное решение задачи (1)-(5),
которые в области
, то существует единственное решение задачи (1)-(5),
которые в области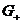 определяется формулами(25)-(29),а в области
определяется формулами(25)-(29),а в области 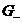 формулами(10),(15),(22),(23),(24).
формулами(10),(15),(22),(23),(24).
Заключение
Материал дипломной работой может вызвать интерес у аспирантов,
занимающихся краевыми задачами для дифференциальных уравнений, а также может
быть использован преподавателями кафедры математического анализа при чтении
студентам спецкурсов “Интегральные уравнения”, “Специальные функции”, “Краевые
задачи”.
Список использованной литературы
1. Бейтмен Г., Эрдейи А. Высшие трансцендентные функции М.:
Наука, 1973. Т. 1. 296 с.
. Берс JI. Математические вопросы дозвуковой и околозвуковой
газовой динамики. М.: ИЛ, 1961, 208 с.
. Вагапов В.З. Краевые задачи для дифференциальных уравнений
с двумя линиями сингулярности коэффициентов: автореферат диссертации на
соискание ученой степени канд. физ.-мат. наук. Самара, 1995, 12 с.
. Векуа И.Н.Обобщенные аналитические функции. М.: Фитматгиз,
1959, 628 с.
. Франкль Ф.И. Избранные труды по газовой динамике. М.:
Наука, 1973, 771с.
. Волкодавов В.Ф., Николаев Н.Я. Интегральные уравнения
Вольтера первого рода с некоторыми специальными функциями в ядрах и их
приложения. Самара: Самарский университет, 1992. -100с.
. Захаров В.Н. Задача Коши для гиперболического уравнения с
двумя линиями вырождения // Матем. моделирование, 1995, т. 7, № 5, с. 55.
. Никифоров А.Ф., Уваров В.Б. Специальные функции
математической физики М.: Интеллект, 2007, 344 с.
. Самко С.Г., Килбас А.А., Маричев О.И. Интегралы и
производные дробного порядка и некоторые их приложения. Минск: Наука и техника,
1987, 315 с.
. Смирнов М.М. Уравнения смешанного типа, ФМЛ, «Наука», 1970,
296 с.
. Франкль Ф.И. Избранные труды по газовой динамике. М.:
Наука, 1973, 771с.