Основы цифровой обработки сигналов
Основы цифровой обработки сигналов
ВВЕДЕНИЕ
цифровой сигнал спектральный
Системой счисления называют систему приемов и правил, которые позволяют
устанавливать взаимно однозначное соответствие между любым числом и его
представлением в виде совокупности конечного числа символов. Системы счисления
делятся на непозиционные и позиционные. В непозиционной системе значение
каждого символа постоянно, где бы символ ни находился в числе (например,
римская система).В позиционной системе значение каждого символа зависит от
места в числе, где записан этот символ (например, арабская система).
Из позиционных систем счисления широко распространена десятичная система,
которая используется в нашей повседневной жизни. Для мира цифровой техники
наибольший интерес представляет двоичная система. Цифровые устройства
используют элементы, которые имеют только два устойчивых состояния, поэтому для
представления и обработки информации удобно применение именно данной системы
счисления.
При работе с цифровыми устройствами гораздо удобнее работать со
спектрами, то есть в частотной области. Это позволяет упростить оборудование и
сократить время обработки сигнала. Переход из временной области в частотную
осуществляют с помощью прямого преобразования Фурье. Оно является взаимно-однозначным,
поэтому представление сигнала в частотной области (спектр) содержит ровно
столько же информации, сколько и исходный сигнал, заданный во временной
области.
1 ЗАДАЧА 1. СИСТЕМЫ СЧИСЛЕНИЯ
1.1 Условие задачи 1. Исходные данные
Провести следующие операции с числом, образованным номером зачетной
книжки:
а) перевести в двоичную систему;
б) перевести в восьмеричную систему;
б) перевести в шестнадцатеричную систему;
в) перевести в десятичную систему числа, полученные в двоичной системе,
восьмеричной системе, шестнадцатеричной системе, то есть сделать обратное
преобразование.
1.2 Выполнение задания 1
При прямом преобразовании производят последовательное деление десятичного
числа и образующихся частных на основание системы счисления до тех пор, пока
остаток от деления не будет меньше основы системы. Полученные при делении
остатки образуют цифры всех разрядов числа, представленного в нужной системе
счисления. Число в новой системе записывается в виде остатков от деления,
начиная с последнего остатка справа налево.
1.2.1 Перевод в двоичную систему счисления
10317210 /2=51586 (0)
/2=25793 (0)
/2=12896 (1)
/2=6448 (0)
/2=3224 (0)
/2=1612 (0)
/2=806 (0)
/2=403 (0)
/2=201 (1)
/2=100 (1)
/2=50 (0)
/2=25 (0)
/2=12 (1)
/2=6 (0)
/2=3 (0)
/2=1 (1)
=110010011000001002
1.2.2 Перевод в восьмеричную систему счисления

.2.3 Перевод в шестнадцатеричную систему счисления

1.2.4 Обратное преобразование
При обратном преобразовании числа в рассматриваемых системах счисления
представляют собой последовательность цифр (цифр разрядов):
…а2 а1 а0
В этой записи а0, а1, … обозначают цифры нулевого, первого и т. д.
разрядов числа. Цифре разряда приписан вес pk, где p -
основание системы счисления, k -
номер разряда, равный индексу при обозначениях цифр разрядов. Приведенная выше
запись означает следующее количество:
N = …
+ a2 ·p2 + a1 ·p1 + a0 ·p0
(1.1)
а) перевод из двоичной системы счисления:
Используем формулу (1.1):
=1*216 + 1*215 + 1*212+ 1*29+ 1*28+ 1*22 = 10317210
б) перевод из восьмеричной системы счисления:
Используем формулу (1.1):
N =
3*85 + 1*84 + 1*83 + 4*82 + 0*81+4*80 =98304+4096+512+256+4=10317210
в) перевод из шестнадцатеричной системы счисления:
Используем формулу (1.1):
N =
1·164 + 9·163 + 3·162 + 0·161 +4= 65536 + 36864 + 768 +4 = 10317210
2. ЗАДАЧА 2. СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ
2.1 Условие задачи 2. Исходные данные
Задан импульс. Требуется:
а) записать математическую модель (формулу), соответствующую импульсу,
согласно варианту;
б) определить спектральную плотность импульса, заданного в таблице,
согласно варианту;
в) построить АЧХ и ФЧХ спектральной плотности при заданной длительности
импульса, амплитуде и других параметрах;
г) используя полученные графики, построить АЧХ и ФЧХ для импульса вдвое
меньшей длительности. Отобразить на графиках влияние задержки импульса на время
τи;
д) дискретизовать заданный сигнал с шагом Т;
е) записать математическую модель (формулу) дискретизованного сигнала;
ж) найти спектральную плотность дискретизованного сигнала;
з) построить амплитудный спектр дискретизованного сигнала;
и) расчет спектральной плотности импульса и построение АЧХ и ФЧХ импульса
и амплитудного спектра дискретизованного сигнала произвести на ЭВМ.
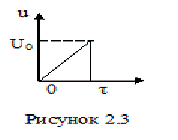
Рисунок
2.1- Вид импульса
Исходные
данные:
Вид
импульса приведен на рисунке 1.
Длительность импульса τи=4 мкс,
α=4 рад/с,
Шаг дискретизации T=0,25
мкс
.2 Выполнение задания 2
2.2.1 Математическая модель импульса
Заданный импульс описывается формулой:
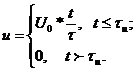 (2.1)
(2.1)
Подставив
значения в (2.1), получим:
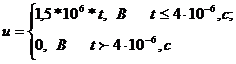
2.2.2 Спектральная плотность импульса
Для определения спектральной плотности импульса воспользуемся прямым
преобразованием Фурье (2.27)[3]:
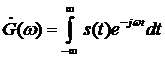
Подставим сигнал (2.1)
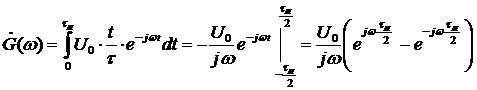 (2.2)
(2.2)
Теперь
воспользуемся формулой Эйлера:
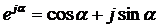 (2.3)
(2.3)
Из
(2.3) нетрудно вывести следующее соотношение:
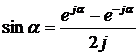 (2.4)
(2.4)
Используем
формулу (2.4) в (2.2):
 (2.5)
(2.5)
Подставим
числовые значения:
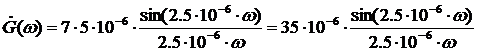
2.2.3 АЧХ и ФЧХ спектральной плотности
График
АЧХ спектральной плотности приведен на рисунке 2. При 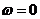
АЧХ
максимальна и численно равна площади импульса. А при 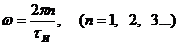 функция
функция  принимает
нулевые значения:
принимает
нулевые значения:
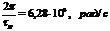 ,
,
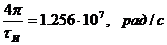 ,
,
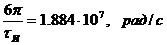
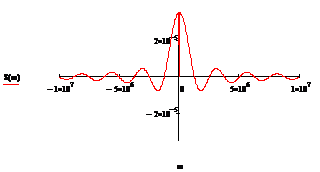
Рисунок
2.2 - АЧХ спектральной плотности импульса

Рисунок 2.3 - ФЧХ спектральной плотности импульса
2.2.4 Влияние задержки и длительности импульса на АЧХ и ФЧХ
спектральной плотности
Изобразим импульс вдвое меньшей длительности:
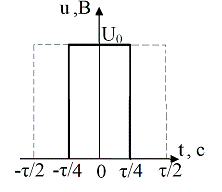
Рисунок 2.4 - Импульс вдвое меньшей длительности
Используем формулу (2.5), получим спектральную плотность импульса вдвое
меньшей длительности:
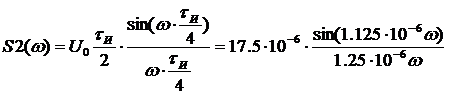
Спектральная
плотность импульса вдвое меньшей длительности:
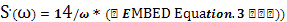
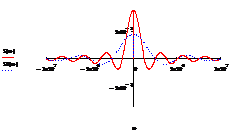
Рисунок
2.4 - АЧХ спектральной плотности импульса вдвое меньшей длительности
(пунктирная линия)
Как
видно из рисунка 2.4, при уменьшении длительности импульса его максимальное
значение F(0) уменьшается, а сам спектр расширяется.
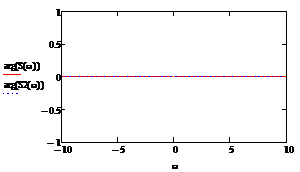
Рисунок
2.5 - ФЧХ спектральной плотности при τ/2
.2.5 Дискретизация сигнала
Количество отсчетов в дискретизованном сигнале:
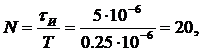 отсчетов
отсчетов
Частота
дискретизации:
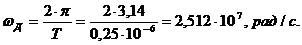
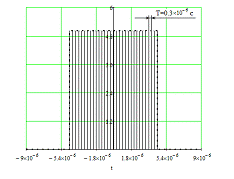
Рисунок
2.6 - Дискретизованный сигнал
2.2.6 Математическая модель дискретизованного сигнала

Дискретизованный импульс описывается формулой:
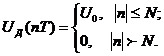
Подставив
значения, получим:
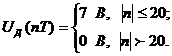
2.2.7 Спектральная плотность дискретизованного сигнала
Спектр
дискретизованного сигнала представляет собой бесконечный ряд сдвинутых между
собой на 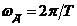 копий спектра исходного непрерывного сигнала u(t).
копий спектра исходного непрерывного сигнала u(t).
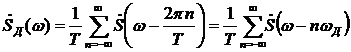
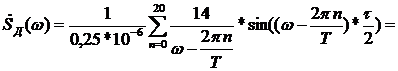
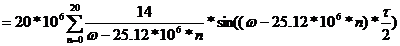
Спектр дискретизованного сигнала представляет собой бесконечный ряд
сдвинутых между собой наωД =2π/Т копий спектра исходного непрерывного
сигнала u(t).
Спектр
расползается по всей шкале частот в обе стороны относительно центральной
частоты 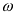 , причем соседние копии спектра расположены
друготносительно друга на длине одной частоты дискретизацииωД.
, причем соседние копии спектра расположены
друготносительно друга на длине одной частоты дискретизацииωД.
Из-за наличия в формуле множителя 1/Т спектр дискретизированного сигнала
имеет размерность, совпадающую с размерностью сигнала.
2.2.8 Амплитудный спектр дискретизованного сигнала
Амплитудный спектр дискретизованного сигнала приведен на рисунке 2.7
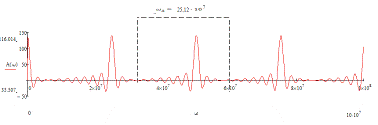
Рисунок 2.7 - Амплитудный спектр дискретизованного сигнала
ЗАКЛЮЧЕНИЕ
По результатам выполнения первого задания видно, что при прямом
преобразовании с увеличением основания новой системы длина записи числа
уменьшается. Самой громоздкой оказывается запись в двоичной системе счисления,
а самой короткой и удобной - шестнадцатеричная система. Обратный же перевод
проще осуществляется при использовании двоичной системы счисления.
В ходе работы была рассчитана спектральная плотность экспоненциального
импульса с помощью формулы прямого преобразования Фурье. По полученным данным
были построены АЧХ и ФЧХ спектральной плотности. Используя полученные графики,
построены аналогичные зависимости для импульса вдвое меньше длительности.
Задержка импульса в данном случае повлияла на АЧХ и ФЧХ сигнала, а именно
периодичность АЧХ и ФЧХ уменьшилась.
Также был построен амплитудный спектр дискретизванного сигнала. Он
идентичен по параметрам спектру непрерывного импульса, но периодичен.
СПИСОК ЛИТЕРАТУРЫ
1. Баскаков С.И. Радиотехнические цепи и сигналы. - М.:
Высшая школа, 2002. - 46.
2. Баскаков С.И. Радиотехнические цепи и сигналы.
Руководство к решению задач. - М.: Высшая школа, 2003.
. Казиева Г.С. Основы цифровой обработки сигналов в
телекоммуникационных системах. Конспект лекций. - Алматы: АИЭС, 2006. - 46 с.
. Казиева Г.С., Богомолова Л.Г. Основы цифровой
обработки сигналов в телекоммуникационных системах. Конспект лекций. - Алматы:
АУЭС, 2011. - 48 с.