|
Авилон
|
М-сервис
|
АвтоХаус
|
Модус
|
Азимут
|
Запасы (машин)
|
|
Дингольфинг
|
7
|
4
|
15
|
9
|
14
|
120
|
|
Регенсбург
|
11
|
2
|
7
|
3
|
10
|
150
|
|
Лейпциг
|
4
|
5
|
12
|
8
|
17
|
100
|
|
Потребности (машин)
|
85
|
65
|
90
|
60
|
70
|
370
|
Содержание
Задача № 1
Задача № 2
1. Перечень сокращений, терминов и их определение
2. Описание используемых методов
2.1 Графический метод
2.2 Симплекс-метод
2.3 Двойственная задача
2.4 Метод потенциалов
3. Решение задачи с помощью нескольких методов
3.1 Решение задачи графическим методом
3.2 Решение задачи симплекс-методом
3.3 Формулировка двойственной задачи
3.4 Моделирование и решение транспортной задачи методом потенциалов
4. Решение симплекс задачи с помощью MS Excel
4.1 Решение двойственной задачи с помощью MS Excel
4.2 Решение транспортной задачи с помощью MS Excel
5. Заключение
6. Список используемой литературы
1. Перечень
сокращений, терминов и их определение
Линейное программирование - это раздел математического
программирования, в котором рассматриваются методы решения элементарных задач с
линейным функционалом и линейными ограничениями, которым должны удовлетворять
искомые переменные.
Система ограничений - называют совокупность уравнений и
неравенств, описывающих ограниченность ресурсов в рассматриваемой задаче.
Целевая функция - функцию переменных задач, которая
характеризует качество выполнения задачи, и экстремум которой требуется найти.
Оптимальное решение - допустимое решение (план) задачи, при
котором целевая функция достигает экстремума.
Каноническая форма - это когда все ограничения являются
уравнениями и все переменные удовлетворяют условию неотрицательности.
ЛП - линейное программирование
Дз - двойственная задачи.
2. Описание
используемых методов
2.1
Графический метод
Графический метод решения задачи линейного программирования - основан на геометрической интерпретации
задачи линейного программирования и применяется в основном при решении задач
двумерного пространства
<#"771270.files/image002.gif">
при ограничениях вида

и
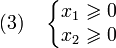
линейное программирование потенциал моделирование
Линейная функция
<#"771270.files/image006.gif"> является уравнением прямой линии <#"771270.files/image007.gif">.
 <#"771270.files/image009.gif">. Тогда поставленной задаче линейного
программирования можно дать следующую интерпретацию
<#"771270.files/image007.gif"> опорная
<#"771270.files/image006.gif"> при этом достигает минимума.
<#"771270.files/image009.gif">. Тогда поставленной задаче линейного
программирования можно дать следующую интерпретацию
<#"771270.files/image007.gif"> опорная
<#"771270.files/image006.gif"> при этом достигает минимума.
Значения  уменьшаются в направлении вектора
<#"771270.files/image011.gif">, поэтому прямую
уменьшаются в направлении вектора
<#"771270.files/image011.gif">, поэтому прямую  передвигаем параллельно самой себе в
направлении вектора
передвигаем параллельно самой себе в
направлении вектора  .
.
Если многоугольник
<#"771270.files/image013.gif"> и  ), причём минимальное значение принимает в
точке
), причём минимальное значение принимает в
точке  . Координаты точки
. Координаты точки  находим, решая систему уравнений
<#"771270.files/image016.gif"> и
находим, решая систему уравнений
<#"771270.files/image016.gif"> и  .
.
Если же многоугольник решений представляет собой неограниченную
многоугольную область, то возможны два случая.
Случай 1. Прямая
 , передвигаясь в направлении вектора
, передвигаясь в направлении вектора  или противоположно ему, постоянно
пересекает многоугольник
<#"771270.files/image018.gif">
или противоположно ему, постоянно
пересекает многоугольник
<#"771270.files/image018.gif">
Симплекс-метод основан на теореме, которая называется
фундаментальной теоремой симплекс - метода. Среди оптимальных планов задачи
линейного программирования в канонической форме обязательно есть опорное
решение ее системы ограничений. Если оптимальный план задачи единственен, то он
совпадает с некоторым опорным решением. Различных опорных решений системы
ограничений конечное число. Поэтому решение задачи в канонической форме можно
было бы искать перебором опорных решений и выбором среди них того, для которого
значение F самое большое. Но, во-первых, все опорные решения неизвестны
и их нужно находить, а во-вторых, в реальных задачах этих решений очень много и
прямой перебор вряд ли возможен. Симплекс - метод представляет собой некоторую
процедуру направленного перебора опорных решений. Исходя из некоторого,
найденного заранее опорного решения по определенному алгоритму симплекс -
метода мы подсчитываем новое опорное решение, на котором значение целевой
функции F не меньше, чем на старом. После ряда шагов мы приходим к опорному
решению, которое является оптимальных планом.
Имея систему ограничений, приведенную к общему виду, то есть
к системе m
линейных уравнений с n переменными (m < n), находят любое базисное
решение этой системы, заботясь только о том, чтобы найти его как можно проще.
Если первое же найденное базисное решение оказалось допустимым, то проверяют
его на оптимальное. Если оно не оптимальное, то, осуществляется переход к
другому, обязательно допустимому базисному решению.
Если первое найденное базисное решение окажется недопустимым,
то с помощью симплексного метода осуществляется переход к другим базисным
решениям, которые приближают нас к области допустимых решений, пока на каком-то
шаге решения базисное решение окажется допустимым и к нему применяют алгоритм
симплексного метода, либо мы убеждаемся в противоречивости системы ограничений.
Таким образом, применение симплексного метода распадается на
два этапа: нахождение допустимого базисного решения системы ограничений или
установление факта ее несовместимости. При этом каждый этап может включать
несколько шагов, соответствующих тому или иному базисному решению. Но так как
число базисных решений всегда ограниченно, то угнетенно и число шагов
симплексного метода.
Не останавливаясь подробнее на сути алгоритма, опишем его
вычислительную сторону. Вычисления по симплекс - методу организуются в виде
симплекс - таблиц, которые являются сокращенной записью задачи линейного
программирования в канонической форме.
Порядок работы с симплекс таблицей:
Первая симплекс - таблица подвергается преобразованию, суть
которого заключается в переходе к новому опорному решению.
Алгоритм перехода к следующей таблице такой:
1) Просматривается последняя строка (индексная) таблицы и
среди коэффициентов этой строки (исключая столбец свободных членов) выбирается
наименьшее отрицательное число при отыскании max, либо наибольшее
положительное при задачи на min. Если такого нет, то исходное базисное решение
является оптимальным, и данная таблица является последней;
) Просматривается столбец таблицы, отвечающий выбранному
отрицательному (положительному) коэффициенту в последней строке-ключевой
столбец, и в этом столбце выбираются положительные коэффициенты. Если таковых
нет, то целевая функция не ограниченна на области допустимых значений
переменных, и задача решений не имеет;
) Среди выбранных коэффициентов столбца выбирается тот, для
которого абсолютная величина отношения соответствующего свободного члена
(находящегося в столбце свободных членов) к этому элементу минимальна. Этот коэффициент
называется разрешающим, а строка в которой он находится ключевой.
) В дальнейшем базисная переменная, отвечающая строке
разрешающего элемента, должна быть переведена в разряд свободных, а свободная
переменная отвечающая столбцу разрешающего элемента, вводится в число базисных.
Строится новая таблица, содержащая новые названия базисных переменных;
) Строка размещающего элемента делится на этот
элемент и полученная строка записывается в новую таблицу на то же место;
6) Столбец размещающего элемента делится на
этот элемент и полученный столбей записывается в новую таблицу на то же
место с противоположным знаком;
7) В остальные клетки новой таблицы
записывается результат преобразования элементов старой
таблицы. (рис.2)

Рисунок 2 Формула вычисления новых элементов.
Элемент ▲ находится в разрешающей строке в одном столбце со
старым элементом; элемент ▼ находится в разрешающем столбце в одной
строке со старым элементом.
В результате получают новую симплекс - таблицу, отвечающую новому
базисному решению.
Теперь следует просмотреть строку целевой функции, если в
ней нет отрицательных значений (в задачи на нахождение максимального значения),
либо положительных (в задачи на нахождение минимального значения) кроме
стоячего на месте (свободного столбца), то значит, что оптимальное
решение получено. В противном случае, переходим к новой симплекс
таблице по выше описанному алгоритму.
2.3
Двойственная задача
Каждой задаче линейного программирования можно сопоставить
определённым образом с ней связанную другую задачу, которая называется
двойственной по отношению к первой. Первоначальная задача называется исходной.
Вместе взятые задачи образуют пару взаимно - двойственных задач. Связь исходной
и двойственной задач заключается главным образом в том, что решение одной из
них может быть получено непосредственно из решения другой. Совместное
рассмотрение таких пар двойственных задач оказывается весьма эффективным
средством теоретического исследования проблем линейного программирования и
построения различных вычислительных методов. Кроме того, рассмотрение
двойственных задач играет большую роль при экономическом анализе результатов
расчета.
Двойственная задача - одно из фундаментальных понятий теории линейного
программирования; инструмент, позволяющий установить, оптимально ли данное допустимое
решение задачи ЛП, без непосредственного сравнения его со всеми остальными
допустимыми решениями.
К каждой задаче ЛП можно построить своего рода симметричную: функционалы
оптимальных решений у обеих задач совпадают, но если в прямой задаче они
отражают наиболее эффективную комбинацию ресурсов, которая дает максимум
целевой функции, то в другой, двойственной - наиболее эффективную
комбинацию расчетных цен (оценок) ограниченных ресурсов. Это такие цены, при
которых полученная продукция оправдывает затраты, а технологические
способы, не включенные в план, по меньшей мере не более рентабельны,
чем примененные. (Впрочем, хотя и принято считать прямой задачу,
ориентированную на максимум целевой функции, а двойственной - ориентированную
на минимум на самом деле эти обозначений условны: обе задачи абсолютно
равноправны, любую можно принять за прямую и искать к ней двойственную.)
Д. з состоит в минимизации затрат при заданных лимитах
ресурсов и формулируется следующим образом
Найти набор переменных v1, v2,…vn (называемых размещающими
множителями, объективно обусловленными (оптимальными) оценками, двойственными
ценами и т.п.), минимизирующих линейную функцию
2.4 Метод
потенциалов
Метод потенциалов - является модификацией симплекс-метода
<#"771270.files/image020.gif"> - пункты производства/потребления,  - дуги
<#"771270.files/image021.gif"> - цены провоза по дугам
- дуги
<#"771270.files/image021.gif"> - цены провоза по дугам  ,
,  - набор базисных столбцов.
- набор базисных столбцов.
Задача формулируется как найти  при условиях
при условиях  , где
, где  - стоимости провоза по дугам,
- стоимости провоза по дугам,  - производсво (+) / потребление (-)
- производсво (+) / потребление (-)  - решение
- решение
Матрица
<#"771270.files/image027.gif">, содержащих всего два ненулевых элемента
- +1 для производителя и −1 для потребителя.
Алгоритм
Метод потенциалов является модификацией симплекс-метода, в котором
базисная матрица  представлена в виде дерева
<#"771270.files/image029.gif"> вычисляются по формуле
представлена в виде дерева
<#"771270.files/image029.gif"> вычисляются по формуле  , что эквивалентно
, что эквивалентно 
Для дуги
<#"771270.files/image032.gif"> потенциалы дуг связаны формулой  .
.
Таким образом, потенциал потребителя равна потенциалу
производителя + стоимость перевозки. С экономической точки зрения это можно
трактовать как стоимость продукта в точке потребления.
Проверка оптимальности плана  легко трактуется с экономической точки зрения - если стоимость
продукта в точке потребления больше стоимости в точке производства + цена
перевоза, по этой дуге следует везти. Величина
легко трактуется с экономической точки зрения - если стоимость
продукта в точке потребления больше стоимости в точке производства + цена
перевоза, по этой дуге следует везти. Величина  называется невязкой дуги.
называется невязкой дуги.
Добавление дуги приводит к возникновению цикла в дереве.
Увеличение провоза по вводимой дуге приводит к пересчету потоков в цикле,
провоз по одной из дуг при этом уменьшится до нуля. Дугу с нулевым потоком
удаляем из базиса, при этом базисный граф остается деревом (цикл разрывается).
Остается только пересчитать потенциалы - добавить (или вычесть -
зависит от направления дуги) ко всем вершинам "повисшей ветки"
величину невязки 
Процесс завершается, когда условие оптимальности  выполняется для всех дуг.
выполняется для всех дуг.
3. Решение
задачи с помощью нескольких методов
3.1 Решение
задачи графическим методом
) Необходимо найти максимальное значение целевой функции F =
34x1+50x2 → max, при ограничениях:
F=34*X1+50*X2 =>max

) Построим прямую 2x1+5x2 = 432 по двум
точкам. Для нахождения первой точки приравниваем x1 = 16. Находим x2
= 80. Для нахождения второй точки приравниваем x2 = 0. Находим x1
= 216. Соединяем точку (16; 80) с (216; 0) прямой линией. Построим прямую 3x1+4x2
= 424 по двум точкам. Для нахождения первой точки приравниваем x1 =
141. Находим x2 = 0. Для нахождения второй точки приравниваем x2
= 8. Находим x1 = 100. Соединяем точку (141; 0) с (8; 100) прямой
линией. Построим прямую 5x1+3x2 = 532 по двум точкам. Для
нахождения первой точки приравниваем x1 = 44. Находим x2
= 104. Для нахождения второй точки приравниваем x2 = 104. Находим x1
= 4. Соединяем точку (44; 104) с (104;
) прямой линией.
|
1
|
X1
|
16
|
216
|
|
|
X2
|
80
|
0
|
|
2
|
X1
|
141
|
8
|
|
|
X2
|
0
|
100
|
|
3
|
X1
|
44
|
104
|
|
|
X2
|
4
|

Рисунок 3 Вектор-градиент
3) Рассмотрим целевую функцию задачи F = 34x1+50x2
→ max.
Вектор-градиент, составленный из коэффициентов целевой
функции, указывает направление максимизации F (X). Начало вектора - точка (0;
0), конец - точка (34; 50). Будем двигать прямую, перпендикулярную вектору,
параллельным образом. Поскольку нас интересует максимальное решение, поэтому
двигаем прямую до последнего касания обозначенной области.
4) Область допустимых решений представляет собой многоугольник
Прямая F (x) = const пересекает область в точке C. Так
как точка C получена в результате пересечения прямых (1) и (2),
то ее координаты удовлетворяют уравнениям этих прямых:

Решив систему уравнений, получим: x1 = 56, x2
= 64 Откуда найдем максимальное значение целевой функции:
(X) = 34*56 + 50*64 = 5104
3.2 Решение
задачи симплекс-методом
Пошаговое описание решения задачи:
1) По данным таблицы из пункта 1 составляем
математическую модель:
F=34*X1+50*X2 =>max

) Приводим модель к каноническому виду:

Базисные переменные входят в целую функцию, а свободные -
нет.
Базисные переменные: Х1, Х2. Свободные переменные: Х3, Х4,
Х5.
3) Выразим свободные переменные через базисные.

) Составим симплекс - таблицу:
|
-Х1
|
-Х2
|
b
|
|
X3
|
2
|
5
|
432
|
|
X4
|
3
|
4
|
424
|
|
X5
|
5
|
3
|
532
|
|
F
|
-34
|
-50
|
|
Столбец свободных членов не содержит отрицательных чисел, но
отрицательные коэффициенты есть в индексной строке.
5) Определение новой базисной переменной: В качестве ведущего
выберем столбец, соответствующий переменной x2, так как в индексной
строке это наибольший коэффициент по модулю.
6) Определение новой свободной переменной:
Вычислим значения Di по строкам как частное от
деления: bi / ai2 и из них выберем наименьшее: min (432:
5, 424: 4, 532: 3) = 862/5 Следовательно, 1-ая строка
является ведущей. Разрешающий элемент равен (5) и находится на пересечении
ведущего столбца и ведущей строки.
7) Преобразуем таблицу по правилу прямоугольника:
) а12=1/5;
) а22=4/ (-5), а32=3/ (-5), а42= (-50) / (-5);
) а11=2/5, а13=432/5;
) а21= (3*5-2*4) /5, а31= (5*5-2*3) /5, а41= (-34*5-2* (-50))
/5, а23= (424*5-432*4) /5, а33= (532*5-432*3) /5, а43= (0*5-432* (-50)) /5.
|
-X1
|
-X3
|
b
|
|
X2
|
2/5
|
1/5
|
432/5
|
|
X4
|
7/5
|
-4/5
|
392/5
|
|
X5
|
19/5
|
-3/5
|
1364/5
|
|
F
|
-14
|
10
|
4320
|
Последний столбец не содержит отрицательных чисел, но
отрицательное число есть в нижней строке, выбираем
min ( ( (432/5) / (2/5)); ( (392/5) / (7/5)); (
(1364/5) (19/5))) = 7/5
) Далее применяем операцию пока не получаем в индексной
строке F
и столбце свободных членов b положительные значения:
|
-X4
|
b
|
|
X2
|
-2/7
|
3/7
|
64
|
|
X1
|
5/7
|
-4/7
|
56
|
|
X5
|
-19/7
|
11/7
|
60
|
|
F
|
10
|
2
|
5104
|
) Из последней таблицы получаем ответ:
X1 = 56; X2 = 64; F = 5104.
3.3
Формулировка двойственной задачи
) Исходная модель:
F=34*X1+50*X2 =>max

2) Составим Матрицу задачи:
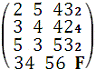
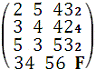 F - Коэффициент
целевой функции.
F - Коэффициент
целевой функции.
) Транспонируем эту матрицу:
At = 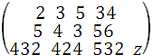
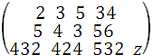
В последней строке находятся коэффициенты целевой функции Z, т.к.,
F=>max, Z=>min. X1 и X2 >=0 поэтому первое и второе
ограничение
Двойственной задачи будут в виде неравенств.
4) Получаем двойственную задачу:
Z = 432 * Y1 + 424 * Y2 + 532 * Y3 =>min

3.4
Моделирование и решение транспортной задачи методом потенциалов
) Стоимость доставки единицы груза из каждого
пункта отправления в соответствующие пункты назначения задана матрицей тарифов.
Проверим необходимое и достаточное условие разрешимости
задачи.
∑a = 120 + 150 + 100 = 370
∑b = 85 + 65 + 90 + 60 + 70 = 370
Условие баланса соблюдается. Запасы равны потребностям.
Следовательно, модель транспортной задачи является закрытой.
Занесем исходные данные в распределительную таблицу.
|
7
|
4
|
15
|
9
|
14
|
120
|
|
11
|
2
|
7
|
3
|
10
|
150
|
|
4
|
5
|
12
|
8
|
17
|
100
|
|
85
|
65
|
90
|
60
|
70
|
370
|
) Проверим оптимальность опорного плана. Найдем потенциалы
ui, vi. по занятым клеткам таблицы, в которых ui
+ vi = cij, полагая, что u1 = 0.
|
7
|
10
|
15
|
11
|
14
|
|
0 (0)
|
0 (6)
|
50
|
0 (2)
|
70
|
120
|
|
-8
|
0 (-12)
|
65
|
25
|
60
|
0 (-4)
|
150
|
|
-3
|
85
|
0 (2)
|
15
|
0 (0)
|
0 (-6)
|
100
|
|
|
85
|
65
|
90
|
60
|
70
|
|
Опорный план не является оптимальным, так как существуют
оценки свободных клеток, для которых ui + vi > 0 max
(6,2,2) = 6.
. Выбирается клетка с наибольшей оценкой (в этом случае: 6);
. От выбранного элемента строится кратчайший прямоугольный
замкнутый контур (а12ðа13ðа23ðа22) Остальные вершины
замкнутого контура кроме первой проходят через заполненные элементы опорного
плана перевозок. Поворот осуществляется только на 90 градусов и только в
заполненных элементах.
. Каждому коэффициенту в вершинах контура строго поочередно
присваивается знак плюс или минус, начиная с пустой клетки: (а13 и а22 будут со
знаком "минус", а а12 и а23 со знаком "плюс").
. Выбираем меньшее по модулю отрицательное значение (в данном
случае 50). Выполняется алгебраическое суммирование по всему контуру:
)
|
149514
|
|
|
|
|
|
|
|
0
|
0 (-6)
|
50
|
0 (-6)
|
0 (-4)
|
70
|
120
|
|
-2
|
0 (-12)
|
15
|
75
|
60
|
0 (2)
|
150
|
|
3
|
85
|
0 (2)
|
15
|
0 (0)
|
0 (0)
|
100
|
|
|
85
|
65
|
90
|
60
|
70
|
|
Проверим оптимальность опорного плана. Найдем потенциалы
ui, vi. по занятым клеткам таблицы, в которых ui
+ vi = cij, полагая, что u1 = 0.
Находим оценки свободных клеток по формуле: ui + vi
- cij;
Опорный план не является оптимальным, так как существуют
оценки свободных клеток, для которых ui + vi - cij
> 0 выполняем перераспределение аналогично предыдущему пункту
)
|
5411714
|
|
|
|
|
|
|
|
0
|
0 (-2)
|
65
|
0 (-2)
|
55
|
120
|
|
-4
|
0 (-12)
|
0 (-2)
|
75
|
60
|
15
|
150
|
|
-1
|
85
|
0 (-2)
|
15
|
0 (-2)
|
0 (-4)
|
100
|
|
|
85
|
65
|
90
|
60
|
70
|
|
Проверим оптимальность опорного плана. Найдем потенциалы
ui, vi. по занятым клеткам таблицы, в которых ui
+ vi = cij, полагая, что u1 = 0.
Опорный план является оптимальным, так все оценки свободных
клеток удовлетворяют условию ui + vi - cij
<= 0
Минимальные затраты составят:
(x) = 4*65 + 14*55 + 7*75 + 3*60 + 10*15 + 4*85 + 12*15 =
2405.
4. Решение
симплекс задачи с помощью MS Excel
1) Запускаем MS Excel. (Пуск - Все программы - MO - Excel 2013).
) Решим данную задачу с помощью команды Данные, Поиск
решения.
Средство поиска решений является одной из надстроек Excel. Если в меню "данные"
отсутствует команда "Поиск решения", то для её установки
необходимо выполнить команду "Надстройка панели быстрого доступа",
"Другие команды", "Надстройки", "Поиск решения".
3) Отведём ячейки A3, B3,C3 под значения перечеренных
Х1-3.
В ячейку C4 введем функцию цели: = 34*А3+ 50 * В3.
В ячейки А7; А9 введём левые части ограничений: =2*А3+5*В3,=3*А3+4*В3,=5*А3+3*В3,
а в ячейки В7; В9 - правые части огничений.
|
переменные
|
|
x1
|
x2
|
|
|
|
|
F (x)
|
0
|
|
ограничения
|
|
0
|
432
|
|
0
|
424
|
|
0
|
532
|
) После этого выберем команду "Данные", "Поиск
решения" и заполним открывшееся диалоговое окно "Поиск решения".

Рисунок 4. Форма поиска решения
) Результаты задачи:
|
переменные
|
|
x1
|
x2
|
|
56
|
64
|
|
F (x)
|
5104
|
|
ограничения
|
|
432
|
432
|
|
424
|
424
|
|
472
|
532
|
4.1 Решение
двойственной задачи с помощью MS Excel
1) Запускаем MS Excel.
) Далее алгоритм решения двойственной задачи будет аналогичен
алгоритму решения симплекс методом.
) Далее идут измененные рисунке 9. т, к некоторые пункты
отличаются:
|
переменные
|
Y2
|
Y3
|
|
|
|
|
|
|
|
Функция цели
|
0
|
|
|
|
|
|
Ограничение
|
|
|
|
|
34
|
|
|
|
|
50
|
|
|

Рисунок 5 Форма поиска решения
|
переменные
|
|
|
Y1
|
Y2
|
Y3
|
|
|
2
|
10
|
0
|
|
|
Функция цели
|
5104
|
|
|
|
|
|
Ограничение
|
|
|
|
34
|
34
|
|
|
|
50
|
50
|
|
|
4.2 Решение
транспортной задачи с помощью MS Excel
1) Запускаем MS Excel.

Рисунок 6 Условия задачи для поиска решений.
) Далее мы создаём аналог таблицы поставленной задачи, а так
же таблицу найденного решения.
)

Рисунок 7 Форма поиска решения.
4) Получаем ответ:

Рисунок 8 Результат поиска решений.
5. Заключение
Целью данного курсового проекта было - составить план
производства требуемых изделий, обеспечивающий максимальную прибыль от их
реализации, свести данную задачу к задаче линейного программирования, решить её
симплекс - методом, методом двойственной задачи и методом потенциалов
(транспортная задача). В ходе выполнения работы данная цель была полностью
выполнена. Симплекс задача и двойственная задача, взаимозаменяемые задачи,
иначе говоря, для проверки одной можно использовать другую.
В данной работе было наглядно рассмотрено решение задач с
помощью MS Excel.
Данные задачи используются в разных областях, например, в
математике или экономике. Следовательно, можно сделать вывод, что данная
курсовая работа может служить наглядным образцом для решения подобных задач.
6. Список
используемой литературы
1.
Аттеков А.В. Галкин С.В. Зарубин В.С. Методы оптимизации: Учебник для вызов /
Под. Ред.В.С. Зарубина, А.П. Крищенко. - 2-е изд., Стереотип. - М. Изд - во
МГТУ им. Н.Э. Баумана, 2033
.
Пинегина М.В. Математические методы и модели в экономике: Учеб. Пособие для
студентов вузов экономических специальностей. - М: Издательство
"Экзамен", 2004.
.
Краев М.С., Чупрынов Б.П. Основы математики и её приложения в экономическом
образовании: Учебник. - 2-е изд., испр. - М.: Дело, 2003.
.
Ларионов А.И., Новоселов А.Л., Юрченко Т.И. Экономико - математические методы в
планировании: Учеб. Для сред. Спец. Заведений. - 2-е изд, перераб, И доп. - М.:
Высш. шк. 1991.
.
Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб.
Пособие. - 3-е изд. - М.: Дело, 2004