Решение задач с использованием производных
Задание 1
функция производные экстремум
Исследовать функцию на непрерывность:
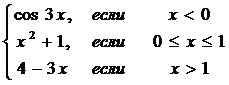
Решение
Функция f(x) -
непрерывна в т х = а, если соблюдаются следующие условия:
при х = а функция f(x) имеет
определенное значение b;
при х → а функция имеет
предел, тоже равный b;
При нарушении хотябы одного из этих
условий функция называется разрывной в т х = а.

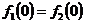 - значит в т х = 0 функция
непрерывна.
- значит в т х = 0 функция
непрерывна.
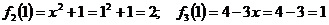
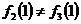 - значит в т х = 1 функция имеет
разрыв.
- значит в т х = 1 функция имеет
разрыв.
Покажем это на графике:
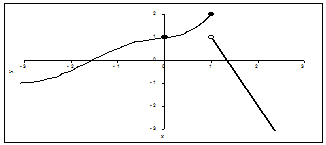
Задание 2
Найти производные функций:

Решение
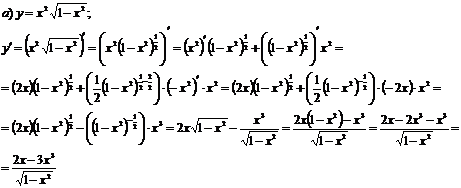
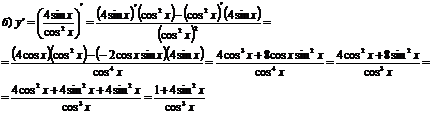
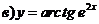
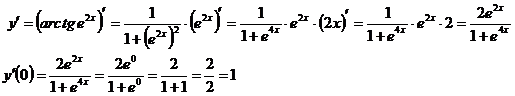
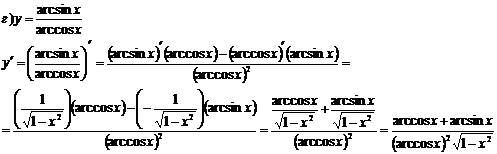
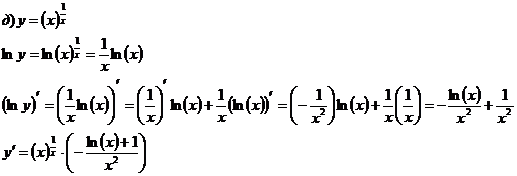
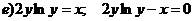
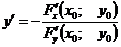

Задание 3
Найти производные первого и второго порядков
функций

Решение
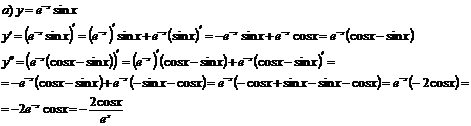
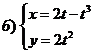
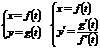
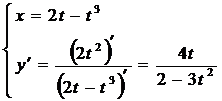

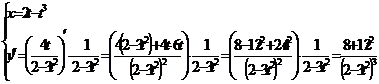
Задание 4
Материальная точка движется
прямолинейно по закону  . Найти
скорость и ускорение в момент времени t = 3c. (S - выражено
в метрах).
. Найти
скорость и ускорение в момент времени t = 3c. (S - выражено
в метрах).
Решение
Найдем скорость:
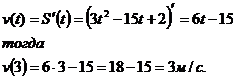
Найдем ускорение
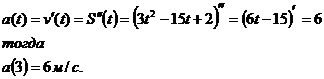
Ответ:  ,
, 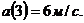
Задание 5
Найти экстремальные значения функции.
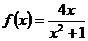
Решение
Исследуем функцию на наличие точек
экстремума (точек максимума и минимума).
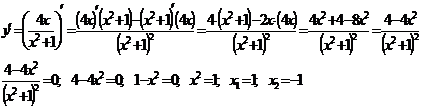
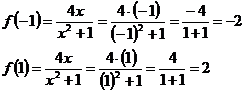
(-1; -2) и (1; 2) - точки
подозрительные на экстремум.
Рассчитаем значение производной
справа и слева от критической точки.

Значит на промежутке (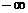 ;-1) и (1;
;-1) и (1; 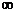 ) функция
убывает, на промежутке [-1; 1] функция возрастает.
) функция
убывает, на промежутке [-1; 1] функция возрастает.
Занесем для ясности полученные
значения в таблицу:
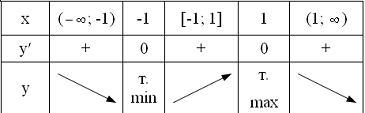
(1; 2) - точка максимума. (-1; -2) -
точка минимума.
Задание 6
Исследовать функции и построить их графики.
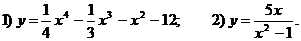
Решение
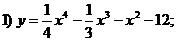
) Область определения:
Функция определена и непрерывна на
всей числовой прямой т.к. f(x) -
многочлен.
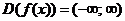
2)Точки пересечения с осями
координат:
С осью ОХ т.е.
у=0: 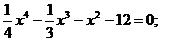
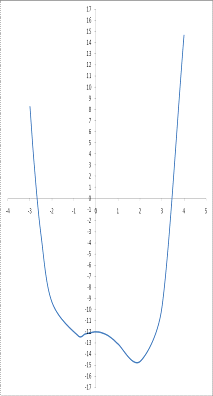
Вычисления сложны, поэтому точку
пересечения с ОХ найдем из графика
С осью ОУ т.е. х=0:
 - точка пересечения с осою ОУ.
- точка пересечения с осою ОУ.
) Исследуем на четность нечетность.
Проверим выполнимость равенств: если f(-x) = f(x), то
функция четная, если f(-x) = -f(x), то
функция нечетная, при х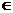 D(y). Если
равенства не выполняются, то функция ни четная ни нечетная.
D(y). Если
равенства не выполняются, то функция ни четная ни нечетная.
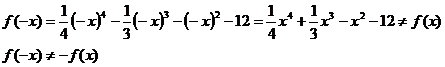
Функция ни четная ни нечетная
)Исследуем на наличие асимптот.
Вертикальных асимптот нет т.к. нет
точек разрыва.
Наклонные асимптоты:
y = kx + b - уравнение
наклонной асимптоты.

тогда

Значит и наклонных асимптот тоже
нет.
)Исследуем функцию на наличие точек
экстремума (точек максимума и минимума), промежутки возрастания и убывания
функции.

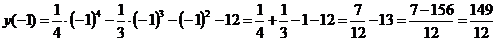
 - точка подозрительная на экстремум.
- точка подозрительная на экстремум.
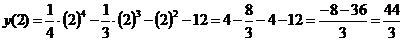
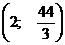 - точка подозрительная на
экстремум.
- точка подозрительная на
экстремум.
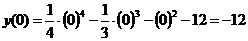
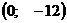 - точка подозрительная на
экстремум.
- точка подозрительная на
экстремум.
Исследуем поведение функции справа и
слева от каждой критической точки
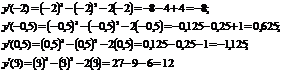
Значит на промежутке (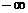 ; -1) [0; 2]
функция убывает, а на промежутке [-1; 0] и (2;
; -1) [0; 2]
функция убывает, а на промежутке [-1; 0] и (2; ) функция возрастает.
) функция возрастает.
Занесем полученные данные в таблицу:
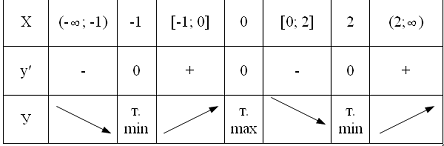
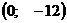 - точка максимума.
- точка максимума.  и
и 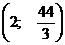 - точки
минимума.
- точки
минимума.
)Исследуем функцию на наличие точек
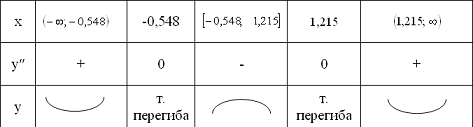
перегиба, промежутки выпуклости и вогнутости функции.
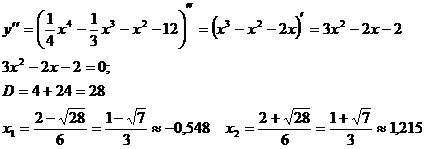

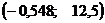 - точка подозрительная на перегиб.
- точка подозрительная на перегиб.
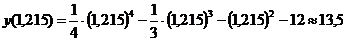
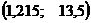 - точка подозрительная на перегиб.
- точка подозрительная на перегиб.

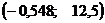 ,
, 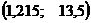 - координата точек перегиба.
- координата точек перегиба.

)Область определения:
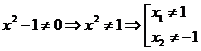 так как на 0 делить нельзя
так как на 0 делить нельзя
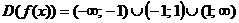
2)Точки пересечения с осями
координат:
С осью ОХ т.е.
у=0: 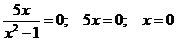
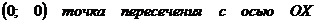
С осью ОУ т.е. х=0: 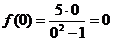
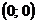 - точка пересечения с осою ОУ.
- точка пересечения с осою ОУ.
) Исследуем на четность нечетность.
Проверим выполнимость равенств: если f(-x) = f(x), то
функция четная, если f(-x) = -f(x), то
функция нечетная, при х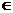 D(y). Если
равенства не выполняются, то функция ни четная ни нечетная.
D(y). Если
равенства не выполняются, то функция ни четная ни нечетная.
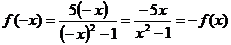
Функция нечетная
)Исследуем на наличие асимптот.
Так как х ≠ -1 и х ≠ 1
то х = -1 и х = 1 вертикальная асимптота.
Наклонные асимптоты:
y = kx + b - уравнение
наклонной асимптоты.
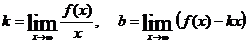
тогда


у = 0 - горизонтальная асимптота
графика функции.
)Исследуем функцию на наличие точек
экстремума (точек максимума и минимума), промежутки возрастания и убывания
функции.

Значит точек экстремума нет
Рассчитаем значение производной
справа и слева от каждой критической точки.
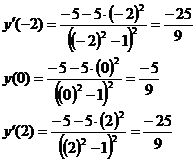
Значит функция убывает на всем
промежутке
)Исследуем функцию на наличие точек
перегиба, промежутки выпуклости и вогнутости функции.
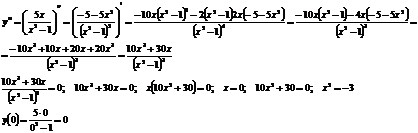
 - точка подозрительная на перегиб.
- точка подозрительная на перегиб.
Исследуем поведение функции справа и
слева от х = -1 и х = 0
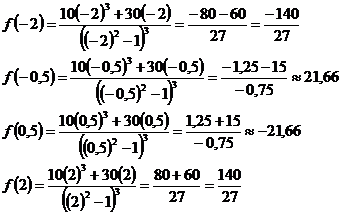
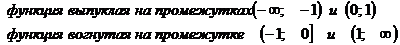
 - координаты точки перегиба.
- координаты точки перегиба.
Список использованной литературы
1.Выгодский М.Я. Справочник по
высшей математике. - М.: АСТ: Астрель, 2006. - 991с.
.Зимина О.В., Кириллов А.И., Сальникова
Т.А. Высшая математика. Под ред. А.И. Кирилова. - 3-е изд., испр. - М.:
ФИЗМАТЛИТ, 2006. - 368с.
.Выгодский М.Я. Справочник по
элементарной математике. - М.: АСТ: Астрель, 2007. - 509с.
.Красс М.С., Чупрыков Б.П.
Математика для экономистов. - СПб.: Питер 2007. - 464с.