Построение треугольника, пирамиды по координатам и использование векторной алгебры
Задание 1
По трем заданным точкам построить треугольник и средствами векторной
алгебры найти:
) длину стороны ВС;
) уравнение линии ВС;
) уравнение высоты, проведенной из точки А;
) длину высоты, проведенной из точки А;
)площадь треугольника АВС;
) угол между сторонами ВА и ВС;
) координаты точки N - середины стороны АС;
) координаты точки М, делящей сторону АВ в отношении 2 : 3, считая от
точки А.
Координаты треугольника: А (-5,3); В (4,6); С (8,4)
Решение:
1. Расстояние d между точками
М1(х1; у1) и М2(х2; у2) определяется по формуле:
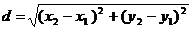
Найдем
длину стороны ВС

.
Уравнение прямой проходящей через точки М1(х1; у1) и М2(х2; у2) имеет вид:

Найдем
уравнение прямой ВС:
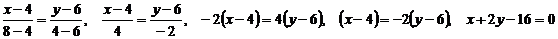
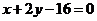 -
уравнение прямой ВС.
-
уравнение прямой ВС.
.Уравнение
высоты, опущенной из вершины А на прямую ВС
Прямая
проходящая через точку М0(х0; у0) и перпендикулярная прямой
Ах
+ Ву + С=0 представляется уравнением
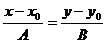
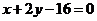 -
уравнение прямой ВС. А (-5,3)
-
уравнение прямой ВС. А (-5,3)
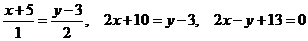 -
уравнение искомой высоты АD.
-
уравнение искомой высоты АD.
.АD.
Расстояние d от точки М1(х1; у1) до прямой Ах+Ву+С=0 определяется
по формуле:


Найдем
длину высоты АD
А(
-5, 3); 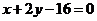 - уравнение прямой ВС
- уравнение прямой ВС
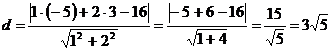
) Площадь треугольника найдем используя
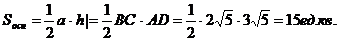
)Косинус
угла между векторами 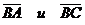 находится по формуле:
находится по формуле:
Косинус
угла α,
образованного векторами 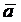 и
и 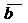 ,равен их
скалярному произведению, деленному на произведение их модулей
,равен их
скалярному произведению, деленному на произведение их модулей
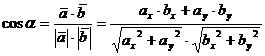
Найдем
координаты векторов 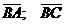
Если
даны точки М1(х1; у1; z1) и М2(х2; у2; z2), то
координаты вектора 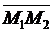 находятся следующим образом:
находятся следующим образом:
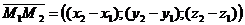
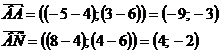
Найдем
угол между векторами  и
и 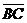
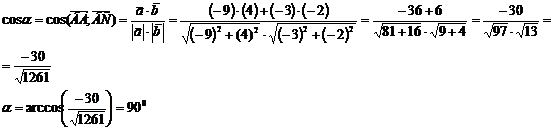
) N
середина АС. Найдем ее координаты по формуле:
А (-5,3); В (4,6); С (8,4)
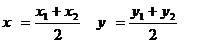

N(1,5; 3,5)
8)координаты точки М, делящей сторону АВ в отношении 2:3, считая от точки
А.
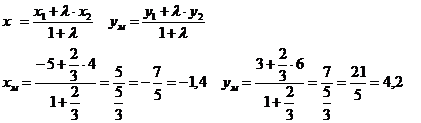
М(-1,4;
4,2)
Сделаем чертеж:

Задание 2
По четырем заданным точкам построить пирамиду и средствами векторной
алгебры найти:
) длину ребра А1А2;
) угол между ребрами А1А2 и А1А4;
) площадь грани А1А2А3;
) объем пирамиды А1А2А3А4;
) составить уравнение прямой А1А2;
) уравнение плоскости А1А2А3.
Координаты пирамиды: А1 (2, -5, 3); А2 (3, 2, -5); А3 (5, 3, 2); А4 (-5,
3, 2)
Решение:
1) Расстояние d между точками
М1(х1; у1; z1) и М2(х2; у2; z2), определяется по формуле:
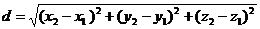
) длину ребра А1А2;
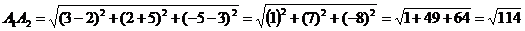
) угол между ребрами А1А2 и А1А4;
косинус
угла между векторами  находится по формуле:
находится по формуле:
Косинус
угла α,
образованного векторами 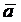 и
и 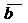 ,равен их
скалярному произведению, деленному на произведение их модулей
,равен их
скалярному произведению, деленному на произведение их модулей
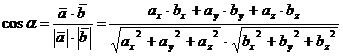
Если
даны точки М1(х1; у1; z1) и М2(х2; у2; z2), то
координаты вектора 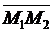 находятся следующим образом:
находятся следующим образом:
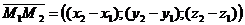
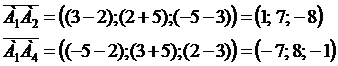
Найдем
угол между векторами 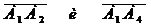
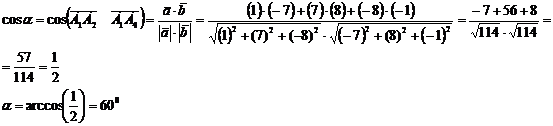
)
площадь грани А1А2А3:
А1
(2, -5, 3); А2 (3, 2, -5); А3 (5, 3, 2); А4 (-5, 3, 2)

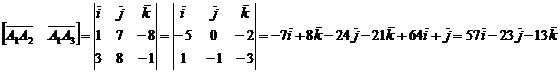
,
то есть вектор векторного произведения имеет координаты (57; -23; -13).
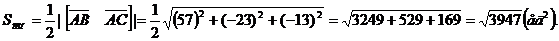
) объем пирамиды А1А2А3А4;
Объем
пирамиды равен 1/6 объема параллелепипеда, построенного на векторах 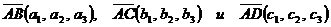 , как на сторонах. Объем параллелепипеда найдем,
используя смешанное произведение векторов:
, как на сторонах. Объем параллелепипеда найдем,
используя смешанное произведение векторов:
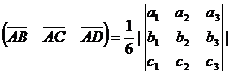
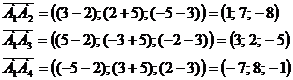
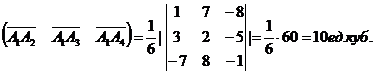
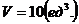
5) составить уравнение прямой А1А2;
Уравнение прямой проходящей через точки М1(х1; у1; z1) и М2(х2; у2; z2), имеет вид:
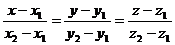
Найдем
уравнение прямой А1А2:
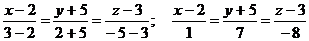
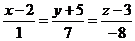 -
уравнение прямой А1А2.
-
уравнение прямой А1А2.
6) уравнение плоскости А1А2А3. Уравнение плоскости проходящей через три
точки М0(х0; у0; z0), М1(х1; у1; z1) и М2(х2; у2; z2), имеет вид:

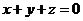 -
уравнение плоскости А1А2А3.
-
уравнение плоскости А1А2А3.

Задание
3
треугольник пирамида уравнение координата
Даны
уравнения линии r = r (ϕ) в полярной системе координат. Требуется:
)построить
линию по точкам на промежутке от ϕ = 0 до ϕ = 2π с шагом, равным π/8;
)
найти уравнение линии в прямоугольной декартовой системе координат, у которой
начало совпадает с полюсом, а положительная полуось абсцисс - с
полярной
осью;
)
назвать линию, найти координаты центра и полуоси.
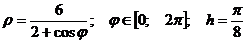
Решение:

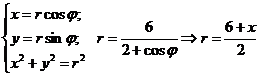

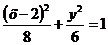 - эллипс
с центром в т(2; 0) малой осью
- эллипс
с центром в т(2; 0) малой осью 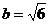 и
большой осью
и
большой осью 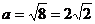
Задание 4
Даны
два комплексных числа 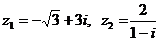 .
.
а) Записать их в тригонометрической форме и отметить полученные числа на
комплексной плоскости;
б) Найти числа z1 + z2, z1 - z2, построить;
в) Найти z1∙z2, z1 / z2, записать в тригонометрической и алгебраической
формах, сравнить результаты;
г) Найти z13;
д) Найти 3√z2,
построить.;
Решение:
Запишем
число 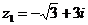 в тригонометрической форме:
в тригонометрической форме:

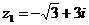

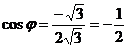
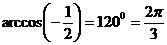
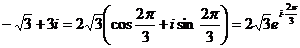

Запишем
число 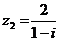 в тригонометрической форме:
в тригонометрической форме:
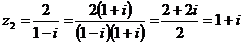
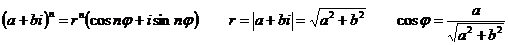
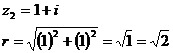
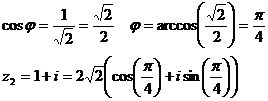

 Сложение
комплексного числа:
Сложение
комплексного числа:


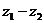 Вычитание
комплексного числа:
Вычитание
комплексного числа:

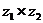 Умножение
комплексного числа:
Умножение
комплексного числа:
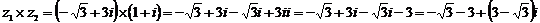
Разделить
комплексное число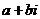 (делимое) на комплексное число
(делимое) на комплексное число 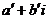 (делитель) - значит найти такое число
(делитель) - значит найти такое число (частное, которое при умножении на делитель даст
делимое.
(частное, которое при умножении на делитель даст
делимое.
На
практике удобно помножить и разделить на сопряженное к знаменателю.
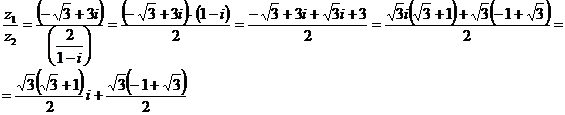
Запишем
число 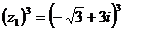 в тригонометрической форме:
в тригонометрической форме:
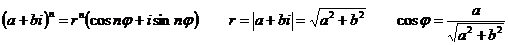
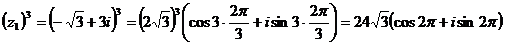
Запишем
число 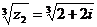 в тригонометрической форме:
в тригонометрической форме:
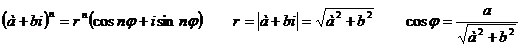
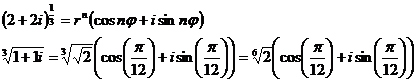
Задание №5
Найти
пределы, не пользуясь правилом Лопиталя
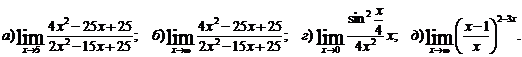
Решение:
а) Вычислим предел подставив в него 5:
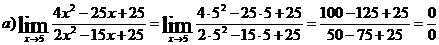 -
-
неопределенность.
Для
устранения неопределенности разложим числитель и знаменатель дроби на множители
по формулам:
ах2
+ bx + с = 0
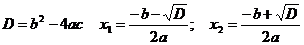
ах2
+ bx + с = а(х-х1)(х-х2)
Тогда
получим:

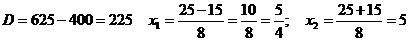

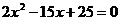
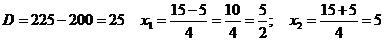
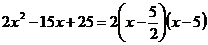
Получаем:
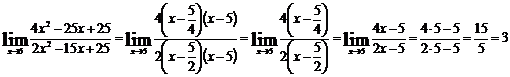
б)
Вычислим предел подставив в него ∞:
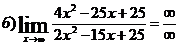 -
неопределенность.
-
неопределенность.
Для
устранения неопределенности разделим числитель и знаменатель на х2. Это можно
сделать, так как значение дроби не изменится если ее числитель и знаменатель
разделить на одно и тоже ненулевое число.
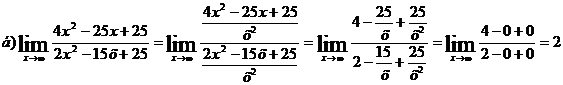
г)
Вычислим предел, подставив в него 0:
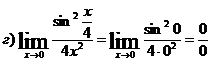 -
неопределенность
-
неопределенность
Для
устранения неопределенности применим формулы 1-го замечательного предела:
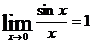
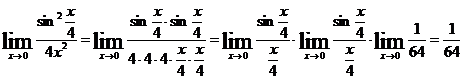
д)
Вычислим предел подставив в него 0:
 -
неопределенность.
-
неопределенность.
Для
устранения неопределенности применим формулы 2-го замечательного предела:
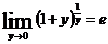
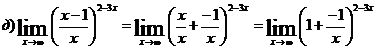
Сделаем
замену 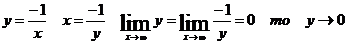
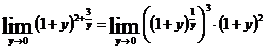
Используя
второй замечательный предел 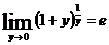
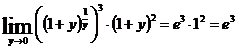
Задание
№6
Исследовать
функцию на непрерывность:

Решение:
Функция
f(x) - непрерывна в т х = а, если соблюдаются следующие
условия:
при
х = а функция f(x) имеет определенное значение b;
при
х → а функция имеет предел, тоже равный b;
При
нарушении хотябы одного из этих условий функция называется разрывной в т х = а.
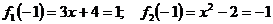
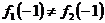 - значит
в т х = -1 функция имеет разрыв.
- значит
в т х = -1 функция имеет разрыв.
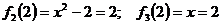
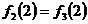 - значит
в т х = 2 функция непрерывна.
- значит
в т х = 2 функция непрерывна.
Покажем
это на графике:
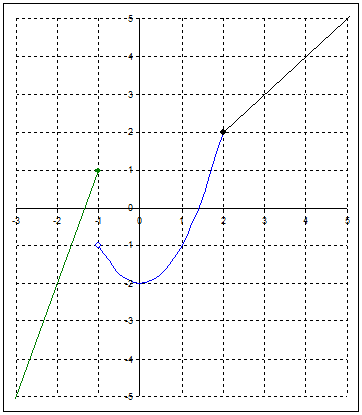
Задание №7
Найти производные функций:
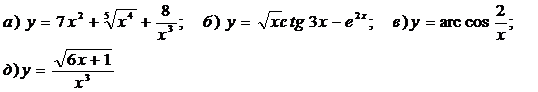
Решение:
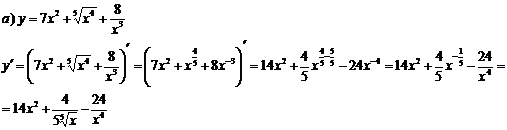
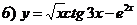
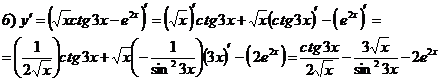
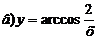


Задание №8
Составить уравнение касательной и нормали к графику функции в точке х0 =
2.
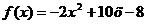
Решение:
Уравнение
касательной к линии: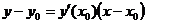
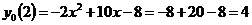
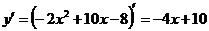

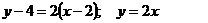
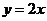 -
уравнение касательной к графику функций
-
уравнение касательной к графику функций 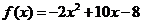 в точке
х=2.
в точке
х=2.
Уравнение нормали имеет вид:
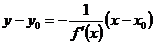
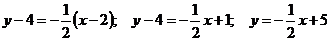
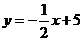 -
уравнение нормали к графику функций
-
уравнение нормали к графику функций 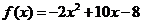 в точке
х=2.
в точке
х=2.
Задание
№9
Найти
пределы функций, применяя правило Лопиталя.
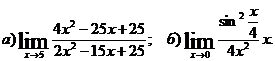
Решение:
а) Вычислим предел, подставив в него 5:
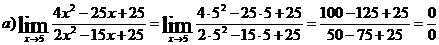 -
-
неопределенность.
Воспользуемся
правилом Лопиталя для устранения неопределенности:
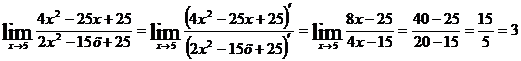
г) Вычислим предел подставив в него 0:
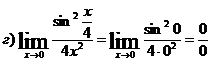 -
неопределенность
-
неопределенность
Воспользуемся
правилом Лопиталя для устранения неопределенности:
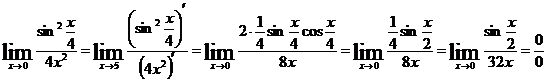 -
-
неопределенность
Воспользуемся
правилом Лопиталя для устранения неопределенности:
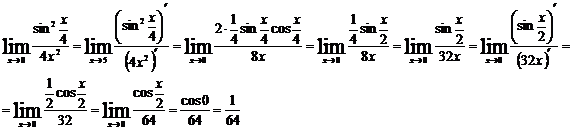
Задача
№ 10
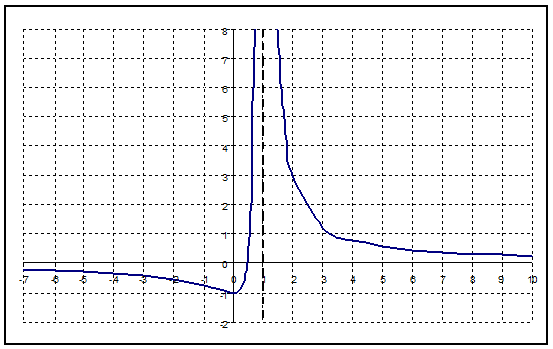
Исследуйте
функцию 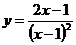 и постройте ее график.
и постройте ее график.
Решение.
1.Область
определения.
Все
предусмотренной формулой функции операции, кроме деления, - т.е. операции
сложения и возведения в натуральную степень - выполняются при любых значениях
аргумента х, а деление возможно, если делитель не равен нулю. Поэтому данная
функция определена, если знаменатель задающей ее дроби не равен нулю: если 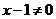 , т.е. если
, т.е. если 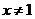 . Таким
образом,
. Таким
образом, 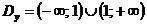 .
.
2)Точки пересечения с осями координат:
С
осью ОХ т.е. у=0: 
 - точка
пересечения с осою ОХ.
- точка
пересечения с осою ОХ.
С
осью ОУ т.е. х=0: 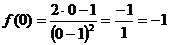
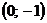 - точка
пересечения с осою ОУ.
- точка
пересечения с осою ОУ.
.Исследуем
на четность нечетность. Проверим выполнимость равенств: если f(-x) = f(x),
то функция четная, если f(-x) = -f(x), то функция нечетная, при х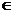 D(y).
Если равенства не выполняются, то функция ни четная ни нечетная.
D(y).
Если равенства не выполняются, то функция ни четная ни нечетная.
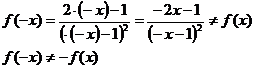
Функция
ни четная ни нечетная
4.Вертикальные асимптоты.
Поскольку
вертикальные асимптоты следует искать лишь в точках разрыва данной функции,
единственным «кандидатом» в нашей задаче является прямая 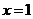 .
.

Следовательно
х=1 точка разрыва 2-го рода и х=1 - вертикальная асимптота.
Наклонные
и горизонтальные асимптоты.
Уравнение
наклонной асимптоты графика функции 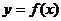 имеет
вид
имеет
вид 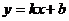 ,
,
где
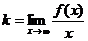 ;
; 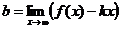 .
.
В
частности, получается, что если 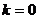 , а
, а 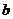 при этом существует, по этим формулам находится
горизонтальная асимптота
при этом существует, по этим формулам находится
горизонтальная асимптота 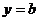 .
.
Выясним
наличие наклонных асимптот.
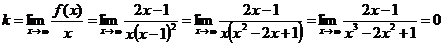 ;
;

 -
уравнение горизонтальной асимптоты.
-
уравнение горизонтальной асимптоты.
.Найдем
экстремумы и интервалы монотонности. Действуем по следующей схеме.
Вычислим
первую производную данной функции:
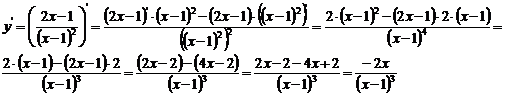
Находим
критические точки функции (т.е. внутренние точки области определения, в которых
первая производная равна нулю или не существует).
Приравняем
нулю найденную производную. Дробь равна нулю, если ее числитель равен нулю. В
числителе стоит произведение двух сомножителей, которое равно нулю, если один
из множителей равен нулю, а второй при этом имеет смысл.
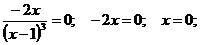
Производная
не существует, если ее знаменатель равен нулю. Это происходит при 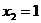 , но это значение аргумента не входит в область
определения данной функции и поэтому не дает критической точки.
, но это значение аргумента не входит в область
определения данной функции и поэтому не дает критической точки.
Таким
образом, у нашей функции две критические точки:  и
и 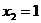 .
.
Исследуем
знак производной слева и справа от каждой критической точки и от точки разрыва.
Найдем
знак производной на каждом из интервалов. Для этого на интервале мы можем
выбрать удобную для вычислений точку и найти в ней знак производной; тот же
знак будет у нее на всем этом интервале.
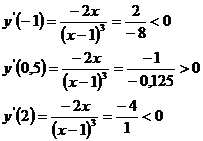
Значит
на промежутке [0; 1) функция возрастает, а на промежутке (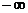 ; 0) и (1;
; 0) и (1; ) функция
убывает.
) функция
убывает.
Занесем
полученные данные в таблицу:
|
х
|
(- ; 0)0[0; 1)1(1; ; 0)0[0; 1)1(1; ) )
|
-
|
0
|
+
|
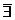 - -
|
|
у  т.
т.
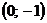 - точка максимума.
- точка максимума.
6.Найдем интервалы выпуклости функции и точки перегиба.
Для этого вычислим вторую производную данной функции:
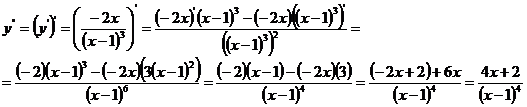
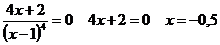
х
= -0,5 - точка подозрительная на перегиб
Исследуем поведение функции справа и слева от точки подозрительной на
перегиб и от т. х=1

|
х
|
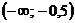 -0,5 -0,5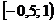 1 1
|
|
|
|
|
|
у′′
|
-
|
0
|
+
|
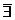 + +
|
|
|
у
|
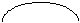  т.
перегиба т.
перегиба 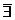 
|
|
|
|
|
Найдем координаты точки перегиба:
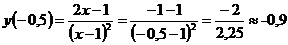
 -
координата точки перегиба.
-
координата точки перегиба.
Список использованной литературы
1.Выгодский М.Я. Справочник по высшей математике. - М.: АСТ:
Астрель, 2006. - 991с.
.Зимина О.В., Кириллов А.И., Сальникова Т.А. Высшая
математика. Под ред. А.И. Кирилова. - 3-е изд., испр. - М.: ФИЗМАТЛИТ, 2006. -
368с.
.Выгодский М.Я. Справочник по элементарной математике. - М.:
АСТ: Астрель, 2007. - 509с.
.Красс М.С., Чупрыков Б.П. Математика для экономистов. -
СПб.: Питер 2007. - 464с.