О пифагорейской математике
Министерство общего и
профессионального образования Российской Федерации
Белгородский государственный
университет
Физико-математический факультета
Кафедра геометрии
Дипломная работа
О пифагорейской математике
Студентки 151 группы д/о
Глумовой Татьяны Анатольевны.
Научный руководитель:
к.ф.-м.н., доцент Проселкова Т.В.
Белгород, 2003
СОДЕРЖАНИЕ
Введение
Глава 1.
Пифагорейские анналы (раннее пифагорейство)
.1 Первый из
семи мудрецов и его школа
.1.1 Жизнь
Пифагора
.1.2
Пифагорейское братство
.2 Классика
греческой науки (пифагорейская школа)
.2.1
Математика
.2.2 Музыка
.2.3
Астрономия
Глава 2.
Великие эллины (среднее пифагорейство)
.1 Евдокс
.2 Платон
.3
Александрийская школа
.3.1 Евклид
.3.2 Архимед
.3.3
Эратосфен
.3.4
Аполлоний
Глава 3. Эллинизм
(позднее пифагорейство)
.1 Никомах
.2 Птолемей
.3 Герон
.4 Диофант
.5 Порфирий,
Ямвлих
.6 Прокл
Заключение
ВВЕДЕНИЕ
Велико значение математики в повседневной жизни человека. Без счета, без
умения правильно складывать, вычитать, умножать и делить числа немыслимо
развитие человеческого общества. Четыре арифметических действия, правила устных
и письменных вычислений не были выдуманы или открыты каким-то одним человеком.
Арифметика возникла из повседневной практики, из жизненных нужд людей и стала такой,
какой ее изучают теперь. Но недостаточно изучать только математические понятия,
правила и теоремы, общепризнанно, что использование элементов историзма в
обучении математике является весьма действенным и эффективным средством
формирования познавательного опыта учащихся. Естественным образом оно
способствует не только лучшему усвоению материала учениками, но и учит их
математическому мышлению, да и мышлению вообще, так как, зачастую только
показав, как человечество пришло к данному открытию, можно показать, какими
путями возможно движение человеческой мысли вообще. Кроме того, изучение
исторических форм математических открытий и математической методологии, их
взаимосвязей и их исторического развития способствует современной тенденции
гуманизации образования, тем самым, имея огромное значение для математиков и
специалистов в области методики математики. Однако, учителя и методисты,
отмечая эту важную роль историко-математического материала, справедливо
указывают на недостаточность методических пособий, разработок, указаний, да и
просто литературы по вопросам подобного рода. Поэтому одной из целей данной
работы является восполнение этого пробела. Выбор темы также диктуется еще одним
немаловажным обстоятельством. А именно тем, что как наука математика сложилась
в религиозно-политическом союзе пифагорейцев в VI в. до н.э. и идейно
господствовала на огромной территории античного мира более тысячелетия (VI в.
до н.э.- V в. н.э.), передалось в непосредственной традиции и будучи (особенно
в начале) строго тайным учением. Между тем фактически в России нет и не было
историко-математической или философской школы, чей задачей было бы изучение
начала начал нашей науки - математики. Во многом это объясняется объективными
причинами. Источников, особенно по раннему пифагорейству, сохранилось очень
мало, а в русском переводе их еще меньше. Без преувеличения можно сказать, что
наша наука только приступает к изучению этой великой философской и научной
школы древности.
Таким образом, выбор данной темы представляется и естественным, и
актуальным.
Пифагорейство разделено на три периода: раннее, среднее, позднее. Более
подробные характеристики каждого из этих периодов, а также персоналии, можно
найти в тексте работы.
ГЛАВА 1. ПИФАГОРЕЙСКИЕ АННАЛЫ (РАННЕЕ ПИФАГОРЕЙСТВО)
.1 Первый из семи мудрецов и его школа
.1.1 Жизнь Пифагора
Пифагор - не только самый популярный ученый, но и самая загадочная
личность, человек-символ, человек-фантом, философ и пророк. Основоположник
дедуктивного научного знания математики и родоначальник многих мистических
учений, учредитель научно-философской школы, ставшей воистину союзом Истины,
Добра и Красоты. Это я только вкратце описала достоинства Пифагора, чтобы вы
представили, какой великой личностью был этот ученый. Если сотни миллионов
учащихся умножить на сотни исписываемых ими тетрадей в клеточку, с каждой из
которой на нас смотрит таблица Пифагора, то получится астрономическая цифра. Ни
одно имя ученого не повторяется так часто. Он был властителем дум,
проповедником собственной «пифагорейской» этики, философом, которого по силе
духа и силе воздействия можно сравнить разве что с его великими современниками:
Конфуцием, Буддой и, возможно, Заратуштрой. Но в отличие от остальных Пифагор
создал самую яркую и самую современную «религию». Пифагор воспитал в
человечестве веру в могущество разума, убежденность в познаваемости природы,
уверенность в том, что ключом к тайнам мироздания является математика.
Этот великий ученый родился на острове Самос в Эгейском море примерно в
570 г. до н. э. Отцом Пифагора был Мнесарх - резчик по драгоценным камням,
когда Мнесарх был в Дельфах по своим торговым делам, он и его жена решили
спросить у Дельфийского оракула, будет ли Судьба благоприятствовать им во время
обратного путешествия в Сирию. Пифия (прорицательница Аполлона), сидя на
золотом триподе над зияющим отверстием оракула, не ответила на их вопрос, но
сказала Мнесарху, что его жена носит в себе дитя и что у них родится сын,
который превзойдет всех людей в красоте и мудрости и который много потрудится в
жизни на благо человечества. Мнесарх столь впечатлен был пророчеством, что
изменил имя собственной жены на Пифазис в честь Пифийской жрицы. Когда родилось
дитя в городе Сидоне, Финикия, оно оказалось, как и говорил оракул, мальчиком.
Мнесарх и Пифазис назвали его Пифагором, потому что они верили в то, что ему
предсказано оракулом.
По многим античным свидетельствам, родившийся мальчик был сказочно
красив, а вскоре проявил и свои незаурядные способности. Среди учителей юного
Пифагора традиция называет имена старца Гермодаманта и Ферекида Сиросского
(хотя и нет твердой уверенности в том, что именно Гермодамант и Ферекид были
первыми учителями Пифагора). Целые дни проводил юный Пифагор у ног старца
Гермодаманта, внимая мелодии кифары и гекзаметрам Гомера. Страсть к музыке и поэзии
великого Гомера Пифагор сохранил на всю жизнь. И, будучи признанным мудрецом,
окруженным толпой учеников, Пифагор начинал день с пения одной из песен Гомера.
Ферекид же был философом и считался основателем италийской школы философии.
Таким образом, если Гермодамант ввел юного Пифагора в круг муз, то Ферекид
обратил его ум к логосу. Ферекид направил взор Пифагора к природе и в ней одной
советовал видеть своего первого и главного учителя. Но как бы то ни было,
неугомонному воображению юного Пифагора очень скоро стало тесно на маленьком
Самосе, и он отправляется в Милет, где встречается с другим ученым - Фалесом.
Эта встреча озарила всю дальнейшую творческую биографию Пифагора. Но он не
копировал учителя, избрал путь, который из античности вел в современность.
Вобрав в себя все знания и умения жителей Милета, Пифагор отправляется в
неблизкий путь до Египта. Во время путешествия Пифагор с равным усердием
постигал секреты морского искусства и таинства церемониалов различных народов.
Прибыв в Египет, Пифагор сначала знакомился с чужой жизни, но вскоре на
смену уличным впечатлениям пришел интерес к внутренней жизни египтян, их
религии, обрядом. Все эти религиозные обряды и ритуалы представляли собой целую
науку. Пифагор понимал, что путь к знаниям, охраняемым кастой жрецов, лежит
через религию. Только изучив в совершенстве сложную иерархию египетских богов,
мифов, обрядов и таинств, можно было надеяться проникнуть в плотный круг
египетского жречества, а значит, получит доступ к научному знанию. Другого пути
не было, и Пифагору на это потребовались годы.
Всякое образование начинается с обучения чтению и письму. Вместе с
египетскими мальчишками сел за известняковые пластинки и возмужалый эллин с
черной курчавой бородой. Очень скоро Пифагор далеко обогнал своих однокашников
и почувствовал себя готовым к осуществлению главной цели своего путешествия -
поездке в святая святых жреческой мудрости город Мемфис.
Блуждая по подземному лабиринту, Пифагор потерял точку отсчета на земле,
счет времени - он слился с ночным небом, он влетел в первозданную стихию и плыл
по ее безграничным просторам. Потоки мыслей о смысле короткой земной жизни и
смысле вечного мироздания несли его по эфирному морю, усыпанному звездами. Его
мысли собирались в тугие пучки, освещая самые сокровенные тайники сознания. Это
путешествие многое изменило в его сознании. Перед жаждущим истины эллином
открылись сияющая красота и разумность устройства мироздания. Какая сила
удерживает эту неизмеримую громаду в вечном движении? Отчего она не распадается
на части и не собирается воедино? Где начало и где конец ее? От этих вопросов
разум приходил в немое оцепенение, которое сменялось оживленной работой мысли.
Видимо, в эти минуты и решился Пифагор назвать звездный мир словом «космос»,
что на языке его далекой родины означало порядок, совершенство, прекрасную
обустроенность.
И все-таки чувство неудовлетворенности не покидало Пифагора. В глубине
души он понимал, что не только под сводом звездного неба, но и над чистым
листом папируса открывается истина. Истина сокрыта в числе! В этом для Пифагора
не оставалось сомнений, но холодной мудрости чисел предстояло еще долго
учиться.
Что же приобрел Пифагор за годы учений в Египте как ученый и, прежде
всего как математик? С высоты сегодняшнего знания, оценивая вклад самого Пифагора
в математику, пожалуй, следует сказать: немногое. Египетская математика была
чисто прикладной наукой: она удовлетворяла потребность в счете (арифметика) и в
измерении земельных участков (геометрия).
Но ни в одном папирусе, ни в одной задаче мы не найдем и намека на
объяснение, почему следовало действовать так, а не иначе. В египетских
папирусах полностью отсутствует главное содержание сегодняшней математики -
доказательство. Этим содержанием наполнил математику Пифагор.
Как бы то ни было, но пора ученичества подходила к концу. Возможно,
неудовлетворенность бездоказательностью египетской математики ускорило
окончательное решение Пифагора возвращаться на родину. Нужно было ехать домой,
и создавать свою школу, в которой ясность логики и твердость доказательства
стали бы главными строительными материалами. Поэтому, научившись всему, что
дали ему жрецы, он, убежав от них, двинулся на родину в Элладу. Однако,
проделав часть пути, Пифагор решается на сухопутное путешествие, во время
которого его захватил в плен Камбиз, царь Вавилона, направлявшийся домой. Не
стоит драматизировать жизнь Пифагора в Вавилоне, т.к. великий властитель Кир
был, терпим ко всем пленникам. Вавилонская математика была, бесспорно, более
развитой (примером этому может служить позиционная система исчисления), чем
египетская, и Пифагору было чему поучится. Но в 530 г. до н.э. Кир двинулся в
поход против племен в Средней Азии. И, пользуясь переполохом в городе, Пифагор
сбежал на родину.
Много трудностей пришлось преодолеть Пифагору, прежде чем вернуться к
берегам родной Эллады. И вот радостное видение, долгие двадцать лет грезившиеся
во снах Пифагору, становились явью: на крутом мысе засверкал знакомый силуэт
храма Геры Самосской. К власти на Самосе пришел тиран Поликрат. Поначалу он
разделил город на три части и правил вместе с братьями Пантагнатом и
Силосонтом. Однако вскоре Поликрат стал безграничным властелином острова. Самым
грандиозным и искусным сооружением его времен был самосский туннель. Пифагор
принимал участие в обсуждении проекта этого сооружения. Вполне возможно, что в
этом проекте нашли воплощение геометрические построения.
Самосский тиран поспешил всячески обласкать знаменитого путешественника,
слава которого уже бежала впереди него. Но Пифагор не спешил принимать милости
Поликрата. Роль придворного полкраба, пусть и украшенного лаврами, никак не
устраивала его. Толстые стены дворца тирана и роскошь придворной жизни не могли
заглушить острую боль, которую причиняла ему царившая в этих стенах
несправедливость. Пифагор не мог жить рядом с источником несчастий своих
сограждан. Он удалился за город и для своих занятий облюбовал пещеру в
окрестностях Самоса.
Непрерывная череда единомышленников, становившихся учениками, старых
друзей и знакомых и просто любопытных потянулись к этой пещере. Дни и ночи
проводил Пифагор в беседах, в которых обсуждалось все - от тайников души
самосского тирана до тайн мироздания. Возможно, в одной из таких бесед
обсуждались геометрические принципы строительства тоннеля.
Жизнь Пифагора в пещере становилась все более уединенной. Но чем дальше
отходил Пифагор от жизни общества, тем теснее сближался он с тайной общиной
орфиков. Орфики исповедовали религиозное учение, основанное, по их верованиям,
самим поэтом Орфеем. Древние мифы утверждали, что Орфей изобрел музыку и
искусство стихосложения. Учение орфиков тесно переплеталось с культом Бога
растительности Диониса - покровителя виноградства и виноделия. Орфей
преобразовал первобытно-разнузданное поклонение Дионису в
религиозно-философское учение. Ради освобождения божественной души, заточенной
в темнице тела, орфики совершали особые очистительные обряды. Свою жизнь они
подчиняли системе особых жизненных правил - "орфическая жизнь".
Орфики верили в то, что душа человека бессмертна и подвержена непрерывной цепи
перевоплощений. После смерти человека его душа переходит в тело одного
животного, потом другого и т.д. Вот почему столь бурно и безудержно исполнялись
орфические обряды - мистерии (таинство). Пифагору нравились мистерии орфиков.
Нравилась чистота их жизни, призванной развивать в человеке лучшие начала,
нравилось стремление орфиков стать частицей единой гармонии природы. Именно
внутренняя философия единения с природой, всеобщей гармонии и непрерывного
творчества природы занимала мудреца. Оставалось только найти единое первоначала
единой природы, отыскать единый источник ее неиссякаемых творческих сил,
увидеть первопричину ее гармонии и прекраснейшего устройства. И такую
первопричину Пифагор отыскал в числе. Теория числа как единого организующего
принципа мироздания стала стержнем всей философской системы Пифагора.
Заметим, что само слово «теория», без которого немыслима современная
наука, имеет орфико-пифагорейское происхождение. Первоначально теория означало
наблюдение, созерцание Однокоренным словом с теорией является и теорема -
зрелище, представление, которое трудами Пифагора стало означать и умозрение,
умозаключение, т.е. математическую теорему.
Но орфики составляли лишь ничтожную часть самосского общества. Пифагора
угнетала сама атмосфера тирании и произвола. Мысль о том, что не пристало
философу, свободному духом, жить в атмосфере насилия, все чаще посещала его.
Как ни горька была эта правда, но она оставалась таковой: родина не дала
Пифагору духовной свободы, столь необходимой мудрецу. То, чего долгие двадцать лет
скитаний он мечтал обрести на родине - душевного равновесия, на родине не было.
Судьба вечного странника вновь выбирала дорогу, и он переселился в Кротон.
Итак, с приездом Пифагора в Кротон начинается самый славный период его
биографии. Возраст акме (40 лет) - вершина творческих сил человека - стал и
временем рассвета философии Пифагора.
.1.2 Пифагорейское братство
Говорят, что Пифагор был первым человеком, который назвал себя философом;
в самом деле, мир обязан как раз ему этим термином. До него умные люди звали
себя мудрецами, что означало человек, который знает. Пифагор был гораздо
скромнее. Он ввел в обращение термин философ, который определил как тот, кто
пытается найти, выяснить.
В Кротоне Пифагор учредил нечто вроде религиозно-этического братства или
тайного монашеского ордена, члены которого обязывались вести так называемый
пифагорейский образ жизни. Сначала в Кротоне на него смотрели искоса, но через
некоторое время власть имущие в этом городе уже искали его совета в делах
огромной важности. Он собрал вокруг себя небольшую группу преданных учеников,
которых посвятил в глубокую мудрость, ему открытую, а также в основы оккультной
математики, музыки, астрономии, которые рассматривались им как треугольное
основание для всех искусств и наук. Это был одновременно религиозный союз, и
политический клуб, и научное общество. Основу пифагорейского союза, скорее
всего, составляли многочисленные братства орфиков. Орфики были близки Пифагору
по духу, и он сумел объединить их единый религиозно-политический союз. Таким
образом, семена учения Пифагора упали на подготовленную орфиками почву, и
именно поэтому союз быстро завоевал в Кротоне широкую известность и стал
ведущим центром духовной и общественной жизни полиса.
Чем же объясняется феноменальная популярность Пифагора в Кротоне?
По-видимому, прежде всего незаурядными личными качествами философа, его умение
увлечь за собой людей. Но не только сила личности и мудрость Пифагора, но и
высокая нравственность проповедуемых им идей и жизненных принципов притягивало
к нему единомышленников. Поначалу именно талант политического оратора и
религиозного проповедника, а не мудрость философа и тем более
естествоиспытателя принесли Пифагору успех. Нравственные принципы и правила,
проповедуемые Пифагором, и сегодня достойны подражания.
Изучение геометрии, музыки и астрономии считалось существенным для
понимания Бога, человека или Природы, и никто не мог полагать себя учеником
Пифагора до тех пор, пока не овладевал в достаточной степени этими науками.
Каждый претендент проверялся по этим трем предметам, и, если обнаруживалось его
невежество, он быстро изгонялся. Ритуал посвящения в члены пифагорейского
братства был окружен множеством таинств, разглашение которых сурово каралось.
Когда к нему приходили младшие и желающие жить совместно, то он не сразу давал
согласие, а ждал, пока их не проверит и не вынесет о них свое суждение.
Философская школа Пифагора была в известной мере также серией инициаций,
поскольку он заставлял учеников проходить через различные ступени и никогда не
вступал с ними в личный контакт, пока они не достигали определенной ступени
совершенства. Согласно его биографам, степеней было три. Во-первых, это
касалось «Математики» - его ученикам вменялось в обязанность знание математики
и геометрии, которое было тогда и могло бы быть сейчас, если бы масонство было
должным образом внедрено, основанием, на котором воздвигалось все знание.
Во-вторых, это касалось «Теории», которая имело дело с искусными приложениями
точных наук. Наконец, речь шла о степени «Избранности», которая присваивалась
кандидату тогда, когда он постигал свет полного просвещения, какого только
можно было достичь. Ученики пифагорейской школы разделялись на «экзотериков»,
или учеников внешних степеней, и «эндотериков», тех, кто проходил третью
степень инициации и был допускаем к секретной мудрости. Молчание, секретность и
безусловное повиновение были кардинальными принципами этого великого ордена» Но
и попав в орден после строгого отбора и испытательного периода, новички могли
только из-за занавеса слушать голос учителя, видеть же его самого разрешалось
только после нескольких лет очищения музыкой и аскетической жизни.
Пифагорейский аскетизм сводился, прежде всего, к обету молчания. Пифагорейцы с
равным усердием заботились и о физическом, и о духовном развитии. Именно в
пифагорейской среде родился термин калокагатия, обозначавший греческий идеал
человека, сочетающего в себе эстетическое (прекрасное) и этическое (добро)
начала, гармонию физических и духовных качеств. Атмосфера высокой
нравственности и самосовершенствования окружала пифагорейский союз, а ее
благотворное дыхание ощущалось и далеко вне его.
В пифагорейское братство принимали не только мужчин, но и женщин. Ямвлих
в жизнеописании Пифагора называет имена 17 женщин - пифагореянок. Но точное
число учеников Пифагора неизвестно.
Пифагор был первым, кто вывел человечество из лабиринтов мифотворчества и
богоискательства к берегам океана точного знания. Он показал, что именно разум,
а не органы чувств приносит человеку истинное знание. Вот почему он советовал
своим ученикам переходить от изучения «телесного», т.е. физических объектов,
которые никогда не бывают в одном и том же состоянии, к изучению
«бестелесного», т.е. к изучению абстрактных математических объектов, дающие
человеку вечные непреходящие истины. Так математика становится у Пифагора
орудием познания мира. А за математикой следует и философия, ибо философия есть
не что иное, как распространение накопленного специального знания на область
мировоззрения. Так рождается знаменитый пифагорейский тезис: «Все есть число» -
кредо философии Пифагора.
и 2 не считались числами у пифагорейцев, потому что они представляют две
надмирские сферы. Пифагорейские числа начинаются с 3, треугольника, и 4,
квадрата. Сложенные между собой и плюс 1 и 2, они дают число 10, великое число
всех вещей, архетип Вселенной. Три мира были названы вместилищами. Первый был
вместилищем принципов, второй - разума, а третий - низший - вместилищем
количеств.
Пифагор учил, что точка символизирует число 1, линия - число 2, плоскость
- число 3, и многогранники - число 4.

1 2 3 4
Число у пифагорейцев трактуется одновременно как оформленное,
материалистически организованное тело, и как душа, которая является
организующим принципом тела. Однако в законченной форме учение о числовой
гармонии можно видеть у Платона в его диалоге "Тимей". Платон
использовал все пифагорейские учения, в частности он пользовался книгами
Филолая, который исходит из антитезы предела и беспредельного. "Все существующее
должно быть пределом или беспредельным или тем и другим вместе, так как оно
состоит ни исключительно из одного предела, ни исключительно из одного
беспредельного.
"Число-это закон и связь мира, сила, царящая над богами и смертными,
условие всего определенного, всего познаваемого", - говорили пифагорейцы.
Основным содержанием пифагорейской математики является учение о числе.
Легенда рассказывает, что на пифагорейцев очень сильное впечатление произвел
тот факт, что звуки, издаваемые тремя струнами, образуют наиболее благозвучное
сочетание, если числа, выражающие их длину, относятся между собой как 3:4:6,
т.е. выражаются отношениями небольших целых чисел. Отсюда якобы и сложилось их
учение о числе, как основе мира и человеческого миропонимания. Однако все
обстояло гораздо сложнее.
Пифагорейское число имеет мало общего с современным понятием числа. Оно,
прежде всего, неотделимо от вещи.
Каждая вещь обладает определенной совокупностью свойств, которые вместе
взятые образуют целое. Но каждое свойство, взятое отдельно теряет свою связь с
вещью, как с целостностью, то есть вещь распадается. Напротив, каждая часть
вещи с ее свойствами, взятые как целое - являются ее элементами. Согласно
античным представлениям, каждая вещь есть целость, состоящая из элементов.
Элементы всегда находятся в определенном структурном взаимоотношении. Отношения
элементов целости могут быть не только разнообразными, но и бесконечными.
Целость можно называть множеством. С современной точки зрения: "
Упорядоченное множество-то, в котором каждые два элемента находятся в
определенном отношении; а вполне упорядоченное множество-то, в котором каждая
его часть обладает первым элементом. Каждая вещь есть не что иное, как
бесконечное и вполне упорядоченное множество.
Между двумя элементами, как бы они не были близки друг к другу, мыслим
всегда и третий элемент; а в каждой из двух образовавшихся половин после
разделения цельного расстояния между двумя элементами тоже мыслимо помещение
еще нового элемента и т.д. То есть расстояние между 2 элементами может быть бесконечно
уменьшаемо до той предельной точки, которая уже не допускает помещения новой
точки; т.е. дробление доводится до полной неразличимости элементов, до полной
их взаимопронизанности.
Число не есть просто результат счета, но всегда содержит в себе идею
порядка и поэтому является структурной целостью. Число способно создавать или,
по крайней мере, расчленять вещи, делая их познаваемыми. Числа обуславливают
свойства вещей и явлений. Чувственным вещам окружающего мира пифагорейцы
приписывали отношения целых чисел.
«Симметричные геометрические тела имели для пифагорейцев и последующих
греческих мыслителей величайшее значение. Для того чтобы быть совершенно
симметричным, геометрическое тело должно иметь равное число граней,
встречающихся в углах, и эти грани должны быть правильными многоугольниками, то
есть фигурами с равными сторонами и углами. Пифагор, вероятно, был первым, кто
сделал величайшее открытие, что есть только пять таких тел.
Пифагорейцы провозглашали борьбу против падения нравов, и ратовали за суровый
образ жизни, прославляя самообладание, смелость и коллективную дисциплину. Они
были связаны строгими обязательствами, в частности, члены этого общества должны
были хранить в тайне учение своего учителя. Живя сообществом, приверженцы
Пифагора совершали тайные обряды и занимались изучением философии и наук. У них
было общее имущество, и свои научные открытия они делали общим (внутри своего
общества) достоянием. Труды, обычно приписываемые Пифагору, таким образом,
относятся не только к легендарному Пифагору, но вообще к трудам этой школы
между 585 и 400 гг. до н.э. (раннее пифагорейство)
Таков был пифагорейский союз - любимое детище великого эллинского
мудреца. Воистину, то был союз истины, добра и красоты. В умножении знания,
постижении гармонии физического и духовного совершенства годы летели как
мгновения. Казалось, так было всегда и так будет вечно. Ничто не предвещало
близкой беды.
В первоначальном виде союз просуществовал недолго, он распался в
результате народного восстания (510 г. до н.э.). Пифагор со своими учениками
переместился в Тарент. Но вскоре и в этом городе народ поднимается против
аристократии. Пифагору пришлось срочно оставить и Тарент, он поспешил в город
Мерапонт.
Когда ему было около 60 лет, Пифагор женился на одной из своих учениц, и у
них родилось семь детей. Его жена была замечательно способной женщиной, которая
не только вдохновляла его всю оставшуюся жизнь, но и после его убийства
продолжала распространять его учение. Как это часто случается с гениями, своей
искренностью Пифагор вызвал и политическую, и личную враждебность со стороны
граждан Кротона. Среди желавших принять посвящение был Килон, человек богатый,
но злой, желая спьяну вступить в братство, которому Пифагор отказал в этом, и
тогда тот решил уничтожить как человека, так и его учение. Через ложные слухи
этот человек возбудил в простых людях недовольство философом. Без всякого
предупреждения банда убийц ворвалась в небольшую группу строений, где обитали
великий учитель и его ученики, подожгли здания и убили Пифагора.
Относительно того, как умер Пифагор, общего мнения нет. Некоторые
говорят, что он был убит собственными учениками; другие говорят, что он бежал
из Кротона с небольшой группой последователей и, попав в засаду, сгорел в
подожженном доме. Еще одна версия говорит о том, что в горящем доме ученики
образовали мост из тел, живыми войдя в огонь, для того, чтобы их учитель прошел
по нему и спасся, и только впоследствии Пифагор умер от разрыва сердца, скорбя
по поводу кажущейся тщетности своих усилий по просвещению и служению
человечеству.
Выжившие его ученика пытались продолжать его учение, но они всякий раз
подвергались гонениям, и к сегодняшнему дню мало что осталось от свидетельств
величия этого философа. Говорят, что его ученики никогда не произносили его
имени, а использовали слова Мастер или Этот Человек. Это происходило, возможно,
потому, что по преданию имя Пифагора состояло из специальным образом
упорядоченных букв и имело огромное священное значение. Журнал «Word»
опубликовал статью Т. Пратера, в которой показывается, что Пифагор посвящал
своих учеников-кандидатов посредством определенной формулы, скрытой в буквах
его имени. Это может быть объяснением того, почему имя Пифагор столь высоко
почиталось.
После смерти Пифагора его школа постепенно распалась, но те, кто был
облагодетельствован его учением, хранили память о великом философе так же, как
они во время жизни почитали человека. Прошло время, и Пифагор стал считаться
уже не человеком, а богом, и его рассеянные по свету ученики были объединены
общим восхищением все превосходящим гением своего учителя.
1.2 Классика греческой науки (пифагорейская школа)
1.2.1 Математика
Пифагорейцы создали науку о числе, положили начало арифметике, очистив ее
от практических приложений, что впоследствии стало уделом
"Логистики", которую греки не признавали настоящей наукой.
Числа пифагорейцы мыслили зримо, и иллюстрировали свое виденье в виде
камешков, разложенных на песке или счетной доске-абаке. По этой причине греки
не знали нуля, так как его невозможно было "увидеть". Но и единица не
была полноправным числом, а представлялась как некий "числовой атом",
из которого образовывались все числа. Пифагорейцы называли единицу "
границей между числом и частями", т.е. между целыми числами и дробями.
Число-множество, составленное из единиц. Первым числом, которое можно
рассматривать как совокупность других чисел, является число четыре. В самом
деле, два нельзя рассматривать как составленное из двух, так как оно состоит из
двух единиц. Аналогично, и число три составляется из одной единицы и еще одного
только числа два.
Числа-камешки раскладывались в виде правильных геометрических фигур. Так
возникло понятие фигурных чисел, в котором нашла свое отражение тесная связь,
существующая между понятиями числа и пространственной протяженностью.
НАПРИМЕР:
1. Линейные числа (простые) - числа, которые делятся только на единицу и самих
себя:
*--*--*--*--* линейное число 5.
2. Плоские числа-числа, представимые в виде произведения двух
сомножителей:
*----*----*
│ │ │ плоское число 6
*----*----*
2. Телесные числа, выражаемые произведением трех сомножителей:
*────────*
*─┼──────* │
│ *──────┼─*
телесное число 8
*────────*
4. Треугольные числа: 3,9
* *
* * * *
* * *
5. Квадратные числа: 9,16
*---*----* *--- * --- * ---- *
│ │ │ │ │ │ │
*---* * *--- * * *
│ │ │ │ │
*---*----* *--- * --- * *
│ │
*--- * ---* ---- *
6. Пятиугольные числа: 5,12
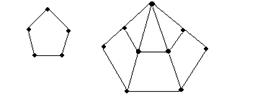
Именно от фигурных чисел пошло выражение "Возвести число в квадрат
или в куб".
Если единица была "числовым атомом", то точка считалась
"геометрическим атомом". Аристотель писал: "Точка есть единица,
имеющая положение, единица есть точка без положения". Для того чтобы быть
отличными друг от друга единицы-точки должны были отделяться пространством,
каждая точка должна была иметь вокруг себя "поле". Благодаря этому
каждое число можно было изображать не только при помощи точек, но и квадратных
полей, или тех и других, как, например, число 3 в виде: * * *
Таким образом, в основе здесь лежит понятие числа, которое изображается
фигурой; арифметика, подчинена геометрии. Их арифметика была геометрична и
наглядна.
Представление чисел в виде правильных геометрических фигур помогало
пифагорейцам находить различные числовые закономерности. Например, чтобы
получить общее выражение для n-го треугольного числа, которое есть не что иное,
как сумма n натуральных чисел 1+2+3+...+n, достаточно дополнить это число до
прямоугольного числа n(n+1) и увидеть (именно увидеть глазами) равенство
* * *  **
* *
**
* *
о * * * 1+2+3+...+n= n(n+1). (1)o o *o o o
n(n+1). (1)o o *o o o
Написав
последовательность квадратных чисел, опять-таки легко увидеть глазами выражение
для суммы n нечетных чисел:
*
o * * o * * * o
o o * *
o * * * o
о
о о * * * о 1 + 3 + 5 + ... + (2n-1)=n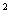 . (2)
. (2)
o o o o
Для
получения квадратных чисел пифагорейцы использовали гномон. Это часть фигуры,
соответствующая нечетному числу, от прибавления которого к квадратному числу
получается следующее квадратное  число.
Вообще гномоном называется такое прибавление к геометрической фигуре, которое
увеличивает, но не меняет ее например, гномоном треугольника является трапеция.
число.
Вообще гномоном называется такое прибавление к геометрической фигуре, которое
увеличивает, но не меняет ее например, гномоном треугольника является трапеция.
Наконец,
разбивая n-е пятиугольное число на три (n-1) треугольных (после чего остается
еще n "камешков"), легко найти его общее выражение:
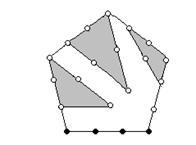
1
+ 4 + 7 + ... + 3n - 2 = n+3 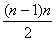 =
=
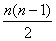 (3)
(3)
Разбиением
на треугольные числа получается и общая формула для n-го k-угольного числа:
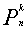
 = n + (k-2n)
= n + (k-2n) 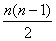 (4)
(4)
откуда при k=2,3,4 следуют формулы 1-3.
Сегодняшний школьник легко заметит, что суммы 1-3 есть не что иное, как
арифметические прогрессии, разность которых d соответственно равны 1,2,3 (для
k-угольного числа d=k-2), и по соответствующей формуле найдет эти суммы и общую
формулу (4).
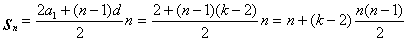
Но
в том-то и прелесть пифагорейских доказательств, что они не требуют никаких
предварительных знаний и в буквальном смысле очевидны.
Фигурное
представление чисел помогало пифагорейцам открывать законы арифметических
операций, а также легко переходить к числовой характеристике геометрических
объектов-измерения площадей и объемов. Так, представим число 10 в двух формах:
*
*
*
*
*
* * * * * * 5 • 2 = 2 • 5 = 10,
*
* * * * * *
*
*
легко
"увидеть" переместительный закон умножения:
ab
= ba.
В
том же числе 10 можно "разглядеть" и распределительный закон сложения
относительно умножения:
(2+3)Ì2 = 2Ì2 + 3Ì2 =10
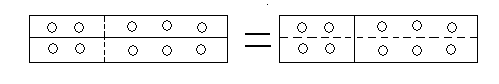
Важнейшей
частью пифагорейской арифметики было учение о четных и нечетных числах. Не
случайно Платон в своих диалогах неоднократно определял арифметику как "
учение о четном и нечетном". Четное и нечетное были для пифагорейцев не
только основными понятиями теории чисел, но и важнейшими философскими
категориями. Пара четное-нечетное наряду с такими, как предел-беспредельное,
доброе-злое, включалась в 10 пар противоположностей, которые пифагорейцы
считали началами всего сущего. Приведем в качестве примера первые пять
положений учения о четном и нечетном:
)
сумма четных чисел является четной;
)
сумма четного количества нечетных чисел четна;
)
сумма нечетного количества нечетных чисел нечетна;
)
четное минус четное есть четное;
)
четное минус нечетное есть нечетное;
Числа
четные делятся на равные части, тем самым они выражают, по мнению пифагорейцев,
некоторую неопределенность. В отличие от них нечетные делятся на неравные
части, и они имеют середину. Числам нечетным приписывается определенность.
Например, семь делится на части три и четыре, число четыре есть середина семи,
так как до четырех содержится три единицы и после четырех надо прибавить еще
три единицы, чтобы получить семь.
Основной
результат учения о четном и нечетном можно сформулировать так: произведение
двух чисел четно тогда и только тогда, когда, по крайней мере, один из
сомножителей четен. Именно на эту теорему опирается доказательство знаменитой
теоремы о несоизмеримости. ( Сторона и диагональ квадрата несоизмеримы.)
Пифагорейцы
изучали некоторые особенные целые числа, как, например, дружественные числа.
Это такие числа, одно из которых равно сумме множителей другого. Неоплатоник
Ямвлих (около 250-325 гг. н.э.), принадлежащий поздней школе пифагорейцев -
неоплатоников, приписывает Пифагору открытие дружественных чисел 220 и 284.
Вершиной
пифагорейского учения о четном и нечетном является учения о совершенных числах.
Совершенным называется натуральное число, равное сумме всех своих правильных
(т.е. меньших этого числа) делителей.
Например:
6
= 1 + 2 + 3; 28 = 1 + 2 + 4 + 7 + 14;
Если
сумма делителей оказывалась больше самого числа, то его называли
"сверхсовершенным", если она была равна числу - «совершенным", а
если меньше - "недостаточным".
Огромную
роль сыграло учение о четном и нечетном в доказательстве утверждения: если
сумма 1 + 2 + 2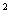 + ... + 2
+ ... + 2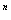 = p
является простым числом, то число 2
= p
является простым числом, то число 2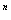 p будет
совершенным.
p будет
совершенным.
Доказательство
этого утверждения сводится к доказательству двух утверждений:
)
других делителей, кроме
1,
2, 2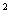 ,..., 2
,..., 2 , 2
, 2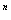 ;
;
p, 2р, 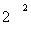 p, ..., 2
p, ..., 2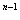 p, (5)
p, (5)
у
числа 2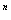 p нет:
p нет:
)
сумма делителей равна самому числу, то есть
1
+ 2 + 2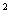 + ... + 2
+ ... + 2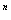 + p (1
+ 2 + 2
+ p (1
+ 2 + 2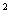 + ... + 2
+ ... + 2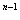 )=2
)=2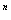 p. (6)
p. (6)
Первое
утверждение доказывается с помощью учения о четном и нечетном
(Книга
II предложение
21-34). Доказательство второго утверждения легко провести на
"камешках".
В
самом деле, так как по условию 1+2+2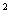 + … +2
+ … +2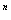 =p, то, сокращая в (6) обе части равенства на p,
имеем:
=p, то, сокращая в (6) обе части равенства на p,
имеем:
1+(1+2+2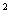 +…+2
+…+2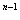 )=2
)=2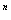 . (7)
. (7)
Теперь
изобразим данную сумму фигурными числами:
┌─┬─┐ 1+1=2;└─┴─┘
┌─┬─┐
├─┴─┤ 1+1+2=4;
└───┘
┌─┬─┬───┐
├─┴─┤ │ 1+1+2+4=8;
└───┴───┘
┌─┬─┬───┐
├─┴─┤ │
├───┴───┤
1+1+2+4+8=16;
│ │
└───────┘
откуда легко «усмотреть» равенство (7).
Учитывая
(7), получим компактную форму записи совершенного числа 2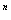 p:
p:
2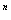 p=2
p=2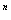 (1+2+2
(1+2+2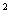 +…+2
+…+2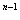 …+2
…+2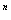 )=2
)=2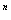 (2
(2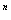 -1+2
-1+2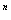 )=2
)=2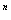 (2
(2 )
)
Итак,
число
q=2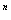 (2
(2 -1) (8)
-1) (8)
является
совершенным при тех значениях n, при которых число p=2 -1 является простым. Легко найти первые подходящие
значения n:
-1 является простым. Легко найти первые подходящие
значения n:
n=1 p=3 q=2p=6;
n=2 p=7 q=2 p=28;=4 p=31 q=2 p=496;=6 p=127 q=2
p=8128.
Первые
четыре совершенных числа были известны пифагорейцам.
Изучение
свойств натуральных чисел привело пифагорейцев к еще одной задаче, задаче о
нахождении тройки чисел (положительных) x,y,z которые были решением уравнения x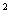 +y
+y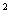 =z
=z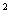 . Решение этой задачи приписывается Пифагору и поэтому
тройки называются пифагорейскими тройками. Ясно, что если x,y,z какая-то тройка
пифагоровых чисел, то nx,ny,nz, тоже пифагоровы тройки. Поэтому будем искать
простые тройки, т.е. не имеющих общих сомножителей. Начало покажем, что в
каждой из таких троек x,y,z один из "катетов"(x или y) должен быть
четным, а другой-нечетным.
. Решение этой задачи приписывается Пифагору и поэтому
тройки называются пифагорейскими тройками. Ясно, что если x,y,z какая-то тройка
пифагоровых чисел, то nx,ny,nz, тоже пифагоровы тройки. Поэтому будем искать
простые тройки, т.е. не имеющих общих сомножителей. Начало покажем, что в
каждой из таких троек x,y,z один из "катетов"(x или y) должен быть
четным, а другой-нечетным.
.
Если предположим, что оба "катета" четные, то четным будет и число 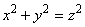 , а значит z-четное. Но это противоречит условию о
том, что числа не имеют общих множителей.
, а значит z-четное. Но это противоречит условию о
том, что числа не имеют общих множителей.
.
X, y - нечетные, следовательно z четное, но и этого не может быть, так как если
x=2p+1, y=2q+1, то . Получим, что z представляет число, которое при
делении на 4 дает остаток 2. Между тем, если считать z=2r, то
z
. Получим, что z представляет число, которое при
делении на 4 дает остаток 2. Между тем, если считать z=2r, то
z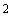 =4r
=4r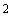 и значит z
и значит z : 4. Опять противоречие. Остается, что один из катетов
четный, другой нечетный. Поэтому x
: 4. Опять противоречие. Остается, что один из катетов
четный, другой нечетный. Поэтому x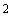 +y
+y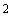 - нечетное, а значит z
- нечетное, а значит z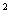 - нечетное.
- нечетное.

Числа
(z+y) и (z-y) взаимно просты. Если бы они не были взаимно просты, то имели бы
общий делитель, предположим d. Тогда
z+y=dk,
а z-y=dm.
Выражая
из этих равенств z и y получаем:
z=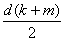 y=
y=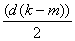
а
это означает, что d является общим делителем z и y, а это противоречит условию
задачи. Но если произведение взаимно простых чисел есть точный квадрат, то
каждое число есть квадрат целого числа, то есть: z+y=m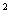 , z-y=n
, z-y=n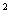 . Решив
систему:
. Решив
систему:

получаем
z= 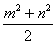 , y=
, y=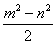 , тогда
x=mn
, тогда
x=mn
|
m
|
n
|
x
|
y
|
z
|
|
3 5 5 7 ∙ ∙
|
1 1 3 1 ∙ ∙
|
3 5 15 7 ∙ ∙
|
4 12 8 24 ∙ ∙
|
5 13 17 25 ∙ ∙
|
Пифагор представил следующие правило для нахождения сторон прямоугольного
треугольника:
|
1-й катет 2n + 1
|
2-й катет 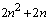 3-й катет 3-й катет 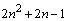
|
|
|
3 5 7 9 ∙ ∙
|
4 12 24 40 ∙
∙
|
5 13 25 41 ∙
∙
|
Пропорции
Характерной особенностью пифагорейского мышления было не просто
стремление все измерить, но и соизмерить, то есть сравнивать измеренные
величины и тем самым раскрывать внутренние связи между ними. Вот почему
пропорции, то есть равенства отношений, стали изучаться раньше, чем сами
отношения. Пифагорейцы разрабатывали: 1) арифметическое учение о пропорциях с
3-мя типами этого рода пропорций: арифметической, геометрической и
гармонической; 2) пропорции 5-ти правильных геометрических тел; 3) музыкальные
пропорции внутри октавы; 4) пропорции основных физических элементов, то есть
земли, воды, воздуха и эфира.
Для того чтобы составить представление о существе этих пропорций и об их
теснейшей взаимосвязи, нужно базироваться на платоновских материалах. Филолай о
пяти правильных телах и присущих им пропорциях, о непрерывной и прерывной
пропорции. Диадическое начало, понимаемое у пифагорейцев и у Платона как
отношение 1:2, повторяется везде совершенно одинаково. Как от точки мы
переходим к прямой, пользуясь этим отношением, так от прямой к плоскости и от
плоскости к телу.
Если считать за точку 1, а 2 за прямую, то 2·2=4 будет плоскостью, а
4·2=8 будет телом. От обычной пропорции диада отличается только тем, что
обладает зрительным характером, в данном случае геометрическим. С помощью диады
греки объединяли переход от одного измерения пространства к другому, то есть
диада есть принцип становления, в отличие от нестановящегося и устойчивого
бытия, которое они называли "монадой".
Итак, дробь как число для пифагорейцев не существовала, поскольку единица
была неделимой. Поэтому дробь (а/b) понималась не как доля единицы, а как
отношение двух целых чисел.
Отношение a:b и c:d называли равными, если у a и b существовал такой
общий делитель p, а у c и d-делитель q, что
a=mp; c=mq
b=np;
d=nq (то есть 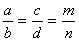 )
)
(в
частности, при n=1 a=mb, c=md). Тогда пары целых чисел разбивались на
пресекающиеся классы пар, имеющих одинаковые отношения:
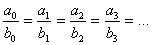
Наименьшая
пара - полностью определяет свой класс. Сегодня эту пару (несократимую дробь)
мы бы назвали рациональным числом, определяющим данный класс. В основе большей
части доказательств теории отношений лежал универсальный способ нахождения
наибольшего общего делителя двух чисел. Этот способ и сегодня с успехом
применяется в теории чисел и называется алгоритмом Евклида. Суть алгоритма
Евклида состоит в том, что а делят на b с остатком, затем b
делят на этот остаток и т.д. В современном виде это можно записать вот так, где
r остаток при делении.
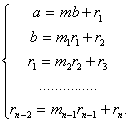 (9)
(9)
Евклид доказал, что:
1) если
r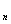 =1, то НОД (а,b)=1, т.е. числа
а и b взаимно простые;
=1, то НОД (а,b)=1, т.е. числа
а и b взаимно простые;
) если
r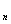 =0, то НОД (а,b)=r
=0, то НОД (а,b)=r .
.
Запишем систему в виде:
 (10)
(10)
подставляя
последующие равенства в предыдущие, получим
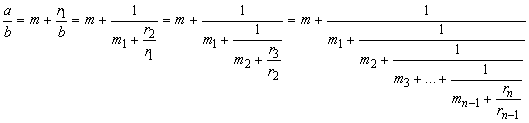 (11)
(11)
где
m целая часть от деления. Дробь (11) называется непрерывной. Из самого принципа
построения непрерывной дроби видно, что если она конечна, то, значит, числа a и
b имеют общую меру, то есть число  является
рациональным. Бесконечная непрерывная дробь будет получатся в случае, если a и
b несоизмеримы, то есть когда число
является
рациональным. Бесконечная непрерывная дробь будет получатся в случае, если a и
b несоизмеримы, то есть когда число  иррациональное.
Таким образом, непрерывная дробь является прекрасным критерием рациональности
или иррациональности числа. Однако переход от алгоритма Евклида к непрерывным
дробям был осуществлен только через 2000 лет, в эпоху Возрождения.
иррациональное.
Таким образом, непрерывная дробь является прекрасным критерием рациональности
или иррациональности числа. Однако переход от алгоритма Евклида к непрерывным
дробям был осуществлен только через 2000 лет, в эпоху Возрождения.
Понятие
величины (отрезка прямой, опр-е см. V кн. "Начал" Евклида)
определялось с помощью аксиом равенства и неравенства, и в частности двумя знаменитыми
аксиомами.
."Говорят,
что величины имеют отношение между собой, если они, взятые кратно, могут
превзойти друг друга" ("Начала", книга V, определение 4). Иначе,
для любых a и b существуют такие числа m и n, что ma>b и nb>a.
."Говорят,
что величины находятся в том же отношении первая ко второй и третья к
четвертой, если равнократные первой и третьей одновременно больше, или
одновременно равны, или одновременно меньше равнократных второй и четвертой
каждая каждой при какой бы то ни было кратности, если взять их в
соответственном порядке" ("Начала", книга V, определение 5).
Иначе, a:b=c:d, если для любых m и n справедливо одно из утверждений:
ma>nb => mc>nd;=nb => mc=nd;<nb => mc<nd.
Эта
аксиома, ставшая через 23 века отправным пунктом современной теории
действительных чисел, позволяла сравнивать отношения несоизмеримых величин.
Оставалось только назвать отношение a:b числом (рациональным, если a и b имели
общую меру, и иррациональным в противном случае). Однако это сделал только
Ньютон в своей "Всеобщей арифметике" в 1707г.: " Под числами мы
понимаем не столько множество единиц, сколько отвлеченное отношение
какой-нибудь величины к другой величине того же рода, принятой нами за
единицу". Но вернемся к пропорциям. И так, пифагорейцы знали три вида пропорций:
арифметическая:
a-b=c-d;
геометрическая:
a:b=c:d; (12)
гармоническая:
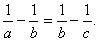
Помимо
пропорций пифагорейцы особое внимание уделяли непрерывным пропорциям, или
средним величинам, то есть таким пропорциям, у которых средние члены совпадали
(b=c). Пифагорейцы не только изучали математические свойства средних, но и
наполняли их глубоким эстетическим содержанием. Об этом красноречиво
свидетельствует следующий отрывок из платоновского "Тимея":
"Невозможно, чтобы две вещи совершенным образом соединились без третьей,
так как между ними должна появиться связь, которая скрепляла бы их. Это
наилучшим образом может выполнить пропорция..."
Полагая
в (12) b=c и переобозначая d через c, получим следующие выражения для средних:
арифметическое
среднее: a-b=d-c => b=
геометрическое
среднее: a:b=b:c => b=  (13)
(13)
гармоническое
среднее: 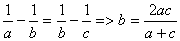
Арифметическое
среднее понималось пифагорейцами арифметически: как отрезок b, меньший большего
отрезка a и больший меньшего c на одну и туже величину a-b=b-c. Геометрическое
среднее (b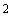 =ac) - геометрически: как площадь квадрата со стороной
b, равновеликого прямоугольнику со сторонами a и c. Наконец, гармоническое
среднее - как арифметическое среднее для обратных величин. Гармоническое
среднее играло большую роль в пифагорейской теории музыки гармонии, откуда и
происходит его название.
=ac) - геометрически: как площадь квадрата со стороной
b, равновеликого прямоугольнику со сторонами a и c. Наконец, гармоническое
среднее - как арифметическое среднее для обратных величин. Гармоническое
среднее играло большую роль в пифагорейской теории музыки гармонии, откуда и
происходит его название.
Среди
множества геометрических средних уникальным свойством обладает одно, делящее
данный отрезок a на две части x и a-x в геометрической пропорции, то есть так,
что отношение целого отрезка a к его большей части x равняется отношению
большей части x к меньшей a-x:
a:x=x:(a-x) (14)
Эта
геометрическая пропорция приводит к уравнению:
x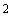 +ax-a
+ax-a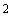 =0,
=0,
которое
имеет один положительный корень:
x=aφ ;
φ =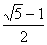
Заметим,
что  = Ф =
= Ф = 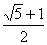 , то есть
φ·Ф=1.
, то есть
φ·Ф=1.
Найдем
разложение φ
в непрерывную дробь. Рассмотрим
бесконечную непрерывную дробь:
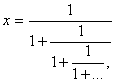 (15)
(15)
в
знаменателе которой нетрудно обнаружить выражение 1+х, т.е.
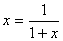

Отсюда
находим уравнение
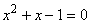
и
его положительный корень х=φ. Следовательно,
дробь (15) и есть искомое разложение для φ.
Эта
удивительная пропорция, в эпоху Возрождения, была названа Леонардо да Винчи
(1452-1519) золотым сечением.
Отметим
одно любопытное свойство всех трех средних величин, которое, как утверждает
Ямвлих во "Введении в никомахову арифметику", Пифагор привез из
Вавилона. Пусть даны две величины a>d. Составим их среднее арифметическое b= и среднее гармоническое c=.
и среднее гармоническое c=.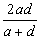
Легко
показать, что b>c:
b>c
<= 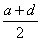 >
> ,
,
то
есть a>b>c>d. Кроме того, легко видеть, что
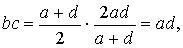
то
есть выполняется основное свойство пропорции (bc=ad), и, следовательно, среднее
арифметическое и среднее гармоническое двух величин a и d образуют с ними
геометрическую пропорцию:
a: (16)
(16)
Эта
пропорция играла значительную роль в пифагорейской теории музыки, отчего ее
часто называют музыкальной.
Построение
средних геометрических было средством извлечения квадратных и кубических корней
у древних греков. Фактически извлечение квадратного корня сводилось к
построению одной средней геометрической к двум данным величинам: a:x=x:b, x=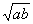 . Извлечение кубического корня сводилось к построению
двух средних геометрических к двум данным величинам: a:x=x:y=y:b. Отсюда x=
. Извлечение кубического корня сводилось к построению
двух средних геометрических к двум данным величинам: a:x=x:y=y:b. Отсюда x=  и y=
и y=  .
.
Гармоническое
среднее (a-b):(b-c)=a:c определялось Архимедом и Платоном. Гармоническое
среднее связывалось с законами музыкальных созвучий, а также и тем, что куб
имеет 12 ребер, 8 вершин и 6 граней, где 8-среднее гармоническое чисел 12 и 6.
Если 12 и 6 крайние члены пропорции находятся в отношении 2:1 длин струн
актавы, то среднее арифметическое 9-образует кварту (отношение 4:3), а среднее
гармоническое 8-квинту (отношение 3:2); вся пропорция имеет вид
12,9,8,6.(Э.Кольман) Пропорции помогали пифагорейцам "извлекать числа из
вещей" и щедро раскрывали перед ними свои сокровища. Возможно, что именно
изучение геометрической пропорции и геометрической средней привело пифагорейцев
к их главному и трагическому открытию - открытию несоизмеримости.
Открытие
несоизмеримости, то есть обнаружение таких величин, отношение которых не может
быть выражено с помощью отношения целых чисел, является наивысшим достижением
пифагорейской школы и поворотным этапом в развитии всей математики.
В
последствии эта ситуация была названа первым кризисом в математике.
Точно
не известно, решение какой конкретной задачи привело пифагорейцев к открытию
несоизмеримости. Это могло быть сделано в любом из пифагорейских учений: т.к. в
арифметике при нахождении средней геометрической чисел 1 и 2, и в геометрии при
отыскании общей меры диагонали и стороны квадрата, и в музыке при попытках
разделить октаву пополам, что также приводит к нахождению средней
геометрической между числами 1 и 2.
ТЕОРЕМА. Сторона AB и диагональ AC квадрата несоизмеримы, т.е. отношение
AC:AB не выражается отношением целых чисел.

ДОКАЗАТЕЛЬСТВО:
Допустим противное. Пусть AC и AB соизмеримы,
то есть их отношение равно отношению целых
чисел: AB=m:n, (17)
причем числа m и n одновременно не являются
четными, так как иначе дробь можно было бы
сократить на 2. Возводя (12) в квадрат, имеем

По
теореме Пифагора 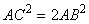 , т.е.
, т.е.  , и,
значит,
, и,
значит,
m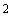 :n
:n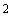 =2 => m
=2 => m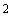 =2n
=2n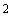 ,
,
то
есть m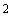 четно. Согласно учению о четном и нечетном
(произведение двух чисел четно тогда и только тогда, когда, по крайней мере,
один из сомножителей четен) m также четно, то есть m=2k, откуда m
четно. Согласно учению о четном и нечетном
(произведение двух чисел четно тогда и только тогда, когда, по крайней мере,
один из сомножителей четен) m также четно, то есть m=2k, откуда m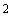 =4k
=4k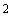 . Тогда
. Тогда
4k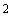 =2n
=2n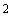 , или 2k
, или 2k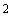 =n
=n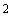 ,
,
то
есть n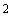 четно, и, следовательно (учение о четном и нечетном),
n также четно. Итак, m и n одновременно являются четными, что противоречит
предположению о не сократимости. Это противоречие доказывает теорему.
четно, и, следовательно (учение о четном и нечетном),
n также четно. Итак, m и n одновременно являются четными, что противоречит
предположению о не сократимости. Это противоречие доказывает теорему.
Как
видим, доказательство несоизмеримости носит чисто пифагорейский характер, так
как целиком основано на учении о четном и нечетном. Но и в этом открытии была
трагедия пифагорейцев, родившись в недрах пифагорейского учения, это доказательство
наносило смертельный удар породившему его учению. Это открытие опрокидывало всю
философскую систему пифагорейцев, которые были убеждены, что элементы чисел
являются элементами всех вещей, и весь мир в целом является гармонией и числом".
Но никаких чисел, кроме целых и их отношений, пифагорейцы не знали.
Согласно
преданию, несоизмеримость открыл сам Пифагор и это открытие долго держалось в
тайне. Лишь ученик Пифагора Гиппас, как утверждает Ямвлих, "открыл
недостойным участия в учениях природу пропорции и несоизмеримости". За
это, продолжает Ямвлих, пифагорейцы "его столь возненавидели, что не
только изгнали его из общего товарищества, но даже соорудили ему могилу, как
будто некогда бывший их товарищ, в самом деле, ушел из земной жизни".
Но,
будучи истинными рыцарями науки, пифагорейцы пытались преодолеть кризис,
вызванный открытием несоизмеримости. Они стали изучать эти
"неразумные" величины, которые мы сегодня называем иррациональными
(от лат. irrationalis - неразумный). Так, иррациональность отношения диагонали
и стороны квадрата пифагорейцы объясняли тем, что оба этих отрезка состоят из
бесчисленного множества точек и поэтому их отношение сводится к отношению двух
бесконечно больших целых чисел. Хотя эта мысль не выдержала критики для геометрических
объектов, находящихся в рациональных отношениях, по отношению к иррациональным
числам она является справедливой. Действительно, всякое иррациональное число
можно с любой степенью точности представить в виде отношения двух целых,
причем, чем больше будут эти числа, тем точнее их отношение будет выражать
иррациональное число.
К
концу Vв.до н.э. пифагореец Теодор из Кирены(? -369 до н.э.),
математик, астроном и музыковед, учитель Теэтета, показал, что стороны
квадратов, площади которых равны 3, 5, 6,…,15, несоизмеримы со стороной
единичного квадрата, т.е. числа √3, √5, √6,…, √15
иррациональные. Мы не знаем доказательства Теодора, но ясно, что он
рассматривал каждую иррациональность в отдельности. Существуют различные
гипотезы относительно того, почему Теодор не смог доказать иррациональность
следующего числа: √17 и выше. Наиболее убедительная из них утверждает,
что все доказательства Теодора основывались только на учении о четном и
нечетном, а первое число, для которого этот способ не проходит, как раз и есть √17.
Но
уже в самом начале IV в. до н.э. (по-видимому, в 399 г. до н.э., в год
казни Сократа) юным и талантливым учеником Теодора Теэтетом было получено общее
доказательство иррациональности чисел вида  , где
N-целое число, не являющееся полным квадратом. В доказательстве Теэтет,
по-видимому, опирался на основную теорему созданной им же теории делимости:
произведение двух целых чисел AB делится на простое число P тогда и только
тогда, когда, по крайней мере, один из сомножителей делится на P. Если бы знать
эту теорему, то доказательство иррациональности
, где
N-целое число, не являющееся полным квадратом. В доказательстве Теэтет,
по-видимому, опирался на основную теорему созданной им же теории делимости:
произведение двух целых чисел AB делится на простое число P тогда и только
тогда, когда, по крайней мере, один из сомножителей делится на P. Если бы знать
эту теорему, то доказательство иррациональности  (N
(N M
M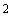 ) фактически не отличается от доказательства
иррациональности √2. Позднее Теэтет доказал иррациональность чисел вида
) фактически не отличается от доказательства
иррациональности √2. Позднее Теэтет доказал иррациональность чисел вида 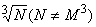 , а также рассмотрел иррациональности вида
, а также рассмотрел иррациональности вида 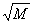
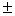
 ,
, 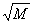
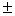 N,
N, 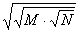 и
предпринял попытку классификации иррациональностей. Эти результаты Теэтета
собраны в X-ой, наиболее трудной, книге "Начал" Евклида.
и
предпринял попытку классификации иррациональностей. Эти результаты Теэтета
собраны в X-ой, наиболее трудной, книге "Начал" Евклида.
Итак,
открытие несоизмеримости не загнало пифагорейцев в тупик, напротив,
стимулировало развитие новых, красивых и глубоких теорий. Открытие
несоизмеримости было едва ли не первым теоретическим результатом, который
невозможно получить с помощью опыта. Более того, оно противоречило всей
измерительной практике, ибо в жизни все величины соизмеримы в пределах точности
измерительного инструмента.
Открытие
несоизмеримости оказало решающее влияние на все дальнейшее развитие греческой
математики. Поскольку некоторые геометрические объекты не измерялись отношением
целых чисел, то есть естественно было предположить, что геометрические объекты
являются величинами более общей природы, чем рациональные числа. Поэтому в
пифагорейской школе предпринимается попытка построить всю математику,
основываясь не на арифметике, а на геометрии. Для этого величины (и в первую
очередь числа) представлялись отрезками, площади и все алгебраические операции
(в том числе и извлечение корня) интерпретировались геометрически. Так в
пифагорейской школе родилась "геометрическая алгебра".
ГЕОМЕТРИЧЕСКАЯ
АЛГЕБРА
Почему
все доказательства теоремы Пифагора были геометрическими? Почему древние греки
боялись алгебры и фактически свели ее к геометрии?
Чтобы
выйти из тупика, в который пифагорейцев поставила задача о несоизмеримости,
рассматривались два пути:
)
либо расширить понятие числа так, чтобы новыми числами стало возможный
характеризовать отношение любых двух геометрических отрезков;
)
либо строить математику на основе геометрии, определив для геометрических
величин все алгебраические операции.
Числа
стали мыслится в виде отрезков, полученных повторением конечного числа раз
некого единичного отрезка. Сложение чисел-отрезков производилось путем
приставления одного отрезка к другому вдоль некоторой прямой, вычитание путем
отбрасывания от большего отрезка меньшего. Умножение представлялось в виде
построения прямоугольника на этих отрезках, площадь которого и выражала
произведение чисел. Складывать и вычитать, позволялось только однородные
величины (либо отрезки, либо площади). Деление определялось как задача
"приложения площадей": "приложить" к данному отрезку c
прямоугольник, равновеликий данному прямоугольнику ab, то есть найти вторую
сторону x прямоугольника так, чтобы xc=ab. "Геометрическое деление":
к стороне a=AB прямоугольника ab приставляется отрезок c, на котором
достраивается прямоугольник BCEF (рис. 1).

Затем проводится диагональ FC до пересечения с продолжением стороны AD в
точке K и строится внешний прямоугольник
AKGF. Тогда закрашенные на рисунке прямоугольники ABCD и CEGH оказываются
равновеликими, так как они получились из равных треугольников AFK и FKG путем
отбрасывания двух равных ab=cx частей:
Δ BCF = Δ FCE и ΔCDK = ΔCKH.
Итак, сторона FG, равная стороне CH искомая сторона x.
Геометрически вводились и многие алгебраические соотношения.
Например:
a(b+c+d)=ab+ac+ad; (18)
(a+b)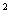 =
=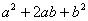 ; (19)
; (19)
 (20)
(20)
Геометрическая
интерпретация тождеств:
┌─────┬──────────┬─────────┐
│
│ │ │
a│ ab │ ac │ ad │
│
│ │ │ a(b+c+d)=ab+ac+ad
│ │ │ │
└─────┴──────────┴─────────┘c
d
Рис. 3
Доказательство
первых двух тождеств очевидно из рисунков 3 и 4.
Для
доказательства третьего к прямоугольнику ab=ABCD достроим квадрат b =BCFE, найдем точку G делящую отрезок AE пополам, то
есть AG=GE=
=BCFE, найдем точку G делящую отрезок AE пополам, то
есть AG=GE=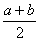 , и построим квадрат GHKE=
, и построим квадрат GHKE=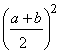 (рис.5). По построению прямоугольник AGMD равен
прямоугольнику BEKL, поэтому исходный прямоугольник ABCD равновелик гномону
GEKLCM, так как у них GBCM - общая часть, а остальные части равны. Но гномон
GEKLMC является разностью двух квадратов: GEKH=
(рис.5). По построению прямоугольник AGMD равен
прямоугольнику BEKL, поэтому исходный прямоугольник ABCD равновелик гномону
GEKLCM, так как у них GBCM - общая часть, а остальные части равны. Но гномон
GEKLMC является разностью двух квадратов: GEKH=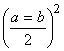 и MCLH=
и MCLH= . Таким образом,
. Таким образом,
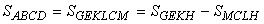 , откуда
ab=
, откуда
ab=
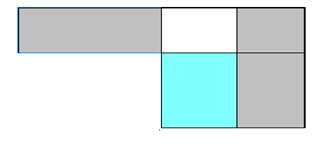
Рис.
5
Однако
уже геометрическое произведение трех величин требовало пространственных
построений, а произведение большего числа сомножителей вообще не поддавалось
геометрической интерпретации в пространстве трех измерений. Вот почему античная
геометрическая алгебра ограничивалась произведениями двух сомножителей, то есть
основывалась на планиметрии, в которой все построения делались с помощью
циркуля и линейки. По этой же причине геометрическая алгебра оказалась хорошо
приспособленной для решения квадратных уравнений и фактически этим и
ограничивалась.
Пифагорейцы
рассматривали три типа геометрических задач, эквивалентных квадратным
уравнениям:
.
Построить квадрат, равновеликий прямоугольнику ab. На языке алгебры это
означает решить уравнение
x = ab. (21)
= ab. (21)
2.
К данному отрезку a приложить прямоугольник, равновеликий прямолинейной фигуре
площади S, так чтобы "недостаток" был квадратом. Иначе, на отрезке
a=AB построить прямоугольник ACDE площади S так, чтобы прямоугольник CBFD был
квадратом. Обозначая сторону квадрата через x, приходим к уравнению
x (a-x) = S. (22)
3.
К данному отрезку a приложить прямоугольник, равновеликий прямоугольной фигуре
площади S, так, чтобы "избыток" был квадратом. Иначе, на отрезке a=AB
построить прямоугольник ACDE площади S так, чтобы прямоугольник BCDF был
квадратом (рис.6). Обозначая сторону квадрата через x, имеем
x (a+x) = S. (23)
Задачи
1-3 решались геометрически путем преобразования произведений ab, x (a-x) и x
(a+x) в разности квадратов по формуле (20). Уравнение (21) при этом принимало
вид:
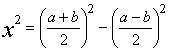 ,
,
то
есть x, согласно теореме Пифагора, находился как катет прямоугольного
треугольника с гипотенузой 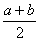 и другим
катетом
и другим
катетом  . Построением такого треугольника и заканчивается II
книга Евклидовских "Начал".
. Построением такого треугольника и заканчивается II
книга Евклидовских "Начал".
Для
этого на отрезке AB=AC+CB=a+b как на диаметре стоим окружность (рис.7). Из
точки C к прямой AB восстанавливаем перпендикуляр до пересечения с окружностью
в точке D. Тогда в треугольнике ODC OD=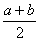 , OC=
, OC= . и, следовательно, по теореме Пифагора CD и есть
искомая величина x. Таким образом, квадрат CDGH=x
. и, следовательно, по теореме Пифагора CD и есть
искомая величина x. Таким образом, квадрат CDGH=x будет равновеликим прямоугольнику ACFE=ab. Итак,
уравнение x
будет равновеликим прямоугольнику ACFE=ab. Итак,
уравнение x =ab решено геометрически, или из величины ab
геометрически извлечен квадратный корень.
=ab решено геометрически, или из величины ab
геометрически извлечен квадратный корень.

Итак, одним из важнейших результатов открытия иррациональности было
быстрое развитие геометрии. Понятие несоизмеримости, иррациональности связано с
понятием бесконечности и непрерывности. Об этом говорил и Зенон в своих парадоксах.
В результате открытия "геометрической алгебры", на первое место
выходит геометрия.
ГЕОМЕТРИЯ
"Пифагор преобразовывал геометрию, придавая ей форму свободной
науки, рассматривая ее принципы чисто абстрактным образом и исследуя теоремы с
нематериальной, интеллектуальной точки зрения. Именно он нашел теорию
иррациональных количеств и конструкцию космических тел". Так оценивал
вклад Пифагора в геометрию Прокл.
В самом деле, в школе Пифагора геометрия оформлялась в самостоятельную
научную дисциплину. Именно Пифагор и его ученики первыми стали изучать
геометрию систематически - как теоретическое учение о свойствах абстрактных
геометрических фигур, а не как сборник прикладных рецептов по землемерию. При
этом, что самое главное, свойства геометрических фигур устанавливались не путем
измерений, а с помощью логических доказательств.
Обладая широчайшей областью практических приложений, геометрия первой из
учений пифагорейцев, сбросила пелену "секретности" и стала популярной
наукой.
Каково было содержание "Предание Пифагора", к сожалению, мы не
знаем. Однако сохранились фрагменты из сочинений замечательного греческого
математика середины V в. до н.э. Гиппократа с ионийского острова Хиоса. Так
вот, в сочинениях Гиппократа Хиосского свойства плоских прямолинейных фигур предполагаются
хорошо известными, тогда как свойства круга и хорд подробно изучаются.
Поскольку до Гиппократа геометрией занимались только пифагорейцы, то
естественно предположить, что все, что Гиппократ считал хорошо известным, было
открыто пифагорейцами.
Пифагорейцы проявляли повышенный интерес к правильным телам. Правильные
геометрические формы благодаря их "правильности", то есть наличию
зеркальной или поворотной (а часто и той и другой) симметрии, как нельзя более
отвечали всей пифагорейской философии о закономерном, структурно-упорядоченном
гармоничном устройстве мироздания. Пифагорейцы доказали теорему о том, что
плоскость можно сплошь (то есть без "дырок" и наложений) покрыть лишь
тремя правильными многоугольниками: треугольниками, квадратами и
шестиугольниками. Не представляет труда и построение этих правильных фигур, а
также фигур, получаемых из них удвоением сторон.
Но вот построение правильного пятиугольника уже не столь очевидно. Мы не
знаем, как строили правильный пятиугольник пифагорейцы. Но известно, что
пятиконечную звезду - свой главный символ и опознавательный знак (пентаграмму)
- они складывали из трех равнобедренных треугольников. А это пересекается с
методом построения правильного пятиугольника, описанным у Евклида
("Начала" кн., пред. 11). Так что метод Евклида, возможно, восходит к
пифагорейцам. Рассмотрим его.
Пусть дан вписанный в окружность равнобедренный треугольник ACD
<C=<D=2<A. Проведем биссектрисы CE и DB углов C и D соответственно.
Тогда углы 1-5 (рис.8) будут равны, а, следовательно, будут равны
соответствующие им дуги и стягивающие их хорды, то есть AB=DC=CD=DE=EA. Итак, вписанный в окружность пятиугольник ABCDE будет
равносторонним. Поскольку <6=<2 и <7=<5 как углы, опирающиеся на
одинаковые дуги AE и AB соответственно, то все углы 1-7 будут равными и,
следовательно, каждый угол пятиугольника ABCDE будет составлен из трех равных
углов, то есть <A=<B=<C=<D=<E=3<1.

Рис. 8
Таким образом, построенный пятиугольник является равносторонним и
равноугольным, то есть правильным. Позднее были найдены и другие способы
построения правильного пятиугольника. Один из них описан в другом выдающемся
сочинении античности - "Альмагесте" Птолемея, которое, подобно
"Началам" Евклида в геометрии, является энциклопедией античных знаний
по астрономии. Другой, в 1525 г., был открыт художником и ученым - Альбрехтом
Дюрером. Однако он указал приближенный способ построения правильного
пятиугольника.
Почему именно пентаграмму пифагорейцы выбрали в качестве символа
приветствия и тайного опознавательного знака? Знакомство с математическими
свойствами пентаграммы поможет ответить на этот вопрос.
Пусть окружность разделена на пять равных частей. Соединяя
последовательно точки деления, получим правильный пятиугольник, диагонали
которого образуют пятиконечную звезду, или звездчатый пятиугольник. Это и есть
пентаграмма. Легко видеть, что внутри пятиконечной звезды вновь образуется
правильный пятиугольник, диагонали которого дают новую звезду, и т.д., (рис. 9)
Рассмотрим треугольник ABC. Он равнобедренный, так как хорды AB и AC
стягивают равные дуги. Далее,<A=36°, <B=<C=72° как вписанные в
окружность углы, опирающиеся на дуги в 72°(=360°:5) и в 144°(=72°∙2)
соответственно. Но <BCD равен 36° как опирающийся на дугу FB в 72°, и,
следовательно, CD является биссектрисой в Δ ABC и отсекает от него
ΔBCD ~ ΔABC. Из подобия этих треугольников имеем
AB:BC=BC:DB. Учитывая, что BC=CD=AD (так как в Δ ADC
<A=<C и,
следовательно, CD=AD), приходим к пропорции
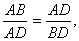 (24)
(24)
то
есть данный отрезок AB так относится к его большей части AD, как большая часть
относится к меньшей AB. Иначе говоря, точка D делит отрезок AB в золотой
пропорции. Равнобедренный треугольник, у которого углы при основании (72°)
вдвое больше угла при вершине (36°), обладает уникальным свойством: биссектриса
угла при основании делит противоположную сторону в золотом сечении. За это
свойство этот треугольник был прозван средневековыми математиками возвышенным.
Именно
золотое свойство возвышенного треугольника и использовал Евклид для его
построения, а значит, и для построения правильного пятиугольника (см. рис.8). В
самом деле, если данный отрезок AB точкой D разделить в золотой пропорции, а
затем циркулем из точки B сделать засечку радиусом AD, а из точки A - радиусом,
AB то точка пересечения C и будет вершиной возвышенного треугольника ABC. Далее
остается лишь описать окружность около ABC и провести биссектрисы углов B и C
до пересечения с окружностью. Окружность разделена на пять равных частей, и,
значит правильный пятиугольник готов.
Остается
показать, как во время Евклида делили отрезок в золотой пропорции. Величина x,
делящая отрезок a в золотом сечении, запишем условие золотого сечения:
а
: х = х : (а-х)
Эта
пропорция приводит к уравнению:
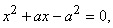
положительный корень, которого можно представить в виде
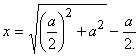
 (25)
(25)
Греки
это решение находили геометрически. Подкоренное выражение в (25), согласно
теореме Пифагора, можно рассматривать как гипотенузу треугольника с катетами а
и  (или как диагональ двойного квадрата со стороной
(или как диагональ двойного квадрата со стороной  ). Отнимая с помощью циркуля от гипотенузы отрезок
). Отнимая с помощью циркуля от гипотенузы отрезок  , мы и найдем искомую величину х. Остается только
(опять - таки с помощью циркуля) перенести отрезок х на отрезок а. (рис. 11).
Золотое сечение отрезка а построено.
, мы и найдем искомую величину х. Остается только
(опять - таки с помощью циркуля) перенести отрезок х на отрезок а. (рис. 11).
Золотое сечение отрезка а построено.

Рис. 10
Вернемся к пентаграмме. Принимая сторону AF=AD=1 исходного правильного
пятиугольника за единицу, полагая DB=x и, следовательно, AB=1+x и подставляя
все это в (24), приходим к уравнению
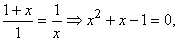
которое
имеет единственный положительный корень :
x=
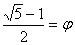
Так
как
1-φ =1- 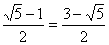 и
и
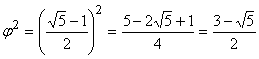 , то
, то
 ,
,
и
мы окончательно находим
AD=DC=CB=AF=...=1;
x=DB=AF=EF=...=
φ;
ED=EG=GH=...=1-
φ =  .
.
повторяя
наши рассуждения для Δ
DGH, в котором DG=φ,
легко видеть,
что
стороны внутренней звезды будут равны φ , а
стороны ее внутреннего правильного пятиугольника - φ
, а
стороны ее внутреннего правильного пятиугольника - φ и т.д.
и т.д.
Таким
образом, последовательность правильных пятиугольников и вписанных в них звезд
образует бесконечно убывающую геометрическую прогрессию со знаменателем
=0,618...<1, или ряд золотого сечения:
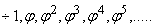 ,
,
причем
стороны правильных пятиугольников образуют ряд четных степеней:
 ,
,
а стороны звезд - ряд нечетных степеней:
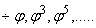
Итак,
пентаграмма обладает массой интереснейших математических свойств:
.
Лучи пентаграммы делят друг друга в золотой пропорции:
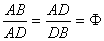
2.
Сторона правильного пятиугольника, сторона вписанной в него пентаграммы и
сторона образованного пентаграммой внутреннего пятиугольника также относятся в
золотой пропорции:

3.
Лучи пентаграммы, выходящие из одной точки, образуют возвышенный треугольник.
.
Последовательность сторон правильных пятиугольников и вписанных в них
пентаграмм образует ряд золотого сечения:
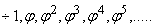 , (26)
, (26)
который
является бесконечно убывающей геометрической прогрессией со знаменателем φ<1 и обладает аддитивным свойством:
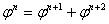 (n=0,1,2,..).
(n=0,1,2,..).
5. Отрезки пентаграммы AB=Ф, AD=1, AE= и ED= связаны между собой всеми
видами средних (11), известных пифагорейцам, а именно
AD=
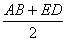 - арифметическое среднее;
- арифметическое среднее;
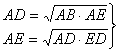 -
геометрическое среднее;
-
геометрическое среднее;
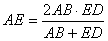 -
гармоническое среднее.
-
гармоническое среднее.
Подведем
итог. Мы видим, что пентаграмма буквально соткана из золотой пропорции и всей
видов средних. К математике присоединялась и числовая мистика: число 5=2+3 было
для пифагорейцев числом любви как сумма первого женского (2) и первого мужского
(3) чисел.
Перейдем
теперь к правильным многогранникам. Их всего пять, и Пифагор знал лишь три тела
- тетраэдр, гексаэдр, куб и додекаэдр, позднее Теэтет открыл и два оставшихся -
октаэдр и икосаэдр.
По-видимому,
сама природа подсказала пифагорейцам форму правильных тел: кристаллы поваренной
соли имеют форму куба, кристаллы кварцев - октаэдра, а кристаллы пирита -
додекаэдра.
Название
правильному многограннику дается по числу его граней
Геометрическая
характеристика правильных многогранников
|
Правильный многоугольник
|
Число граней
|
вершин
|
ребер
|
Геометрия грани
|
m
|
|
Тетраэдр Октаэдр Гексаэдр
Икосаэдр Додекаэдр
|
4(тетра) 8 (окто) 6 (гекса)
20(икоси) 12(додека)
|
4 6 8 12 20
|
6 12 12 30 30
|
|
3 4 3 5 3
|
Буква m в таблице обозначает число граней при вершине.
Пифагорейцы заметили, что в кубе число вершин (8) есть среднее гармоническое
числа граней (6) и числа ребер (12) и поэтому назвали куб гармоническим телом.
Позднее, ко времени Евклида было замечено, что куб и октаэдр, а также додекаэдр
и икосаэдр дуальны (двойственны),т.е. число граней одного тела равно числу
вершин другого и наоборот. Тогда одно тело может быть получено из другого, если
центры тяжести граней одного принять за вершины другого или наоборот. Тетраэдр
дуален сам себе.
Как построение правильного многоугольника начинается с окружности, точно
также и сфера является основой для построения правильного многогранника. Как в
правильном многоугольнике центры вписанной и описанной окружностей совпадают,
так и в правильном многограннике совпадают центры вписанной и описанной сфер.
И все - таки самым интригующим свойством правильных тел является то, что
их существует всего пять. Доказательством этого факта завершается последняя
X111 книга "Начал" Евклида. В самом деле, сумма плоских углов S при
вершине выпуклого многогранника должна быть строго меньше 360 , а число граней при
вершине m>3. Значит, гранями правильных тел могут быть только три правильных
многоугольника: треугольник, квадрат, и пятиугольник, ибо уже для
шестиугольника S=120º 3=360º. Из правильных треугольников можно
составить три правильных тела: m=3 - тетраэдр, m=4 - октаэдр и m=5 - икосаэдр (m=6 S=60º 6=360º).
Из квадратов и
правильных пятиугольников - только по одному (куб и додекаэдр) при m=3 (при m=4
S=90º
4=360º) - для
квадратов и S=108º 4=432º - для пятиугольников.
Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с
теоремой Пифагора. Пожалуй, даже те, кто в своей жизни навсегда распрощался с
математикой, сохраняют воспоминания о «пифагоровых штанах» - квадрате на
гипотенузе, равновеликом двум квадратам на катетах. Причина такой популярности
теоремы Пифагора триедина: это простота - красота - значимость. В самом деле,
теорема Пифагора проста, но не очевидна. Это сочетание двух противоречивых
начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме
того, теорема Пифагора имеет огромное значение: она применяется в геометрии
буквально на каждом шагу, и тот факт, что существует около 500 различных
доказательств этой теоремы (геометрических, алгебраических, механических и
т.д.), свидетельствует о гигантском числе ее конкретных реализаций. Открытие
теоремы Пифагором окружено ореолом красивых легенд. Прокл, комментируя
последнее предложение первой книги «Начал» Евклида, пишет: «Если послушать тех,
кто любит повторять древние легенды, то придется сказать, что эта теорема
восходит к Пифагору; рассказывают, что он в честь этого открытия принес в
жертву быка». Впрочем, более щедрые сказители одного быка превратили в одну
гекатомбу, а это уже целая сотня. И хотя еще Цицерон заметил, что всякое
пролитие крови было чуждо уставу пифагорейского ордена, легенда эта прочно
срослась с теоремой Пифагора и через две тысячи лет продолжала вызывать горячие
отклики. Так, оптимист Михаил Ломоносов (1711--1765) писал: «Пифагор за
изобретение одного геометрического правила Зевсу принес на жертву сто волов. Но
ежели бы за найденные в нынешние времена от остроумных математиков правила по
суеверной его ревности поступать, то едва бы в целом свете столько рогатого
скота сыскалось». А вот ироничный Генрих Гейне (1797-1856) видел развитие той
же ситуации несколько иначе: «Кто знает! Кто знает! Возможно, душа Пифагора
переселилась в беднягу кандидата, который не смог доказать теорему Пифагора и
провалился из-за этого на экзаменах, тогда как в его экзаменаторах обитают души
тех быков, которых Пифагор, обрадованный открытием своей теоремы, принес в
жертву бессмертным богам».
Сегодня теорема Пифагора обнаружена в различных частных задачах и
чертежах: и в египетском треугольнике в папирусе времен фараона Аменемхета
первого (ок. 2000 до н.э.), и в вавилонских клинописных табличках эпохи царя
Хаммурапи (XVIII в. до н.э.), и в древнеиндийском геометрическо-теологическом
трактате VII -V вв. до н.э. «Сульва сутра» («Правила веревки»). В древнейшем
китайском трактате «Чжоу-би суань цзинь», время создания которого точно не
известно, утверждается, что в XII в. до н. э. китайцы знали свойства
египетского треугольника, а к VI в. до н.э. и общий вид теоремы. Несмотря на
все это, имя Пифагора столь прочно сплавилось с теоремой Пифагора, что сейчас
просто невозможно представить, что это словосочетание распадется. То же
относится и к легенде о заклании быков Пифагором. Да и вряд ли нужно
препарировать историко-математическим скальпелем красивые древние предания.
Сегодня принято считать, что Пифагор дал первое доказательство носящей его имя
теоремы. Увы, от этого доказательства также не сохранилось никаких следов.
Я рассмотрю некоторые классические доказательства теоремы Пифагора,
известные из древних трактатов. Сделать это полезно еще и потому, что в
современных школьных учебниках дается алгебраическое доказательство теоремы.
При этом бесследно исчезает первозданная геометрическая аура теоремы, теряется
та нить Ариадны, которая вела древних мудрецов к истине, а путь этот почти
всегда оказывался кратчайшим и всегда красивым. Итак, Теорема Пифагора.

Рис. 11
"Квадрат, построенный на гипотенузе прямоугольного треугольника,
равновелик сумме квадратов, построенных на его катетах".
Простейшее доказательство теоремы получается в простейшем случае
равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась
теорема. В самом деле, достаточно просто посмотреть на мозаику равнобедренных
прямоугольных треугольников (рис. 11), чтобы убедиться в справедливости
теоремы. Например, для ∆ABC:
квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а
квадраты, построенные на катетах,- по два. Теорема доказана.
Древнекитайское доказательство. Математические трактаты Древнего Китая
дошли до нас в редакции II в. до н.э. Дело в том, что в 213 г. до н.э. китайский
император Ши Хуан-ди, стремясь ликвидировать прежние традиции, приказал сжечь
все древние книги. Во II в. до н.э. в Китае была изобретена бумага и
одновременно начинается воссоздание древних книг. Так возникла тематика в
девяти книгах» - главное из сохранившихся математико-астрономических сочинений
в книге «Математики» помещен чертеж (рис. 12, а), доказывающий теорему
Пифагора.

Рис.
12
Ключ
к этому доказательству подобрать нетрудно. В самом деле, на древнекитайском
чертеже четыре равных прямоугольных треугольника с катетами а, b и
гипотенузой с уложены так, что их внешний контур образует квадрат со стороной
а+b, а внутренний - квадрат со стороной с, построенный на
гипотенузе (рис. 12, б). Если квадрат со стороной с вырезать и оставшиеся 4
затушеванных треугольника уложить в два прямоугольника (рис. 12, в), то ясно,
что образовавшаяся пустота, с одной стороны, равна с2, а с другой - а2+Ь2,
т.е. с2=а2+Ь2. Теорема доказана. Заметим, что
при таком доказательстве построения внутри квадрата на гипотенузе, которые мы
видим на древнекитайском чертеже (рис. 12, а), не используются. По-видимому,
древнекитайские математики имели другое доказательство. Именно если в квадрате
со стороной с два заштрихованных треугольника (рис.12, б) отрезать и приложить
гипотенузами к двум другим гипотенузам (рис.12, г), то легко обнаружить, что
полученная фигура, которую иногда называют «креслом невесты», состоит из двух
квадратов со сторонами а и b, т.е. с2=а2+Ь2
На
рисунке 13 воспроизведен чертеж трактата «Чжоу-би». Здесь теорема Пифагора
рассмотрена для египетского треугольника с катетами 3, 4 и гипотенузой 5 единиц
измерения. Квадрат на гипотенузе содержит 25 клеток, а вписанный в него квадрат
на большем катете - 16. Ясно, что оставшаяся часть содержит 9 клеток.

Это
и будет квадрат на меньшем катете
Древнеиндийское
доказательство. Математики Древней Индии заметили, что для доказательства
теоремы Пифагора достаточно использовать внутреннюю часть древнекитайского
чертежа. В написанном на пальмовых листьях трактате «Сиддханта широмани»
(«Венец знания») крупнейшего индийского математика XII в. Бхаскары помещен
чертеж (рис.14,а) с характерным для индийских доказательств словом «смотри!».
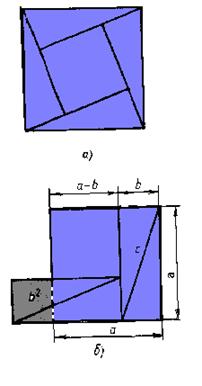
Рис.
13
пифагор математический философия число
Как
видим, прямоугольные треугольники уложены здесь гипотенузой наружу и квадрат с2
перекладывается в «кресло невесты» а2-b2 (рис.14, б). Заметим, что частные случаи теоремы
Пифагора (например, построение квадрата, площадь которого вдвое больше площади
данного квадрата) встречаются в древнеиндийском трактате «Сульва сутра» (VII -V
вв. до н.э.).
Доказательство
Евклида
Приведено
в предложении 47 первой книги «Начал». На гипотенузе и катетах прямоугольного
треугольника АВС строятся соответствующие квадраты (рис. 15) и доказывается,
что прямоугольник BJLD равновелик квадрату ABFH, а
прямоугольник ICEL - квадрату АСКС. Тогда сумма квадратов на катетах будет
равна квадрату на гипотенузе. В самом деле, затушеванные на рисунке
треугольники ABD и BFC равны по двум сторонам и углу между ними: FB=AB, BC==BD и ÐFBC=d+ÐABC=ÐABD. Но SABD=1/2 SBJLD, так как у треугольника ABD и прямоугольника BJLD
общее основание BD и общая высота LD. Аналогично SFBC=1\2 SABFH (BF-общее основание, АВ-общая высота).

Рис.
15
Отсюда,
учитывая, что SABD=SFBC ,
имеем SBJLD= SABFH. Аналогично, используя равенство треугольников ВСК. и
АСЕ, доказывается, что SJCEL=SACKG. Итак, SABFH+SACKG=SBJLD+SJCEL= SBCED , что и требовалось доказать. Доказательство Евклида
в сравнении с древнекитайским или древнеиндийским выглядит чрезмерно сложным.
По этой причине его нередко называли «ходульным» и «надуманным». Но такое
мнение поверхностно. Теорема Пифагора у Евклида является заключительным звеном
в цепи предложений 1-й книги «Начал». Для того чтобы логически безупречно
построить эту цепь, чтобы каждый шаг доказательства был основан на ранее
доказанных предложениях, Евклиду нужен был именно выбранный им путь.
Еще
давно была изобретена головоломка, называемая сегодня «Пифагор». Нетрудно
убедиться в том, что в основе семи частей головоломки лежат равнобедренный
прямоугольный треугольник и квадраты, построенные на его катетах, или, иначе,
фигуры, составленные из 16 одинаковых равнобедренных прямоугольных
треугольников и потому укладывающиеся в квадрат. Такова лишь малая толика
богатств, скрытых в жемчужине античной математики - теореме Пифагора. Далее я
рассмотрю несколько алгебраических доказательств теоремы.
ДОКАЗАТЕЛЬСТВО
ТЕОРЕМЫ ПИФАГОРА
Пусть
Т- прямоугольный треугольник с катетами а, b и гипотенузой с (рис.16, а).
Докажем, что с2=а2+Ь2.
Построим
квадрат Q со стороной а+Ь (рис.16, б). На сторонах квадрата Q
возьмем точки А, В, С, D так, чтобы отрезки АВ, ВС, CD, DA
отсекали от квадрата Q прямоугольные треугольники Т1, Т2,
Т3, Т4 с катетами а и b. Четырехугольник ABCD
обозначим буквой Р. Покажем, что Р - квадрат со стороной с.
Все
треугольники Т1, Т2, Т3, Т4 равны
треугольнику Т (по двум катетам). Поэтому их гипотенузы равны гипотенузе
треугольника Т, т. е. отрезку с. Докажем, что все углы этого четырехугольника
прямые.
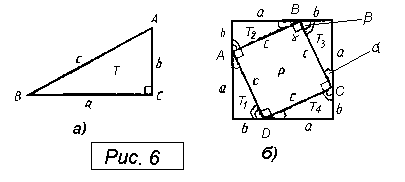
Пусть
a и b- величины острых углов треугольника Т. Тогда, как вам известно, a+b= 90°. Угол у при вершине А четырехугольника Р вместе
с углами, равными a и b, составляет развернутый угол.
Поэтому a+b=180°. И так как a+b= 90°, то g=90°. Точно так же доказывается, что и остальные углы
четырехугольника Р прямые. Следовательно, четырехугольник Р - квадрат со
стороной с.
Квадрат
Q со стороной а+Ь слагается из квадрата Р со стороной с
и четырех треугольников, равных треугольнику Т. Поэтому для их площадей
выполняется равенство S(Q)=S(P)+4S(T).
Так
как S(Q)=(a+b) 2; S(P)=c2 и S(T)=1/2(ab), то, подставляя эти выражения в S(Q)=S(P)+4S(T),
получаем равенство (a+b)2=c2+4(1/2)ab Поскольку (a+b)2=a2+b2+2ab,
то равенство (a+b)2=c2+4(1/2)ab можно записать так: a2+b2+2ab=c2+2ab. Из равенства a2+b2+2ab=c2+2ab следует, что с2=а2+Ь2.
ЕЩЕ
ОДНО АЛГЕБРАИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО
Пусть
АВС - данный прямоугольный треугольник с прямым углом С. Проведем высоту CD из
вершины прямого угла С (рис.17).
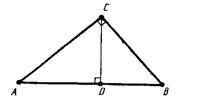
По
определению косинуса угла (Косинусом острого угла прямоугольного треугольника
называется отношение прилежащего катета к гипотенузе) соsА=AD/AC=AC/AB.
Отсюда AB*AD=AC2.
Аналогично соsВ=BD/BC=BC/AB. Отсюда AB*BD=ВС2.
Складывая полученные равенства почленно и замечая, что AD+DB=AB,
получим: АС2+ВС2=АВ(AD + DB)=АВ2.
Теорема доказана.
В
заключении еще раз хочется сказать о важности теоремы. Значение ее состоит,
прежде всего, в том, что из нее или с ее помощью можно вывести большинство
теорем геометрии. К сожалению, невозможно здесь привести все или даже самые
красивые доказательства теоремы, однако хочется надеется, что приведенные
примеры убедительно свидетельствуют об огромном интересе сегодня, да и вчера,
проявляемом по отношению к ней.
Все задачи, связанные с решением квадратных уравнений, решались
пифагорейцами геометрически с помощью циркуля и линейки. Геометрические методы
этих уравнений были хорошо разработаны, причем никаких проблем с
несоизмеримостью при геометрических построениях не возникало. Казалось, в
геометрической алгебре надолго воцарился безоблачный покой.
Однако уже в V в. до н.э. появились задачи, которые никак не удавалось
решить с помощью циркуля и линейки. Это знаменитые три классические задачи
древности, которые были окончательно решены только в XIX в., то есть через два
с половиной тысячелетия! Вот эти задачи:
1. Удвоение куба. Построить куб, объем которого в два раза больше объема
данного куба.
2. Трисекция угла. Произвольный угол разделить на три равные части.
. Квадратура круга. Построить квадрат, равновеликий данному кругу.
Остановимся подробно лишь на первой задачи, поскольку ее поразительное по
красоте решение было найдено на рубеже - вв. до н.э. последним и наиболее
выдающимся представителем пифагорейской школы Архитом. Что касается двух других
классических задач, то они также были решены примерно в это же время софистом
Гиппием из Элиды и его учеником Диностратом. Гиппий дал способ построения
особой линии, называемой квадратрисой, (должна быть сноска) с помощью которой и
было найдено решение задач о трисекции угла и квадратуре круга. Но ни решение
Архита, ни решение Гиппияи Динострата не были классическими решениями задач
древности, так как они либо привлекали другие построения, кроме построений
циркулем и линейкой, либо (как у Архита) выходили их плоскости в пространство.
Начиная с эпохи Возрождения, с возрождением интереса к античному наследию
и развитием математики, страсти вокруг классических задач разгораются с новой
силой. Простота постановки задач завораживала и притягивала как магнит. Поток
"решений" рос как снежный ком, так что в 1775г. Парижская Академия
наук. Лишь в 1837 г. французский математик Пьер Ванцель (1814-1848) доказал,
что задачи удвоения куба и трисекции угла сводятся к решению кубических
уравнений
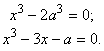
которые
неразрешимы в квадратных радикалах и, значит, не могут быть решены с помощью
циркуля и линейки. Еще через 50 лет, в 1882 г., немецкий математик Карл
Линдеман (1852-1939) доказал трансцедентность (от лат. transcendent - выходящий
за пределы) числа (т.е. тот факт, что число не удовлетворяет никакому
алгебраическому уравнению с целыми коэффициентами), а значит, и невозможность
построения квадратуры круга с помощью циркуля и линейки.
Но
вернемся к задаче об удвоении куба. Эту задачу называют делосской проблемой,
ибо с ней связана красивая легенда. Однажды на острове Делос вспыхнула эпидемия
чумы. Испуганные жители острова обратились за советом к Дельфийскому оракулу,
который сказал, что нужно удвоить золотой жертвенник богу Аполлону, имеющий
форму куба. Простодушные делосцы отлили еще один куб и поставили его на первый.
Однако чума не унималась. Тогда они вновь обратились к оракулу, и оракул
ответил, что они не решили поставленной задачи: новый жертвенник имел вдвое
больший объем, но не имел формы куба. Не найдя нужного решения, жители Делоса
обратились к Платону, но великий философ ответил уклончиво: "Боги
недовольны вами за то, что вы мало занимаетесь геометрией". Платон сам не
знал решения задачи, которую вскоре блестяще решил его друг Архит.
Архит
из Тарента (ок. 428-365 гг до н.э.) ярчайшая личность в античной истории. Живое
воплощение пифагорейского идеала, последний представитель раннего
пифагорейства. Математик и механик, философ и музыкант, полководец и
политический деятель, Архит первым упорядочил механику на основе математики,
работал над деревянной моделью летающего голубя. Архит является автором
арифметической теории пропорций, изложенной в VII книге "Начал"
Евклида.
И
все-таки самой яркой страницей в научной биографии Архита является решение
делосской проблемы. Если ребро данного куба равно a, а ребро искомого-x, то
задача об удвоении куба приводит к уравнению
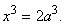 (27)
(27)
Сегодня
его решение без труда найдет каждый школьник
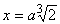 (28)
(28)
но
вот построит ли он циркулем и линейкой 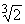 ?
?
Пифагорейцы
не знали иррациональных чисел, поэтому они искали геометрическое решение
задачи. В V в. до н.э. Гиппократ Хиосский показал, что решение делосской
проблемы можно свести к отысканию двух средних пропорциональных x и y,
называемых вставками, которые, будучи "вставленными" между данными a
и 2a, образуют непрерывную пропорцию
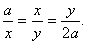 (29)
(29)
В
самом деле, из первого равенства имеем x =ay, а
из второго y
=ay, а
из второго y =2ax. Следовательно,
=2ax. Следовательно,
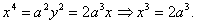
Итак,
первая вставка x и есть ребро искомого куба.
Архит
заметил, что если из вершины M прямоугольного треугольника, опирающегося на
диаметр, опустить перпендикуляр в точку C, а из C опустить перпендикуляр на
другой катет (рис.18), то получится пять подобных треугольников. Назовем их
треугольниками Архита. Достаточно рассмотреть три из них:
∆ADC ~
∆AMC ~ ∆AMB,
отсюда
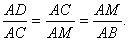
Это
и есть непрерывная пропорция вида (29).
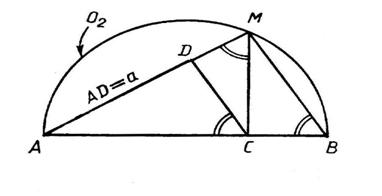
Рис.
18
Пусть
теперь AB=2a и пусть точка M движется по полуокружности диаметра 2a от точки B
к точке A. Тогда точка C будет двигаться по диаметру AB от точки B к точке A, а
длина отрезка AD примет все возможные значения от 2a (при M=B) до 0 (при M=A).
Следовательно, найдется такое промежуточное положение точки M, при котором
AD=a. Тогда AC=x= и AM=y=
и AM=y= .Это и
будет решение делосской проблемы. Осталось только найти его.
.Это и
будет решение делосской проблемы. Осталось только найти его.
Для
этого Архит фиксирует в плоскости окружность диаметра, AB=2a. Назовем ее  . На диаметре AB строится окружность
. На диаметре AB строится окружность  в перпендикулярной плоскости (по этой окружности и
будет пробегать точка M). Далее Архит начинает вращать
в перпендикулярной плоскости (по этой окружности и
будет пробегать точка M). Далее Архит начинает вращать  вокруг точки A, причем положение точки M на
вокруг точки A, причем положение точки M на  определяется положением тоски C, которая все время
движется по
определяется положением тоски C, которая все время
движется по  .Таким образом, точка M пробегает
.Таким образом, точка M пробегает  от точки B к точки A (рис19). Поверхность, которую
окружность
от точки B к точки A (рис19). Поверхность, которую
окружность  опишет в пространстве, будет тором с внутренним
диаметром, равным нулю. Поверхность, описываемая в пространстве перпендикуляром
CM, будет круговым цилиндром с радиусом a и образующей CM. Наконец, траектория
точки M будет линия пересечения
опишет в пространстве, будет тором с внутренним
диаметром, равным нулю. Поверхность, описываемая в пространстве перпендикуляром
CM, будет круговым цилиндром с радиусом a и образующей CM. Наконец, траектория
точки M будет линия пересечения  тора и
цилиндра. Линия
тора и
цилиндра. Линия 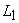 в плоскостях, перпендикулярных плоскости окружности
в плоскостях, перпендикулярных плоскости окружности  , определяет совокупность треугольников Архита (рис.19),
у которых наибольшая гипотенуза постоянна AB=2a, а катет AD изменяется от
2a(когда
, определяет совокупность треугольников Архита (рис.19),
у которых наибольшая гипотенуза постоянна AB=2a, а катет AD изменяется от
2a(когда 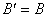 ) до 0 (когда
) до 0 (когда 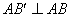 ).
).
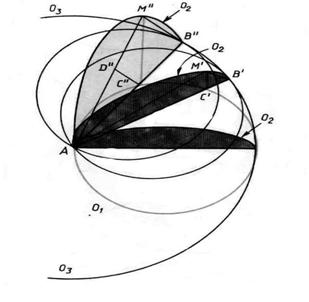
Остается
"поймать" нужное положение точки M на, 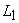 при
котором AD=a. Для этого Архит делает следующее построение (рис.20) (Для большей
наглядности на рисунках прямая
при
котором AD=a. Для этого Архит делает следующее построение (рис.20) (Для большей
наглядности на рисунках прямая  показана
не как касательная.) Из точки A на
показана
не как касательная.) Из точки A на  .
откладывается хорда
.
откладывается хорда  =a, прямая
=a, прямая  продолжается
до пересечения в точке
продолжается
до пересечения в точке  с касательной к
с касательной к  . в точке
B, и затем строится конус с образующей
. в точке
B, и затем строится конус с образующей  и осью
AB. Угол полураствора конуса
и осью
AB. Угол полураствора конуса 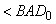 =60° (так
как ∆
=60° (так
как ∆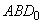 прямоугольный, как опирающийся на диаметр, и AB=2a,
прямоугольный, как опирающийся на диаметр, и AB=2a,  =a). Конус пересекает цилиндр по некоторой линии
=a). Конус пересекает цилиндр по некоторой линии  . Так вот, пространственные линии
. Так вот, пространственные линии 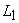 и
и  пересекаются
и их точка пересечения M* и дает искомое положение точки M на окружности
пересекаются
и их точка пересечения M* и дает искомое положение точки M на окружности  или торе. Докажем это.
или торе. Докажем это.
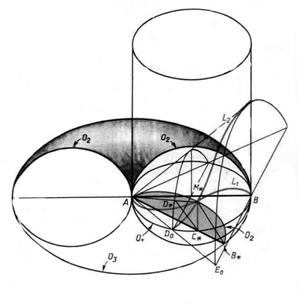
Пусть
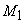 - произвольная точка на
- произвольная точка на  (рис. 21). Образующая цилиндра, проходящая через
(рис. 21). Образующая цилиндра, проходящая через 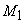 , пересекает
, пересекает  . в точке
. в точке
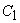 . Пусть <
. Пусть < =α (α ≤ 60), перпендикуляр, опущенный из точки
=α (α ≤ 60), перпендикуляр, опущенный из точки 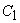 на
на 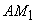 ,
попадает в точку
,
попадает в точку  , а перпендикуляр, восстановленный из точки
, а перпендикуляр, восстановленный из точки 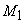 к
к 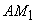 , попадает
в точку
, попадает
в точку 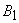 и пусть проходящее через
и пусть проходящее через 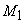 круговое сечение конуса пересекает AB в точке
круговое сечение конуса пересекает AB в точке 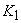 . Тогда линия
. Тогда линия  также
будет определять совокупность треугольников Архита, которые также располагаются
в плоскостях, перпендикулярных плоскости окружности
также
будет определять совокупность треугольников Архита, которые также располагаются
в плоскостях, перпендикулярных плоскости окружности  . Рассмотрим подробнее эти треугольники.
. Рассмотрим подробнее эти треугольники.

Из
Δ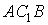 находим
находим
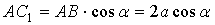 (30)
(30)
Из
Δ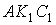 , учитывая (30), имеем
, учитывая (30), имеем
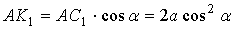 . (31)
. (31)
Из
Δ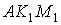 , учитывая (31), находим
, учитывая (31), находим
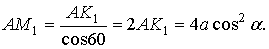 . (32)
. (32)
Из
Δ , обозначая <
, обозначая < и
учитывая (30) и (32), имеем
и
учитывая (30) и (32), имеем
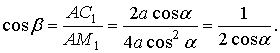 (33)
(33)
Наконец,
из Δ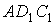 , учитывая (30) и (33), находим
, учитывая (30) и (33), находим
 .
.
Итак,
точки 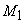 линии
линии  определяют
треугольники Архита, у которых катет
определяют
треугольники Архита, у которых катет 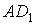 постоянен
и равен a:
постоянен
и равен a: 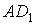 =a, а наибольшая гипотенуза
=a, а наибольшая гипотенуза 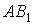 изменяется от a (при
изменяется от a (при  ) до 8a
(при
) до 8a
(при 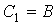 ).
).
Таким
образом, линия 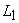 определяет треугольники Архита с постоянной
гипотенузой AB=2a, а линия
определяет треугольники Архита с постоянной
гипотенузой AB=2a, а линия  в тех же
плоскостях определяет треугольники Архита, у которых наибольшая гипотенуза
в тех же
плоскостях определяет треугольники Архита, у которых наибольшая гипотенуза 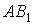 изменяется от a до 8a, а катет
изменяется от a до 8a, а катет 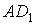 =a постоянен. Из соображений непрерывности следует,
что найдется такая точка M*, на
=a постоянен. Из соображений непрерывности следует,
что найдется такая точка M*, на  в
которой AB*=2a. При этом точка
в
которой AB*=2a. При этом точка 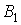 треугольников
Архита, определяемых
треугольников
Архита, определяемых  (см. рис.21), попадает на окружность
(см. рис.21), попадает на окружность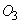 , то есть лежит на поверхности тора (см. рис.20 ).
Следовательно, линии
, то есть лежит на поверхности тора (см. рис.20 ).
Следовательно, линии 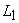 и
и  пересекаются
и в точке их пересечения у треугольников Архита AB*=2a, AD*=a и, значит, AC*=a
пересекаются
и в точке их пересечения у треугольников Архита AB*=2a, AD*=a и, значит, AC*=a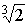 , что и дает решение делосской проблемы.
, что и дает решение делосской проблемы.
Итак,
проекция точки пересечения цилиндра, тора и конуса на окружность  - точка C* - определяет решение задачи об удвоении
куба. Таково решение делосской проблемы Архита- жемчужины античной геометрии.
- точка C* - определяет решение задачи об удвоении
куба. Таково решение делосской проблемы Архита- жемчужины античной геометрии.
2.2.2 Музыка
Музыка и математика. Сегодня эти два слова редко стоят вместе. Между тем
в пифагорейской "математике" именно музыке суждено было стать первым,
и, пожалуй, единственным физическим свидетелем, подтверждающим справедливость
пифагорейского тезиса: «Все есть число". Родство с арифметикой в
пифагорейской "математе" обогатило музыку методами построения ее
фундамента - музыкальной гаммы, фундамента, на котором и было возведено
прекрасное здание искусства музыки.
Согласно
преданию, сам Пифагор обнаружил, что приятные слуху созвучия - консонансы (от
лат. consonantia- созвучие) - получается лишь в том случае, когда длины струн,
издающих эти звуки, относятся как целые числа первой четверки, то есть как 1:2,
2:3, 3:4. При этом также было замечено, что, чем меньше число n в отношении  (n=1,2,3), тем созвучнее интервал. Это открытие
потрясло Пифагора. Еще бы: ведь столь эфемерное физическое явление, как звук и
тем более приятное созвучие, поддавалось числовой характеристике. Именно это
открытие впервые указывало на существование числовых закономерностей в природе,
и именно оно послужило отправной точкой в развитии пифагорейской философии.
(n=1,2,3), тем созвучнее интервал. Это открытие
потрясло Пифагора. Еще бы: ведь столь эфемерное физическое явление, как звук и
тем более приятное созвучие, поддавалось числовой характеристике. Именно это
открытие впервые указывало на существование числовых закономерностей в природе,
и именно оно послужило отправной точкой в развитии пифагорейской философии.
Закон
целочисленных отношений в консонансах был открыт Пифагором. Он ставил
эксперименты, не меняя натяжение струны с помощью различных грузов, а меняя
длину струны на монохорде.
Монохорд
был одним из перовых музыкальных инструментов древних греков. Он представлял
собой длинный ящик, необходимый для усиления звука, над которым натягивалась
струна. Снизу струна поджималась передвижкой подставкой. Таким образом, струна
имела постоянное натяжение, но разную длину.
Видимо,
на монохорде и было впервые обнаружено, что струна, вдвое короче данной струны,
звучит на октаву выше. Но полной ясности в том, каков физический смысл чисел n
в отношении  , определяющим консонанс, у древних долгое время не
было. Одни толковали их как силу натяжения струны, другие - как длину струны,
третьи - как высоту тона, хотя никто не знал, что такое высота тона. Ясность в
этом вопросе наступила, пожалуй, только после Архита, который сущность высоты
тона видел не в длине струны и не в силе ее натяжения (ведь один и тот же тон
можно получить на струнах разной длины и разного натяжения), а в скорости ее
движения, то есть в скорости ударения струны по частичкам воздуха. Сегодня эту
"скорость движения" мы называем частотой колебания струны. Далее
Архит установил, что высота тона (или частота колебания струны) обратно
пропорциональна ее длине.
, определяющим консонанс, у древних долгое время не
было. Одни толковали их как силу натяжения струны, другие - как длину струны,
третьи - как высоту тона, хотя никто не знал, что такое высота тона. Ясность в
этом вопросе наступила, пожалуй, только после Архита, который сущность высоты
тона видел не в длине струны и не в силе ее натяжения (ведь один и тот же тон
можно получить на струнах разной длины и разного натяжения), а в скорости ее
движения, то есть в скорости ударения струны по частичкам воздуха. Сегодня эту
"скорость движения" мы называем частотой колебания струны. Далее
Архит установил, что высота тона (или частота колебания струны) обратно
пропорциональна ее длине.
Два
закона легли в основу пифагорейской теории музыки:
.
Две звучащие струны дают консонанс лишь тогда, когда их длины относятся как
целые числа, составляющие треугольное число 10=1+2+3+4, то есть как 1:2, 2:3,
3:4. При этом интервал тем созвучнее, чем меньше число n в отношении
 (n=1,
2, 3,). (34)
(n=1,
2, 3,). (34)
2.
Высота тона определяется частотой колебания струны, которая обратно
пропорциональна длине струны l:
 (35)
(35)
Гаммой,
или звукорядом, называется последовательность звуков (ступеней звукоряда)
некоторой музыкальной системы, расположенных начиная от основного звука
(основного тона) в восходящем или нисходящем порядке. Интервалом между тонами
называется порядковый номер ступени верхнего тона относительно нижнего в данном
звукоряде, а интервальным коэффициентом I двух
тонов - отношение частоты колебаний верхнего тона к частоте нижнего:
двух
тонов - отношение частоты колебаний верхнего тона к частоте нижнего:
 (36)
(36)
Интервальные
коэффициенты (34) и соответствующие им интервалы в средние века были названы
совершенными консонансами и получили латинские названия:
Октава

Квинта
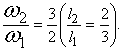
Кварта
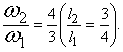
Звуки
в музыкальной системе связаны между собой определенными зависимостями. Одни из
них являются неустойчивыми и тяготеют к другим - устойчивым. В каждой
музыкальной системе существует наиболее устойчивый, основной тон, именуемый
тоникой, с которого начинается данная система. Ладом называется приятная для
слуха взаимосвязь музыкальных звуков, определяемая зависимостью неустойчивых
звуков от устойчивых, и прежде всего от тоники, и имеющая определенный характер
звучания - наклонение. Наиболее распространенные лады состоят из семи основных
ступеней. Наконец, математическое выражение системы звуковысотных отношений
(лада) называется музыкальным строем.
В
основу музыкальной шкалы - гаммы - пифагорейцы положили интервал октавы. Октава
настолько созвучный консонанс, что верхний звук кажется уменьшенной корней
нижнего, поэтому его и принято называть октавным повторением нижнего тона и
обозначать той же нотой. Далее октаву предстояло разделить на какие-то
благозвучные части. И здесь пифагорейцы, конечно, обратились к средним
величинам.
Составляя
арифметическое среднее для основного тона 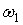 и его
октавного повторения
и его
октавного повторения 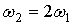 :
:
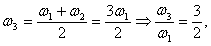
мы
обнаруживаем прекрасный результат: это арифметическое среднее дает следующий
совершенный консонанс - квинту.
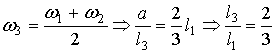 и т.д.
и т.д.
Пифагорейцы
не только нашли строгие математические методы построения музыкальных ладов,
которые практически без изменения вошли в современную музыку, но и заложили
основы учения об этосе каждого лада. В пифагорейской теории музыки был
достигнут союз математики и искусства, союз, принесший неоценимую пользу и
науке математике, и искусству музыке.
2.2.3 Астрономия
Неотъемлемой частью пифагорейской философии, также как и музыка была
астрономия.
Во все времена вселенная своей неизмеримой громадностью и красотой
притягивала внимание людей. Разумеется, звездное небо не оставило равнодушным и
разум пифагорейцев, и в пифагорейской системе знаний астрономия была наиболее
мировоззренчески значимой и наиболее поэтической наукой.
В своих астрономических гипотезах пифагорейцы исходили из одной основной
идеи - гармонического устройства Мироздания. Они верили в его стройную
организованность, симметрию, а значит, и красоту. Вот почему Вселенную
пифагорейцы называли словом КОСМОС, что в буквальном переводе означает строй,
порядок, прекрасное устройство. К сожалению, сегодня это первоначальное
пифагорейское значение слова "космос" забыто.
Пифагор из всех плоских линий самой совершенной считал окружность, а из
пространственных тел - шар. Вероятно, что мерой совершенства этих
геометрических объектов служила их симметрия: только окружность и шар обладают
центральной симметрией бесконечного порядка, т.е. при любом повороте вокруг
центра они совмещаются сами с собой. Именно из соображений совершенства
пифагорейцы считали, что планеты имеют шарообразную форму, а их траекториями
являются окружности. Эти соображения являются важнейшими астрономическими
догадками пифагорейцев.
Издревле люди наблюдали на небосводе две самые яркие звезды. Они сияли в
течение недолгого времени сразу после захода солнца и незадолго до его восхода
и были названы Вечерней и Утренней звездами. Пифагор впервые высказал
предположение о том, что эти звезды есть не что иное, как планета Венера.
По преданию, Пифагору принадлежит и первая космологическая модель
устройства Вселенной. В центре Мироздания он помещает Землю, вокруг которой
вращаются три сферы: Луны, Солнца и сфера звезд вместе с планетами. Очень скоро
эта модель была заменена более совершенной моделью (например, моделью Филолая),
в которой каждой планете выделялась своя круговая траектория.
Пифагореец Филолай, живший столетием позже своего учителя, по-видимому,
является первым в истории астрономии, кто убрал Землю из центра Мироздания и
поместил ее на круговую орбиту. Убрав Землю из центра Мироздания Филолай тем
самым исключает особую роль Земли, а, следовательно, и особую роль человечества
в этом мире. Филолай также и Луну животными и растениями, причем более
крупными, красивыми, чем земные. Важнейшей особенностью модели Филолая было то,
что он считал Землю подвижной.
Но Филолай не был гелиоцентристом, он сделал лишь первый шаг в этом
направлении. В центре космоса Филолай поместил Центральный огонь, являющийся по
Филолаю источником жизни. Кроме того, Вселенная и замыкается огненной сферой,
служащей ее наружной границей.
Между двух огней Филолай на концентрических сферах располагает Землю,
Луну, Солнце, пять планет: Меркурий, Венеру, Марс, Юпитер, Сатурн (точная
последовательность их расположения неизвестна) и сферу неподвижных звезд.
Помимо этих космических тел Филолай между Центральным огнем и Землей помещает
Противоземлю (Антихон), вероятно для того, чтобы защитить Землю от сильного
разогревания Центральным огнем или для объяснения солнечных затмений.
Но вскоре эта модель была заменена космологической моделью Платона, где
уже не было ни Центрального огня, ни Противоземли.
Вот таким был космос пифагорейцев.
ГЛАВА 2. ВЕЛИКИЕ ЭЛЛИНЫ (среднее пифагорейство).
2.1 Евдокс
Евдокс Книдский, ученик Архита Тарентского, был непосредственно
предшественником Евклида, родился около 408 г. до н.э. в Книде, на юго - западе
Малой Азии, и был известен не только как математик, но и как астроном, врач,
философ, географ, оратор и общественный деятель. Недаром друзья его называли "Евдокс
Знаменитый". В молодости он изучал математику у Архита Тарентского, а
затем философию в Академии Платона. Евдокс совершил путешествие в Египет, где
изучал астрономию. По возвращению на родину, он основал собственную школу,
сыгравшую большую роль в греческой науке.
После открытия несоизмеримости, прежняя пифагорейская теория, основанная
на понимании отношения двух отрезков как отношения двух целых чисел, не могла
дальше служить для решения геометрических задач.
Среди астрономов Евдокс получил известность благодаря описанию звездного
неба, восходов и заходов неподвижных звезд. Именно Евдоксу принадлежит одна из
первых попыток построения теории движения планет.
Важнейшим вкладом Евдокса в математику является его теория отношений,
которая выясняется в трех определениях (Евклид "Начала", опр.3,4,5).
. "Необходимым условием того, что две величины находятся в
отношении, является их однородность, а основанием отношения служит
количество".
. "Говорят, что величины имеют отношение между собой, если они,
взятые кратно, могут превзойти друг друга" ("Начала", книга,
опр.4). Иначе, для любых a и b существуют такие числа m и n, что ma>b и
nb>a.
. "Говорят, что величины находятся в том же отношении первая ко
второй и третья к четвертой, если равнократные первой и третьей одновременно
больше, или одновременно равны, или одновременно меньше равнократных второй и
четвертой каждая каждой при какой бы то ни было кратности, если взять их в
соответственном порядке" ("Начала", книга, опр. 5).
Иначе, a:b=c:d, если для любых m и n справедливо одно из утверждений:
ma>nb => mc>nd;=nb => mc=nd;<nb => mc<nd.
Евдоксова теория отношений покончила с арифметической теорией
пифагорейцев, применяемой только к соизмеримым величинам, т.е. понятие
"отношения" стало применимым и для несоизмеримых отрезков. Это была
чисто геометрическая теория, изложенная в строго аксиоматической форме.
По словам Архимеда, Евдокс разработал один из важнейших методов в
математике, " метод исчерпывания " (предвестник современного метода
пределов), с помощью которого он дал первое строгое доказательство формулы
объема пирамиды. Метод исчерпывания доказывает единственность предела, но не
решает вопрос о существовании предела.
2.2 Платон
Развитие математики, приведшей к созданию "Начал" Евклида,
стимулировалось борьбой между существующими тогда философскими школами. Не
последнюю роль в этой борьбе играла платоновская школа.
Платон (427-347 гг. до н.э.), ученик Сократа, жил в период упадка Афин.
Платон основал философскую школу, получившую название Академии, которая в
течение целого века руководила всей интеллектуальной жизнью города.
Начиная изучение Платона, следует учитывать некоторые трудности: внешнюю
и внутреннюю. Внешняя трудность заключается в том, что отсутствует не только
специальное и систематическое изложение, но и отсутствует вообще система всей
философии. Ее приходится извлекать из массы диалогов Платона, где спорящие
стороны часто не приходят ни к какому ясно выраженному выводу.
Еще большую трудность представляет внутреннее понимание философии
Платона. Существует ряд интерпретаций платонизма, отличающихся друг от друга.
По Диогену Лаэртскому платоновский диалог имеет два самых общих вида:
наставительный и исследовательский. Наставительный в свою очередь разделяется
на два вида: теоретический и практический; теоретический разделяется на
физический и логический, а практический - на этический и политический.
Исследовательский разделяется на два вида: упражнительный и состязательный;
упражнительный разделяется на повивальный (рождающий мысль) и испытательный, а
состязательный - на доказующий и опровергающий.
К физическому роду диалогов принадлежит, например: "Тимей"; к
логическому роду - "Политик", "Парменид, или Об идеях"; к
этическому - "Федр, или о любви", "Пир, или О благе"; к
политическому - "Государство, или О справедливости", "Законы,
или О законодательстве"; к повивальному - "Лахет, или О
мужестве", оба "Алкивиада"; к испытательному - "Менон, или
О добродетели", "Феэтет, или О знании"; к доказующему -
"Протагор" и к опровергающему - оба "Гиппия".
Самым трудным для понимания является платоновское учение об идеях. Очень
сложно дать ясный анализ этого учения.
Платоновская идея не есть просто субстанция, не просто миф, не просто тот
или иной Бог и не просто причина соответствующего рода вещей - это их смысловой
образец, их предельная структура, из которой вещи истекают не только
натуралистически но и логически.
Не будучи сам математиком, Платон отделял математике важное место в своей
воспитательной системе и энергично поощрял её изучение. Уже то обстоятельство,
что над входом в "Академию" помещалась надпись: "Пусть не
знающий геометрии не войдет сюда " - сыграло положительную роль для
развития математики.
Платон и платоники считали, что математические объекты занимают
промежуточное место между чувственными вещами и идеями. Как известно, лишь
идеям платоники приписывали подлинное существование, наделяя их
единственностью, вечностью и не изменчивостью. Материальные вещи являются лишь
тенью идей. Они множественны, преходящи и изменчивы. Любой математический
объект, например треугольник, хотя и обладает вечность, обладает и
множественностью, т.е. существует много треугольников, которые являются лишь
образами абсолютного треугольника, пребывающего в мире идей.
Назревшая в V в. до н.э. в Греции необходимость полного и окончательного
синтеза софистов и Сократа привела к небывалому расцвету философской мысли, без
предварительной формулировки которого останется совсем неясной вся философия
Платона. Формулировка эта сводится к синтезу космологизма и антропологизма.
Синтезировать это значит:
во-первых, понять человеческое сознание, разум с его идеями и
человеческую душу с ее вечными стремлениями как объективную реальность, как
достояние космоса:
во-вторых, прежний космос понять как рождающее человеческой души со всеми
ее разумными идеями и жизненными стремлениями.
Космический разум рассматривал уже Сократ, но это происходило у него не
систематически и было далеко от философско-эстетической системы. Необходимо
было конструировать такое космическое бытие, которое было бы и понятным для
человека разумным миром идей, создаваемых рассуждающей способностью человека, и
конструировать такой разум, который был бы столь же объективно реален и в своей
реальности столь же понятен и очевиден. Здесь и появляется платоновский термин
" ИДЕЯ ".
Платоновская идея не есть просто субъективно - человеческая идея, это
объективно - реальное бытие, независимое от человеческого сознания и
существующее до и вне всякого человека. Эта платоновская идея, с одной стороны,
уже не имеет ничего общего с материальной действительностью; а с другой
стороны, она и есть не что иное, как разумно жизненная и вполне материальная
действительность. Она и есть порождающая модель всего чувственного мира.
Мы привыкли думать, что субъективная идея есть отражение объективной материальной
действительности. Платон же прямо признавал идеи существующими вне и независимо
от вещей, хотя они и были для него принципами оформления этих вещей.
Платоновскую идею следует понимать как тождество субъективного и объективного,
мысленного и материального.
Разум Платона со всеми своими идеями реален, а материя со всей своей
непреодолимой реальностью воплощает в себе идеи разума и без них повисает в
воздухе, превращаясь в непознаваемое.
Высоким принципом для античной философии был чувственный и идеально
организованный космос. Этот принцип и положил в основание всей своей эстетики
Платон.
Платон исходит из геоцентрической модели космоса: центром Мироздания для
него является неподвижная Земля, вокруг которой на семи сферах вращаются Луна,
Солнце, Венера, Меркурий, Марс, Юпитер и Сатурн. Далее следует сфера
неподвижных звезд. На базе этой системы Мироздания Платон развивает теорию
небесного гептахорда (семиструнника) т.е. теорию семи неподвижных сфер,
построенных на музыкальных отношениях. Согласно Платону, небесный гептахорд
описывается рядом чисел
1 2 3 4 8 9 27
Однако порядок членов этого ряда в космической системе Платоном не
указан.
Ключ к платоновскому гептахорду спрятан в числах 1, 2, 3, именно в
пифагорейском понимании единицы как символа неделимого начала, двойки как
символа неопределенной бесконечности и тройки - как символа определенности. Но
Платон добавляет к этому ряду в качестве символа беспредельного куб со стороной
2, площадью грани 4 и объемом 8. А в качестве символа определенности - куб со
стороной 3, площадью грани 9 и объемом 27.
Платон погружает свои идеи в недра живого телесного космического бытия.
Тот самый, живой, вполне физический космос, который был воспет досократиками.
Платон никуда не пошел дальше пифагорейских сфер, Парменидова
"единого", Демокритовых атомов. А никуда и невозможно было идти,
оставаясь греческим и античным мыслителем. Но он интерпретировал этот космос с
точки зрения его идеальных связей, расчленил в нем физическое и смысловое и
опять отождествил это но уже по смыслу при помощи чистых понятий.
Слово "идея" имеет своим корнем "вид". Идея - то, что
видно в вещи. В греческом языке это слово очень часто служит для обозначения
внешнего вида вещи, наружности человека. Если всмотреться в сущность вещи, в ее
смысл, то он ("вид") тоже будет "виден" и глазу и главным
образом уму. Вот эта видимая умом ("умная") сущность вещи, ее
внутренне - внешний облик, и есть ИДЕЯ вещи.
Однако идея вещи есть не только видимая умом пассивная фигурность вещи.
Она есть в то же время и самая субстанция вещи, ее внутренне определяющая сила.
Лосев А.Ф. говорит: "Платон вовсе не гонится за философской
системой, но считает своим главным философским методом вечное искание, вечный
переход от одних концепций к другим, сплошное становление философской мысли, и
притом становление ценою полной неустойчивости употребляемой терминологии,
ценой разнобоя в самом существенном словоупотреблении ".
2.3 Александрийская школа
2.3.1 Евклид
В конце IV в. до н.э. после походов Александра Македонского, была создана
огромная, но недолговечная империя, включавшая Грецию, Египет, Месопотамию,
Персию и др. страны Средиземноморья и Ближнего и Среднего Востока. Период
эллинизма длился до завоевания эллинистических стран Римом, закончившегося I в.
до н.э. Крупнейшими центрами культурной жизни эллинистических стран были
Александрия, Пергам и остров Родос. Александрия становится крупнейшим научным
центром.
К первым представителям Александрийской школы принадлежит Евклид, который
жил около 300 г. до н.э. Его жизнь мало известна. В одном из своих сочинений
поздний пифагореец - неоплатоник Папп, живший в Александрии в - вв. н.э.,
изображает Евклида, как человека исключительно честного, скромного, которому
были чужды гордость и эгоизм Он очень строго относился к изучению математики,
об этом можно судить из рассказа неоплатоника Прокла: царь Птолемей спросил
Евклида, нельзя ли найти более короткий и менее утомительный путь к изучению
геометрии, чем его "Начала". Евклид ответил: " Нет царской
дороги к геометрии!".
Из трудов Евклида, кроме "Начал", до нас дошли: 1)
"Данные" - задачи, решаемые с помощью геометрической алгебры; 2)
"О делении фигур" - задачи на построение; 3) "Феномена"
(явления) - астрономическое сочинение; 4) "Оптика". Другие
произведения утеряны.
Славу Евклиду принесли его "Начала", состоящие из тринадцати
книг. Первые шесть книг этого труда посвящены планиметрии, 7-10 - учению о числе, 11-13 -
стереометрии. Содержание книг 1-4, 7-9 происходят в основном от ионийской и
пифагорейской школ, 5 и 12 - от Евдокса, 10 и 13 - от Теэтета. Оригинальная
рукопись "Начал", которая долгое время сохранялась в Александрийском
музее, не дошла до нас. "Начала" распространялись в многочисленных
рукописях, которые на протяжении десятков и сотен лет комментировались,
снабжались примечаниями и исправлениями, местами дополнялись и изменялись.
Отсюда понятно, почему тексты дошедших до нашего времени рукописных копий не
совпадают полностью. "Начала" Евклида были переведены на десятки
языков, изданы и переизданы в разных странах много раз. На русском языке
"Начала" были изданы три раза в 18 в. и четыре раза в 19 в. Последний
и самый совершенный перевод с греческого на русский язык был осуществлен
советским ученым, профессором Д.Д. Мордухай - Болтовским и опубликован в
1948-1950 гг.
Начиная с III в. до н.э. и до середины прошлого века "Начала"
были образцом строго логического изложения геометрии. Евклид исходил из
определений геометрических понятий и аксиом. Характер определений у Евклида
различен. В большинстве случаев они описательные, например: "Точка есть
то, что не имеет частей" книга I. Но встречаются словесные определения,
вроде определения 19 книги I: "Прямоугольные фигуры суть те, которые
содержатся между прямыми", и аксиоматические, т.е. те, которые могут быть
сформулированы в виде аксиом, например, определение I книги III: "Равные
круги суть те, у которых диаметры равны или прямые из центра (радиусы)
равны". Если определения предписаны почти каждой книге (кроме VIII, IX,
XII и XIII), постулаты (их пять) и аксиомы (их девять) помещены впереди всего
труда - в первой книге.
Постулаты - это требования построить некоторые простейшие фигуры.
Построения, допустимые постулатами, предполагают линейку без делений, не
допускающую измерения расстояний. Циркуль предназначался для описания из данной
точки окружностей с данным радиусом.
Ограничения, наложенные на употребление линейки и циркуля, по-видимому,
были связаны с тем, что эти инструменты заменили собой веревку, первоначально
служившую как для проведения прямых, так и для описания окружностей.
Первые три постулата гласят: "Что от всякой точки до всякой точки
«можно» провести прямую линию"; "Что ограниченную прямую «можно»
непрерывно продолжать по прямой"; "Что из всякого центра и всяким
раствором «может быть» описан круг". Четвертый постулат выдвигает
требование равенства всех прямых углов между собой, которое теперь не считается
постулатом, а доказывается. Смысл пятого постулата заключается в том, что точка
пересечения двух прямых считается построенной, если при пересечении третьей
прямой внутренние односторонние углы в сумме меньше двух прямых. Этот постулат
получил название постулата параллельности. Попытки доказательства данного
постулата делались еще со времен Евклида и продолжались на протяжении двух
тысячелетий, пока в 1826 г. Русский математик Н.И. Лобачевский не создал свою
неевклидову геометрию. Из этого вытекало, что пятый постулат доказать нельзя.
Каждое геометрическое предложение формулируется в общих выражениях, затем
конкретно указывается на чертеже что дано и что требуется доказать или
построить. После доказательства следует заключение, повторяющее начальную
формулировку и заканчивающееся словами: "что и требовалось доказать"
или "что и требовалось сделать".
На протяжении многих столетий до 19 в. изучение геометрии велось по
"Началам" Евклида. Наши современные учебники имеют много общих черт с
"Началами": планиметрия и стереометрия излагаются раздельно; теоремам
предшествуют определения и аксиомы. Многие теоремы по содержанию совпадают с
теми, которые имеются в "Началах".
2.3.2 Архимед
Величайшим математиком эпохи эллинизма был Архимед (287-212 гг. до н.э.),
живший в Сиракузах, где он был советником царя Гиерона. Он - один из немногих
ученых древности, которых мы знаем не только по имени, сохранились немногие
сведения о его жизни. Архимед был убит, когда римляне взяли Сиракузы, при осаде
которых было использовано защитниками техническое искусство ученого. Подобная
склонность к практическим применениям представляется весьма необычной, если
учесть как относились к этому ученые раннего периода.
Наиболее важный вклад Архимеда в математику относится к той области,
которую теперь мы называем интегральным исчислением:
теоремы о площадях, плоских фигур и об объемах тел. Архимед впервые ввел
понятие и рассмотрение верхней и нижней сумм, ограничивающих искомую величину
(площадь или объем), разность между которыми становилась сколь угодно малой.
Для прямой, окружности, конических сечений и спирали он доказал важнейшее
свойство непрерывных величин: т.е. то, что они между двумя своими значениями
принимают все промежуточные значения. Архимед нашел также способ сведения
большого класса задач на экстремум к задачам на построение касательной.
В "Измерении круга" он нашел приближенное выражение для
окружности, пользуясь вписанными и описанными правильными многоугольниками.
Одной ярко выраженной особенностью математического творчества Архимеда
является его связь с механикой, гидростатикой и астрономией, сближение теории с
практикой, вычислительной математике и развитие ее приемов.
В математике Архимеду принадлежит сочинение относящееся к полуправильным
многогранникам, т.е. таких выпуклых многогранников, все грани которых -
правильные многоугольники, более чем одного вида. Архимед нашел тринадцать
таких тел, ограниченных 8,14,26,32,38,62 или 92 гранями, имеющими форму
треугольников, квадратов, пятиугольников, шестиугольников, десятиугольников или
двенадцати угольников.
Обилие вычислений у Архимеда отличает его от большинства математиков
Греции.
.3.3 Эратосфен
Также одним из выдающихся математиков периода эллинизма был Эратосфен. О
нем сохранилось сравнительно много биографических данных, родившемся в 276 или
275 (а по другим сведениям в 284) г. до н.э. в Кирене, на северном побережье
Африки. Прожил почти всю свою жизнь в Александрии. Некоторое время Эратосфен провел
в Афинах. Умер около 194 г. до н.э., ослепший и в полной нищете.
Дарования Эратосфена были разносторонни; Архимед их высоко ценил, но
выдающихся трудов Эратосфен не создал.
До нас дошли лишь два собственно математических открытия Эратосфена: это
его знаменитое "решето" ("коскинон") и его решение
делийской проблемы. Решето Эратосфена представляет собой известный прием для
нахождения всех простых чисел, меньших чем заданное число n, кроме числа 2,
которое нужно добавить.
В комментарии к сочинению Архимеда "О шаре и цилиндре" Евтохий
рассказывает историю делийской проблемы, ее легендарное возникновение и
решения, предложенные Архитом, Евдоксом и Менехмом, причем все это в виде
письма Эратосфена Птолемею. Хотя само письмо является подложным, но содержащееся
в нем решение Эратосфена подлинно. Решение Эратосфена является механическим и
осуществляется при помощи простого прибора, названного "месолабон".
Эратосфен придавал своему открытию столь большое значение, что воздвиг колонну,
посвященную Птолемею, с надписью, излагающей суть построения, и бронзовым
изображением прибора.
Эратосфен является также автором сочинения "Платоникос", в
котором основные математические понятия, в частности пропорции, а также
принципы музыки рассматривались в свете платоновой философии.
Наряду с чисто математическими нельзя, однако, не упомянуть и
астрономические работы Эратосфена, среди которых находится прославившее его имя
измерение Земли, описанное им в отдельном сочинении. Это - первое исторически
установленное определение размеров Земли. Эратосфен нашел, что длина большой
окружности земного шара равна 250 000 египетских стадий, т.е. в зависимости от
различных оценок, даваемых этой мере, заключена между 39 и 46 тысячами
километров; эта оценка более точна, чем у Архимеда, и должна считаться
необыкновенно удачной.
Сочинение "Измерение Земли" содержало и многие другие сведения
по математической географии и астрономии. Эратосфен занимался также
хронологией; ему приписывают разработку взамен старого египетского календаря с
високосным годом в 366 дней каждый четвертый год. Этот календарь, приводивший в
соответствие календарные даты с действительными временами года, был введен
указом от 7 марта 238 г. до н.э., объявленном на собрании жрецов в Канопе.
2.3.4 Аполлоний
Третьим и последним из великих математиков эпохи эллинизма наряду с
Евклидом и Архимедом был Аполлоний Пергский. Ели Евклиду мы обязаны знакомством
с элементарной геометрией древних, то их теорию конических сечений мы знаем по
великому труду Аполлония.
Аполлоний из Перги (ок. 260-170 гг. до н.э.),по-видимому, вел обучение в
Александрии, где изучал математику у учеников Евклида, и в Пеогаме. Ярчайшим
его достижением является трактат из восьми книг о конических сечениях ("О
кониках"). Сохранилось семь книг из восьми, три из них только в арабском
переводе.
Первые четыре книги содержат систематическое изложение главных свойств
данных сечений. Эти свойства служат для приложения теории к решению задач на
построение посредством пространственных мест. Навина исходной точки
исследования Аполлония заключается в следующем : вместо того, чтобы
рассматривать сечения конусов вращения плоскостями, находящихся в определенном
положении, Аполлоний сразу же приступает к изучению произвольных плоских
сечений. Затем, чтобы связать с этими сечениями некоторое планиметрическое
свойство, способное лечь в основу для дальнейших исследований, Аполлоний
обобщает прием изучения сечений, перпендикулярных к плоскости симметрии конуса,
на произвольные сечения. Это обобщение позволяет относить конические сечения к
любому ее диаметру и сопряженным с ним хордам.
Книга первая "Конических сечений" открывается определением
кругового конуса, причем конус рассматривался по обе стороны от вершины. Здесь
же выводились основные понятия теории конических сечений, вершина конического
сечения, его диаметры, сопряженные диаметры.
Аполлоний получает эллипс, гиперболу или параболу в зависимости от того,
пересекает ли плоскость одну только полость конуса, обе его полости или она
параллельна одной из образующих конуса. Мы называем данные кривые, следуя
Аполлонию, который впервые ввел эти термины. Данные названия выражают одно из
свойств этих кривых, связанное с площадями и выражаемое, в наших обозначениях,
уравнениями :
y =px, y
=px, y =px+
=px+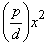
(у
Аполлония p и d - отрезки; знак "+" дает гиперболу, знак
"-"дает эллипс). Парабола здесь значит "приложение", эллипс
- "приложение с недостатком", гипербола - "приложение с
избытком".
В
первой книге Аполлоний также доказывает, что вид уравнения, которым
характеризуется каждое из трех конических сечений, не зависит от линий
(диаметра и сопряженной ему хорды), к которым оно отнесено. Т.е. доказывается
инвариантность этого свойства при переходе от одной системы координат к другой.
Вторая
книга начинается разделом об асимптотах гиперболы, а далее Аполлоний находит
касательные и асимптоты к кривым второго порядка.
В
III книге содержатся предложения о равенстве площадей прямоугольных фигур,
образованных касательными и секущими конических сечений, выводятся фокусы
эллипса, гиперболы и исследуются их свойства.
В
IV книге Аполлоний определяет число точек пересечения двух кривых второго
порядка и доказывает, что это число не превышает 4. Этот вопрос был важен для
греков, так как именно точки пересечения нужны были для решения таких задач,
как задача удвоения куба, для которой эти кривые и были изобретены. Четвертой
книгой как бы завершалась более элементарная часть учения о конических
сечениях.
В
оставшихся четырех книгах Аполлоний рассматривает подобные сечения двух прямых
подобных конусов; хорды, параллельные сопряженным диаметрам и доказывает
теоремы о постоянстве суммы квадратов сопряженных диаметров и площади
построенного на них параллелограмма и др.
Аполлоний
занимался усовершенствованием системы счисления, значительно облегчил умножение
больших чисел в греческой нумерации.
Теория
конических сечений Аполлония была положена в основу "Введения" Ферма
и "Геометрии" Декарта. У Аполлония не было общих произвольно взятых
координат, но были координатный угол и координатные линии, всегда
ориентированные по двум сопряженным направлениям кривой второго порядка. Этим
он и предвосхитил идеи аналитической геометрии.
ГЛАВА 3. ЭЛЛИНИЗМ (ПОЗДНЕЕ ПИФАГОРЕЙСТВО)
После завоевания римлянами главных эллинистических стран характер
математики в Александрии стал отличатся от математики периода эллинизма.
Основной причиной изменения характера математики было широкое усвоение традиций
математиков и астрономов Вавилона. В результате этого усвоения область
практического применения математики расширилась, в особенности за счет
применения к астрономии. На первое место начинает выдвигаться вычислительная
математика, в частности возникает нужная астрономии тригонометрия.
Рассмотрение александрийской математики римской эпохи начнем с одного из
самых ранних математиков Никомаха из Герасы.
3.1 Никомах
Никомах из Герасы (около 100 г.), его "Введения к арифметике"
наиболее полное из сохранившихся изложений пифагорейской арифметики. Там
рассматриваются большей частью те же вопросы, что и в арифметических книгах
Евклида, но в отличие от Евклида Никомах пользуется арифметическими
обозначениями.
"Введение к арифметике" следует считать не столько научным
произведением, сколько популярным введением в пифагорейское учение о числах. По
уровню изложения оно далеко отстает от Евклида. Никомах не дает настоящих
доказательств, а только подтверждает предложения конкретными примерами. Из
содержания "Введения к арифметике", кроме классификации чисел и
отношений между ними, включая и многоугольные, пирамидальные и другие фигурные
числа, заслуживает внимания, что Никомах, не давая формулы суммирования кубов
чисел, тем не менее указывает, что в ряду нечетных чисел 1, 3, 5, 7, 9, 11, ...
кубами являются 1, 3+5=2, 7+9+11=3, ... Однако, одним из крупнейших
произведений Александрийской школы римского периода являются сочинения
Птолемея.
3.2 Птолемей
Знаменитый греческий астроном, географ и оптик Птолемей, производивший
свой наблюдения с 127 г. по 151 г. в Александрии, написал "Математическое
собрание в XIII книгах", получившие позднее арабизированное название
"Альмагест" ("Величайшее построение"). Это труд является
превосходным изложением всех астрономических знаний того времени.
Книга I "Альмагеста" излагает теорию плоской и сферической
тригонометрии, необходимой для составления таблиц хорд (синусов) и пользование
ею.
Кроме "Альмагеста" Птолемей оставил нам "Съемку" и
"Планисферий" - астрономические сочинения, широко применяющие
математику. Первое сочинение излагает теорию ортогональной проекции небесной
сферы на три взаимно перпендикулярные плоскости: меридиана, горизонта и
вертикального круга. С помощью этих проекций решалась задача нахождения
положения Солнца над горизонтом в определенный день и час для определенной
широты.
"Планисферий" сохранился лишь в переводе с арабского и содержит
сведения о проекции северной небесной полусферы на плоскость экватора из точки,
помещенной в южном полюсе.
Однако, Птолемей занимался не только астрономией, но и уделял время
математике. Как свидетельствует Прокл (см.[6]) у Птолемея был труд посвященный
доказательству V постулата Евклида о параллельности. Итак, Птолемей сделал
первую попытку из тех многочисленных попыток доказать V постулат, которые
делались математиками разных веков и народов.
3.3 Герон
Одним из виднейших математиков эпохи эллинизма, писавшим почти по всем
вопросам математики, механики, астрономии, был Герон Александрийский,
родившийся в III в н.э. Сочинения Герона носили больше прикладные, чем
теоретические цели. Им было создано практическое и теоретическое руководство по
геодезии, служившее этой цели на протяжении многих веков.
В чисто теоретической области Герон оставил после себя комментарии к
"Началам" Евклида. В другом сочинении, "Определения", он
излагает геометрические термины, опираясь на учение Евклида. Ценность этого
сочинения в том, что здесь даны различные определения отдельных геометрических
понятий в их историческом развитии. (см. [32])
Наиболее важным геометрическим сочинением Герона является его
"Метрика" (учение об измерении) в трех книгах. В них содержатся
правила измерения площадей и объемов поверхностей; формула для вычисления
площади неравностороннего треугольника, так называемая "формула
Герона", которая была известна еще Архимеду. Причем, все эти правила
строго доказываются. Другое же сочинение Герона, "Геометрия",
напротив не содержит ни каких доказательств и даже формулировок в общем виде, а
представляет собой набор конкретных задач.
В механике и оптике Герону принадлежат следующие достижения:
доказательство того, что равномерное движение складывается по правилу
параллелограмма; доказательство равенства углов падения и отражения.
3.4 Диофант
До 300 г. к сокровищнице арифметики в том объеме, в котором она имелась
во времена расцвета греческой геометрии, были присоединены лишь отдельные
открытия. Только у Диофанта александрийского мы встречаем нечто новое,
представляющее большой интерес.
Родился Диофант вероятно в III в., о его жизни нет почти никаких
сведений, наши представления ограничиваются стихотворением-задачей, в которой
говорится, что его отрочество составляло 1/6 его жизни, борода начала расти
спустя 1/12, женился он после 1/7, и спустя пять лет у него родился сын,
который прожил 1/2 возраста отца, а последний умер спустя четыре года после
смерти сына. Составив и решив уравнение получаем, что Диофант прожил 84 года.
Диофант напрямую не принадлежал к пифагорейской традиции, хотя многое
заимствовал у пифагорейцев. Главной отличительной чертой было понятие числа.
Диофанта фактически разрушает понимание числа как величины. Для него число
несет отголосок функциональной зависимости и появляются дроби.
Сохранилось часть математического трактата Диофанта
"Арифметика", состоящая из 13 книг (до нас дошли только 6 книг).
Теоретическая основа труда Диофанта и цель его исследований заключается в том,
чтобы избежать иррациональных количеств. При помощи этой теории он в состоянии
дать примеры определенных задач, приводимых к уравнениям с рациональными
решениями, и, кроме того, дать обширный ряд неопределенных задач, для которых
можно всегда найти рациональные решения.
Специфика Диофанта заключается в том, что он занимается лишь специальными
числовыми задачами и для их решения пользуется лишь чисто числовыми операциями,
не устанавливая никогда общих теорем.
Диофант не нуждается в геометрическом представлении чисел, чем резко и
отличается от пифагорейцев, однако заимствует свою терминологию из мира
геометрических представлений, говоря, например, прямоугольник вместо
произведения.
У Диофанта мы впервые встречаем систематическое использование
алгебраических символов.
Диофант нашел решения около 130 неопределенных уравнений, принадлежащих
более чем к 50 различным классам. Общих методов решения неопределенных
уравнений или их классификации у Диофанта нет. Нет и доказательств
справедливости полученного результата, его истинность проверяется
непосредственной подстановкой.
В "Арифметике", помимо изложения начал алгебры, приведено много
задач, сводящихся к неопределенным уравнениям различных степеней, и указаны
методы нахождения решений таких уравнений в рациональных положительных числах.
Неопределенные квадратные уравнения встречаются в "Арифметике" прежде
всего в виде :
Ax + Bx + C=y
+ Bx + C=y
В
зависимости от значений коэффициентов A,B,C возникают различные случаи решения.
В случае когда В=0 Диофант дает способ нахождения произвольного числа неполного
уравнения, если известен один из них. Диофант замечает, что уравнение решается
лишь тогда, когда А является суммой двух квадратов. В случае полного уравнения
он не сводит его к неполному виду, а рассматривает лишь случай, когда либо А,
либо С являются полными квадратами, либо когда таковым является выражение В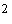 - АС.
- АС.
Кроме
этих уравнений, Диофант решает и системы (см. [29],[32]):
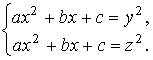
Типично
для Диофанта то, что его интересуют только положительные рациональные решения.
Иррациональные решения он называет "невозможными" и тщательно
подбирает коэффициенты так, чтобы получались искомые положительные рациональные
решения. Имел также представление об отрицательных числах, например знал, что
квадрат отрицательного числа равен положительному числу.
Имя Диофанта прочно закрепилось и в той части теории чисел, которая
изучает приближения действительных чисел рациональными. Эти приближения
называются диофантовыми. К теории диофантовых приближений относят вопросы,
касающиеся решения в целых числах неравенств или их систем.
Именем Диофанта названы два больших раздела теории чисел: теория
диофантовых уравнений и теория диофантовых приближений. Сочинение Диофанта были
отправной точкой для теоретико-числовых исследований Ферма, Эйлера, Гаусса и
др. математиков.
В дальнейшем, следовавшие за Диофантом математики Римской эпохи были
больше комментаторами, чем самостоятельными созидателями. К ним относятся
например: Порфирий, Ямвлих, Прокл. Но наиболее яркими были Ямвлих и Прокл.
3.5 Ямвлих
Порфирий (233-304 гг.), ученик виднейшего представителя мистической
философской школы неоплатонизма Плотина, написал комментарии к
"Началам" Евклида. Его учеником был Ямвлих, который родился около
240-245 г. на севере Сирии в городе Халкиде. Было очень много споров о дате его
рождения, остановились на данной.
Однако, спорными оказались не только даты жизни Ямвлиха, но и его место
его ученичества и сами его учителя. Наиболее приемлемым считается, что Ямвлих
учился в Александрии и Риме, где учился у Анатолия, а затем у Порфирия.
Александрия к этому времени стала центром платонизма. Что незамедлительно
сказалось на Ямвлихе. Нельзя было учится в Александрии и не быть платоником.
Ямвлих продолжает и углубляет основную тенденцию всего неоплатонизма, а
именно тенденцию о трех ипостасях - единого, ноуменальной сферы и души.
К математическим трактатам Ямвлиха относится трактат "Телогумены
арифметики" ("Арифметическая теология"), причем считается, что
большая часть произведения приписывается кому-нибудь из учеников (точных
сведений на этот счет нет). Данный трактат имеет очень большую ценность, так
как это единственное дошедшее до нас произведение, в котором учение о числах,
преимущественно пифагорейское учение о числах, изложено полно и разнообразно.
Трудность изучения возникает во-первых из-за разрозненности, иногда
противоречивости материала; во-вторых, отсутствие внутренней системы; с одной
стороны, речь идет о числах, тем не менее выводы делаются иной раз из чисел, а
иногда выводы ничего общего с арифметикой не имеют, а носят философский
характер.
Трактат включает в себя учение о единицы, двоицы, троицы и т.д. до
девятерицы. Очень важно выделить учение о единице, которая мыслится как принцип
всякого числа. Но
это не просто единица как начало числового ряда это неделимая единица. Т.е.
представить себе какое-нибудь отдельное число не значит представить его в виде
механической суммы ничем не связанных единиц. Допустим говоря
"миллион" мы не представляем себе огромное количество единиц, а
представляем в виде одного неделимого целого.
Ямвлих также написал девять сочинений о союзе пифагорейцев, из которых
сохранилось четыре. Наибольший интерес для истории математики представляет
книга IV "О введении в арифметику Никомаха". Здесь Ямвлих приводит
различные предложения пифагорейцев о квадратных и "продолговатых"
числах, т.е. о числах вида n(n+1).
3.6. Прокл
Вторым великим комментатором данного периода был Прокл, родившийся
родился в 412 г. в Византии (Константинополь), получил обычное образование для
юноши хорошего происхождения (отец его был адвокатом), затем отправился в
Александрии, где изучал риторику, латинский язык и право. Отправившись в
Константинополь начинает изучать философию, а возвратившись в Александрию
становится учеником Герона, который обучает его математики. Так как толкования
философских текстов, предлагаемые его учителями, представлялись Проклу
"недостойными философской мысли", Прокл отправляется в Афины, где
продолжает свое обучение, приступив к таинствам Платонова учения. Впоследствии,
после смерти Сириана, возглавлявшего Академию, Прокл становится главой
Платоновской Академии в Афинах. (см. [6])
Прокл продолжает и углубляет философию Платона, особенно это касается
философии числа. Им написаны комментарии ко всем диалогам Платона. Для
математики наибольшее значение имеют его комментарии к книге "Начал"
Евклида, являющиеся одним из важнейших источников истории геометрии. При
составлении своих "Комментариев" Прокл пользовался рядом трудов,
которые были затем утеряны, и сведения о них дошли до нас лишь благодаря
Проклу.
"Комментарии" к первой книге Евклида начинаются двумя
введениями (книгами). В первом говорится об отношении математики к философии,
во втором - о геометрии ее предмете.
Всего в первой книге пятнадцать пунктов. Некоторые авторы отмечают ее
сходство с Ямвлихом. Однако у Прокла отмечается почти полное отсутствие
специальных и подчеркнутых отсылок к пифагорейским учениям, столь характерное
для Ямвлиха. Прокл почти всегда ссылается на тексты Платона.
План второй книги состоит из 11 пунктов. В отличие от первой книги она
более разнородна. В ней можно выделить три части: первая посвящена философии
геометрии; вторая представляет собой "каталог геометров"; третья
посвящена конкретно Евклиду, его сочинениям, характеристике "Начал" в
целом и их первой книге.
Приступая затем к ее комментированию, Прокл разбирает по порядку
исторически и критически каждое определение, постулат и аксиому, после чего
переходит к предложениям. Как правило, он сначала объясняет доказательство,
данное Евклидом, а потом указывает несколько конкретных примеров для
упражнения, и в конце опровергает возражения, которые делались или могут быть
сделаны относительно аргументов доказательства. Лишь в одном случае он
добавляет самостоятельно от себя новое, а именно, пытаясь доказать V постулат о
параллельности после того, как он привел попытку Птолемея и возражения против
нее. Прокл, при доказательстве опирался на неявное предположение о том, что
расстояние между непересекающимися прямыми, лежащими в одной плоскости,
ограничено, что равносильно доказываемому постулату. Попытка Прокла также как и
Птолемея оказалась неудачной. (см. [6], [32])
Попытки доказательства пятого постулата продолжались вплоть до открытия
великим русским ученым Лобачевским Неевклидовой геометрии. Это открытие
поставило точку на пятом постулате Евклида
ЗАКЛЮЧЕНИЕ
"Лучший метод для предвидения будущего развития математических наук
заключается в изучении истории и нынешнего состояния этих наук". А.
Пуанкаре
Очевидно, что незнание опыта развития науки, неумение его анализировать
делает нас беспомощными перед задачами будущего. Отсюда вытекает необходимость
изучения истории любой науки и, конечно, математика не является исключением.
Мы, естественно не претендуем на полноту изложения и анализа, тем не менее,
надеемся, что в данной работе достаточно адекватно отразили историю развития и
отличительные особенности более, чем тысячелетней научной и философской
традиции пифагорейства. Вообще говоря, в методологии каждой науки принято
различать 4 уровня ее структурного состава:
. факты, накопленные в результате экспериментов и наблюдений в
ходе развития этой науки;
. гипотезы, т.е. основанные на обобщении этих фактов научные
предложения, которые объясняют их и которые подвергаются в дальнейшем проверке
опытом;
. теории и законы, т.е. подтвердившиеся гипотезы;
. методология, т.е. общетеоретические и философские
истолкования этих законов и теорий, характеризующее общий подход к изучению
данного предмета.
Все эти элементы тесно связаны и находятся в постоянном развитии. В
работе была сделана попытка раскрыть содержание всех четырех пунктов на всех
этапах развития пифагорейства. И хотя их общая характеристика была уже дана
выше, все-таки хотелось еще раз остановиться на этом.
Бессмертную славу неоплатоникам-пифагорейцам принесла не только их
непревзойденная философия числа и не только дедуктивно-аксиоматический метод,
дошедший до нас почти в неизменном виде в "Началах" Евклида.
Изучая пифагорейскую математику мы на каждом шагу убеждаемся в
поразительном их умении находить глубокие, "вечные" проблемы мироздания.
До сегодняшнего дня ждет своего решения проблема совершенных чисел,
единственную пока формулу для которых нашли пифагорейцы. Ждет объяснения
(математиков и философов) тайна "золотого сечения". Лишь в 19 веке
было строго доказано, что все три знаменитые задачи древности (трисекция угла,
квадратура круга, удвоение куба), также восходящие к трудам пифагорейцев,
неразрешимы с помощью циркуля и линейки. Однако пифагорейцы умели не только
ставить задачи, но блестяще их решать, как показано в данной работе. Кроме
того, они создавали универсальные методы, пригодные для решения не просто
отдельных, а целого класса задач. Несмотря на скудность источников, мы также
можем явно проследить процесс дифференциации отдельных математических дисциплин
в рамках единой математики, осуществленный пифагорейцами и их последователями.
Так уже в школе Пифагора из арифметики была выделена в отдельную область теории
чисел, т.е. совокупность математических знаний, относящихся к общим свойствам
операций с натуральными числами. В это же время происходит интенсивная
систематизация геометрических сведений. Были написаны специальные книги, в
которых излагались накопившиеся к этому времени геометрические знания, причем
уже делались попытки аксиоматизации. Открытие пифагорейцами иррациональности
послужило толчком к созданию геометрической алгебры. Ее первичными элементами
были отрезки прямой, а одним из ее методов был метод приложения площадей. Это в
свою очередь повлекло за собой необходимость создания общей теории отношений,
способной оперировать с несоизмеримыми величинами, т.е. с иррациональными. Такая теория
была создана Евдоксом во второй половине IV в. до н.э.
Недостаточность геометрической алгебры как общей математической теории
была особенно подчеркнута выделением класса задач, не поддающихся решению с
помощью циркуля и линейки. В попытках решить эти задачи были открыты
"луночки" Гиппократа, "конические сечения " Аполлония, в
свою очередь конические сечения предопределили появление координатной сетки. А
методы Архимеда для нахождения площадей криволинейных фигур на плоскости
представляют собой зачаток интегрального исчисления, построенного через две
тысячи лет трудами Ферма, Ньютона, Лейбница и др.
Если апофеозом всей математики стали "Начала" Евклида, то
апофеозом физики стали труды Архимеда по механике.
Достижения пифагорейцев не ограничиваются только математическими или
физическими. Ими была создана теория музыки, которая более 2 тысячелетий
является фундаментом искусства музыки. Нельзя также себе представить развитие
греческой науки без астрономии.
Пифагорейцы впервые выделили астрономию как науку. И здесь им принадлежит
множество открытий: измерение Земли, создание календаря Эратосфеном,
определение времени солнцестояния и т.д. Но главным достижением является
построение геоцентрической модели мира, достаточно эффективно служившей вплоть
до появления коперниковской системы. Даже уже сказанного достаточно для вывода
о том, что своими открытиями пифагорейцы заложили фундамент европейской науки.
Совершенство и одновременно простота многих открытий пифагорейства делает
их вполне доступными современным школьникам. Опыт, хотя и небольшой, позволяет
сделать вывод о значительном повышении уровня усвоения материала учениками при
введении элементов истории математики, значительный интерес вызывают
оригинальные доказательства древних, особенно изложенных в занимательной форме.
Так будем помнить сами и дадим нашим ученикам знание того неоспоримого и
часто забываемого факта, что Древняя Греция - колыбель нашей науки, а открытия
эллинского гения не только сопоставимы с современными, но и часто превышают их
по глубине проникновения в самую суть природы вещей.
ЛИТЕРАТУРА
1. Лосев А.Ф. / История античной
эстетики т. 1 М., 1994 г.
.
Лосев А.Ф. / История античной эстетики. т. 2 М., 1994 г.
.
Лосев А.Ф. / Миф. Сущность. Число./
.
Прокл / Комментарий к первой книге "Начал" Евклида. Введение /
Греко-латинский кабинет, М. 1994г.
.
Евклид "Начала" I-VI книги. / Перевод и комментарии Д.Д.
Мордухай-Болтовского. / М.; Л.: Гостехиздат, 1949 г.
Евклид
"Начала" VII-X книги. / Перевод и комментарии Д.Д.
Мордухай-Болтовского. / М.; Л.: Гостехиздат, 1949 г.
.
Евклид "Начала" VII-X книги. / Перевод и комментарии Д.Д.
Мордухай-Болтовского. / М.; Л.: Гостехиздат, 1949 г.
.
Лебедев В.И. / Очерки по истории математики. Знаменитые задачи древности.
.
Лебедев В.И. / Очерки по истории математики. Кто автор первых теорем.
.
Цейтен Г.Г. / История математики в древние и средние века. перев. Юшкевича П.
Государственное технико-теоретическое издательство . М.,1932 г.
.
Стройк Д.Я. / Немного истории.
.
Стройк Д.Я. / Краткий очерк истории математики. М."Наука" Главная
редакция физико - математической литературы. 1984г.
.
Чистяков В.Д. / Три знаменитые задачи древности. М. 1963 г.
.
Смышляев В.К. / Знакомые имена.
.
Кольман Э.Я. / Математика до эпохи возраждения.
.
Гегель т. 1
.
Гегель т. 2
.
Даан-Дальмедико. / Пути и лабиринты. М 1986 г.
.
Лицман В. / Теорема Пифагора. М. 1960 г.
.
Башмаков Ю.А. / Хрестоматия по истории математики. М. 1976 г.
.
Волошинов А.В. / Пифагор. М. 1993 г.
.
Глейзер Г.И. / История математики. М. 1990 г.
.
Глейзер Г.И. / История математики в школе 9-10 кл. М. 1983 г.
. Глейзер
Г.И. / История математики в школе 6-9 кл.
.
Диоген Лаэртский. / О жизни, учениях и изречениях знаменитых философов.
"ТАНАИС", М., 1995г.
.
Бородин А.И., Бугай А.С. / Выдающиеся математики. Биографический словарь -
справочник. Киев. "Радянська школа" 1987 г.
.
Рыбников / История математики./ "Московский университет" 1979 г.
.
Жмудь Л.Я. / Пифагор и его школа. / Л."Наука", 1990 г.
.
Юшкевич П. / История математики./
.
Кольман Э.Я./ История математика в древности. / Издательство
физико-математической литературы, М., 1961 г.